Version française abrégée
Comprendre et prédire la propagation d'une épidémie dépend de manière cruciale de notre capacité à modéliser les mouvements et interactions des individus dans des systèmes possédant de nombreuses échelles de temps et d'espace, allant de déplacements locaux et de contacts directs entre individus jusqu'aux flots de transport à l'échelle mondiale. Dans ce contexte, la modélisation en épidémiologie a évolué depuis des modèles compartimentaux simples jusqu'à des modèles intégrant de plus en plus de détails sur la structure de la population considérée et les interactions entre individus.
Ces approches de plus en plus détaillées ont été rendues possibles ces dernières années grâce une croissance spectaculaire de la puissance des ordinateurs. Cette croissance a permis d'obtenir et de manipuler un grand nombre de données sur la structure démographique des populations, et d'étudier de manière extensive certains réseaux de transports qui permettent à l'épidémie de se propager. Ces données ont en particulier permis aux chercheurs de caractériser quantitativement les propriétés statistiques de ces réseaux et de mettre en évidence des propriétés complexes, telles que de très fortes hétérogénéités.
Ces avancées ont permis de montrer les limites de certaines hypothèses habituellement utilisées en épidémiologie. En particulier, l'hypothèse d'homogénéité selon laquelle tous les individus ont le même environnement semble être une approximation très brutale dans de nombreux cas. La description de la propagation d'épidémies par un simple processus de diffusion spatiale est également très irréaliste dans de nombreuses situations. De façon générale, la complexité des réseaux sociaux et de transport, ainsi que leurs différents niveaux d'hétérogénéité, ne doivent donc surtout pas être négligées.
Ces considérations peuvent apparaître comme justifiant une modélisation des systèmes complexes contenant le plus de détails possible. Le débat entre réalisme, précision et généralité n'est certes pas nouveau, mais la possibilité d'intégrer un très grand nombre de détails le remet à une place centrale. D'un côté, les modèles très simplifiés peuvent permettre de mettre en évidence le mécanisme principal d'un phénomène, mais au détriment de la précision et du réalisme. À l'autre extrême, des modèles intégrant un très grand nombre de paramètres rendent une description réaliste des phénomènes possible, au risque cependant de rendre opaque les mécanismes fondamentaux.
Il est donc très difficile de proposer un modèle qui reste à un niveau raisonnable de réalisme et de précision afin d'être utile à la prévision et à la mise en place de stratégies de contrôle, mais qui soit aussi suffisamment simple pour maîtriser les approximations utilisées et comprendre la nature des mécanismes sous-jacents. Les récentes avancées dans la compréhension des systèmes complexes jouent ici un rôle majeur. Pour ces systèmes complexes, qui sont généralement composés d'un grand nombre de composants dont l'interaction donne lieu à des comportements collectifs non triviaux, il est en général possible d'identifier les paramètres qui sont réellement pertinents pour leur description à grande échelle. Ceci permet alors d'étudier de manière systématique les caractéristiques fondamentales de phénomènes dynamiques, et en particulier de la propagation d'épidémies.
Dans cet article, nous passons en revue les progrès récents dans la modélisation de propagation d'épidémies qui intègrent nos connaissances sur les réseaux complexes. Nous discutons en premier lieu les caractéristiques des systèmes complexes, qui se révèlent particulièrement pertinentes pour la modélisation de la propagation d'épidémies. Nous rappelons ensuite les effets des fortes fluctuations de degré, typiques de nombreux réseaux complexes, sur la propagation d'épidémies. Enfin, dans la dernière partie, nous considérons des modèles plus réalistes dits de « métapopulations ». En particulier, nous discutons les directions prises ces dernières années, qui ouvrent la voie à la construction d'une « épidémiologie numérique » capable de prédictions quantitatives.
1 Complexity and epidemic modelling
Epidemic forecast is crucially depending on our ability to model the spread of epidemics in spatially extended systems and the movement of individuals at various levels, from the global scale of transportation flows to the local scale of the activities and contacts of individuals. In this context, modelling in mathematical and statistical epidemiology has evolved from simple compartmental models into structured approaches in which the heterogeneities and details of the population and system under study are becoming increasingly important features [1] (see Fig. 1). In the case of spatially extended systems, modelling approaches have been extended into schemes that explicitly include spatial structures and consist of multiple sub-populations coupled by travelling fluxes, while the epidemic within the sub-population is described according to approximations depending on the specific case studied [2–10]. This patch or meta-population modelling framework has then grown into a multiscale framework in which the various possible granularities of the system (country, intercity, intracity) are considered through different approximations and coupled through interaction networks describing the flows of people and/or animals [10–17]. At the most detailed level, the introduction of agent-based models (ABM) has enabled to stretch even more the usual modelling perspective, by simulating the propagation of an infectious disease individual by individual [18,19].

Different scales structure used in epidemic modelling. Circles represent individuals and each colour corresponds to a specific stage of the disease. From left to right: homogeneous mixing, in which individuals are assumed to homogeneously interact with each other at random; social structure, where people are classified according to demographic information (age, gender, etc.); contact network models, in which the detailed network of social interactions between individuals provide the possible virus propagation paths; multi-scale models, which consider sub-population coupled by movements of individuals, while homogeneous mixing is assumed on the lower scale; agent-based models, which recreate the movements and interactions of any single individual on a very detailed scale (a schematic representation of a city is shown). Masquer
Different scales structure used in epidemic modelling. Circles represent individuals and each colour corresponds to a specific stage of the disease. From left to right: homogeneous mixing, in which individuals are assumed to homogeneously interact with each other at random; ... Lire la suite
The above modelling approaches are based on actual and detailed data on the activity of individuals, their interactions and movement, as well as the spatial structure of the environment, transportation infrastructures, traffic networks, and travel times. While for a long time this kind of data was limited and scant, recent years have witnessed a tremendous progress in data gathering, thanks to the development of new data-processing tools and the increase in computational power. A huge amount of data, collected and meticulously catalogued, has become finally available for scientific analysis and study. The scientific community has subsequently uncovered in such data the presence of complex properties and heterogeneities that cannot be neglected in epidemic-modelling description. In particular, the ever-increasing level of interconnectedness and globalization of our modern society along with a high level of diversity and heterogeneity induces a novel epidemiological context: the mathematical and computational modelling of disease spread needs to integrate such complex features.
Although there is no commonly accepted definition of complex systems, they share a number of characteristics. They are made of a large number of interacting components and there is not a global blueprint controlling their evolution. One of the most peculiar features of complex systems is their non-trivial collective behaviour and their resilience to perturbations; i.e. their ability to adapt to a fluctuating environment and to evolve. This last point in particular allows one to distinguish complex from complicated systems, since random perturbations on complicated systems will lead in most cases to their failure.
These considerations might appear as a call for a modelling approach of complex systems that considers as many possible parameters and details as we can possibly handle. The debate about the amount of “realism, precision, and generality” needed in a model is not new, but still very vivid [20,21]. As noted by May and previous authors (see [20] and references therein), there is a broad spectrum of models ranging from ‘toy’ models to highly detailed models. Toy models sacrifice precision and sometimes realism in order to capture the essence of the phenomenon and the general mechanisms. On the other side of the spectrum, models with a high level of detail provide the opportunity of analyzing the spreading process in a very realistic way, making all assumptions explicit, the main drawback being that the key mechanisms underlying the epidemic evolution are difficult to identify and discriminate because of the numerous assumptions and of the large number of elements of the system. It is thus a difficult task to obtain finally a model that stays at a reasonable level of precision, but still captures enough realism to be useful in practical situations, such as forecasting and control strategies' assessment. In the case of complex systems, this task is simplified by the fact that it is possible to distinguish different classes of parameters and to identify which ones are really relevant in the description of the large-scale behaviour of the system. By leveraging on the recent understanding of complex systems, it is then possible to complement the basic approaches developed in mathematical and statistical epidemiology with the introduction of large scale systems (104 to 106 degrees of freedom), and to isolate the main features responsible for their behaviour. This allows the systematic investigation of the impact of the various complex features of real systems on the basic properties of epidemic spreading.
In the following, we provide a discussion of the various instances at which the inclusion of complex features is relevant in epidemic modelling. We will then discuss the spread of epidemics in complex networks and the effect of large-degree fluctuations on the spreading process. In Section 4, we discuss a further step towards realism with the implementation of metapopulation models. In this Section, we will focus especially on the new directions emerged in the last years in the context of large computational approaches that pave the way to the establishment of computational infrastructures able to provide quantitative forecast of epidemic spreading.
2 From Euclidian space to networks
In the pre-industrial times, disease spread was mainly a spatial diffusion phenomenon. For instance, during the spread of the so-called Black Death, which occurred in the 14th century, only few travelling means were available and typical trips were limited to relatively short distances on the time scale of one day.
Historical studies confirm that the propagation (Fig. 2) indeed followed a simple scheme, with a spatio-temporal spread mainly dominated by spatial diffusion. More precisely, ballpark calculations on the historical data show that the Black Death essentially spread through Europe from south to north, with the invasion front moving at an approximate velocity of 200–400 miles/year [22]. Mathematically, this process can be described with a simple Susceptible-Infected-Removed (SIR) model with diffusion, which can be written as:
| (1) |
| (2) |
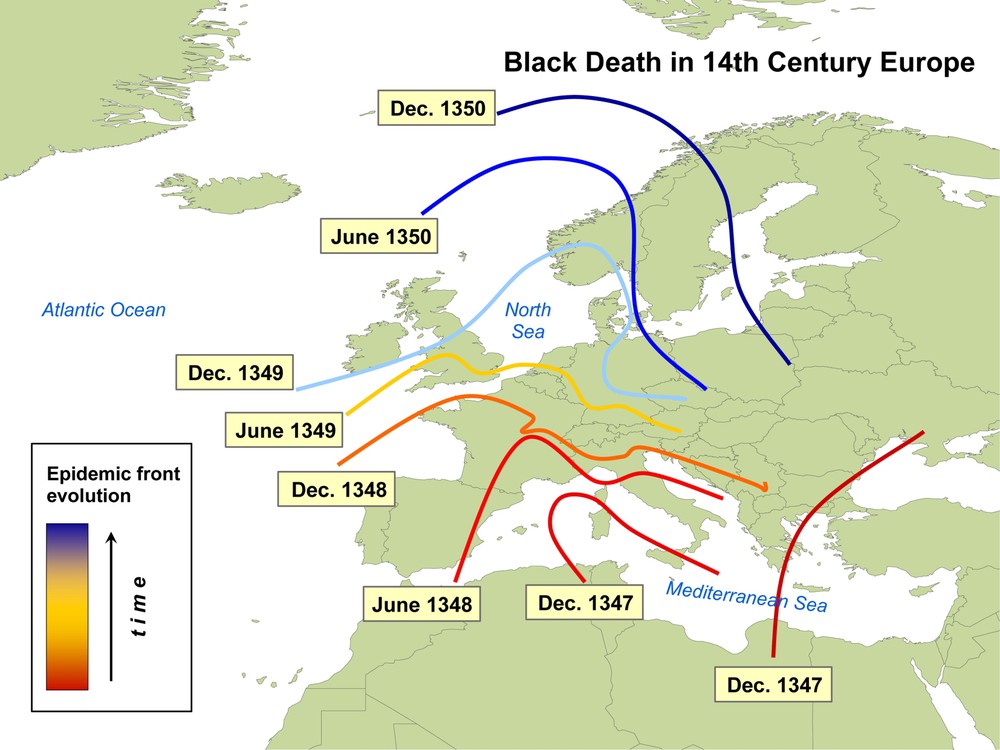
Map of the propagation of the Black Death in the 14th century. The epidemic front spread in Europe with a velocity of the order of 200–400 miles per year.
Our modern societies are sharply contrasting with the previous example: due to the large variety of travelling means with different distance and time-scales associated, epidemiology cannot simply rely on an approximate spatial description of the disease spread. The interplay between social networks and infrastructures was argued to be at the origin of the spreading pattern of a disease already observed in the 19th century, when the English physician John Snow analyzed on a map the relation between the public water-supply system and cholera cases in London [23]. As anticipated moreover already in 1933 [24], the large scale and geographical impact of infectious diseases on populations in the modern world is mainly due to commercial air travel. This has been repeatedly and dramatically demonstrated in several circumstances, such as the international airline hub-to-hub pandemic spread of acute hemorrhagic conjunctivitis in 1981 [25], and more recently the evolution of SARS epidemic [26]. While this epidemic indeed first diffused out of its origin in China and spread in South-East Asia, it also reached very rapidly much farther regions, such as North America and Europe, brought by infected individuals travelling by plane (see Fig. 3). One of the most dangerous aspects of the SARS epidemic was in fact its very fast spread on worldwide scales. This picture, therefore, cannot be simply described in terms of diffusive phenomena, but ought to explicitly incorporate the spatial structure of modern transportation networks [27,28], which have been identified as one of the main mechanisms for propagation on a global scale. In this perspective, epidemic modelling thus changes from a description in terms of local diffusion to one in which long-range interactions (i.e. flights connecting far apart airports) play a crucial role. The identification and characterization of the underlying network of infrastructures is therefore fundamental.
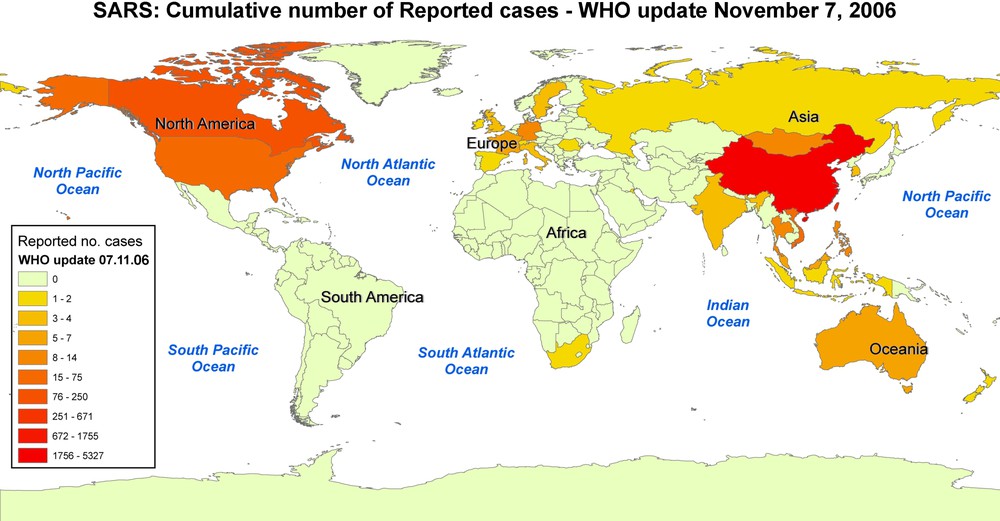
Map of the cumulative number of reported cases of SARS infection, according to WHO data of 7 November 2006.
Networks that trace the activities and interactions of individuals, social patterns, transportation fluxes, and population movements on a local and global scale [18,27,29,30] are therefore the key ingredients in our understanding of epidemic behaviour and in our capabilities to predict their evolution. The importance of networks in epidemiology has not to be stressed here. The population connectivity pattern and the structure of meta-population models are for example naturally defined in terms of networks. The recent progresses in the field stem from the increased ability to gather data on several large sets of networked structures and populations, finding that they exhibit complex features encoded in large-scale heterogeneity, self-organization and other properties typical of complex systems [31–33]. While heterogeneity has been acknowledged since long as a relevant factor in determining the properties of epidemic spreading phenomena [1,34], many real world networks exhibit levels of heterogeneity that were not anticipated until a few years ago. Moreover, the presence of such features was recently found to have a strong impact on the resulting infection dynamics, breaking down the standard epidemiological framework. In order to discuss the relevance of complex systems' properties on the spread of an infectious disease, we will distinguish in the following between two different levels of modelling approaches corresponding to two different granularity scales – the population and meta-population description levels.
2.1 Single population level
Accurate data on the human interaction between individuals is usually rather difficult to obtain. Data on single populations are not abundant and generally troubled by issues such as the concurrency of relations or the sampling biases. Several recent studies on the network of sexual contact [29,30] are however showing that the number of sex partners is broadly distributed. This is a very peculiar feature typical of many natural and artificial complex networks, characterized by virtually infinite degree fluctuations, where the degree of a given node represents its number of connections to other nodes. In contrast with the homogeneous random graphs characterized by nodes having a typical degree k close to the average
2.2 Meta-population level
Patch or meta-population modelling frameworks consider multiple sub-populations coupled by movements of individuals. These models are defined by the network describing the coupling among the populations along with the intensity of the coupling, which in general represents the rate of exchange of individuals between two populations. Meta-population models can be devised at various granularity levels (country, intercity, intracity) and the corresponding networks are therefore including very different systems and infrastructure. This implies scales ranging from the movement of people within locations of a city to the large flows of travellers among urban areas.
At the lowest scale, the urban level, an impressive characterization of the human flows was recently conducted by the TRANSIM group [18]. This study focused on the network of locations in the city of Portland, Oregon, including homes, offices, shops, and recreational areas. The temporal links between locations represent the flow of individuals going at a given time from one place to another. The resulting network is characterized by broad distributions of the degrees and of the flows of individuals travelling on a given connection [18]. Strong heterogeneities are thus present, not only at the topological level, but also at the level of the traffic on the network: a simultaneous characterization of the system in terms of both topology and weights associated with connections is needed to integrate the different levels of complexity in a unifying picture [27].
Similar results have been found in commuting patterns among cities and counties within a given geographical region/country. In this case, the nodes of the network represent cities, counties and in general municipalities or urban aggregations coupled by connections that correspond to the commuting flows of individuals. The analysis of these networks uncovered rather homogeneous topologies – mainly due to strong spatial constraints – associated with very large fluctuations in the travel flows of individuals [38]. The broad distribution of travel flows plays an important role in the predictability of an epidemic spread, as will be discussed in the following sections, and needs therefore to be taken into account for a complete understanding of the process.
Finally, the global scale is characterized by the air connections infrastructure, composed by airports (nodes) and direct flights among them (links). Data representing the travel flow of passengers defines the weight to each connection [27]. This transportation network displays several strong levels of heterogeneity. The distribution of degrees (i.e., of the number of connections of an airport) is scale-free and the traffic is very broadly distributed, varying over several orders of magnitude [27,28]. This points to a structure that is composed by airports having large fluctuations in their number of connections to other airports and, moreover, to number of passengers travelling on a given route ranging from few individuals to millions of individuals in a given amount of time.
All these features have important implications on the dynamical processes occurring in the system. Modelling frameworks that neglect any of these heterogeneity properties would therefore miss crucial ingredients of the propagation dynamics of epidemics. In the following chapter, we will review some basic results concerning the effect of fluctuations in our understanding of epidemic spreading.
3 Complex networks: effect of degree fluctuations on epidemic processes
The heterogeneity found in the connectivity pattern of the contact networks described in the previous section has a strong impact on the properties of the dynamical processes occurring on the networks. A striking example is provided by the different expressions of the necessary condition for the spread of a disease across a population, depending on the homogeneous or heterogeneous character of the contact network of this population.
In the framework of homogeneous approximations, the SIR model described by Eq. (1) leads to a major outbreak, thus infecting a finite fraction of the population, if the following condition – called epidemic threshold – is satisfied:
In order to account for contact networks in which different individuals can have very different numbers of contacts (degrees), Eq. (1) has to be generalized to describe the evolution of the numbers of infected individuals of degree k. It can then be shown that the disease will affect a finite fraction of the population if
The previous result on the epidemic threshold concerns the stationary properties of endemic states or the final percentage of cases of an epidemic. The impact of topological heterogeneities of the contact network on the dynamical evolution of the outbreaks has also been investigated [43]. It turns out that the time behaviour of epidemic outbreaks and the growth of the number of infected individuals are governed by a time scale τ proportional to the ratio between the first and second moment of the network's degree distribution:
| (3) |
4 Meta-population models: Integrating several levels of complexity
The relevant impact of heterogeneity and connectivity fluctuations in the epidemic modelling at the level of a single population leads us to investigate the role of complex connectivity patterns and traffic in meta-population models. Let us consider as a prototypical case the worldwide spreading of epidemics through air travel. As a basic modelling strategy, it is possible to use a meta-population approach [7–9] in which individuals are allowed to travel from one city to another by means of the airline transportation network, while the disease within the city is described with opportune compartmental models or more detailed description of the disease dynamics. This amounts to write for each urban area the set of equations:
| (4) |
| (5) |
This modelling program dates back to the work of Rvachev and Longini [11], and it has been used along the years to simulate diseases such as pandemic influenza [44–46], HIV [47], and SARS [13]. While these earlier studies were considering a limited number of urban areas and travel connections, it has recently become possible to scale up this approach by including the full International Air Transport Association (IATA) [48] database. This has led to a modelling framework [16,17] considering up to 3100 airports with demographic data for the surrounding urban areas and 17 182 connections among them, each representing the presence of a direct flight. This corresponds to more than 99% of the worldwide commercial traffic by plane. To each link connecting airports i and j is attached the weight
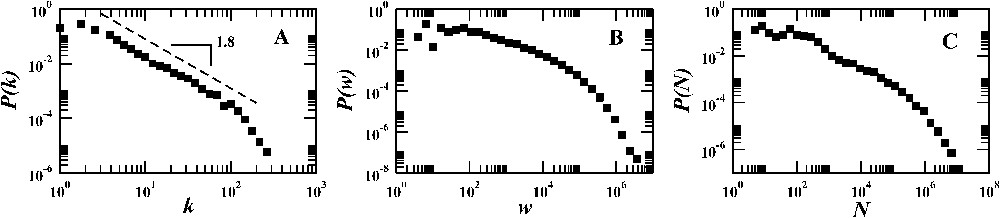
Probability distributions of (A) the number of connections of each airport, (B) the number of passengers travelling on a given connection between a pair of airports, (C) the population size of the urban area surrounding each airport. Topology and traffic data are obtained from the IATA [48] database, while population data are extracted from several different census databases, available on the web.
The model obtained by integrating all these data and the aetiology of the disease within each city can be used to forecast the behaviour of emerging diseases as well as to validate the approach. Strikingly, this modelling appears to provide very good results in agreement with historical data [13,49], thus spurring the issue of identifying the fundamental limits in epidemic evolution predictability with computational modelling and their dependence on the underlying complex features of the system.
A major question in the modelling of global epidemics consists indeed in providing adequate information on the reliability of the obtained epidemic forecast, i.e. the epidemic predictability. The intrinsic stochasticity of the epidemic spreading will make each realization unique and reasonable forecast can be obtained only if all epidemic outbreak realizations starting with the same initial conditions and subject to different noise realizations are reasonably similar. A convenient quantity to monitor in this respect is the vector
| (6) |
If we consider a model in which the cities are linked by a completely homogeneous transport network (HOMN), where both degrees of each city and traffic flows on each connection are close to their average values, we find a significant overlap (
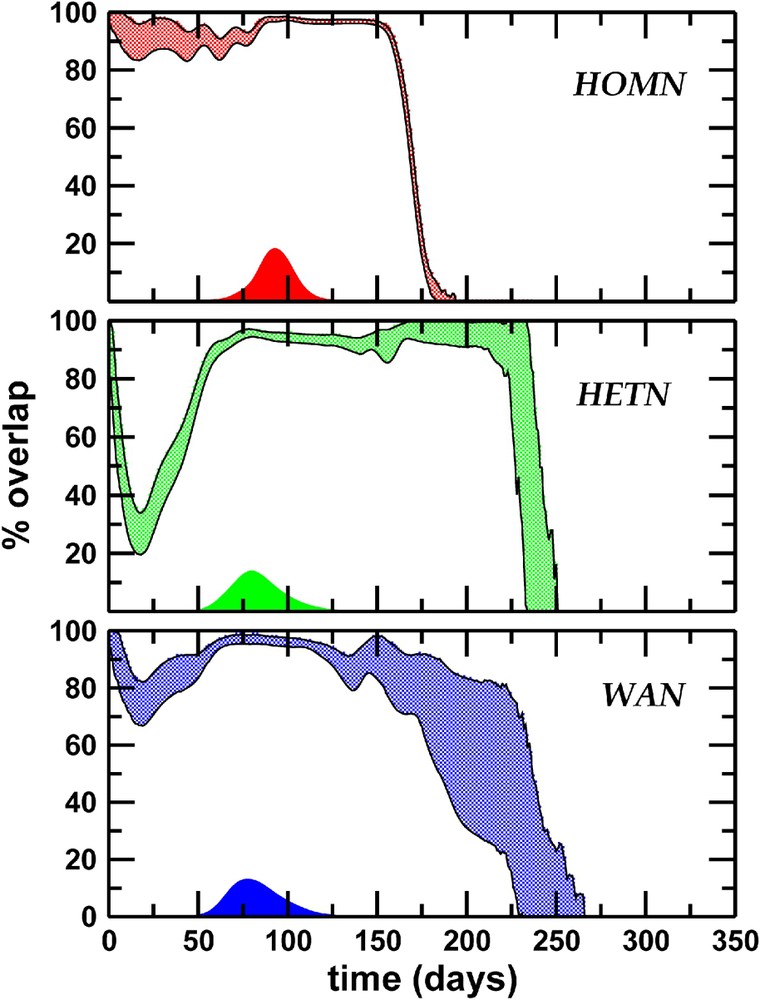
Epidemics predictability. Percentage of overlap as a function of time: the shaded area corresponds to the standard deviation obtained with 5×103 couples of different realizations. Topological heterogeneity plays a dominant role in reducing the overlap in the early stage of the epidemics. Large fluctuations at the end of the epidemics are observed when a heterogeneous topology is considered, due to the different lifetime of the epidemics in distinct realizations, induced by the large topological fluctuations of the network. We also report the prevalence profile as a function of time, showing that the maximum predictability corresponds to the prevalence peak. Masquer
Epidemics predictability. Percentage of overlap as a function of time: the shaded area corresponds to the standard deviation obtained with 5×103 couples of different realizations. Topological heterogeneity plays a dominant role in reducing the overlap in the early stage of ... Lire la suite
These results may be rationalized by considering the conflicting effects of the various levels of heterogeneity (see Fig. 6). On the one hand, the heterogeneity of the connectivity pattern (broad distribution of degrees), and in particular the existence of hubs, provides a multiplicity of equivalent channels for the travel of infected individuals, depressing the predictability of the evolution, as the comparison of HETN and HOMN shows. On the other hand, the heterogeneity of traffic flows introduces dominant connections that select preferential pathways, increasing the epidemic predictability. The backbone of such dominant spreading channels thus defines specific ‘epidemic pathways’, which are weakly affected by the stochastic noise. In the case of the worldwide airport network, the heterogeneity of the fluxes thus partially compensates for the decrease in predictability due to the topological heterogeneity.
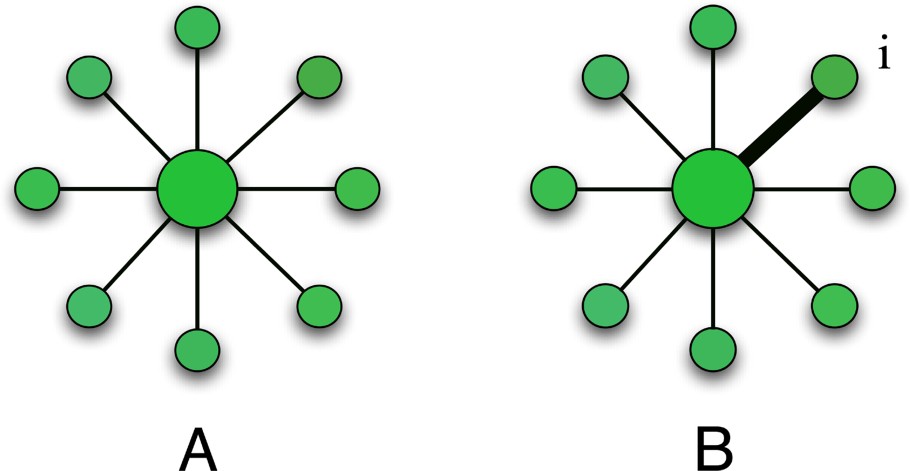
Influence of heterogeneity on the predictability. (A) Large degrees lower the predictability. Starting from the hub if all weights are equal, a disease can spread on all the nodes with equal probability. (B) For the same topology, weight heterogeneity selects a particular path (from the hub to the node i) and thus increases the predictability.
In summary, different levels of complexity of the system affect our ability to predict the spatio-temporal spread of a disease in opposite ways. The intrinsic stochastic nature of the propagation of directly transmitted diseases – inherent both in the infection dynamics and in the movements of individuals – makes it harder to forecast the process evolution on a complex pattern of interactions. However, an additional level of heterogeneity, here encoded in the broad distribution of passenger travel flows, plays a crucial role at our advantage, making epidemic forecasts a feasible problem to address. This result clearly shows how the interplay and the integration of several levels of complexity of the system produce unexpected phenomena, which needs to be accounted for in order to obtain a better general understanding of the process.
5 Conclusions and perspectives
Taking into account the complexity of real systems in epidemic modelling has shown to be unavoidable, and the corresponding approaches have already produced a wealth of interesting results. While this has stimulated the recent focus on large-scale computational approach to epidemic modelling, it is clear that many basic theoretical questions are still open. How does the complex nature of the real world affect our predictive capabilities in the realm of computational epidemiology? What are the fundamental limits in epidemic evolution predictability with computational modelling? How do they depend on the level of accuracy of our description and knowledge on the state of the system? Tackling such questions necessitates exploiting several techniques and approaches. Complex systems and networks analysis, mathematical biology, statistics, non-equilibrium statistical physics, and computer science are all playing an important role in the development of a modern computational epidemiology approach. While such an integrated approach might still be in its first steps, it seems now possible to imagine ambitiously the creation of computational epidemic forecast infrastructures able to provide reliable, detailed, and quantitatively accurate predictions of global epidemic spread.
Acknowledgements
We are grateful to the International Air Transport Association for making the airline commercial flight database available to us. A.V. is partially funded by the NSF award IIS-0513650. A.B. and A.V. are partially funded by the EC contract 001907 (DELIS).



Vous devez vous connecter pour continuer.
S'authentifier