HIV treatment models with time delay

Mostafa Bachar; Anita Dorfmayr

doi:10.1016/j.crvi.2004.08.007

Biological modelling / Biomodélisation

HIV treatment models with time delay
[Modèles de traitement des maladies HIV avec retard temporel.]

Présenté par : Pierre Auger

Mostafa Bachar ¹ ; Anita Dorfmayr ²

¹ Institute for Mathematics, University of Graz, Heinrichstraße 36, 8010 Graz, Austria
² Institute for Discrete Mathematics and Geometry, Vienna Univesity of Technology, Wiedner Hauptstraße 8/104, 1040 Vienna, Austria

Comptes Rendus. Biologies, Volume 327 (2004) no. 11, pp. 983-994.

Résumés

Anglais
Français

The present paper shows possible effects of antiretroviral treatment on the dynamics of the spread of the disease of human immunodeficiency virus infection in a population of varying size. By introducing time delays, we model the latency period and the delayed onset of positive treatment effects in the patients. The Hopf bifurcation and stability behaviour of the delay differential-equation model are analysed and simulations for different scenarios depending on the size of the treatment-induced delay are presented, and the results are discussed in detail.

Cet article montre les effets possibles du traitement anti-rétroviral de la dynamique de la propagation de l'infection par le virus de la maladie immunodéficitaire humaine au sein d'une population de taille variable. En introduisant des retards temporels, nous modélisons la période de latence et l'apparition des effets positifs du traitement sur les patients. La bifurcation de Hopf et le comportement en termes de stabilité du modèle d'équations différentielles à retard sont analysés et des simulations de différents scénarios dépendant de l'ampleur du retard induit par le traitement sont présentées, et les résultats discutés en détail.

Métadonnées

Reçu le : 2004-02-09
Accepté le : 2004-08-10
Publié le : 2004-11-01

PMID

DOI : 10.1016/j.crvi.2004.08.007

Keywords: HIV, time delay, Hopf bifurcation, delay differential equations
Mot clés : HIV, retard temporel, bifurcation de Hopf, équations différentielles à retard

Affiliations des auteurs :

Mostafa Bachar ¹ ; Anita Dorfmayr ²

¹ Institute for Mathematics, University of Graz, Heinrichstraße 36, 8010 Graz, Austria
² Institute for Discrete Mathematics and Geometry, Vienna Univesity of Technology, Wiedner Hauptstraße 8/104, 1040 Vienna, Austria

@article{CRBIOL_2004__327_11_983_0,
     author = {Mostafa Bachar and Anita Dorfmayr},
     title = {HIV treatment models with time delay},
     journal = {Comptes Rendus. Biologies},
     pages = {983--994},
     publisher = {Elsevier},
     volume = {327},
     number = {11},
     year = {2004},
     doi = {10.1016/j.crvi.2004.08.007},
     language = {en},
}

TY  - JOUR
AU  - Mostafa Bachar
AU  - Anita Dorfmayr
TI  - HIV treatment models with time delay
JO  - Comptes Rendus. Biologies
PY  - 2004
SP  - 983
EP  - 994
VL  - 327
IS  - 11
PB  - Elsevier
DO  - 10.1016/j.crvi.2004.08.007
LA  - en
ID  - CRBIOL_2004__327_11_983_0
ER  -

%0 Journal Article
%A Mostafa Bachar
%A Anita Dorfmayr
%T HIV treatment models with time delay
%J Comptes Rendus. Biologies
%D 2004
%P 983-994
%V 327
%N 11
%I Elsevier
%R 10.1016/j.crvi.2004.08.007
%G en
%F CRBIOL_2004__327_11_983_0

Mostafa Bachar; Anita Dorfmayr. HIV treatment models with time delay. Comptes Rendus. Biologies, Volume 327 (2004) no. 11, pp. 983-994. doi : 10.1016/j.crvi.2004.08.007. https://comptes-rendus.academie-sciences.fr/biologies/articles/10.1016/j.crvi.2004.08.007/

Version originale du texte intégral

1 Introduction

The disease of human immunodeficiency virus (HIV) infection has become a worldwide pandemic [1,2]. UNAIDS reports about an estimated number of 34–46 million people living with HIV worldwide by the end of 2003, and 5 million new infections in 2003 show that it is still growing rapidly. The disease is a major problem first of all in the developing countries of Sub-Saharan Africa. This region accounts for 25.0–28.2 million people infected with HIV by the end of 2003 and 4.2–5.8 million new infections in 2003 (source: UNAIDS http://www.unaids.org/).

Very effective treatments for HIV infected individuals have been developed, and drug prices dropped significantly the last years according to UNAIDS (http://www.unaids.org/). Therefore, they may be widely distributed, not only in the industrial, but also in the developing countries. Thus, it is worth studying the effects that the wide use of antiretroviral can have on the spread of the disease.

HIV predominantly infects CD $4^{+}$ T cells that are crucial for the functioning of the human immune system. In the course of the disease of HIV infection, an increasing amount of viruses in the blood of the patients leads to a decrease in the CD $4^{+}$ T cell count, and finally to the destruction of the immune system [3].

Several groups of anti-HIV drugs have been developed that interfere with several processes in the replication cycle of HIV. The most important ones among those are reverse transcriptase inhibitors and protease inhibitors, antiretroviral drugs that inhibit the process of reverse transcription and the viral maturation process, respectively. To interfere with the integration process, integrase is used as another target for the development of anti-HIV drugs. Multiple coreceptors for different types of HIV strains have been identified that probably play an important role in the process of binding to the host cell. These coreceptors are also promising targets for anti-HIV drugs. Starting with highly active antiretroviral therapy (HAART), an anti-HIV combination therapy that includes one protease inhibitor and two reverse transcriptase inhibitors, combination therapy has been used to reduce resistance effects. In many cases, combination therapy leads to a delayed progression of HIV disease. If initiating therapy is used and if dose reductions and inconsistent therapy are avoided, a long-term suppression of the virus below the limit of detection is possible. However, recent studies have shown that HIV persists in a replication-competent form in resting CD $4^{+}$ T cells, despite aggressive antiretroviral therapy. Therapy-induced decreases in viral load and an increasing number of CD $4^{+}$ T cells were the most significant prognostic indicators of positive clinical treatment benefit [4,5]. As a result, treated individuals can live longer free of HIV-related symptoms.

The influence that antiretroviral therapy has on the battle between the human immunodeficiency virus and the human immune system has widely been analysed, see e.g. [6–12]. The spread of HIV/AIDS amongst a population or among interacting communities without treatment has also been investigated [13–19]. Some mathematical and statistical models deal with the spread of HIV/AIDS amongst a population including treatment and/or change of behaviour [8,17,20–25]. For more details on the mathematical modelling of the dynamics of infectious diseases, see [15,26–30].

In [31], the authors formulated and analysed a model for HIV transmission for a homosexual population of varying size with recruitment into the susceptible class proportional to the active population size and with stages of progression to AIDS in [31]. In [32–34], the authors modified this ordinary differential-equation model by incorporating treatment effects. The underlying assumption in [32,33] is that of a worst-case scenario, where infected individuals – no matter if they are treated or not – do not change their behaviour despite their knowledge of the risks. In [32], a general staged progression model with n infectious stages, including anti-HIV drug treatment, was formulated and analysed in detail. A similar model with staged progression based on clinical stages was discussed in detail and simulations were shown in [23].

Although there are lots of research going on in the field of modelling the disease of HIV infection, many effects that antiretroviral treatment has on the spread of HIV infection in a population remain unknown. First of all, it has not been investigated, how the delayed onset of positive treatment effects influences the spread of the disease. Secondly, it is worth studying the possible effects of the latency period, although it is assumed to be very short in the case of HIV (in the range of a few days, see [5]).

In the following, we will study the dynamics of the spread of the disease of HIV infection in a population depending on this treatment-induced delay. We will present an ordinary differential-equation model based on clinical stages as given in [32,33] and the main results in Section 2. In Section 3, we will then modify it by introducing two time delays λ and τ to model the delayed onset of treatment effects (τ) and the latency period (λ). As there is no data on the size of τ, we will show simulations for different scenarios according to the size of this treatment-induced delay. A detailed discussion of the results is given in Section 4.

2 ODE model with two infectious stages: model formulation and main results

In the following transmission via sexual contact is assumed. Thus, we consider a sexually active population of varying size N. AIDS patients are assumed to be too sick to be sexually active. Thus, the total population can be divided into a susceptible class of size S and an infectious class before the onset of AIDS. As the infectious period is very long (⩾10 years), it is further divided into several stages. The widely-used CDC-classification suggests 2–6 stages of infection before AIDS with the classes defined by either viral load or CD $4^{+}$ T cell count, and clinical symptoms (see [5]). In our model, we use two stages according to clinical stages, that is the asymptomatic and the symptomatic phases as defined in [18]. The numbers of individuals in the infectious classes are given by $I_{1}$ and $I_{2}$ , respectively. All individuals entering the population are assumed to be susceptible, because vertical transmission can be almost excluded by means of antiretroviral treatment [5]. The number of individuals entering the population per unit of time is bN with birth-rate constant b, where ‘birth’ means that an individual becomes sexually active. Similarly, d is the natural death rate constant for all subpopulations. For simplicity reasons, the total population size is assumed to grow exponentially with rate constant $b - d$ in the absence of the disease. It is further assumed that infected individuals do not change their behaviour, no matter if they are treated or not. Thus, the average number of contacts of an individual per unit of time is a constant c for all subpopulations. The disease progression rate constant from stage j to stage $j + 1$ or the AIDS-stage is given by $k_{j}$ for $j = 1, 2$ , respectively. To model treatment effects as described in Section 1, it is assumed that an infected individual in the second stage can move back to the first stage by means of successful drug treatment. The corresponding transfer-rate constant is denoted by α. By β and $a β$ we denote the probability of disease transmission during one contact with an infected individual in stages 1 and 2, respectively.

See Table 1 for an overview of the parameters and variables used in the formulation of the model equations. Here also the parameter values used in the simulations below are given. The values for the disease progression rates $k_{j}$ are taken from [18]. The reasons for using these quite old estimates are obvious: as today antiretroviral treatments are widely used, new estimates on these transfer rates always include treatment effects. The main goal of our work was to study the effects of treatment on the population growth and the spread of the epidemic. This is why we have to use these very old estimates for the $k_{j}$ that hopefully represent the spread of the epidemic in an untreated population. In case $b < d$ , an epidemic of HIV infection can only speed up extinction of the population, whereas in case $b ⩾ d$ , the disease of HIV infection can slow down the population growth or even reverse growth to decay. As the latter case is much more interesting, the simulations shown in this paper use parameter values b and d chosen such that the population grows in the absence of the disease. According to [5], the probability of disease transmission per contact is between 11% and 50%. It is highest right after infection and in the last stage before AIDS, thus we take $β = 0.5$ and $a β = 0.6 β$ . In the simulations we analyse two treatment levels – medium level and high level treatment with $α = 0.1$ and $α = 0.2$ , respectively. It has to be pointed out that there is no data available for the size of parameter α, thus our values are only reasonable estimates for different treatment levels. Parameter c reflects the level of risky behaviour in the population.

S	number, proportion of susceptibles
$I_{j}$ for j=1,2	number, proportion of infectives in stage j
$I_{1} (0) = 0.05$ , $I_{2} (0) = 0$	initial numbers of infectives (in thousands)
$N = S + I_{1} + I_{2}$	total active population size
$N_{0} = 5000$	initial population size (in thousands)
A	number of AIDS cases
b=0.001	‘birth’ rate constant (number of people becoming sexually active per unit of time)
d=0.0006	natural death rate constant
c=0.3	average number of contacts of an individual per unit of time
β=0.5	probability of disease transmission per contact by an infective in the first stage
a β=0.6 β	probability of disease transmission per contact by an infective in the second stage
$k_{1} = 0.0190, k_{2} = 0.0159$	transfer rate constant $\begin{matrix} I_{1} \end{matrix} \to \begin{matrix} I_{2} \end{matrix}$ and $\begin{matrix} I_{2} \end{matrix} \to \begin{matrix} A \end{matrix}$ , respectively (disease progression)
α=0.1 or 0.2	transfer rate constant $\begin{matrix} I_{2} \end{matrix} \to \begin{matrix} I_{1} \end{matrix}$ (successful treatment: medium or high level treatment)
$c β \frac{S}{N} (I_{1} + a I_{2})$ with	average number of new infections per unit of time (standard incidence)

Let $\dot{X}$ denote the derivative of X with respect to time. The model equations are then given by:

\begin{matrix} N = S + I_{1} + I_{2} \\ {\dot{I}}_{1} = c β \frac{S}{N} (I_{1} + a I_{2}) - (d + k_{1}) I_{1} + α I_{2} \\ {\dot{I}}_{2} = k_{1} I_{1} - (d + k_{2} + α) I_{2} \\ \dot{N} = (b - d) N - k_{2} I_{2} \end{matrix}

(1)

The treatment reproduction number R is used to define a threshold condition for the existence and stability of equilibrium points. It can be interpreted as the average number of infections a typical infective causes in a completely susceptible population. In [32], a formula for R was derived for a very general model with n infectious stages. The complexity of this formula increases significantly with increasing n. In the case of two infectious compartments, it yields the following expression for R:

R = \frac{c β}{D_{2}} (D_{1} + a k_{1}) with D_{1} = d + k_{2} + α D_{2} = (d + k_{1}) D_{1} - k_{1} α

(2)

In the absence of virus, the total sexually active population size of initial size

N_{0}

is assumed to grow exponentially:

N (t) = N_{0} e^{(b - d) t}

Reasonable initial conditions for an infection-free population of initial size

N_{0}

are:

I_{1} (0) = 0.05, I_{2} (0) = 0, N (0) = N_{0}

If system (1) with an initial infection free steady state

E_{0} = (0.05, 0, N_{0})

has a positive (infected) steady state

E^{*} = (I_{1}^{*}, I_{2}^{*}, N^{*})

, then:

I_{1}^{*} = (1 - \frac{1}{R}) \frac{D_{1}}{D_{1} + k_{1}} N^{*}

(3)

I_{2}^{*} = (1 - \frac{1}{R}) \frac{k_{1}}{D_{1} + k_{1}} N^{*}

(4)

N^{*} = \frac{k_{1}}{b - d} I_{2}^{*}

(5)

We can see easily that R is a bifurcation parameter: in case

R < 1

,

I_{1}^{*}

is negative and therefore the steady state

E^{*}

is unphysical and does not exist. When

R = 1

, the infection-free and endemic (positive) steady states collide and there is a transcritical bifurcation. Thus,

E^{*}

exists if and only if

R > 1

. Note that at the positive equilibrium point

E^{*}

, a proportion

1 - \frac{I_{1}^{*} + I_{2}^{*}}{N^{*}} = \frac{1}{R}

of the population will stay susceptible, that is uninfected. The higher the treatment reproduction number R gets, the lower this proportion will be.

To discuss the local stability of the endemic steady state $E^{*}$ , we consider the linearized system of (1) at $E^{*}$ . The Jacobian at $E^{*}$ is given by:

J = (\begin{matrix} M_{1} & M_{2} & M_{3} \\ k_{1} & - D_{1} & 0 \\ 0 & - k_{2} & b - d \end{matrix})

where

M_{1} = - (R - 1) \cdot \frac{D_{2}}{D_{1} + k_{1}} - \frac{a k_{1} (d + k_{1}) + k_{1} α}{D_{1} + a k_{1}}

(6)

M_{2} = α + \frac{a D_{2}}{D_{1} + a k_{1}} - (R - 1) \cdot \frac{D_{1}}{D_{1} + k_{1}}

(7)

M_{3} = \frac{{(R - 1)}^{2}}{R} \cdot \frac{D_{2}}{D_{1} + k_{1}}

(8)

Then the characteristic equation of the linearized system is

λ^{3} + a_{1} λ^{2} + a_{2} λ + a_{3} = 0

(9)

where

a_{1} = - (b - d) + D_{1} - M_{1}

(10)

a_{2} = - D_{1} (b - d) - k_{1} M_{2} - M_{1} (D_{1} - b + d)

(11)

a_{3} = M_{1} D_{1} (b - d) + k_{1} k_{2} M_{3} + k_{1} M_{2} (b - d)

(12)

By using the Routh–Hurwitz criterion [35], it follows that all eigenvalues of the characteristic equation (9) have negative real parts if and only if the following condition is satisfied:

a_{1}, a_{3}, a_{1} a_{2} - a_{3} > 0

(13)

Theorem 1

The endemic population steady state $E^{*}$ exists if and only if $R > 1$ and is asymptotically stable if the inequalities in (13) are satisfied.

For the parameter values as given in Table 1 and $M_{1}, M_{2}, M_{3}$ as defined in (6)–(8), we get:

(14)

Thus, all the conditions given in (13) are satisfied, and it follows from Theorem 1 that the infected steady state

E^{*} = (I_{1}^{*}, I_{2}^{*}, N^{*})

as given in Eqs. (3)–(5) is asymptotically stable. The numerical simulation for the case of high-level treatment (

α = 0.2

) is given in Fig. 1.

Fig. 1
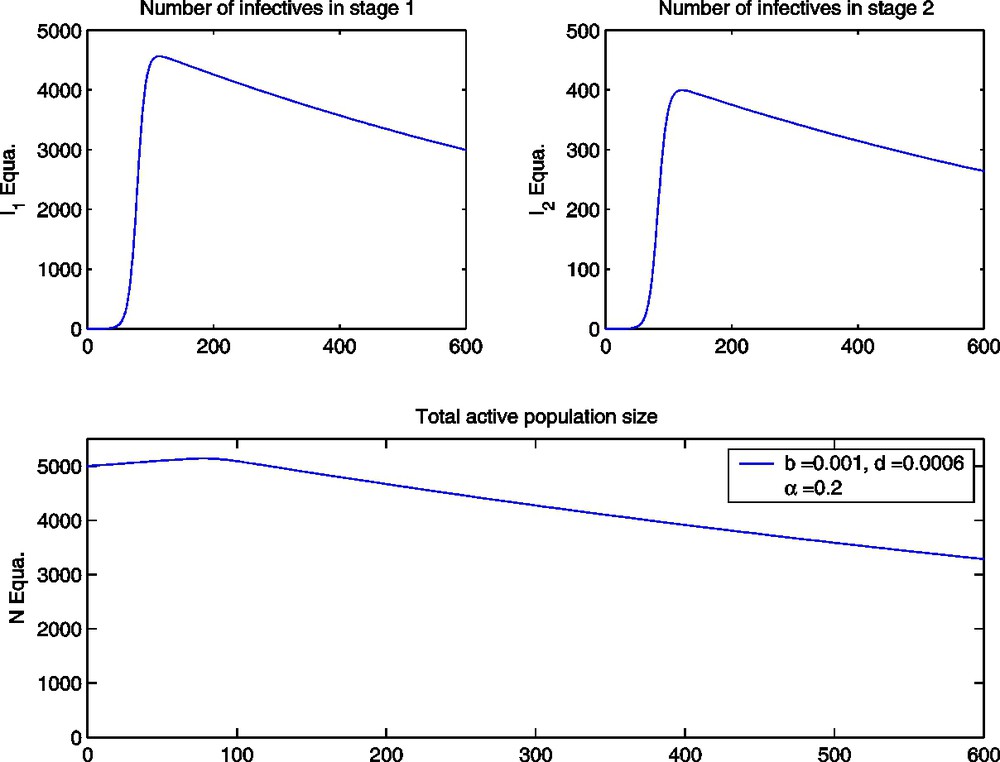
The ODE model with high level treatment (α=0.2) and all parameter values as given in Table 1.

In [32], it was shown in detail that $E^{*}$ is asymptotically stable for n infectious stages whenever it exists.

3 Models with time delay: latency period and treatment induced delay

Let constant τ (in months) be the time delay from the start of treatment in the symptomatic stage $I_{2}$ until treatment effects become visible. As with every virus infection, one has to distinguish between infected individuals having the virus in their bloodstream and infectious individuals, who also can infect others. When a patient is infected with HIV, he typically can transmit the disease not at once, but after a short timespan (in the range of a few days, see [5]) called the latency period. In the following the latency period will be modelled by a time-delay constant λ (in months).

We incorporate these two delays into our ordinary differential-equation model (1) and use the same parameters as in Table 1. We then get the following delay differential-equation model:

(15)

As for the ODE model (1), we assume that the population is completely susceptible in the beginning. That is, the initial conditions are taken to be:

N (0) = N_{0}, I_{1} (s) = 0.05, I_{2} (s) = 0 s \in [- \max (λ, τ), 0]

Again, we find the infected steady state

E^{*} = (I_{1}^{*}, I_{2}^{*}, N^{*})

, where

I_{1}^{*}

,

I_{2}^{*}

, and

N^{*}

are given by Eqs. (3)–(5). To derive stability results of the steady state

E^{*}

for the delay system (15), we study the linearised system of (15) at

E^{*}

. By using the notation

X (t) = (I_{1}^{l} (t), I_{2}^{l} (t), N^{l} (t))

, corresponding to the linearised model around

E^{*}

, we then have:

\dot{X} = A_{1} X (t) + A_{2} X (t - λ) + A_{3} X (t - τ)

(16)

where

A_{1}

,

A_{2}

and

A_{3}

are the following matrices (with

M_{1}

,

M_{2}

,

M_{3}

as given in (6)–(8)):

A_{1} = (\begin{matrix} M_{1} - c β \cdot \frac{1}{R} & M_{2} - α + c β \cdot (1 - \frac{1}{R}) \cdot \frac{D_{1}}{D_{1} + k_{1}} & M_{3} \\ k_{1} & - (d + k_{2}) & 0 \\ 0 & - k_{2} & b - d \end{matrix})

A_{2} = (\begin{matrix} c β \cdot \frac{1}{R} & - c β \cdot (1 - \frac{1}{R}) \cdot \frac{D_{1}}{D_{1} + k_{1}} & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{matrix}), and

A_{3} = (\begin{matrix} 0 & α & 0 \\ 0 & - α & 0 \\ 0 & 0 & 0 \end{matrix})

The characteristic equation of (16) is given by:

Δ (ζ) = \det (ζ I - A_{1} - e^{- ζ λ} A_{2} - e^{- ζ τ} A_{3}) ζ \in C

(17)

We say that

E^{*}

is asymptotically stable if all roots of the characteristic equation (17) have negative real parts (see for example [36,37]).

Definition 1

The steady state $E^{*}$ of system (15) is called absolutely stable (i.e. asymptotically stable independently of delay) if it is asymptotically stable for all delays λ and τ. $E^{*}$ is called conditionally stable (i.e. asymptotically stable depending on the delays) if it is asymptotically stable for λ and τ in some intervals, but not necessarily for all delays λ and τ.

The characteristic equation (17) of the linearised system at the endemic steady state $E^{*}$ can be written as a third-degree polynomial equation of the following form:

ζ^{3} + (a_{1}^{'} + a_{2}^{'} e^{- ζ λ} + e^{- ζ τ} a_{3}^{'}) ζ^{2} + (a_{4}^{'} + a_{5}^{'} e^{- ζ λ} + e^{- ζ τ} a_{6}^{'} + a_{7}^{'} e^{- ζ (τ + λ)}) ζ + a_{8}^{'} e^{- ζ (τ + λ)} + e^{- ζ λ} a_{9}^{'} + e^{- ζ τ} a_{10}^{'} + a_{11}^{'} = 0

Here we have (again with $M_{1}$ , $M_{2}$ , $M_{3}$ as given in (6)–(8)):

a_{1}^{'} = - b - M_{1} + k_{2} + 2 d + c β \cdot \frac{1}{R}

a_{2}^{'} = - c β \cdot \frac{1}{R}

a_{3}^{'} = α

a_{4}^{'} = (M_{1} - c β \cdot \frac{1}{R}) \cdot (b - 2 d - k_{2}) - (b - d) (d + k_{2}) + k_{1} (α - M_{2}) - c β \cdot (1 - \frac{1}{R}) \cdot \frac{k_{1} D_{1}}{D_{1} + k_{1}}

a_{5}^{'} = c β \cdot (1 - \frac{1}{R}) \cdot \frac{k_{1} D_{1}}{D_{1} + k_{1}} - c β \cdot \frac{1}{R} (k_{2} + 2 d - b)

a_{6}^{'} = - α (b - d + M_{1} + k_{1} - c β \cdot \frac{1}{R})

a_{7}^{'} = - c β \cdot \frac{1}{R} α

a_{8}^{'} = c β \cdot \frac{1}{R} α (b - d)

a_{9}^{'} = - c β (b - d) \cdot ((1 - \frac{1}{R}) \cdot \frac{k_{1} D_{1}}{D_{1} + k_{1}} + \frac{1}{R} (d + k_{2}))

a_{10}^{'} = α (b - d) (k_{1} + M_{1} - c β \cdot \frac{1}{R})

a_{11}^{'} = k_{1} k_{2} M_{3} + (b - d) \cdot (k_{1} (M_{2} - α) + M_{1} (d + k_{2})) + c β (b - d) \cdot ((1 - \frac{1}{R}) \cdot \frac{k_{1} D_{1}}{D_{1} + k_{1}} - \frac{1}{R} (d + k_{2}))

Remark 1

We have $a_{1}^{'} + a_{2}^{'} + a_{3}^{'} = a_{1}$ , $a_{4}^{'} + a_{5}^{'} + a_{6}^{'} + a_{7}^{'} = a_{2}$ and $a_{8}^{'} + a_{9}^{'} + a_{10}^{'} + a_{11}^{'} = a_{3}$ , where ${(a_{i})}_{i = 1, 2, 3}$ are defined in Eqs. (10)–(12).

The location of the roots of Eq. (17) has been studied by many authors (see [38–46]). The following result, giving necessary and sufficient conditions for the absolute stability of (16), was proved by Hale et al. in [37,47].

Lemma 1

The delay differential-equation system(16)is absolutely stable if and only if:

(1) $Re [A]$ $ξ < 0$ with $A = A_{1} + A_{2} + A_{3}$ ,
(2) $\det [i ω I - A_{1} - e^{- i ω λ} A_{2} - e^{- i ω τ} A_{3}] \neq 0$ for all $ω > 0$ .

To study the delay case, we consider the ordinary differential-equation model (1) first (with $λ = τ = 0$ for model (15)), and assume that condition (13) for the asymptotic stability of $E^{*}$ is satisfied. Thus, all the roots of (1) have negative real parts, and assumption (1) in Lemma 1 is fulfilled. Assumption (2) in Lemma 1 means that iω, $ω > 0$ is not a root of Eq. (17). Then by using Lemma 1, the delay system is asymptotically stable if and only if the ODE system is asymptotically stable and the characteristic equation (17) has no purely imaginary roots.

Let $θ (τ, λ) = η (τ, λ) + i ω (τ, λ)$ , with $ω > 0$ , be the eigenvalues of the characteristic equation (17), where $η (τ, λ)$ and $ω (τ, λ)$ depend on the delays τ and λ.

If, on the other hand, the characteristic equation (17) has a pair of purely imaginary roots iω, $ω > 0$ , then the delay system (15) is not absolutely stable, but could be conditionally stable. For example in the case of one delay, say for τ, and we suppose that $ω_{0}$ is given, for some value $τ_{0}$ . Hence, when $τ < τ_{0}$ , the real parts of all roots of the characteristic equation (17) still remain negative and the system is conditionally stable. When $τ = τ_{0}$ , the characteristic equation (17) has a purely imaginary root iω, $ω > 0$ , and the system (15) loses its stability. By using Rouché's theorem (Dieudonné [48], Theorem 9.17.4) and continuity in τ, and if the transversality condition holds ( $\frac{d η (τ)}{d τ} |_{τ_{0}} > 0$ ) at $τ = τ_{0}$ , then the characteristic equation (17) will have at least one root with positive real part when $τ > τ_{0}$ and becomes unstable.

To be able to find a condition for all eigenvalues to have negative real parts, we will determine if (17) has purely imaginary roots.

Since the positive equilibrium $E^{*}$ of the ODE model is stable, we have $η (0) < 0$ when $τ = λ = 0$ . By continuity, if $τ > 0$ , $λ > 0$ are sufficiently small, we still have $η (τ, λ) < 0$ and $E^{*}$ still remains stable. If $η (τ_{0}, λ_{0}) = 0$ for certain values $τ_{0} > 0$ and $λ_{0} > 0$ , the steady state $E^{*}$ loses its stability and becomes unstable when $η (τ, λ) > 0$ . On the other hand, if such an $ω (λ_{0}, τ_{0})$ does not exist for all delays, that is the characteristic equation (17) does not have purely imaginary roots, the system will always be stable.

If $i ω (τ, λ) = i ω$ , $ω > 0$ is a root of the characteristic equation (17), then we have:

- i ω^{3} - (a_{1}^{'} + a_{2}^{'} (\cos ω λ - i \sin ω λ) + a_{3}^{'} (\cos ω τ - i \sin ω τ)) ω^{2} + i (a_{4}^{'} + a_{5}^{'} (\cos ω λ - i \sin ω λ) + a_{6}^{'} (\cos ω τ - i \sin ω τ) + a_{7}^{'} (\cos ω (τ + λ) - i \sin ω (τ + λ))) ω + a_{8}^{'} (\cos ω (τ + λ) - i \sin ω (τ + λ)) + (\cos ω λ - i \sin ω λ) a_{9}^{'} + (\cos w τ - i \sin w τ) a_{10}^{'} + a_{11}^{'} = 0

Separating the real and imaginary parts, we have the following:

- (a_{2}^{'} \cos ω λ + a_{3}^{'} \cos ω τ) ω^{2} + (a_{5}^{'} \sin ω λ + a_{6}^{'} \sin ω τ + a_{7}^{'} \sin ω (τ + λ)) ω + a_{8}^{'} \cos ω (τ + λ) + a_{9}^{'} \cos ω λ + a_{10}^{'} \cos ω τ = a_{1}^{'} ω^{2} - a_{11}^{'}

(18)

and

(a_{2}^{'} \sin ω λ + a_{3}^{'} \sin ω τ) ω^{2} + (a_{5}^{'} \cos ω λ + a_{6}^{'} \cos ω τ + a_{7}^{'} \cos ω (τ + λ)) ω - a_{8}^{'} \sin ω (τ + λ) - a_{9}^{'} \sin ω λ - a_{10}^{'} \sin ω τ = ω^{3} - a_{4}^{'} ω

(19)

For complexity and practically reasons, we study the system (15) when

λ = 0

. In this case, the model (15) reduces to a system with only one delay

τ > 0

, where

τ > 0

is the time from the start of treatment in

I_{2}

until treatment effects become visible.

The resulting differential-equation model including delayed onset of treatment effects but no latency period is formulated as follows:

\begin{matrix} N = S + I_{1} + I_{2} \\ {\dot{I}}_{1} = c β \frac{S}{N} (I_{1} + a I_{2}) - (d + k_{1}) I_{1} + α I_{2} (t - τ) \\ {\dot{I}}_{2} = k_{1} I_{1} - (d + k_{2}) I_{2} - α I_{2} (t - τ) \\ \dot{N} = (b - d) N - k_{2} I_{2} \end{matrix}

(20)

In this case, Eqs. (18) and (19) reduce to:

(- a_{3}^{'} ω^{2} + a_{8}^{'} + a_{10}^{'}) \cos ω τ + (a_{6}^{'} + a_{7}^{'}) ω \sin ω τ = ω^{2} (a_{1}^{'} + a_{2}^{'}) - (a_{11}^{'} + a_{9}^{'})

(21)

and

(a_{3}^{'} w^{2} - a_{8}^{'} - a_{10}^{'}) \sin ω τ + (a_{6}^{'} + a_{7}^{'}) ω \cos w τ = ω^{3} - (a_{4}^{'} + a_{5}^{'}) ω

(22)

Adding up the squares of both equations, we obtain the following:

ω^{6} + ω^{4} ({(a_{1}^{'} + a_{2}^{'})}^{2} - 2 (a_{4}^{'} + a_{5}^{'}) - {(a_{3}^{'})}^{2}) + ω^{2} ({(a_{4}^{'} + a_{5}^{'})}^{2} - 2 (a_{2}^{'} + a_{1}^{'}) (a_{11}^{'} + a_{9}^{'}) - {(a_{6}^{'} + a_{7}^{'})}^{2} + 2 (a_{8}^{'} + a_{10}^{'}) a_{3}^{'}) + {(a_{11}^{'} + a_{9}^{'})}^{2} - {(a_{8}^{'} + a_{10}^{'})}^{2} = 0

Then we have

f (u) = u^{3} + κ u^{2} + ν u + ι = 0

(23)

where

u = ω^{2}, κ = {(a_{1}^{'} + a_{2}^{'})}^{2} - 2 (a_{4}^{'} + a_{5}^{'}) - {(a_{3}^{'})}^{2}

ι = {(a_{11}^{'} + a_{9}^{'})}^{2} - {(a_{8}^{'} + a_{10}^{'})}^{2}

ν = {(a_{4}^{'} + a_{5}^{'})}^{2} - 2 (a_{2}^{'} + a_{1}^{'}) (a_{11}^{'} + a_{9}^{'}) - {(a_{6}^{'} + a_{7}^{'})}^{2} + 2 (a_{8}^{'} + a_{10}^{'}) a_{3}^{'}

Remark 2

If $ι ⩾ 0$ and $ν ⩾ 0$ , then Eq. (23) has no positive real roots.

Notice that in the case of a population with high-level treatment ( $α = 0.2$ ) and all parameter values as given in Table 1, we have: $ν ≅ - 7.9222 e - 004 < 0$ and $ι ≅ 1.5178 e - 009 > 0$ . Thus, the equation has a positive root $ω_{0}$ . Hence the characteristic equation (17) with $λ = 0$ has a purely imaginary root $i ω ≅ 0.1983 i$ .

Again, let $θ (τ) = η (τ) + i ω (τ)$ be the eigenvalues of Eq. (17) – with $λ = 0$ – such that $η (τ_{0}) = 0, ω (τ_{0}) = ω_{0} ≅ 0.1983$ . From (21) and (22), we have

τ_{j} = \frac{1}{ω_{0}} \arccos (\frac{f_{1}}{f_{2}}) + \frac{2 j π}{ω_{0}}, j = 1, 2, \dots

where

f_{1} = (a_{6}^{'} + a_{7}^{'}) ω_{0} (ω_{0}^{3} - (a_{4}^{'} + a_{5}^{'}) ω_{0}) + (- a_{3}^{'} ω_{0}^{2} + a_{8}^{'} + a_{10}^{'}) (ω_{0}^{2} (a_{1}^{'} + a_{2}^{'}) - (a_{11}^{'} + a_{9}^{'}))

(24)

f_{2} = {(a_{3}^{'} ω_{0}^{2} - a_{8}^{'} - a_{10}^{'})}^{2} + {(a_{6}^{'} + a_{7}^{'})}^{2} ω_{0}^{2}

(25)

We can verify that the following conditions hold:

{\frac{d η (τ)}{d τ} |}_{τ = τ_{0}} ≅ 0.02321 > 0

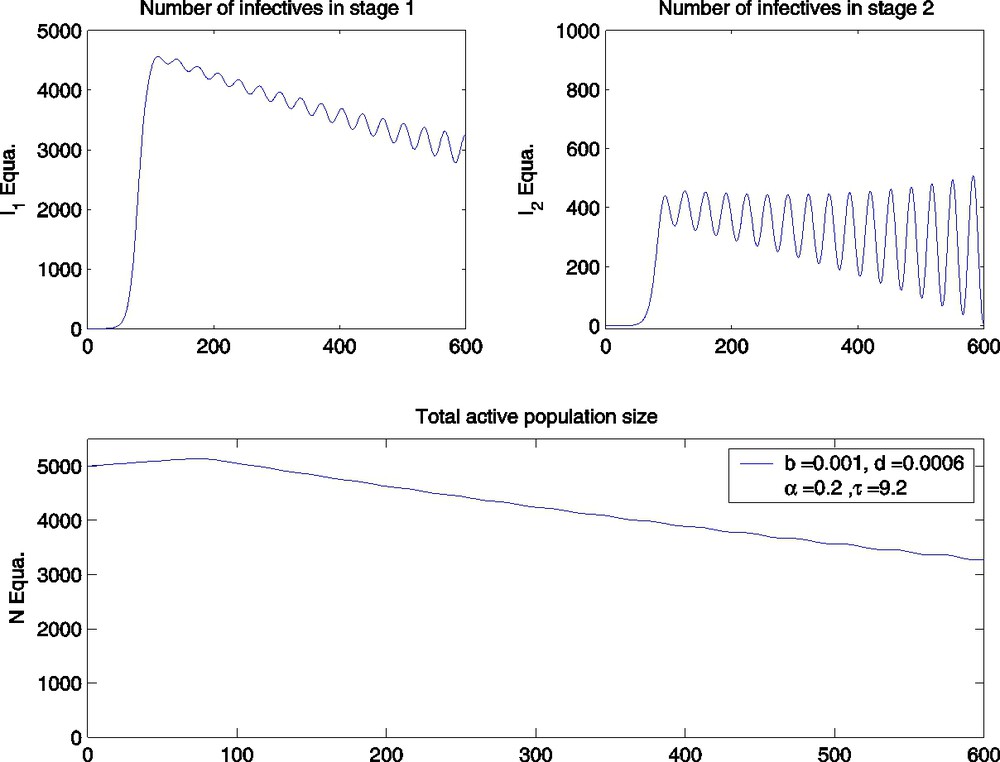
Then the real part of $θ (τ)$ becomes positive when $τ > τ_{0} ≅ 8.82035$ , and the steady state becomes unstable (see Fig. 4). From that, it follows that $τ_{0}$ is a bifurcation value, and a Hopf bifurcation (see [49]) occurs when τ passes through the critical value $τ_{0}$ in Fig. 3. We can see in Fig. 2 that the steady state $E^{*}$ still is stable for delay $τ < τ_{0}$ , allthough the delay causes transient oscillations. Thus, we have the following theorem.

Fig. 4
The DDE model with α=0.2,τ=9.2 and parameter values as given in Table 1.

Fig. 3
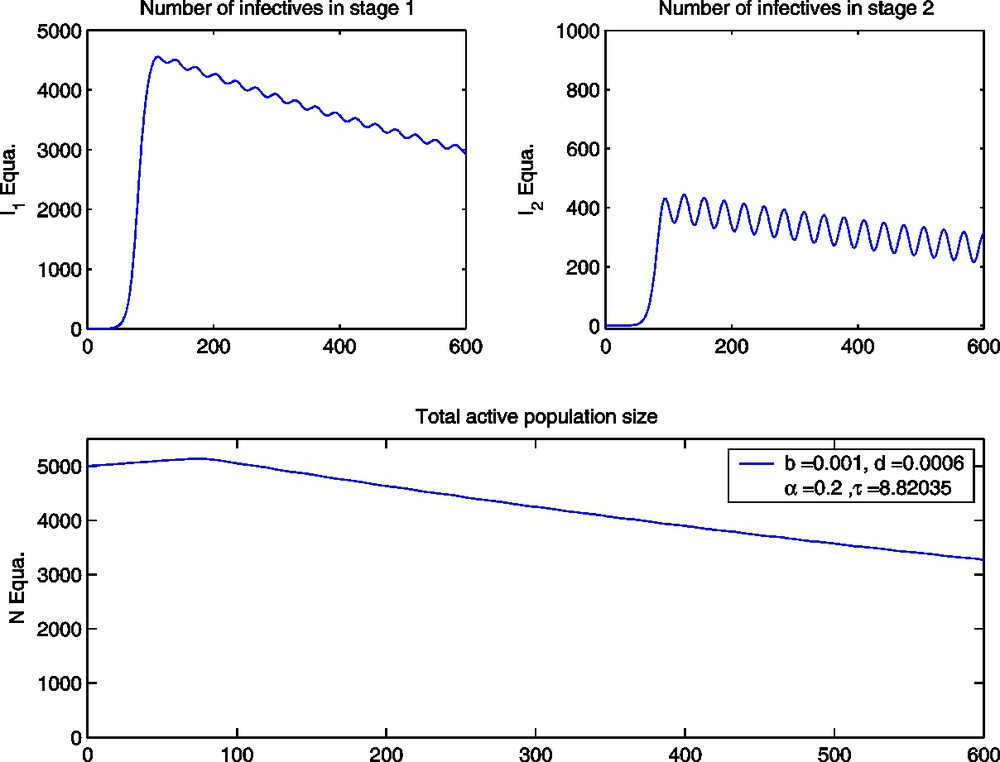
The DDE model with α=0.2,τ≅8.82035 and parameter values as given in Table 1.

Fig. 2
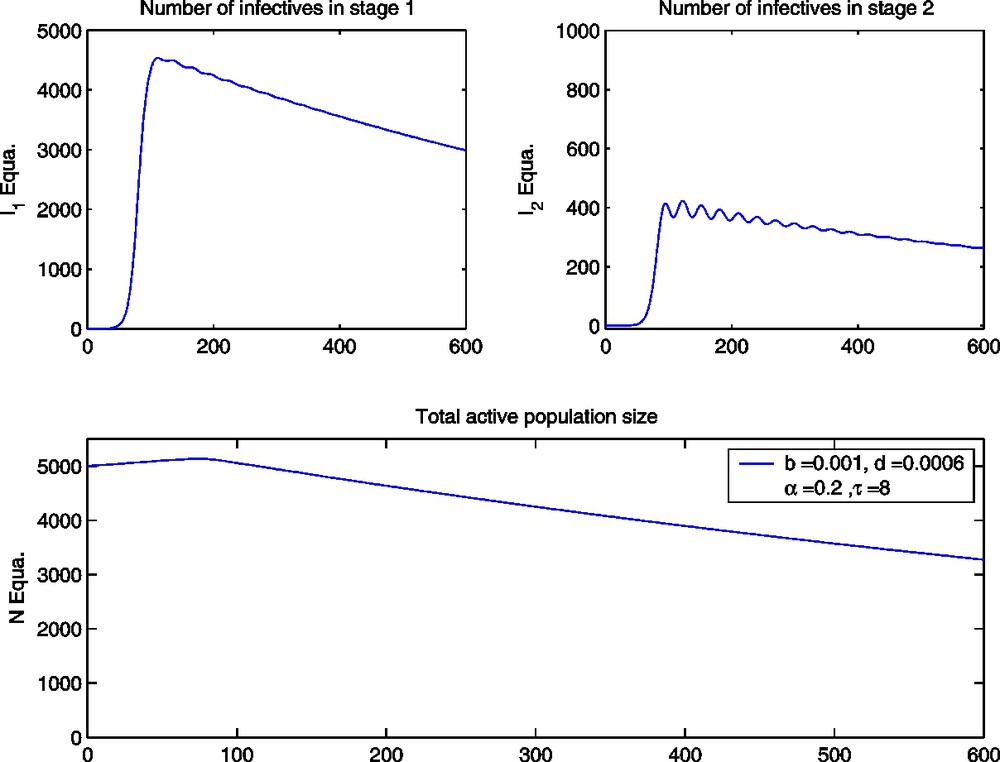
The ODE model with α=0.2,τ=8 and parameter values as given in Table 1.

Theorem 2

The infected steady state $E^{*}$ of the delay model (20) is asymptotically stable when $τ < τ_{0}$ and unstable when $τ > τ_{0}$ , where

τ_{0} = \frac{1}{ω_{0}} \arccos (\frac{f_{1}}{f_{2}}) ≅ 8.82035

and

f_{1}, f_{2}

are given by (24) and (25) .

If $τ = τ_{0} ≅ 8.82035$ , a Hopf bifurcation occurs, that is, a family of periodic solution bifurcates from $E^{*}$ as τ passes through the critical value $τ_{0} ≅ 8.82035$ .

Biologically, this means that there is a critical value for the treatment-induced delay $τ_{0}$ , that determines the stability of the endemic equilibrium point $E^{*}$ . With the parameter values given in Table 1, the endemic equilibrium point is asymptotically stable when antiretroviral drugs in average show positive effects in the patients within less than $τ_{0} ≅ 8.82035$ months. In this case (see Fig. 2) the population will reach the infected steady state $E^{*}$ as given in Eqs. (3)–(5). As soon as it takes more than $τ_{0} ≅ 8.82035$ months for the patients to feel better, the infected steady state $E^{*}$ loses its stability (see Fig. 4).

4 Discussion

The underlying assumption in the present paper is that people who are infected with HIV do not change their behaviour despite the knowledge of the risks. In [50], S. Blower states that incidence rates of HIV will fall as more HIV-positive individuals gain access to treatment (HAART), but that this public health benefit will only occur if the levels of risky behaviour do not increase. Computer simulations based on a simple ordinary differential-equation model for an HIV epidemic (see [33]), on the contrary, show that treatment without reduction of risky behaviour may even increase the proportion of infected individuals. This effects can also be seen in the delay differential-equation models presented in the present paper. The simulations for the ODE model in [33] show that the combination of reduction of risky behaviour together with antiretroviral drug treatment is a very promising strategy in fighting the epidemic of HIV infection. This has to be taken into account, when anti-HIV regimens are distributed in the poorest countries of the world, where behaviour change is hard to achieve because of low educational levels or cultural reasons.

In our delay differential-equation models we do have two threshold parameters: The treatment reproduction number R serves as a threshold for the existence of an endemic equilibrium point, and the size of the treatment-induced delay τ has enormous effects on the dynamics of the spread of the disease of HIV infection in the population. This treatment-induced delay τ can be seen as the minimum time span that patients have to be under medical treatment until positive treatment effects occur. If and only if the treatment reproduction number R is above one, there is a positive steady state. If in this case, the treatment induced delay τ is below a critical value, the total sexually active population will reach the infected equilibrium point (see Fig. 2). Note that at this positive steady state there are still people that have not been infected with HIV. The proportion of these susceptibles is given by $\frac{1}{R}$ . As soon as τ increases and reaches the critical value, a Hopf bifurcation occurs (see Fig. 3), and, finally, the endemic equilibrium point loses its stability above the critical value (see Fig. 4).

The present work wants to be understood as a starting point for further research on analysing treatment effects including time delay on the spread of an HIV epidemic. The next step will be to analyse the general model with n infected stages. We also have to point out that we assumed exponential growth for the total population in the absence of the disease, what is a very restrictive assumption. The simulations with logistic growth for the ODE model given in [32] show that the disease of HIV infection also could lower the carrying capacity or give rise to a second positive steady state below the carrying capacity. It remains to analyse the delay differential-equation model with other than exponential population growth and the role of treatment and behaviour change under these circumstances.

Acknowledgments

The first author was supported by the Fonds zur Förderung der wissenschaftliche Forschung under SFB F003, ‘Optimierung und Kontrolle’, and by EC programme Centers of Excellence of State in phase of pre-accession, No. ICA1-CT-2000-70024.

Bibliographie

[1] D.E. Bloom River path associates something to be done: Treating HIV/AIDS, Science, Volume 288 (2000), pp. 2171-2173

[2] J.M. Mann; D.J.M. Tarantola HIV 1998: The global picture, Sci. Am., Volume 279 (1998), pp. 82-83

[3] Retroviruses (J.M. Coffin; S.H. Hughes; H.E. Varmus, eds.), Cold Spring Harbor Laboratory Press, Cold Spring Harbor, New York, 1997

[4] J.H. Condra; E.A. Emini Preventing HIV-1 drug resistance, Sci. Med., Volume 4 (1997), pp. 2-11

[5] B.S. Kamps; H.-R. Brodt; E.B. Helm AIDS 2000: Diagnostik und Therapie, Steinhäuser Verlag, 2000

[6] S. Blower; A.N. Aschenbach; H.B. Gershengorn; J.O. Kahn Predicting the unpredictable: Transmission of drug-resistant HIV, Nat. Med., Volume 7 (2001), pp. 1016-1020

[7] A.A. Ding; H. Wu Relationships between antiviral treatment effects and biphasic viral decay rates in modeling HIV dynamics, Math. Biosci., Volume 160 (1999), pp. 63-82

[8] S.-F. Hsu Schmitz Effects of treatment or/and vaccination on HIV transmission in homosexuals with genetic heterogeneity, Math. Biosci., Volume 167 (2000), pp. 1-18

[9] D. Kirschner Using Mathematics to Understand HIV Immune Dynamics, Not. AMS, Volume 43 (1996), pp. 191-202

[10] R.M. Ribeiro; S. Bonhoeffer Production of resistant HIV mutants during antiretroviral therapy, Proc. Natl Acad. Sci. USA, Volume 97 (2000), pp. 7681-7686

[11] D. Wick On T-cell dynamics and the hyperactivation theory of AIDS pathogenesis, Math. Biosci., Volume 158 (1999), pp. 127-144

[12] D. Wick; S.G. Self Early HIV infection in vivo: branching-process model for the studying timing of immune responses and drug therapy, Math. Biosci., Volume 165 (2000), pp. 115-134

[13] Mathematical and Statistical Approaches to AIDS Epidemiology (C. Castillo-Chavez, ed.), Lect. Notes Biomath., vol. 83, Springer Verlag, New York, 1989

[14] V.R. Haynatzka; J. Gani; S.T. Rachev The spread of AIDS among interactive transmission groups, Math. Comput. Modelling, Volume 32 (2000), pp. 169-180

[15] H.W. Hethcote The mathematics of infectious diseases, SIAM Rev., Volume 42 (2000), pp. 599-653

[16] H.W. Hethcote; J.W. Van Ark; I.M. Longini A simulation model of AIDS in San Francisco: I. Model formulation, and parameter estimation, Math. Biosci., Volume 106 (1991), pp. 203-222

[17] H.W. Hethcote; J.W. Van Ark; J.M. Karon A simulation model of AIDS in San Francisco: II. Simulations, therapy, and sensitivity analysis, Math. Biosci., Volume 106 (1991), pp. 223-247

[18] H.W. Hethcote; J.W. Van Ark Modeling HIV Transmission and AIDS in the United States, Lect. Notes Biomath., vol. 95, 1992

[19] F. Lewis; D. Greenhalgh Three stage AIDS incubation period: a worst-case scenario using addict needle interaction assumptions, Math. Biosci., Volume 169 (2001), pp. 53-87

[20] S. Blower; H.B. Gershengorn; R.M. Grant A tale of two futures: HIV and antiretroviral therapy in San Francisco, Science, Volume 287 (2000), pp. 650-654

[21] D. Greenhalgh; M. Doyle; F. Lewis A mathematical treatment of AIDS and condom use, IMA J. Math. Appl. Med. Biol., Volume 18 (2001), pp. 225-262

[22] A.B. Gumel; E.H. Twizell; P. Yu Numerical and bifurcation analyses for a population model of HIV chemotherapy, Math. Comput. Simul., Volume 54 (2000), pp. 169-181

[23] Y.-H. Hsieh; K. Cooke Behaviour change and treatment of core groups: its effect on the spread of HIV/AIDS, IMA J. Math. Appl. Med. Biol., Volume 17 (2000), pp. 213-241

[24] Y.-H. Hsieh; S.-P. Sheu The effect of density-dependent treatment and behavior change on the dynamics of HIV transmission, J. Math. Biol., Volume 43 (2001), pp. 69-80

[25] E. Massad; F.A.B. Coutinho; M.N. Burattini; L.F. Lopez Modeling the Impact of Imperfect HIV Vaccines on the Incidence of the Infection, Math. Comput. Model., Volume 34 (2001), pp. 345-351

[26] S. Busenbery; K. Cooke Vertically Transmitted Diseases, Springer-Verlag, New York, Berlin, Heidelberg, 1993

[27] S. Busenberg; P. van den Driessche Analysis of a disease transmission model in a population with varying size, J. Math. Biol., Volume 28 (1990), pp. 257-270

[28] O. Diekmann; J.A.P. Heesterbeek Mathematical Epidemiology of Infectious Diseases: Model Building, Analysis and Interpretation, Wiley Series in Mathematical and Computational Biology, Wiley, Chichester, 2000

[29] H.W. Hethcote; M. Zhien; L. Shengbing Effects of quarantine in six endemic models for infectious diseases, Math. Biosci., Volume 180 (2002), pp. 141-160

[30] P. van den Driessche, J. Watmough, Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission (preprint)

[31] X. Lin; H.W. Hethcote; P. Van den Driessche An epidemiological model for HIV/AIDS with proportional recruitment, Math. Biosci., Volume 118 (1993), pp. 181-195

[32] A. Dorfmayr, HIV treatment models in mathematical epidemiology, PhD thesis, Vienna University of Technology, Vienna, 2002

[33] A. Dorfmayr The effects of antiretroviral therapy on an HIV/AIDS epidemic, Proc. PRIM 2002 (‘Mathematics in Medicine and Pharmacy’), Novi Sad, 2002 (accepted for publication)

[34] C.C. McCluskey A model of HIV/AIDS with staged progression and amelioration, Math. Biosci., Volume 181 (2003), pp. 1-16

[35] M. Reimer Grundlagen der Numerischen Mathematik II, Akademishe Verlagsgesellschaft Wiesbaden, 1982

[36] J. Hale Theory of Functional Differential Equations, Springer Verlag, New York, 1993

[37] J.K. Hale; E.F. Infante; F.-S. Tsen Theory and Applications of Hopf Bifurcation, Cambridge University Press, Cambridge, 1981

[38] M. Baptistini; P. Táboas On the stability of some exponential polynomials, J. Math. Anal. Appl., Volume 205 (1997), pp. 259-272

[39] R. Bellman; K.L. Cooke Differential-Difference Equations, Academic Press, New York, 1963

[40] F. Brauer Absolute stability in delay equations, J. Diff. Equat., Volume 69 (1987), pp. 185-191

[41] R.V. Culshaw; S. Ruan A delay-differential equation model of HIV infection of CD4+ T-cells, Math. Biosci., Volume 165 (2000), pp. 27-39

[42] K.L. Cooke; Z. Grossman Discrete delay, distributed delay and stability switches, J. Math. Anal. Appl., Volume 86 (1982), pp. 592-627

[43] K.L. Cooke; P. van den Driessche On zeros of some transcendental equations, Funkcialaj Ekvacioj, Volume 29 (1986), pp. 77-90

[44] J.M. Mahaffy A test for stability of linear differential delay equations, Quart. Appl. Math., Volume 40 ( 1982/83 ), pp. 193-202

[45] S. Ruan; J. Wei On the zeros of transcendental functions with applications to stability of delay differential equations to stability of delay differential equations with two delay, Dyn. Contin. Discrete Impulsive Syst., Volume 10 (2003), pp. 863-874

[46] R. Ouifki; M.L. Hbid; O. Arino Attractiveness and Hopf bifurcation for retarded differential equations, Commun. Pure Appl. Anal., Volume 2 (2003) no. 2, pp. 147-158

[47] F.G. Boese Stability criteria for second-order dynamical systems models with time delays, SIAM J. Math. Anal., Volume 26 (1995), pp. 1306-1330

[48] J. Dieudonné Foundations of Modern Analysis, Academic Press, New York, 1960

[49] B.D. Hassard; N.D. Kazarinoff; Y.H. Wan Stability in linear delay equations, J. Math. Anal. Appl., Volume 105 (1985), pp. 533-555

[50] S. Blower Calculating the consequences: HAART and risky sex, AIDS, Volume 15 (2001), pp. 1309-1310

Commentaires - Politique