1 Introduction
Epilepsy, one of the most common neurologic disorders, is a major public health issue, affecting about 4% of individuals over their lifetime [1]. One of the most disabling aspects of this disease is the apparently random nature of epileptic seizures. This unpredictability of seizure is responsible for enhanced risk for morbidity [2] and represents a major factor of worse quality of life [3]. Despite progress in understanding the pathogenesis of seizures and epilepsy [4], the interictal–ictal transition remains a mystery. Anticipation of seizure onset, even of short term, would provide time for the application of preventive measures to minimize seizure risk and, ultimately, improve quality of life. Moreover, successful completion of this goal will provide some light to the characterization of basic pathophysiological mechanisms responsible for individual seizures, the so-called ‘ictogenesis’, and to the development of an epileptic condition [5].
The motivation for the search of seizure anticipation is straightforward. The electroencephalographic (EEG) correlate of the seizure in partial epilepsy is characterized by the sudden appearance of an ictal discharge out of the ongoing background activity [5]. These ictal patterns are identified by the expert's visual inspection of EEG recordings – still the ‘gold standard’ for seizure identification. There are no other known electrographic clues in advance predicting the occurrence of a seizure [6–8]. Specifically, the term ‘seizure anticipation’ is used to refer to the process of identifying a state in the EEG signals by moving backward in time from the unequivocal seizure onset [9–11]. Rather than referring to a declaration in advance of the time, anticipation refers to the time between the earliest identification of a preseizure state and the onset of the clinical seizure or the time at which a well-trained clinician can pick up evidences by visual inspection of the EEG (Fig. 1). Therefore, in contrast to seizure detection, anticipation involves the detection of hidden electrographic patterns that can not be directly detected by traditional signal analysis, at least until the ictogenesis issue is clearly resolved.
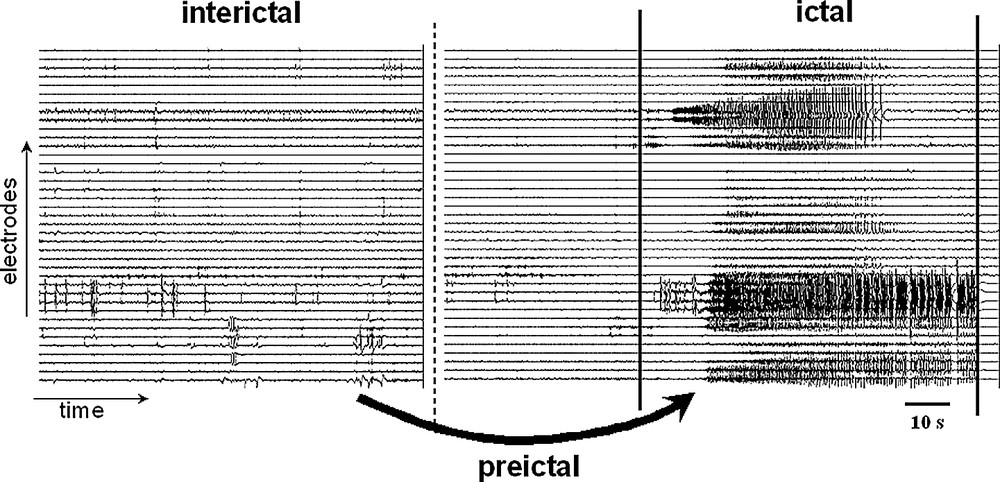
The interictal–ictal transition. An epoch of intracranial EEG from a patient implanted with hippocampal depth electrodes is shown. The seizure onset is here characterized by the sudden appearance of an ictal discharge out of the ongoing background activity. The objective of the seizure anticipation is to understand the process of changes mediating the transitions from the interictal to the ictal state and to find out whether systematic preictal changes may anticipate the occurrence of the seizures.
The search for preictal changes is further motivated by a number of clinical observations indicating that an epileptic seizure is not an abrupt phenomenon that occurs like a bolt from the blue. For example, many patients are aware of periods when seizures are more likely and various warning symptoms (called prodomi) have been reported to precede epileptic seizures from several minutes to hours [12]. There is also physiological support for preictal changes. Some studies demonstrated that modifications in the cerebral blood flow occur around 10 min prior to temporal-lobe seizures [13,14]. In the course of the last decade, the search in EEG signals for hidden dynamical patterns, anticipating an impending seizure, has been also motivated by new advances in mathematical methods to analyse complex systems. According to this new approach of the brain large-scale activities, often called neurodynamics [15], EEG signals are no longer be regarded as a purely stochastic phenomenon, but reflect the complex dynamics of coupled nonlinear interactions between neuronal populations [16].
Using non-linear analyses of the EEG signals, several studies have provided strong evidences that the interictal–ictal transition is not an abrupt phenomenon [9–11]. Rather, findings indicate that it is possible to detect a preseizure state of several minutes anticipating the electrical onset of a seizure. On the basis of our own work, we review here some recent evidences and introduce the used neurodynamical approach that offers a conceptual and mathematical framework to analyse large-scale epileptic phenomena. Hypotheses on the neuronal mechanisms underlying the preictal period are also discussed. In particular, we hypothesize that the preictal phase may reflect an alteration of normal large-scale brain synchronizations, inducing a state of higher susceptibility for seizure activity.
2 The neurodynamics at the large scale
Although much is known about the structure and functional attributes of the brain, a comprehensive understanding of its large-scale dynamical properties remains unknown. At this macroscopic level, a prevalent feature of the brain activity is the presence of metastable spatiotemporal patterns of neural activity distributed over many distinct brain regions [17]. The existence of large-scale cortical dynamics is confirmed by numerous functional brain mapping studies, employing electro- and magneto-encephalography (EEG-MEG), functional Magnetic Resonance Imaging (fMRI) or Positron Emission Tomography (PET). As suggested by these observations, a key property of this large-scale dynamics is its extraordinary degree of coordination: The different parts of the brain through their rich network of connections cooperate to produce an unified whole, typically including multiple modalities and submodalities, that cannot be subdivided into independent components without a loss in its meaning. Specifically, brain imaging reported that this endogenous dynamics has three main characteristics [17–22]: First, the large-scale dynamics constantly gives rise to new patterns in succession and thus is dynamically unstable. This notion of metastability is central to the entire idea of large-scale neurodynamics presented here since it underscores that the global activity enters into different states of coordination of its constituent areas without becoming trapped in one particular state (Fig. 2A). Second, the large-scale dynamics modulates the microscopic cellular interactions and locally constrains their behaviours. A reciprocal interplay between a relative local autonomy of the elementary neuronal components and the global web of interdependences creates a wide variety of complex, global states able to carry out different behaviours. Finally, the large-scale dynamics must emerge very quickly, on a time period between 100 to 300 ms. Such a rapid integration can be achieved through the strong cortico-cortical as well as cortico-thalamic projections generating a coherent neuronal process through ongoing re-entrant, recursive, and highly parallel interactions among widely distributed brain areas. These three main characteristics permit the brain as a whole to switch rapidly between different functions through the reorganization of its component areas into different coordinated networks. A major question of the modern neuroscience is how the (non-linear) coupling among neuronal components can give rise to a wide variety of complex, coordinated behaviours [18–22].
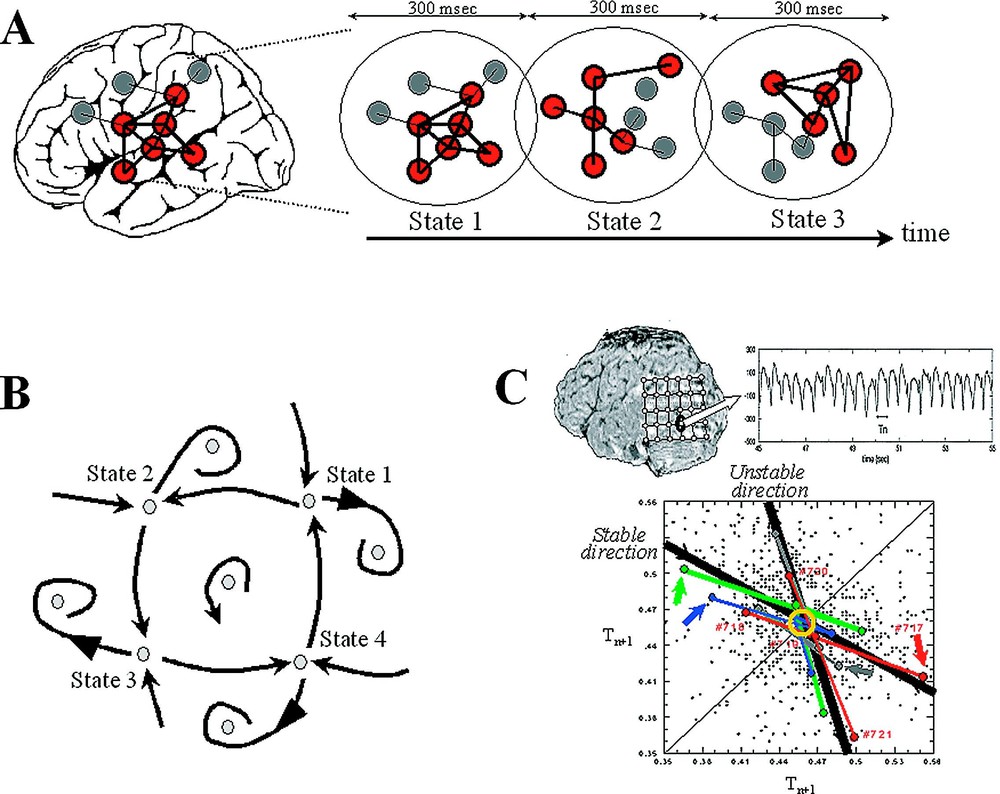
Neurodynamics at the large scale. (A) At the macroscopic level, a prevalent feature of the brain activity is the presence of metastable and distributed patterns of neural activity on a time period between 100 to 300 ms. (B) The dynamics for this emergent behaviour can be described geometrically, in terms of positions, regions and trajectories in a state space. (C) An example of complex dynamic patterns observed in a local EEG activity recorded from an epileptic focus. The temporal intervals between successive discharges were analysed in a first-return map intervals . Various unstable periodic activities are observed with recurrent deterministic trajectories toward them (stable direction) and diverging away (unstable direction).
Clearly, better understanding of these large-scale brain processes remains hampered by the lack of a theoretical language for expressing these complex behaviours in dynamical terms. Despite still in its infancy, a significative theoretical framework to afford this issue has been proposed by the physical-mathematical framework of nonlinear dynamics. From the physics of complex systems, it is well known that systems possessing a large number of elements interacting in a nonlinear way can give rise to the spontaneous formation of well-organized structures, patterns, or behaviours, which is usually referred to as self-organization. The earliest example for this behaviour in a simple physical system is the convection cells (Bénard instability) in a horizontal water layer with a thermal gradient. When the thermal gradient has reached a critical value, the initially uncorrelated, random motions of billions of molecules synchronize spontaneously without any external control, leading to a spontaneous emergence of long-range correlated macroscopic structures [23]. During the early 1970s, the growing need for a better understanding of these types of cooperative behaviours has led to a general theoretical description based on a branch of mathematics called dynamic system theory [24]. In a nutshell, the traditional starting point of all these descriptions consists in conceptualizing the dynamics geometrically, in terms of positions, regions and trajectories in the space of possible states. Collectively, they constitute what is known as the system flow. The shape of the flow is determined by the system's intrinsic dynamics – the force that push the system state in one direction or another, depending on where the current state is located. They can be thought of as constituting a kind of landscape over which the behaviour of the system moves. The global shape of dynamical landscape is determined by the so-called order parameters. For autonomous dynamical systems, these global parameters are solely created by the intrinsic interactions among the individual parts of the system. They in turn govern the behaviour of the individual parts. The dynamics of these order parameters (by definition, this dynamics is slower than that of the system) characterizes how the dynamical landscape is formed and evolves in time.
In a general way, nonlinear dynamics has a natural appeal for neurosciences, since it provides ways to conceptualize systems undergoing continual change, ways to characterize the relative stability of possible patterns of change as a function of system parameters, and ways to think about couplings between complex processes such as local neural activities distributed over many distinct brain regions. In particular, the dynamical system descriptions address the fundamental conflict between stability and instability of brain dynamics at different levels of organization of the nervous systems [16,25,26]. Applied to large-scale brain processes, dynamical system descriptions may provide guidance to a new interpretation of the global brain dynamics as a flow [27]. Why is this of importance here? First, these descriptions lead us directly to an explicit view of brain dynamic as a trajectory in a state space (Fig. 2B). Because of its intrinsic instability, no stable region exists in the phase space, but rather ongoing sequences of transient visits of specific weakly attracting places in a complex pattern of motion, modulated by external influences. Second, these descriptions make explicit generic structures of the brain dynamics, i.e., characteristics that are observed independently of the particular variation of the context or of the components of the network under consideration. The key feature is here given by the intrinsic dynamical landscape that brings the flow into particular trajectories, depending on where the current state is located. Finally, dynamic system theory can help us to describe order parameters of brain dynamics, characterizing how its intrinsic dynamics is constituted and unfolds in time, possibly around some instabilities. Again, these global parameters emerge from the intrinsic activity of the nervous system itself and constrain the behaviour of the individual parts of the brain.
From our own work, a good example of dynamical patterns has been reported in the case of a patient with an unusually focal and stable occipito-temporal epileptic discharge [28]. The corresponding EEGs were recorded intracranially in the course of presurgical evaluation of this patient who was not responsive to medication and became candidate for surgery. Characteristic for this epileptogenic tissue, the EEG signals exhibited spontaneous and nearly periodic interictal spikes (Fig. 2C), reflecting the manifestation of pathological recruitment of local neuronal populations, which did not produce cognitive impairments. The temporal intervals between successive discharges were analysed in a first-return map, reconstructing the dynamical structure through the ‘method of delays’ (see Section 4). This analysis revealed various clusters of unstable rhythms having underlying short-time causality: a tendency in successive time steps to follow recurrent trajectories that approach the clusters along a specific direction and remain nearby before they diverge away along another unstable direction. Although the positions of the periodic points are shifted between different behavioural conditions, the related slope of approach to the instabilities appears as invariant features of the dynamics for all experimental conditions. This kind of dynamics is very similar to a chaotic trajectory, which typically includes an infinite number of unstable periodic orbits [25,26]. Thus the state never remains long in any of these unstable motions, but continually switches from one periodic motion to another, thereby giving an appearance of randomness [29]. Another interesting observation here was that the local activity under study can be transiently modulated by the subject's cognitive states. This modulation can be accomplished because the epileptogenic zone is embedded in a complex network of other brain regions that actively participate in normal large-scale interactions. From these observations, it follows that the global pattern of integration can produce ‘downward’ effects (global-to-local), acting on the local level of cellular assemblies [30].
3 Disentangling the brain web
Brain complexity has a temporal, but also a spatial aspect. Spatial complexity implies the coordination of many different regions through a kind of temporal resonance or ‘glue’. Neural synchrony is an important candidate for this integration, mediated by neuronal groups that oscillate in specific bands and enter into precise phase-locking over a limited period of time [17]. This role of synchronization of neuronal discharges, although not a new idea, has been greatly highlighted by results from microelectrodes in animals [31]. These single-unit recording studies in animals have been complemented by studies at coarser levels of resolution in humans and animals. These are not spikes, but local field potentials (LFP) of various degrees of spatial resolution, including human subdural electrocorticograms [32], scalp EEG [33] or MEG [34]. Also, there is some recent evidence to suggest that not only local activities, but also long-range synchronization comparable to those found in single-unit studies in animals can also be detected between surface recordings [35]. Specifically, it has been shown that large-scale integration implicates not only the establishment of dynamical links, but also their dismantling to give way for a next cognitive moment. The key finding is here that synchronous patterns are short-lived (lasting on the order of 50 to 250 ms) with new patterns continually being created, destroyed and subsequently recreated. These results are based on the analysis of phase synchronization, which involves the pairwise comparison of phase relations between different electrode recordings. In this context, a classical definition of synchronization is the adjustment of the rhythmicity of two oscillators in a phase-locking and assumes the constancy of phase difference within a limited window of time, typically of a few hundreds of milliseconds (Fig. 3A). In the case of neural signals (such as EEG, MEG, and intracranial), detecting phase locking between two distant brain recordings is, however, not straightforward and this quantification requires methods that are entirely different that the cross-correlograms between spike discharges of microelectrode studies. Furthermore, especially for non invasive signals, the true synchronies are buried in a considerable background noise, which can give rise to spurious phase-locking between their signals. Consequently, the question “synchronous or not synchronous” can only be treated in a statistical sense. This statistical analysis of phase synchronization between neuronal signals was introduced by Lachaux et al. [36] and Tass et al. [37] to overcome some limitations of conventional methods which not disentangle amplitudes and phases. Fig. 3B shows an example of synchrony characterization between intracranial EEG recordings. In contrast to scalp recordings, human intracranial EEGs are generally highly differentiated and local in respect to measures of cooperative interactions, at least down to millimetre dimensions, and fluctuate in time within seconds [38]. Fig. 3B shows successive graphs of synchronization in the alpha range (8–13 Hz) linking different deep structures during an awaken state, far away from any seizures. Elevated large-scale phase synchronization can transiently be observed during periods on the order of 100 ms to a few seconds. Phase-locked patterns of activity appear highly variable both temporally and spatially, sometimes linking different cortical regions separated by several centimeters. This complexity leads naturally to a dynamical description of these cooperative behaviours [39,40].
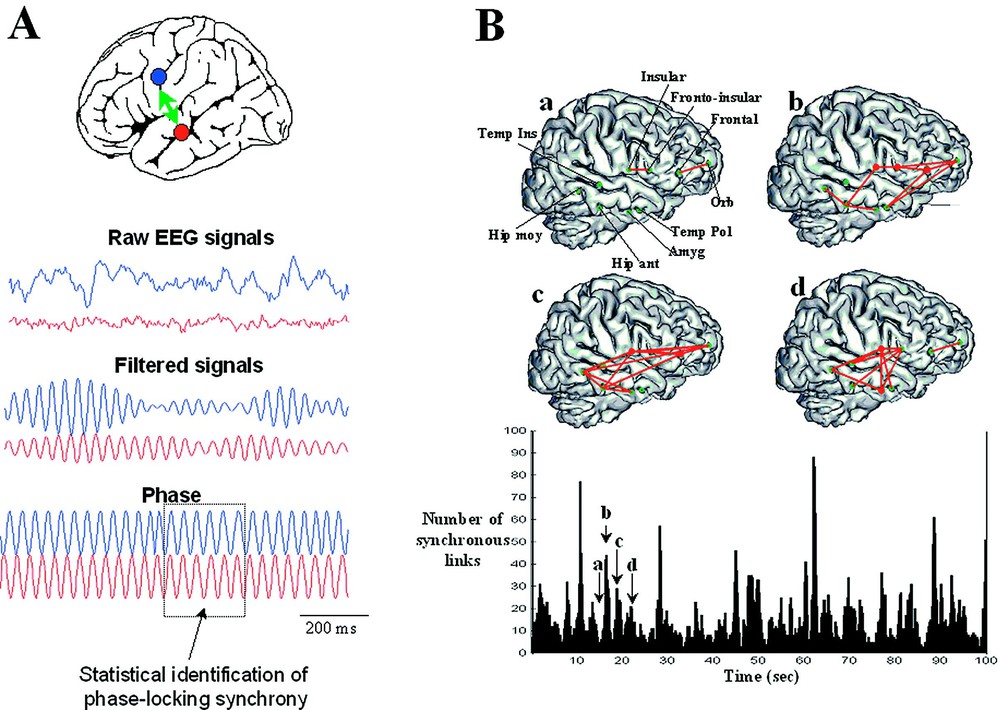
Measuring brain synchronization. (A) Synchronization measures are needed to describe weak interdependences between two distant EEG signals. The phase synchrony measures the degree of temporal relations between the phases of the brain signals regardless of the signal amplitudes. A phase-locking is detected when the phase differences between the signals fluctuate around a constant value within a limited window of time. Practically, raw EEG signals have broad bands and it is difficult to directly interpret an instantaneous phase from the activity. Therefore, the first step is to filter the signals within a particular frequency band of a few hertz. In the second step, the instantaneous phase of each signal is extracted in this frequency band. The degree of phase-locking is then quantified by a statistical measure and phase-locking episodes are detected. (B) Example of transient phase-synchrony: spatial projection of synchronous patterns on a 3D MRI reconstruction at four successive moments of time (a, b, c, d) and, below, the link numbers as function of time. We can observe that these phase-locked patterns of brain activity appear highly variable both temporally and spatially, transiently linking different cortical regions.
4 The first generation of nonlinear studies: potentials and limitations of phase-space techniques for seizure anticipation
Given that a complex dynamic system can involve an enormous number of interrelated dependent variables that are impossible to measure directly, the main problem is how to analyse a multidimensional dynamic system knowing only a few variables that can be measured. In this context, it has been mathematically established that, if we can measure any single variable with sufficient accuracy over a sufficiently long period of time, then it is possible to make quantitatively meaningful inferences about the underlying dynamical structure of the system from the behaviour of that single variable [41]. A well-established implementation of this important mathematical fact for the reconstruction of the dynamical structure from one observable is through the ‘method of delays’. A ‘phase space’ can be constructed by taking successive points of the original time series separated by a fixed time delay τ. Let be the neuronal activity recorded at time t and let m delayed amplitudes be recorded on an individual channel. At each time t, the state of the neuronal activity is represented as a point in a m-dimensional space: . This mathematical representation permits the introduction of independent coordinates as the dynamic variables needed to specify the instantaneous state of the system. A sequence of such states followed in time defines a trajectory. An “attractor” is a trajectory in phase space to which the system will converge from any set of initial conditions. The geometrical properties of the trajectories evolving in the phase-space can then be expressed quantitatively using nonlinear measures [42]. An important measure is the dimensionality of the dynamics, referred to as the ‘correlation dimension’ (D2), which characterizes the minimum number of variables that must be considered in the description. A periodic oscillation would have a dimension of 1. If the system has a dimension larger than 2 and is not an integer, then we would expect the system to exhibit ‘chaotic dynamics’ that is governed by low-dimensional deterministic models and show a exponential divergence of originally nearby trajectories.
The phase-space techniques have prompted an intensive search for low-dimensional deterministic phenomena in EEG signals. In the field of epilepsy, Babloyantz and Destexhe [43] were the first to demonstrate that phase-space analysis of EEG recordings from patients with epilepsy can provide new perspectives regarding ictogenesis. They estimated the correlation dimension of scalp EEG signals recorded during a human absence seizure and found that the dimension for seizure activity is of considerably lower value than for normal activity. These findings suggested that the generation of ictal activity in the brain corresponds with a specific dynamical state, which is different from normal ongoing activity. These findings are in line with the work of Iasemidis and Sackellares [44] who described similar variations in the largest Lyapunov exponent (i.e. the mean rate of divergence of initially neighbouring states in the phase space). How the phase transition from interictal state to the ictal state occurs has been explored by our group with comparable phase-space techniques [45]. We estimated the dynamical complexity of intracranial recordings one hour before the seizure onsets of patients with temporal epilepsy. We demonstrated that in most cases (90%), changes toward long-lasting states occurred before the seizure (between 2–6 min) and were more pronounced compared to maximal changes occurring during interictal states, thus suggesting the existence of a ‘preictal state’. This phenomenon could not be directly detected by visual inspection of the original signal or by other more traditional methods of signal processing such as Fourier analysis. Lehnertz and Elger [46] confirmed these findings in a comparable group of patients. These converging evidences suggest that the dynamical properties of the preictal, ictal and postictal states are different. The seizure might be interpreted as the end of a process of changes that starts long before. This transition or route towards the seizure seems to reflect a process from ‘disorder to order’ and argues that epilepsy belongs to the ‘dynamical diseases’ [47].
Nevertheless, after an initial euphoric period in the field of seizure anticipation, several difficulties have been pointed out in a careful application of these phase-space techniques to brain signals and in the interpretation of the results. The major difficulties resulted in the sensitivity of these nonlinear measures to noise and artefacts that are hard to avoid in clinical situations or in non-invasive recording techniques. Even small amounts of noise have a pronounced adverse effect on the estimation of the nonlinear measures [48]. Furthermore, it has been shown that finite values of the correlation dimension can be found even for ‘coloured’ random noise (i.e., for high-dimensional processes characterized by spectra with power-law dependence and random uniformly distributed phases that are clearly not related to low-dimensional dynamics) [49]. Consequently, measures of system complexity do not, in themselves, give any insight into whether the system under study shows a complexity change in terms of the number of degrees of freedom. This limitation has led to doubts about the interpretation of preictal changes in terms of ‘low complexity’. Finally, up to now, most seizure anticipation methods have been evaluated by analysing few and brief preseizure data sets to obtain their sensitivity. No or insufficient interictal data have been investigated to determine their specificity. Indeed, state changes in the interictal dynamics induced by different physiological states of the brain (like the wakefulness–sleep transition) may contribute to spurious detection of preseizure changes whatever the type of analysis. Recent studies concluded that both sensitivity and specificity of phase-space techniques are not yet sufficient to allow a clinical application [50–52].
5 The second generation of nonlinear studies: long-term evaluation of brain synchronization
Nonlinear EEG analysis requires new developments to improve further our understanding of the spatiotemporal dynamics of the epileptogenic process. In this context, the quantification of transient phase-locking between different cortical areas, ubiquitous during normal physiological conditions such as sensory-motor processing [17], can give a better insight into subtle dynamic interactions between pathologic disturbances and surrounding brain regions. These used methods are based on direct estimation of the instantaneous phase of the signal and, hence, are ideal for analysing epileptic EEG recordings whose synchronization properties evolve over time (see Section 3). Using these multivariate techniques, we have recently examined the degree of phase synchronization in long-term intracranial EEG recordings of five patients suffering from mesial temporal lobe epilepsy [53]. These data were part of an international database (1st International Conference on Seizure Anticipation, Bonn, Germany, 2002), containing continuous multi-channel EEG signals (total analysed duration: 305 h, covering 52 seizures). With the statistical measure introduced by Lachaux et al. [36], we examined the synchronies between all possible combinations of electrode pairs for the entire frequency range (0–100 Hz) and detected quantifiable spatial or temporal shifts in preictal synchronization far in advance of seizure onset detectable on the EEG. Because normal EEG synchronization is enormously varied, manifesting qualitative changes depending on behavioural state, we paid close attention to potentially confounding factors for seizure anticipation such as normal behavioural state changes. Toward this end, a classification technique was used to identify if a synchronization pattern is likely or not to be a member of a library of synchronization reference patterns representing long periods of interictal activity (duration ranging from 5 to 24 h, including alert wakefulness or drowsiness, different sleep states including REM). Otherwise, it is classified as an altered state of brain synchronization, deviating from all interictal reference patterns. In most of the cases (36/52 of all seizures, i.e., 70%), we observed a specific state of brain synchronization several hours before the actual seizures. Mean time from declaration of impending seizure to seizure EEG onset was min using optimal parameters to obtain near 100% specificity. Examining the spatial distribution of these changes, we observed that pairs of electrodes near the primary epileptogenic zone appear to increase or decrease their synchronization before the seizures. Very often, these phase synchronization alterations involved a preictal decrease in synchrony within the 5–20-Hz range (the so-called alpha and beta band) (Fig. 4A). This decrease is the exact converse of phase-locking, and is best described as phase-scattering where the probability of finding synchrony between two electrodes drops well below the interictal level [17]. In accordance with other observations [54–56], these findings suggest that local networks within the temporal lobe are engaged in the slow changes detected during the preseizure time. Despite some scepticism about preliminary reports using phase-space techniques (see Section 4 for a critical point of view), these findings give very promising evidences of preictal changes in brain electrical activity prior to seizure and suggest that the analysis of phase synchronization might offer a way to distinguish between a preictal state and normal interictal activity [56]. Nevertheless, it is important to point out that these results do not constitute genuine seizure anticipation, because this would require a prospective analysis of data when time to seizure is unknown. Furthermore, it is important to stress that the anticipation times are strongly dependent on the criteria we used and should be regarded as a weak estimate that allows both intra- and intercomparisons. Nevertheless, in the present state, our analysis could, after more extensive validation, be used for warning purposes. Further improvements can be obtained by selecting (on- or offline) multiple preseizure segments for training purposes or by adding continuously new synchronization patterns in the interictal library. Also, expert-selected signal information can also be included, depending on the type of signal characteristics or changes the physician/user wants to detect (or not detect).
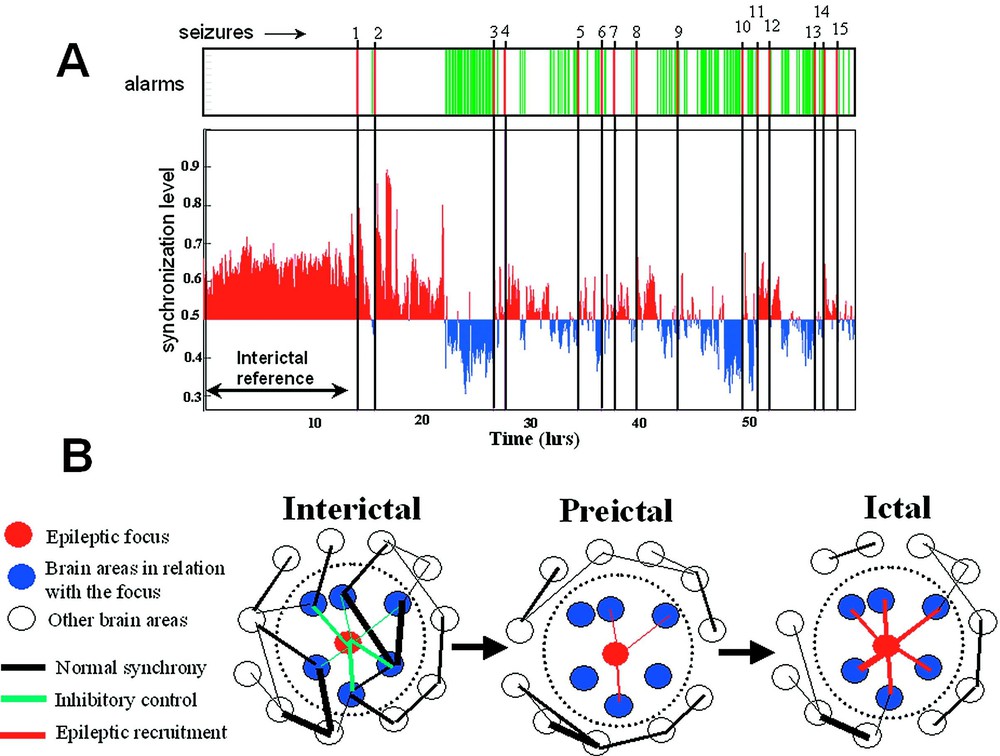
Dys-synchronization prior to seizure. (A) Synchronization analysis of a long term recordings of a patient with a epileptic focus in the temporal lobe. The phase-synchronization was estimated using a sliding window analysis between 10 and 20 Hz, for all pairs of EEG channels in the epileptogenic temporal lobe (14 channels). Fifteen seizures were recorded. Thirteen hours of interictal activity (including periods of wakefulness and sleep) are defined as a reference state. Before most of the seizures, a specific decrease (blue) in the synchrony level can be seen before seizure onset. An alarm is declared when the synchronization crosses an adjustable threshold. Clearly, this analysis could be used for warning purposes. (B) A possible mechanism for preictal changes: During the interictal state, the neuronal populations in relation to the epileptic focus are implicated in large scale dynamics of normal brain functioning. During the preictal state, these populations lose their synchronization with other cortical areas and with themselves. This condition isolates the epileptic pacemakers from the ongoing large-scale brain influences and facilitates the development of a focal hyperexcitable state. This condition also provides an ‘idle’ population of neurons that become easily recruited into the epileptic process. Additionally, during this preictal state, the inhibitory control of the epileptogenic zone can also progressively break down. Seizure activity will be initiated when a critical mass is recruited.
6 Towards a neurodynamical understanding of ictogenesis
Although the observations of preictal changes are still limited, and do not provide a direct physiological mechanism, some hypotheses can be made (see also [53–56]). Specifically, it was hypothesized that the transient phase-locking between different parts of the brain could be a basic mechanism for the functional large-scale integration observed during cognition and normal functions [17–22]. Thus, given this central role of synchrony in normal states, our results suggest that the participation of particular networks in normal physiological synchronizations appears to be preictally altered, inducing a state of higher susceptibility for seizure activity. This is also in accordance with experimental models of epilepsy showing that specific networks around the epileptic focus seem to be of crucial importance in determining whether or not a seizure is likely to occur and spread [57]. Specifically, our present observations suggest that two related processes seem to be involved here (Fig. 4B): (1) a state of increased synchronization – this state may reflect recruitment phenomena within the primary epileptogenic area and its surroundings regions –, (2) a state of decreased synchronization – this state may isolate pathologically discharging neuronal populations of the epileptic focus from the influence of activity in wider brain areas, thus facilitating the development of local pathological recruitments. On the other hand, a loss of synchrony might also provide an ‘idle’ population of neurons that may be more easily recruited into the epileptic process [53–56]. Finally, the preictal loss of synchrony could reflect a depression of synaptic inhibition in areas surrounding the epileptogenic focus, as shown in certain experimental models of epilepsy [58]. Further investigations of the spatial characteristics of phase synchronization or studies at a cellular level [59] are necessary to validate these hypotheses.
7 Conclusion
Although the field of seizure anticipation is still in its infancy, there are good reasons to be optimistic about the development of robust method for seizure anticipation [9–11]. This ability to anticipate seizures using the intracranial or scalp EEG may have considerable practical implications for the large population of patients with uncontrolled epilepsy. For example, implementing a bedside system of seizure anticipation in a video/EEG unit would be of considerable help for efficient seizure monitoring and for the preparation of the radioactive tracer injection in SPECT examinations. Optimally the tracer must be injected as close to seizure onset as possible. Very often, this procedure is not informative enough due to a late injection, tens of seconds after the onset, which marks much more of the areas of propagation than the actual epileptogenic zone. Considerable resources could be spared by an efficient anticipation.
The perspective opened by the ability to anticipate a seizure several minutes in advance would also provide a time window during which therapeutic measures may be taken to avoid the occurrence of a seizure. In this context, pharmacological control may be possible using rapidly acting antiepileptic drugs with a quick delivery procedure. But probably best adapted to real time therapy are electrical stimulations. Direct brain stimulations for the control of epileptic seizures have already been tested [60], although several questions have not been answered: where and when should the stimulation be applied? Should they be done regularly or only in relation to emergence of epileptic activity? In this second option, seizure anticipation offers, in principle, the possibility to deliver precise electrical stimulations in order to deviate the epileptogenic activities away from their route towards the seizure. This has been already done for rat hippocampal slices by using nonlinear control [29] and in vivo by electric field modulation of brain structures [61].
For basic epilepsy research, the findings are promising to characterize in dynamical terms the preictal state, and thus establish the necessary conditions for the occurrence of a seizure. Of course, a large patient population may be useful for better characterization and understanding of mechanisms of generation and timing of epileptic seizures. Nevertheless, on the basis of our present knowledge, our understanding of the mechanism that underlies the generation of seizures has progressed to the point where it is clear that most seizures are unlikely to arise from random fluctuations of brain activity. Clearly, seizures cannot be regarded in isolation, but require a process of global changes in brain dynamics that starts long before its manifestation. In particular our analysis of preictal synchronizations reaffirms the point that epileptic seizures do not occur in a behavioural vacuum, but that the integrated, normal functioning of the brain before the seizure occurs is critical. Indeed, seizure foci are surrounded by pools of neurons functioning in local and large-scale interactions and are ‘pulled’ into the seizure discharge once the seizure has started. From our most recent observations, we hypothesize that the preictal period may reflect the dys-synchronization of these specific populations of neurons.


