1 Introduction
In a previous paper [1], we have modelled the storage, recall and final effect of abiotic signals in seedlings of Bidens pilosa L. by use of an asynchronous, logical (discrete) formulation [2]. This was especially useful to determine toward which direction the system would tend to move and its steady-state conditions of functioning. The present paper represents the differential (continuous) approach of the same problem. The aim is to describe the system evolution by introducing a continuous term coming from non-linear enzyme kinetics into the equations of the dynamics of the seedling growth.
2 Summarizing the experimental data
See, e.g., Desbiez et al. [3–5] for original experimental data on the Bidens system and Thellier et al. [6] for a review. Briefly, the Bidens seedlings exhibit a bilateral symmetry with their two opposite cotyledons (cotyledon A on the left and cotyledon B on the right when all the seedlings under study are oriented parallel to one another), their actively growing apex (or terminal bud) and their two cotyledonary buds (i.e. the buds at the axil of the cotyledons). As long as the apex is present, it inhibits the growth of the ‘cotyledonary buds’ (apical dominance); however, after apex removal (seedling ‘decapitation’), the cotyledonary buds can start to grow. Stimulating (for instance, pricking) one of the seedling cotyledons (e.g., cotyledon A), i.e. delivering an asymmetrical stimulus to each seedling, tends to alter the symmetry of the growth of the ‘cotyledonary buds’. More precisely, the stimulation of one of the seedling cotyledons gives a statistical advantage to the axillary bud of the opposite cotyledon (the ‘distal’ bud) relative to the bud at the axil of the stimulated cotyledon (the ‘proximal’ bud). In a population of seedlings, this relative advantage of one bud upon the other can be measured by the use of a parameter, g, which corresponds to the difference (normalised to the total number of plants) between the number of plants where bud B starts growing before bud A and the number of plants where bud A starts growing before bud B. For instance,
When cotyledon stimulation is carried out on non-decapitated seedlings, this has no externally apparent effect on plant morphogenesis; however, if the apical bud is finally removed, the cotyledonary buds start to grow with the same g-values as when cotyledon stimulation is carried out simultaneously to seedling decapitation. A ‘symmetry-breaking signal’ (initiated by cotyledon stimulation) thus is stored (‘STO’ function) within the seedlings, without taking effect, during the time lapse between cotyledon stimulation and seedling decapitation. From many experiments, it was inferred that this signal storage was an irreversible and an all-or-nothing process. Now, depending on the conditions of seedling decapitation and on the possible application of a variety of other treatments, the g-values appeared to be sometimes close to zero and sometimes significantly different from zero, although all the seedlings had been subjected to the same asymmetrical pricking treatment. This means that, apart from their STO function, the seedlings possess a recall (RCL) function that can be reversibly switched ‘on’ or ‘off’ and that the stored signal can take effect (differential growth of the cotyledonary buds) only when the RCL function is ‘on’. Typical experimental data taken from the first two Tables in Thellier et al. [6] are grouped in Table 1. By successively switching the recall function, ‘off’, then ‘on’, then ‘off’ again, etc., the observed g-values were close to zero, significantly above zero, close to zero again, etc. This shows that the stored symmetry-breaking signal can be repeatedly solicited, which is strikingly similar to the storage and evocation functions existing in animal and human brain [7,8].
Experimental results relative to bud growth asymmetry, following various sorts of pricking treatments, or combinations of pricking treatments, and plant decapitation [6]
| Ref. No. | Pricking treatment | Plant decapitation at | g | Bud growth asymmetry |
| 1 | non-pricked control | onset of daylight | 0.02 | bud A ≈ bud B |
| 2 | 4A | onset of daylight | 0.35±0.2 | bud B > bud A |
| 3 | 4A | midday | 0.08±0.15 | bud A ≈ bud B |
| 4 | 1A | onset of daylight | 0.01 | bud A ≈ bud B |
| 5 | 4B | onset of daylight | −0.35 | bud A > bud B |
| 6 | 1A(1h)4B | onset of daylight | 0.39 | bud B > bud A |
| 7 | 2A | onset of daylight | 0.06 | bud A ≈ bud B |
| 8 | 2A(1h)2A/2B | onset of daylight | 0.32 | bud B > bud A |
| 9 | 2A(1h)2A/2B(3h)2A/2B | onset of daylight | 0.05 | bud A ≈ bud B |
| 10 | 2A(1h)2A/2B(3h)2A/2B(5h)2A/2B | onset of daylight | 0.34 | bud B > bud A |
3 The differential modelling of the Bidens system
3.1 Statement of the problem
The interpretation given below is based upon the assumption that the growth of any of the three buds of each seedling (the apex and the two cotyledonary buds) tends to further favour its own growth and to inhibit the growth of the other two buds, as a consequence of the synthesis by a growing bud of appropriate ‘growth metabolites’ [9].
3.2 The differential symbolism
In the present differential formulation, we are going to use specific symbols, which may be different from those used in the previous asynchronous, logical formulation [1]. In particular, here we are using the unique symbol A (respectively B) in order to represent, both, the left (respectively right) side of the seedlings (cotyledons and cotyledonary buds) and the size (i.e. also the content in growth metabolites) of the cotyledonary buds. We term ‘mnesic opernet’ (Fig. 1) the system obtained by combining the genetic (operon) and epigenetic parts (metabolic net) of the system ruling the growth of the cotyledonary buds [6,8]. In Fig. 1, the genetic part of the mnesic opernet has been modelled using a Boolean system [1,8]: the variable
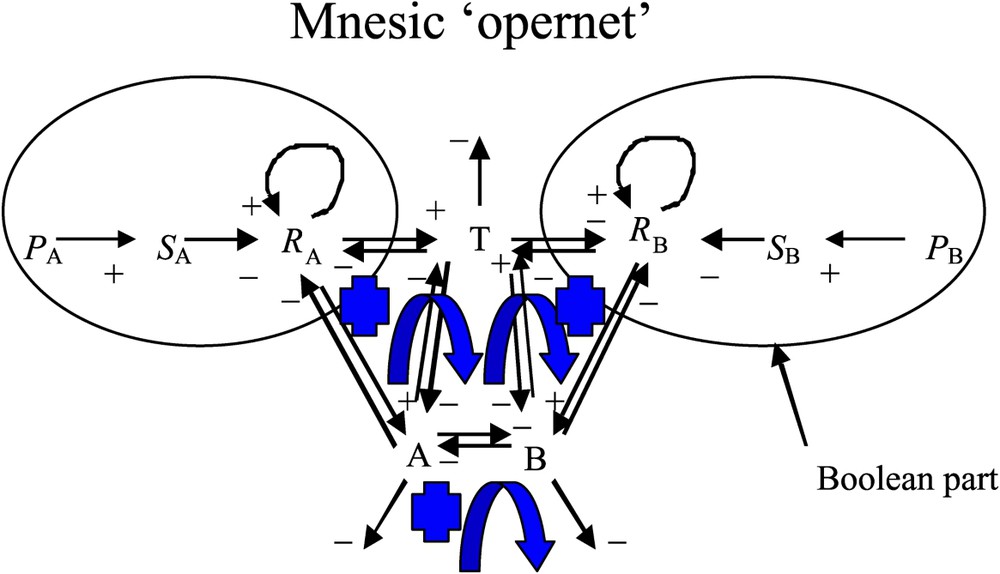
The mnesic ‘opernet’ summarizing the regulation of the plant growth at two levels, the genetic control (Boolean part) and the epigenetic metabolism (differential part). The arrows + (respectively −) correspond to an activation (respectively an inhibition) and the blue arrows correspond to positive regulatory loops. (For interpretation of the references in colour in this figure legend, the reader is referred to the web version of this article.)
Fig. 2 describes the interaction graph denoted G. The connectivity coefficient of this graph (i.e. the number of interaction arrows divided by the number of vertices)
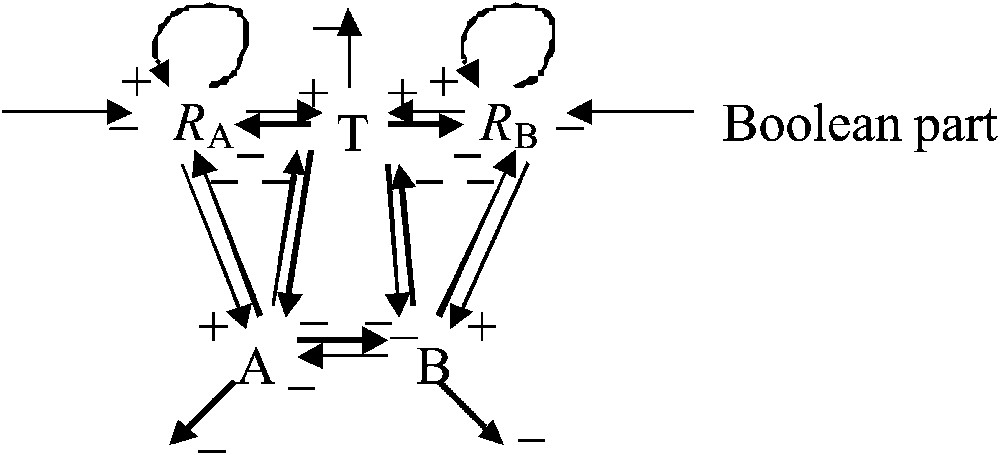
Interaction graph G of the epigenetic part representing the metabolic core of the growth system. The central regulation triangle between T, A and B is an inhibitory 3-switch.
3.3 The system of differential equations
The differential system governing the variables
The first two equations correspond to the dynamics of
- – (i) an auto-catalytic term,
- – (ii) a negative term
- – (iii) a negative term, corresponding to the production of growth metabolites
- – (iv) instantaneous perturbations
Note that, in these first two equations, the coefficients 4/5 and 1/5, and 1 and 1/2, have been chosen arbitrarily, just to express that the effect of one bud upon itself is much larger than its effect upon the other bud. Given the robustness of the system, the results would not be changed significantly by choosing other parameter values (e.g., 5/6 and 1/6, and 1 and 1/3).
The last three equations correspond to the dynamics of the concentrations of growth metabolites in the apex and the cotyledonary buds,
In order to be able to interpret a minima the experimental results given in Table 1, let us assume that F is a ‘dual-phasic’ function possessing two successive inflection points [12] (Fig. 3). Moreover, dual-phasic kinetic curves have also been shown to exist with natural or artificial enzymatic or transport systems [13–15].
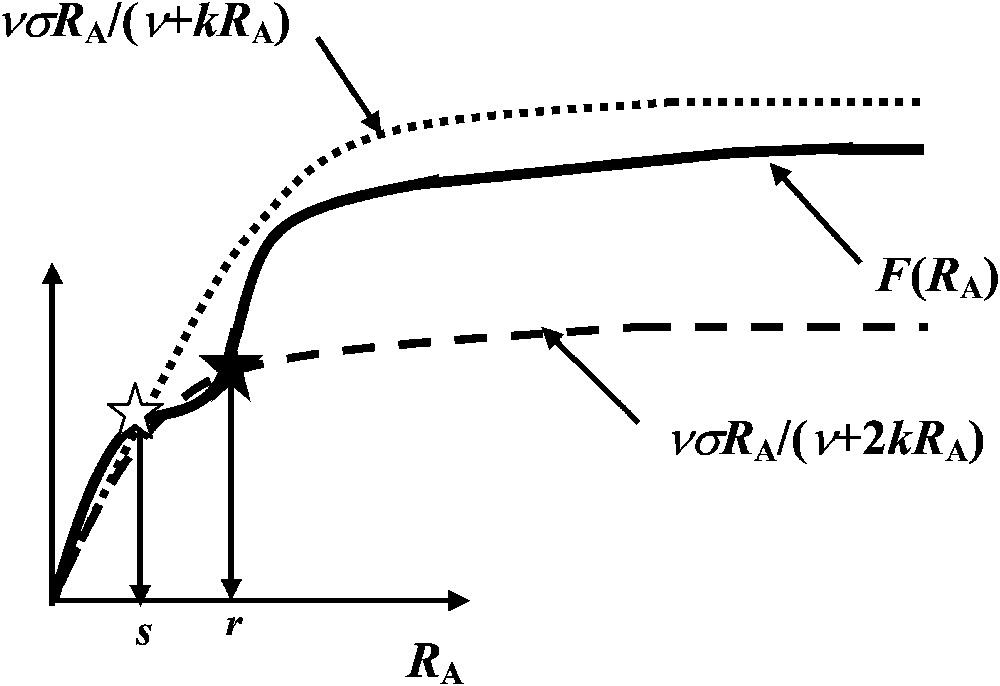
The function
The function
Let us consider the stationary state equation of the differential system as described above. In the absence of any perturbation, it is written:
If the value of the derivative of F,
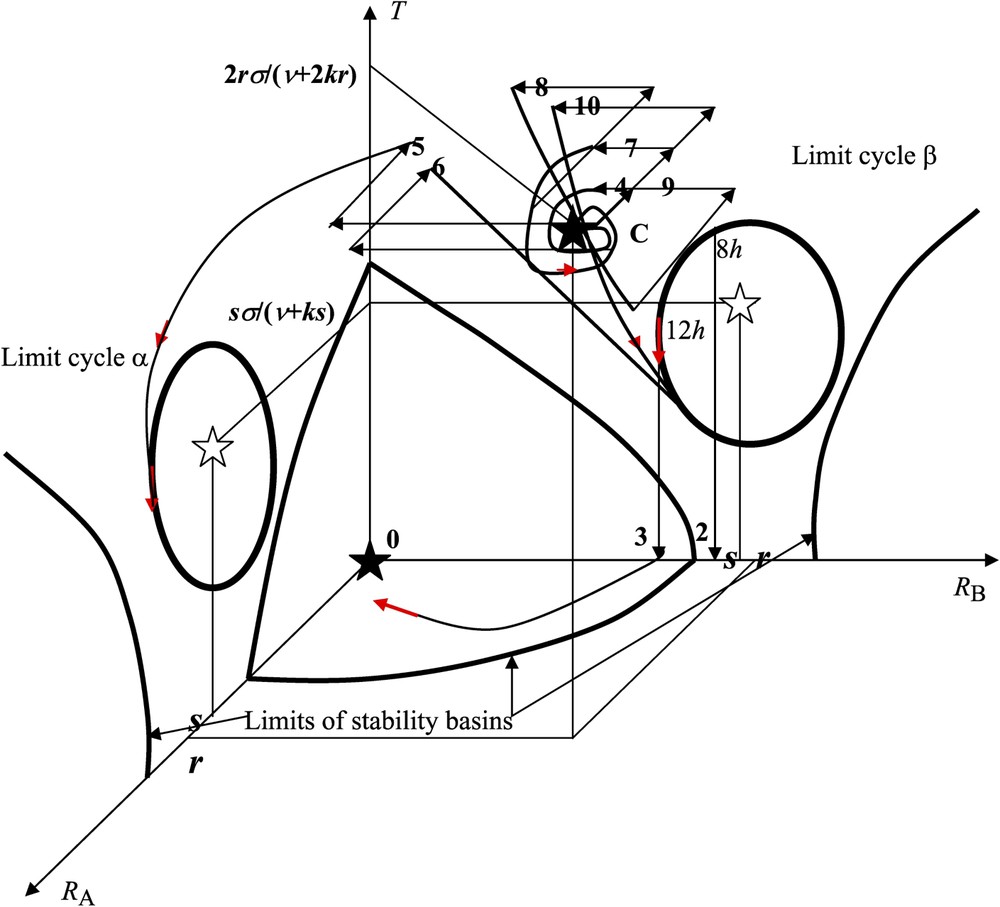
Experimental perturbations in the state space (
In our reasoning below, we assume that the dynamics of the inhibitory 3-switch representing the interactions between T, A and B is already known [10]. Note that, if we consider an inhibitory n-switch between the entities
- – (i) if
then the steady state is - – (ii) if
then the steady state is - – (iii) the third case is identical to the second case, except that the roles of A and B have been inverted, and it is bud B that takes precedence over bud A.
4 Application to the interpretation of the experimental data
When examining the experimental data represented in Table 1, the phenomenology of the growth response of the cotyledonary buds looks rather intricate: (i) the asymmetry of the response (
- –
(1) if the initial conditions (non-pricked controls) are within the basin of stability of the stable steady state C (i.e. close enough to C), then, in the absence of any perturbation, the whole trajectory lies within this basin and tends towards C (where
- –
(2)–(3) with seedlings subjected to a 4-pricks treatment on cotyledon A, there is a shift from the initial conditions close to C (non-pricked controls) to the basin of the limit cycle β. That the final response depends on the time of the day when seedling decapitation was carried out (
- –
(4) if the system is initially close to C and if a 1-prick treatment is applied to cotyledon A (respectively B), then we assume that this perturbation results in an instantaneous decrease w of the intensity of
- –
(5) when a 4-prick treatment is applied to cotyledon B, then the point representing the system leaves the basin of C with a decrease of, for instance, 4w in
- –
(6) when the seedlings are subjected to a 1-prick treatment on cotyledon A followed, 1 h later, by a 4-prick treatment on cotyledon B, then the system goes into the basin of the limit cycle β, with the consequence that
- –
(7) when the seedlings are subjected to a 2-prick treatment on cotyledon A, then the system remains in the basin of C and
- –
(8) when the seedlings are subjected to a 2-prick treatment on cotyledon A followed, 1 h later, by a symmetrical 2-prick treatment on both cotyledons A and B, then the system goes into the basin of the limit cycle β, again with the consequence that
- –
(9) when the seedlings are subjected to a 2-prick treatment on cotyledon A followed, 1 h later, by a symmetrical 2-prick treatment on both cotyledons A and B, again followed, 3 h later, by a symmetrical 2-prick treatment on both cotyledons A and B, then the system returns into the basin of C with the consequence that
- –
(10) when a 2-prick treatment on cotyledon A is followed by three symmetrical 2-pricks treatments on both cotyledons A and B after 1 h, 3 h and 5 h, respectively, the system goes into the basin of C after the second symmetrical pricking treatment (same behaviour as in case (9)), but it leaves the basin of C to go towards the limit cycle β after the third symmetrical treatment. In that case, we have again
It is noteworthy that our above reasoning still holds if C is an attractor (e.g., a limit cycle). Because of its qualitative character, this reasoning is robust and depends only on the general features that have been chosen for function F: in particular, its dual-phasic non-linearity is absolutely requisite to be able to account for all the experimental observations.
5 Conclusions
By using the qualitative description of both the genetic (after a pricking treatment or other stresses) and epigenetic forces exerted on the opernet, all the simulated behaviours were shown to fit qualitatively the observed phenomenology as it is summarized in Table 1. In our present interpretation (i) the storage (STO) function corresponds to the existence of the limit cycles α and β in the state space (
Acknowledgements
We acknowledge the support of the National Network for Technology Research RNTS ‘Technologies for Health’ of the French Ministry of Research.



Vous devez vous connecter pour continuer.
S'authentifier