1 Introduction
The concept of molecular evolutionary clocks is central to modern comparative genomics. From the pioneering work of Zuckerlandl and Pauling [1], it is commonly admitted that amino-acid substitutions between orthologous proteins accumulate with the time separating them from their common ancestor, and differences between aligned sequences are, therefore, used to build phylogenetic trees and to estimate the dates of separation between living species (or groups of species). With the increasing availability of genome sequence data, it became clear, however, that the rate at which protein sequences evolve varies among lineages [2], leading to the idea of relaxed molecular clocks [3–5], and raising the question of appropriate calibration to date major phylogenetic separations. In fungi, for example, this problem was remarkably illustrated by the work of Taylor and Berbee [6]: depending upon the reference used to calibrate the clock, the separation date between Ascomycota and Basidiomycota varies between 400 and 1800 Myr. Similarly, the origin of Saccharomycotina (budding yeasts) is dated, according to calibrations, at 250 Myr ago or 900 Myr ago, i.e. a range of uncertainty linking the Permian-Trias transition to deep precambrian times. Even when calibration is properly set, extrapolation of molecular clocks to large evolutionary scales can only give seemingly precise results if one takes the statistical limits of confidence into proper consideration [7]. Greater precision would require independent calibration points within short evolutionary timescales using increased taxon sampling or continuous fossil records, two conditions not always readily accessible. The identification of Paleopyrenomycites devonicus as the oldest fossil ascomycete dated to 400 Myr [8] played an important role to calibrate the fungal tree of life, but such fossils remain rare in fungi. Also, they are non-existent in yeasts, if one excepts amber inclusions which have received only limited attention so far [9,10] and are, anyway, too recent for setting clocks over long evolutionary times. Increasing taxon sampling is not easier for yeasts, since it is unlikely that living intermediates exist, given their very mode of propagation that creates constant bottlenecks.
Another important problem for dating using molecular data is that substitution rates also vary between the different genes of a same organism. In yeasts, for example, a dispersion of nearly three orders of magnitude exists in the rate of non-synonymous substitutions per site (dN) between the fastest and the slowest evolving proteins [11]. The dispersion is lower in organisms with smaller genetically effective population sizes such as Drosophila and mammals [12], hence the necessity to compare homogeneous groups of organisms sharing similar life style and mode of propagation to properly date evolutionary changes. Yeasts offer such a case with more than three dozens of species fully sequenced [13] and population genomic studies now available for a few of them [14,15]. These fungi proved particularly meaningful to elucidate the mechanisms of unicellular eukaryotic genome evolution by allowing us to easily confront hypotheses based on comparative genome analysis with the results of direct experimental approaches [16]. Most yeasts whose genomes have been fully sequenced so far belong to the Saccharomycotina (also called hemiascomycetes), a large subphylum of Ascomycota that includes Saccharomyces cerevisiae. Despite the conservation of their unicellular mode of life with bud formation, these yeasts cover a very broad evolutionary range, and very important degrees of sequence divergence exist between orthologous genes of distinct yeast species, even those belonging to the same clade [17,18]. Dating major evolutionary changes in yeast genomes, such as the change of codon assignation in the CTG group [19], the triplication of mating cassettes in Saccharomycetaceae [13], or the whole-genome duplication in the ancestry of Saccharomyces sensu stricto and related clades [20], remains, therefore, highly imprecise. Phylogenetic interpolation within the fungal tree of life has been attempted [21–23], but the specific mode of propagation of yeasts with rapid clonal expansions raises the question of the validity of the comparisons with multicellular organisms having obligate sexual reproduction and possibly distinct evolutionary rates. A specific calibration of the molecular clock of yeasts is, therefore, desirable. But, besides the genomic changes themselves, no independent piece of information such as fossils records, is available to cover their very large evolutionary range.
In this work, we have addressed this question from two different viewpoints. Starting from the mutation rates that have been precisely measured by experiments in S. cerevisiae [24–26], we have computed the minimal number of successive generations separating distinct lineages in this yeast, and extrapolated similar calculations to the separation of species within clades. This clock is appropriate for short evolutionary timescales but gradually loses precision with increasing evolutionary range. We have, therefore, looked for a second clock more appropriate to larger evolutionary timescales by examining the relationship between sequence divergence and degrees of chromosomal rearrangements. This relationship has been quantitatively established over the entire evolutionary range of Saccharomycotina, and compared to a similar relationship established for insects.
2 Calibrating sequence divergence in terms of the minimal number of successive generations
The spontaneous mutation rate has recently been determined with precision in S. cerevisiae by three independent approaches. A per-base-pair mutation rate (μ) was established for two genes using the classical Luria-Delbrück fluctuation assays [24]. Figures of 3.80 × 10−10 and 6.44 × 10−10 mutations per nucleotide per generation were obtained for the URA3 and the CAN1 genes, respectively, indicating that, even if not entirely uniform across the genome, the mutation rate shows a limited variation range (ca. two times). An independent estimation of the per-base-pair mutation rate (μ) along the entire genome was obtained using novel sequencing technology in mutation-accumulation experiments [25]. Partial resequencing (ca. 40% genome coverage) of four independent cultures of S. cerevisiae grown in rich medium for a total of ca. 4800 generations after 200 successive single-cell bottlenecks gave a complete description of the spectrum and frequencies of spontaneous mutations. Although some variations were again observed between the different parts of the S. cerevisiae genome, results converge to an average figure of 3.3 × 10−10 mutations per nucleotide per generation, ca. 90% of which being nucleotide substitutions and 10% indels. This figure is in excellent agreement with the Luria-Delbrück assays on reporter-construct studies cited above. Finally, figures of 3.8 × 10−10 to 2.0 × 10−10 base substitutions per nucleotide per generation were reported for three strains of S. cerevisiae using sequencing of cell lines grown with or without meiotic cycles [26]. We, therefore, admitted for this work that the spontaneous rate of nucleotide substitution in S. cerevisiae under laboratory conditions is 3 × 10−10 mutations per site per generation. Assuming that such mutations are independent and neutral, one can then simply calculate the theoretical frequency of mutants (m) after n successive generations from the initial genome using the following equation:
| (1) |
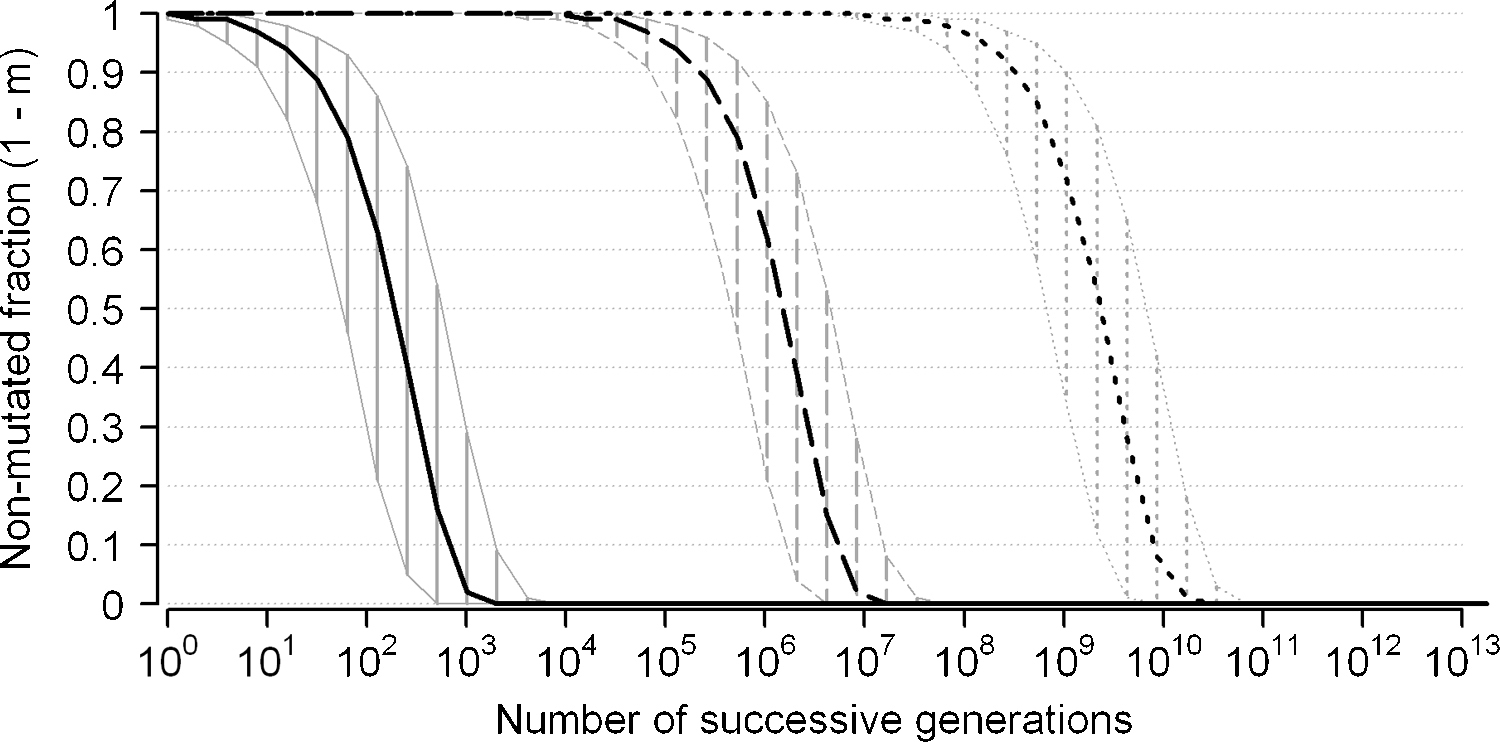
Theoretical mutant frequency as a function of successive generations. Theoretical curves representing the predicted fraction of non-mutated genetic elements (nucleotides, genes or genomes) in yeasts (ordinate) after increasing numbers of successive cellular generations (abscissa, log scale) under the hypothesis of a constant mutation rate and independent and neutral mutations (see text). Dotted curve refers to the fraction of non-mutated nucleotides for a mutation rate μ = 3 × 10−10 mutation per nucleotide per generation. Hatched area gives expected limits for mutational rates of 1 × 10−10 (right limit) and 10 × 10−10 (left limit), respectively. Similar curves and hatched areas are drawn for the same mutational rates for genes (assuming an average gene size of 1500 nucleotides, dashed curve and area) and for complete yeast genomes (assuming a genome size of 12 millions nucleotides, plain curve and area).
Such short times on the geological scale are to be compared with the estimated age of Saccharomycotina yeasts (above). This perspective predicts that presently living yeast species, even those usually regarded as “closely related”, can only be distantly related from one another in terms of molecular evolution. Of course, results of Fig. 1 only represent the maximum possible frequency of mutants after a given number of successive generations (or the minimum time necessary to reach a given level of sequence divergence between two yeasts derived from a common ancestor). In reality, mutations are not all neutral (in particular in compact genomes such as yeasts), and those affecting fitness will have a decreased or increased probability of becoming fixed in populations. For yeasts, however, this bias against mutation fixation is probably limited because, although not quantitatively established for wild populations, bottlenecks are likely to play a major role, hence increasing genetic drift at the expense of selection [25].
Since several S. cerevisiae strains have now been sequenced [14,15,28–30], we found interesting to calculate the theoretical number of generations separating each of these strains to the reference laboratory strain S288c. Table 1 gives such figures for several frequently used S. cerevisiae laboratory strains, as well as for a few isolates of S. paradoxus. As can be seen, the least diverging strain of S. cerevisiae, A364A, appears to have undergone at least one million generations from its common ancestor with S288c, i.e. more than the total number of generations since the human-chimpanzee separation. The most divergent S. cerevisiae strain, SK1, has undergone 6.8–11 million successive generations (depending upon dataset, resequencing and array hybridization give slightly different results) from its common ancestor with S288c. Similarly, the closest strain of S. paradoxus has undergone ca. one million generations since its common ancestor with the reference strain, but divergence of other strains appear much more ancient (up to 63.3 million generations). Using recent population genomics studies [14,15] and similar calculations, we have reanalyzed the population structures of S. cerevisiae and S. paradoxus (Fig. 2). A striking difference appears between the two species using the available references. In S. cerevisiae, less than 10% of strains are separated from the reference by a relatively small number of generations (1–3 million(s)), whereas the majority of strains have undergone 5–10 million generations after separation (or 4 to 7, depending on datasets). Whether the latter forms a homogeneous population or not can only be determined by using different references. The population of S. paradoxus (only available from [14]) is made of a homogeneous majority of strains very closely related to the reference (less than one million generations) and two subpopulations having separated much longer before (ca. 20 and 65 million generations from the last common ancestor, respectively). This heterogeneity coincides with the idea that S. paradoxus strains remain limited within geographic boundaries for a long time while the homogeneity of the S. cerevisiae population is related to the frequent formation of mosaics among strains [14].
Sequence polymorphism between strains of S. cerevisiae and S. paradoxus.
| Species | Reference strain | Compared strain | Number of SNPs | SNP frequency (%) | n | Ref. |
| S. cerevisiae | S288C | A364A | 6,538 | 0.060 | 1,000,300 | [15] |
| S288C | W303 | 11,976 | 0.110 | 1,834,342 | [15] | |
| S288C | CENPK | 16,406 | 0.150 | 2,501,877 | [15] | |
| S288C | FL100 | 22,446 | 0.210 | 3,503,680 | [15] | |
| S288C | RM11 | 29,508 | 0.270 | 4,506,086 | [15] | |
| S288C | SK1 | 44,148 | 0.410 | 6,847,380 | [15] | |
| S288C | W303 | - | 0.072 | 1,200,432 | [14] | |
| S288C | RM11-1a | - | 0.364 | 6,077,734 | [14] | |
| S288C | SK1 | - | 0.659 | 11,019,682 | [14] | |
| S. paradoxus | CBS432 | CBS5829 | - | 0.068 | 1,133,719 | [14] |
| CBS432 | N-44 | - | 1.209 | 20,272,796 | [14] | |
| CBS432 | DBVPG6304 | - | 3.736 | 63,459,609 | [14] | |
| CBS432 | YPS138 | - | 3.727 | 63,303,795 | [14] |

Dating populations of Saccharomyces from sequence polymorphism. The figure represents the cumulative frequency distributions of strains from S. cerevisiae (black lines) and S. paradoxus (grey line) as a function of the number of successive generations (abscissa) they have each undergone from their common ancestor with the cognate reference strain (S288c for S. cerevisiae strains, and CBS432 for S. paradoxus strains). The number of successive generations (abscissa) is calculated from the SNP rate of each strain relative to the reference, using the equation:
N1/2 = ½ × log (1 − m)/log (1 − μ)
where μ is the mutation rate per nucleotide per generation (here 3 × 10−10) and m is the observed frequency of SNP. The ½ factor compared to Eq. (1) is due to the assumption of equivalent mutational rates in both lineages (reference and studied strain) from their common ancestor. SNP data are taken from the I40 rates in [14] (triangles) for the 37 strains of S. cerevisiae and the 35 strains of S. paradoxus (resequencing of references ignored) and from [15] (dots) for 62 strains of S. cerevisiae (resequencing of reference ignored).
We have tried to extend our calculations to larger evolutionary distances, such as those observed between species of a same clade, even if precision should diminish. An interesting case of a hybrid yeast genome has recently been discovered and fully sequenced (Leh-Louis et al., in preparation). This yeast was formed by hybridization between two parents differing from each other by ca. 12% nucleotide substitutions on average, a figure which, according to our calculations, corresponds to ca. 210 million generations from their common ancestor, i.e. an order of magnitude probably comparable to the separation of fishes from mammals. Other interesting cases are, in principle, offered by the existence of pseudogenes since they are expected to diverge in sequence at the neutral rate [31]. However, the original sequences of the ancestral functional gene are unfortunately very rarely available. Pseudogenes corresponding to duplicated ohnologs in the genome of S. cerevisiae offer a means to alleviate this difficulty. For example, a pseudogene corresponding to an ancient copy of the Lys-tRNA synthetase gene lies between YBR060c and YBR061c after duplication of the functional KRS1 ancestral gene [32]. Given the fact that the two functional copies conserved in S. uvarum (660.15 and 678.163) are 98.8% identical in sequence (consistent with a strong functional constraint on this essential enzyme) and are 89% identical in sequence to the functional gene of S. cerevisiae (KRS1, YDR037w), it is possible to conclude that the S. cerevisiae pseudogene differs from its ancestral sequence by ca. 30–40% of nucleotide substitutions which, according to our calculation corresponds to a minimum of 1.1–1.7 billion successive generations. This estimate is, of course, not precise but it gives us an order of magnitude for the minimal age of the whole-genome duplication at the origin of Saccharomyces sensu stricto and related clades. Extension of this method to larger phylogenetic distances becomes increasingly problematic, however. First because nucleotide sequence alignments become more uncertain as sequence divergence increases, and second because of the over-simplification of the reality inherent to the hypothesis of neutrality and clonal expansion. Given the large evolutionary span covered by the sequenced yeast genomes, another method is, therefore, needed.
3 Chromosomal rearrangements as an estimation of species divergence times
Our second method to estimate the evolutionary divergence between yeasts is based on the conservation of synteny. In the group of S. sensu stricto and related clades, the genome duplication followed by extensive gene loss, has so profoundly affected the gene order map by creating a 1:2 relationship with the non-duplicated yeasts of the same family [33,34], that synteny conservation cannot be used as a simple evolutionary clock. The subsequent release of complete genome sequences of numerous other yeasts now allows us to examine this problem across a very broad evolutionary range. In a previous investigation, five protoploid species of Saccharomycetaceae have been compared, giving us a first description of the number and size of conserved syntenic blocks in yeasts [18]. We have now extended this analysis to another group of yeasts, collectively designated as “CTG”, and separated from the Saccharomycetaceae family at an early branching point within the Saccharomycotina yeasts ([13], see also Santos et al., this issue). Many sequenced species of this group are only known as diploids and were, therefore, disregarded to eliminate possible artifacts on synteny conservation (available sequences correspond to the haploid equivalent). We have, therefore, only studied the five fully sequenced haploid species from this group: Debaryomyces hansenii [35], Pichia (Scheffersomyces) stipitis [36], Candida (Meyerozyma) guilliermondi, Clavispora lusitaniae and Lodderomyces elongisporus [17]. As an outgroup, we have used the genome of Yarrowia lipolytica [35] which is neither a Saccharomycetaceae nor a member of the CTG group. All pairwise comparisons were performed between the 11 yeast species, as described in Fig. 3, and conserved syntenic blocks were defined using the same parameters as [18], namely a minimum of five conserved orthologs and a maximum of 10 intervening genes. As published previously, the five protoploid Saccharomycetaceae share 200 to 300 short syntenic blocks (average size of 20 genes) in all pairwise comparisons, except for the Kluyveromyces (Lachancea) thermotolerans/Saccharomyces (Lachancea) kluyveri pair. These two species belong to the same clade (Lachancea) within the Saccharomycetaceae family. Similar number and size distributions of conserved syntenic blocks are observed among the pairwise comparisons between the five CTG species. This time, the D. hansenii/C. guillermondi pair forms the exception, indicating that these two species are more closely related to each other than are the other three (despite the fact that they belong to two distinct clades, Debaryomyces and Meyerozyma, respectively). If one now compares species of the Saccharomycetaceae family to those of the CTG group, the number of conserved syntenic blocks and their average size drop (100–200 blocks of average size 14 genes).
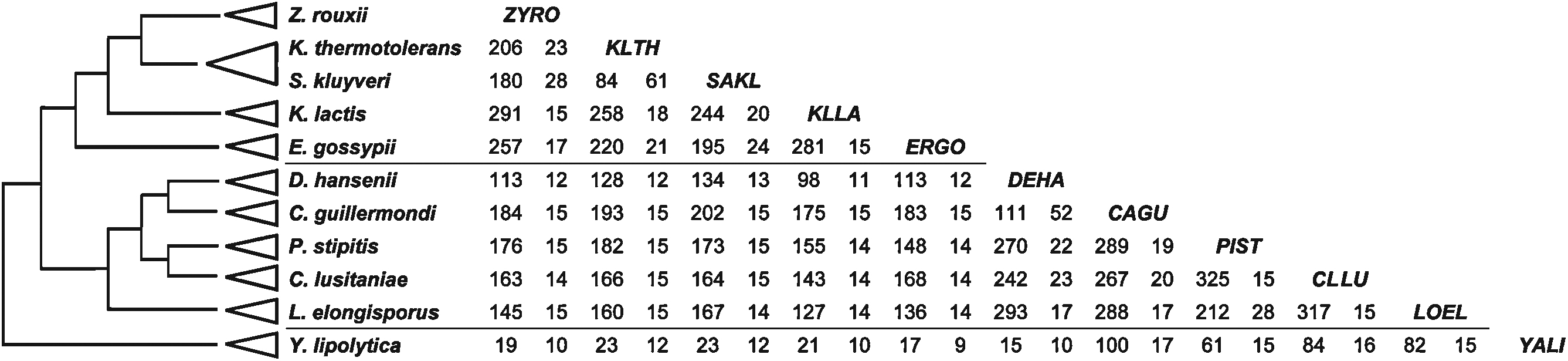
Number and size of conserved syntenic blocks between Saccharomycotina yeasts. On the left, the commonly accepted topology is shown [57] (top: protoploid Saccharomycetaceae, middle: CTG yeasts, bottom: Y. lipolytica). For each pairwise comparison, the table indicates the total number of conserved syntenic blocks (left) and their average size (in coding genes, right). Conserved syntenic blocks are defined by sets of at least five adjacent orthologous genes (defining anchor points), conserved in order between two species, and separated by a maximum of 10 intervening genes [18]. Orthologous genes were previously extracted by the IONS method using sequence and neighborhood similarity (Seret and Baret, in preparation) for Zygosaccharomyces rouxii, K. thermotolerans, S. kluyveri, Kluyveromyces lactis, Eremothecium (Ashbya) gossypii, D. hansenii and Y. lipolytica. Orthology relationships between the protoploid and CTG species, and between the CTG group and Y. lipolytica, was deduced from Reciprocal Best Hits (RBH), using blastp program [58].
Z. rouxii: ZYRO; K. thermotolerans: KLTH; S. kluyveri: SAKL; K. lactis: KLLA; E. gossypii: ERGO; D. hansenii: DEHA; C. guillermondi: CAGU; P. stipitis: PIST; C. lusitaniae: CLLU; L. elongisporus: LOEL; Y. lipolytica: YALI.
To quantitatively estimate the conservation of synteny between any two yeasts (in order to further support comparisons across the entire group of species studied), we calculated for all pairs of compared species the number of orthologous genes present in conserved syntenic blocks and reported it to the total number of orthologous genes between the two species. We found 3600–4300 orthologous genes in conserved syntenic blocks for comparisons within the Saccharomycetaceae (corresponding to 85% to 95% of all orthologs, Fig. 4A). Similarly, 3100–4300 orthologous genes are in conserved syntenic blocks for comparisons within the CTG group (68% to 92%). Now, comparisons between the protoploid Saccharomycetaceae and the CTG yeasts reveals only 750–1400 orthologous genes in conserved syntenic blocks (15% to 35%). When Y. lipolytica is compared to any member of the previous two groups, even lower conservation of synteny is observed.
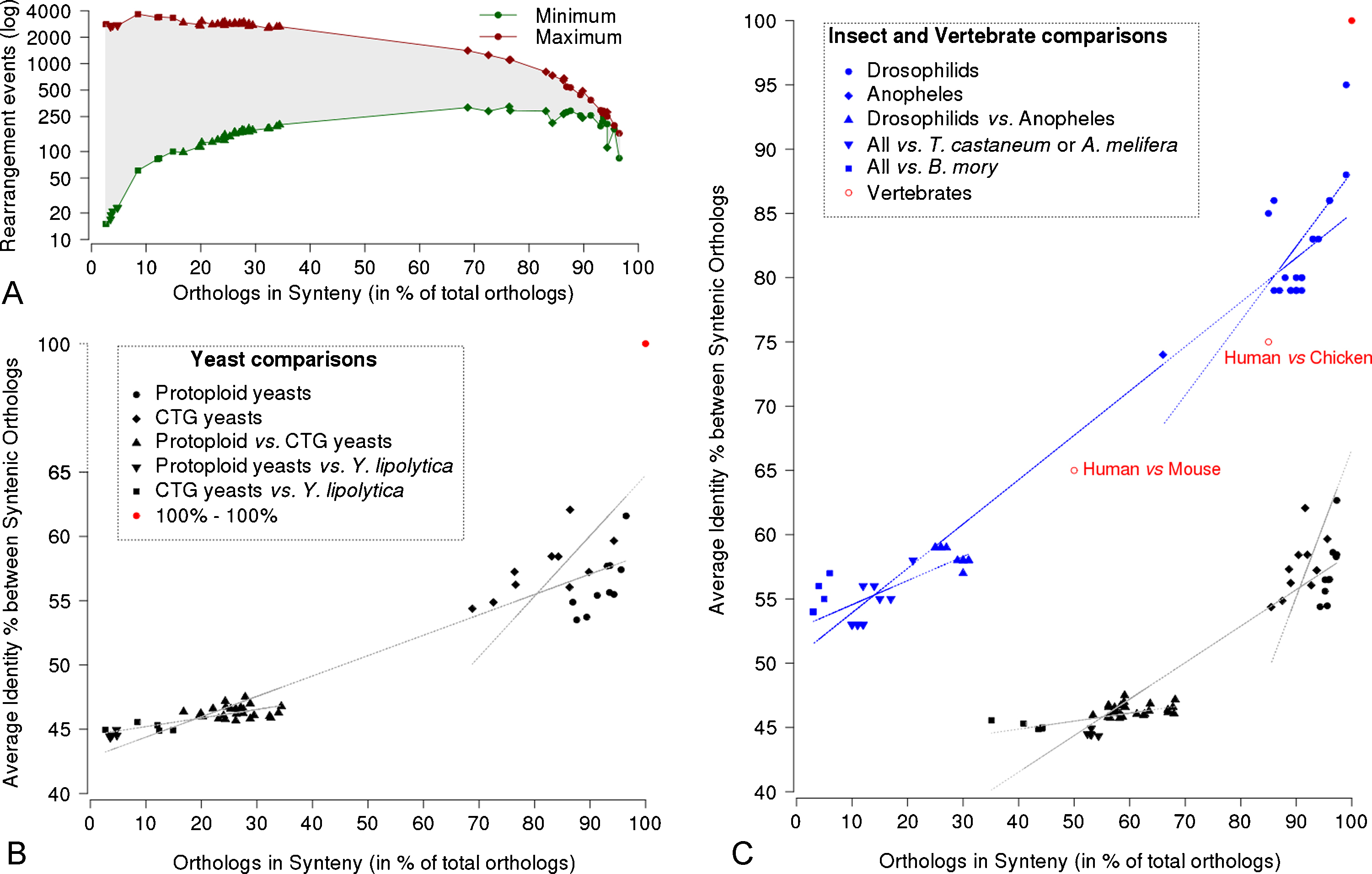
Conservation of synteny and its relationship with sequence divergence. A. Estimation of the minimal (green) and maximal (red) numbers of genome rearrangements (ordinate) between Saccharomycotina yeasts. Abscissa represents the ratio of the number of orthologs in conserved synteny blocks over the total number of identified orthologs in the pair of yeast species compared. Symbols correspond to those described in (B). B. Relationship between conserved synteny and sequence divergence among Saccharomycotina yeasts. Syntenic blocks considered are defined in Fig. 3. Abscissa represents the ratio of the number of orthologs in conserved synteny blocks over the total number of identified orthologs in the pair of yeast species compared. Ordinate represents the average amino-acid identity between all orthologous proteins for each pair of yeast species considered. The red dot corresponds to comparison of any species with itself. Linear correlations have been fitted for the whole dataset, and independently for the two subsets corresponding to less than 40% or more than 60% of orthologs in synteny, respectively. C. Comparison of yeasts to insects. Abscissa and ordinate, same as (B). Insect and vertebrate data have been extracted from [45]. Yeast data have been recomputed using the same parameters as for insect data. Conserved syntenic blocks were reconstructed from aligned orthologs defined from RBH (with more than 30 amino-acid long alignments to avoid domain detection), assuming a minimum of two anchor points and a maximum of one intervening gene (compare to (B)). Linear correlations have been fitted for each of the two datasets, and for corresponding subsets as in (B). Abscissa limits are less than 35% and more than 60% for insects, and less than 70% and more than 80% for yeasts.
Ancestral genome reconstruction is generally done by trying to minimize the postulated rearrangements necessary to account for extant genomes [37–41]. Given the large evolutionary distances between studied yeasts, the estimation of the number of actual rearrangements from the observed syntenic blocks is not trivial. We have, therefore, opted for minimal and maximal estimates using the following principles: the minimal number of rearrangements should be at least equal to the number of identified syntenic blocks, and the maximum number of rearrangements is equal to the total number of orthologs minus those present in syntenic blocks (Fig. 4A). For example, between K. thermotolerans and S. kluyveri, the minimal number of rearrangements is 84, and the maximal one is 161 (4609 identified orthologs – 4448 orthologs in syntenic blocks). Interestingly, the two numbers are very close for this comparison, as is the case for D. hansenii and C. guillermondi (minimum 111 and maximum 281), but diverge for longer evolutionary distances. For species presenting more than 65% of orthologs in synteny, the number of rearrangements ranges from 250 to 1500 (Fig. 4A). For species presenting less than 35% of orthologs in synteny, the difference between minimum and maximum values is too large to allow reliable reconstruction of ancestral genomes. In addition to the broadening of observable figures, the number of rearrangements becomes more and more difficult to evaluate with increasing evolutionary distance due to the superposition of events. Following the original work of [42], breakpoint reuse has been proposed to have a great impact on the dynamics of genomes. Micro-inversions involving one or a few genes, and consequently forming short conserved blocks, have been shown to deeply affect the estimation of breakpoint reuse in human and mouse evolution [43]. More recently, the analysis of 12 closely related Drosophila species has shown that breakpoint reuse is stronger in internal branches of the phylogenetic tree, while uniquely used breakpoints are specific to more derived lineages [44]. By analyzing the distribution of synteny block sizes in protoploid Saccharomycetaceae, it has been shown that breaks are not random in genomes [18], as previously reported for insects [45]. Although different in nature, breakpoint reuse is not different from the presence of hot-spots and cold-spots in meiotic recombination (see [46] for S. cerevisiae, for example).
At this point, it is interesting to analyze the relationships between the conservation of synteny and the divergence of sequences. Fig. 4B shows the results. We observe two groups of points, corresponding respectively to intra-family comparisons (protoploid, on the one hand, and CTG species, on the other) and to interfamily comparisons, including Y. lipolytica. By fitting two independent regression lines, we show that the relationship between the percentage of orthologs in syntenic blocks and the sequence divergence is described by two linear correlations. The greatest slope for the first group of points (short evolutionary distances) indicates rapid sequence divergence for limited loss of synteny. The flattened slope for the second group of points suggests saturation of sequence divergence due to functional constraints for very long evolutionary distances.
The data previously reported by [45] for eight members of the Drosophila genus and four other insects, show an astonishing similarity with our yeast results. Because they used slightly different parameters to calculate conserved syntenic blocks, we have recalculated the yeast data using their parameters (minimum of two conserved orthologous genes separated by a maximum of one intervening gene) to allow direct comparisons (Fig. 4C). As can be seen by comparing Fig. 4B to Fig. 4C, application of the insect parameters to the yeast dataset results in a translation to higher synteny values, without altering the overall shape of the curves. Remarquably, we observe a similar split into two groups of points for both insects and yeasts, despite the fact that sequences are globally less diverged in insects than in yeasts. For a similar interval of sequence identity (ca. 50–60%), the insect genomes are clearly much more rearranged than the yeast genomes. Alternatively, for similarly high conservation of synteny (above 80%), yeast sequences are much more divergent than insect sequences. Several hypotheses can account for the accelerated chromosomal reshuffling in insects compared to yeasts, including the very distinct architectures of their genomes, and their sexual reproduction. Insect genomes vary in size from 152 to 231 Mb [47], as compared to 8.7 to 15.5 Mb for most yeast genomes, except Y. lipolytica genome of 20.5 Mb [13]. They contain numerous and diverse transposable elements (for example 1572 partial or full-size elements in D. melanogaster [48]), as compared to only few in yeast genomes (zero in some protoploid genomes [18] to a dozen in most S. cerevisiae strains [14]). Insect genomes have larger intergenic regions than yeast genomes (ca. 4800 bp on average for insects [49] compared to ca. 490 bp for yeasts [50]) and larger and more numerous spliceosomal introns [49] (Neuvéglise et al., this volume). The accelerated chromosomal reshuffling in insects compared to yeasts is further magnified by the fact that the mutational rate of Drosophila melanogaster (3.5 × 10−9 mutations per nucleotide per generation, a value experimentally measured by sequencing three strains [51]), is roughly ten times greater than that of S. cerevisiae. Consequently, similar sequence divergence values correspond to a smaller number of generations in insects than in yeasts.
4 Discussion
In the absence of a properly set evolutionary clock for yeasts, based on reliable external data, and in view of the difficulty to apply clocks that would simultaneously be valid over short and very long evolutionary ranges, we have developed here two methods to relate sequence divergence, number of generations and genome rearrangements. Calculations based on the known mutational rate of S. cerevisiae illustrate that the minimum number of successive generations separating different strains of a same species is necessarily large, and rapidly becomes very large when two related species of a same clade are compared. Given generation times in nature, the mutational clock for yeast genomes is, therefore, necessarily very rapid. Our theoretical assumption about neutrality of mutations and exclusively clonal expansion (used to simplify the calculations) does not alter this conclusion. If anything, the number of generations needed to obtain the sequence divergence observed between yeast genomes can only be larger than the one calculated here on the neutrality hypothesis. Indeed, disadvantageous mutations will have a lower probability to be fixed in populations and advantageous ones cannot represent the majority. A systematic analysis of the fitness of mutations in yeasts would certainly be very informative. However, the repetitive bottlenecks predicted to occur in natural yeast populations (to keep sustainable cell numbers), indeed create a trend to neutrality, the genetic drift becoming prominent over selection. The existence of sexual reproduction in natural yeast populations does not change our conclusions, since similar base substitution rates were found in S. cerevisiae between purely vegetative lines and lines undergoing one meiotic cycle every 20 vegetative divisions [26].
The clock based on synteny conservation also presents some limits with increasing evolutionary distances. First, with current methods to assign gene orthology relationships based on sequence similarity, the number of recognizable orthologs diminishes when sequences diverge too much. Second, the observable number of conserved syntenic blocks tends to underestimate the actual number of chromosomal rearrangements due to superposition of events and accumulation of micro-rearrangements embedding a few genes. These limitations are also discussed by Drillon and Fischer, this volume for yeast and vertebrate comparisons. The similarity of the relationship between synteny and sequence divergence among yeasts and insects, however, shows that a synteny-based clock is very appropriate for intra-family taxa and becomes less appropriate for inter-family comparisons. At this larger evolutionary scale, a better taxon sampling remains central to the correct estimation of evolutionary times.
Whatever the progresses in setting appropriate clocks, the correct construction of phylogenetic trees will have to better incorporate non-vertical exchanges. In yeasts, the formation of interspecific hybrids appears to be frequent [52,53], even though the contribution of this phenomenon to yeast evolution remains to be quantified. Similarly, acquisition of horizontally transferred genes [54] and introgression of large chromosomal segments from distantly related species [30] contribute to alter the clocks. In principle, building gene-specific and lineage-specific clocks would be the solution [55] but it results in complex models whose biological relevance remains to be established. Finally, to complete the evolutionary clocks of eukaryotes, one should note the accelerated mutation rate of mitochondrial DNA (e.g. 12.9 × 10−9 mutations per nucleotide per generation as experimentally determined for S. cerevisiae [25]), and the fact that pieces of mitochondrial DNA (NUMTs) enter chromosomes of yeasts [56] and other species, reminding us of the intensity of novel sequence acquisition within nuclear genomes of eukaryotes.
Disclosure of interest
The authors declare that they have no conflicts of interest concerning this article.
Acknowledgements
We thank our colleagues from the Génolevures Consortium (GDR2354 CNRS) for helpful discussions, and particularly Philippe Baret, Laurence Despons, Véronique Leh-Louis and Marie-Line Seret for communicating unpublished results. T.R. is the recipient of a fellowship from the French Ministère de l’Enseignement Supérieur et de la Recherche. B.D. is a member of Institut Universitaire de France.


