1 Introduction
L’étude des processus de croissance du fœtus appliquée à la détermination de l’âge concerne plusieurs disciplines, dont l’obstétrique, la médecine légale et l’anthropologie biologique 〚1–8〛.
Dans la littérature, de nombreux paramètres ont été étudiés pour l’estimation de l’âge fœtal sur la base de méthodes anthropométriques, radiographiques et échographiques 〚6, 8–16〛. Ces dernières ont l’avantage d’être applicables in vivo et de constituer de très larges séries 〚15–16〛. Cependant, les mesures échographiques sont dépendantes de l’observateur, et très peu d’études ont recherché des corrélations écho-anatomiques. L’originalité de notre approche est de proposer une nouvelle équation, établie sur un large échantillon de fœtus normaux, d’âge connu, utilisant la mesure sur radiographie de la portion ossifiée du fémur et validée biométriquement par la mise en évidence d’une parfaite corrélation anatomo-radiologique 〚17, 18〛 et statistiquement par l’utilisation d’une méthodologie séparant échantillon d’apprentissage et de validation 〚19〛.
2 Population d’étude
La création des centres de diagnostic prénatal (décret n° 97-578 du 28 mai 1997) a permis de systématiser les examens fœtaux post mortem. Ces examens sont obligatoirement effectués après une interruption médicale de grossesse, mais peuvent être pratiqués dans le cadre de fausses couches et de morts in utero.
De 1998 à 2001, nous avons examiné plus de 2 000 fœtus issus de fausses couches et de morts in utero. Dans cette population, nous avons sélectionné 782 fœtus dont l’âge est réparti de 12 à 41 semaines d’aménorrhée (Fig. 1). Ces fœtus ont été considérés comme normaux après vérification anatomique complète, caryotype et radiographie du squelette entier de face et de profil.

Répartition des effectifs dans notre échantillon total en fonction de l'âge, exprimé en semaines d'aménorrhée (SA).
3 Méthodes
Nous avons exclu de l’étude les fœtus dont les mères ont présenté pendant la grossesse une hypertension artérielle (potentiellement responsable d’hypotrophie fœtale ou de retard de croissance) ou un diabète (pouvant générer une macrosomie) 〚20〛. De plus, nous avons exclu les grossesses gémellaires, causes fréquentes d’hypotrophie fœtale 〚21〛 et les fœtus macérés, dont on n’a pu préciser le moment exact du décès.
L’âge fœtal de référence a été déterminé en fonction de la date des dernières règles (règle de Naegele) corrigée le cas échéant 〚10〛 par la datation de la première échographie 〚22〛. Nous avons exclu les fœtus pour lesquels il existait une discordance entre âge estimé selon la règle de Naegele et l’âge obtenu lors de la première échographie.
La population fœtale a été divisée en deux échantillons : un échantillon d’apprentissage (A), sur lequel nous avons établi notre équation, et un échantillon de validation (V), permettant d’évaluer cette estimation sur un échantillon n’ayant pas servi à l’établir. L’estimation de l’âge est ainsi testée sur l’échantillon de validation, qui a été constitué après tirage au sort de 30 fœtus, et comparée aux formules classiquement utilisées en anthropologie 〚5, 23, 24〛. Cette méthode constitue un moyen de validation statistique de la formule de régression établie, et non une méthode de validation inter-populationnelle, les deux échantillons étant issus de la même population d’origine.
3.1 Protocole de prise des mesure de la longueur fémorale
La mesure a porté sur la longueur de la portion ossifiée de la matrice cartilagineuse de cet os en cours de formation. Elle est effectuée avec une règle graduée au demi-millimètre. L’intégrité fœtale a été préservée en utilisant un protocole radiographique de mesure 〚17, 18〛.
La mesure radiologique de ces diaphyses nécessite des précautions : d’une part, il a été nécessaire de s’assurer que l’os était parfaitement parallèle au film, pour éviter toute erreur de parallaxe ; d’autre part, il a été nécessaire que l’os soit posé contre la plaque radiographique pour éviter le phénomène dit de « cône de projection ». Nous avons ainsi effectué la mesure sur le cliché de profil pour être certain que l’un des membres repose correctement sur la plaque. Malgré ce choix, la reconnaissance d’un profil vrai des membres n’a pas été toujours facile, nous amenant ainsi à définir et à valider un critère qualitatif autorisant la prise de la mesure 〚17〛. Ce critère est l’observation d’une plaque conjugale nette (définie par la limite entre la métaphyse et le cartilage de conjugaison) 〚17〛. Nous avons également montré qu’il n’existait pas de différence significative entre les fémurs droit et gauche, ce qui nous a permis de ne pas tenir compte de la latéralisation 〚17〛. Une corrélation radio-anatomique, validée sur 60 paires de fémurs disséqués, nous a permis d’établir un facteur de correction assurant l’exacte correspondance de la mesure avec la pièce osseuse réelle 〚18〛.
3.2 Comparaison avec les équations, courbe et table de référence
Nous avons comparé notre formule avec les formules classiquement utilisées par les anthropologues et les médecins légistes 〚5, 23, 24〛.
La formule de régression linéaire uniparamétrée et les comparaisons des différences entre âge prédit et âge réel ont été établies avec le logiciel SPSS 10®.
4 Résultats
L’utilisation du critère qualitatif 〚17〛 a permis d’effectuer la mesure 374 fois. L’échantillon total a alors été réparti en 344 cas pour l’échantillon A et en 30 cas pour l’échantillon V. les valeurs moyennes des mesures effectuées et leur variation en fonction de l’âge sont représentées sur la Fig. 2.
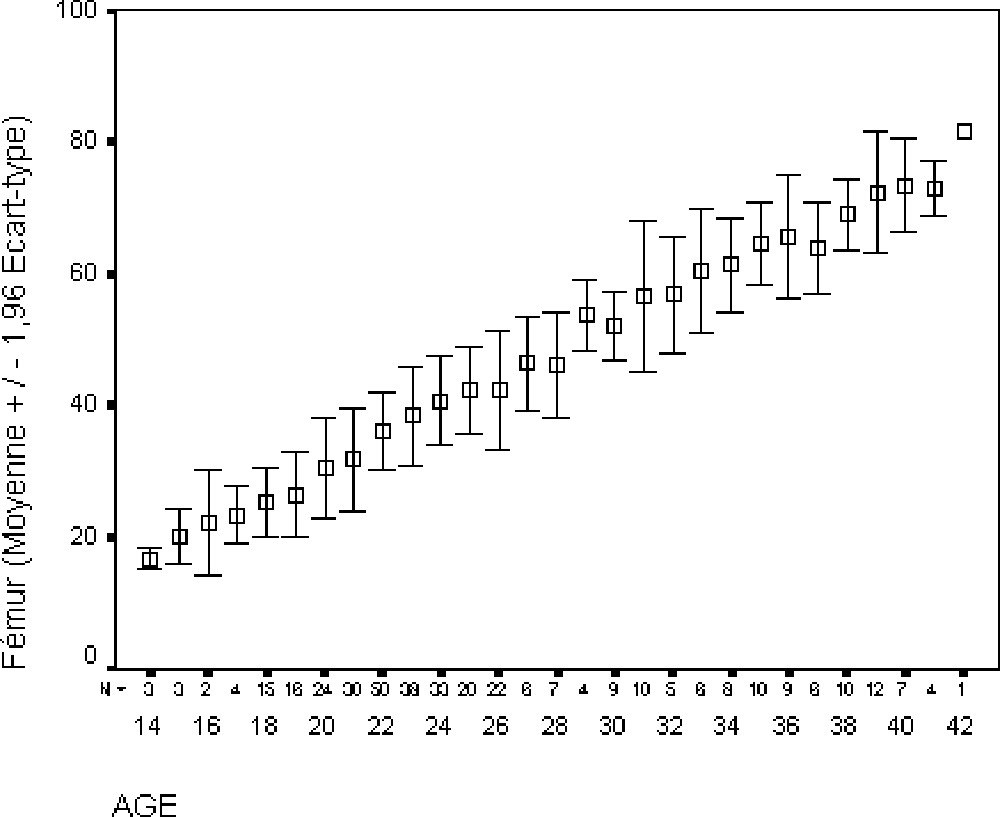
Présentation des longueurs diaphysaires fémorales selon l'âge. Le carré central représente la valeur moyenne et les barres d'erreurs symbolisent la variabilité de la mesure (±1,96 écart type). Pour chaque âge, l'effectif (N) ayant servi au calcul des moyennes et écarts types est précisé sous l'axe des abscisses.
4.1 L’équation uniparamétrée
Dans l’échantillon A, la longueur du fémur présente une très bonne corrélation avec l’âge (Pearson de 96,6% ; p < 0,001). La statistique de Durbin–Watson (2,053) assure la non-autocorrélation des résidus, dont la distribution est normale et dont la valeur du carré moyen (2,881) témoigne de la bonne adéquation du modèle aux données.
La régression décrite ci-dessous permet d’estimer l’âge fœtal avec un intervalle de confiance de +/- 3,34 semaines :
4.2 Comparaison de nos estimations de l’âge fœtal avec les tables, courbes et équations données dans la littérature
Le tableau présentant les valeurs des résidus pour chacun des 30 fœtus de l’échantillon V, nous permet d’observer que les erreurs moyennes sont proches de 0 (Tableau 1). Cependant, les résidus engendrés sur l’ensemble des âges par la formule de Fazekas et Kosa 〚23〛 présentent un écart type, élevé témoignant de l’importance de certaines erreurs (Tableau 2). Notre formule présente, par rapport aux autres méthodes (Tableau 2), l’avantage de ne pas fournir de résidus plus importants pour les âges les plus élevés.
Prédictions et résidus générés par chacune des formules testées sur l’échantillon V. Les âges prédits sont en semaines d’aménorrhée (SA) et les résidus sont en semaines. Les « prédictions » d’âge des formules de Fazekas et Kosa 〚23〛, Balthazard et Dervieux 〚24〛 et Olivier et Pineau 〚5〛 font suite à une détermination de la stature (pour chacune de ces trois méthodes, aucun intervalle de confiance ne peut être précisé). Pour notre formule, le calcul se fait directement à partir de la mesure de la diaphyse fémorale (la prédiction est nommée « centre » pour rappeler qu’elle est donnée avec un intervalle de confiance à 95% = centre ± 3,34).
| Âge (SA) | Fazekas | Balthazard | Olivier | Notre formule | ||||
| Prédictions | Résidus | Prédictions | Résidus | Prédictions | Résidus | Centre | Résidus | |
| 17 | 13,95 | 3,05 | 15,40 | 1,60 | 16,73 | 0,27 | 15,64 | 1,36 |
| 19 | 17,26 | 1,74 | 18,27 | 0,73 | 18,62 | 0,38 | 18,43 | 0,57 |
| 19 | 16,84 | 2,16 | 17,91 | 1,09 | 18,37 | 0,63 | 18,08 | 0,92 |
| 19 | 18,61 | 0,39 | 19,44 | 0,44 | 19,44 | 0,44 | 19,56 | 0,56 |
| 19 | 14,98 | 4,02 | 16,29 | 2,71 | 17,30 | 1,70 | 16,51 | 2,49 |
| 20 | 20,58 | 0,58 | 21,16 | 1,16 | 20,72 | 0,72 | 21,23 | 1,23 |
| 20 | 14,95 | 5,05 | 16,26 | 3,74 | 17,28 | 2,72 | 16,48 | 3,52 |
| 21 | 16,98 | 4,02 | 18,03 | 2,97 | 18,45 | 2,55 | 18,20 | 2,80 |
| 21 | 17,16 | 3,84 | 18,19 | 2,81 | 18,56 | 2,44 | 18,35 | 2,65 |
| 22 | 21,92 | 0,08 | 22,33 | 0,33 | 21,64 | 0,36 | 22,36 | 0,36 |
| 22 | 19,04 | 2,96 | 19,82 | 2,18 | 19,72 | 2,28 | 19,93 | 2,07 |
| 22 | 18,68 | 3,32 | 19,50 | 2,50 | 19,49 | 2,51 | 19,62 | 2,38 |
| 22 | 24,02 | 2,02 | 24,15 | 2,15 | 23,16 | 1,16 | 24,13 | 2,13 |
| 22 | 23,23 | 1,23 | 23,46 | 1,46 | 22,58 | 0,58 | 23,46 | 1,46 |
| 22 | 22,47 | 0,47 | 22,81 | 0,81 | 22,03 | 0,03 | 22,82 | 0,82 |
| 22 | 22,84 | 0,84 | 23,12 | 1,12 | 22,29 | 0,29 | 23,13 | 1,13 |
| 23 | 23,01 | 0,01 | 23,27 | 0,27 | 22,41 | 0,59 | 23,27 | 0,27 |
| 23 | 24,16 | 1,16 | 24,27 | 1,27 | 23,26 | 0,26 | 24,24 | 1,24 |
| 23 | 25,60 | 2,60 | 25,52 | 2,52 | 24,37 | 1,37 | 25,45 | 2,45 |
| 23 | 23,40 | 0,40 | 23,61 | 0,61 | 22,70 | 0,30 | 23,60 | 0,60 |
| 25 | 25,26 | 0,26 | 25,22 | 0,22 | 24,10 | 0,90 | 25,17 | 0,17 |
| 26 | 22,86 | 3,14 | 23,14 | 2,86 | 22,31 | 3,69 | 23,15 | 2,85 |
| 26 | 25,22 | 0,78 | 25,19 | 0,81 | 24,07 | 1,93 | 25,13 | 0,87 |
| 28 | 30,17 | 2,17 | 29,49 | 1,49 | 28,24 | 0,24 | 29,30 | 1,30 |
| 29 | 29,75 | 0,75 | 29,14 | 0,14 | 27,87 | 1,13 | 28,96 | 0,04 |
| 30 | 30,17 | 0,17 | 29,49 | 0,51 | 28,24 | 1,76 | 29,30 | 0,70 |
| 35 | 37,25 | 2,25 | 35,65 | 0,65 | 35,49 | 0,49 | 35,27 | 0,27 |
| 35 | 37,93 | 2,93 | 36,24 | 1,24 | 36,27 | 1,27 | 35,84 | 0,84 |
| 36 | 35,91 | 0,09 | 34,49 | 1,51 | 33,98 | 2,02 | 34,14 | 1,86 |
| 39 | 42,35 | 3,35 | 40,09 | 1,09 | 41,84 | 2,84 | 39,57 | 0,57 |
Moyennes et écarts types des résidus engendrés par chacune des formules testées. Les valeurs sont calculées pour l’échantillon total, puis pour les fœtus âgés de moins de 22 semaines d’aménorrhée et pour les fœtus âgés de plus de 22 semaines d’aménorrhée (SA).
| Fazekas | Balthazard | Olivier | Notre formule | |
| Échantillon total | ||||
| Moyenne | 0,45 | 0,30 | 0,62 | 0,32 |
| Ecart type | 2,34 | 1,72 | 1,50 | 1,63 |
| Âge < 22 SA | ||||
| Moyenne | 1,75 | 0,93 | 0,86 | 0,81 |
| Ecart type | 2,23 | 1,88 | 1,37 | 1,81 |
| Âge > 22 SA | ||||
| Moyenne | 0,86 | 0,33 | 0,37 | 0,17 |
| Ecart type | 1,66 | 1,33 | 1,63 | 1,32 |
5 Discussion
Dans ce travail, nous avons montré que l’équation obtenue permet une estimation de l’âge fœtal proche de l’âge réel, d’autant meilleure que les fœtus sont âgés (deuxième partie de gestation), ce qui correspond aux cas les plus fréquemment retrouvés dans un contexte anthropologique et médico-légal.
5.1 Choix de notre méthodologie
La nature du matériel étudié n’autorise pas le suivi longitudinal préconisé dans les travaux sur la croissance fœtale in vivo 〚25–27〛. Néanmoins, Deter et Harrist 〚28〛 ont démontré que les courbes de croissance obtenues par une étude longitudinale et celles obtenues par une étude transversale sont similaires, bien que ces dernières nécessitent, selon ces auteurs, l’inclusion d’un plus grand nombre d’individus. Cependant, la détermination de l’âge fœtal à partir d’études transversales doit être pondérée par la variabilité auxologique inter- et intra-populationnelle 〚29–32〛. Cette pondération est représentée par l’importance des bornes de l’intervalle de confiance à 95% de l’âge prédit à partir de la longueur fémorale, quel que soit l’âge. Cet intervalle n’est jamais précisé dans les autres travaux qui sont classiquement utilisés en anthropologie 〚5, 23, 24〛.
La distinction entre échantillon d’apprentissage et échantillon de validation n’a pas été considérée dans les travaux antérieurs. Elle permet de valider statistiquement la formule de régression établie sur un échantillon différent.
Enfin, le choix méthodologique de relever les mesures diaphysaires sur radiographies a permis d’établir de nombreuses validations quant à leur fiabilité et leur correspondance avec les mesures anatomiques réelles 〚17, 18〛. Ceci n’est pas le cas des études échographiques, qui n’ont que rarement fait l’objet de tests de validation 〚33, 34〛. Plusieurs auteurs ont montré que le manque de reproductibilité et de répétabilité des études était lié au fœtus (position et mouvements, quantité de liquide amniotique), à la mère (importance du pannicule adipeux), à la qualité de la résolution de l’image et à l’observateur 〚33, 34〛. Une étude récente concernant les corrélations écho-anatomiques a montré que, selon le type de mesure (échographique ou anatomique), on pouvait observer des différences allant jusqu’à deux semaines lors de l’estimation de l’âge avec la même formule 〚35〛.
5.1.1 La population d’étude
Sherwood et al. 〚4〛 ont confirmé récemment que l’existence de malformations ou d’anomalies du caryotype était une source d’erreur dans l’estimation de l’âge fœtal.
Nous avons délibérément exclu de cette étude non seulement les fœtus présentant une pathologie identifiable, mais aussi ceux pour lesquels une pathologie maternelle était connue. Cette précaution n’est pas systématiquement prise dans les travaux antérieurs.
5.1.2 L’effectif
La moitié de notre population d’étude se répartit entre 20 et 28 semaines d’aménorrhée (Fig. 1). Cette distribution a probablement diminué la précision dans l’estimation de l’âge. Les déséquilibres observés sont en partie liés aux dates légales des échographies obligatoires, générant dans leurs suites des interruptions de grossesses. Néanmoins, il ne nous a pas paru adéquat de présenter nos résultats en deux ou plusieurs équations en fonction de tranches d’âge définies arbitrairement, comme ils sont souvent présentés dans l’analyse des données échographiques 〚36–38〛. Cette méthode a l’avantage d’améliorer l’intervalle de confiance de la prédiction, mais nécessite l’utilisation d’un autre estimateur d’âge pour le choix de l’équation pertinente, ce qui n’est pas la situation rencontrée en pratique anthropologique courante.
5.1.3 L’âge gestationnel de référence
Notre méthode a été établie à partir d’un échantillon d’âge connu (confirmation de la règle de Naegele lors de la première échographie obligatoire). Cet échantillon ne présente pas l’inconvénient d’une détermination indirecte à partir de la stature, comme c’est le cas dans les travaux antérieurs, qui utilisent deux formules de régression successives pour déterminer l’âge fœtal (longueur diaphysaire/stature ; stature/âge fœtal) 〚5, 23, 24〛.
Par ailleurs, il n’existe dans ces travaux que peu ou pas d’informations obstétricales sur le déroulement de la grossesse et sur les antécédents maternels ou familiaux.
5.2 Comparaison des méthodes classiques
Nous avons mesuré la longueur du fémur pour estimer l’âge fœtal, en raison de la facilité de mesure de cet os par radiographie.
Ce seul paramètre permet d’estimer l’âge à ±3,34 semaines. Pour éliminer les différents biais de mesure observés dans les études échographiques, nous avons initialement validé un critère qualitatif de mesure—une plaque conjugale nette—et pratiqué des tests de reproductibilité et de répétabilité 〚17, 18〛. La prise de mesure sur cliché radiographique permet de conserver le fœtus intact.
Notre étude se base sur des effectifs plus réduits que les études portant sur la croissance fœtale in vivo, quantifiée par échographie. Ces dernières ont permis de définir la variabilité de la croissance diaphysaire, augmentant en fonction de l’âge 〚15, 16, 39–41〛. Cependant, selon certains de ces travaux, l’augmentation de la variabilité avec l’âge est la moins importante pour le fémur par rapport à l’ensemble des autres paramètres 〚16〛. Dans notre étude (Fig. 2), la variabilité maximale que nous retrouvons est comparable à celle décrite par ces auteurs 〚16〛. Cette concordance permet vérifier la nécessité de prise en compte de la variabilité dans la détermination de l’âge fœtal et valide pro parte l’utilisation d’une seule formule sur l’ensemble des âges. Cette démarche est dictée par trois impératifs principaux. Le premier est dépendant du contexte anthropologique (ostéo-archéologique ou médico-légal) dans lequel cette recherche se développe. Ce contexte fournit un objet d’analyse (osseux) souvent isolé, ne permettant pas l’application d’une autre méthode que celle d’une formule prédictive à partir d’un os. Dans ce cas, on ne peut présumer d’un âge, et par conséquent choisir la formule de détermination la mieux adaptée. Le second prend en compte l’importance de la détermination de l’âge dans le domaine médico-légal : au-delà de 22 semaines d’aménorrhée, la qualification d’homicide peut être retenue, et au-delà de 28 semaines, il peut y avoir un enregistrement à l’état civil. Ces deux éléments justifient les recherches sur des fœtus âgés de moins de six mois. Enfin, la dernière contrainte doit privilégier la fiabilité à la précision, dans cette application où la problématique est individuelle et non populationnelle.
En anthropologie, il faut souligner que la plupart des publications antérieures ont été établies à partir d’effectifs réduits 〚5, 23〛. Dans certaines études, la variabilité naturelle a été artificiellement diminuée par exclusion des individus atypiques ou la prise en compte exclusive d’individus « moyens » 〚6〛. De même, l’intervalle de confiance lié à l’estimation n’est que très rarement précisé et la marge d’erreur présentée est établie sur l’échantillon qui a servi à établir la régression, la sous-estimant donc très certainement.
Les facteurs socio-économiques et environnementaux présentant d’importantes répercussions sur la croissance fœtale 〚42–44〛, on peut considérer que notre échantillon n’a pas une valeur de représentation universelle. L’existence de facteurs socio-environnementaux influençant la croissance fœtale est illustrée par l’étude de Hohler, qui a établi deux équations différentes pour les villes de Washington et de Miami avec une méthodologie identique 〚11〛. Plusieurs travaux récents ont également présenté la variabilité inter-populationnelle dans la croissance 〚30–32〛 et souligné l’utilité d’établir des équations adaptées à chaque population d’étude.
Cependant, si notre population de référence ne peut pas prétendre être identique à une population archéologique, l’équation proposée conserve l’intérêt d’avoir été établie sur une méthodologie biométrique validée sur une collection de fœtus dont l’histoire obstétricale et l’âge sont parfaitement connus, ce qui n’était pas le cas des travaux de référence antérieurs 〚5, 23, 24〛.
6 Conclusion
Nous avons établi, sur 344 longueurs diaphysaires fémorales, une nouvelle formule d’estimation de l’âge fœtal. Celle-ci présente cinq caractéristiques importantes :
- • les mesures sont relevées sur des radiographies selon un protocole validé qui garantit leur fiabilité ;
- • les mesures ont été vérifiées et corrigées pour obtenir une parfaite corrélation radio-anatomique ;
- • l’établissement d’une seule formule pour l’ensemble des âges ne nécessite pas une évaluation préalable de l’âge ;
- • la formule établie est validée sur un échantillon de 30 individus qui n’ont pas servi à l’établir ;
- • la fiabilité de l’évaluation d’âge selon notre méthode est quantifiée : nous pouvons estimer l’âge d’un fœtus avec un intervalle de confiance de 95% ; quel que soit l’âge, cet intervalle est défini par une prédiction centrée ±3,34 semaines.
Abridged version
1 Introduction
Human foetal growth has widely been studied, mainly in order to assess foetal age in the fields of obstetrics, forensic medicine and physical anthropology. These studies led to the development of several reference tables and regression equations, which demonstrated a strong correlation between foetal age and long bones size. However, none of these methods have been tested on other samples than the one they were established on.
The aim of this study is to create a new formula, based on the examination of a large sample of known age foetuses, and to compare it with some previously proposed methods. In order to establish this new formula, we measured the femoral diaphysis length with the help of an already validated method, which shows an excellent radio-anatomic correlation, and we did separate learning and validation samples.
2 Studied population
Owing to the creation of prenatal diagnostic centres, we had the possibility to study more than 2000 foetuses, among which 782 were considered as normal on the basis of several clinical examinations (X-ray examination, normal caryotype and normal aspect of the viscera for both macroscopic and histologic examinations). Moreover, we did take care to exclude the ones whose intra uterine growth retardation was detected during the first legal ultrasonography.
3 Methods
Real foetal age has been assessed with the last menstruation period, and verified with the help of the first ultrasonographic dating.
The complete sample of normal foetuses has been separated into learning and validation samples. This methodology allows testing the established formula on a sample that was not used for its computation, and avoids the bias of auto-validation. Nevertheless, this validation can only be considered as a statistic one, and does not represent an external validation, since the two samples are coming from the same population.
3.1 Measurement method
The radiographic measurements of the femoral diaphysis were carried out with respect to a previously established and validated protocol: the observation of a net and clear-cut conjugal plate. The measurements were made using a half-millimetre ruler, on both right and left bones, since we already stated that there were no significant differences. We established our age prediction with a linear regression model using the least squares method.
3.2 Comparison with equations, curve and reference table
In order to compare our formula with similar prediction equations, we selected the three formulas which are the most frequently used by forensic physicians and anthropologists: Balthazard and Dervieux 〚24〛, Olivier and Pineau 〚5〛, Fazekas and Kosa 〚23〛. The age predictions were statistically compared with the SPSS® 10 software.
4 Results
4.1 The established formula
The use of the qualitative criterion allowed us to measure 374 femoral diaphysis. The complete sample has therefore been divided as follows: 344 foetuses constituted the learning sample and 30 foetuses were used to test the formula (validation sample).
The femoral diaphyseal length showed an excellent correlation with age (Pearson = 0.966 with p < 0.001) and allowed an age estimation with a 95% confidence interval of ±3.34 weeks when using the formula:
4.2 The predictions comparison
Age estimation using each one of the tested formulas revealed that the average errors were very small. Nevertheless, the important standard deviation of the differences between real age and estimated age (called residues) for Fazekas and Kosa’s method indicates that there were important errors. The second important point of this comparison is that our formula does not show any increase of the errors when age increases.
5 Discussion
In this work, we demonstrated that the established formula allows an age estimation that is close to the real age, and that this estimation is even better in the second part of the gestational period, which corresponds to the most frequently encountered case in both forensic and anthropologic fields.
The chosen methodology, i.e. a transversal study, necessitated the consideration of a bigger sample than in the case of longitudinal studies, in order to take into account the variability of human growth. This variability is illustrated by the width of the 95% confidence interval, which is very rarely explicit in the previously published studies. Moreover, the separation of learning and validation samples is essential to avoid an important methodological bias, especially when we compare the established formula with other ones, which is actually not the case in previously published methods.
Our knowledge of the medical history of both foetuses and mothers ensured us not to consider pathologic cases, and to be precise in our estimation concerning the date of conception: all the foetuses whose first ultrasonographically evaluated age was different from the one calculated from the last menstruation period were excluded. In this way, we could avoid the bias of two successive evaluations, seen in Naegele’s and Haase’s methods.
The choice of a radiographic measurement protocol allowed us to establish several validation tests concerning the reliability and the correspondence with the real anatomic size. These validations are rarely seen in ultrasonographic studies, and some authors even demonstrated that there were a significant lack of reliability because of the foetal position, the scanning resolution and the observer’s experimentation. All these biases could generate some age estimation differences up to two weeks.
The age repartition of the examined material is also important. For example, nearly half of our foetuses were between 20 and 28 weeks old. Although the used least squares regression method is influenced by this imbalance, we considered that the formation of age groups to create several age prediction formulae, as it is frequently seen in other studies, entails important difficulties in the choice of the applicable equation. Therefore, our choice to create a unique regression formula applicable all along foetal life can be justified for three main reasons.
The first one is depending on the context of bones finding in anthropology: the object to analyse can be isolated, and we cannot apply any first age estimation to choose the applicable formula.
The second one takes into account the interest of age estimation in forensic anthropology: after 20 gestational weeks, the homicide qualification can be applied, and after 26 gestational weeks, the foetus can be notified on civil registries. These two elements explain the need of age estimation before six month.
The third reason is the necessity to favour reliability rather than precision in our field of investigation, where individual age estimation is more frequent than population age profile reconstruction.
The radiographic measurement of the femur seemed to be preferable because of its good reliability and its excellent correlation with age. Furthermore, since this method did not necessitate any dissection, the foetuses remained in a good state of preservation, and were therefore available for further examinations. We have to note that ultrasonographic studies are not always applicable (e.g. on foetal remains), and show some imprecision in the measurements.
Concerning the methods that are classically used in anthropology, they are old, were established on small samples that consider only ‘average’ foetuses, and their error margin is underestimated, since their calculation is based on the sample used for the examination.
However, we have to underline that even if the chosen methodology can be a source of error, the existing differences between the different populations can also be responsible of the observed variability. Actually, there are strong evidences to assert that the French population of the 21st century shows different growth patterns than several decades ago, or than other populations living in other countries. This has been recently demonstrated by Hohler, who obtained two different formulae when using the same methodology for the populations of Washington and Miami.
6 Conclusion
We have established, on 344 foetal femoral diaphyseal lengths, a new age estimation formula. This one shows five important characteristics:
- • the measurements were carried out on X-ray pictures, following an already validated protocol, which ensured their reliability;
- • all the measurements were verified and corrected in order to present a perfect radio-anatomical correlation;
- • the establishment of a unique formula applicable all along foetal life did not necessitate ‘first age’ estimation;
- • the formula has been validated on 30 cases that were not used in its calculation;
- • the reliability of our method is clearly defined: we can estimate the age of a foetus from an isolated femoral diaphysis with a 95% confidence interval, which is defined as a calculated value ±3.34 weeks.



