1 Introduction
Dans une expérience de RMN, les signaux sont de deux types : d’une part, le signal RMN, porteur de l’information, d’autre part, le bruit, qui ne contient pas d’information utile et tend à masquer le signal 〚1〛. Le rapport signal/bruit S/B d’une expérience de RMN est défini par le signal crête recueilli rapporté à la tension de bruit efficace 〚2〛 ; dans ces conditions :
2 Le bruit en RMN
Les origines du bruit sont multiples. Celui-ci conduit à une pollution du signal dans l’ensemble du domaine spectral. On distingue essentiellement les bruits aléatoires, inhérents à tout dispositif électronique, et des bruits cohérents, provoqués par le voisinage d’appareils électroniques. Nous nous intéresserons aux bruits qui sont internes au système antenne–échantillon ; les autres causes de bruit ne seront pas prises en compte dans cette analyse. La sensibilité maximale du capteur est donc recherchée. Aux bornes de l’antenne, on constate que l’amplitude du bruit obéit essentiellement à une statistique gaussienne. Ce bruit gaussien est un « bruit blanc », du fait de sa répartition d’énergie uniforme sur le domaine spectral étudié. C’est l’agitation thermique des porteurs de charges à l’intérieur de l’antenne ou de tout autre circuit électrique couplé à celle-ci (échantillon conducteur par exemple) qui induit la tension de bruit. Nous constatons ainsi que l’échantillon peut être une source importante de bruit.
Les phénomènes qui produisent une augmentation de la résistance équivalente sont l’effet pelliculaire et l’effet de proximité ; lorsque l’échantillon est conducteur, la résistance équivalente de bruit doit aussi tenir compte des pertes induites dans celui-ci : courants de Foucault (pertes magnétiques) et pertes diélectriques (pertes capacitives).
Les pertes magnétiques sont liées à l’échantillon par sa conductivité. Elles sont dues au fait que le champ alternatif produit par l’antenne entraîne l’apparition de courants de Foucault dans l’échantillon (conducteur), lequel dissipe de l’énergie par effet Joule. La résistance de pertes magnétiques augmente très rapidement avec le volume de l’échantillon et la fréquence.
Les pertes diélectriques sont dues à la capacité distribuée (Cd) entre l’antenne et l’échantillon. La distribution de potentiel le long de l’antenne entraîne l’apparition d’un champ électrique, dont les lignes de champ traversent l’échantillon 〚3〛. Ce dernier se trouve à un potentiel très proche de celui des masses métalliques qui l’entourent et auxquelles il est fortement couplé. Ces masses métalliques sont elles-mêmes reliées au potentiel de référence (masse). On observe alors des pertes diélectriques de l’antenne vers l’échantillon, puis vers la masse. La résistance des pertes diélectriques augmente très rapidement avec la fréquence. Cette résistance est très difficile à évaluer, puisqu’elle dépend autant de l’environnement de l’antenne que des caractéristiques propres de celle-ci 〚3〛.
La tension de bruit efficace (la valeur quadratique moyenne) dépend essentiellement de la résistance équivalente de l’antenne. Ces dissipations supplémentaires provoquent l’augmentation de la résistance équivalente de perte de l’antenne.
Pour un échantillon donné, seules les pertes magnétiques sont irréductibles, les deux autres sources des pertes pouvant être minimisées : les pertes diélectriques, par la minimisation du champ électrique dû à la bobine, et les pertes résistives, par l’optimisation de la géométrie des conducteurs.
Pour nos microbobines, et même à fréquence de travail élevée, la source majeure de bruit reste la résistance de la bobine (Rt ≈ Rb) 〚4〛, donc l’effet pelliculaire et l’effet de proximité. Les deux effets simulés pour un solénoïde de cinq tours, de diamètre interne Dint = 200 μm, avec un espacement entre tours s = 1 μm et un diamètre de fil d = 16 μm pour un courant de 1 mA, sont mis en évidence sur la Fig. 1.
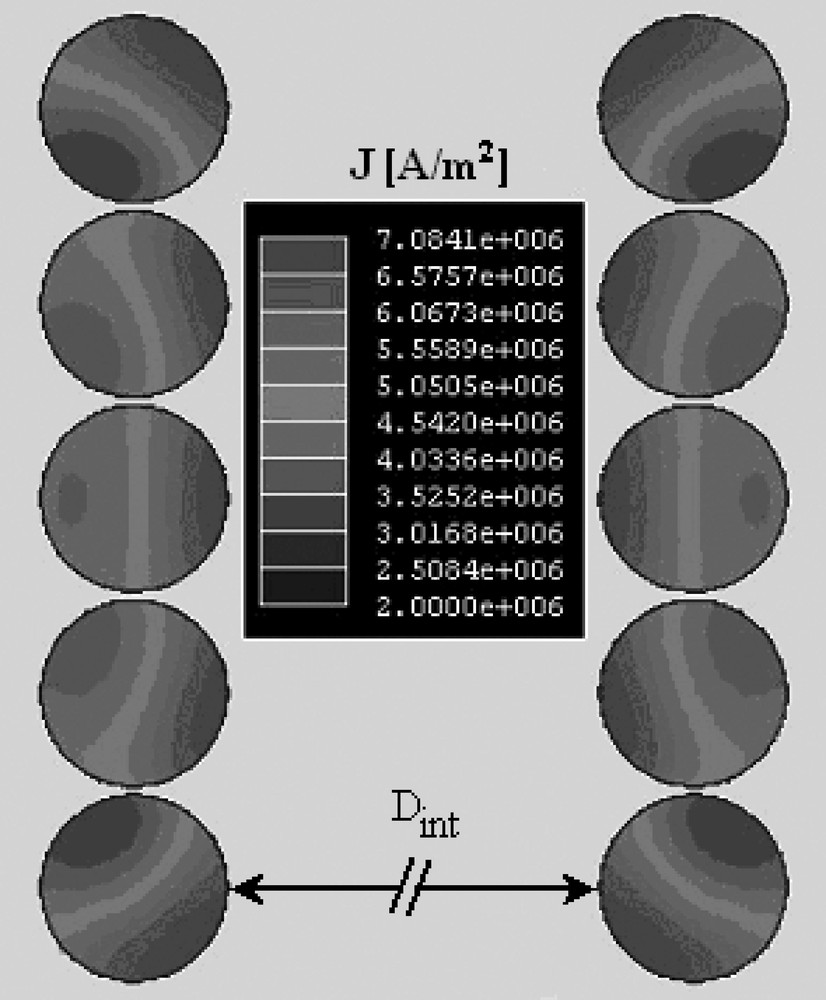
Distribution de la densité de courant J pour un solénoïde.
2.1 L’effet pelliculaire
Le passage du courant alternatif dans un conducteur est affecté par les courants induits par le champ alternatif né du courant lui-même. La concentration du courant à la surface d’un conducteur s’appelle « effet pelliculaire » ou « effet de peau ».
La distribution du courant dans la section d’un conducteur cylindrique est donnée par la relation suivante :
avec
Quand la pulsation ω augmente, et ce d’autant plus vite que μ et σ sont grands, on trouve que plus on pénètre dans le conducteur, plus la densité de courant, maximale à la périphérie, diminue rapidement. On peut même, pour des pulsations ω élevées, avoir une ou plusieurs inversions du sens du courant en allant de la périphérie vers le centre.
Donc, plus la fréquence est élevée, plus l’effet pelliculaire augmente la résistance Rt de la bobine et donc la tension de bruit Vb.
Pour un fil isolé, on peut écrire :
2.2 L’effet de proximité
La variation du champ magnétique créé par le solénoïde induit des courants dans les spires voisines, de sorte que la distribution du courant à l’intérieur du conducteur est perturbée. Quand deux ou plusieurs conducteurs traversés par un courant alternatif sont voisins (c’est le cas des antennes multi-spires), la répartition du courant dans l’un est affectée par le flux magnétique produit par le conducteur adjacent, de même que le flux magnétique produit par le courant dans le conducteur lui-même. Par exemple, si on suppose deux conducteurs parallèles, les courants sont concentrés sur les faces intérieures pour des courants de directions opposées et sur les faces extérieures pour des courants de même direction.
Le calcul analytique de la résistance ajoutée par l’effet de proximité est difficile, même pour deux conducteurs parallèles ; pour des bobines plus complexes, le calcul numérique devient indispensable.
Pour deux conducteurs parallèles, d’une longueur infinie, le rapport entre la résistance en courant alternatif et la résistance en courant continu (qui prend en compte les effets de peau et de proximité) est donné par la relation suivante 〚5〛 :
3 Méthode
Pour augmenter le rapport signal/bruit au maximum, il faut donc optimiser la bobine de réception.
Dans nos simulations, menées à l’aide des logiciels Maxwell 2D/3D (Ansoft Corp., Pittsburgh, USA) et Magnetic@ (MagneticaSoft, Nice, France), nous avons fait varier le nombre de tours (n = 1, 3, 5, 7 à 12, 15, 17 et 20), le diamètre interne du solénoïde (Dint = 100 à 300 μm), le diamètre du fil de cuivre (d = 8 à 100 μm) et enfin l’espacement entre tours (s = 1 à 100 μm). On considère que l’échantillon se trouve dans un tube capillaire placé à l’intérieur du solénoïde et que le fil est en cuivre. La section de la microbobine est représentée sur la Fig. 2.
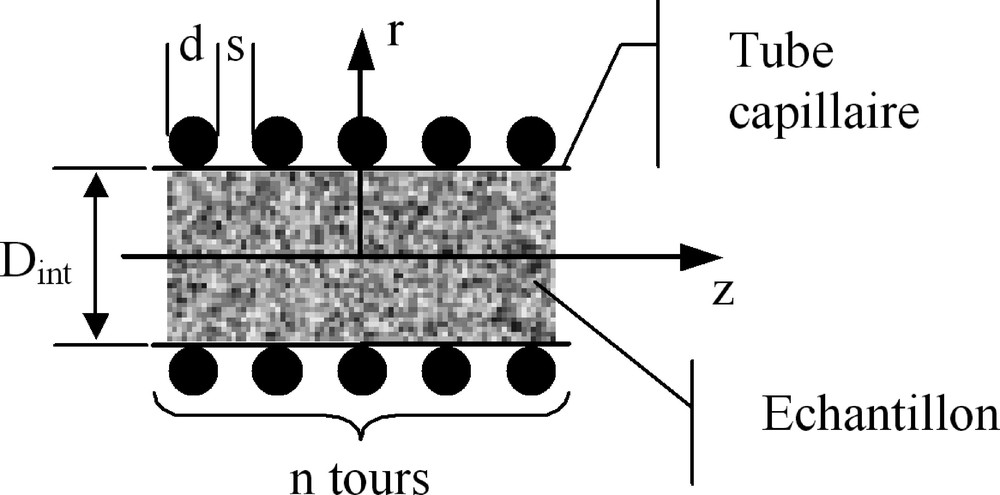
Section de la microbobine.
Maxwell 2D/3D est un logiciel de calcul des champs magnétiques statique et dynamique fondé sur la méthode des éléments finis. Il permet, en particulier, d’analyser la distribution du courant à l’intérieur des milieux conducteurs et prend en compte l’effet de peau et l’effet de proximité.
Le logiciel Magnetic@ 〚6〛 est, quant à lui, fondé sur la méthode de dérivation du potentiel vecteur et/ou du potentiel scalaire associé à un développement du champ en harmoniques sphériques. Il permet de faire très rapidement de calculs de champ magnétique d’une très haute précision.
Ces deux logiciels, très complémentaires, fournissent tous les paramètres nécessaires à l’évaluation des performances des microbobines : l’inductance L, la résistance R et le champ magnétique B produit.
Les calculs du rapport signal/bruit par unité de volume d’échantillon ont été réalisés pour le proton de l’eau à 2 T (85,13 MHz), à une température T = 310 K et pour une largeur spectrale Δf/f = 6 ppm.
Pour calculer l’intensité du signal, nous avons simulé le champ magnétique créé par des microbobines radiofréquence. Ainsi, ces simulations fournissent non seulement les résultats quantitatifs indispensables pour le calcul du rapport signal/bruit, mais également une cartographie précise du champ magnétique, qui permet d’optimiser la position de l’échantillon pour obtenir les meilleurs résultats en termes de rapport signal/bruit par unité de volume. La composante axiale (BZ) du champ magnétique à l’intérieur d’un solénoïde de diamètre interne Dint = 200 μm, pour un espacement entre tours s = 10 μm, un diamètre de fil d = 60 μm et n = 10 tours est représentée sur la Fig. 3, pour un courant I = 1 mA.
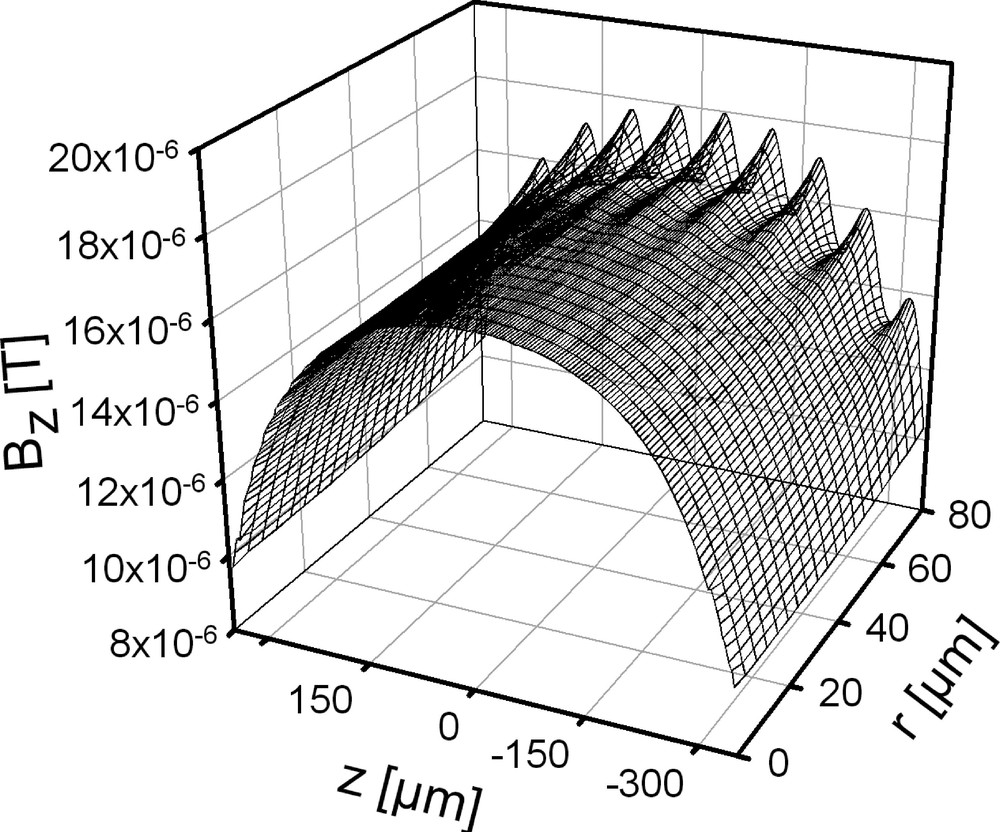
Composante axiale Bz du champ magnétique à l’intérieur d’un solénoïde.
4 Résultats et discussion
Pour valider la précision du logiciel Maxwell, nous avons simulé et mesuré quelques microbobines. Nous avons également comparé les résultats obtenus avec des calculs effectués à l’aide du logiciel Magnetic@ spécifiquement développé pour la résolution précise de problèmes de magnétostatique. Les comparaisons prouvent que les résultats obtenus par simulation sont valides.
Les contributions des différents effets (résistance en continu, effets de peau et de proximité) à la résistance totale de la microbobine pour un diamètre interne du solénoïde Dint = 200 μm, le diamètre du fil d = 40 μm et n = 10 tours sont représentées sur la Fig. 4 en fonction de l’espacement entre tours, noté s.
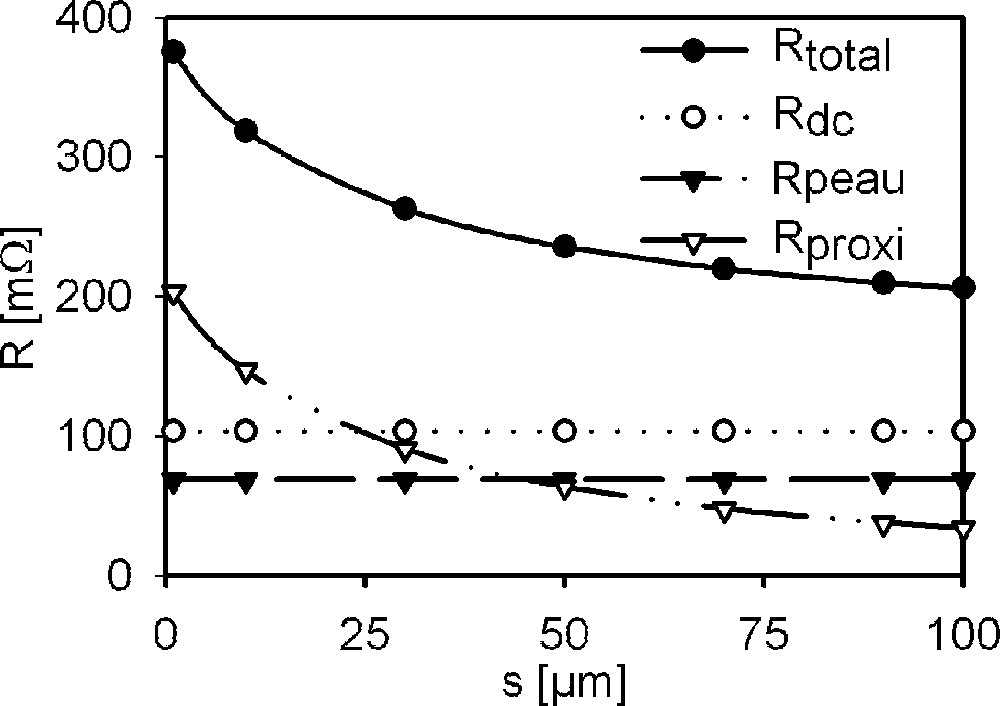
Contribution des différents effets à la résistance totale de la microbobine en fonction de l’espacement entre tours.
La résistance totale de la bobine dépend de l’espacement entre les tours, car l’effet de proximité varie très rapidement avec la distance entre les conducteurs de la microbobine. Cette résistance additionnelle due à l’effet de proximité est environ trois fois plus importante que la résistance additionnelle due à l’effet de peau lorsque les tours sont jointifs, égale à cette résistance pour un espacement entre tours comparable au diamètre du fil, et jusqu’à deux fois plus faible pour un espacement entre tours double du diamètre du fil. Mais évidement, la résistance totale de la bobine n’est pas le seul paramètre qui décide des performances d’une bobine RMN.
Le rapport signal/bruit par unité de volume, et le facteur de qualité Q de la bobine pour des solénoïdes avec Dint = 200 μm, n = 10 et différents diamètres du fil d sont donnés en fonction de s (Figs. 5 et 6). On observe que le rapport signal/bruit par unité de volume augmente sensiblement lorsque l’espace intertour s décroît de 100 à 1 μm (l’effet pelliculaire est compensé par une augmentation de la sensibilité du capteur) ; parallèlement le facteur de qualité Q présente un maximum pour un espacement entre tours s de quelques microns, si le diamètre du fil est d = 40 μm, ou pour des spires jointives, si le diamètre du fil est réduit à d = 20 μm.
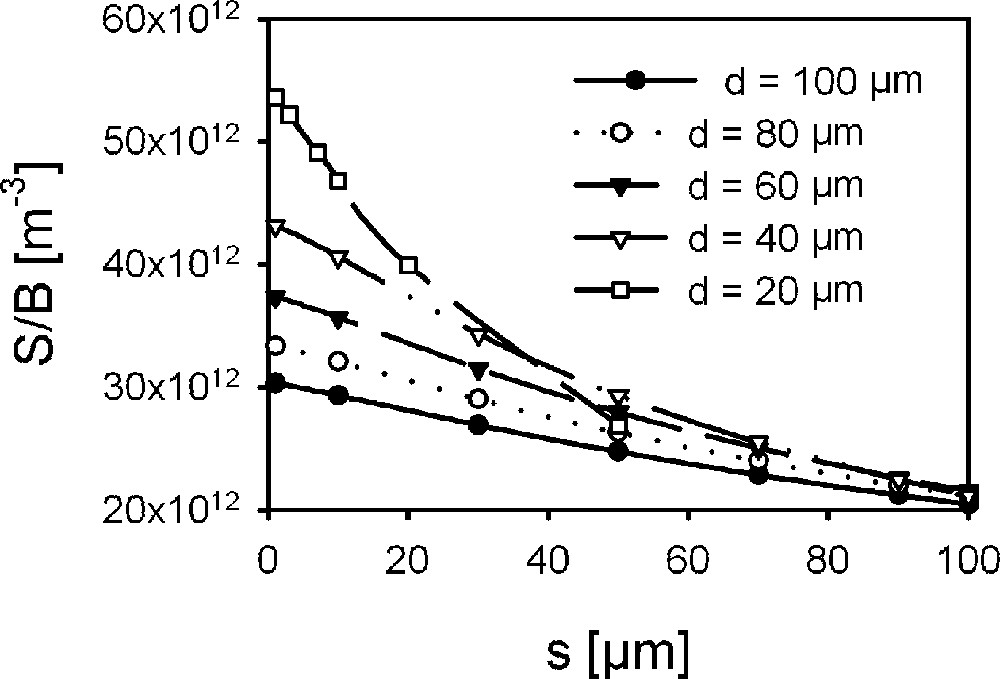
Rapport signal/bruit par unité de volume en fonction de l’espacement entre tours.
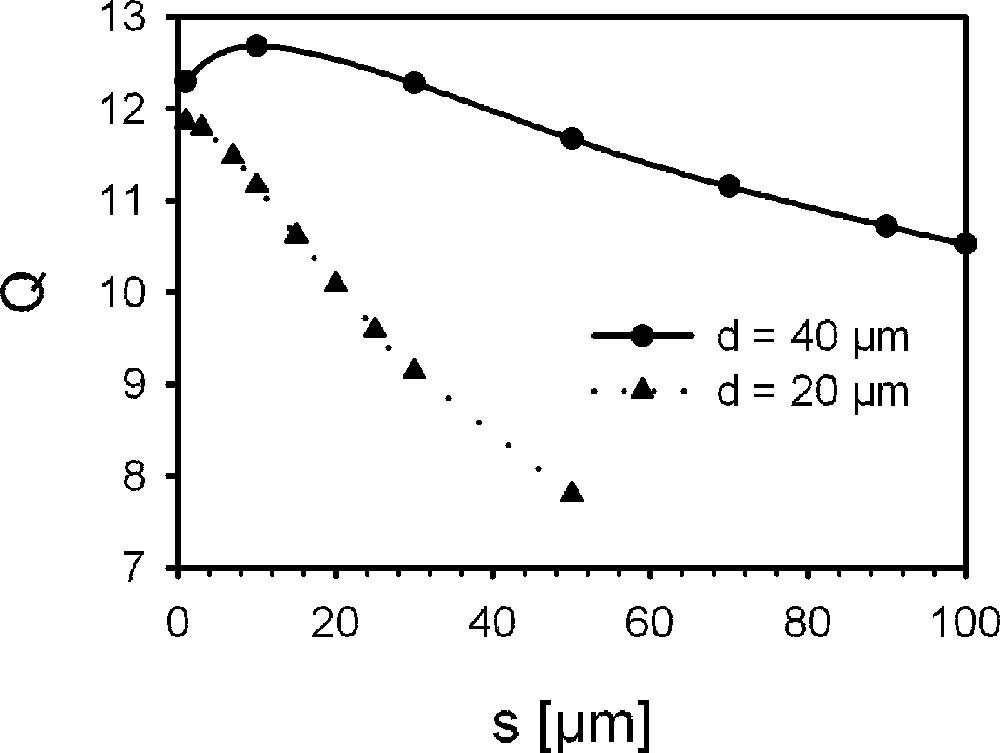
Variation de Q en fonction de l’espacement entre tours.
Pour le même diamètre Dint et s = 1 μm, l’optimum en termes de rapport signal/bruit par unité de volume est trouvé pour un diamètre de fil d ≈ 16 μm (Fig. 7).
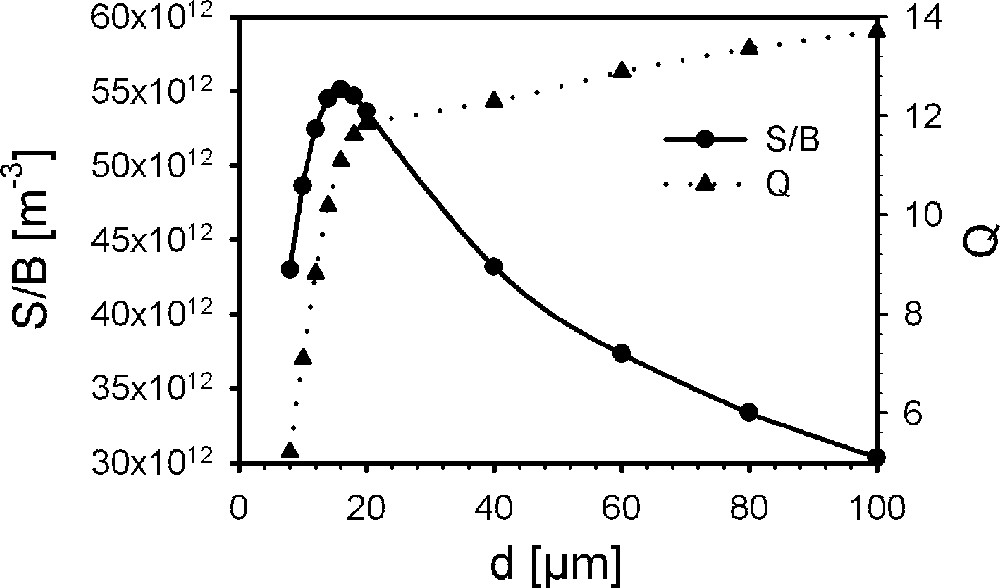
Variations du rapport signal/bruit par unité de volume et de Q en fonction du diamètre du fil.
Ces simulations confirment qu’une réduction du diamètre du solénoïde se traduit par un accroissement du rapport signal/bruit par unité de volume 〚4〛, malgré une décroissance rapide du facteur de qualité de la bobine (Fig. 8).
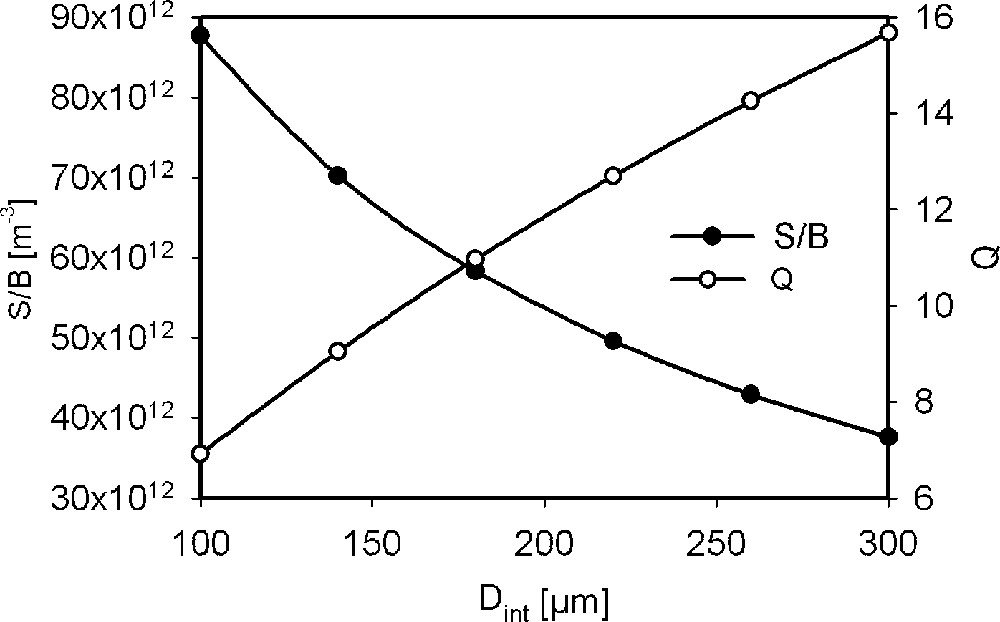
Variations du rapport signal/bruit par unité de volume et de Q en fonction du diamètre interne du solénoïde.
Pour des solénoïdes de diamètre Dint = 200 μm, avec un diamètre de fil d = 16 μm et un espacement entre tours s = 1 μm le rapport signal/bruit par unité de volume passe par un maximum pour n = 8 tours environ, alors que le facteur de qualité Q augmente régulièrement avec le nombre de tours n (Fig. 9).
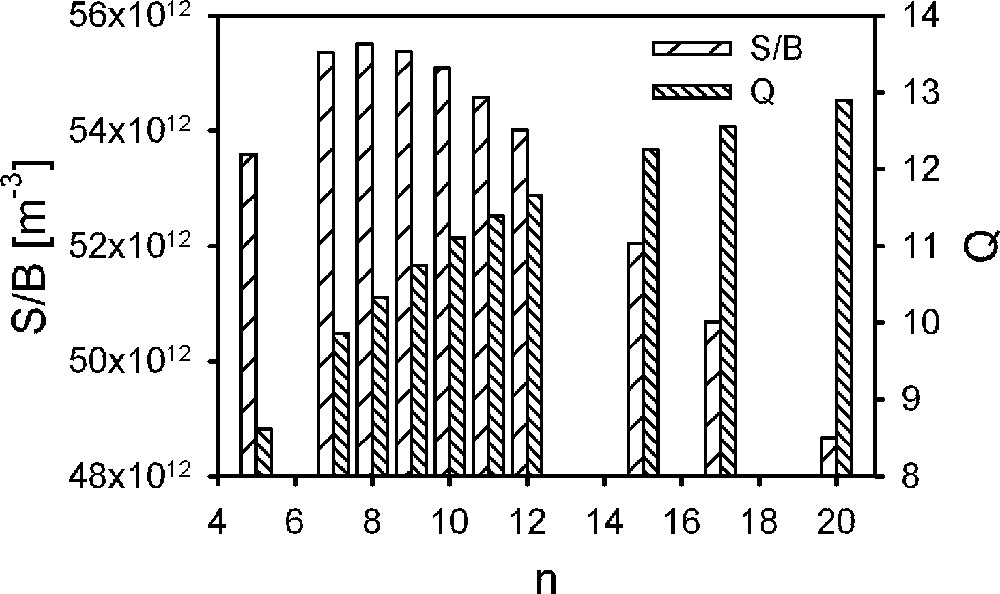
Variations du rapport signal/bruit par unité de volume et de Q en fonction du nombre de tours.
5 Conclusions et perspectives
Les calculs et les simulations effectuées ont donné des résultats très intéressants. Ainsi, lorsque la bobine réceptrice devient très petite (rayon du fil comparable à l’épaisseur de peau), les règles de conception classiques 〚4〛 ne sont plus applicables ; la mise en œuvre d’un logiciel de simulation électromagnétique est alors indispensable pour optimiser les performances des microbobines et conduire ainsi à des capteurs biologiques de plus en plus efficaces.
Les perspectives ouvertes par cette étude sont vastes ; à court terme, il faut envisager d’améliorer la rapidité de la simulation des structures des capteurs à l’aide d’un logiciel plus adapté à l’optimisation automatique. Dans une seconde étape, il faudra minimiser les élargissements des raies spectrales en adaptant les susceptibilités du capteur et de l’échantillon. En effet, la différence entre les susceptibilités magnétiques du cuivre et du milieu extérieur crée des variations du champ magnétique B0 ; ceci entraîne un élargissement de la raie 〚7–10〛. Les solutions envisageables pour remédier à ce problème sont l’utilisation d’un fluide de susceptibilité magnétique très proche de celle du cuivre (FC – 40 fluorinert) 〚8〛 ou l’utilisation d’un fil spécial présentant une susceptibilité magnétique χ ≅ 0, qui est obtenu par la combinaison de plusieurs matériaux (cuivre, aluminium, or, argent, rhodium) de susceptibilités différentes 〚7〛. La deuxième solution est la seule applicable pour les bobines de réception RMN implantables.
Enfin, le passage à des réalisations faisant appel aux technologies de la micro-électronique permettra certainement d’optimiser au mieux tant le capteur que la transmission du signal.
Remerciements
Ce travail a été réalisé avec la participation financière d’Ezus-Lyon 1, société de recherche sous contrat bénéficiant de l’abondement Anvar.
Abridged version
The extraction of the Nuclear Magnetic Resonance (NMR) spectra of samples having smaller and smaller volumes is a real challenge. Either that these reductions of volume are dictated by the difficulties of production of sufficiently large samples or by necessities of miniaturisation of the analysing system, in both cases a careful design of the radiofrequency coil, ensuring an optimum reception of the NMR signal, is required. We have also evaluated the usefulness of electromagnetic simulation software for the design and optimisation of these radio-frequency coils, which are more and more used in biology and health research projects.
The solenoidal microcoils are used in NMR spectroscopy for mass-limited samples analysis including contaminants in the pharmaceutical industry, reactions involving the breakdown of agrochemicals, multistep chemical synthesis of natural products and compounds formed by single-bead solid-state combinatorial chemistry.
The magnetic coupling between a RF coil and a sample is maximised by physically designing the coil as small as possible as to just accommodate the sample. Maximum coupling corresponds directly to an optimal sensitivity for the signal reception.
For optimising not only the quality factor (Q) but also the signal-to-noise ratio, we simulated the electromagnetic parameters (the electrical resistance Rt, the inductance L and the RF field B1) of planar rectangular RF coils using ANSOFT Maxwell 2D/3D software (Ansoft Corp., Pittsburgh, USA) and Magnetic@ (MagneticaSoft, Nice, France). The Maxwell 2D/3D software is based on advanced finite element technology and uses electromagnetic AC and DC field simulation to predict product performance with physical and geometric inputs. Magnetic@, works under Mathematica software (Wolfram Research, Inc., USA) and provides high accurate computations of static magnetic field. This software offers the choice of two modes of calculation: a method derived from the vector potential, which is applicable to all space including the winding and the magnetic materials, and a method using spherical harmonics, which is restricted to the space without magnetic field generator. The simulations were been performed using AC excitation and magnetostatic approximation in order to calculate the B1 field and sinusoidal excitation of the RF coil in order to calculate the resistance Rt of the coils and the magnetic losses.
The signal-to-noise ratio S/N of a NMR experiment is defined as the peak signal divided by the root mean square (rms) noise:
The origins of noise in NMR are multiple. The total resistance of the coil contains the electrical resistance of the isolated coil (in vacuum) and the equivalent electrical resistance due to the magnetic losses in the sample.
The electrical resistance of the isolated coil is due to the ohmic losses, the skin effect and the proximity effect in the coil wires. The current is concentrated towards the outer edge of the conductor (skin effect) with the current density decreasing exponentially from the wire surface to the centre. The magnetic field lines from a given turn of coil induce eddy currents in adjacent turns (proximity effect), further distorting the current distribution and increasing the resistance of the coil.
At the dimensions of our coils, for a frequency of 85.13 MHz (proton frequency resonance at 2 T), the noise originating from the sample is negligible in comparison with the noise produced by the coil wires.
In our simulations we have varied the turn number (n = 1, 3, 5, 7–12, 15, 17 and 20 turns), the internal diameter of solenoidal microcoil (Dint = 100 to 300 μm), the copper wire diameter (d = 8 to 100 μm) and the interturn spacing (s = 1 to 100 μm). The signal-to-noise ratio per unit sample volume computation was made for proton in water at 2 T (f = 85.13 MHz), T = 37 °C and Δf/f = 6 ppm.
To start we have evaluated the contributions of different effects (dc, skin, proximity) to the total resistance of microcoil Rt in function of the geometrical parameters of the coils (n, Dint, d and s). For this purpose, we have simulated the current distributions in the coils wire.
A decrease in the diameter of solenoidal microcoil produces an increase in the signal-to-noise ratio per unit sample volume but in the same time Q will quickly decrease. For a solenoidal microcoil with n = 10 turns and Dint = 200 μm, if the interturn spacing s decreases from 100 μm to 1 μm, the signal-to-noise ratio per unit sample volume increases. The proximity effect on Rt is compensated by a significant increase in sensitivity. In the same conditions, Q is maximal for adjacent turns if d = 20 μm or for few microns interturn spacing if d = 40 to 100 μm. For the same Dint and s = 1 μm, with d decreasing from 100 to 8 μm, the signal-to-noise ratio per unit sample volume increases to a maximum for d ≈ 16 μm; after that, it will quickly decrease.
In conclusion, when the coil size becomes small (e.g., the wire radius is comparable to the skin depth), standard design rules are no more relevant, and the help of electromagnetic simulation software is mandatory in order to optimise the quality of the microcoil.



