1. Introduction
Les animaux présentent une multitude de formes, de couleurs et de comportements. Particulièrement intrigants, de nombreux personnages se répètent dans l’espace à travers les organes selon des motifs essentiels à la forme physique, tels que des hexagones, des anneaux, des motifs labyrinthiques, des rosettes, des rayures ou des taches. Ces motifs périodiques apparaissent au cours du développement embryonnaire à partir de structures initialement homogènes, qui acquièrent des informations de position déclenchant une réponse moléculaire et cellulaire, conduisant finalement à des changements locaux dans le destin des cellules et la différenciation des tissus. La compréhension des mécanismes qui contrôlent la formation des motifs naturels est l’une des tâches des biologistes de l’évolution, des biologistes du développement et des mathématiciens, qui se sont attaqués à ce défi pendant plus d’un demi-siècle. Leurs méthodes complémentaires ont conduit à deux grandes théories de la formation des modèles. Dans la première, l’information positionnelle est fournie par une source externe au tissu formant le modèle [1]. Ce mécanisme d’ « instruction » a été décrit pour la première fois dans l’embryon de drosophile. Dans ce système, des segments corporels se forment progressivement le long de l’axe antéro-postérieur en fonction des concentrations locales d’ARNm bicoïde maternel, qui forme un gradient à partir de sa source antérieure [2, 3]. Depuis cette découverte pionnière, de nombreuses autres molécules se diffusant à longue distance et induisant différents destins en fonction de la dose, appelées morphogènes, ont été liées à la formation d’une pléthore de caractères organisés en motifs, tant chez les invertébrés que chez les vertébrés par exemple, [4, 5]. Comme les morphogènes émanent de structures embryonnaires précoces orientées le long des axes du corps, la formation de motifs explique intuitivement que de nombreux motifs périodiques sont reproductibles et ont conservé leur orientation au sein des taxons. Cependant, cette stratégie de formation de modèles ne fournit pas de principes mécanistes simples permettant d’établir des modèles périodiques plus complexes. Dans le second cas, des instabilités intrinsèques dans les tissus non structurés provoquent spontanément une « auto-organisation » des caractères émergents sur une surface en développement. Les dynamiques d’auto-organisation ont été théorisées pour la première fois dans le modèle de réaction-diffusion de Turing, un système d’équation différentielle partielle (EDP) qui décrit l’interaction dynamique d’au moins deux facteurs, une molécule auto-activante qui diffuse à longue distance et son inhibiteur à courte distance, produit en réponse à l’activateur, qui diffuse plus rapidement [6]. Les simulations numériques de la dynamique réaction-diffusion reproduisent des motifs périodiques tels que des bandes ou des points [7, 8, 9], ainsi que des domaines de grande taille dans certaines conditions particulières (par exemple, une diffusion élevée de l’inhibiteur ; [8, 10]. Plus récemment, des modèles de type Turing avec un seul facteur moléculaire mais intégrant des paramètres mécaniques, et d’autres systèmes auto-organisés tels que la chimiotaxie, qui décrit le mouvement des cellules vers un facteur chimio-attractif, ont également réussi à produire des motifs périodiques in silico [11, 12]. Le dessin par auto-organisation est donc théoriquement compatible avec la répétition périodique de motifs de base. De nombreux travaux empiriques confirment en effet l’existence d’une dynamique d’auto-organisation dans les systèmes biologiques : les profils d’expression des molécules candidates ou la dynamique cellulaire — y compris les forces mécaniques qu’elles exercent sur leur substrat, correspondant potentiellement aux paramètres des équations de Turing, contrôlent la formation d’organes à motifs périodiques tels que les écailles de tortue et de requin, les dents d’alligator, les follicules de plumes, ou les dents, les poils et les doigts de mammifères [13, 14, 15, 16, 17, 18]. En outre, les modèles auto-organisés sont très malléables, car de subtiles modifications des paramètres stochastiques peuvent avoir un impact considérable sur les modèles finaux [8], ce qui peut expliquer la façon dont la variation se produit. Cependant, la grande flexibilité des systèmes auto-organisateurs ne se concilie guère avec la reproductibilité et l’orientation conservée de la plupart des modèles périodiques. La signalisation pédagogique et l’auto-organisation ont toutes deux souffert d’un manque de preuves expérimentales en raison des difficultés cumulées [1] d’effectuer des expériences histologiques et génétiques dans des organismes non modèles présentant des modèles pertinents sur le plan écologique, et [2] d’associer à des modèles finaux des événements candidats se produisant avant l’existence d’une référence spatiale.
2. Utilisation de la variation naturelle dans les études de formation de modèles
Les scientifiques ont toujours profité de la biodiversité pour dévoiler les lois mathématiques et physiques de la vie ou améliorer la technologie et la médecine. La génétique et la biologie du développement, en particulier, sont nées de l’observation des variations phénotypiques, des premières classifications d’organismes d’Aristote aux lois de l’héritage de Mendel. Avec l’avènement de la biologie moléculaire moderne et la nécessité d’explorer les mécanismes fondamentaux du développement dans des systèmes de modèles standardisés, l’étude des populations naturelles est progressivement tombée en désuétude, en plus de la recherche écologique et environnementale. L’ère post-génomique actuelle a marqué le retour de la variation des traits comme outil d’étude de l’évo-dévo et de la génétique des populations : beaucoup profitent des différences morphologiques ou comportementales entre quelques espèces pour identifier les bases moléculaires de l’évolution phénotypique par des méthodes de génétique prospective (c’est-à-dire des analyses GWAS ou QTL) ou des analyses comparatives d’expression [19, 20, 21, 22, 23]. Le domaine des mathématiques appliquées a également été profondément influencé par la diversité biologique et son origine développementale, les systèmes mathématiques tels que les EDP étant préférés parce qu’ils produisent une dynamique opportune et sont permissifs à une variation importante par la modification minimale des paramètres. Dans notre laboratoire, nous travaillons à la normalisation et à l’extension de l’utilisation de la variation naturelle dans les études sur le développement, en combinant des enquêtes à grande échelle et des expérimentations fonctionnelles sur des espèces non modèles pour l’étude de la formation des modèles. Notre méthode consiste à identifier les attributs communs et différents d’un modèle en étudiant ses variations entre les espèces et en les corrélant aux processus embryonnaires communs et différents, ce qui permet de repérer les événements candidats à la formation de modèles.
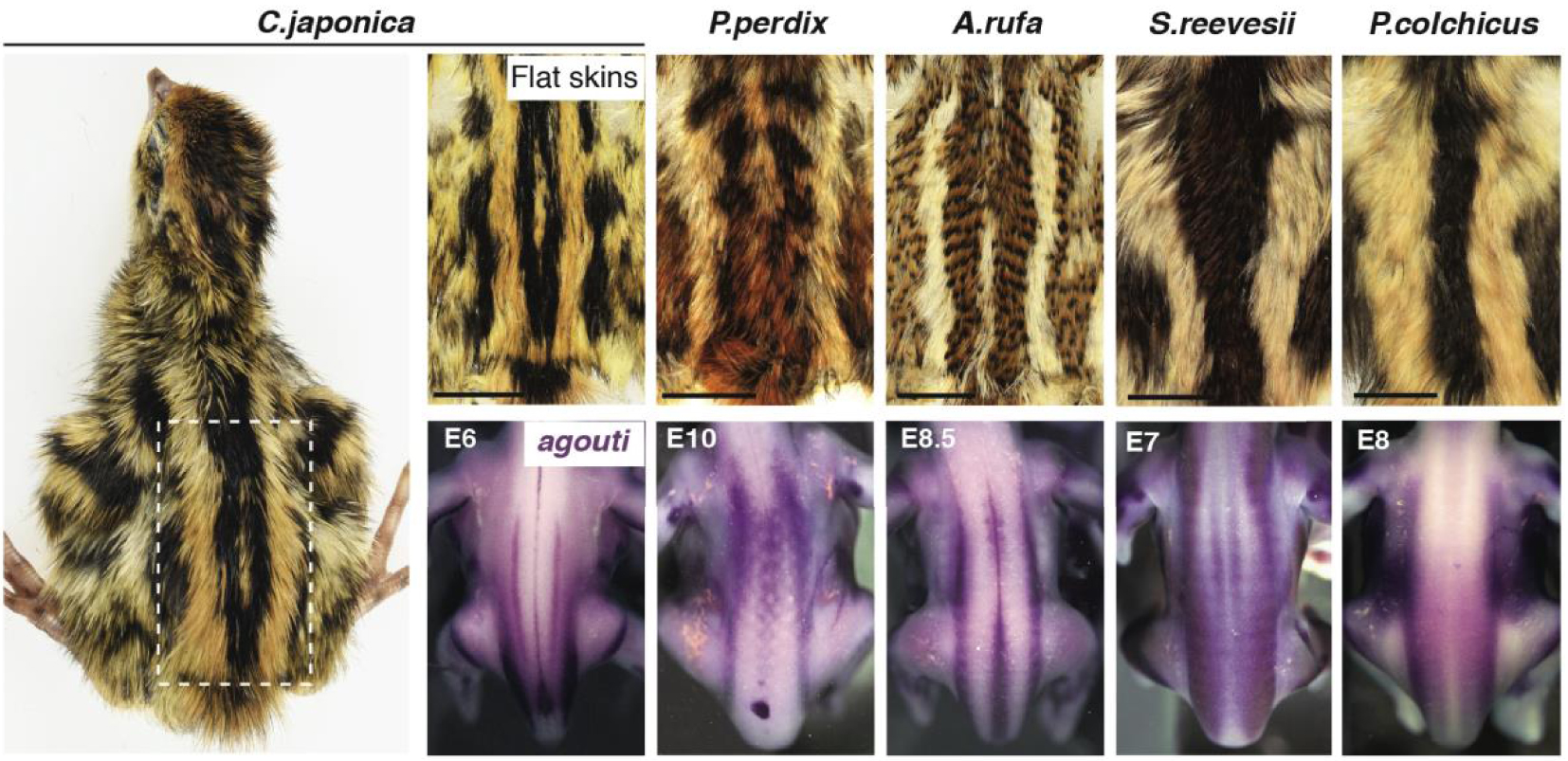
Le motif rayé varie selon les espèces et est pré-modelé par l’agouti. L’étude de la coloration des plumes à tous les endroits de la peau dorsale chez des spécimens à peau plate de 10 espèces d’oiseaux galliformes (5 sont présentés ici) a montré que les bandes longitudinales médianes ont conservé leur emplacement absolu mais varient en largeur. Ces deux attributs sont préfigurés par l’expression précoce, spécifique à l’espèce, de l’agouti dans l’embryon, avant la production de pigments. E : période embryonnaire. Masquer
Le motif rayé varie selon les espèces et est pré-modelé par l’agouti. L’étude de la coloration des plumes à tous les endroits de la peau dorsale chez des spécimens à peau plate de 10 espèces d’oiseaux galliformes (5 sont ... Lire la suite
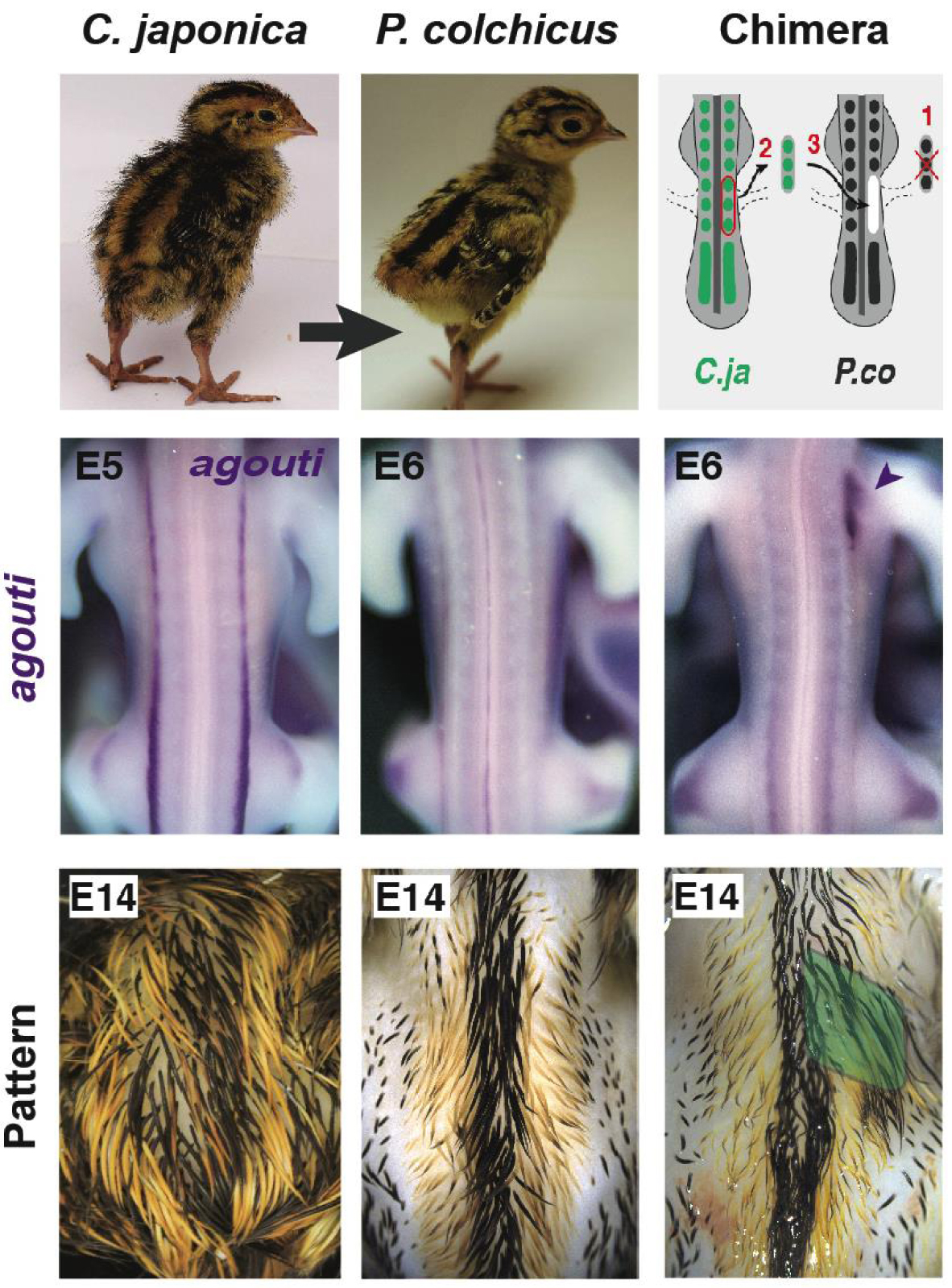
La greffe hétéro-spécifique caille-faon a montré que les somites indiquent l’emplacement des rayures. Les tissus des donneurs de cailles japonais ont été transférés dans des faisans hôtes. Lors de la transplantation de somites, les chimères présentaient un profil d’expression de type donneur d’agouti et, plus tard, de plumage, au niveau de la greffe (c’est-à-dire la région de l’aile droite, en pointe de flèche à E6, en vert à E14). Les deux sont restés inchangés après la transplantation des moitiés du tube neural. Ces résultats ont démontré que les signaux de position contrôlant l’établissement du pré-modèle et du motif rayé d’agouti émanent du somite. E : période embryonnaire. Masquer
La greffe hétéro-spécifique caille-faon a montré que les somites indiquent l’emplacement des rayures. Les tissus des donneurs de cailles japonais ont été transférés dans des faisans hôtes. Lors de la transplantation de somites, les chimères présentaient un profil d’expression de ... Lire la suite
3. Motifs périodiques de couleur, systèmes d’icônes pour les biologistes et les mathématiciens
Des exemples vivants de la plupart des géométries périodiques définies mathématiquement (c’est-à-dire des rayures, des pointillés) peuvent être trouvés dans le pelage des mammifères, des oiseaux, des reptiles et des poissons. Ces motifs résultent de la distribution différentielle des pigments dans des compartiments discrets à la surface de la peau ou le long des appendices cutanés [24]. Chez les oiseaux et les mammifères, des cellules spécialisées dans la production de pigments (mélanocytes) synthétisent l’eumélanine noire et la phaeomélanine jaune, qui sont à la base de la plupart des motifs visibles [25, 26]. Des études de lignée ont montré que les mélanocytes sont spécifiés à partir de la crête neurale lors de la fermeture du tube neural, et migrent ventralement dans le derme pour atteindre leur emplacement [24, 27]. La présence de compartiments colorés visibles peut donc être due à différents mécanismes, notamment des différences dans le type et la quantité de pigments produits, la durée de leur production, la présence/absence de cellules productrices de pigments ou des changements dans leur comportement. Au moment où nous avons conçu notre étude, plusieurs gènes de pigmentation connus pour contrôler la synthèse des pigments (par exemple, agouti, Alx3, end3b) présentaient des profils d’expression spatialement restreints dans la peau embryonnaire, de sorte qu’ils préfigurent les futures différences de couleur dans le ventrum ou des bandes périodiques dans le dos chez les rongeurs [28, 29, 30, 31]. Chez le poisson zèbre Danio rerio, en revanche, il a été démontré que les rayures colorées longitudinales résultent de changements locaux dans l’interaction pigment-cellule au cours de la différenciation de la peau, un mécanisme d’attraction-répulsion similaire à la dynamique de Turing, qui ne nécessite pas de pré-modélisation préalable du tissu [32, 33]. Cependant, la distribution spatiale des pigments est souvent visiblement liée à des repères anatomiques chez les poissons [34, 35, 36, 37], ce qui suggère que l’activité des cellules pigmentaires peut être commandée par des sources précoces. Plus généralement, les modèles périodiques sont souvent très reproductibles au sein des espèces, présentant une orientation/périodicité spécifique, ce qui suggère que leur émergence pourrait être étroitement liée à des références spatiales préexistantes. Ensemble, les études ont mis en évidence le rôle clé des événements moléculaires et cellulaires en jeu dans la peau des embryons précoces, ouvrant la voie à l’établissement d’un lien entre les motifs périodiques de couleur et les premières morphologies.
4. Agouti pré-modèle des rayures périodiques chez les oiseaux de basse-cour
Pour relever ce défi, nous avons entrepris d’identifier les attributs communs et variables du motif de rayures périodiques transitoires visible chez de nombreux oiseaux de chasse. Dans ce groupe (c’est-à-dire les Galliformes), les juvéniles sont généralement caractérisés par des rayures longitudinales dorsales présentant une séquence noire-jaune-noir. Nous avons étudié 10 espèces en enregistrant la coloration de toutes les plumes dorsales et en établissant des cartes de référence du motif rayé, qui est très reproductible au sein de l’espèce. Les quantifications ont montré que le nombre de rayures est proportionnel à la taille du dos. Par rapport à ce facteur, la largeur de chaque raie homologue varie selon les espèces, mais notamment, la position absolue des raies les plus médianes le long de l’axe dorso-ventral est comparable (Figure 1). Nous avons établi un lien entre la largeur des bandes et la production opportune de la coloration jaune à des endroits spécifiques. Nous avons montré que la variation de cet attribut n’est pas due à des changements dans la croissance des plumes ou dans le moment où elles déclenchent la production de jaune, mais plutôt à des différences spécifiques à l’espèce dans le profil d’expression du gène de pigmentation bien connu agouti. Ce gène est exprimé par des bandes longitudinales qui préfigurent les rayures médianes les plus importantes de chaque espèce, et des analyses du motif rayé chez des souches de cailles japonaises (fournies par D. Gourichon, INRA) dans lesquelles le niveau d’expression de l’agouti est augmenté (dans la souche Fawn) ou diminué (dans la souche Recessive Black) ont démontré fonctionnellement qu’il contrôle localement la largeur des rayures en ajustant la durée de l’impulsion de production de jaune de manière dose-dépendante.
5. Le pré-modèle Agouti est commandé par le somite
Une observation frappante de notre étude phénotypique était la position conservée des bandes médianes, ce qui nous a incités à rechercher une source précoce d’informations positionnelles contrôlant cet attribut. Pour ce faire, nous avons réexaminé la technique de lignage instrumental qui a révélé l’origine embryonnaire de la plupart des organes et des populations cellulaires en développement, à savoir la greffe hétéro-spécifique de caille-quick [38]. Ici, nous avons transplanté des tissus embryonnaires de cailles japonaises donneuses dans des faisans communs (car le poulet domestique ne présente pas de rayures). Nous avons constaté qu’après la transplantation du tube neural (d’où proviennent les cellules productrices de pigments), le schéma d’expression de l’agouti et plus tard, le schéma de couleur, étaient inchangés chez les chimères. Cependant, après avoir greffé des somites (d’où proviennent les cellules dermiques), les chimères présentaient localement une expression d’agouti semblable à celle de la caille au niveau de la greffe dans la peau en développement des hôtes, et à long terme, un motif de couleur rayé typique des donneurs. Ces résultats ont montré que le mésoderme somatique commande de manière autonome l’expression de l’agouti et, par conséquent, la position des bandes jaunes (Figure 2 ; [39, 40]).
6. Conclusion
L’ensemble des résultats a montré que le motif rayé des juvéniles de gibier à plumes est produit dans un processus en deux étapes. Tout d’abord, les somites donnent des informations de position dans le derme au début de son développement, ce qui contrôle l’établissement du profil d’expression de l’agouti dans un pré-modèle qui préfigure les rayures jaunes. La position des rayures est conservée entre les oiseaux, ce qui suggère que cette référence de développement précoce limite l’étendue de l’évolution du motif. Deuxièmement, l’agouti contrôle localement la production de jaune de manière dose-dépendante, ce qui définit la largeur de la bande. Cette dernière varie selon les espèces, ce qui suggère que cet événement de développement, qui se produit plus tard et donc potentiellement libéré des contraintes pléiotropiques, est le mécanisme sur lequel l’évolution agit. Une telle organisation séquentielle de l’espace, combinant des mécanismes locaux précoces et tardifs, peut façonner la formation et l’évolution de nombreux modèles périodiques.
Remerciements
We thank Professors Cossart, Postaire and Chapron for their invitation to contribute to « Les Comptes Rendus Biologies de l’Académie des Sciences ». This work was funded by a Labex Memolife Grant, an ERC Starting Grant, and a Schlumberger Foundation for Education and Research Grant.
English version
1. Introduction
Animals display a multitude of shapes, colours and behaviours. Particularly intriguing, many characters spatially repeat across organs in patterns key to fitness, such as hexagons, rings, labyrinthine motifs, rosettes, stripes or spots. These periodic patterns arise during embryonic development from initially homogeneous structures, which acquire positional information triggering molecular and cellular response, eventually leading to local changes in cell fate and tissue differentiation. Understanding the mechanisms that control the formation of natural patterns has been a culprit of evolutionary biologists, developmental biologists and mathematicians, who tackled this challenge for more than half a century. Their complementary methods led to two major patterning theories. In the first, positional information is provided by a source external to the pattern-forming tissue [1]. This “instruction” mechanism has been first described in the drosophila embryo. In this system, body segments gradually form along the antero-posterior axis according to local concentrations of maternal Bicoid mRNA, which forms a gradient from its anterior source [2, 3]. Since this pioneering discovery many other molecules diffusing at long-range and inducing different fates in a dose-dependent manner—so-called morphogens, have been linked to the formation of a plethora of characters organised in patterns, both in invertebrates and in vertebrates (e.g., [4, 5]). Because morphogens emanate from early embryonic structures oriented along body axes, instructional patterning intuitively explains that many periodic patterns are reproducible and have conserved orientation within taxa. However, this patterning strategy does not provide simple mechanistic principles of establishment of more complex, periodic patterns. In the second, intrinsic instabilities within the un-patterned tissue spontaneously cause a “self-organisation” of emerging characters across a developing surface. Self-organising dynamics have been first theorised in the Turing reaction-diffusion model, a partial differential equation (PDE) system which describes the dynamic interplay of at least two factors, a self-activating molecule which diffuses at long range and its short range inhibitor, produced as a response to the activator, which diffuses faster [6]. Numerical simulations of reaction–diffusion dynamics reproduce periodic motifs such as stripes or spots [7, 8, 9], as well as large size domains under certain particular conditions (e.g., high diffusion of the inhibitor; [8, 10]). More recently, Turing-like models with only one molecular factor but integrating mechanical parameters, and other self-organising systems such as chemotaxis, which describes the movement of cells towards a chemo-attractant factor, have also been successful at producing periodic patterns in silico [11, 12]. Patterning through self-organisation is thus theoretically compatible with the periodic repetition of basic motifs. A breadth of empirical work indeed supports the existence of self-organising dynamics in biological systems: expression profiles of candidate molecules or cellular dynamics—including mechanical forces they exert on their substrate, potentially corresponding to parameters of Turing’s equations, control the formation of periodically patterned organs such as turtle and shark scales, alligator teeth, feather follicles, or mammalian teeth, hair, and digits [13, 14, 15, 16, 17, 18]. In addition, self-organising models are highly malleable as subtle changes in stochastic parameters may drastically impact final patterns [8], and this can explain how variation arises. However, high flexibility of self-organising systems hardly reconciles with the reproducibility and conserved orientation of most periodic patterns. Long-opposed, instructional signalling and self-organisation both suffered from lack of experimental evidence due to the cumulative difficulties of (1) performing histological and genetic experiments in non-model organisms displaying ecologically-relevant patterns, and (2) associating candidate events occurring before spatial reference exists to final patterns.
2. Using natural variation in pattern formation studies
Scientists have always taken advantage of biodiversity to unveil the mathematical and physical laws of life or improve technology and medicine. Genetics and developmental biology in particular were born from observations of phenotypic variation, from Aristotle’s first organismal classifications to Mendel’s laws of inheritance. With the advent of modern molecular biology and the necessity to explore core developmental mechanisms in standardised model systems, studying natural populations gradually fell in desuetude besides ecological and environmental research. The current post-genomic era marked the return of trait variation as a tool for evo-devo and population genetics studies: many take advantage of morphological or behavioural differences between few species to identify the molecular bases of phenotypic evolution through forward genetics methods (i.e., GWAS or QTL analyses) or comparative expression analyses [19, 20, 21, 22, 23]. The field of applied mathematics was also deeply influenced by biological diversity and its developmental origin, mathematical systems such as PDEs being prefered because they produce timely dynamics and are permissive to extensive variation through minimam parameter modification. In our laboratory, we work to standardise and extend the use of natural variation in developmental studies, combining large scale surveys and functional experimentation in non-model species for the study of pattern formation. Our method consists in identifying common and differing attributes of a pattern by surveying its variation between species, and correlating those to common and differing embryonic processes, which allows pinpointing candidate patterning events.
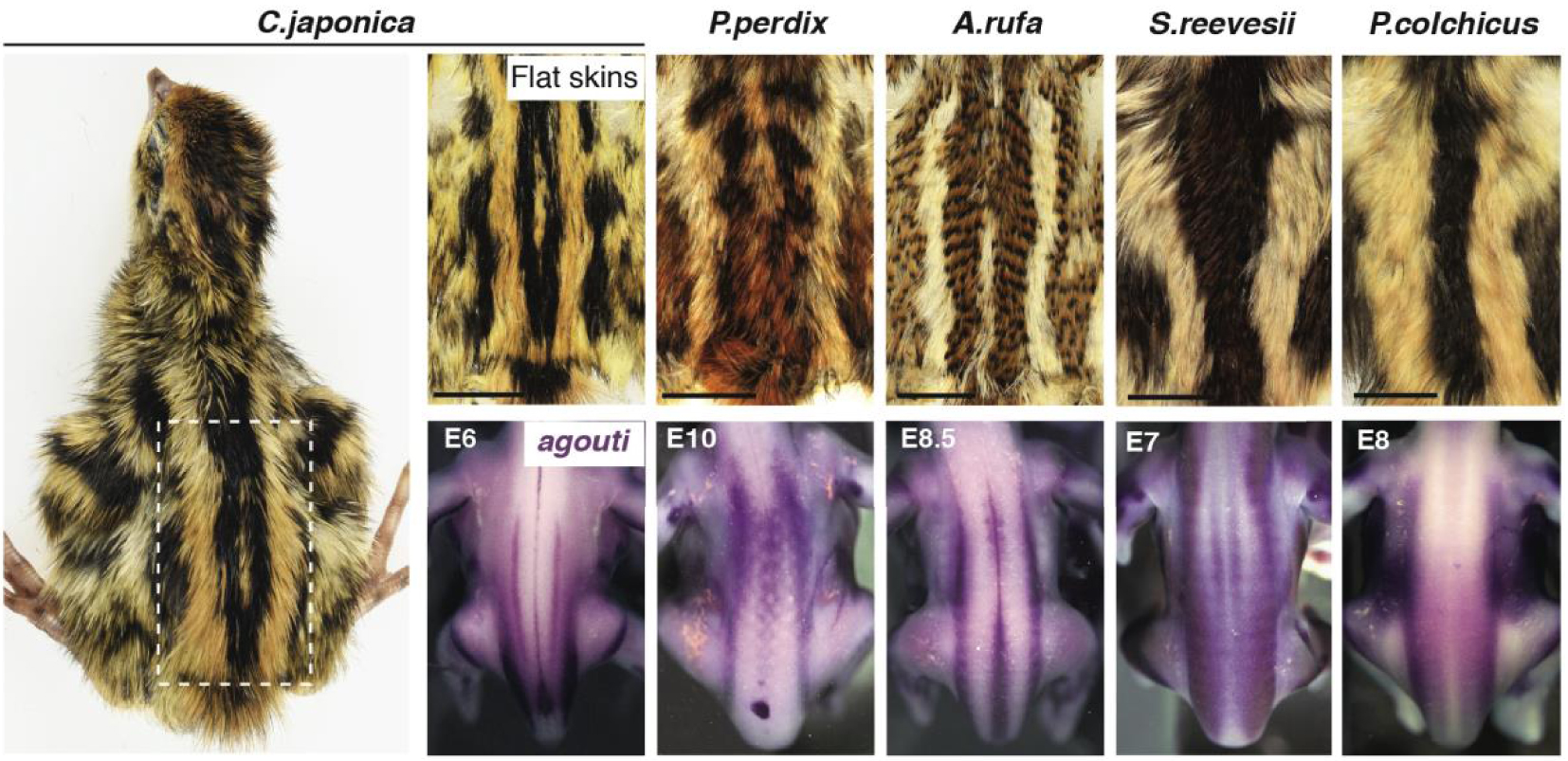
The striped pattern varies between species and is pre-patterned by agouti. Surveying feather colouration at all location of the dorsal skin in flat skin specimens of 10 species of Galliform birds (5 are shown here) evidenced that medial-most longitudinal stripes have conserved absolute location but vary in width. Both attributes are foreshadowed by early, species-specific expression of agouti in the embryo, prior to pigment production. E: embryonic day.
3. Periodic colour patterns, iconic systems for biologists and mathematicians
Living examples of most mathematically defined periodic geometries (i.e., stripes, dotted arrays) can be found in the coat of mammals, birds, reptiles and fish. These motifs result from the differential distribution of pigments in discrete compartments across the skin surface or along cutaneous appendages [24]. In birds and mammals, specialized pigment producing cells (melanocytes) synthesize black eumelanin and yellow phaeomelanin, basis of most visible motifs [25, 26]. Lineage studies showed that melanocytes are specified from the neural crest upon closure of the neural tube, and migrate ventrally in the dermis to reach their location [24, 27]. The presence of visible colour compartments may thus be due to different mechanisms, including differences in the type and amount of pigments produced, the duration of their production, a presence/absence of pigment-producing cells, or changes in their behaviour. At the time we designed our study, several pigmentation genes otherwise known to control pigment synthesis (e.g., agouti, Alx3, end3b) had been shown to display spatially restricted expression profiles in the embryonic skin such that they foreshadow future colour differences in the ventrum or of periodic stripes in the dorsum in rodents [28, 29, 30, 31]. In the zebra fish Danio rerio however, longitudinal colored stripes were shown to arise from local changes in pigment-cell type interaction during skin differentiation, an attraction-repulsion mechanism akin to Turing dynamics, which does not necessitate prior pre-patterning of the tissue [32, 33]. However, the spatial distribution of pigments is often visibly linked to anatomical landmarks in fish [34, 35, 36, 37], suggesting that pigment cell activity may be instructed by early sources. More generally, periodic patterns are often highly reproducible within species, displaying specific orientation/periodicity, which suggests their emergence could be tightly linked to pre-existing spatial references. Together, studies evidenced the key role of molecular and cellular events at play in the early embryonic skin, paving the way to link periodic colour patterns to early morphologies.
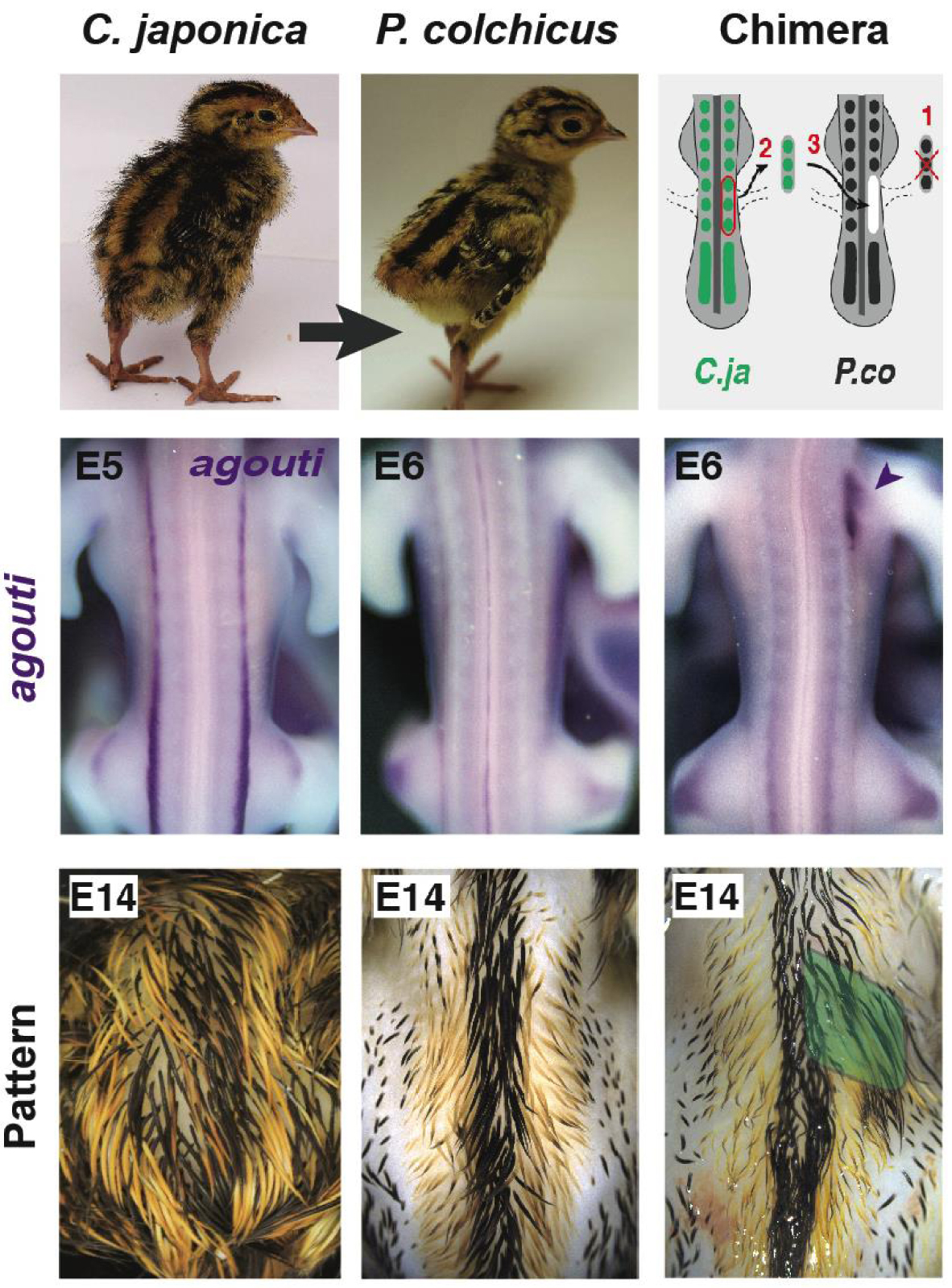
Quail-pheasant hetero-specific grafting showed somites instruct stripe location. Tissues from Japanese quail donors were transferred into pheasant hosts. When somites were transplanted, chimeras displayed a donor-like expression profile of agouti and later, plumage pattern, at the level of the graft (i.e., right under-wing region, arrowhead at E6, in green at E14). Both remained unchanged were neural tube halves were transplanted. These results demonstrated that positional signals controlling agouti pre-pattern and striped pattern establishment emanate from the somite. E: embryonic day. Masquer
Quail-pheasant hetero-specific grafting showed somites instruct stripe location. Tissues from Japanese quail donors were transferred into pheasant hosts. When somites were transplanted, chimeras displayed a donor-like expression profile of agouti and later, plumage pattern, at the level of the ... Lire la suite
4. Agouti pre-patterns periodic stripes in poultry birds
To tackle this challenge, we set to identify varying and common attributes in the transient, periodic striped pattern visible in many game birds. In this group (i.e., Galliformes) juveniles are typically characterised by dorsal longitudinal stripes displaying a black-yellow-black sequence. We surveyed 10 species by recording the colouration of all dorsal feathers and building reference maps of the striped pattern, which we found is highly reproducible within species. Quantifications showed that the number of stripes is proportional to dorsum size. Relative to this factor, the width of each homologous stripe varied between species, but notably, the absolute position of medial-most stripes along the dorso-ventral axis was comparable (Figure 1). We linked stripe width to the timely production of yellow colouration at specific locations. We showed that variation in this attribute is not due to changes in feather growth or in the time at which they trigger yellow production, but rather to species-specific differences in the expression profile of the well-known pigmentation gene agouti. This gene is expressed in longitudinal bands that foreshadow medial-most stripes in each species, and analyses of the striped pattern in strains of Japanese quails (provided by D. Gourichon, INRA) in which the expression level of agouti is increased (in the Fawn strain) or decreased (in the Recessive Black strain) functionally demonstrated that it locally controls stripe width by adjusting the duration of the yellow-production pulse in a dose-dependent manner.
5. The Agouti pre-pattern is instructed by the somite
A striking observation from our phenotypic survey was the conserved position of medial-most stripes, which prompted us to seek for an early developmental source of positional information controlling this attribute. To do so, we revisited the instrumental lineage technique that unveiled the embryonic origin of most developing organs and cell populations, namely quail-chick hetero-specific grafting [38]. Here, we transplanted embryonic tissues from donor Japanese quails were into Common pheasant hosts (as the domestic chicken does not display stripes). We found that after transplanting the neural tube (from which pigment-producing cells originate), the expression pattern of agouti and later, the colour pattern, were unchanged in chimeras. However, after grafting somites (from which dermal cells originate), chimeras locally displayed quail-like expression of agouti at the level of the graft in the developing skin of hosts, and at long-term, a typical donor striped colour pattern. These results showed that the somitic mesoderm autonomously instructs agouti expression and consequently the position of yellow stripes (Figure 2; [39, 40]).
6. Conclusion
Taken together, results showed that the striped pattern of juvenile game birds is produced in a two-step process. First, somites instruct positional information in the early developing dermis, which controls the establishment of agouti expression profile in a pre-pattern that foreshadows yellow stripes. Stripe position is conserved between birds, suggesting this early developmental reference constrains the extent of pattern evolution. Second, agouti locally controls yellow production in a dose-dependent manner, which defines stripe width. The latter varies between species, suggesting this developmental event, occurring later and thus potentially released from pleiotropic constrains, is the mechanism upon which evolution acts. Such sequential organisation of space combining early instructive foundation and late local mechanisms may shape the formation and evolution of many periodic patterns.



 CC-BY 4.0
CC-BY 4.0