1 Introduction
Synthesising magnets starting from molecular building blocks offers the opportunity to combine magnetism with other physicochemical properties. Oxalate-based compounds appear as first choice candidates in the design of polyfunctional magnets [1]. We have centred our research efforts on the synthesis of optically active magnets [2, 3] in order to study cross-effects such as magneto-chiral dichroism [4].
X-ray Magnetic Circular Dichroism is a valuable tool in the comprehension of the properties of molecule-based magnets, since it brings local information about the magnetisation of the elements present in the compounds [5]. Most of the studies are undertaken using high magnetic field in order to saturate the sample and therefore increase the signal. We will present here XMCD measurements performed at zero field. We will show how they can bring valuable information about the local remnant magnetisation of each element that is expected to be influenced by the local magnetic anisotropy.
We report in this paper the enantiomeric synthesis of {[TBA][NiIICrIII(ox)3]}n (TBA = N(C4H9)4) together with its optical and magnetic properties and then focus on the detailed description of the XMCD results. {A[MIIM′III(ox)3]}n two-dimensional compounds are made of {[MIIM′III(ox)3]}n n– honeycomb layers with n A+ cations located between these layers [6]. For M′ = CrIII, the compounds can be obtained in their enantiomeric forms starting from resolved tris(oxalato)chromate(III) [2, 3]. Within this wide family of compounds, we have chosen the nickel-chromium derivative for several reasons. First, it is possible to synthesise it in its optically active forms. We will therefore be able to demonstrate experimentally that XMCD is indeed independent of the choice of the enantiomer. Second, it is a ferromagnet below 16 K [7], which is an easily reachable temperature with the cryostat designed for XMCD experiments. Finally, using (ferrocenylmethyl)trialkyl ammonium cations, we showed that the coercive force at 2 K was over 0.2 T with high remnant magnetisation [3]. Hence, the XMCD remnant signal is expected to be important for this compound.
2 Results and discussion
2.1 Enantioselective synthesis
The synthesis of the optically active form of the compound is very alike those previously described for two- [3] and three- [2] dimensional compounds. The enantioselective reaction starting from the Δ enantiomer of tris(oxalato)chromate(III) writes:
As previously demonstrated, the rapid precipitation of the compound prevents the racemisation of the starting building block [2]. The circular dichroism (CD) spectra shown in Fig. 1 are, within concentration difference due to solid-state measurements, symmetrical with respect to the x-axis. This symmetry assesses the enantiomeric character of the two networks and hence the enantioselectivity of the reaction. The main feature (λmax = 565 nm) is attributed to CrIII d–d transitions and allows us to determine the absolute configuration of the propeller-like metallic centre in the compound: a positive (respectively negative) CD signal corresponds to the Λ (respectively Δ) configuration. The nickel signal is not obvious and cannot be attributed in an unambiguous manner, because (i) it is smaller and (ii) it cannot be compared to any tris(oxalato)nickelate(II) building block [3]. Therefore, the determination of the absolute configuration of the tris(bischelated) nickel ion follows from the heterochiral arrangement of the metal ions in the 2D compounds [1, 3].

Normalised circular dichroism spectra of the two enantiomers of {[TBA][NiCr(ox)3]}n at room temperature.
2.2 Magnetic properties
The molar susceptibility χM has been measured as a function of temperature for the two enantiomers. The χM T versus T curves show a smooth monotonic increase when decreasing the temperature and diverge at low T. The χM–1 versus T curves are linear in the 50–300-K temperature range. They can be fitted by a Curie–Weiss law χM–1 = (T – Θ)/C. The Weiss constants have the same magnitude (32 K) for the two enantiomers. The χM T value at room temperature is 3.16 cm3 K mol–1. The Field-Cooled (FC) magnetisation curves present a steep increase at 16 K. The magnetisation at saturation equals 4.45 μb at 2 K and 4.15 μb at 11 K (Fig. 2a). The magnetisation at 11 K under 2 T is 3.70 μb. The remnant magnetisation is 2.10 μb at 2 K and 1.05 μb at 11 K (Fig. 2b). The coercive force at 2 K is as high as 280 mT, while its value at 11 K is 12 mT.

Hysteresis loops at 2 K (squares) and 11 K (triangles) of {[TBA][Δ–NiΛ–Cr(ox)3]}n. (a) presents the full-scale loops while (b) focuses on the low-field region.
Both the shape of the χM T versus T curves and the sign of the Weiss constant indicate the existence of a short-range ferromagnetic interaction between the nearest paramagnetic ions in these compounds. As previously stated, the compound is a ferromagnet below 16 K [7]. The saturation value of the magnetisation is close to the spin-only value expected for a ferromagnet (5 μb). The coercive forces at 2, 5 [7] and 11 K are high for molecule-based magnets, which are most generally soft magnets. As exemplified in three-dimensional nickel(II)-containing oxalate-based networks (structural data are unfortunately unavailable for 2D compounds), the Ni(II) environment is slightly trigonally distorted [8]. The high coercive force observed in the 2D compounds can thus be related either to single ion anisotropy of the nickel(II) ion [9] associated to the magnetocrystalline anisotropy arising from the two-dimensional character of the network or to shape anisotropy [3].
2.3 X-ray Magnetic Circular Dichroism
Isotropic XANES and XMCD signals have been recorded for the two enantiomeric forms. The shape and intensities of the spectra have been found to be the same for the two isomers. We thus provide a direct proof that, as expected, they are not influenced by the structural chirality of the compounds. The isotropic XANES, the XMCD signals (× 200) and the XMCD signals in zero field (× 2000) obtained at the nickel and chromium K-edges for the Λ-isomer are reported in Fig. 3. K-edge XANES structures correspond to transitions of the 1s photoelectron to p-symmetry bound or continuum states according to the usual atomic selection rules in the electric dipolar approximation. XANES spectra at the nickel and chromium K-edges display the main features expected for transition metal ions in nearly octahedral surroundings (Fig. 3a) [10].
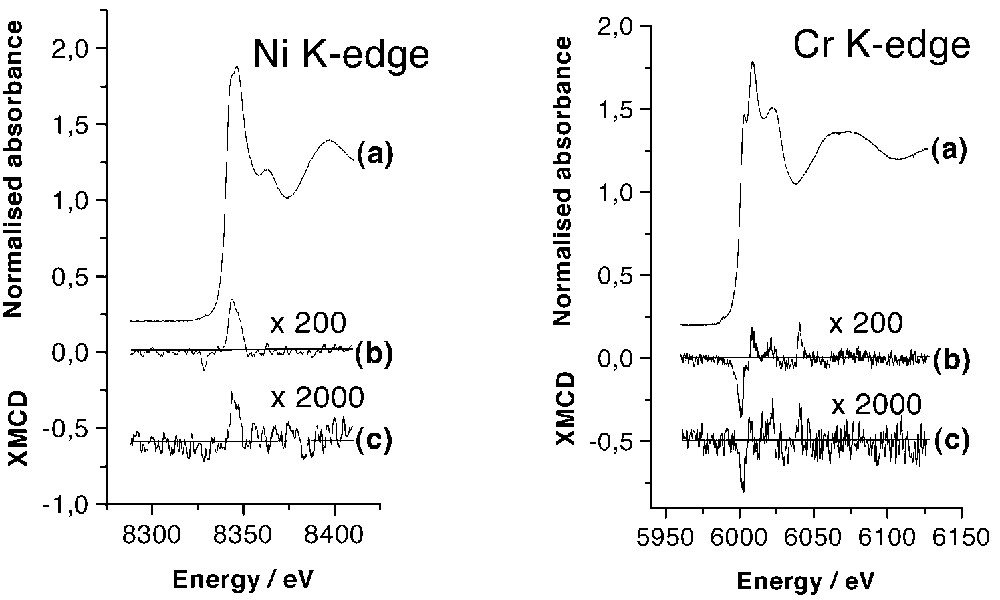
Isotropic XAS spectra: (a) XMCD signals (× 200) measured at 11 K in H = ±2 T; (b) XMCD signals (× 2000) measured in zero field after applying H = ±2 T (c) XMCD signals of {[TBA][Δ–NiΛ–Cr(ox)3]}n at Ni K-edge (left) and Cr K-edge (right).
A XMCD signal of weak intensity (< 0.35% of the isotropic spectra) is present at the two edges, in the energy range corresponding to the allowed transition to the p-symmetry levels of the metal (Fig. 3b). The intensity is quite the same at the two edges. In contrast with the L2,3-edges, for which XMCD signals can be as large as 100%, the XMCD signals at the K-edges are never larger than a few tenths of a percent of the atomic cross-section. The small intensity of the signals is due to the absence of spin-orbit coupling in the 1s level and to the weakness of the spin-orbit coupling in the final state [11]. The sign of the dichroic signal is directly related to the direction of the magnetic moments compared to the one of the magnetic field, due to the 3d unpaired electrons [12]. So, the magnetic exchange interaction between the nickel and chromium ions can be directly deduced from the analysis of the sign of the XMCD signals. In the compound, the shape of the XMCD signal, negative then positive, is the same at the two edges. Moreover, the signals have the same shape as those obtained for the molecule-based magnet CsINiII[CrIII(CN)6], in which the exchange interaction between CrIII and NiII cations is ferromagnetic [13]. Hence XMCD results directly evidence the ferromagnetic exchange interaction between the nickel and the chromium cations deduced from the analysis of the macroscopic magnetic measurements.
At the chromium K-edge, an additional structure is observed 40 eV after the absorption edge in the XMCD signal. This feature was predicted by multiple scattering calculations performed with potentials taking into account the spin-orbit coupling, which is responsible for XMCD [13, 14]. These calculations show that close to the edge, the spin-orbit scattering of the photoelectron by the magnetic neighbouring sites with also part scattering by the potential of the absorbing atom is the major contribution to the XMCD signal. At higher energy, XMCD comes essentially from the difference between spin-up and spin-down density of empty states.
After applying a magnetic field of H = ±2 T, a remnant signal is observed at the two edges (Fig. 3c). The shape is the same as the one of XMCD spectra recorded with H = ±2 T, but the intensity of the two remnant signals is ten times smaller. ±2 T XMCD and remnant XMCD signals can be compared to the macroscopic remnant magnetisation measured at T = 11 K by conventional magnetometry (Fig. 2). At this temperature, the remnant macroscopic magnetisation is divided by 4 compared to the value reached at ±2 T. Hence, the XMCD intensities appear more than two times smaller than expected from macroscopic measurements. Two explanations can be put forward for this difference: (i) the temperature of the sample can be a little bit higher than the value given by the thermocouple (nevertheless, the existence of the remnant signal indicates that the temperature is well below the Curie temperature, e.g. 16 K); (ii) since the acquisition time is long (several hours), the magnetisation may partly reverse during the XMCD measurement. The similarity of ±2 T XMCD and remnant XMCD signals for the two ions means that, despite the anisotropic character of the NiII ion compared to the CrIII, the local magnetic moments relax in the same way for the two cations. In other words, the exchange interaction between the two metal ions is strong enough to impose a similar evolution of the magnetisation born by each element, regardless the difference of single ion anisotropy of NiII and CrIII cations.
3 Concluding remarks
We report XMCD results at the Ni and Cr K-edges for the optically active oxalate-based magnet {[TBA][NiCr(ox)3]}n. As expected, the XMCD signal is independent of the choice of the enantiomer. The XMCD signals at Ni and Cr K-edges, which are proportional to the local magnetic moments born by the two spin carriers, confirm the local ferromagnetic exchange interaction between the two ions deduced from the analysis of macroscopic magnetic measurements. We evidenced a remnant XMCD signal at H = 0 T at the two edges. Surprisingly, the relative remnant local magnetic moments are the same for CrIII and NiII cations, despite the expected anisotropic character of the nickel(II) ion. To evidence the relative role of local anisotropy, magnetocrystalline anisotropy and exchange interaction, a better system would be the Co–Cr analogue, for which the important spin-orbit coupling for the CoII cation is well known [15].
These experiments in zero field open new perspectives. They can be used to suppress undesirable signals arising from paramagnetic impurities in the studied compounds [16]. Moreover, a remnant XMCD signal of a paramagnetic ion included in a magnetically long-range-ordered material would arise from the internal magnetic field created by the magnetic network. This new probe of the internal magnetic field, compared to Mössbauer spectroscopy, would not be restricted to iron-containing compounds.
4 Experimental section
4.1 Synthesis
4.1.1 Materials
K3[Cr(ox)3]·3 H2O was prepared and resolved according to the literature methods [17]. The other reagents are commercially available and were used as purchased.
4.1.2 Synthesis of optically active {[TBA][NiCr(ox) 3]}n
To a methanolic solution of tetrabutylammonium bromide (0.428 g in 0.5 ml, 1.33 mmol) was added an aqueous solution (1.5 ml) containing NiCl2·6 H2O (158 mg, 0.66 mmol) and, dissolved just before addition, resolved K3[Cr(ox)3]·3 H2O (325 mg, 0.66 mmol) ([α]D = 1250° for Λ and [α]D = –1200° for Δ). The mixture was scratched in order to provide a rapid precipitation of the compound. The solution was filtered off, washed twice with water, twice with methanol and dried with diethyl ether. 200 mg (yield: 50%) of product was collected starting from Λ–[Cr(ox)3]3– and 225 mg (yield: 56%) of product was collected starting from Δ–[Cr(ox)3]3–.
{[TBA][Λ–NiΔ-Cr(ox) 3]} n: IR (KBr) cm–1: 2966, s; 2936, m; 2878, m; 1622, vs; 1466, m; 1438, m; 1384, w; 1340, w;1298, m; 1093, m; 912, w; 822, m; 546, m; 475, m; 432, m; 406, m; anal. calc. for C22H36NO12CrNi: C, 42.81; H, 5.88; N, 2.27; found: C, 41.8; H, 6.3; N, 2.6
{[TBA][Λ–NiΔ-Cr(ox) 3]} n: IR (KBr) cm–1: 2970, s; 2940, m; 2879, m; 1623, vs; 1467, m; 1440, m; 1384, w; 1341, w;1299, m; 912, w; 822, m; 546, m; 475, m; 432, m; 406, m; anal. calc. for C22H36NO12CrNi: C, 42.81; H, 5.88; N, 2.27; found: C, 42.95 ; H, 6.31; N, 2.77.
4.2 Physical techniques
The IR spectra were recorded on a Bio-Rad IRFT spectrophotometer as KBr pellets in the 4000–250 cm–1 region. Elemental analyses were completed at the SIAR–UPMC, Paris. Specific rotations of the starting materials were measured at 20 °C, in a 1-dm tube containing the aqueous solution, using the sodium D line in a polarimeter Ameria A5. Circular dichroism spectra were recorded with a Jasco model J-710 spectropolarimeter. Measurements were made on 0.1–1 mg of solid dispersed in 100 mg of oven-dried KBr. 13-mm diameter disks were made in a standard disk press. The displayed absorption spectra result from substraction of the spectrum of a pure KBr disk, followed by a normalisation at one of the dichroic signal for the extremum observed at 565 nm.
4.3 Magnetic measurements
The magnetic measurements of powdered samples were performed between 2 and 300 K using a Quantum Design MPMS5 SQUID magnetometer. The hysteresis loops were measured at 2 and 11 K. The field-cooled (FC) magnetisation versus temperature curves were measured in a 0.01-T external field. The susceptibility curve was measured in a 0.1-T external field and corrected for diamagnetism and temperature independent paramagnetism.
4.4 XAS and XMCD data collection
The spectra were recorded at the Cr and Ni K-edges at the energy dispersive absorption line of the DCI ring at LURE (Orsay), using a Si (111) curved polychromator focusing the beam on the sample between the poles of a magnetic coil. Right circularly polarised photons were selected by positioning a 1-mm wide slit 5.5 mm below the ‘orbit plane’ and the circular polarisation rate was 70%. The spectra were recorded at T = 11 K. To obtain the XMCD signals, spectra were recorded with an applied magnetic field of H = 2 T alternatively parallel and antiparallel to the direction of the photon beam. The XMCD signal was taken as the difference between the two spectra. The remnant XMCD signals was recorded at H = 0 T after applying alternatively the H = 2 T magnetic field parallel and antiparallel to the direction of the photon beam.
Acknowledgements
The authors thank Laurent Legrand (GPS, UPMC, Paris, France) for his efficiency to solve magnetometry problems. They also thank the CNRS (France), ‘Université Pierre-et-Marie-Curie’, ‘Paris-6’ (France), the European Community (TMR ERBFMBICT972644 and FMRXCT980181), and the European Science Foundation (Molecular Magnets Programme) for financial support.



