Multiphase structure and physical properties of organic composites obtained by mechanochemical reaction between BEDT–TTF and iodine-derived acceptors. An overview

Andrzej Graja; Mykola Golub

doi:10.1016/S1631-0748(03)00055-9

Multiphase structure and physical properties of organic composites obtained by mechanochemical reaction between BEDT–TTF and iodine-derived acceptors. An overview

Andrzej Graja ¹ ; Mykola Golub ¹

¹ Institute of Molecular Physics, Polish Academy of Sciences, 60–179 Poznań, Poland

Comptes Rendus. Chimie, Volume 6 (2003) no. 3, pp. 367-375.

Résumés

Anglais
Français

The results of the studies of the physical properties of organic composites obtained by direct solid–solid charge-transfer (CT) reaction between bis(ethylenedithio)tetrathiafulvalene (BEDT–TTF) and iodine or gold iodide are presented and discussed. It is shown that the analysis of experimental data of dc conductivity and thermoelectric power and the relation between morphology of composites and their electrical properties result in understanding the charge transport phenomena and allow to propose the model of electrical transport in these materials. The main factors that affect the electrical properties of composites are recognized and the ways of controlling these factors and tuning the electrical properties are proposed.

Nous présentons les résultats de nos études sur les propriétés physiques de composites organiques obtenus par une réaction de transfert de charge réalisée directement à l’état solide entre le bis(éthylènedithio)tétrathiafulvalène (BEDT–TTF) et l’iode ou l’iodure d’or. L’analyse des études de la conductivité électrique, de la force thermoélectrique ainsi que de la relation entre la morphologie des composites et leurs propriétés électriques est donnée. Cette analyse a permis d’expliquer l’effet du transfert de charge et de proposer un modèle représentatif du transport électrique dans ces matériaux. Les principaux facteurs déterminant les propriétés électriques de composites sont indiqués. Le rôle de ces facteurs ainsi que les possibilités d’obtention des propriétés électriques sont proposés.

Métadonnées

Reçu le : 2002-10-15
Accepté le : 2003-02-12
Publié le : 2003-03-01

DOI : 10.1016/S1631-0748(03)00055-9

Keywords: Full paper, electrical conductivity, thermoelectric power, organic conducting composites, BEDT–TTF, hot-pressing
Mots clés : Mémoire, conductivité électrique, force thermoélectrique, composites organique de haute conductivité, BEDT–TTF, hot-pressing

Affiliations des auteurs :

Andrzej Graja ¹ ; Mykola Golub ¹

¹ Institute of Molecular Physics, Polish Academy of Sciences, 60–179 Poznań, Poland

@article{CRCHIM_2003__6_3_367_0,
     author = {Andrzej Graja and Mykola Golub},
     title = {Multiphase structure and physical properties of organic composites obtained by mechanochemical reaction between {BEDT{\textendash}TTF} and iodine-derived acceptors. {An} overview},
     journal = {Comptes Rendus. Chimie},
     pages = {367--375},
     publisher = {Elsevier},
     volume = {6},
     number = {3},
     year = {2003},
     doi = {10.1016/S1631-0748(03)00055-9},
     language = {en},
}

TY  - JOUR
AU  - Andrzej Graja
AU  - Mykola Golub
TI  - Multiphase structure and physical properties of organic composites obtained by mechanochemical reaction between BEDT–TTF and iodine-derived acceptors. An overview
JO  - Comptes Rendus. Chimie
PY  - 2003
SP  - 367
EP  - 375
VL  - 6
IS  - 3
PB  - Elsevier
DO  - 10.1016/S1631-0748(03)00055-9
LA  - en
ID  - CRCHIM_2003__6_3_367_0
ER  -

%0 Journal Article
%A Andrzej Graja
%A Mykola Golub
%T Multiphase structure and physical properties of organic composites obtained by mechanochemical reaction between BEDT–TTF and iodine-derived acceptors. An overview
%J Comptes Rendus. Chimie
%D 2003
%P 367-375
%V 6
%N 3
%I Elsevier
%R 10.1016/S1631-0748(03)00055-9
%G en
%F CRCHIM_2003__6_3_367_0

Andrzej Graja; Mykola Golub. Multiphase structure and physical properties of organic composites obtained by mechanochemical reaction between BEDT–TTF and iodine-derived acceptors. An overview. Comptes Rendus. Chimie, Volume 6 (2003) no. 3, pp. 367-375. doi : 10.1016/S1631-0748(03)00055-9. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/S1631-0748(03)00055-9/

Version originale du texte intégral

1 Organic charge-transfer complexes: single crystals and composites

As a rule, organic conductors are produced by means of a charge-transfer (CT) reaction, in an appropriate solvent, between two crystalline insulating components, one being an electron donor, the other being an electron acceptor. The charge-transfer reaction results in the ionisation of these two neutral moieties and in their molecular association to form a third crystalline and conducting solid. Hundreds of crystalline CT solids have so far been synthesised and investigated, and their electrical properties are covering quite a wide range from poor semiconducting to superconducting [1, 2].

CT complexes and cation- or anion-radical salts usually exhibit a higher packing density of the molecules as compared with the molecular crystals, hence the forming ion radicals are located close to each other. Their three-dimensional structures consist of regular arrangements of either conducting chains or conducting planes and, hence, they often exhibit highly anisotropic properties.

Single crystals of the organic semiconductors obtained by a partial reduction of the acceptor molecule (e.g., TCNQ) to the anion-radical state, under the influence of appropriate donors or of the organic metals and superconductors prepared by anodic oxidation of the solution of the donor (e.g., BEDT–TTF), in the presence of a supporting electrolyte, are of relatively good quality. Their habit is adequate to the crystal symmetry and their faces are well developed and glassy. Number of the crystal defects can be kept low by the choice of solvents and suitable conditions of the crystallisation. The single crystals exhibit distinct anisotropy reflecting the specific ordering of the molecules/ions (usually one-dimensional in organic semiconductors and one- or two-dimensional in organic metals or superconductors). Unfortunately, the dimensions of the single crystals of organic metals based on BEDT–TTF or related donor molecules are usually much less than 1 mm. In addition, they are brittle and mechanically not resistant; this is why they are not of great practical interest.

The way chosen by Brau and Farges [3, 4] to overcome these shortcomings rests on producing the conducting material, as a composite material, by the way of CT reaction between the organic electron donor and acceptor moieties occurring directly in the solid phase. The reaction between almost any donor or acceptor component is accomplished directly in the solid state, simply by grinding the two components together. The resulting powdered mixture would then be compacted under 5-kbar pressure to form a disk, for example. The method is quite simple and inexpensive; it works for almost any donor–acceptor pair and it is a convenient way to produce samples of nearly unlimited size. The size without limit and any form of the composite samples are their main advantages over the single-crystal technology. The physical properties of such composites roughly resemble the properties of their crystalline analogues obtained by the traditional ways [5–7]; their isotropic properties are the only exception. However, the grains forming the composite sample are anisotropic and show all the properties typical of single crystals. The method of Brau and Farges [3, 4] has already been widely exploited by our group [7–10].

2 Principles and remarks on the composite technology

To understand the physics and chemistry of the process in mechanically treated solid mixtures, it is necessary to consider what makes the interface between two solids. When two phases are brought into contact, their properties are changed substantially in the contact area. The depth of this interface region and the character of the changes depend on the physical nature of the two solids. Among these changes, the following have to be noted [11]: (1) distortion of the crystal structures of contacting solids, (2) redistribution of electrons at the contact between two solids with different contact potential and (3) redistribution of the point defects at the interface. As a result of changes in the structure, composition, concentration of electrons and ionic defects, the physicochemical properties at the interface are essentially different from those in the bulk. In particular, an approach of easy deformable organic grains of different electron properties (electron donor or acceptor) can lead to the CT reaction between them, and formation of the CT complexes.

As it was shown by Brau et al. [12], the first step of the solid–solid reaction and its kinetics can be investigated by direct observation under microscope of the contact established between the two microcrystals, e.g., TCNQ and TEA⁺I^–. The solid–solid CT reaction is evidenced by a significant blackening which starts just at the contact between the two crystals and it involves a diffusion process that goes from the donor to the acceptor moieties.

To make a composite, the two polycrystalline moieties have to be ground together, so that the mean size of the individual grains gradually decreases. During this process, not only the number of instantaneous contact points increases, but also these point contact interfaces change randomly. This is why the kinetics of the reaction, and thus, its efficiency, are significantly dependent on grinding conditions [5]. When two polycrystalline reactants are ground together, two effects are in fact competing: together with the expected CT reaction effect, there is also a charge localisation side effect. The first effect results in the increase of an electrical conductivity, σ, of the sample, via the increase of the charge-carrier density, while the second effect inhibits the conductivity due to the decrease of the charge carrier mobility. In the first step of the reaction, the first effect is dominant and σ increases; in the second step, the reaction is almost completed, the charge localisation effect becomes dominant, and σ decreases [5]. Thus, it is evident that a particular grinding time is a valuable reference parameter for making the composites with optimal conductivity.

When two solids are treated mechanically the temperature of the contact also changes. In the case of organic solids, this effect is not so important, because of the considerable deformation of the grains while crashed. On the other hand, the mechanochemical reaction can be completed by the appropriate thermal treatment of the sample [4]. This is why the composite samples are usually annealed at the defined time and temperature. It was found experimentally that the electrical conductivity of annealed BEDT–TTF-derived composites changes its value [13] and also its character. For example, the composite (BEDT–TTF)₂/I₃ becomes not only metallic, but shows the onset of superconductivity after the annealing, first for 2 h at 85 °C then for 5 min at 155 °C [14]. The composites of BEDT–TTF with gold iodides acceptors annealed at 80–85 °C during 2 hours and at 155 °C during several minutes, offer metallic properties though they were semiconducting just after preparation [9, 13, 15].

3 Multiphase structure of the organic highly conducting composites

Morphology of the surface of the composites of general formulae (BEDT–TTF)_x/(AuI) and (BEDT–TTF)_x/(AuI₃) depends on their composition, conditions of the synthesis and annealing procedure [8]. Usually, the morphology of the composite resembles the texture of a sponge. It has been suggested from X-ray diffractograms and Raman spectra that these composites are mainly built of (BEDT–TTF)₂I₃ and (BEDT–TTF)₂AuI₂ grains [16]. This composition was confirmed and detailed by SEM imaging, and first of all an energy dispersive X-ray analysis (EDX) [8, 10]. From these studies, it is clear that besides (BEDT–TTF)₂I₃ and (BEDT–TTF)₂AuI₂ crystallites, the neutral grains of metallic gold occur in the composites. This structure corresponds to the donor to acceptor molecular ratio of x_opt = 0.8 for (BEDT–TTF)_x/(AuI) and of x_opt = 2.0 for (BEDT–TTF)_x/(AuI₃) samples, i.e. the compositions corresponding to the maximum of the electrical conductivity, σ. It was also determined that the conducting grains are separated by amorphous matter of various composition and different electrical properties. A typical SEM micrograph of (BEDT–TTF)_2.17/(AuI₃) composite surface is shown in Fig. 1. Almost regular microparticles can be attributed to (BEDT–TTF)₂I₃ and (BEDT–TTF)₂AuI₂ crystallites, but the clear, light spots can be attributed to the neutral Au grains.

Fig. 1
Scanning electron microscope micrograph of the surface of the (BEDT–TTF)_2.17/(AuI₃) composite after sample annealing.

EDX microanalysis of (BEDT–TTF)_x/(AuI) and (BEDT–TTF)_x/(AuI₃) composites performed for their various areas of 2–4 μm in diameter [10] confirmed the above-suggested composition of the samples. This was revealed from the energy spectra showing the contents of elements in the investigated areas or as two-dimensional images visualising a surface distribution of elements (Fig. 2) with reference to the SEM image of the examined surface. These pictures show contents and surface distribution for such elements as: C, O, S, I, and Au. For analysis of mutual arrangement of the elements, the images have been processed by using a two-point spatial correlation function of element distribution [10]. Among other things, the analysis gives the evidence for a coincidence between light spots localisation and groups of points representing the gold contents. The concentration of points representing the iodine element is lower at these places. Contrary to the free gold, free iodine does not form separate grains, but is evenly distributed between other microparticles. Grey areas in the images should be attributed mainly to (BEDT–TTF)₂I₃ and (BEDT–TTF)₂AuI₂ crystallites.

Fig. 2
Two-dimensional image visualising a surface distribution of the elements: carbon, oxygen, sulphur, iodine and gold in reference with SEM image of the (BEDT–TTF)_0.82/(AuI) composite before the sample annealing.

From the SEM and EDX investigations, one can state also that the annealing of the composite leads to development and completion of the CT reaction, as well as to the chemical exchange between components.

4 Some aspects of the theory of electrical transport in the multiphase materials

The composites show a granular structure with grains and voids of different electrical properties. The grains facilitate transport properties of crystalline materials. Usually, their transport shows metal-like nature with electrical conductivity dominated by delocalised electrons. If grains have many defects, interaction of electrons with these defects tends to localisation of electrons in the grains. The voids are empty or are filled with amorphous matter of various compositions, usually insulating, which is opposite to the grains. Thus, the electrical conductivity of such heterogeneous composites is restricted by electron transfer between large conducting grains.

There are several mechanisms of charge transport between conducting grains in heterogeneous materials. Which mechanism wins depends on the shape and size of grains, the distance between grains and other factors. The most probable mechanism that takes place in our composites is fluctuation-induced tunnelling conduction. The model of this mechanism was elaborated by Sheng [17] to describe the conductivity in heterogeneous materials with relatively large conducting islands separated by small insulating barriers. According to this model, the thermally activated voltage fluctuations across insulating gaps modulate the effective barrier height and play an important role in the determination the temperature and field dependencies of the conductivity. Assuming a parabolic barrier, the temperature dependence of the fluctuation-induced tunnelling conductivity, σ(T) is given by:

σ (T) = σ_{0} \exp (- \frac{T_{1}}{T + T_{0}})

1

where σ₀ is a slowly varying function of T as compared to the exponential term. Parameters T₀ and T₁ depend on properties of contacts between grains: their length w, area A and height of potential barrier V [18].

In the case when only two process of transport dominate, i.e. metallic conduction in grains and fluctuation-induced tunnelling between these grains, one can use the simplest model of composite as a system of arrays of resistors of two types: one represents the resistance of contacts and the other represents the resistance of the grains. The resistance of contact is described by the formula (1) for field-induced tunnelling. The resistance of grains can be expected to vary as T^α. Hence, the temperature dependence of conductivity of such a system would be:

σ (T) = {[C_{1} \exp (\frac{T_{1}}{T + T_{0}}) + C_{2} T^{α}]}^{- 1}

2

where C_i are geometrical factors depending on the fraction L_i, of the sample length and of the sample cross-section area A_i. Index i = 1, 2 for the intergrain regions and for the conducting grains, respectively.

Investigations of the temperature dependence of thermoelectric power can yield additional information about the transport properties of these materials. Thermoelectric properties of inhomogeneous materials were accounted by Webman et al. [19] in terms of the effective-medium theory and by numerical simulations. In particular, two phase system has been considered and the following constrains were imposed:

σ_{1} < < σ_{1}, P_{1} < < P_{2}

3

where σ_i is the electrical conductivity, P_i = σ_i S_i, and S_i is the thermoelectric power of phase i. In this case, for all concentrations C of the conducting phase for which σ₁ << σ(C) , i.e. C ≥ 0.5, only the conducting phase gives a contribution to the thermoelectric power:

S \approx S_{2}

4

The influence of the insulating phase appears only at small concentration of the conducting phase. Below the percolation threshold C*, when σ₁ << σ₂, S₁ >> S₂, and the thermal conductivities of phases are approximately equal, the thermoelectric power as a function of C is described by the formula:

S (C) = S_{1} \frac{σ_{1}}{σ (C)} = S_{1} \frac{C * - C}{C *}

5

Assuming a constant thermal conductivity for both phases, the following formula applies for the whole range of concentrations C [20]:

S (C) = \frac{\sum_{i} f_{i} σ_{i} S_{i}}{\sum_{i} f_{i} σ_{i}}

6

where f_i is the volume fraction of phase i.

We will use these relations for the interpretation of our experimental data for (BEDT–TTF)_x/(AuI) and (BEDT–TTF)_x/(AuI₃) composites.

5 Transport properties of the conducting BEDT–TTF-derived composites: their dc conductivity and the thermoelectric power

For dc conductivity measurements by four-probe method, samples were shaped in the form of bars on which gold contacts were evaporated and silver wires were glued with silver paint. In thermoelectric power measurements, a rectangular sample is mounted between two silver blocks through an indium layer. A temperature difference from 0 to 1 K is established by gradually heating one of the silver blocks and is monitored with differential thermocouple. The thermoelectric power is deduced from the slope of electromotive force between two ends of the sample vs. the temperature difference. Both dc conductivity and the thermoelectric power are measured in temperature range of 4–300 K. For more detailed description of the experiment, see [9, 21].

The values of the conductivity measured at room temperature of the composites strongly depend on their composition expressed by the parameter x, as is shown in Fig. 3. The maximum of the conductivity occurs at x_e_x_p = 0.82 for (BEDT–TTF)_x/(AuI) and x_e_x_p = 2.0 for (BEDT–TTF)_x/(AuI₃). These two values correspond well with those obtained on the basis of the stoichiometry of the two composites: x_cal = 0.8 and x_cal = 2.0, respectively [8].

Fig. 3
The dc electrical conductivity of the (BEDT–TTF)_x/(AuI₃) (a) and (BEDT–TTF)_x/(AuI) (b) composites vs. parameter x, for annealed samples.

The results of the dc conductivity study of (BEDT–TTF)_x/(AuI) and (BEDT–TTF)_x/(AuI₃) composites were reported earlier [9]. Here we will only draw the attention to the relevant aspects of these studies. As an example, the temperature dependencies of the dc electrical conductivity for some selected composites are presented in Fig. 4. The conductivity of both (BEDT–TTF)_x/(AuI) and (BEDT–TTF)_x/(AuI₃) composites shows a semiconducting character before annealing. The most probable origins of this behaviour are: (1) an interaction of charge carriers with defects in conducting grains, which tends to their localisation, and (2) electron tunnelling between the grains. These undesirable processes can be suppressed by annealing, when two processes take place: (1) completion of the CT reaction effects (the grains growth and an enhancement of the intergrain contacts), and (2) recrystallisation of grains that tend to the formation of a β-phase [8, 16, 22]. The first process eliminates charge localisation and the second improves the electron transport between the grains.

Fig. 4
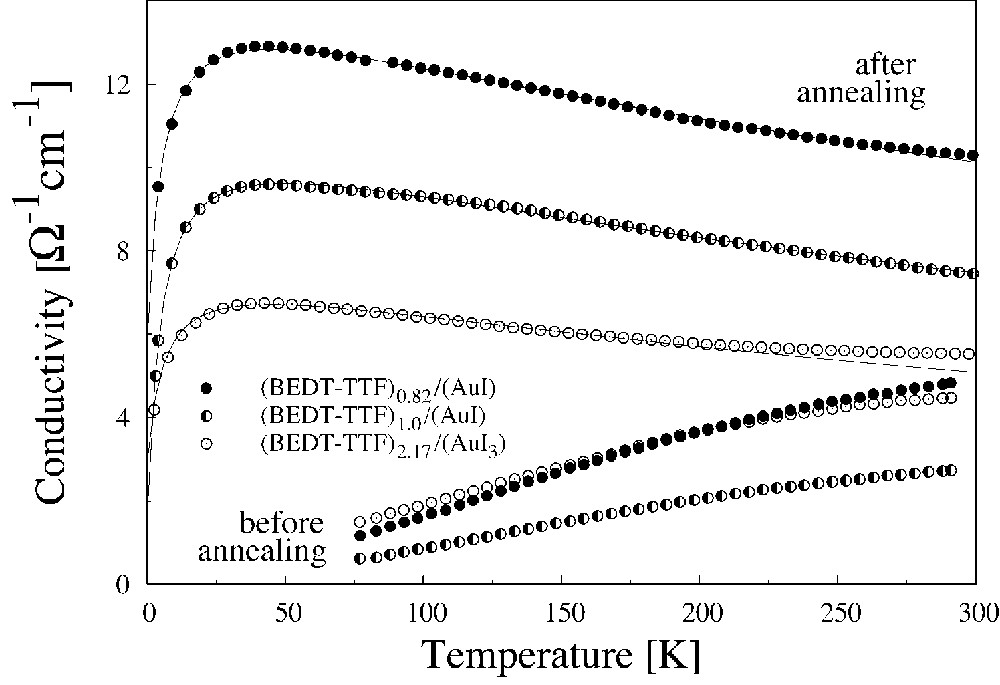
Typical temperature dependence of the dc electrical conductivity of (BEDT–TTF)_x/(AuI) and (BEDT–TTF)_x/(AuI₃) before and after annealing. Solid curves are fits to Eq. (2).

Conductivity of the annealed composites shows metal-like properties (if their compositions are not very far from the optimal). The metallic character of conductivity is observed down to about 25–30 K. Below this temperature the T-dependence of conductivity shows the exp[–T₁/(T+T₀)] character and therefore is mainly determined by fluctuation-induced tunnelling of electrons between grains. The experimental data can be fitted by Eq. (2). This allows us to assume that the annealing of the composites makes the influence of electron localisation negligible and inhibits (but does not eliminate entirely) the undesirable effect of intergrain tunnelling. From fitting parameters T₀ and T₁, one can obtain information about such characteristics of the composites as their length w, area A of contacts between grains and height of potential barrier V [18]. An analysis of changes of these values with x, annealing conditions, grinding time and other parameters of composite preparation can give us useful information to understand processes taking place during composite formation. As an example, Fig. 5 shows the changes of A and w with x for (BEDT–TTF)_x/(AuI) composites. At x ≈ x_opt, there is a minimum for the contact width w and therefore there are the best conditions for electron transport between the grains. So, one of the way of an increase of the composite conductivity and thus of obtaining materials of better electrical properties is to decrease the grain separation through an improvement of contacts between the grains.

Fig. 5
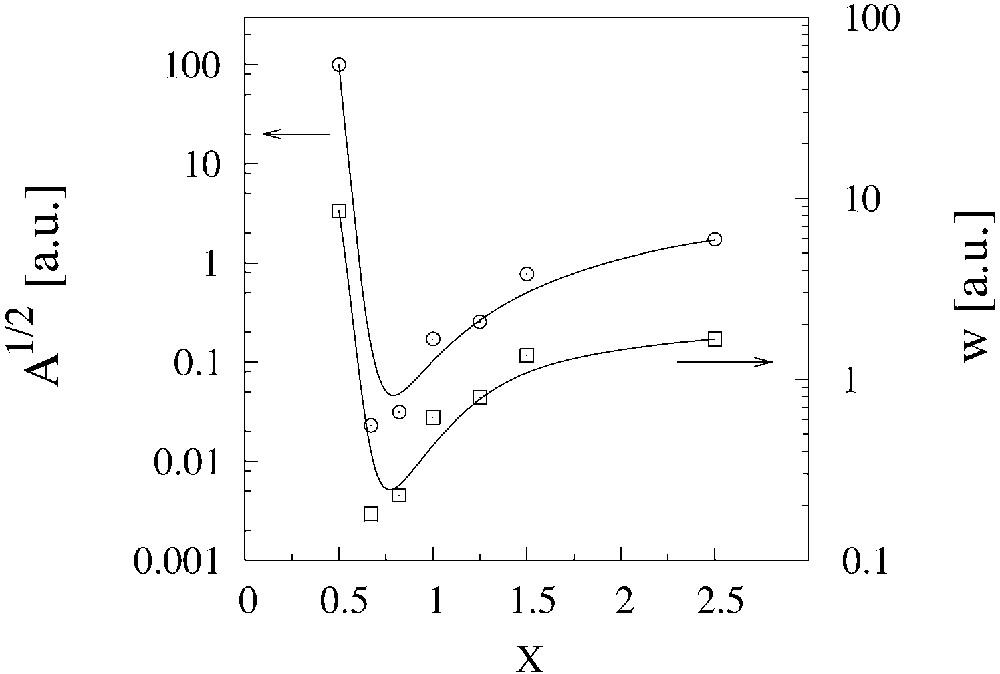
Dependence of the intergrain contact width w and area A vs. composition x for the (BEDT–TTF)_x/(AuI) composites. Values of w and A are obtained from fitting parameters T₀ and T₁ using equations from [20].

However it is difficult to suppress the intergrain effect to such a degree that the character of the conductivity could be metallic in the whole range of temperatures. In some cases, it can be achieved by careful tuning of the conditions of composites preparation, especially of the procedure of their annealing. By this way, the metallic (BEDT–TTF)₂/I₃ composite in the whole range of temperature was obtained by Smirani et al. [6], but the preparation of fully metallic (BEDT–TTF)_0.82/(AuI) composite was reported by us [13].

To make the technology of composite preparation more reliable and produce composites with better electrical properties, we have adopted and developed a hot pressing technique [21]. Two procedures, pressing of a milled donor–acceptor mixture and its annealing, were combined together to achieve better conditions of contact formations between conducting grains. The milled reacted powder is pressed in temperature 80–85 °C for several hours. Then the composite is annealed some more at temperature 155 °C during about 10 min. The procedure of annealing at 155 °C cannot be a part of the hot-pressing procedure, because the powder begins to react with an iron press at such temperatures and cannot be pulled out from it without damage.

The effect of the hot-pressing technology of preparation of the (BEDT–TTF)₂/I₃ composite is shown in Fig. 6. The composites obtained by hot pressing method show sharper decrease of their resistivity with the temperature decreasing and remain metallic in the whole temperature range. This method permitted us to obtain the metallic (BEDT–TTF)_0.82/(AuI) composite down to lowest temperatures (Fig. 7).

Fig. 6
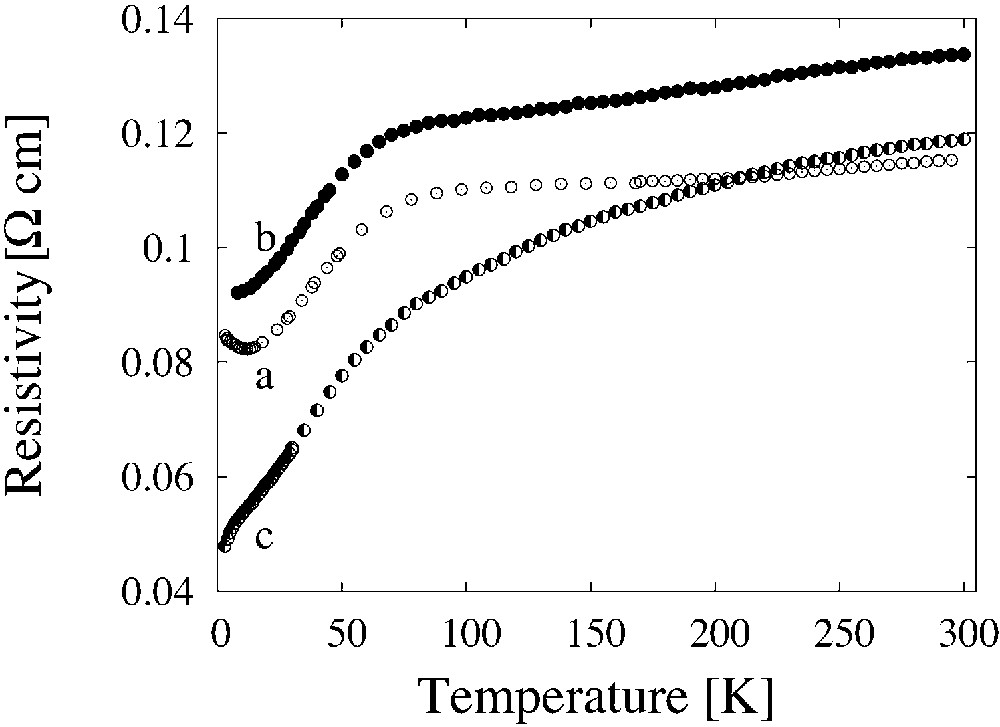
Temperature dependence of the resistivity of the composites (BEDT–TTF)₂/I₃ obtained by different technologies: (a) ordinary method, annealing 2 h at 90 °C and 10 min at 155 °C; (b) hot pressing during 2 h at 60 °C, annealing during 2 h at 90 °C and 10 min at 155 °C; (c) hot pressing during 2 h at 80 °C, annealing during 10 min at 155 °C.

Fig. 7
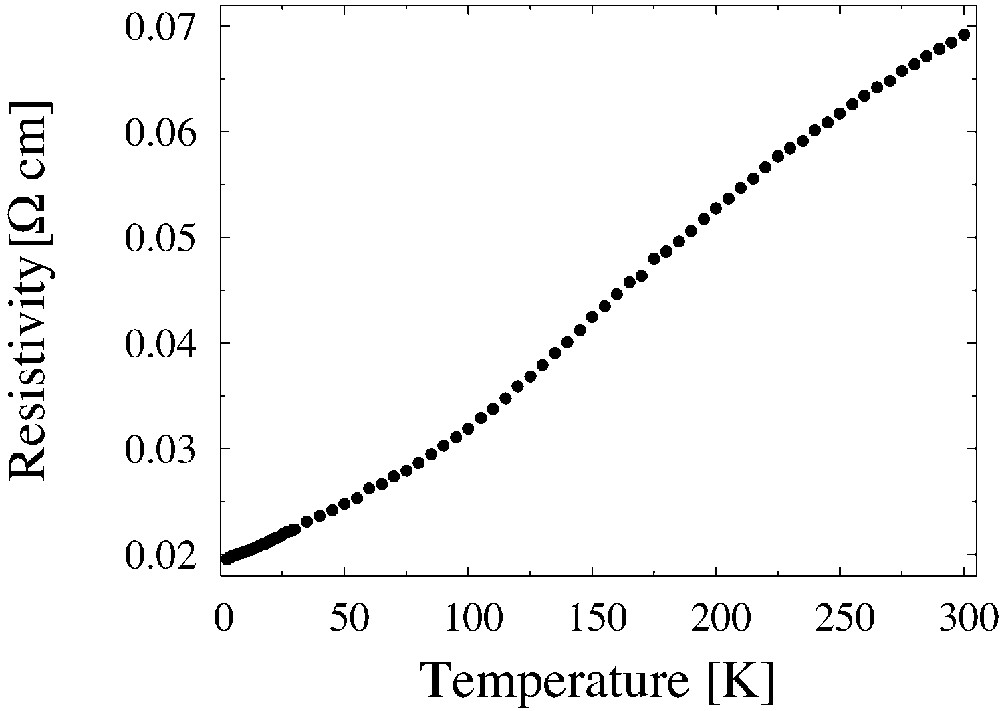
Temperature dependence of the resistivity of the composite (BEDT–TTF)_0.82/(AuI) obtained by hot-pressing method.

As it was mentioned previously, the investigations of the thermoelectric power give important information on the electrical transport properties of the composites. The temperature dependence of the thermoelectric power, S(T) of (BEDT–TTF)_x/(AuI) composites is shown in Fig. 8, but in Fig. 9 the room temperature thermoelectric power as a function of x is presented. The thermoelectric power of the composites, with x not very far from the optimal one, shows a metallic character and it varies slowly with x. Moreover, S(T) of the composites with x ≈ x_opt is similar to S(T) of the single crystals of (BEDT–TTF)₂I₃ [23]. Only for x much smaller than the optimal one S(T) changes drastically. The changes are observed also for high values of x. Such behaviour of the thermoelectric power is fully understandable in Eqs. (3)–(7). For x close to x_opt, the concentration of conducting grains is large and the thermoelectric properties of the composites are fully determined by properties of grains and do not depend on their concentration, as it is suggested by Eq. (4). For an x value far from the optimal one, the concentration of the grains is small and an insulating phase contributes to the thermoelectric properties of the composite. The influence of this phase grows with the decrease of the conducting-grain concentration and x dependence of the thermoelectric power can be expressed by Eq. (5) in this range. Eq. (6) can be used for description of S(x) dependence in the whole range of x. The fact that S(T) of the composites with x ≈ x_opt is similar to S(T) of the single crystals of (BEDT–TTF)₂I₃ is of great importance. It means that the electrical properties of grains are close to properties of single crystals (BEDT–TTF)₂I₃ and (BEDT–TTF)₂AuI₂.

Fig. 8
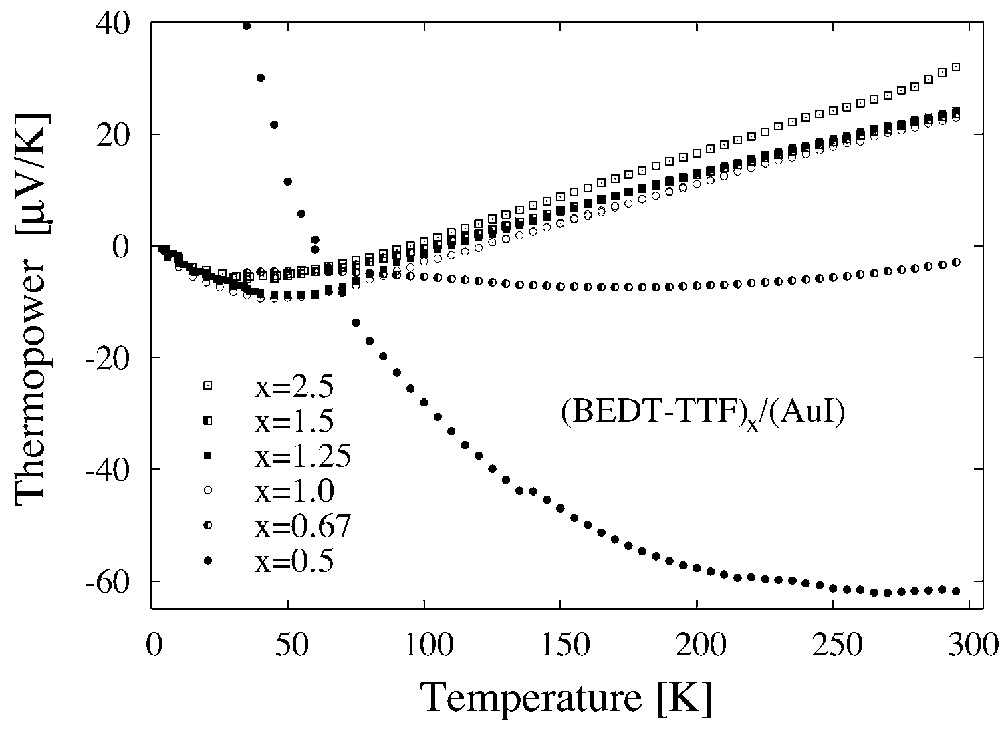
Thermoelectric power vs. temperature of the composites (BEDT–TTF)_x/(AuI) obtained by the ordinary method.

Fig. 9
Room-temperature thermoelectric power and the conductivity vs. parameter x of the composites (BEDT–TTF)_x/(AuI) obtained by the ordinary method.

The thermoelectric properties of the composites (BEDT–TTF)_x/(AuI₃) are similar to the properties of (BEDT–TTF)_x/(AuI). Therefore, all conclusions made for (BEDT–TTF)_x/(AuI) composites are fair for (BEDT–TTF)_x/(AuI₃) ones.

6 Concluding remarks and prospects

Synthesis of non-traditional organic materials that possess good physical properties, in particular high electrical conductivity and good stability, is an important aspect of contemporary molecular engineering. It is possible to fabricate various organic conductors not only in the crystal form but also in the form of thin conducting films [24], conducting reticulate doped polymeric films [25] or polycrystalline samples of organic metals [26] and other. Although these materials present great practical importance, they exhibit, unfortunately, some shortcomings. One of them is relatively poor understanding of their physical properties. On the other hand the materials based on BEDT–TTF or its derivatives form especially interesting and promising group of new organic solids. They show metal-like high electrical conductivity, relatively good stability and reproducibility. The technology of their production by direct solid–solid CT reaction, proposed by Farges and Brau several years ago [6] and developed by both Nice and Poznań groups [4, 7–11, 13–16, 22, 27–30], is very simple and inexpensive. Another great advantage of this technology is that many new composites can be obtained with the same technique, which have no single crystals equivalent.

We have given here a discussion of basic problems concerning the physical properties of BEDT–TTF-derived composites. Present efforts to develop the composite technology testing the hot-pressing technique are also presented. More thorough understanding and description of phenomena occurring in this type of new materials are necessary both to develop the method of composite preparation and to find out the potential opportunities of their application.

Acknowledgements

The authors thank J.-P. Farges and A. Brau from the University of Nice–Sophia Antipolis for their discussions and co-operation.

Bibliographie

[1] (J.-P. Farges, ed.), Organic Conductors: Fundamentals and Applications, Dekker, New York, 1994

[2] J.M. Williams; J.R. Ferraro; R.J. Thorn; K.D. Carlson; U. Geiser; H.H. Wang; A.M. Kini; M.-H. Whangbo Organic Superconductors (Including Fullerenes), Prentice Hall, Englewood Cliffs, New Jersey, 1992

[3] J.P. Farges; A. Brau; P. Dupuis Solid-State Commun, 54 (1985), p. 531

[4] J.P. Farges; A. Brau; F.A. Sahraoui Mol. Cryst. Liq. Cryst., 186 (1990), p. 143

[5] J.P. Farges; A. Brau (H.S. Nalwa, ed.), Handbook of Advanced Electronic and Photonic Materials and Devices, Academic Press, San Diego, 2001, p. 329

[6] I. Smirani; A. Brau; J.P. Farges Synth. Met., 93 (1998), p. 203

[7] V.N. Semkin; A. Graja; I. Smirani; A. Brau; J.P. Farges J. Mol. Struct., 9 (1999) no. 512, p. 49

[8] M. Golub; L. Szcześniak; A. Graja; A. Brau; J.P. Farges J. Mater. Sci., 36 (2001), p. 5543

[9] M. Golub; A. Graja; A. Brau; J.P. Farges Synth. Met., 125 (2002), p. 301

[10] M. Golub; A. Graja; A. Brau; J.P. Farges Synth. Met., 125 (2002), p. 337

[11] V. Boldyrev; E. Boldyreva Mat. Sci. Forum, 88–90 (1992), p. 711

[12] A. Brau; J.P. Farges; F.A. Sahraoui Mol. Cryst. Liq. Cryst., 186 (1990), p. 131

[13] A. Brau; I. Smirani; J.P. Farges; R. Lipiec; A. Graja Synth. Met., 108 (2000), p. 75

[14] I. Smirani; P. Auban-Senzier; D. Jérome; A. Brau; J.P. Farges Synthetic Met., 102 (1999), p. 1259

[15] I. Smirani; R. Lipiec; A. Brau; J.P. Farges; A. Graja J. Mater. Sci., 36 (2001), p. 1227

[16] A. Graja; A. Brau; J.P. Farges; M. Golub; A. Tracz; J.K. Jeszka Synth. Met., 120 (2001), p. 753

[17] P. Sheng Phys. Rev. B, 21 (1980), p. 2180

[18] G. Paasch; S. Karg; T. Schimmel; W. Riess; M. Schwoerer Synth. Met., 55–57 (1993), p. 4872

[19] I. Webman; J. Jortner; M.H. Cohen Phys. Rev. B, 16 (1977), p. 2959

[20] J. Joo; S.M. Long; J.P. Pouget; E.J. Oh; A.G. MacDiarmid; A.J. Epstein Phys. Rev. B, 57 (1998), p. 9567

[21] M. Golub, A. Graja (to be published).

[22] I. Smirani PhD thesis, University of Nice–Sophia Antipolis, 1998

[23] K. Mortensen; J.M. Williams; H.H. Wang Solid-State Commun., 56 (1985), p. 105

[24] K. Kawabata; K. Tanaka; M. Mizutani Solid-State Commun., 74 (1990), p. 83

[25] J.K. Jeszka; J. Ulański; M. Kryszewski Nature, 298 (1981), p. 390

[26] D. Schweitzer; P. Bele; H. Brunner; E. Gogu; U. Haeberlen; I. Hennig; T. Klutz; R. Świetlik; H.J. Keller Z. Phys. B: Condens. Matter, 67 (1987), p. 489

[27] M. Golub; A. Graja; M. Połomska Phys. Status Solidi A, 194 (2002), p. 226

[28] A. Brau; J.P. Farges; E. Ghezzal Solid-State Ionics, 44 (1991), p. 331

[29] A. Graja; R. Świetlik; M. Połomska; A. Brau; J.P. Farges Synthetic Met., 125 (2002), p. 319

[30] A. Brau; I. Smirani; J.P. Farges; V.N. Semkin; A. Graja Mol. Cryst. Liq. Cryst., 354 (2000), p. 63

Commentaires - Politique