1 Introduction
In the last few years we have been interested in the theoretical analysis of transition metal compounds containing o-phenylenediamido ligands or, in general, ene-diamido ligands. Initially, we paid attention to the bonding capabilities of the dianionic ene-diamido functionality that coordinates metals with a formal d0 electron configuration [1]. The reasons that favor the observed folded 2,5-diazacyclopent-3-ene metallacycle were investigated in a number of Group 5 [2,3] and Group 4 derivatives [4]. Concerning the o-phenylenediamido ligand, their complexes with Group 6 metals in different oxidation states, were studied from the structural and electronic points of view [5]. The o-phenylenediamido/o-diiminobenzene dichotomy of this non-innocent ligand was investigated as well in some mononuclear Group-8 derivatives [6].
In the last decade, the number of theoretical papers dedicated to the investigation of mononuclear species containing ene-diamido or diimino ligands have increased markedly [7–16]. Today, the number of theoretical studies devoted to binuclear systems with a bridging diimino ligand is still limited [17], although the chemistry of binuclear species containing bridging diimino ligands was initiated and developed several years ago by Vrieze and coworkers [18,19]. We have recently shown that the oxidation of binuclear ruthenium complexes of this type affects mainly the bridge and transforms the o-phenylenediamido ligand into a o-diiminobenzene one. The experimental results were justified by DFT calculations [20]. As a logical expansion of this work, this paper presents an overview of the different coordination modes found in known binuclear transition metal compounds, which contain bridging diimino or ene-diamido ligands. The electronic structures of the corresponding bridging ligands are analyzed and discussed in terms of the results of DFT calculations.
2 Results and discussion
2.1 Structural arrangements of ene-diamido and diimino ligands in binuclear compounds
We have centered our attention on structurally characterized compounds that contain the ene-diamido or the diimino fragments as a bridge between two metal atoms. Clusters of higher nuclearity are not considered in this paper [21–24]. From a search in the Cambridge Structural Database [25] three different coordination modes are identified (see Fig. 1). They are, respectively, μ-η2-(N, N′),η2-(N, N′), I, μ-η2-(N, N′),η2-(N, C), II, and μ-η2-(N, N′),η4-(N, N′, C, C′), III. The bridging ligand in the coordination modes I and III behaves as a eight electron donor. However, in I the bridge has the dianionic ene-diamido character, while in mode III displays a neutral diimino nature. In the latter coordination mode, two nitrogen σ lone pairs and two π contributions of C=N bonds are donated to each metal respectively. Finally, the ligand in II is also neutral and behaves as a six electron donor. Four electrons are donated to one metal through the nitrogen σ combinations of diimino, whereas the third pair of electrons come from the π contribution of one C=N bond and are donated to the second metal (Fig. 1).
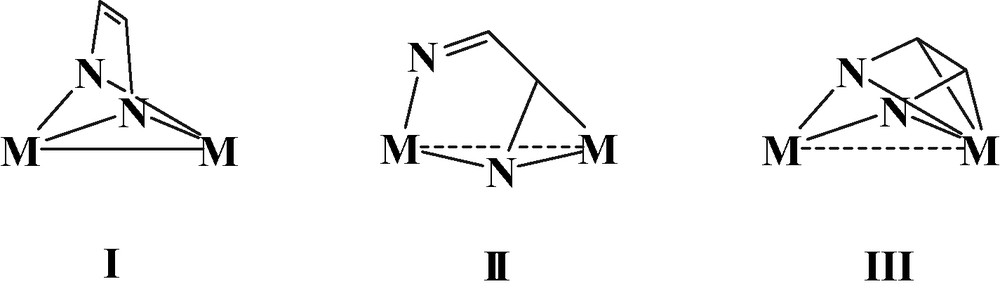
Schematic representation of the three different coordination modes of bridging 1,4-diaza-1,3-butadiene skeleton in binuclear compounds. Substituents at N and C atoms are not shown.
On the basis of the structural features, the complexes may be distinguished in seven different categories. Tables 1 and 2 show a simplified scheme for each structural type, the complex formula and the corresponding CCDC refcode. Table 1 displays the examples in which the bridging ligand is of C6H4(NR)2-o type, whereas Table 2 shows those in which the bridge does not contain the arylic backbone.
Structural arrangements of the C6H4(NR)2-o ligand in binuclear compoundsa
| Structural types | Formula | Refcode and reference |
| [Ru2{μ-C6H4(NH)2-o}(CO)4(PPh3)2] | JETPED, JETPIH [26] | |
| [Fe2{μ-C6H4(NH)(NPh)-o}(CO)6] | SEMFEC10 [27] | |
| [Fe2{μ-C6H4(NH)(NtBu)-o}(CO)6] | SIYXED [28] | |
| [Ru2{μ-C6H4(NH)2-o}(μ-dppm)(CO)2(PPh3)2] | SOGCUM [29] | |
| [Ru2{μ-C6H4(NH)2-o}(μ-dppm)(CO)2(PPh3)2](PF6)2 | AROQAZ [20] |
a The phenylene ring is not drawn in the charts.
Structural arrangements of the R,R′-DAD diimino ligand in binuclear compoundsa
| Structural types | Formula | Refcode and reference |
| [Fe2(μ-p-C6H4Me,OCH2CH(CH2)3N-DAD)(CO)6] | CUQLAB [30] | |
| [Fe2(μ-p-C6H4OMe,OCH2CH(CH2)3N-DAD)(CO)6] | CUQLEF [30] | |
| [(CO)3Ru(μ-iPr,H-DAD)Fe(CO)3] | GIFXIC [31] | |
| [Fe2(μ-Cy,H-DAD)(CO)6] | HXBCFE [32] | |
| [Mn2(μ-Ph,Ph-DAD)(CO)6] | JAPTEZ [33] | |
| [Mn2(μ-Me,Me-DAD)(CO)6] | MEAZMN [34] | |
| [Mn2(μ-p-C6H4Me,p-CH2C6H4Cl-DAD)(CO)6] | MNCLPD10 [33] | |
| [Ru2(μ-iPr,H-DAD)2(CO)4] | COGXRU [35] | |
| [CpRu(μ-tBu,H-DAD)(μ-CO)Co(CO)2] | GIFXUO [36] | |
| [(CO)3Mn(μ-tBu,H-DAD)(μ-CO)Co(CO)2] | GXCOMN [37] | |
| [(CO)2ClRu(μ-iPr,H-DAD)(μ-H)Ru(CO)3] | WAGKOE [38] | |
| [(CO)2MeRu(μ-iPr,H-DAD)(μ-H)Fe(CO)3] | YAJXAI [39] | |
| [(CO)2MeRu(μ-iPr,H-DAD)(μ-I)Ru(CO)2(PMe2Ph)] | YAJXOW [39] | |
| [Ru2(μ-iPr,H-DAD)(μ-CO)(CO)4] | CIYRAD [40] | |
| [Ru2(μ-iPr,H-DAD)(μ-HCCH)(CO)4] | GLXRUA10 [41] | |
| [Fe2(μ-iPr,H-DAD)(μ-HCCCOOMe)(CO)4] | JANFEJ [42] | |
| [(CO)3Ru(μ-iPr,H-DAD)(μ-CCCOOMe)Fe(CO)2] | SASYAM [43] | |
| [(CO)2MeRu(μ-iPr,H-DAD)(μ-I)Ru(CO)2] | YAJXEM [39] |
a R,R′-DAD represents the substituted 1,4-diaza-1,3-butadiene RN=CR′CR′=NR.
The general arrangements of the bridging ligand, displayed in Fig. 1, are encountered in both Tables 1 and 2, although with some sub-distinctions. In I the ligand bridges the two metals through the N atoms and maintains its molecular plane perpendicular to the M–M bond (μ-η2-(N, N′),η2-(N, N′) bonding type). In mode IIa the diazabutadiene ligand binds one metal through the N=C bond, while the second metal atom is coordinated by both nitrogen atoms (μ-η2-(N, N′),η2-(N, C) bonding type). The modes IIb and IIc, which differ for the presence or absence of M–M bond, are similar to that of IIa but the diazabutadiene bridge is not unique, but there is an additional bridge X. The latter coordinates both metals through a single atom (e.g., CO, H or halide) or two linked atoms (e.g. acetylene type ligand). Alternatively, the additional bridge is a second diazabutadiene ligand. In mode IIIa the diazabutadiene molecule is bent towards one metal atom and the short M–C contacts are indicative of a bonding interaction. Again, types IIIb and IIIc feature the same coordination mode of IIIa, μ-η2-(N, N′),η4-(N, N′, C, C′), and have an additional bridging ligand X. Their main difference is the presence or absence of a direct metal–metal bond, respectively.
In order to gain a general overview of the structural and electronic features of the coordinated 1,4-diaza-1,3-butadiene skeleton in these binuclear complexes, representative models for each subclass were selected and theoretical calculations were carried out followed by a bonding analysis.
2.2 Ene-diamido μ-η2-(N, N′),η2-(N, N′) bridging ligand
Recently, the MO distribution of [Ru2{μ-C6H4(NH)2-o}(μ-dppm)(CO)2(PPh3)2] complex, in which the o-phenylenediamido ligand symmetrically bridges the two metal atoms (μ-η2-(N, N′),η2-(N, N′), type I), has been analyzed by DFT methods [20]. Model compound [Ru2{μ-C6H4(NH)2-o}(μ-H2PCH2PH2)(PH3)2(CO)2] has been adopted and the bonding scheme, previously discussed by EHMO method [44] has been consistently confirmed. Curiously enough, from the inspection of Tables 1 and 2 one can see that the μ-η2-(N, N′),η2-(N, N′) arrangement is specific for o-phenylenediamido ligand and not for structurally characterized examples containing the 1,4-diaza-1,3-butadiene ligand (that is, without the arylic bakbone). In fact, the ligands of type R,R′-DAD adopt the bridging coordination modes II or III exclusively.
In order to gain further information about the bonding capabilities of the o-phenylenediamido ligand, calculations on the simplest model compounds [M2{μ-C6H4(NH)2-o}(CO)6] (M = Fe, 1a; Ru, 2a) were performed with the coordination mode μ-η2-(N, N′),η2-(N, N′), I. The optimized structure of the iron derivative 1a is displayed in Fig. 2, while its computed structural parameters are reported in Table 3. A good correlation with the experimental values of the [Fe2{μ-C6H4(NH)(NR)-o}(CO)6] complexes was found. The calculated C–C and N–C lengths are in agreement with a dianionic ene-diamido character of the C6H4(NH)2-o ligand. Also, the results for 2a are consistent with the geometry of the [Ru2{μ-C6H4(NH)2-o}(PPh3)2(CO)4] complex (see Section 5). For both, 1a and 2a derivatives, the MO analysis previously reported for o-phenylendiamido ruthenium complexes of type I is well suited and does no require further comment. The computed HOMO for the model 1a comes from interaction of the filled π3* orbital with the 1b1 metal combination and is largely ligand centered, whereas HOMO-1 accounts for the direct Fe–Fe interaction. The computed charges of both iron atoms are 1.27 and the Fe–Fe interaction is a non-polarized metal–metal bond in a d7–d7 L3M–ML3 system.

Optimized structure of model compound [Fe2{C6H4(NH)2-o}(CO)6], 1a, and its HOMO and HOMO-1 orbitals.
Selected structural parameters of calculated iron complexes [Fe2{C6H4(NH)2-o}(CO)6], 1a, and [Fe2(DAD)(CO)6], 1b, (coordination mode I) and comparison with experimental data
| Bond distances (Å) and angles (°) | Calculated | Experimental, [Fe2{μ-C6H4(NH)(NR)-o}(CO)6] | ||
| 1a | 1b | R = Ph, SEMFEC10 | R = tBu, SIYXED | |
| Fe1–Fe2 | 2.367 | 2.361 | 2.37 | 2.384(1) |
| Fe1–N | 2.014 | 2.021 | 1.98 | 1.963(5) |
| 2.02 | 2.066(5) | |||
| Fe2–N | 2.014 | 2.021 | 2.00 | 1.963(6) |
| 2.02 | 2.062(5) | |||
| N–C | 1.423 | 1.433 | 1.44 | 1.421(7) |
| 1.45 | 1.476(7) | |||
| C–C | 1.408 | 1.339 | 1.36 | 1.38 |
| Fe1–CO(up) | 1.806 | 1.805 | 1.80 | 1.822(8) |
| Fe2–CO(up) | 1.806 | 1.805 | 1.82 | 1.807(8) |
| Fe1–CO(down) | 1.796 | 1.796 | 1.78 | 1.756(7) |
| 1.78 | 1.763(8) | |||
| Fe2–CO(down) | 1.796 | 1.796 | 1.76 | 1.755(8) |
| 1.77 | 1.787(8) | |||
| C–C–N | 109.7 | 110.6 | 109.8 | 109.6(5) |
| 111.4 | 111.0(6) | |||
| Fe2–Fe1–CO(up) | 148.3 | 148.1 | 146.9 | 147.2(3) |
| 149.3 | 147.5(2) |
The ruthenium derivative [Ru2(DAD)(CO)6], 2b, (DAD = HNCHCHNH) was previously optimized [20]. The suitable results obtained after simplification of the o-phenylendiamido group by DAD ligand prompted us to optimize as well the simplest model compound [Fe2(DAD)(CO)6], 1b, with the DAD ligand arranged as in I and without symmetry constrains. The resulting structure of 1b is shown in Fig. 3. The computed structural parameters are close to those of 1a and are also collected in Table 3 for the appropriate comparison. No noteworthy differences can be observed after the oversimplification of the o-phenylendiamido ligand (dismissal of the aryl backbone).
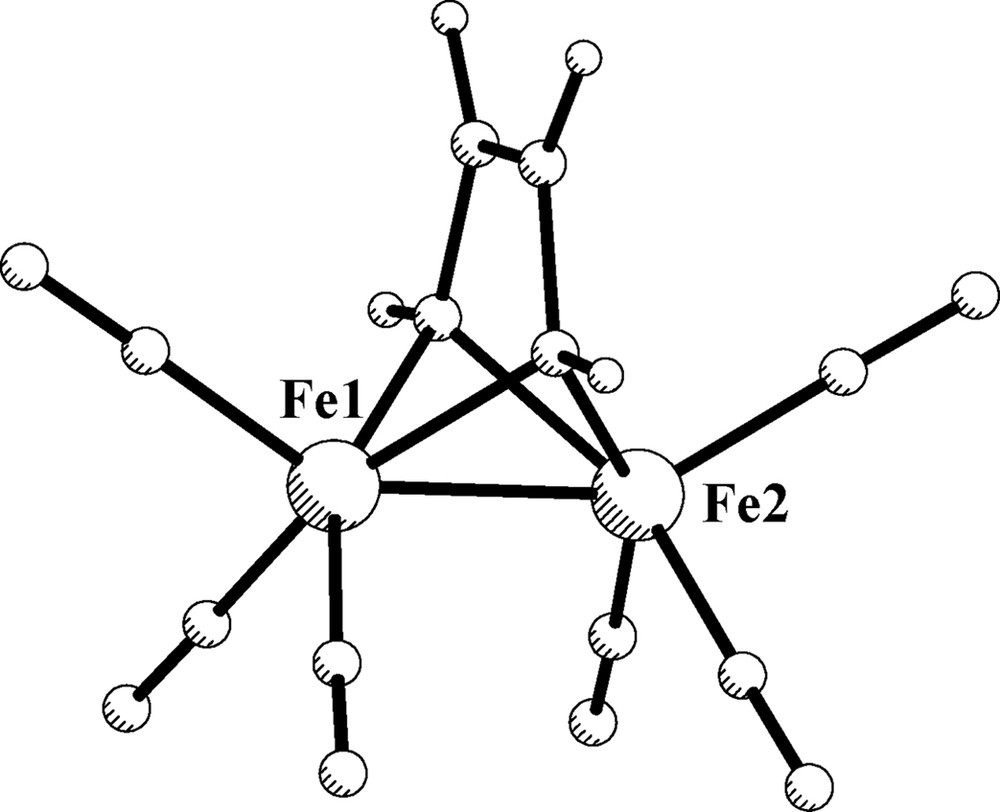
Optimized structure of 1b.
2.3 Diimino μ-η2-(N, N′),η2-(N, C) bridging ligand
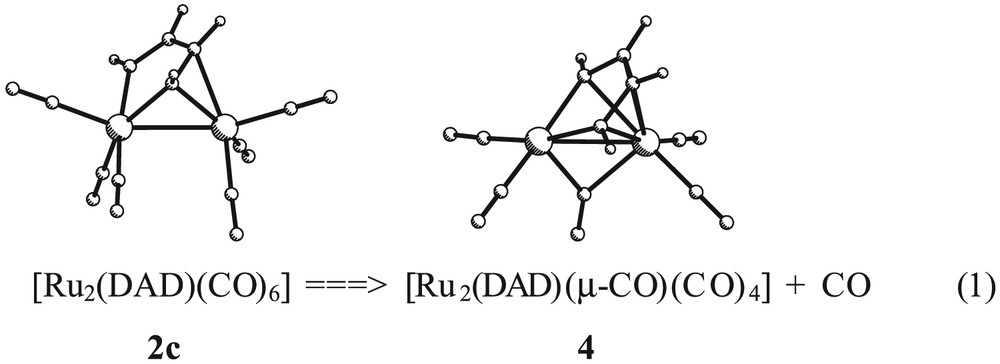
Concerning the coordination mode μ-η2-(N, N′),η2-(N, C) (type II), the model compounds [M2(DAD)(CO)6] (M = Fe, 1c; Ru, 2c) were optimized without symmetry restrictions. The resulting structures are displayed in Fig. 4. The computed structural parameters for the iron derivative 1c are grouped in Table 4. Bond distances and angles show a reasonable agreement when compared with those found experimentally. The calculated N–C bonds are characterized by two different distances of 1.299 and 1.405 Å, N1–C1 and N2–C2, respectively. The former distance is close to that of a typical double N=C bond, while the latter is slightly shorter than the computed NC bond in the ene-diamido complex 1a. These values are in conformity with a diimino description of the diazabutadiene bridging ligand. Selected calculated bond lengths and angles of compound [Ru2(DAD)(CO)6], 2c, are only included as Supplementary Material because no structural data are available for comparison. However, it is important to highlight that the computed IR spectrum of 2c in the ν(CO) region (2054, 2012, 1992, 1983, 1958 and 1956 cm–1) fits quite well with the reported IR spectra of [Ru2(R,R′-DAD)(CO)6] complexes [35].
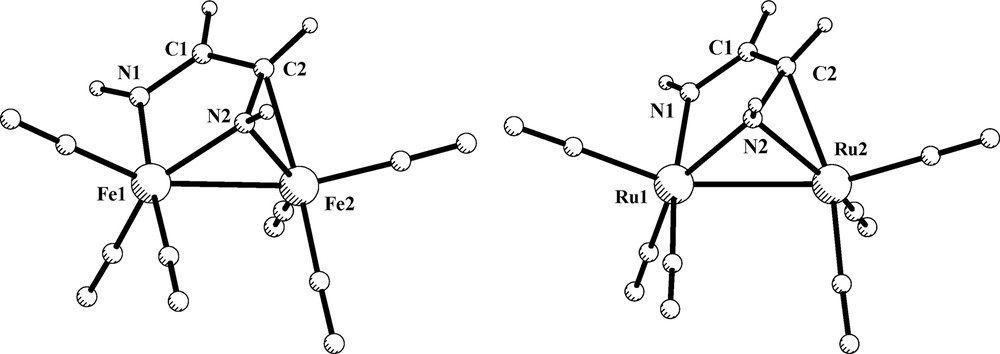
Optimized structures of compounds [M2(DAD)(CO)6] (M = Fe, 1c; Ru, 2c).
Selected structural parameters of calculated [Fe2(DAD)(CO)6] complex, 1c, (coordination mode II) and comparison with experimental data
| Bond distances (Å) and angles (°) | Calculated | Experimental | ||
| 1c | HXBCFE | CUQLAB | CUQLEF | |
| Fe1–Fe2 | 2.628 | 2.60 | 2.565(1) | 2.592(9) |
| Fe1–N1 | 2.004 | 1.97 | 2.015(6) | 2.015(4) |
| Fe1–N2 | 1.962 | 1.99 | 1.959(6) | 1.968(4) |
| Fe2–N2 | 1.915 | 1.93 | 1.926(6) | 1.929(4) |
| Fe2–C2 | 2.098 | 2.07 | 2.021(6) | 2.045(5) |
| N1–C1 | 1.299 | 1.28 | 1.304(8) | 1.313(6) |
| N2–C2 | 1.405 | 1.40 | 1.394(8) | 1.397(6) |
| C1–C2 | 1.429 | 1.43 | 1.497(9) | 1.495(6) |
| C–C–N | 117.3 | 115.5 | 116.0(6) | 116.4(4) |
| 115.0 | 118.6 | 112.3(6) | 112.9(4) |
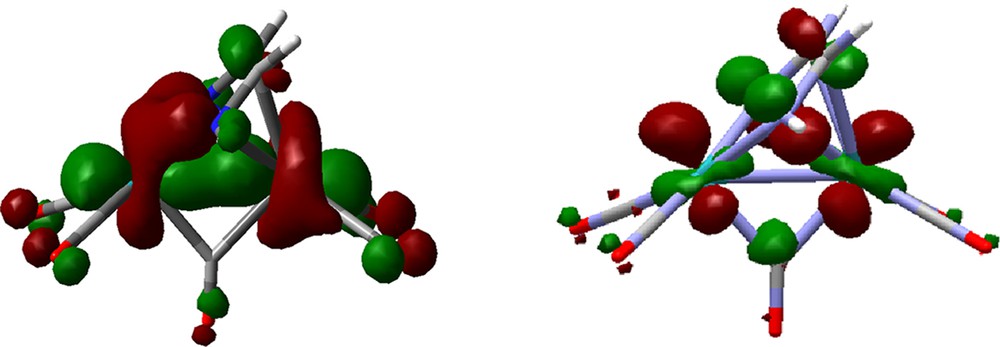
The bridging diimino ligand in these [M2(DAD)(CO)6] complexes behaves as a six electron donor to the d8–d8 L3M–ML3 system, behaving the dihapto bonded C=N bond as the equivalent of a two electron donor. Each metal displays pseudo-octahedral and trigonal bipyramidal coordination environments at the atoms Fe1 and Fe2, respectively (see 1c, Fig. 4). As a possible interpretation, the metal–metal bond can be considered of dative nature. According to the latter, the metal–metal interaction stems from the donation of a filled σ-ML5 hybrid onto an empty σ-ML4 one. The calculated HOMO for 1c, shown in Fig. 5, supports the viewpoint. The computed metal charges (0.41 and 0.12 for the Fe1 and Fe2 atoms in 1c, respectively) account well for the presence of a polarized metal–metal bond.
HOMO of 1c.
2.4 Comparison of the coordination modes μ-η2-(N, N′),η2-(N, N′), type I, and μ-η2-(N, N′),η2-(N, C), type II, in compounds with the same general formulation [M2(DAD)(CO)6] (M = Fe, Ru)
The optimizations of iron and ruthenium binuclear complexes with similar formulation [M2(DAD)(CO)6] and different coordination modes μ-η2-(N, N′),η2-(N, N′), I, and μ-η2-(N, N′),η2-(N, C), II, computed at the same level of theory, allow us to adequately compare their structural and energetic features (1b vs. 1c and 2b vs. 2c). Regarding the bond distances, the C–C bond length of the metallacycle is longer in compounds 1c and 2c (diimino μ-η2-(N, N′),η2-(N, C), coordination mode II) than the same value in 1b and 2b (for example, 1.429 versus 1.339 Å for M = Fe), in agreement with the ene-diamido formulation of the bridge (mode I) in the latter complexes. Additionally, both C–N distances in the complexes of type c (diimino) are shorter than those found for b complexes (for example, 1.299 and 1.405 versus 1.433 Å for M = Fe). These structural differences accompany also to different formal charges of the metal atoms. Comparison of the iron charges in compounds 1b (0.79 for the two atoms) and 1c (0.41 and 0.12 for the Fe1 and Fe2 atoms, respectively) confirms the different formulation of the bridge.
Concerning the energies, the [M2(DAD)(CO)6] isomers of type c are found to be slightly more stable than those of type b. The energy differences are computed to be 2.5 and 3.0 kcal mol–1, for M = Fe and Ru, respectively. This fact suggests that the μ-η2-(N, N′),η2-(N, C) coordination mode for the 1,4-diaza-1,3-butadiene ligand is slightly privileged with respect to the μ-η2-(N, N′),η2-(N, N′) one. However, when the bridging ligand contains the o-phenylenediamido group the structural situation is that represented by I, according to the experimental evidence. A plausible explanation for this fact is the following: generally, the H–C–C–H (or R′–C–C–R′) torsion angle of coordinated diimine ligands are close to 0°. However, the computed H–C–C–H torsion angle for DAD in the complexes 1c and 2c is ca. 17°, a value that is not compatible with the planar o-phenylene backbone.
2.5 μ-η2-(N, N′),η4-(N, N′, C, C′) bridging ligand
The chemical oxidation of [Ru2{μ-C6H4(NH)2-o}(μ-dppm)(CO)2(PPh3)2] complex affords [Ru2{μ-C6H4(NH)2-o}(μ-dppm)(CO)2(PPh3)2](PF6)2, in which the C6H4(NH)2-o ligand adopts the μ-η2-(N, N′),η4-(N, N′, C, C′) coordination mode (III) and behaves as an eight-electron donor in the diimino form. The structural characterization of the latter compound, together with a theoretical analysis of the simplest model compound [Ru2(DAD)(CO)6]2+, has recently appeared [20]. In order to generalize the attributes of the bonding mode III, the formally isoelectronic model compound [Mn2(DAD)(CO)6], 3, has also been studied for a convenient comparison. The optimized geometry of 3 is depicted in Fig. 6. Table 5 shows selected structural data (experimental and calculated) corresponding to the known [Mn2(R,R′-DAD)(CO)6] complexes. In general, there is a satisfactory agreement between the calculated and experimental geometric parameters, the bond distances agree within 0.05 Å, except for the Mn–Mn separation. Although the latter is clearly overestimated, its value of 2.723 Å is still consistent with a direct metal–metal bond [45]. The C–C and N–C lengths of 1.399 and 1.379 Å, respectively, are in conformity with a diimino constitution of the DAD ligand.
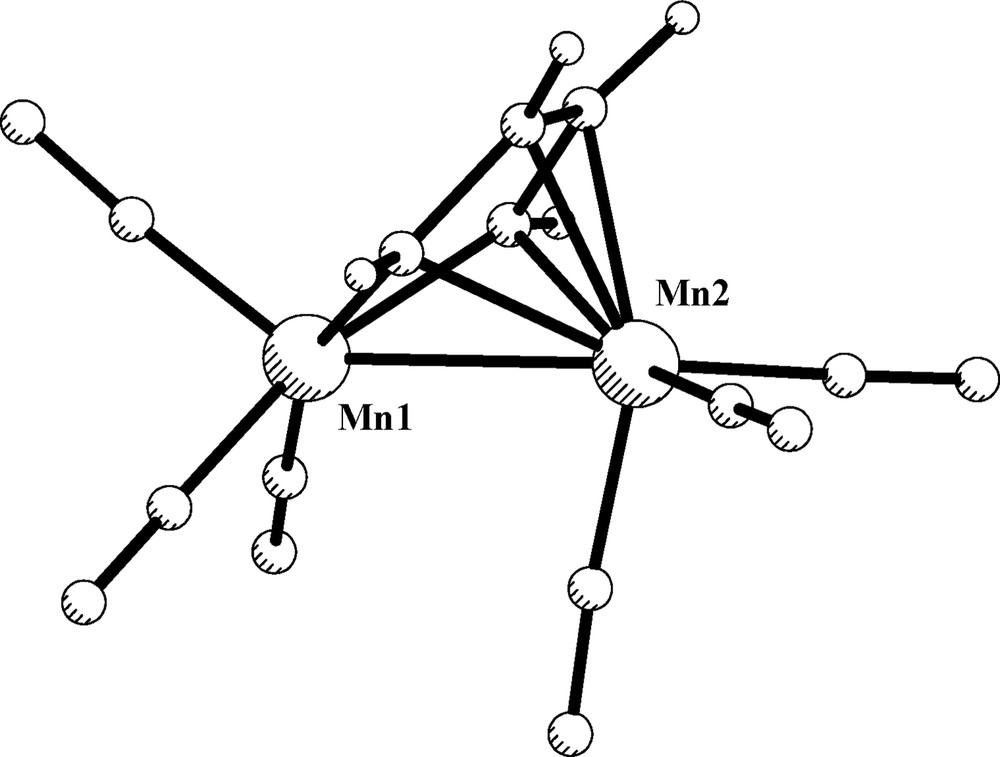
Optimized structure of model compound [Mn2(DAD)(CO)6], 3.
Selected structural parameters of [Mn2(R,R′-DAD)(CO)6] manganese complexes (coordination mode III) and comparison with experimental data
| Bond distances (Å) and angles (°) | Calculated | Experimental | ||
| 3 | R = R′ = Ph, JAPTEZ | R = p-C6H4-Me, R′ = p-C6H4-Cl, MNCLPD10 | R = R′ = Me, MEAZMN | |
| Mn1–Mn2 | 2.723 | 2.612(1) | 2.633(1) | 2.615(1) |
| Mn1–N | 1.986 | 1.984(4) | 1.962(5) | 1.977(3) |
| 1.975(3) | 1.958(5) | 1.995(3) | ||
| Mn2–N | 2.141 | 2.092(4) | 2.087(5) | 2.108(3) |
| 2.137(3) | 2.084(5) | 2.111(3) | ||
| Mn2–C | 2.141 | 2.149(4) | 2.131(6) | 2.137(4) |
| 2.153(4) | 2.124(6) | 2.147(4) | ||
| N–C | 1.379 | 1.387(5) | 1.387(8) | 1.392(5) |
| 1.397(5) | 1.377(8) | 1.388(5) | ||
| C–C | 1.399 | 1.418(6) | 1.397(8) | 1.407(5) |
| Mn1–CO(up) | 1.779 | 1.760(6) | 1.748(8) | 1.789(4) |
| Mn1–CO(down) | 1.818 | 1.804(6) | 1.809(7) | 1.804(4) |
| 1.791(6) | 1.811(8) | 1.810(4) | ||
| Mn2–CO(up) | 1.805 | 1.788(5) | 1.803(7) | 1.801(4) |
| 1.802(6) | 1.804(7) | 1.804(4) | ||
| Mn2–CO(down) | 1.809 | 1.804(6) | 1.811(7) | 1.808(4) |
| C–C–N | 112.3 | 111.3(4) | 112.0(6) | 112.3(3) |
| 111.8(4) | 110.5(5) | 112.7(3) | ||
| Mn1–Mn2–CO(down) | 77.0 | 74.3(2) | 75.5(2) | 75.9(1) |
| Mn2–Mn1–CO(up) | 143.5 | 148.8(2) | 146.4(3) | 148.5(1) |
The frontier MOs of the diimino DAD ligand include two filled σ lone pairs (in phase σip and out phase σop) that correspond to the HOMO and HOMO-1 of the molecule; two filled, lower in energy, π1 and π2 combinations and two empty π* combinations (π3* and π4*). Consequently, the bonding capabilities of this ligand arises from the two nitrogen σ lone pairs and the two filled π MOs, making possible the donation to the metals of eight electrons. On the basis of a FMO analysis, essentially, the qualitative picture of the bonding in 3 may be described as the ligand-to-metal donation of the two σ lone pairs to Mn1 atom and of the two π combinations to Mn2 atom. The different Mn1–N and Mn2–N distances accounts well with this explanation. Moreover, the specific orientation of the MnL3 fragment at the atom Mn2 atom is well rationalized with the backdonation from one of the well known dπ metal hybrids (2e levels) of a C3v–ML3 fragment [46] into the empty π3* level of the bridging ligand.
The two-electron chemical oxidation of ruthenium complexes of type I determines the reorganization of the C6H4(NH)2-o ligand to the structural type III. This experimental fact has been studied theoretically in the model compounds [Ru2(DAD)(CO)6] and [Ru2(DAD)(CO)6]2+. However, the removal of two electrons in the binuclear system may formally occur by the simple elimination of one ligand acting as 2e donor. For example, Vrieze and coworkers reported the dissociation of CO from [Ru2(R,R′-DAD)(CO)6] complexes (coordination type I) to give [Ru2(R,R′-DAD)(μ-CO)(CO)4] (coordination type III). Analogously, the same authors observed the formation of [Ru2(R,R′-DAD)(HCCH)(CO)4] compounds (coordination type III) by interaction of species [Ru2(R,R′-DAD)(CO)6] with acetylene. Both types of compounds have been studied through the respective models [Ru2(DAD)(μ-CO)(CO)4], 4, and [Ru2(DAD)(μ-HCCH)(CO)4], 5. Full geometry optimizations were performed for 4 and 5 (both with imposed symmetry Cs) and the resulting final geometries are shown in Fig. 7. Selected calculated parameters and, for comparison, selected experimental data from X-ray crystallography have been collected in Tables 6 and 7, respectively. The geometrical features of the diimino ligand in 4 and 5 are similar and adequately match the reported structures. Furthermore, the computed IR bands concerning the CO region (2029, 2000, 1964, 1958, 1848 cm–1 for 4 and 2020, 2001, 1958, 1956 cm–1 for 5) correctly reproduce the experimental trends.

Optimized structures of model compounds [Ru2(DAD)(μ-CO)(CO)4], 4, and [Ru2(DAD)(μ-HCCH)(CO)4], 5.
Selected structural parameters of [Ru2(R,R′-DAD)(μ-CO)(CO)4]
| Bond distances (Å) and angles (°) | Calculated | Experimental |
| R = R′ = H, 4 | R = iPr, R′ = H, CIYRAD | |
| Ru–Ru | 2.796 | 2.741(1) |
| Ru1–N | 2.158 | 2.14(1) |
| 2.14(1) | ||
| Ru2–N | 2.319 | 2.27(1) |
| 2.25(1) | ||
| Ru2–C | 2.360 | 2.27(1) |
| 2.28(1) | ||
| Ru1–Cbridging | 2.063 | 2.03(1) |
| Ru2–Cbridging | 2.121 | 2.15(1) |
| N–C | 1.383 | 1.43(1) |
| 1.43(1) | ||
| C–C | 1.397 | 1.39(2) |
| Ru–N–Ru | 77.2 | 76.7(3) |
| 77.1(3) | ||
| C–C–N | 114.4 | 115.9(9) |
| 114.7(10) | ||
| Ru1–C–Obridging | 137.0 | 138.7(10) |
| Ru2–C–Obridging | 139.1 | 139.4(10) |
Selected structural parameters of [Ru2(R,R′-DAD)(μ-HCCH)(CO)4]
| Bond distances (Å) and angles (°) | Calculated | Experimental |
| R = R′ = H, 5 | R = iPr, R′ = H, GLXRUA10 | |
| Ru1–Ru2 | 3.049 | 2.936(1) |
| Ru1–N | 2.139 | 2.117(6) |
| 2.111(6) | ||
| Ru2–N | 2.311 | 2.226(6) |
| 2.225(6) | ||
| Ru2–C | 2.295 | 2.226(7) |
| Ru1–Cbridging | 2.065 | 2.062(9) |
| Ru2–Cbridging | 2.093 | 2.092(8) |
| Ru1–CO | 1.889 | 1.862(9) |
| 1.844(9) | ||
| Ru2–CO | 1.878 | 1.869(8) |
| 1.864(8) | ||
| N–C | 1.394 | 1.40(1) |
| 1.451(9) | ||
| C–C (DAB) | 1.396 | 1.396(11) |
| C–C (acetylene) | 1.321 | 1.34(1) |
| Ru–N–Ru | 86.4 | 84.2(2) |
| 84.5(2) | ||
| C–C–N | 113.9 | 116.4(7) |
| 112.1(6) |
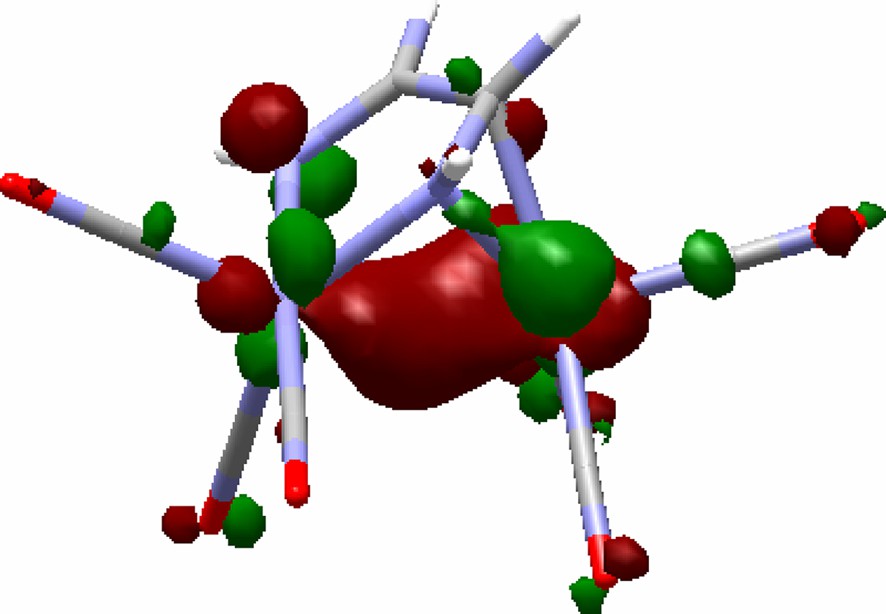
Both compounds were analyzed theoretically in an early work [17]. Our results are in agreement with the bonding description presented in that paper except for the proposed lack of the metal–metal bond. This fact may be re-interpreted on the basis of our results. At variance with complex 2c in which the metal–metal interaction appears in the HOMO (see Fig. 5), an analogs level for complex 4 is found in the HOMO-7 and it is significantly delocalized (Fig. 8). Moreover, the higher filled MOs feature also some antibonding metal–metal character and determine the poor metal–metal overlap population, pointed out by the authors [17]. Metal–metal bonds are frequently difficult to investigate and new approaches are continuously emerging [47,48]. Although no additional deeper studies have been performed, on the basis of our results the existence of a metal–metal interaction in 4 is a conclusion preferable to that of its non-existence. In fact, the computed Ru–Ru bond length in 4 is slightly shorter than in 2c (2.819 Å), where the Ru–Ru bond is not questionable.
HOMO-7 and LUMO of 4.
The experimental evidence of CO dissociation in [Ru2(R,R′-DAD)(CO)6] complexes has a theoretical confirmation from the present calculations. In 2c, the dissociated CO molecule is precisely the ligand that displays the longest M–CO distance. The computed energy for the process represented in Eq. (1) is –10.64 kcal mol–1. This value agrees with the experimental observation of dissociation of CO upon refluxing the [Ru2(R,R′-DAD)(CO)6] complexes in toluene [40]. The LUMO of 4 is characterized by a hybrid directed toward the created vacant position (see Fig. 8).
Finally, a representative example of the structures of type IIIc has been chosen. The model compound [(CO)2MeRu(μ-DAD)(μ-I)Ru(CO)2], 6, has been optimized with no symmetry constrains. Fig. 9 shows the resulting structure and Table 8 summarizes selected structural parameters and their comparison with the experimental data [39].
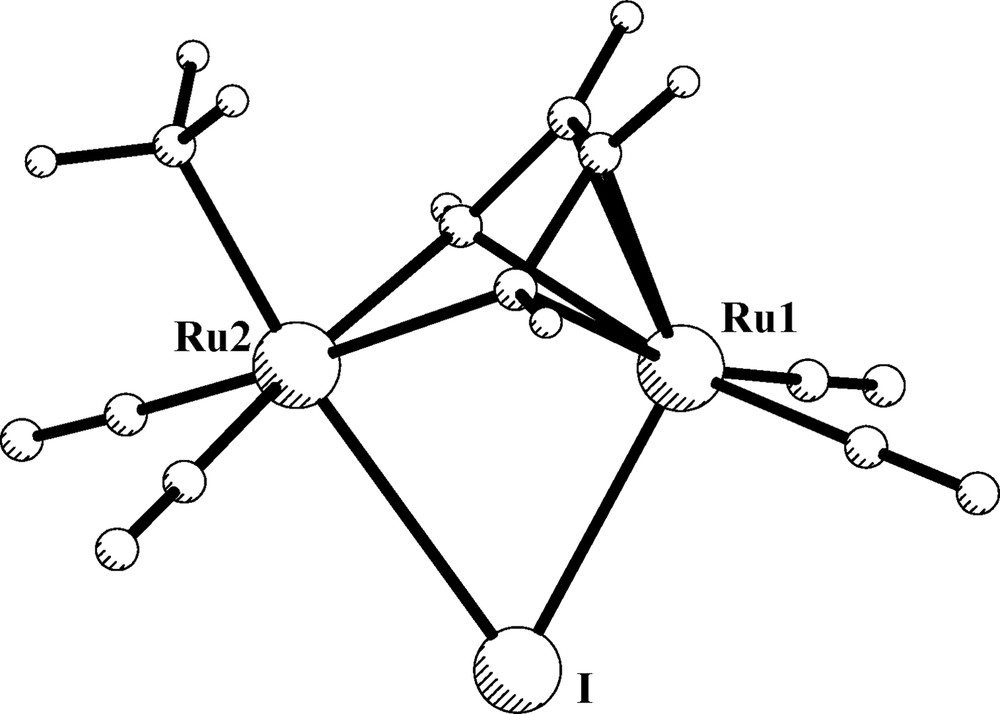
Optimized structure of model compound [(CO)2MeRu(μ-DAD)(μ-I)Ru(CO)2], 6.
Selected structural parameters of [(CO)2MeRu(μ-R,R′-DAD)(μ-I)Ru(CO)2]
| Bond distances (Å) and angles (°) | Calculated | Experimental |
| R = R′ = H, 6 | R = iPr, R′ = H, YAJXEM | |
| Ru1–Ru2 | 3.150 | 3.0635(6) |
| Ru1–N | 2.245 | 2.196(3) |
| 2.197(3) | ||
| Ru2–N | 2.180 | 2.150(4) |
| 2.162(4) | ||
| Ru1–C | 2.231 | 2.162(4) |
| 2.160(5) | ||
| Ru2–CH3 | 2.121 | 2.115(5) |
| N–C | 1.377 | 1.377(6) |
| 1.366(6) | ||
| C–C | 1.417 | 1.422(7) |
| Ru1–I | 2.806 | 2.7517(5) |
| Ru2–I | 3.172 | 3.0215(5) |
| Ru1–CO | 1.899 | 1.870(5) |
| 1.891(5) | ||
| Ru2–CO | 1.887 | 1.856(5) |
| 1.860(4) |
The calculated geometry of 6 is in good agreement with the experimental structure of complex [(CO)2MeRu(μ-iPr,H-DAD)(μ-I)Ru(CO)2]. In addition, the computed carbonyl IR bands (2030, 2017, 1977 and 1988 cm–1) are in accord with the experimental values. Again, the bond distances support the diimino formulation of the DAD ligand, which behaves as a 8e donor. Thus, the complex features a d6-RuL4 fragment (at Ru2) saturated from the nitrogen σ lone pairs and a d8-RuL3 fragment (at Ru1) which is η4 coordinated by the π system of DAD (four π electrons, donation and backdonation). No metal–metal bond exists in view of the long Ru–Ru distance (3.063 Å experimental and 3.150 Å computed).
3 Conclusions
The diazabutadiene skeleton may bridge two metal centers by adopting three different coordination modes in the diimino or the ene-diamido formulation. The bonding mode μ-η2-(N, N′),η2-(N, N′), I, is exclusively found when the bridge is an ene-diamido C6H4(NR)2-o ligand (aryl backbone), which behaves as eight electron donor to a d7–d7 L3M–ML3 system. The HOMO is essentially centered at the C6H4(NR)2-o ligand. In absence of the phenylene ring the diazabutadiene skeleton acts as diimino bridge with two possible bonding modes, namely μ-η2-(N, N′),η2-(N, C), II, and μ-η2-(N, N′),η4-(N, N′, C, C′), III. In these modes the bridge behaves as six and eight electron donor ligand, respectively. In particular, the arrangement of type II is only observed for diimino ligands without the arylic backbone. In this case, the ligand has sufficient freedom to twist at the C–C linkage. The same torsion is more difficult for a phenyl ring, which would lose aromaticity. Concerning the C6H4(NR)2-o ligand, the conversion of ene-diamido to diimino is chemically possible through a two electron oxidation process [20], which changes the coordination mode of the bridge from I to III. The chemical conversion of compounds [Ru2(R,R′-DAD)(CO)6] into [Ru2(R,R′-DAD)(μ-CO)(CO)4] derivatives by CO dissociation and the energetics associated to this process are also analyzed. The removal of a two electron donor induces the reorganization of the bridge from the coordination type II toward the bonding of type III. In this manner, the bridge is enabled to donate an additional electron pair to the binuclear moiety and, most importantly, allows metal backdonation into a suited π* level. This causes weakening but not disappearance of the metal–metal bond.
4 Computational details
The electronic structure and geometries of the model complexes were computed within the density functional theory at the B3LYP [49,50] level using the LANL2DZ [51,52] basis set for the iron and ruthenium atoms. The basis set used for the remaining atoms was 6-31G + (d, p). All the optimized geometries were characterized as local energy minima by diagonalization of the analytically computed Hessian (vibrational frequencies calculations). The computed IR spectra were scaled by a factor of 0.96 [53,54]. The DFT calculations were performed using the Gaussian 98 suite of programs [55]. Molecular orbitals were visualized using the GaussView program [56]. Cartesian coordinates for the optimized molecules are available from the authors upon request. The FMO analyses were done with CACAO [57] using the coordinates of the optimized model complexes.
5 Supplementary material available
Tables 9 and 10 contain bond distances and angles of the computed model compounds 2a and 2c, respectively.
Comparison of the computed model compound [Ru2(μ-C6H4(NH)2-o)(CO)6], 2a, with experimental [Ru2{μ-C6H4(NH)2-o}(PPh3)2(CO)4] complexes
| Bond distances (Å) and angles (°) | Calculated | Experimental | |
| 2a | JETPED | JETPIH | |
| Ru–Ru | 2.613 | 2.558(1) | 2.560(1) |
| Ru–N | 2.177 | 2.167(8) | 2.163(2) |
| 2.178 | 2.149(8) | 2.161(2) | |
| Ru–CO(up) | 1.977 | – | – |
| 1.978 | – | – | |
| Ru–CO(down) | 1.922 | 1.87(1) | 1.866(3) |
| 1.85(1) | 1.858(3) | ||
| N–C | 1.427 | 1.44(1) | 1.419(4) |
| 1.42(1) | 1.431(4) | ||
| C–C | 1.410 | 1.41(1) | 1.403(5) |
| Ru–N–Ru | 73.7 | 73.1 | 72.6 |
| 72.3 | 72.6 | ||
| C–C–N | 111.3 | 111.9 | 111.5 |
| 110.7 | 111.0 | ||
| Ru–Ru–CO(up) | 148.4 | – | – |
| CO(down)–Ru–CO(down) | 91.6 | 91.4(5) | 89.7(1) |
| CO(down)–Ru–CO(up) | 97.2 | – | – |
Computed bond distances (Å) and angles (°) for model compound [Ru2(DAD)(CO)6], 2c
| Ru–Ru | 2.819 |
| Ru1–N | 2.130 |
| 2.142 | |
| Ru2–N | 2.105 |
| Ru2–C | 2.252 |
| N–C (bonded) | 1.415 |
| N–C (non bonded) | 1.303 |
| C–C | 1.429 |
| Ru1–CO(up) | 1.976 |
| Ru2–CO(up) | 1.950 |
| Ru1–CO(down) | 1.930 |
| 1.923 | |
| Ru2–CO(down) | 1.925 |
| 1.950 | |
| Ru–N–Ru | 83.5 |
| Ru–Ru–CO(up) | 154.7 |
| 156.7 | |
| C–C–N | 117.1 |
| 119.5 | |
| H–C–C–H | 17.4 |
Acknowledgments
This paper is the result of a sabbatical at ICCOM (Firenze, Italy) with financial support from the Spanish Secretaría de Estado de Educación y Universidades. My gratitude to Professor Carlo Mealli, who was a kind host and an excellent guide through the ‘forest’ of theoretical chemistry. I would like to thank to Dr. Ienco and Mr. Masi, from the same group, for their hospitality. My thanks also to all the people in the Italian Institute. Finally, I am indebted to my colleagues of our research group for allowing me to spend one year away.