Order-from-disorder in a spin-dimer magnet

Wolfram Brenig

doi:10.1016/j.crci.2006.11.008

Résumé

We study the magnetism of a two-dimensional model of coupled spin dimers in the presence of disorder. Using a quantum Monte-Carlo approach, we evaluate the staggered structure factor as a function of the exchange coupling strength and for various disorder concentrations. We show that substitutional disorder in terms of non-magnetic defects leads to long-range magnetic order at zero temperature.

There is a growing suspicion that thermodynamic properties of many novel materials at finite temperatures may be a consequence of their vicinity to quantum critical points, i.e. changes of the ground-state symmetry as a function of some intrinsic parameter p. Such quantum phase transitions (QPTs) may play a key role in the high-temperature cuprate superconductors, in heavy fermion materials, and in low-dimensional quantum magnets. Regarding the latter, antiferromagnetically (AFM) coupled spin-1/2 dimer magnets are of particular interest. Many molecular magnetic materials can be understood in terms of one-, two- and three-dimensional networks of spin dimers [1]. In dimer magnets, p can be identified with the ratio J/j of the intra-dimer exchange to an effective inter-dimer coupling. For $| p | ≫ 1$ and J > 0, the ground state can be understood in terms of a product state of weakly interacting spin-singlets which display no magnetic long-range order (MLRO). However, as p is lowered to $| p | \sim 1$ and in spacial dimensions D ≥ 2, a QPT to MLRO may arise with a commensuration vector Q depending on the details of the inter-dimer coupling. In this context, the impact of disorder has become a recent topic. Here we focus on the effects of substitutional disorder arising from non-magnetic defects. In molecular dimer magnets, such defects can be introduced in a controlled way, as e.g. in the coupled ladder compound [Ph(NH₃)](18C₆)[Ni(dmit)₂]_1–x[Au(dmit)₂]_x, where the [Ni(dmit)₂]⁻ ion leads to spin-1/2, while for Ni → Au spin-0 results [2]. To be specific, we study the 2D version of the so-called Kondo-necklace model of coupled spin-1/2 dimers:

H_{SKN} = j \sum_{l m} S_{P l} \cdot S_{P m} + J \sum_{l} S_{P l} \cdot S_{I l},

(1)

shown in Fig. 1. The clean limit of this model has been discussed in Refs. [3–5].

Fig. 1
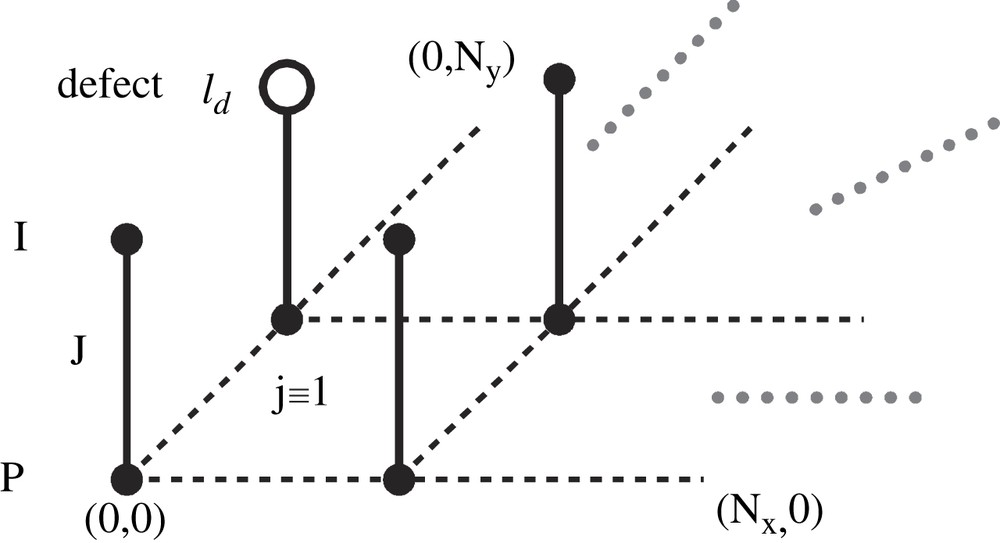
2D Kondo-necklace with 2 × N_x × N_y sites (periodic boundary conditions assumed). Spin-1/2 moments are located on the solid bullets. Solid (dashed) lines refer to inter(intra)-dimer exchange J(j ≡ 1).

The disorder we consider amounts to a random removal of spins from sites l_d of the upper layer ‘I’ of Fig. 1, thereby introducing non-magnetic defects at a concentration c. It has been conjectured that generically such defects in AFM quantum spin systems will enhance local AFM spin correlations and therefore stabilize or trigger MLRO on unfrustrated lattices [6,7]. To test this conjecture in the present case, we have evaluated the AFM order parameter, i.e. the longitudinal staggered structure factor:

S_{n} (Q) = 〈 {(m_{n Q}^{z})}^{2} 〉

(2)

where

m_{n Q}^{z} = \sum_{l} S_{n l}^{z} \exp (i Q \cdot r_{l}) / N_{n}

is the staggered magnetization, with

Q = (π, π, π)

m_{n Q}^{z}

selects between n = P, I, A, for which r_l runs over the lower (upper) layer for n = P(I) and all sites for n = A. The calculation of S_n(Q) proceeds via a quantum Monte-Carlo (QMC) technique, namely the stochastic series expansion (SSE) with loop-updates introduced in Refs. [8,9]. Details will be reported elsewhere.

Fig. 2 summarizes our results. It shows the low-temperature squared staggered moment $M_{Q}^{2} = 3 S_{n} (Q)$ vs. J for various defect concentrations and for fixed inter-dimer exchange j ≡ 1 at a system size of N = 2 × N_x × N_y = 2 × 24 × 24. Extensive finite-size scaling analysis has been performed at various J and c to ensure that the systematic finite-size corrections to $M_{Q}^{2}$ are on the order of, or less than ∼10% and have no impact on the results discussed here [10]. Moreover, the inverse temperature β = 1/T has been chosen such as to represent the zero-temperature limit. At c = 0, $M_{Q}^{2}$ is finite below a critical value of J = J_c and drops to approximately zero for J > J_c. Extrapolation of $M_{Q}^{2} (J < J_{c})$ by a power law leads to J_c ≈ 1.41(2). We identify J_c with the QPT and expect AFMLRO for J < J_c in the thermodynamic limit at T = 0. For J > J_c we find no other transitions, i.e. the systems connect adiabatically to the limit of J = ∞. Therefore, it is in a dimerized state with no MLRO. For a finite defect density, c > 0, the situation changes dramatically. For all values of J investigated, we find that the staggered moment, i.e. the order parameter of the AFM state remains finite, also for J > J_c. Our results do not rule out a large upward renormalization of the QPT as a function of c, i.e. beyond the range of J considered here. However, it is rather likely that the QPT is suppressed by the disorder and $J_{c} (c \neq 0) = ∞$ for all c. In any case Fig. 2 demonstrates the main point of this short note, i.e. that non-magnetic disorder can induce MLRO in a state which is non-magnetic otherwise in the clean limit, i.e. we find order-from-disorder.

Fig. 2
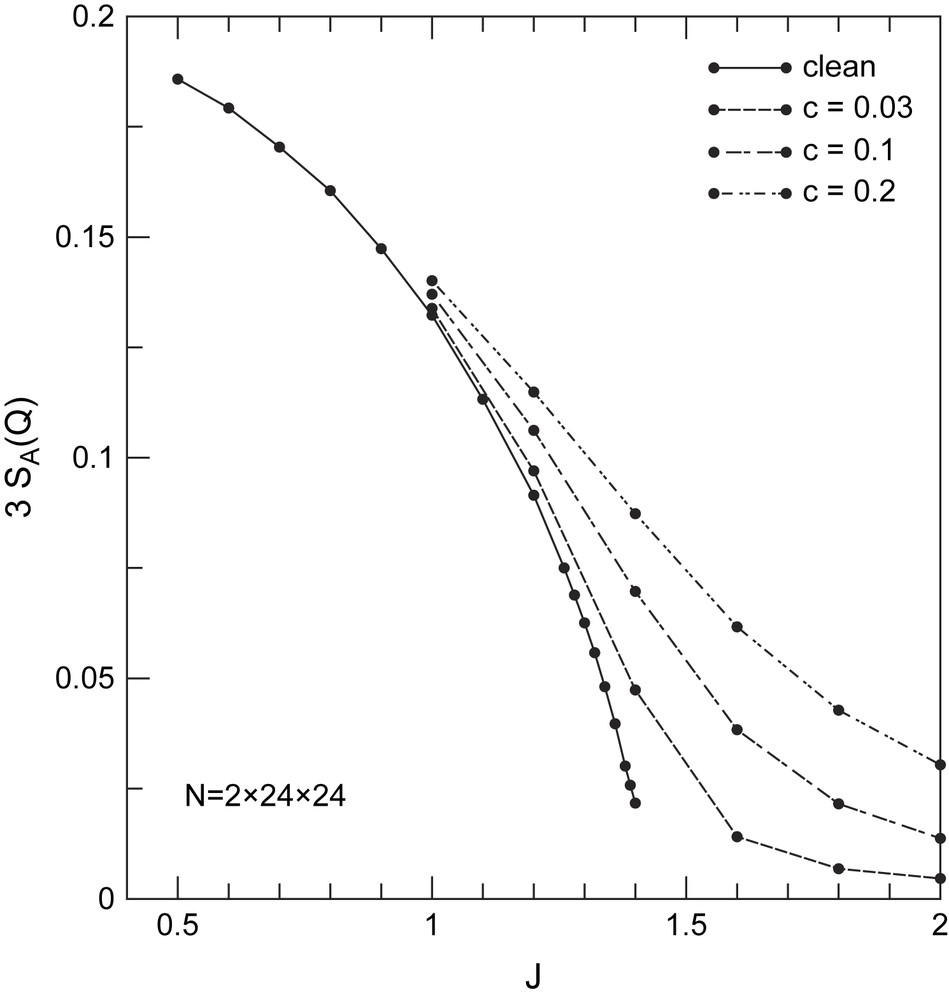
Staggered structure factor S_A(Q) vs. J close to the QPT for various defect concentrations c. Inverse temperatures β = 1/T are β = 100 at c = 0 and β = 1024 at c = 0.03, 0.1, and 0.2. Disorder results include averages over ∼900 system realizations each. Statistical errors are less than the solid-circle marker size.

Acknowledgement

Part of this work has been funded by the German Science Foundation, DFG, under Grant Nos. BR 1084/2-2 and BR 1084/4-1.