Theoretical investigation of structures and electronic states of a series of phenyl-capped oligothiophenes

Hossein Nikoofard; Mohamad Gholami

doi:10.1016/j.crci.2013.11.001

Theoretical investigation of structures and electronic states of a series of phenyl-capped oligothiophenes

Hossein Nikoofard ¹ ; Mohamad Gholami ¹

¹ Faculty of Chemistry, Shahrood University of Technology, Shahrood 36199-95161, Iran

Comptes Rendus. Chimie, Volume 17 (2014) no. 10, pp. 1034-1040.

Résumé

The structures and electronic states of a series of phenyl-capped oligothiophenes (PnTs) and their ionic species were investigated by means of the density functional theory (DFT). The calculations were performed on the oligomers formed by n repeating units, where n ranges from 2 to 6, using the B3LYP/6-31G** level of theory. The results obtained show that the end-substitution plays a fine-tuning effect on the geometries, electronics, and excitation states. It was found that the oligomers in the doped state have more satisfactory structural and electronic characteristics for the conducting polymers. The conjugated system in the doped oligomers has more aromaticity, with expanded and planar chains. The calculated energy gap values between the frontal molecular orbitals for the PnTs indicate that with increasing the oligomer chain length, the conductive band gap decreases. The calculated ﬁrst excitation energies of the PnTs at the TD-B3LYP/6-31G** level reveal that the doped PnTs have lower excitation energies than the neutral states. The oligomer chains with a phenyl ring as the end-capped group display red shifts in their absorption spectra. The end-caped substituted oligothiophenes display better characteristics than the unsubstituted ones. It could be anticipated that the phenyl-caped substitution would be helpful to charge-carrier hopings between chains, and thereby, enhance the conductivity.

Métadonnées

Reçu le : 2013-09-08
Accepté le : 2013-11-04
Publié le : 2014-07-10

DOI : 10.1016/j.crci.2013.11.001

Mots clés : Phenyl-capped thiophene (PnT), Oligomer, Density functional theory (DFT), Semi-conductor

Affiliations des auteurs :

Hossein Nikoofard ¹ ; Mohamad Gholami ¹

¹ Faculty of Chemistry, Shahrood University of Technology, Shahrood 36199-95161, Iran

@article{CRCHIM_2014__17_10_1034_0,
     author = {Hossein Nikoofard and Mohamad Gholami},
     title = {Theoretical investigation of structures and electronic states of a series of phenyl-capped oligothiophenes},
     journal = {Comptes Rendus. Chimie},
     pages = {1034--1040},
     publisher = {Elsevier},
     volume = {17},
     number = {10},
     year = {2014},
     doi = {10.1016/j.crci.2013.11.001},
     language = {en},
}

TY  - JOUR
AU  - Hossein Nikoofard
AU  - Mohamad Gholami
TI  - Theoretical investigation of structures and electronic states of a series of phenyl-capped oligothiophenes
JO  - Comptes Rendus. Chimie
PY  - 2014
SP  - 1034
EP  - 1040
VL  - 17
IS  - 10
PB  - Elsevier
DO  - 10.1016/j.crci.2013.11.001
LA  - en
ID  - CRCHIM_2014__17_10_1034_0
ER  -

%0 Journal Article
%A Hossein Nikoofard
%A Mohamad Gholami
%T Theoretical investigation of structures and electronic states of a series of phenyl-capped oligothiophenes
%J Comptes Rendus. Chimie
%D 2014
%P 1034-1040
%V 17
%N 10
%I Elsevier
%R 10.1016/j.crci.2013.11.001
%G en
%F CRCHIM_2014__17_10_1034_0

Hossein Nikoofard; Mohamad Gholami. Theoretical investigation of structures and electronic states of a series of phenyl-capped oligothiophenes. Comptes Rendus. Chimie, Volume 17 (2014) no. 10, pp. 1034-1040. doi : 10.1016/j.crci.2013.11.001. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2013.11.001/

Version originale du texte intégral

1 Introduction

Five-membered oligoheterocyclic compounds, such as oligthiophene, oligopyrrole, and oligofuran have raised an extensive interest in the last decade because they display fascinating semi-conductivity, photo-conductivity, and electroluminescence properties [1,2]. Intrinsic conducting polymers with conjugated double bonds are newly considered as a very important class of electroactive and photoactive materials. Some of these polymers exhibit physical properties that lend them to the development of display devices, transistors, sensors, etc. [3–5]. These applications have received a great deal of attention from both the academic and industrial research centres [6–9]. During the past decade, thiophene-based electronic materials have been extensively investigated. The ease in the chemical modification of the structures of these materials can potentially allow us to fine-tune their optical and electronic properties [10–14]. These properties strongly depend upon the degree of electronic delocalization present in such materials, effective conjugated length (ECL), and introduction of substituents at specific positions. However, a significant drawback of oligothiophenes is their low fluorescence and poor stability with respect to the oligomers consisting of substituted derivatives [15].

In order to develop a higher performance of oligothiophene, several modified oligothiophenes have been synthesized, and their electronic properties symmetrically investigated. One approach is to substitute the side-chain of the thiophene ring. Substituents at the β-position of the monomer rings prevent the undesirable α-β couplings that decrease the conjugated length and solubility of the polymers, and also the substitution plays an important role in the electrical and electro-optical properties of the polymers [16]. Conducting polymers with modified solubility in some industrially important solvents have recently been synthesized by introducing a proper substitution on the monomer ring [17,18]. It is clear that the electronic and structural properties of a substituent contribute to the delocalization of the polymer π-conjugate system, and the introduction of an electron-donating substituent at the β-position of the thiophene ring might be an interesting strategy to prevent defects, and withhold or even surpass the desirable properties of polymers [19–23].

The other approach is to synthesize the capped oligothiophene, where both ends of the thiophene chain are capped by the substituted groups [24–29]. The capped oligothiophenes have a well-defined molecular size and a high chemical stability. Recently, it has been found that phenyl groups as the end-substituents have novel light-emitting properties [24–29]. Although these features, obtained experimentally, are one of the interesting points in capped-oligoheterocyclics, the electronic structures of both neutral and doped states of the capped-oligoheterocyclics are not clearly understood due to the lack of theoretical works. However, in the last few decades, theoretical calculations have been employed to investigate different aspects related to the molecular and electronic structures of thiophene and its β-position substituted derivatives using ab initio and DFT calculations [30–37]. In our previous works [38,39], we studied a series of substituted pyrroles as potential monomers for the synthesis of conductive polymers and the corresponding oligomers with modified physical and electrical characteristics.

Theoretical investigations on a series of end-substituted oligoheterocycles are thereby desirable for designing novel functional materials, which is the main purpose of this work. In the present study, we investigated the phenyl group effect as the end-substitution on the structural and electronic properties of a series of oligothiophenes in the ground and exited forms and their doped states, as obtained with the aid of DFT calculations. To this end, we investigated characteristics of the π-conjugate system and bond length alternation pattern, HOMO–LUMO gaps, electron affinity (EA), ionization potential energy (IP), and the first excited energies of a series of PnTs including di-, tri-, tetra-, penta-, and hexamers.

2 Computational details

The ground-state geometry of each oligomer studied in this work was fully optimized using gradient procedures at the hybrid density functional B3LYP level of theory. A preliminary basis set test carried out for calculations on the electronic ground state showed that 6-31G** was the best basis set that can be used within our available hardware/software facilities within a reasonable time. Our previous studies [38,39] and reports by others [40–46] have shown that the DFT appeared notably adapted to describe oligoheterocyclics. Thus, the DFT-B3LYP level of theory was selected for the present study of PnTs using the 6-31G** basis set as implemented in the Gaussian 03 program package [47].

The optimized geometries were calculated for both the neutral and doped states of the oligomers. There was no symmetric constraint on geometry optimization. The nature of the optimized stationary point was characterized by frequency calculations at the same level of theory with the same basis set. The analysis of the obtained results showed that all the optimized structures were obtained as minima on the potential energy surface without any imaginary mode. The energies of the different states in the relevant geometries were obtained for calculating the IP values using the Koopman theorem [48]. The time-dependent density functional theory (TD-DFT) [49,50] was employed to calculate the optical properties on the basis of B3LYP/6-31G** optimized geometries. Ten lowest excitation states of each compound were computed, from which the excitation spectra were theoretically simulated with a Gaussian broadening of 0.6 eV of full-width half maximum.

3 Results and discussion

3.1 Molecular geometry

The sketch map of the structure for the hexamer type (n = 6), P6Ts, is depicted in Scheme 1, as an example of the PnTs. It is noticeable that the carbon atoms adjacent to the heteroatom in the thiophene ring α positions are branching centers in the electropolymerizationelectro-polymerization process, and thus controls the stereochemistry of the polymer chains. Also, the β carbon atoms are in appropriate positions for substitution. However, in this study, the phenyl substitution was fixed at the head and tail of an oligomer chain. It is known that the well-defined polymer structure contains almost exclusively the head-to-tail (HT) conformation, due to the α–α couplings between adjacent heterocyclic monomers in the backbone of polymer chains [38,39]. Thus, geometry optimization of PnTs was performed on the HT conformation at the B3LYP/6-31G** level of theory.

Scheme 1
Structure and numbering scheme used for the phenyl-capped hexathiophene P6Ts.

One of the important factors related to the extent of the π-conjugation is the chain planarity, which can be reflected by the tortional angle D, as defined in Scheme 1. Dihedral angles defining the torsion between two adjacent building units along the oligomer chain for nTs, PnTs, and their ionic species were collected in Table 1. The calculations indicate that nTs and PnTs, in neutral states, are non-planar structures, in which the phenyl ring substituents are largely twisted from the plane of backbone structure of PnTs due to their steric hindrances. These angles are largely changed in the ionic states. With increase in the repeating units, there is a significant reduction in the inter-ring torsion angle at the centre of the oligomer, compared to the outside. It is interesting that the doped oligomers have less torsion angles than the corresponding neutral ones. It is known that the planarity of the polymer chains plays an important role in their electric conductivity. In general, crystalline oligothiophenes have been found to be nearly planar, as a result of more favorable crystal packing [51]. The DFT-optimized geometries are in agreement with the solid-state structure.

Species	D₁	D₂	D₃	D₄	D₅	D′	D″
2Ts	21.9	—	—	—	—	—	—
3Ts	18.1	18.2	—	—	—	—	—
4Ts	17.1	14.7	17	—	—	—	—
5Ts	16.4	9.8	9.7	16.3	—	—	—
6Ts	16.4	10.3	0.3	10.7	16.6	—	—

P2Ts	13.8	—	—	—	—	25.3	25.5
P3Ts	12.8	12.9	—	—	—	25.9	25.8
P4Ts	15.3	13.9	15.4	—	—	26.4	25.8
P5Ts	15.5	12.6	12.7	15.6	—	25.5	25.5
P6Ts	15.6	12.5	12.6	12.5	15.5	26.3	25.6

P2Ts(+)	0.1	—	—	—	—	7.7	7.5
P3Ts(+)	1	1	—	—	—	16.7	16.6
P4Ts(+)	1.5	0.6	1.7	—	—	19.8	19.5
P5Ts(+)	2.8	0.5	0.6	2.9	—	21.2	20.8
P6Ts(+)	3.2	0.4	0	0.4	3.2	22.1	22.6

P2Ts(–)	0	—	—	—	—	0	0
P3Ts(–)	0	0	—	—	—	0.1	0.1
P4Ts(–)	0	0	0.1	—	—	0.1	0.3
P5Ts(–)	1.3	0.1	0.2	1.4	—	6.8	7
P6Ts(–)	2.3	0.1	0	0.1	2.4	11.4	11.3

Another important parameter of interest with respect to the π-conjugation is the bond alternation parameter, δ, defined here as the bond length difference between two adjacent single and double bonds. A small δ value may correspond to a good π conjugation [52]. Here, the two bond alternation parameters, δ_intra and δ_inter, are defined as:

δ_intra = r_ββ – r_αβ and δ_inter = r_αα − r_αβ

(1)

where r_αβ and r_ββ are the intra-ring bond lengths, and r_αα denotes the inter-ring bond length, as labeled in Scheme 1. The average intra- and inter-ring bond alternation parameters for neutral, cationic, and anionic species are listed in Table 2. The investigation of the bond alternation parameter shows a decrease in phenyl-capped oligothiophenes, compared with the corresponding oligothiophenes. Thus, phenyl-capped oligothiophenes show a better π-conjugation. In cationic and anionic species of oligomers,

{\bar{δ}}_{intra}

and

{\bar{δ}}_{inter}

are very little, as expected. It is clear that the doped oligomers show a better π-conjugation system, and the length of all singlet and doublet bonds in π-conjugated backbone come between the values for the singlet and doublet bonds. Therefore, we expect a very little

{\bar{δ}}_{intra}

and

{\bar{δ}}_{inter}

for ionic species, in which the results of the bond alternation parameter are in agreement with this subject.

Species	${\bar{δ}}_{intera}$ /Å	${\bar{δ}}_{intra}$ /Å	f_n
2Ts	0.052	0.073	1.0441
3Ts	0.046	0.069	1.0411
4Ts	0.042	0.066	1.0391
5Ts	0.04	0.066	1.0377
6Ts	0.038	0.063	1.0367

P2Ts	0.038	0.066	1.0347
P3Ts	0.036	0.064	1.0344
P4Ts	0.035	0.062	1.0342
P5Ts	0.034	0.062	1.0339
P6Ts	0.034	0.061	1.0337

P2Ts(+)	0.021	0	0.9902
P3Ts(+)	–0.013	0.008	0.997
P4Ts(+)	–0.008	0.014	1.0016
P5Ts(+)	–0.003	0.019	1.0052
P6Ts(+)	0	0.023	1.0081

P2Ts(–)	0.006	0.066	0.9987
P3Ts(–)	0	0.064	1.0037
P4Ts(–)	0.004	0.062	1.0074
P5Ts(–)	0.007	0.062	1.0103
P6Ts(–)	0.009	0.061	1.0127

Furthermore, the quinoid term refers to a structure in which the inter-ring bond has a greater double bond character than that in the standard aromatic configuration, and it is determined by the quinoid coefficient, f_n [53–56]. This geometry parameter is defined as:

f_{n} = \frac{{\bar{R}}_{s ingle}}{{\bar{R}}_{double}}

(2)

where

{\bar{R}}_{single}

and

{\bar{R}}_{double}

are the mean lengths for the single and double C–C bonds along the conjugated π-system for oligomer chain with n repeating units, respectively. It is clear that a f_n value closer to unity (f_n → 1) corresponds to an increase in the aromatic character of C–C bonds along the conjugated polymer chain. The calculated values for the quinoid coefficient for all PnTs and their ionic states are reported in Table 2 (last column). As shown in this table, with growth in the polymer chain, the quantity of f_n decreases towards the unit value. It is also evidenced that the calculated results for the f_n coefficient are consistent with the behavior of bond alternation parameters for the PnT species studied. Inspection of the quinoid coefficients obtained show a decrease in the value of f_n for the PnTs compared with the corresponding nTs. In cationic and anionic species, the value for f_n is close to unity, as expected. Compared to oligothiophenes, the presence of phenyl groups as the end-caped substituents could improve the electron delocalization along the π-conjugation system. Delocalization of the π-electron onto the oligomer chain leads to satisfactory resonance structures and improves the stabilization of the PnTs species. It has been shown that a small bond length alternation may correspond to the narrow gap for the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO), HLG, and low TD-DFT excitation energy, E_g [44,45].

3.2 Electronic properties

It is useful to examine the highest occupied orbitals and the lowest virtual orbitals for these oligomers and polymers because the relative ordering of the occupied and virtual orbitals provides a reasonable qualitative indication of the excitation properties and the ability of electron or hole transport [57]. Since the first dipole allowed electron transitions as well as the strongest electron transitions with largest oscillator strength correspond almost exclusively to the promotion of an electron from HOMO to LUMO, we calculated the HLGs for all the studied oligomers in both the neutral and doped states. The HLG values for the neutral form are illustrated in Fig. 1 schematically. As we can see in this figure, reduction of HLGs for all oligomers becomes more obvious with increasing the conjugation length. As shown in this figure, the HLG values for the PnT species are less than those for the corresponding nT species. According to this figure, closing the end-sides of oligothiophenes by phenyl groups destabilizes both the HOMO and LUMO levels. The results obtained show an increase in the HOMO orbital level and a decrease in the LUMO orbital level after closing the end-sides of oligothiophenes by phenyl groups, and then, a reduction value for the HOMO–LUMO gap for phenyl-capped oligothiophenes.

Fig. 1
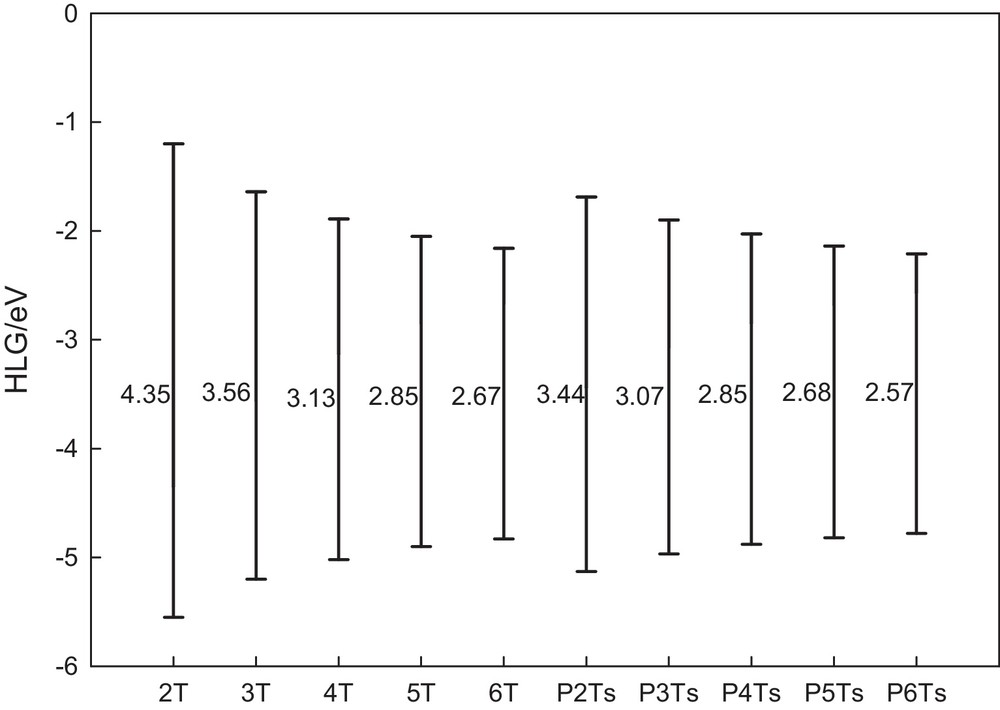
Variation in HOMO, LUMO, and HLG with the number of units (n) for PnTs and nTs, schematically.

In addition, another important tool to qualitatively judge the excitation state is the TD-DFT technique. It is clear that the low-lying excited states of the polymer, oligomer, and organic semi-conductors are correlated with the electron and hole conductivities. In particular, the first excited state is strongly correlated with these transport processes. Therefore, studying the excited states is important in the elucidation of the mechanism of the electron and hole conductivities in organic semi-conductors. Here, the excitation energies from the first to 6th excited states of each oligomer are calculated at the B3LYP/6-31G(d,p) level of theory. For instance, the simulated excitation spectra obtained using a Gaussian broadening for six lowest excitation states of hexamers are described in Fig. 2. The results obtained for the TD-DFT excitation energy (E_g) and the longest wavelength (λ_max) of the maximum absorption peaks with corresponding oscillator strengths (f) of each oligomer are collected in Table 3. For all the oligothiophene derivatives, the calculated λ_max values show the increasing order of dimer < trimer < tetramer < pentamer < hexamer, which is in good accordance with the corresponding reverse order of E_g values. The obtained results show that the attachment of phenyl groups to the end-sides of oligothiophenes leads to an evident bathochromic shift and increase in the intensity of the maximum absorption peak. This indicates that PnTs will have large λ_max values in the solid state due to higher conjugation length and flat structures. Moreover, as expected, the simulated absorption spectra and behavior of the maximum absorption peaks are qualitatively in agreement with the results obtained in studying the HOMO and LUMO orbitals.

Fig. 2
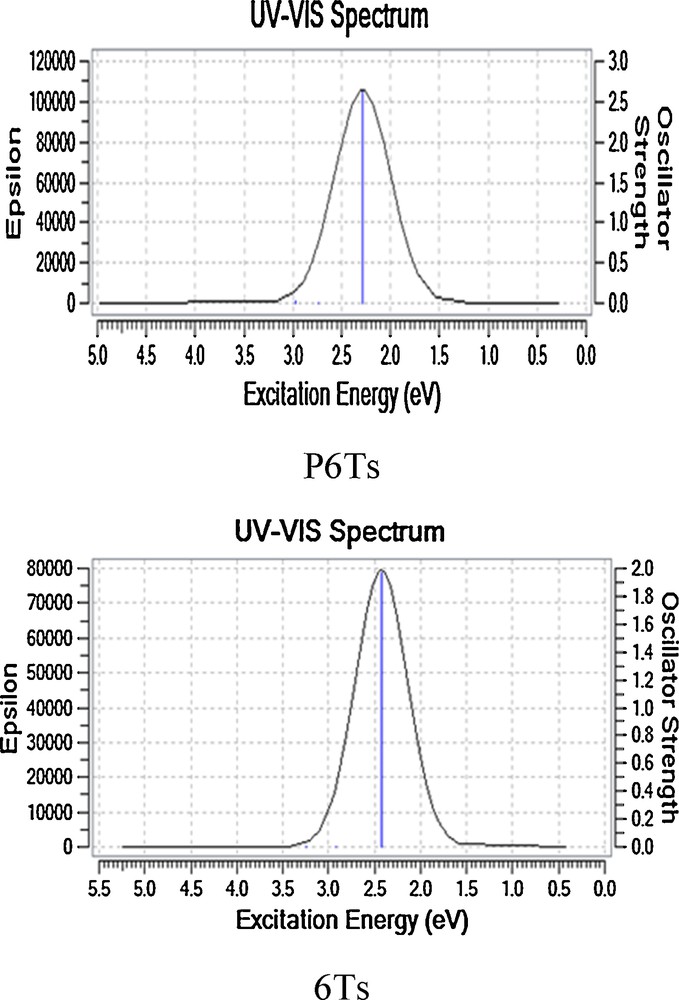
Simulated absorption spectra for both hexamers 6Ts and P6Ts calculated at the Td-B3LYP/6-31G(d,p) level of theory.

Compound	λ_max/nm	E_g/eV	f
2Ts	301.5	4.11	0.41
3Ts	369.88	3.35	0.8
4Ts	424.78	2.92	1.2
5Ts	472.66	2.62	1.58
6Ts	511.2	2.42	1.96

P2Ts	390.66	3.17	1.2
P3Ts	441.61	2.81	1.57
P4Ts	480.63	2.58	1.94
P5Ts	515.17	2.41	2.28
P6Ts	542.96	2.28	2.62

As mentioned in the introduction section, efficient injection and transport of both holes and electrons are important parameters for the rational design of optimized light-emitting diodes, and lead to the good performance of conductive polymers in device, such as organic light-emitting diodes (OLEDs) [52]. The ionization potential and electron affinity are closely related to the degree of electron extraction (hole injection) to form p-type semi-conductors and electron injection to form n-type semi-conductors [44]. Electronic energies for the neutral, cationic, and anionic species of the oligomers were calculated at the B3LYP/6-31G** level of theory, and used for calculation of the ionization potential (IP) and electron affinity (EA) of each oligomer, which are listed in Table 4. The results obtained for IPs and EAs show a decrease in the energy barrier for the hole and electron injection after closing the end-sides of oligothiophenes by phenyl groups, and show better p-type and n-type conducting for phenyl-capped oligothiophenes than the corresponding oligothiophenes. It was found that as the fraction of thiophene increases, the IP values decrease, which corresponds to an improvement in the hole injection properties, and this is also consistent with the trend of changes in the case of HLGs. With increase in the conjugated length, influence of the substituent type is not considerable. It is known that the formation of the intermediate radical cations from the monomers, as the first step in the polymerization mechanism of conductive polymers, has an important role in their polymerization process. This reaction can be considered as an ionization reaction [58–60]. In general, it may be concluded that the initiation step of electropolymerization of PnT species requires a lower applied potential. In other words, this potential is reduced when the electron conjugation of molecules increases. This behavior is in agreement with the lower oxidation potentials measured experimentally [60].

Species	IP/eV	EA/ev
2Ts	7.11	–0.34
3Ts	6.49	–0.36
4Ts	6.14	–0.78
5Ts	5.9	–1.05
6Ts	5.74	–1.25
P2Ts	6.28	–0.63
P3Ts	6	–0.94
P4Ts	5.81	–1.15
P5Ts	5.67	–1.31

The organic field-effect transistor and the organic light-emitting diode experiments show that a Schottky-type injection barrier for hoping-type carrier transport can satisfactorily describe the charge injection properties of electrode/organic interface [61,62]. Thus, for a given electrode, the hole and electron injection rates are mainly decided by the HOMO and LUMO levels. The relationship of the charge carrier injection rate between the unsubstituted and substituted molecules can be expressed as:

\frac{υ_{e}^{sub}}{υ_{e}^{unsub}} = \exp (\frac{E_{L}^{unsub} - E_{L}^{sub}}{k T})

(3)

\frac{υ_{h}^{sub}}{υ_{h}^{unsub}} = \exp (\frac{E_{H}^{unsub} - E_{H}^{sub}}{k T})

(4)

where

υ_{e}^{sub}

and

υ_{e}^{unsub}

are the electron injection rates for the substituted and unsubstituted molecules, respectively;

E_{L}^{sub}

and

E_{L}^{unsub}

are the LUMO energies for the substituted and unsubstituted molecules, respectively;

υ_{h}^{sub}

and

υ_{h}^{unsub}

are the hole injection rates for the substituted and unsubstituted molecules, respectively;

E_{H}^{sub}

and

E_{H}^{unsub}

are the HOMO energies for the substituted and unsubstituted molecules, respectively. Table 5 lists the carrier injection rates for phenyl-capped oligothiophenes relative to the corresponding oligothiophenes. Due to the exponential dependence of carrier injection rate on the injection barrier, ΔE, the difference of a few barrier heights can significantly influence the injection rate. The results obtained show a large increase in the charge-carrier injection rate for phenyl-capped oligothiophenes with respect to the corresponding oligothiophenes. With an increase in the chain length, the relative charge-carrier injection rate decreases. It shows a larger charge-carrier injection rate for the electron carrier than for the hole carrier, which exhibits the phenyl-capped oligothiophene tendency towards n-type transport. In practice, the substitution technique is usually used to tune the doping types for designing novel materials with desirable conductive behaviors. For example, the unsubstituted and the–CH₃/–CH₃ end-capped oligothiophenes show p-type conductivity [63–68], while the–CN/–CN end-capped oligothiophenes exhibit n-type transport [69–72]. Our recommended polymer possessing phenyl group as end-capped is a good candidate for the design of charge transport and/or solar cell materials. This study may be helpful in further theoretical investigations on such kind of systems and also to the experimental study of charge transport and/or solar cell materials.

Compound	n-type	p-type
2Ts	1.00	1.00
3Ts	1.00	1.00
4Ts	1.00	1.00
5Ts	1.00	1.00
6Ts	1.00	1.00

P2Ts	1.06 × 10⁷	1.78 × 10⁸
P3Ts	7.11 × 10³	2.794 × 10⁴
P4Ts	2.04 × 10²	3.29 × 10²
P5Ts	26.15	26.15
P6Ts	7.41	5.99

4 Conclusion

In this work, the effect of the end-substitution of phenyl group on the geometry, electron conjugation and electronic properties of oligothiophenes was investigated using DFT. The presence of the phenyl substituent at the ends of an oligothiophene chain exerts fine-tuning effects on the structures, electronic and excitation states. The calculations carried out on both neutral and doped phenyl-caped oligorthiophenes show that the doped oligomers have more satisfactory structural and electronic characteristics for conducting polymers. The conjugated π-system in the doped oligomers is expanded more, with a higher planarity, and the quinoid coefficient is close to unity. The obtained results reveal that with increasing the oligomer chain length, the bond alternation parameter in a conjugated system tends towards zero, corresponding to higher aromaticity. Also, the calculated energy gap values between the frontal orbitals, electron affinities, and ionization potentials indicate that with increasing the oligomer chain length, the conductivity band decreases. The absorption spectra were evaluated at the TD-B3LP/6-31G(d,p) level. Among the molecules investigated, those derivatives with a phenyl ring as the end-capped group display the largest λ_max value, which is in good agreement with the results obtained for the HOMO–LUMO energies. In addition, all the PnTs investigated have better hole- and electron-transporting rates, and can act as nice ambipolar materials.

Acknowledgement

The authors wish to thank the Shahrood University of Technology for the financial support of this work.

Bibliographie

[1] H. Meng; J. Zheng; A.J. Lovinger; B.C. Wang; P.G. Van Patten; Z. Bao Chem. Mater., 15 (2003), pp. 1778-1787

[2] M. Mushrush; A. Facchetti; M. Lefenfeld; H.E. Katz; T.J. Marks J. Am. Chem. Soc., 125 (2003), pp. 9414-9423

[3] P.N. Prasad; D.J. Williams Introduction to Nonlinear Effects in Monomers and Polymers, Wiley, New York, 1991

[4] K. Naoi; K.-I. Kawase; Y. Inoue J. Electrochem. Soc., 144 (1997), p. L170-L172

[5] J.J. Halls; C.A. Walsh; N.C. Greenham; E.A. Marseglia; R.H. Friend; S.C. Moratti; A.B. Holmes Nature, 376 (1995), pp. 498-500

[6] J.H. Burroughes; D.D.C. Bradley; A.R. Brown Nature, 347 (1990), pp. 539-541

[7] G. Gustafsson; Y. Cao; G.M. Treacy; F. Klavetter; N. Colaneri; A.J. Heeger Nature, 357 (1992), pp. 477-479

[8] P.L. Burn; A.B. Holmes; A. Kraft; D.D.C. Bradley; A.R. Brown; R.H. Friend; R.W. Gymer Nature, 356 (1992), pp. 47-49

[9] A. Kraft; A.C. Grimsdale; A.B. Holmes Angew. Chem., 110 (1998), pp. 416-443

[10] Handbook of Oligo- and Polythiophenes (D. In; Fichou, eds.), Wiley, New York, 1999

[11] M. Kobayashi; J. Chem; T.C. Chung; F. Moraes; A.J. Heeger; F. Wudl Synth. Met., 9 (1984), pp. 77-96

[12] T.C. Chung; J.H. Kaufman; A.J. Heeger; F. Wudl Phys. Rev. B, 30 (1984), pp. 702-710

[13] S. Hotta Molecular conductive materials: polythiophenes and oligothiophenes (H.S. Nalwa, ed.), Handbook of Organic Conductive Molecules and Polymers, vol. 2, Wiley, Chichester, 1997, pp. 309-387

[14] C. Ziegler Thin film properties of oligothiophenes (H.S. Nalwa, ed.), Handbook of Organic Conductive Molecules and Polymers, vol. 3, Wiley, Chichester, 1997

[15] W. Yu; H. Meng; J. Pel; W. Huang J. Am. Chem. Soc., 120 (1998), pp. 11808-11813

[16] G. Zotti; S. Zecchin; G. Schiavon; B. Vercelli; A. Berlin; S. Grimoldi Macromol. Chem. Phys., 205 (2004), pp. 2026-2031

[17] X.-L. Wei; Y.Z. Wang; S.M. Long; C. Bobeczko; A.J. Epstein J. Am. Chem. Soc., 118 (1996), pp. 2545-2552

[18] M. Tsuchiya; S. Matsui; K. Sano; T. Kojima J. Appl. Polym. Sci., 70 (1998), pp. 471-475

[19] M. Charton J. Am. Chem. Soc., 97 (1975), pp. 1552-1556

[20] R.W. Taft, Wiley, New York (1956), p. 556

[21] R.J. Waltman; J. Bargon; A.F. Diaz J. Phys. Chem., 87 (1983), pp. 1459-1466

[22] M. Sato; H. Morii Polym. Commun., 32 (1991), pp. 42-48

[23] M. Sato; H. Morii Macromolecules, 24 (1991), pp. 1196-1201

[24] S.A. Lee; Y. Yoshida; M. Fukuyama; S. Hotta Synth. Met., 106 (1999), pp. 39-43

[25] K. Waragai; H. Akimichi; S. Hotta; H. Kano Phys. Rev. B, 52 (1995), pp. 1786-1792

[26] S. Hotta; Y. Ichino; Y. Yoshida; M. Yoshida Synth. Met., 121 (2001), pp. 1353-1354

[27] G. Zotti; G. Schiavon Chem. Mater., 5 (1993), pp. 620-624

[28] H. Yanagi; A. Yoshiki; S. Hotta; S. Kobayashi Appl. Phys. Lett., 83 (2003), pp. 1941-1943

[29] S. Hotta; M. Goto; R. Azumi; M. Inoue; M. Ichikawa; Y. Taniguchi Chem. Mater., 16 (2004), pp. 237-241

[30] A. Dkhissi; F. Louwet; L. Groenendaal; D. Beljonne; R. Lazzaroni; J.L. Bredas Chem. Phys. Lett., 359 (2002), pp. 466-472

[31] A. Dkhissi; D. Beljonne; R. Lazzaroni; F. Louwet; L. Groenendaal; J.L. Bredas Int. J. Quantum Chem., 91 (2002), p. 517

[32] C. Aleman; D. Curco; J. Casanovas Chem. Phys. Lett., 386 (2004), pp. 408-413

[33] C. Aleman; J. Casanovas J. Phys. Chem., 108 (2004), pp. 1440-1447

[34] Y. Dai; E. Blaisteu-Barojas J. Chem. Phys., 129 (2008), pp. 164903-164908

[35] S. Suramitr; A. piriyagagoon; P. Wolschann; S. Hannongbua Theor. Chem. Acc., 131 (2012), pp. 1209-1217

[36] U. Salzner; P.G. Pickup; R.A. Poirier; J.B. Lagowski J. Phys. Chem. A, 102 (1998), pp. 2572-2578

[37] R. Colle; A. Curioni J. Am. Chem. Soc., 120 (1998), pp. 4832-4837

[38] H. Sabzyan; H. Nikoofard Chem. Phys., 107 (2004), pp. 105-113

[39] H. Nikoofard; H. Sabzyan J. Fluo. Chem., 128 (2007), pp. 668-673

[40] D. Jacquemin; E.A. Perpete Chem. Phys. Lett., 429 (2006), pp. 147-152

[41] E.A. Perpete; J. Preat; J.M. Andre; D. Jacquemin J. Phys. Chem. A, 110 (2006), pp. 5629-5635

[42] D. Jacquemin; V. Wathelet; E.A. Perpete J. Phys. Chem. A, 110 (2006), pp. 9145-9152

[43] D. Jacquemin; J. Preat; V. Wathelet; M. Fontaine; E.A. Perpete J. Am. Chem. Soc., 128 (2006), pp. 2072-2083

[44] G. Zhang; J. Ma; Y. Jiang J. Phys. Chem. B, 109 (2005), pp. 13499-13509

[45] H. Cao; J. Ma; G. Zhang; Y. Jiang Macromolecules, 38 (2005), pp. 1123-1130

[46] G. Zhang; J. Ma; Y. Jiang Macromolecules, 36 (2003), pp. 2130-2140

[47] M.J. Frisch; G.W. Trucks; H.B. Schlegel; G.E. Scuseria; M.A. Robb; J.R. Cheeseman; V.G. Zakrzewski; J.A. Montgomery; R.E. Stratmann; J.C. Burant; S. Dapprich; J.M. Millam; A.D. Daniels; K.N. Kudin; M.C. Strain; O. Farkas; J. Tomasi; V. Barone; M. Cossi; R. Cammi; B. Mennucci; C. Pomelli; C. Adamo; S. Clifford; J. Ochterski; G.A. Petersson; P.Y. Ayala; Q. Cui; K. Morokuma; D.K. Malick; A.D. Rabuck; K. Raghavachari; J.B. Foresman; J. Cioslowski; J.V. Ortiz; B.B. Stefanov; G. Liu; A. Liashenko; P. Piskorz; I. Komaromi; R. Gomperts; R.L. Martin; D.J. Fox; T. Keith; M.A. Al-Laham; C.Y. Peng; A. Nanayakkara; C. Gonzalez; M. Challacombe; P.M.W. Gill; B. Johnson; W. Chen; M.W. Wong; J.L. Andres; C. Gonzalez; M. Head-Gordon; E.S. Replogle; J.A. Pople Gaussian 03W, Gaussian Inc., Pittsburgh PA, 2003

[48] T. Koopmans Physica, 1 (1934), pp. 104-113

[49] Z.H. Levine; P. Soven Phys. Rev. A, 29 (1984), pp. 625-635

[50] A. Zangwill; P. Soven Phys. Rev. A, 21 (1980), pp. 1561-1572

[51] G. Horowitz; B. Bachet; A. Yassar; P. Lang; F. Demanze; J.-L. Fave; F. Garnier Chem. Mater., 7 (1995), pp. 1337-1345

[52] G. Zhang; H. Zhang; D. Li; D. Chen; X. Yu; B. Liu; Z. Li Theo. Chem. Acc., 121 (2008), pp. 109-122

[53] M. Levy; A. Nagy Phys. Rev. Lett., 83 (1999), pp. 4361-4364

[54] R. Colle; A. Curioni J. Phys. Chem. A, 104 (2000), pp. 8546-8550

[55] H. Sabzyan; A. Omrani J. Phys. Chem. A, 107 (2003), pp. 6476-6486

[56] A. Omrani; H. Sabzyan J. Phys. Chem. A, 109 (2005), pp. 8874-8879

[57] M.A. De Oliveira; H. Duarte; J. Pernaut; W.B. De Almeida J. Phys. Chem. A, 104 (2000), pp. 8256-8262

[58] R.J. Waltman; A.F. Diaz; J. Bargon J. Phys. Chem., 88 (1984), pp. 4343-4346

[59] W. Su; J.O. Iron Synth. Met., 95 (1998), pp. 159-167

[60] S. Sadki; P. Scottland; N. Brodie; G. Sabouraud Chem. Soc. Rev., 29 (2000), pp. 283-293

[61] A.K. Mahapatro; S. Ghosh Appl. Phys. Lett., 80 (2002), pp. 4840-4842

[62] A.B. Chwang; C.D. Frisbie J. Phys. Chem. B, 104 (2000), pp. 12202-12209

[63] A. Facchetti; Y. Deng; A. Wang; Y. Koide; H. Sirringhaus; T.J. Marks; R.H. Friend Angew. Chem. Int. Ed., 39 (2000), pp. 4547-4551

[64] C. Zhang; S.J. Sun Polym. Sci. Part A Polym. Chem., 45 (2007), pp. 41-48

[65] M.H. Yoon; S.A. Di Benedetto; A. Facchetti; T.J. Marks J. Am. Chem. Soc., 127 (2005), pp. 1348-1349

[66] J. Casado; M.Z. Zgierski; R.G. Hicks; D.J.T. Myles; P.M. Viruela; E. Ortí; M.C.R. Delgado; V. Hernández; J.T.L. Navarrete J. Phys. Chem., A109 (2005), pp. 11275-11284

[67] C.R. Newman; C.D. Frisbie; D.A. daSilva Filho; J.L. Brédas; P.C. Ewbank; K.R. Mann Chem. Mater., 16 (2004), pp. 4436-4451

[68] J. Casado; L.L. Miller; K.R. Mann; T.M. Pappenfus; H. Higuchi; E. Ortå; B. Milián; R. Pou-Amérigo; V. Hernández; J.T.L. Navarrete J. Am. Chem. Soc., 124 (2002), pp. 12380-12388

[69] H.E. Katz; A. Dodabalapur; L. Torsi; D. Elder Chem. Mater., 7 (1995), pp. 2238-2240

[70] P. Bauerle; U. Segelbacherf; A. Maier; M. Mehring J. Am. Chem. Soc., 115 (1993), pp. 10217-10223

[71] S. Hotta; K. Waragai J. Mater. Chem., 1 (1991), pp. 835-842

[72] K. Waragai; S. Hotta Synth. Met., 41 (1991), pp. 519-522

Commentaires - Politique