Quantum chemical studies of non-covalent interactions between the ethyl cation and rare gases

Boaz G. Oliveira

doi:10.1016/j.crci.2014.01.014

Quantum chemical studies of non-covalent interactions between the ethyl cation and rare gases

Boaz G. Oliveira ¹

¹ Instituto de Ciências Ambientais e Desenvolvimento Sustentável, Universidade Federal da Bahia, 47801-100 Barreiras, BA, Brazil

Comptes Rendus. Chimie, Volume 17 (2014) no. 10, pp. 1041-1049.

Résumé

By taking into consideration the facts that rare gases (Ar, He, Kr, and Ne) are practically inert and that the structure of the ethyl cation (C₂H₅⁺) is stabilized through the hyperconjugation effect, a theoretical study at the B3LYP/6-311 + +G(d,p) level of calculation was carried out here in order to investigate the formation of the C₂H₅⁺···Ar, C₂H₅⁺···He, C₂H₅⁺···Kr, and C₂H₅⁺···Ne complexes. The charge transfers among H and Ar, He, Kr or Ne prove that the loss of electronic density on the rare gases are clearly noticeable. Additionally, the synergism between the structural changes and the vibration shifts have been demonstrated and justified on the basis of the Bent rule and QTAIM calculations. In complement, the interaction strength in H⁺···Ar, H⁺···He, H⁺···Kr, and H⁺···Ne was examined, although the covalent character is completely null because these contacts are very weak.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

mmc1.docx

Métadonnées

Reçu le : 2013-07-22
Accepté le : 2014-01-21
Publié le : 2014-08-01

DOI : 10.1016/j.crci.2014.01.014

Mots clés : Ethyl cation, Rare gases, B3LYP, QTAIM, NBO

Affiliations des auteurs :

Boaz G. Oliveira ¹

¹ Instituto de Ciências Ambientais e Desenvolvimento Sustentável, Universidade Federal da Bahia, 47801-100 Barreiras, BA, Brazil

@article{CRCHIM_2014__17_10_1041_0,
     author = {Boaz G. Oliveira},
     title = {Quantum chemical studies of non-covalent interactions between the ethyl cation and rare gases},
     journal = {Comptes Rendus. Chimie},
     pages = {1041--1049},
     publisher = {Elsevier},
     volume = {17},
     number = {10},
     year = {2014},
     doi = {10.1016/j.crci.2014.01.014},
     language = {en},
}

TY  - JOUR
AU  - Boaz G. Oliveira
TI  - Quantum chemical studies of non-covalent interactions between the ethyl cation and rare gases
JO  - Comptes Rendus. Chimie
PY  - 2014
SP  - 1041
EP  - 1049
VL  - 17
IS  - 10
PB  - Elsevier
DO  - 10.1016/j.crci.2014.01.014
LA  - en
ID  - CRCHIM_2014__17_10_1041_0
ER  -

%0 Journal Article
%A Boaz G. Oliveira
%T Quantum chemical studies of non-covalent interactions between the ethyl cation and rare gases
%J Comptes Rendus. Chimie
%D 2014
%P 1041-1049
%V 17
%N 10
%I Elsevier
%R 10.1016/j.crci.2014.01.014
%G en
%F CRCHIM_2014__17_10_1041_0

Boaz G. Oliveira. Quantum chemical studies of non-covalent interactions between the ethyl cation and rare gases. Comptes Rendus. Chimie, Volume 17 (2014) no. 10, pp. 1041-1049. doi : 10.1016/j.crci.2014.01.014. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2014.01.014/

Version originale du texte intégral

1 Introduction

Nowadays, the studies of interatomic interactions have attained a level of complexity never seen before [1–5]. Besides dihydrogen bonds [6–10], halogen bonds [11–14], dihydride–halogen bonds [15–17], beryllium bonds [18], and pnicogen bonds [19,20], in general the electron flux on these interactions occur from high-electron-density centers, such as proton acceptors, towards the electron-depleted ones, which are represented by hydrogen donors [21–24]. Clearly, this electronic gearing controls the formation of these non-covalent links [25–27]. Anyhow, the research of new forms of intermolecular contacts is focused on the analysis of the high electron-density entity, because it is from the hyperconjugative interaction (charge transfer) [28] between the frontier molecular orbitals occurs. Otherwise, in some circumstances, hybridization (ab initio wave function) can manifest itself and outweigh hyperconjugation [29,30]. Actually, depending on the strength of the interaction, these two interpretative lines rationalize the state-of-the-art to evaluate whether an intermolecular system is a stronger or a weaker bound.

Regarding proton donating in hydrogen bonding, it is known that they must not necessarily be neutral acids, and indeed, they can originate from ionic species. In agreement with this, it was established a very long time ago that some carbonium ions have the capability to acquire extra stability [31], but in this case, the occurrence of inconstant electronic fluxes plays a great role in the formation of electron-depleted molecular sites. If it happens, the carbocation may function as a proton donor, such as the ethyl cation (C₂H₅⁺) does, for instance. Beyond being a typical representative of carbocations [32], C₂H₅⁺ has been already examined and validated as a proton donor in the formation of hydrogen complexes with similar neutral molecules, such as acetylene, ethylene, as well as cyclopropane [33], wherein π···H hydrogen bonds appear. Moreover, C₂H₅⁺ is also able to form dihydrogen bonds when it binds to magnesium hydride or beryllium hydride to form binary (C₂H₅⁺···MgH₂ and C₂H₅⁺···BeH₂) and ternary (C₂H₅⁺···2MgH₂ and C₂H₅⁺···2BeH₂) complexes [34,35].

Concerning the proton's acceptor nature, it is well known that molecules with lone pairs of electrons [36,37], unsaturated bonds [22,38] or even those with hydride groups [16,17] are able to receive acid protons. Otherwise, there is also another possibility of unusual proton receptors, for instance, the rare gases. In line with this, Cappelletti et al. [39] have stated the “birth of the hydrogen bond” between water and some rare gases, Barreto et al. [40] described van der Waals forces in complexes of water and peroxides with rare gases, whereas Jamshidi et al. [41] have asserted that metals and rare gases bind to each other in a stable form. Although the existence of protonated rare gas clusters is known [42], the main goal of the current work is focused on a quantum chemical study of intermolecular interactions between rare gases, such as argon, helium, krypton, or neon, and the ethyl cation (C₂H₅⁺), whose H···Ar, H···He, H···Kr, and H···Ne contacts will be examined by means of structural investigation, determination of electronic parameters, infrared spectroscopy analysis, topological integrations of charge densities, and molecular orbital calculations.

From a spectroscopic standpoint, the researches related to hydrogen bonds or any other similar interaction are currently performed on the basis of the s-(H) and p-(X) orbitals in the H−X proton donor system (wherein X is more electronegative than hydrogen) [43], whose contributions as well as variations accord well with the Bent rule [44]. Being aware of this statement, the analysis of these orbitals should be one of the objectives to be fulfilled here because the Bent rule corroborates the hybridization theory and justifies the frequency shifts of the proton donors. As such, the shortening in the bond length of the proton donor is followed by a decrease in its polarity, by which an increase in the s-character of the orbital of X (within the H−X molecule) is evidenced. If this occurs, displacements in the coordinates of H and X are expected, and surely this can be justified through the computation of their atomic radii by means of the Quantum Theory of Atoms in Molecules (QTAIM) [45]. Specifically, if the distance between these atoms is reduced, the relationship Δr_H > Δr_X is valid. This inequality is related to the shortening of the bond length and with a blue shift in the stretch frequency [43]. On the other hand, if Δr_H < Δr_X, it means that a weakness in the proton donor bond is testified, which leads to an increase in the bond length, which, in turn, causes the appearance of a red shift in the H−X oscillator [43].

On a purely theoretical viewpoint, these atomic radii are computed in the light of the QTAIM approach, with localization of Bond Critical Points (BCP) along each internuclear axis [46]. In addition, other topological properties are also determined, namely: electronic density (ρ), Laplacian (▿²ρ), kinetic (G) and potential (U) electronic density energies. It is through the low and high values of ρ, the positive and negative ones of ▿²ρ, and finally if G outweighs U or vice-versa, that all H···RG (with RG = Ar, He, Kr, and Ne) interactions and π bond of C₂H₅⁺ are modeled. In practice, it is expected that the interaction strength profile of the C₂H₅⁺···RG systems may be in good agreement with these kinds of analysis presented above, although it is widely known that the charge transfer mechanism still governs the formation of some intermolecular interactions [28,47–50], even if partially. Due to this, the algorithms of the Charges from Electrostatic Potentials using a grid-based method (ChelpG) [51], Natural Bond Orbitals (NBO) [52], the traditional Mulliken population analysis [53], and naturally the QTAIM integrations [54] were applied during routine calculations. By these codes, the loss of atomic charge on the rare gases being transferred towards H, the phenomenon of shift in the frequency of the proton donor (C₂H₅⁺), and of course the formation of the H···RG interaction can be certainly evidenced.

2 Computational procedure

The optimized geometries of the C₂H₅⁺···RG complexes (with RG = Ar, He, Kr, and Ne) were modeled at the B3LYP/6-311 + +G(d,p) level of theory. All calculations were carried out by the GAUSSIAN 98 W quantum software [55], by which the calculations of the ChelpG, NBO, and Mulliken atomic charges were also obtained. Moreover, the Boys and Bernardi function counterpoise method [56] implemented to eliminate the Basis Sets Superposition Error (BSSE) [57] and the Zero-Point vibrational Energy (ZPE) [58] were also included to correct the interaction energies. Regarding the QTAIM calculations, they were performed by AIMAll 11.05.16 software [59] after generation of the “wfn” archive by GAUSSIAN 98W.

3 Results and discussions

3.1 Structure and spectrum

Through the calculations performed at the B3LYP/6-311 + +G(d,p) level of theory, Fig. 1 illustrates the optimized geometries of the C₂H₅⁺···Ar (I), C₂H₅⁺···He (II), C₂H₅⁺···Kr (III), and C₂H₅⁺···Ne (IV) complexes. The distance values of 2.5822 (I), 2.4116 (II), 2.6126 (III), and 2.3956 Å (IV) for the H···RG interactions are shorter than the corresponding sum of the van der Waals radii [60–62], whose amounts are 2.97 (H = 1.09 + Ar = 1.88), 2.490 (H = 1.09 + He = 1.40), 3.11 (H = 1.09 + Kr = 2.02), and 2.63 Å (H = 1.09 + Ne = 1.54). In conformity with these assertions, but in view of the applicability in investigations of chemical bonds and interatomic distances [63,64], the interaction distance at the B3LYP/6-311 + +G(d,p) of I is shorter than the values reported by Goswani and Arunan [65] regarding the H₂O···2Ar and H₂S···2Ar complexes at the MP2(full)/aug-cc-pVTZ level of theory. Absolutely, this is not enough to discriminate the efficiency between these levels of theory, but otherwise it also serves to show that ternary structures have not necessarily shorter intermolecular distances and higher interaction energies compared with binary ones [21,27,66,67].

Fig. 1
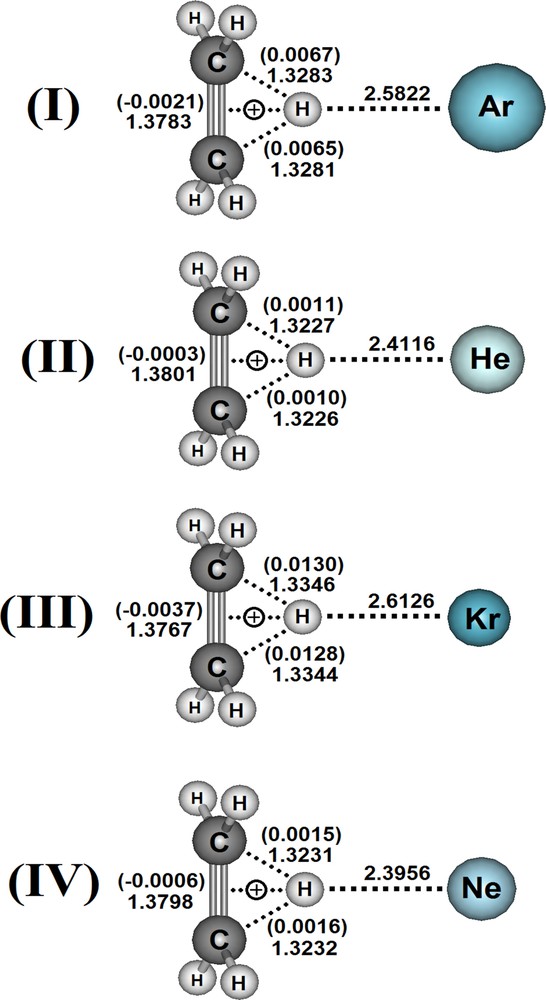
(Color online.) Optimized geometries of the C₂H₅⁺···Ar (I), C₂H₅⁺···He (II), C₂H₅⁺···Kr (**III**), and C₂H₅⁺···Ne (IV) complexes obtained via B3LYP/6-311 + +G(d,p) calculations.

In addition to H···RG, the values of the bond lengths of both C···H and π are also depicted in Fig. 1. Unlike many other intermolecular systems [68–70], the shorter interactions of II and IV are not responsible for the most intense molecular changes, in particular on the ethyl cation. Note that IV is a much shorter bound than III, although the corresponding values of Δr_π are –0.0006 and –0.0037 Å. Because the hyperconjugation controls the stabilization of C₂H₅⁺, this effect shows itself sensitive to the changes in the π···H and C···H contacts [71,72]. These bond lengths vary between 0.0199 and 0.0371 Å as well as between 0.0011 and 0.0130 Å; these profiles are not in line with the interaction strengths, obviously at this stage of the study regarding only the interatomic distances. However, all these results show a good concordance with the phenomenology of the infrared stretch modes, whose values are displayed in Table 1.

IR modes	Interatomic and molecular systems
	I	II	III	IV
υ_H···RG	80	68.10	89	62.8
I_H···RG	30.88	6.21	42.7	16.9
υ_π···H,c	2093.1	2142.7	2035.9	2140.4
υ_π···H,m	2144.8 (2217)^e	2144.8	2144.8	2144.8
Δυ_π···H^a	–51.7	–2.1	–108.9	–4.4
I_π···H	179.2	55.73	338.9	67.88
I_π···H/I_π···H,m^b	4.1	1.3	7.8	1.6
υ_π	1574.4	1572.8	1575.6	1572.9
Δυ_π^c	+1.8	+0.2	+3	0.3
I_π	19.99	10.4	34	11.2
I_π/I_π,m^d	2.1	1.01	3.6	1.2

^a Δυ_π···H = υ_π···H,c–υ_π···H,m (complex - monomer), in which the value of υ_π···H,m is 2144.8 cm⁻¹ at the B3LYP/6-311 + +G(d,p) level of theory.

^b I_π···H/I_π···H,m, in which the value of I_π···H,m is 43 km·mol⁻¹ at the B3LYP/6-311 + +G(d,p) level of theory.

^c Δυ_π = υ_π,c–υ_π,m (complex–monomer), in which the value of υ_π,m is 1572.63 cm⁻¹ at the B3LYP/6-311 + +G(d,p) level of theory.

^d I_π/I_π,m, in which the value of I_π,m is 9.47 km·mol⁻¹ at the B3LYP/6-311 + +G(d,p) level of theory.

^e Experimental value: Ref. [80].

Although supported by the van der Waals radii, the long interatomic distances present weak stretch frequency modes, which oscillate between 62.8 and 89 cm⁻¹; their absorption intensities are not so low (e.g., 30.88 and 42.70 km·mol⁻¹ for II and III, respectively). As aforementioned, the π bonds are reduced and strengthened after the formation of the I–IV complexes, but now, the vibration analysis point out slight blue shifts with increasing absorption intensity ratios [73,74]. Bearing in mind that the ethyl cation is a proton donor, the distance shortening reaffirms that π···H possesses the same profile observed in a large number of systems stabilized via H-bond [75,76]. Similar to a selected group of systems [77,78], however, red and blue shifts also coexist in the ethyl cation. Just like mentioned by Yen et al. [79] in studies of complexes, such as H–Ng–F···H–F and H–F···H–Ng–F, actually there is a synergism between Δr_π···H and Δυ_π···H, although all computed red shifts of –51.7 (I), –2.1 (II), –108.9 (III), and –4.4 cm⁻¹ (IV) are not concordant with the profile of the interatomic strength. In other words, the intensities of the shifted frequencies are not affected by the interatomic distances. Note that the experimental value of 2217 cm⁻¹ obtained by Duncan et al. [80] was satisfactorily reproduced by the value of 2144.8 cm⁻¹ determined via B3LYP/6-311 + +G(d,p) calculations.

3.2 Energy and charge transfer: attraction, repulsion and eventual retro-donation

Some time ago, Salazar et al. [81] have mentioned the difficulty in studying complexes formed by rare gases. Especially about interaction energy, it is widely known that its quantity is negative if the geometry of the intermolecular complex falls at the minimum of the potential energy surface [82]. According to the values listed in Table 2, it can be perceived how I–IV complexes are weakly bound. As can be seen, the ΔZPE corrections outweigh BSSE, although in some cases, the BSSE values are negative [83], even though the interaction energy of –7.69 kJ·mol⁻¹ reveals that III is the most stable complex. Contrary to what one might point out, intermolecular interactions with low energies are not unusual, as can confirmed by a work by Lu et al. [84]. Of course, small BSSE amounts were also obtained, and above all else, this was also verified in weakly bound complexes modeled through the B3LYP/6-311 + +G(d,p) theoretical level [85]. Likewise, it may be highlighted that H···RG is a non-covalent interaction with low results of BSSE and ΔE^C, although this is not relevant because other intermolecular interactions also present a similar aspect [19]. What is quite clear in other works [86,87] is not evidenced here regarding the direct relationship between distances and energies of H···RG interactions.

Energies	Interatomic and molecular systems
	I	II	III	IV
ΔE	–4.62	–0.61	–8.66	–2.21
BSSE	–0.40	0.02	–0.20	0.48
ΔZPE	1.29	0.93	1.17	1.07
ΔE^C	–3.73	+0.034	–7.69	–0.66

One of the most applied procedures in the investigations of intermolecular interactions is the analysis of the charge-transfer mechanism, which has proven extremely efficient in several applications [88,89], although it is also neglected because the atomic charge has no physical basis and thereby is not included into the Schrödinger equation. Despite this, many are the algorithms implemented to compute atomic charges, namely those inserted into the ChelpG, NBO, Mulliken, and QTAIM schemes. From these approaches, Table 3 lists the values of the charge transfer (ΔQ_RG^ChelpG, ΔQ_RG^NBO, ΔQ_RG^Mull, and ΔQ_RG^QTAIM), whose mechanism was admitted as being initialized by donations of electronic density from rare gases towards the ethyl cation. In this manner, the positive values of ΔQ_RG reaffirm the transference of charge previously quoted, although it must be also asserted that the negative and small results of –0.00032 and 0.00088 au of II and IV are somewhat realistic because undoubtedly these systems are not only non-covalent but almost non-bonded. This scenario suggests that an electronic retro-donation from ethyl cation towards to neon and helium may be reliable.

Charges	Interatomic and molecular systems
	I	II	III	IV
ΔQ_RG^ChelpG	+0.063 (–0.088) [0.000]	+0.018 (–0.035) [+0.002]	0.102 (–0.131) [–0.001]	+0.023 (–0.042) [–0.003]
ΔQ_RG^NBO	+0.019 (+0.002) [–0.006]	+0.0020 (+0.002) [–0.001]	+0.036 (+0.01) [–0.011]	+0.004 (+0.002) [–0.001]
ΔQ_RG^Mull	+0.062 (–0.032) [–0.012]	+0.017 (–0.019) [–0.001]	+0.081 (–0.031) [–0.017]	+0.028 (–0.016) [–0.008]
ΔQ_RG^QTAIM	+0.0183 (+0.006) [–0.005]	+0.0008 (+0.002) [–0.001]	+0.032 (+0.010) [–0.007]	–0.0003 (+0.007) [–0.0009]

Throughout the chemical literature with mention to hydrogen bonding [90,91], the great applicability of the charge transfers is concentrated in the characterization and/or justification of the shifting frequencies of the proton donors when these species bind with high density centers [92]. By contrasting all amounts of ΔQ_RG^ChelpG, ΔQ_RG^NBO, ΔQ_RG^Mull, and ΔQ_RG^QTAIM versus the values of Δυ_π···H, four relationships were equated as follows:

Δυ_π···H = –1277.5 ΔQ_RG^ChelpG + 24.0, R² = –0.997

(1)

Δυ_π···H = –3182.1 ΔQ_RG^NBO + 6.75, R² = –0.999

(2)

Δυ_π···H = –1639.5 ΔQ_RG^Mull + 35.3, R² = –0.968

(3)

Δυ_π···H = –3124.6 ΔQ_RG^QTAIM – 0.8, R² = –0.993

(4)

The role of charge transfer is well understood on the basis of the frontier molecular orbitals, in which the electron-density flows between them from the HOMO towards the LUMO of the proton acceptor and donor [93,94], respectively. Here, charge transfer is not entirely absolute because in the weakest bound systems, for instance II and IV, an electronic density retro-donating phenomenon (LUMO to HOMO) determined via QTAIM calculations is evidenced. Even though the linear and direct relationship between ΔQ_RG^NBO and Δυ_π···H was established, Fig. 2 shows that NBO is an efficient approach in view of the linear coefficient of –0.999.

Fig. 2
Relationship between NBO charge transfer on rare gases (ΔQ_RG^NBO) and red shifts on the π···H contact (Δυ_π···H).

3.3 NBO and QTAIM analysis: Bent rule and interaction strength

In a forward analysis of the molecular orbital, in Table 4 are listed other NBO parameters, such as the percentages of the s-character and p-character of carbon (π) and hydrogen (H···RG) in the ethyl cation. Increases of 0.03 and 0.09% as well as decreases of –0.02 and –0.01% in the s-character can be noted; these are closely related with the interaction strength of the I and III complexes as well as of the II and IV ones, respectively. For the first two complexes, which are the longer bound ones, conclusively the Bent rule is satisfied, whereas it is not for the last two complexes, because they are weakly bound and even energetically non-bonded. This analysis is not applied to interaction energy, but surely is treated as one additional justification to the frequency shifts of the proton donors [43]. In this context, Fig. 3 illustrates the relationship between Δυ_π···H and Δ%_s(C), whose linear profile with a coefficient of –0.997 yielded by the equation (5) can be considered highly satisfactory.

Δυ_π···H = –1004.18 Δ%s(C) – 19.18, R² = –0.997

(5)

Hybridizations	Interatomic and molecular systems
	I	II	III	IV
%s(C)	33.51	33.46	33.57	33.47
Δ%s(C)^a	0.03	–0.02	0.09	–0.01
%p(C)	66.32	66.38	66.28	66.37
Δ%p(C)^b	–0.04	0.02	–0.08	0.01
%s(H)	99.84	99.94	99.94	99.94
Δ%s(H)^c	–0.10	0.0	0.0	0.0
%p(H)	0.16	0.06	0.06	0.06
Δ%p(H)^d	0.1	0.0	0.0	0.0

^a Δ%s(C) = %s(C)–%s(C)_,m, in which the values of %s(C)_,m is 33.48;

^b Δ%p(C) = %p(C)–%p(C)_,m, in which the values of %p(C)_,m is 66.36;

^c Δ%s(H) = %s(H)–%s(H)_,m, in which the values of %s(H)_,m is 99.94;

^d Δ%p(H) = %p(H)–%p(H)_,m, in which the values of %p(H)_,m is 0.06.

Fig. 3
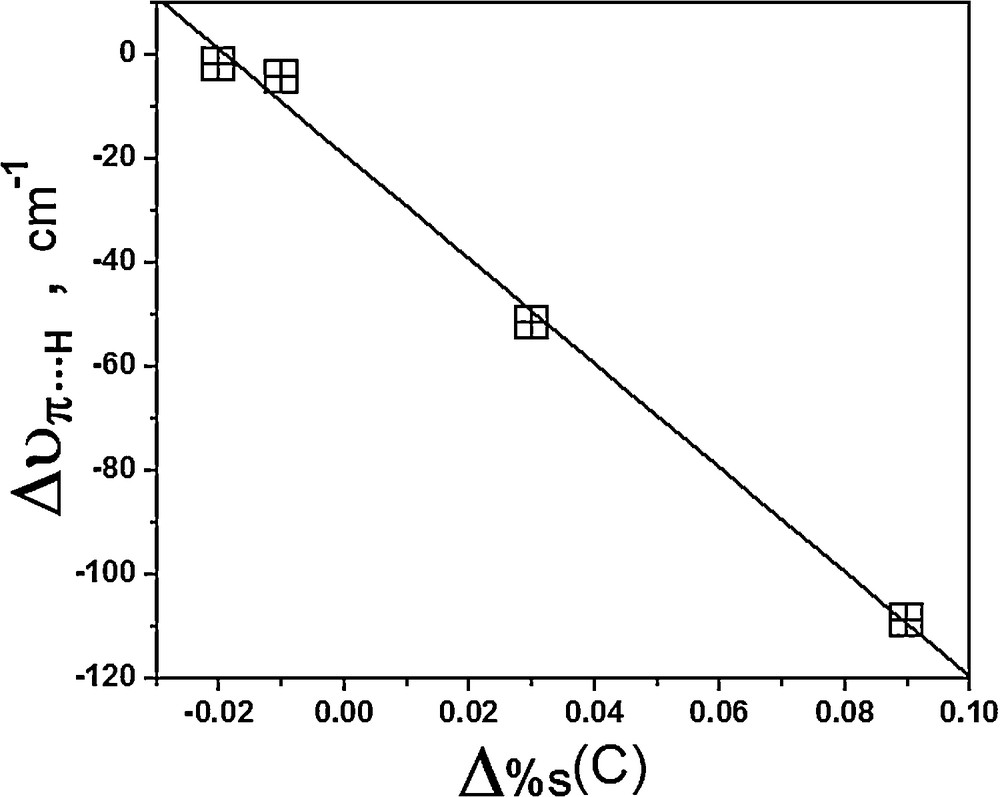
Relationship between the red shifts on π···H contact (Δυ_π···H) and the variations of the s-character of the carbons (Δ%sC).

Another information must be registered regarding the blue shifts: the increase of %_s(X) in X reinforces the characterization of the hybridization effect as dominant rather than the hyperconjugation upon the formation of the Y···H−X H-bond. So, hybridization would be present in stronger H-bond systems containing blue shifts on their proton donors [43]. Nevertheless, it should be pointed out that none of these events was identified here. On the contrary, this work presents a unanimous scenario with weakly bonded systems with interactions varying between 0.343 up to –7.69 kJ·mol⁻¹ followed by red shifts in the stretch frequencies of π···H proton donors oscillators.

In Tables 5–7 are organized several topological parameters (ρ, ▿²ρ, G, U, –G/U, Δr^o, and є) obtained from QTAIM calculations. In addition to the first four terms previously presented, other QTAIM parameters were introduced, such as Δr^o and є. About Δr^o, it represents a measurement of the distance between the nucleus and the BCP along a bond path as well as how much this distance varies by the formation of the complex (r^o_π−BCP,c) in comparison with the monomer (r^o_π−BCP,m), which is often a proton donor in which the following subtraction is valid: Δr^o_π−BCP = r^o_π−BCP,c–r^o_π−BCP,m [43]. In accordance with the hybridization theory, it was admitted that the manifestation of the blue shifts on proton donors would not be caused only by the increase in the s-character of the orbital of X (elements bound to H to form H − X) supported by the Bent rule, but the increase in the H radius compared with the value of X also reinforces this statement. Through the values of Δr^o_π−BCP and Δr^o_BCP−H (see Table 5), the inference of π···H can be discussed, in which H is the proton donor site. In all complexes, QTAIM computation revealed that Δr^o_π−BCP increases while Δr^o_BCP−H is reduced, meaning then Δr^o_π−BCP > Δr^o_BCP−H, which undoubtedly justifies the red-shift frequencies of –51.7 (I), –2.1 (II), –108.9 (III), and –4.4 cm⁻¹ (IV).

Properties	Interatomic and molecular systems
	I	II	III	IV
ρ_π···H	0.0179 (–0.0018)	0.1809 (–0.0002)	0.1772 (–0.0039)	0.1808 (–0.0002)
▿²ρ_π···H	–0.2218 (–0.0027)	–0.2193 (–0.0005)	–0.2213 (–0.0026)	–0.2201 (–0.0014)
G_π···H	0.0606 (–0.0022)	0.0625 (–0.0002)	0.0588 (–0.0039)	0.0622 (–0.0005)
U_π···H	–0.1766 (0.0036)	–0.1798 (0.0004)	–0.1730 (0.0072)	–0.1795 (0.0007)
–G/U_(π···H)	0.3432	0.3400	0.3400	0.3470
r^o_{π(π···H)}	0.6947 (0.0095)	0.6863 (0.0011)	0.7034 (0.0182)	0.6872 (0.0020)
r^o_H(π···H)	0.4857 (–0.0018)	0.4874 (–0.0001)	0.4844 (–0.0032)	0.4872 (–0.0003)
є_π···H	1.7873 (–0.0075)	1.8557 (–0.0071)	1.7189 (–0.1438)	1.8481 (–0.0147)

Properties	Interatomic and molecular systems
	I	II	III	IV
ρ_π	0.3155 (0.0009)	0.3147 (0.0001)	0.3164 (0.0017)	0.3147 (0.00008)
▿²ρ_π	–0.8909 (–0.0042)	–0.8871 (–0.0004)	–0.8955 (–0.0088)	–0.8867 (–0.00004)
G_π	0.1133 (0.0010)	0.1125 (0.0001)	0.1140 (0.0016)	0.1126 (0.0002)
U_π	–0.4495 (–0.0030)	–0.4468 (–0.0004)	–0.4519 (–0.0054)	–0.4469 (–0.0005)
–G/U_(π)	0.2522	0.2520	0.2520	0.2520
r^o_π	0.6906 (–0.0011)	0.6915 (–0.0002)	0.6898 (–0.0019)	0.6914 (–0.0003)
є_π	0.1999 (0.0040)	0.1965 (0.0005)	0.2017 (0.0058)	0.1972 (0.0013)

Properties	Interatomic and molecular systems
	I	II	III	IV
ρ_H···RG	0.0098	0.0036	0.0126	0.0066
▿²ρ_H···RG	0.0300	0.0139	0.0328	0.0267
G_H···RG	0.0060	0.0026	0.0068	0.0056
U_H···RG	–0.0045	–0.0018	–0.0054	–0.0045
–G/U_(H···RG)	1.337	1.45	1.256	1.2300
є_H···RG	0.0412	0.0430	0.0360	0.0452

Since we had a peculiar interest in assessing the sub-part of the proton donor, blue shifts on the frequencies of the π bonds were identified in opposition to the red shifts of π···H discussed above. Due to the symmetry of the ethyl cation, the negative values of Δr°_C−C (see Table 6) indicate a mutual movement of the carbon atoms toward the BCP located between them. Independently, the reductions of Δr°_C−C are consistent with the blue shift results of +1.8 (I), +0.2 (II), +3.0 (III), and +0.3 cm⁻¹ (IV). In agreement with the Bent rule [95], particularly the stronger bound complexes I and III are those in which the s-character of the carbon is enhanced. For the remaining complexes whose intermolecular stabilization is ruled by the lowest interaction energies, in other words as what has been observed in II and IV, there was no variation of the s-character of C and thereby the lowermost blue shift values of 0.2–0.3 cm⁻¹ could not be explained.

Furthermore, it should be stressed that either the strengthening or the weakness of the π bond and π···H interaction can be interpreted in the light of the ellipticity (є) [96,97], whose values are also displayed in Tables 5 and 6. Briefly speaking, it is well known that є mimics the unsaturated character of the C − C bond in the 0.0–0.45 range (from ethane, benzene, up to ethylene) [46], indicating that the bond will be strengthened if the profile of є is enlarged. Here, by focusing justly on π and π···H, the є values for these centers are enhanced and reduced after I–IV complexes have been formed. Because these events attest to stronger and weaker contacts, of course they can be also used as argument to justify the frequency changes, namely those shifted either to red or blue regions. As such, we plotted in Fig. 4, the relationship between the frequency shifts and ellipticity variations for π and π···H, and an excellent linear correlation was yielded by equation (6) below:

Δυ_π/π···H = 746.64 Δɛ_π/π···H + 1.18, R² = 0.996

(6)

Fig. 4
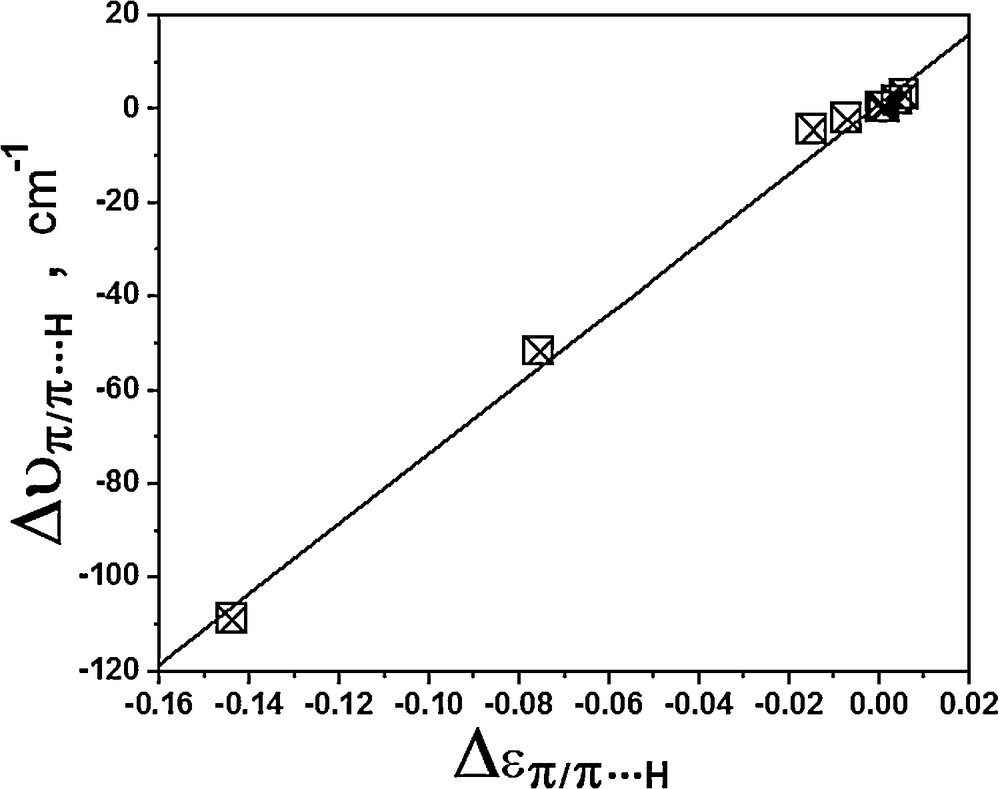
Relationship between the frequency shifts and ellipticity variations of the π bonds and π···H contacts.

One of the foundations of the QTAIM is devoted to the characterization (See Fig. 5) of BCPs (w, y, and z) and Bond Paths (BP) along the chemical bonds [98] (through the BCP pointed by w) and interatomic interactions (through the BCP pointed by z), in which it can be formed by low, median or high charge density concentrations [99–103]. Such designations can be predicted through the obtained values of ▿²ρ listed in Table 7 (the relief map of the C₂H₅⁺···Ar complex is illustrated in Fig. 6). It can be seen that the ▿²ρ values for H···RG are positive, whereas they are negative for π···H and π (see Tables 5 and 6). In other words, the interaction H···RG is recognized as a closed-shell one and assumed to be non-covalent, albeit the very low energetic values have already revealed this before. In spite of this, the ratio values of G and U conduct the debate of the interaction strength as follows:

• –G/U < 0.5 indicates a total covalent character;
• –G/U < 1.0 indicates a partial covalent character;
• –G/U > 1 a non-covalent character [15,16,26].

Fig. 5
(Color online.) Indication of the BCPs and BP for the C₂H₅⁺···Kr complex.

Fig. 6
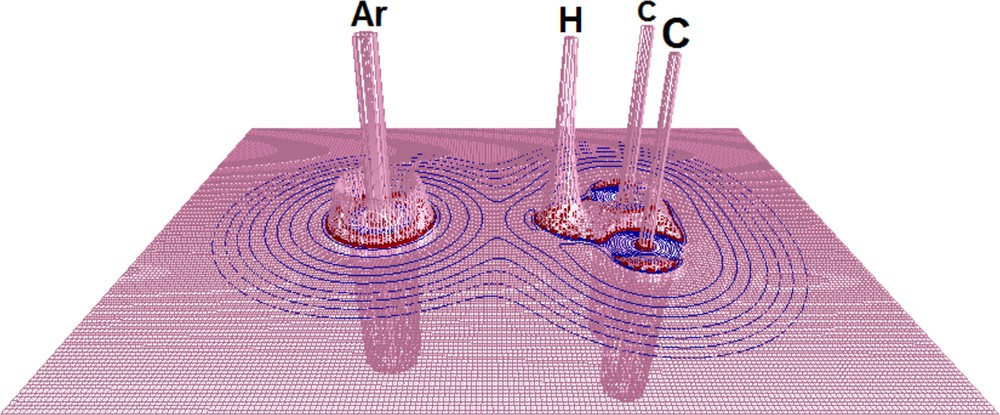
(Color online.) Laplacian relief map of the C₂H₅⁺···Ar complex.

Through this, it can be seen that all H···Rg interactions have no covalent character, whereas π···H and π are totally covalent. This scenario corroborates directly the slight frequency shifts and the low interaction energies.

Meanwhile, even though the interactive system is located in an energy minimum with low attraction strength, the prediction of its interaction strength is absolutely allowed, and it can be performed in conformity with the equation presented below [104,105]:

Δmol = [(υ_o–υ/υ_o)² + (ρ_o–ρ/ρ_o)² + (▿²ρ_o–▿²ρ/▿²ρ_o)²]^1/2

(7)

As a first result, the relationship between the interaction energies and the values of the Δmol parameter is graphically illustrated in Fig. 7, in which a linear coefficient of –0.994 was yielded by equation (8):

ΔE^C = –141.08 Δmol_π···H + 0.19, R² = –0.994

(8)

Fig. 7
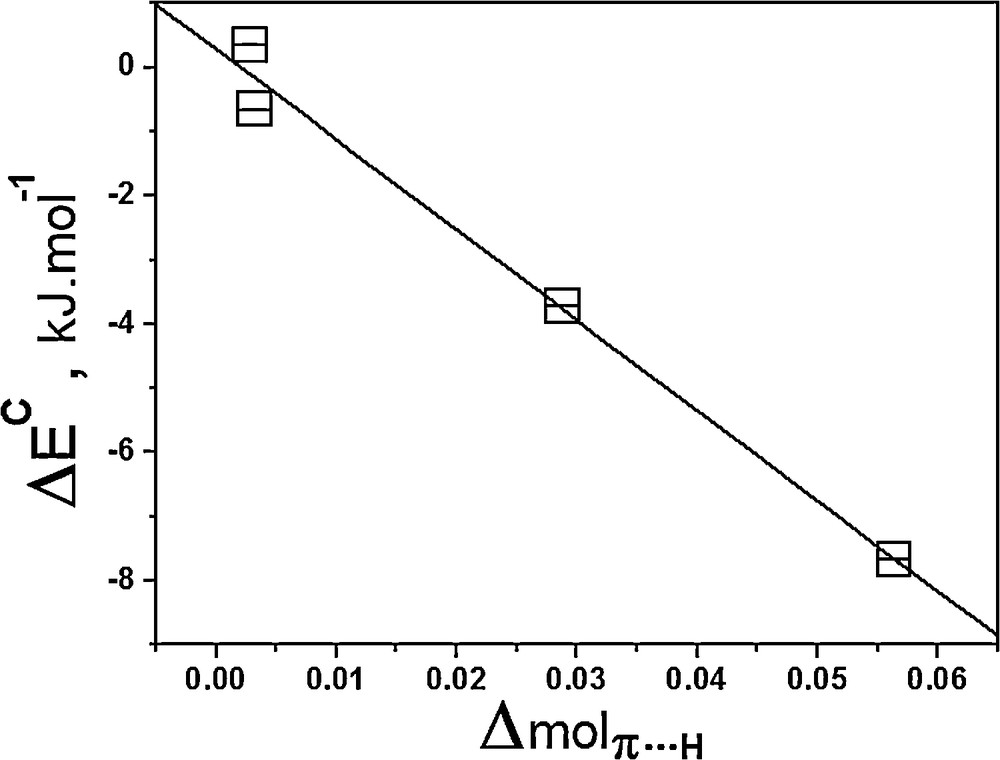
Relationship between the interaction energies and the values of the Δmol_π···H parameter.

In this, the vibration and topological properties used to generate the Δmol parameter were collected from the π···H contact. On the other hand, if the π bond is used instead of π···H, the value of the linear coefficient of –0.988 obtained from the analysis of Fig. 8 is symbolized by equation (9):

ΔE^C = –101.12 Δmol_π–0.25, R² = –0.988

(9)

Fig. 8
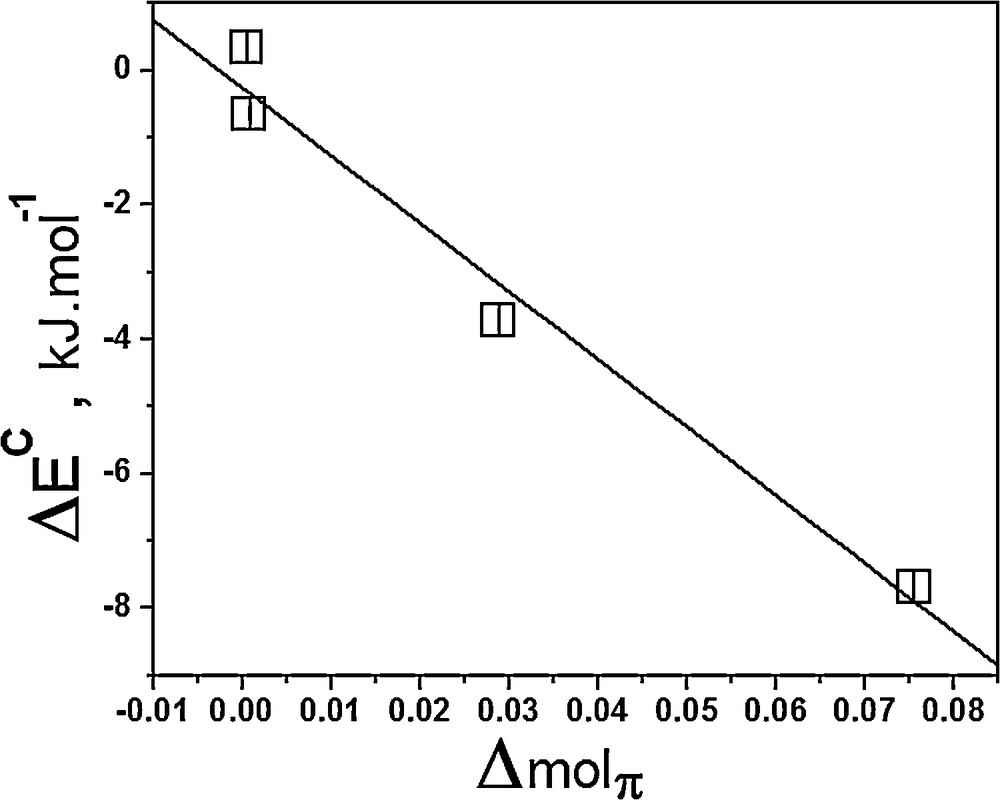
Relationship between the interaction energies and the values of the Δmol_π parameter.

Regarding the construction of these two models, vibration modes (red and blue shifts) were used instead of structural parameters [26], although it has been demonstrated that the vibration frequencies produce relationships well satisfactorily [104]. In any event, it should be emphasized that the ethyl cation disposes of two centers to predict the interaction strength with rare gases, namely the π bond and the π···H interaction.

4 Conclusions

After a discerning discussion of geometry data, vibration modes, and electronic parameters of the C₂H₅⁺···Ar, C₂H₅⁺···He, C₂H₅⁺···Kr and C₂H₅⁺···Ne complexes, it can be affirmed that they are unusual intermolecular systems because the shifted frequencies of the π bonds and π···H contacts are partially supported by the hybridization orbital. About this, the C₂H₅⁺···Ar and C₂H₅⁺···Kr systems are stronger bound with interaction energies from –3.73 up to –7.69 kJ·mol⁻¹, and thereby, they are fitted into the context of the Bent rule. The QTAIM calculations identified bond critical points and bond paths, wherein the high and low electronic densities followed by the negative and positive value of the Laplacian and electronic energy ratio (kinetic/potential) characterized π and π···H contacts as covalent, whereas the H···RG interaction as non-covalent. Moreover, the arising of blue and red shifts in π and π···H are accounted for by their strengthening and weakening, which can be explained via a decrease and an increase, respectively, in their values of ellipticity. The interpretation of the blue shifts is in line with the enhancements of the atomic radii of C computed by the QTAIM protocol, and in turn, reductions of the atomic radii of H are closely related to the appearance of the red shifts. At the end, even if C₂H₅⁺···He and C₂H₅⁺···Ne are weakly bound systems, the prediction of the interaction strength was successfully performed on the basis of vibration modes and of QTAIM parameters.

Acknowledgements

The author would like to thank to CNPq, CAPES and FAPESB Brazilian funding agencies.

Bibliographie

[1] G.A. Arteca; R.E. Cachau; K. Veluri Chem. Phys. Lett., 319 (2000), pp. 719-724

[2] S. Stadler; S. Hansen; I. Kröger; C. Kumpf; E. Umbach Nat. Phys., 5 (2009), pp. 153-158

[3] N. Pan; R.-Z. Wei; Y.-H. Chi; J.-M. Shi; W. Wei; Y.-Q. Zhang; Z. Anorg Allg. Chem., 639 (2013), pp. 1026-1031

[4] M.S. Gordon; Q.A. Smith; P. Xu; L.V. Slipchenko Ann. Rev. Phys. Chem., 64 (2013), pp. 553-578

[5] Z. Burghard; A. Leineweber; P.A. van Aken; T. Dufaux; M. Burghard; J. Bill Adv. Mater., 25 (2013), pp. 2468-2473

[6] B.G. Oliveira; R.C.M.U. Araújo; M.N. Ramos Spectrochim. Acta A, 68 (2007), pp. 626-631

[7] B.G. Oliveira; R.C.M.U. Araújo; M.N. Ramos Struct. Chem., 19 (2008), pp. 185-189

[8] B.G. Oliveira; R.C.M.U. Araújo; M.N. Ramos Struct. Chem., 19 (2008), pp. 665-670

[9] B.G. Oliveira; R.C.M.U. Araújo; J.J. Silva; M.N. Ramos Struct. Chem., 21 (2010), pp. 221-228

[10] B.G. Oliveira; M.N. Ramos Int. J. Quantum Chem., 110 (2010), pp. 307-316

[11] B.G. Oliveira; R.C.M.U. Araújo; E.S. Leite; M.N. Ramos Int. J. Quantum Chem., 111 (2011), pp. 111-116

[12] P.-P. Zhou; W.-Y. Qiu; S. Liub; N.-Z. Jinc Phys. Chem. Chem. Phys., 13 (2011), pp. 7408-7418

[13] R. Wilcken; M.O. Zimmermann; A. Lange; A.C. Joerger; F.M. Boeckler J. Med. Chem., 56 (2013), pp. 1363-1388

[14] M.R. Scholfield; C.M.V. Zanden; M. Carter; P.S. Ho Protein Sci., 22 (2013), pp. 139-152

[15] M. Jabłoński; M. Palusiak J. Phys. Chem. A, 116 (2012), pp. 2322-2332

[16] B.G. Oliveira Comput. Theor. Chem., 998 (2012), pp. 173-182

[17] B.G. Oliveira Phys. Chem. Chem. Phys., 15 (2013), pp. 37-79

[18] M. Yáñez; P. Sanz; O. Mó; I. Alkorta; J. Elguero J. Chem. Theory Comput., 5 (2009), pp. 2763-2771

[19] S. Scheiner J. Chem. Phys., 134 (2011), pp. 0932159-0943151

[20] J.E. Del Bene; I. Alkorta; G. Sánchez-Sanz; J. Elguero J. Phys. Chem. A, 116 (2012), pp. 9205-9213

[21] B.G. Oliveira; R.C.M.U. Araújo; A.B. Carvalho; E.F. Lima; W.L.V. Silva; M.N. Ramos; A.M. Tavares J. Mol. Struct. (Theochem), 775 (2006), pp. 39-45

[22] B.G. Oliveira; R.C.M.U. Araú jo; M.N. Ramos; A.B. Carvalho Struct. Chem., 20 (2009), pp. 663-670

[23] G.R. Desiraju Angew. Chem. Int. Ed., 50 (2011), pp. 52-59

[24] P. Goymer Nat. Chem., 4 (2012), pp. 863-864

[25] B.G. Oliveira; R.C.M.U. Araújo; A.B. Carvalho; M.N. Ramos J. Mol. Model., 15 (2009), pp. 421-432

[26] S.J. Grabowski Chem. Rev., 111 (2011), pp. 2597-2625

[27] B.G. Oliveira; R.C.M.U. Araújo; A.B. Carvalho; M.N. Ramos J. Mol. Model., 17 (2011), pp. 2847-2862

[28] B.G. Oliveira; R.C.M.U. Araújo Quim. Nova, 30 (2007), pp. 791-796

[29] P.-P. Zhou; W.-Y. Qiu; N.-Z. Jin J. Chem. Phys., 137 (2012), pp. 084311-084315

[30] I.V. Alabugin; M. Manoharan; S. Peabody; F. Weinhold J. Am. Chem. Soc., 125 (2003), pp. 5973-5987

[31] J.E. Williams; V. Buss; L.C. Allen J. Am. Chem. Soc., 93 (1971), pp. 6867-6873

[32] H.-S. Andrei; N. Solc; O. Dopfer Angew. Chem. Int. Ed., 47 (2008), pp. 395-397

[33] B.G. Oliveira; M.L.A.A. Vasconcellos; R.R. Olinda; E.B.A. Filho Struct. Chem., 20 (2009), pp. 81-90

[34] B.G. Oliveira; M.L.A.A. Vasconcellos Inorg. Chem. Commun., 12 (2009), pp. 1142-1144

[35] B.G. Oliveira; M.L.A.A. Vasconcellos Struct. Chem., 20 (2009), pp. 897-902

[36] B.G. Oliveira; R.C.M.U. Araújo; A.B. Carvalho; M.N. Ramos J. Mol. Model., 15 (2009), pp. 123-131

[37] B.G. Oliveira; R.C.M.U. Araújo; A.B. Carvalho; M.N. Ramos; M.Z. Hernandes; K.R. Cavalcante J. Mol. Struct. (Theochem), 802 (2007), pp. 91-97

[38] B.G. Oliveira; R.C.M.U. Araújo; F.S. Pereira; E.F. Lima; W.L.V. Silva; A.B. Carvalho; M.N. Ramos Quim. Nova, 31 (2008), pp. 1673-1679

[39] V. Aquilanti; E. Comicchi; M.M. Teixidor; N. Saendig; F. Pirani; D. Cappelletti Angew. Chem. Int. Ed., 44 (2005), pp. 2356-2360

[40] P.R.P. Barreto; F. Palazzetti; G. Grossi; A. Lombardi; G.S. Maciel; A.F.A. Vilela Int. J. Quantum Chem., 110 (2010), pp. 777-786

[41] Z. Jamshidi; K. Eskandari; S.M. Azami Int. J. Quantum Chem., 113 (2013), pp. 1981-1991

[42] F. Moncada; L.S. Uribe; J. Romero; A. Reyes Int. J. Quantum Chem., 113 (2013), pp. 1556-1561

[43] S.J. Grabowski J. Phys. Chem. A, 115 (2011), pp. 12789-12799

[44] H.A. Bent Chem. Rev., 61 (1961), pp. 275-311

[45] R.F.W. Bader Atoms in Molecules – A Quantum Theory, Oxford University Press, Oxford, UK, 1990

[46] R.F.W. Bader Chem. Rev., 91 (1991), pp. 893-928

[47] J. Goodman; L.E. Brus J. Chem. Phys., 67 (1977), pp. 4858-4865

[48] N. Gresh; P. Claverie; A. Pullman Int. J. Quantum Chem., 29 (1986), pp. 101-118

[49] R. Yerushalmi; A. Brandis; V. Rosenbach-Belkin; K.K. Baldridge; A. Scherz J. Phys. Chem. A, 110 (2006), pp. 412-421

[50] D. Chaturvedi; V. Gupta; P. Tandon; A. Sharma; C. Baraldi; M.C. Gamberini Spectrochim. Acta A, 99 (2012), pp. 150-159

[51] C.M. Breneman; K.B. Wiberg J. Comput. Chem., 11 (1990), pp. 361-373

[52] F. Weinhold; C.R. Landis Discovering Chemistry With Natural Bond Orbitals, John Wiley & Sons, New Jersey, 2012

[53] R.S. Mulliken J. Chem. Phys., 23 (1955), pp. 1833-1840

[54] R.F.W. Bader; C.F. Matta J. Phys. Chem. A, 108 (2004), pp. 8385-8394

[55] M.J. Frisch; G.W. Trucks; H.B. Schlegel; G.E. Scuseria; M.A. Robb; J.R. Cheeseman; J.A. Montgomery; T. Vreven; K.N. Kudin; J.C. Burant; J.M. Millam; S.S. Iyengar; J. Tomasi; V. Barone; B. Mennucci; M. Cossi; G. Scalmani; N. Rega; G.A. Petersson; H. Nakatsuji; M. Hada; M. Ehara; K. Toyota; R. Fukuda; J. Hasegawa; M. Ishida; T. Nakajima; Y. Honda; O. Kitao; H. Nakai; M. Klene; X. Li; J.E. Knox; H.P. Hratchian; J.B. Cross; C. Adamo; J. Jaramillo; R. Gomperts; R.E. Stratmann; O. Yazyev; A.J. Austin; R. Cammi; C. Pomelli; J.W. Ochterski; P.Y. Ayala; K. Morokuma; G.A. Voth; P. Salvador; J.J. Dannenberg; V.G. Zakrzewski; S. Dapprich; A.D. Daniels; M.C. Strain; O. Farkas; D.K. Malick; A.D. Rabuck; K. Raghavachari; J.B. Foresman; J.V. Ortiz; Q. Cui; A.G. Baboul; S. Clifford; J. Cioslowski; B.B. Stefanov; G. Liu; A. Liashenko; P. Piskorz; I. Komaromi; R.L. Martin; D.J. Fox; T. Keith; M.A. Al-Laham; C.Y. Peng; A. Nanayakkara; M. Challacombe; P.M.W. Gill; B. Johnson; W. Chen; M.W. Wong; C. Gonzalez; J.A. Pople Gaussian, Gaussian, Inc, Pittsburgh PA, 2003

[56] S.F. Boys; F. Bernardi Mol. Phys., 19 (1970), pp. 553-566

[57] F.B. Van Duijneveldt; J.G.C.M. van Duijneveldt-van de Rijdt; J.H. van Lenthe Chem. Rev., 94 (1994), pp. 1873-1885

[58] A. Ruzsinszky; C. Van Alsenoy; G.I. Csonka J. Phys. Chem. A, 107 (2003), pp. 736-744

[59] T.A. Keith AIMAll Version 11.05.16, 2011

[60] A. Bondi J. Phys. Chem., 68 (1964), pp. 441-451

[61] R.S. Rowland J. Phys. Chem., 100 (1996), pp. 7384-7391

[62] S. Alvareza Dalton Trans., 42 (2013), pp. 8617-8636

[63] H. Böhm; R. Ahlrichs J. Chem. Phys., 77 (1982), pp. 2028-2034

[64] G.P. Schiemenz Z. Naturforsch., 62b (2007), pp. 235-243

[65] M. Goswani; E. Arunan Phys. Chem. Chem. Phys., 11 (2009), pp. 8974-8983

[66] B.G. Oliveira; R.C.M.U. Araújo J. Mol. Model., 18 (2012), pp. 2845-2854

[67] B.G. Oliveira; R.C.M.U. Araújo; F.F. Chagas; A.B. Carvalho; M.N. Ramos J. Mol. Model., 14 (2008), pp. 949-955

[68] B. Makiabadi; M. Zakarianejad; S. Bagheri; H.R. Masoodi; R.S. Aghaie Int. J. Quantum Chem., 113 (2013), pp. 2361-2371

[69] S. Scheiner Acc. Chem. Res., 46 (2013), pp. 280-288

[70] B.G. Oliveira; R.C.M.U. Araújo Can. J. Chem., 90 (2012), pp. 368-375

[71] J.J. Dannenberg; T.D. Berke Theor. Chem. Acc., 24 (1972), pp. 99-101

[72] P.D.B. de la Mare Pure Appl. Chem., 56 (1984), pp. 755-1766

[73] B.G. Oliveira; R.C.M.U. Araújo; M.N. Ramos J. Mol. Struct. (Theochem), 908 (2009), pp. 79-83

[74] B.G. Oliveira; R.C.M.U. Araújo; M.N. Ramos J. Mol. Struct. (Theochem), 944 (2010), pp. 168-172

[75] P. Hobza; Z. Havlas Chem. Rev., 100 (2000), pp. 4253-4264

[76] I.V. Alabugin; M. Manoharan; F.A. Weinhold J. Phys. Chem. A, 108 (2004), pp. 4720-4730

[77] W. Yu; Z. Lin; Z. Huang ChemPhysChem., 7 (2006), pp. 828-830

[78] B.G. Oliveira; M.C.A. Lima; I.R. Pitta; S.L. Galdino; M.Z. Hernandes J. Mol. Model., 16 (2010), pp. 119-127

[79] S.-Y. Yen; C.-H. Mou; W.-P. Hu Chem. Phys. Lett., 383 (2004), pp. 606-611

[80] A.M. Ricks; G.E.P. Douberly; V.R. Schleyer; M.A. Duncan Chem. Phys. Lett., 480 (2009), pp. 17-20

[81] M.C. Salazar; J.L. Paz; A.J. Hernández; C. Manzanares; E.V. Ludeña Int. J. Quantum Chem., 95 (2003), pp. 177-183

[82] Z. Latajka; S. Scheiner J. Chem. Phys., 87 (1987), pp. 1194-1204

[83] P. Salvador; M.M. Szczęśniak J. Chem. Phys., 118 (2003), pp. 537-549

[84] Y. Lu; H. Li; X. Zhu; H. Liu; W. Zhu Int. J. Quantum Chem., 112 (2012), pp. 1421-1430

[85] M.C. Daza; J.A. Dobado; J.M. Molina; P. Salvador; M. Duran; J.L. Villaveces J. Chem. Phys., 110 (1999), pp. 11806-11813

[86] P.S. Kushawaha; P.C. Mishra Int. J. Quantum Chem., 76 (2000), pp. 700-713

[87] I. Mata; I. Alkorta; E. Espinosa; E. Molins Chem. Phys. Lett., 507 (2011), pp. 185-189

[88] A. Vogler; H. Kunkely Coord. Chem. Rev., 208 (2000), pp. 321-329

[89] T. Kubař; M. Elstner J. Phys. Chem. B, 112 (2008), pp. 8788-8798

[90] J.M. Herbert; M. Head-Gordon J. Am. Chem. Soc., 128 (2006), pp. 13932-13939

[91] S.G. Ramesh; S. Re; J.T. Hynes J. Phys. Chem. A, 112 (2008), pp. 3391-3398

[92] A.M. Wright; A.A. Howard; J.C. Howard; G.S. Tschumper; N.I. Hammer J. Phys. Chem. A, 117 (2013), pp. 5435-5446

[93] E. Ramos-Cordoba; D.S. Lambrecht; M. Head-Gordon Faraday Discuss., 150 (2011), pp. 345-362

[94] V. Balachandran; G. Mahalakshmi; A. Lakshmi; A. Janaki Spectrochim. Acta A, 97 (2012), pp. 1101-1110

[95] S. Noorizadeh J. Mol. Struct. (Theochem), 713 (2004), pp. 27-32

[96] K. Durka; R. Kamiński; S. Luliński; J. Serwatowski; K. Woźniak Phys. Chem. Chem. Phys., 12 (2010), pp. 13126-13136

[97] R.N. Singh; V. Baboo; P. Rawat; V.P. Gupta J. Mol. Struct., 1037 (2013), pp. 338-351

[98] R.F.W. Bader J. Phys. Chem. A, 113 (2009), pp. 10391-10396

[99] B.G. Oliveira; M.L.A.A. Vasconcellos J. Mol. Struct. (Theochem), 774 (2006), pp. 83-88

[100] E.B.A. Filho; E. Ventura; S.A. do Monte; B.G. Oliveira; C.G.L. Junior; G.B. Rocha; M.L.A.A. Vasconcellos Chem. Phys. Lett., 449 (2007), pp. 336-340

[101] B.G. Oliveira; L.F.C.C. Leite J. Mol. Struct. (Theochem), 915 (2009), pp. 38-42

[102] B.G. Oliveira; R.C.M.U. Araújo Monatsh. Chem., 142 (2011), pp. 861-873

[103] B.G. Oliveira; R.C.M.U. Araújo; M.N. Ramos Quim. Nova, 33 (2010), pp. 1155-1162

[104] B.G. Oliveira; F.S. Pereira; R.C.M.U. de Araújo; M.N. Ramos Chem. Phys. Lett., 427 (2006), pp. 181-184

[105] B.G. Oliveira; R.C.M.U. de Araújo; M.N. Ramos Chem. Phys. Lett., 433 (2007), pp. 390-394

Commentaires - Politique

Ces articles pourraient vous intéresser

The interaction strength of intermolecular systems formed by NaH⋯2(HF) and NaH⋯4(HF): Hydrogen bonds, dihydrogen bonds and halogen–hydride bonds

Boaz G. Oliveira

C. R. Chim (2016)

Effect of Al- and Ga-doping on the adsorption of H $_{2}$ SiCl $_{2}$ onto the outer surface of boron nitride nanotube: a DFT study

Mohsen Doust Mohammadi; Hewa Y. Abdullah; George Biskos; ...

C. R. Chim (2021)

First nanoparticles of Per $_{2}$ [Au(mnt) $_{2}$ ]

Dominique de Caro; Kane Jacob; Christophe Faulmann; ...

C. R. Chim (2020)