1. Introduction
The consequences of Einstein’s special theory of relativity [1, 2] manifest themselves in virtually every aspect of the chemistry of gold [3, 4, 5, 6, 7, 8, 9]. Relativistic destabilization of the 5d orbitals allows for the existence and stability of such pentavalent Au species as the AuF6− anion [10, 11] and Au2F10 [12]. Relativistic stabilization of the 6s orbitals on the other hand allows for the existence and stability of the auride anion, a unique metal-based pseudohalide [13, 14, 15]. The latter effect is also responsible for gold having the highest electronegativity among all nonradioactive metals, essentially the same as carbon. It is worth mentioning in passing that even more dramatic relativistic effects have been postulated for roentgenium, gold’s superheavy congener, notably a 6d97s2 atomic ground state and a heptavalent D5h-symmetric fluoride, RgF7 [16].
Relativistic effects also explain why stable, structurally characterized Au(II) porphyrins have long remained elusive, in sharp contrast to Cu(II) and Ag(II) porphyrins [17]. The Au(III) center in porphyrins was long thought to be electrochemically inert [18, 19] and only in 2002 was the one-electron reduction of Au(III) porphyrins identified as metal-centered [20, 21]. Only in 2017 was Au[TPP] reported as the first structurally characterized Au(II) porphyrin [22]. The structure turned out to be more than a synthetic feat: the metalloporphyrin core was found to exhibit a unique lateral distortion (Figure 1), in contrast to the usual D4h geometry. The distortion, whereby the Au–N bonds in one direction are longer than those in the other direction, was also attributed to a second-order Jahn–Teller effect involving the relativistically destabilized 5dx2‐y2 orbital and the relativistically stabilized 6s orbital. A mild wave distortion of the porphyrin was also noted, but was assumed to be incidental to the lateral distortion [22].
Top left: crystal structure of Au[TPP] (CSD: TEHZOY). Bottom left: view of porphyrin core exhibiting wave distortion. Right: selected bond distances (black) and out-of-plane deformations (red) in Å.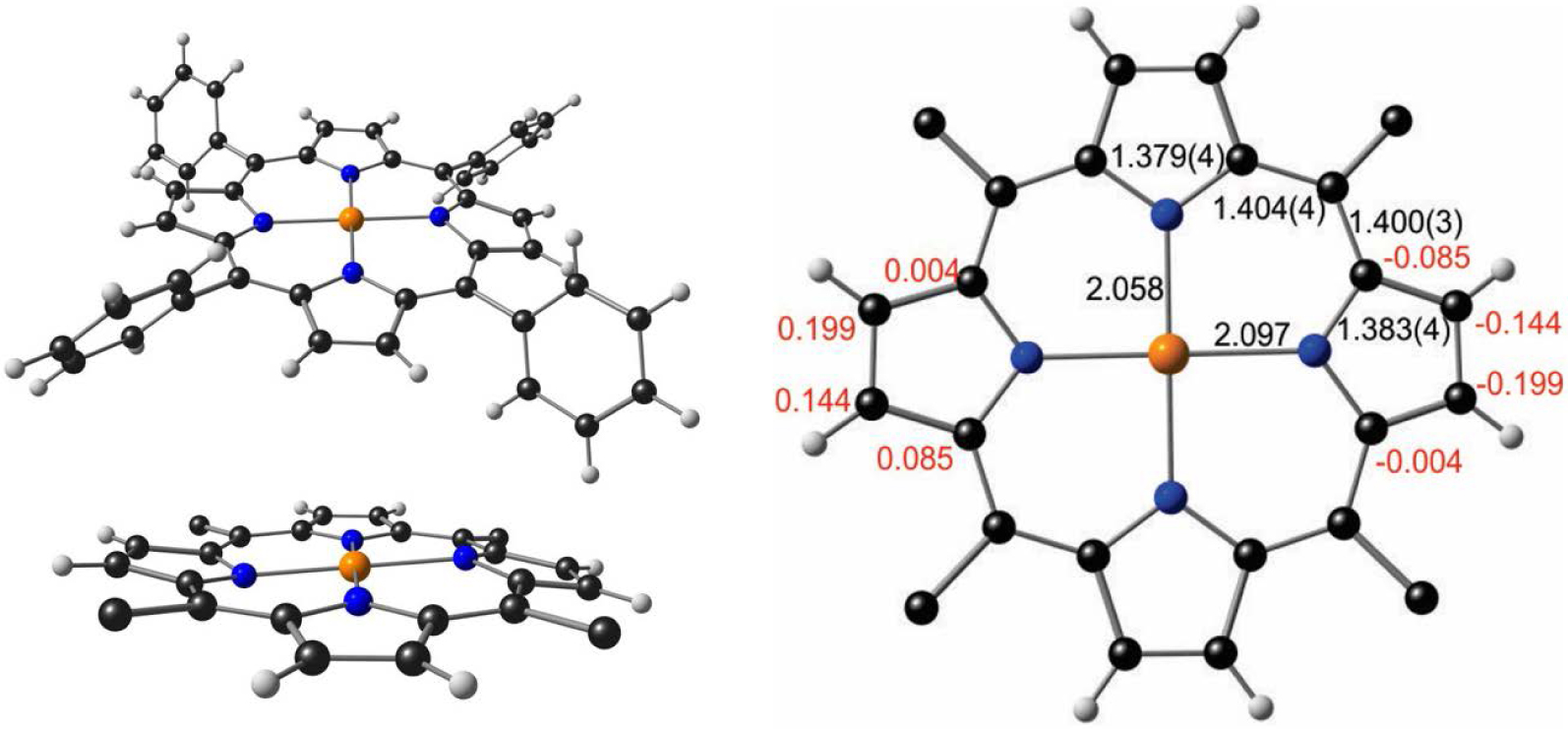
In this study, we have critically examined two key aspects of Au(II) porphyrins—their ionization potentials and the putative second-order Jahn–Teller distortion. Relativity was found to downshift the ionization potentials of Au(II) porphyrins by ∼0.6 eV, which is severalfold that calculated for Ag(II) porphyrins. Significantly, the present study also places the unusual geometrical distortions of Au[TPP] in an entirely new light. On account of a heretofore unsuspected orbital interaction, ultimately attributable to relativity, it is the wave distortion that emerges as the preeminent stereoelectronic effect in Au(II) porphyrins; the lateral distortion appears merely incidental to the wave distortion.
2. Results and discussion
In this study, we have critically examined the role of relativity in determining two key aspects of Au(II) porphyrins, their ionization potentials and the putative Jahn–Teller distortion. Three Au(II) porphyrins were studied in this work—Au[P], Au[TPP], and Au[TPFPP]—where P, TPP, and TPFPP denote porphine, tetraphenylporphyrin, and tetrakis(pentafluorophenyl)porphyrin, respectively. For comparison purposes, the analogous Ag porphyrins were also studied. Each molecule and its corresponding cation were optimized with scalar-relativistic and two-component spin–orbit DFT as described in the Computational methods section.
The relativistic calculations revealed unusually low adiabatic IPs for the Au(II) porphyrins (Table 1), which are about 1 eV lower than those of Ag(II) porphyrins and a little under 2 eV lower than those of Zn(II) porphyrins [23] (DFT has long excelled at predicting ionization potentials and photoelectron spectra of porphyrins [24, 25, 26, 27]). Both scalar-relativistic and spin–orbit calculations yielded very similar IPs, to within 0.05 eV. For Au, the relativistic effects are large, some 0.7 eV, compared with only 0.05–0.2 eV for Ag, in line with analogous findings from our laboratory on other pairs of 4d and 5d transition metal complexes [28, 29, 30, 31, 32, 33]. Substituent effects were also found to be important [25, 34]: both for the Ag and Au series, the IP of the TPFPP complex is some three-quarters of an eV higher than that of the TPP complex. Electron-deficient porphyrins thus appear clearly poised to deliver more oxidatively robust Au(II) derivatives.
Adiabatic OLYP ionization potentials obtained with nonrelativistic (NR), scalar-relativistic (SR), and two-component spin–orbit (SO) ZORA calculationsa
| Molecule | NR | SR | SO |
|---|---|---|---|
| Ag[P] | 6.13 | 5.93 (6.17) | 5.93 |
| Au[P] | 5.55 | 4.90 (4.96) | 4.87 |
| Ag[TPP] | 5.64 | 5.57 (5.88) | 5.59 |
| Au[TPP] | 5.14 | 4.60 (4.57) | 4.60 |
| Ag[TPFPP] | 6.50 | 6.34 (6.67) | – |
| Au[TPFPP] | 5.91 | 5.36 (5.48) | 5.34 |
aThe values shown in parentheses are based on single-point B3LYP∗ calculations on OLYP geometries.
Turning now to the question of geometry, the Ag(II) complexes all optimized to their expected point groups: D4h for Ag[P] and D2d for Ag[TPP] and Ag[TPFPP] (Figures 2 and 3) [35, 36]. In contrast, for the Au analogues of the three molecules, both scalar and spin–orbit relativistic calculations revealed a lateral compression–elongation, much as observed experimentally. Furthermore, like the experimental [22] structure, and DFT-optimized structures evinced a distinct wave distortion. The optimized equilibrium geometries of all the Au(II) structures, accordingly, were found to conform to only C2h symmetry, with the C2 axis passing through a pair of opposite nitrogen atoms.
Top: selected OLYP-D3 optimized distances (black), out-of-plane distortions (red), and Mulliken spin populations (blue) for Au[P] (left) and Ag[P] (right). Middle row: HOMOs (SOMOs). Bottom: spin densities.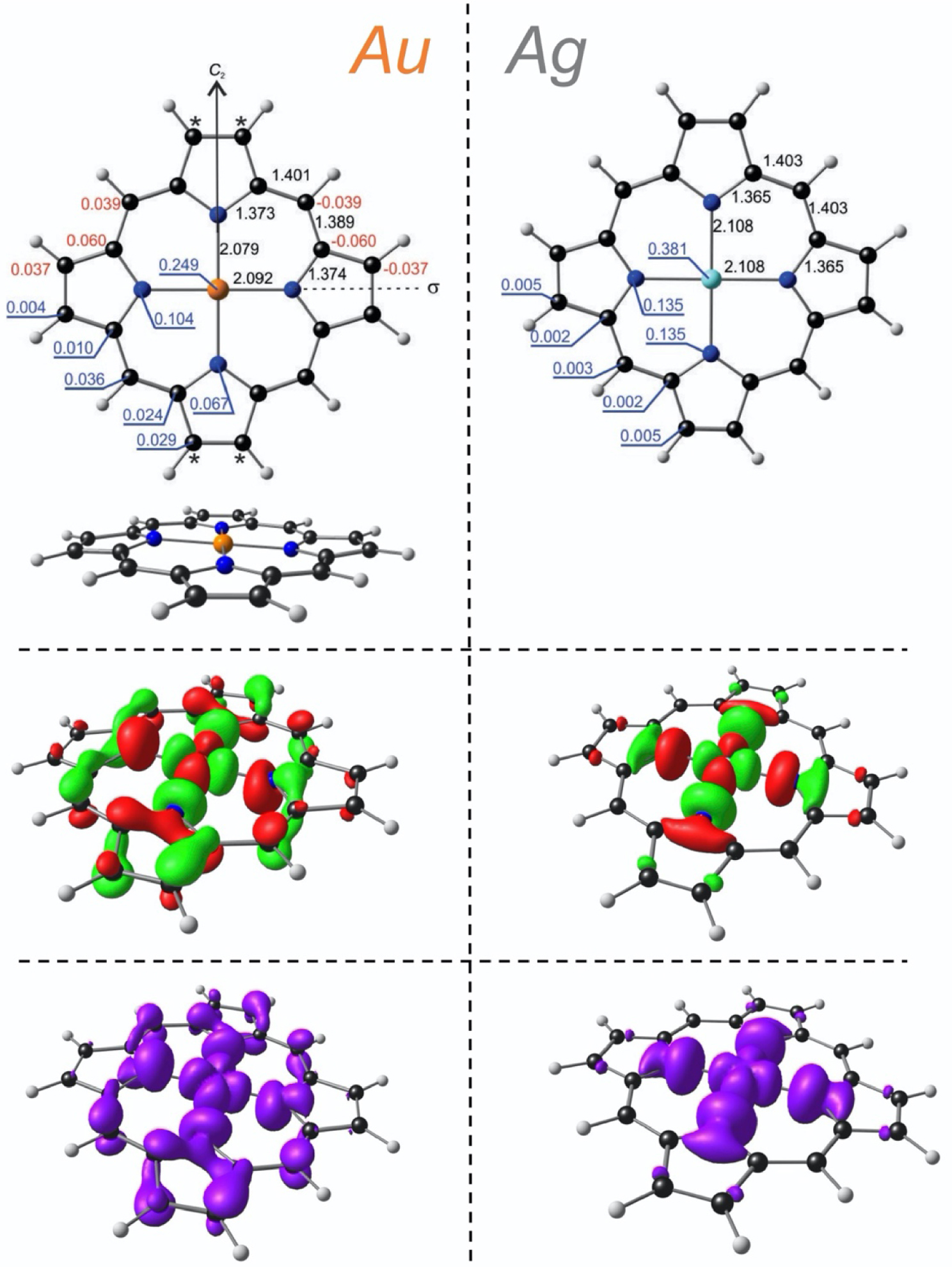
Selected OLYP-D3 optimized distances (black), out-of-plane distortions (red), and Mulliken spin populations (blue) for M[TPP] and M[TPFPP], where M = Ag, Au. All distances are in Å. Note: HOMOs (SOMOs) and spin density plots are omitted for these complexes as these are visually almost indistinguishable from those shown in Figure 2 (in spite of quantitative differences).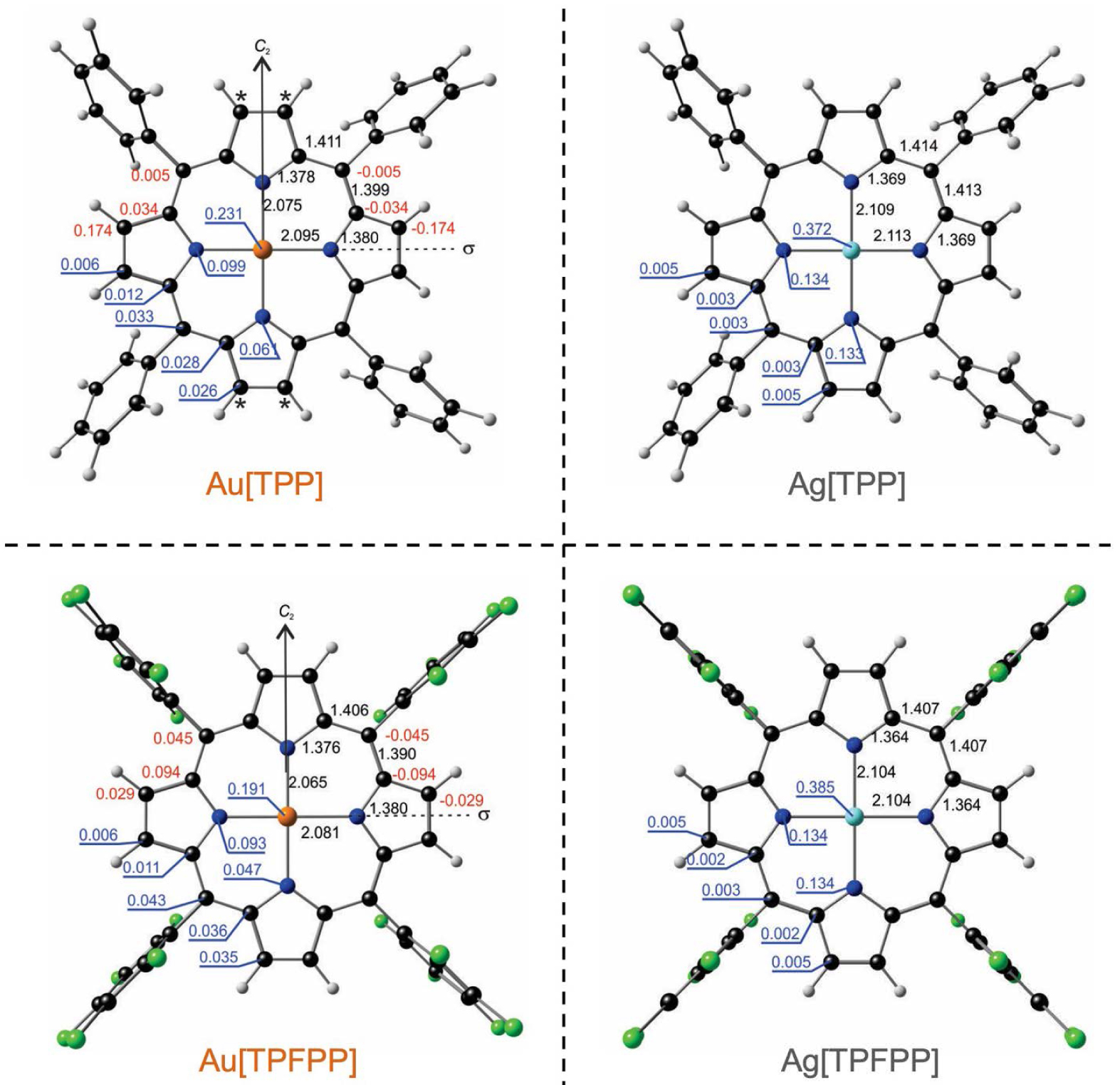
As of now, the unusual core geometry of Au[TPP] has been ascribed to a second-order Jahn–Teller distortion involving the Au 5dx2‐y2 and 6s orbitals [22]. An examination of the scalar-relativistic frontier MOs of each of the three Au(II) porphyrins studied indeed revealed varying degrees of mixing of the dz2, dx2‐y2, and 6s orbitals. Unlike in a simple Jahn–Teller system (but not uncommonly for second-order Jahn–Teller systems [37, 38]), however, the OLYP-D3 Kohn–Sham MOs with major contributions from the three atomic orbitals were found to exhibit a remarkable 8-eV span of orbital energies in these systems. For Au[P], the orbital energies for the α or majority-spin orbitals were −7.63 eV for the primarily dz2-based HOMO-18, −3.27 eV for the primarily dx2‐y2-based HOMO, and 0.56 eV for the primarily 6s-based LUMO+27. Of the three MOs, it was the lower-energy, primarily dz2-based HOMO-18, not the dx2‐y2-based HOMO, that was found to exhibit the greatest degree of dx2‐y2 and 6s admixture. The HOMO, it turned out, engages in a very different orbital interaction, namely one with the porphyrin’s π-HOMO. Thus, both the HOMOs and spin density profiles of the complexes exhibit surprisingly significant π-amplitudes at the meso positions of porphyrin (Figure 2). The Au(II) centers, as a result, carry correspondingly smaller spin populations than the Ag(II) centers in the analogous complexes (Figures 2 and 3). The latter finding greatly intrigued us, as it seemed to indicate an electronic imperative underlying the porphyrin’s wave distortion: the Au(II) center appears to exploit the nonplanar wave geometry to suck electron density from the porphyrin’s π-HOMO into its 5dx2‐y2 orbital.
To gauge the relative importance of the lateral compression–elongation and the wave distortion, we next optimized Au[P] with scalar-relativistic OLYP-D3 calculations under three different symmetry constraints, D4h, D2h, and C2h, with all MO irreps worked out by hand. Both the D4h and D2h calculations led to non-aufbau orbital occupations (i.e., where LUMO is below the HOMO), an indication of the instability of the molecule under those symmetry constraints. Most interestingly, the D2h optimized geometry did not exhibit the expected lateral distortion and proved essentially identical to the D4h geometry. In other words, the lateral distortion does not occur in the absence of the wave distortion. We are thus led to conclude that it is the wave distortion that is fundamental and drives the lateral distortion, and not the other way around.
The above findings lend an entirely new complexion to the electron structure of Au(II) porphyrins. The tendency of the Au(II) center to increase its effective d-electron count parallels a recent study in which a variety of formally Au(III) complexes have been described as quasi-d10, based on theoretical analyses of their bonding interactions [39]. These complexes nevertheless exhibit distinct 2p→5d XANES features, indicative of a 5d hole. Like many d10 complexes, on the other hand, they also exhibit weak, low-energy MLCT transitions in the near-infrared [22]. In this study, TDDFT calculations, which do a rather good job of reproducing the visible absorption spectrum of Au[TPP] (details of which are not particularly relevant), also predict two infrared absorptions with almost vanishingly small oscillator strengths. The wavelengths of the two absorptions vary considerably with details of the computational method, such as the choice of the exchange–correlation functional and basis set, but the assignment of the two features seems stable with respect to such details. With the well-calibrated range-separated CAMY-B3LYP functional [40] and the COSMO solvation model [41], the two absorptions in dichloromethane are at 0.55 eV (2215 nm) and 0.66 eV (1863 nm, Figure 4). Given their low energies and intensities, these two features have not been experimentally detected so far, but may be viewed as computational signatures of Au[TPP]. Comfortingly, the electrochemical HOMO-LUMO gaps (defined as the algebraic difference between the oxidation and reduction potentials) of Au(II) porphyrins of ∼0.6 eV, which may be inferred from the literature [20, 21] are in almost perfect agreement with the CAMY-B3LYP excitation energy.
CAMY-B3LYP/STO-TZ2P-derived infrared transitions and their MO composition for Au[TPP].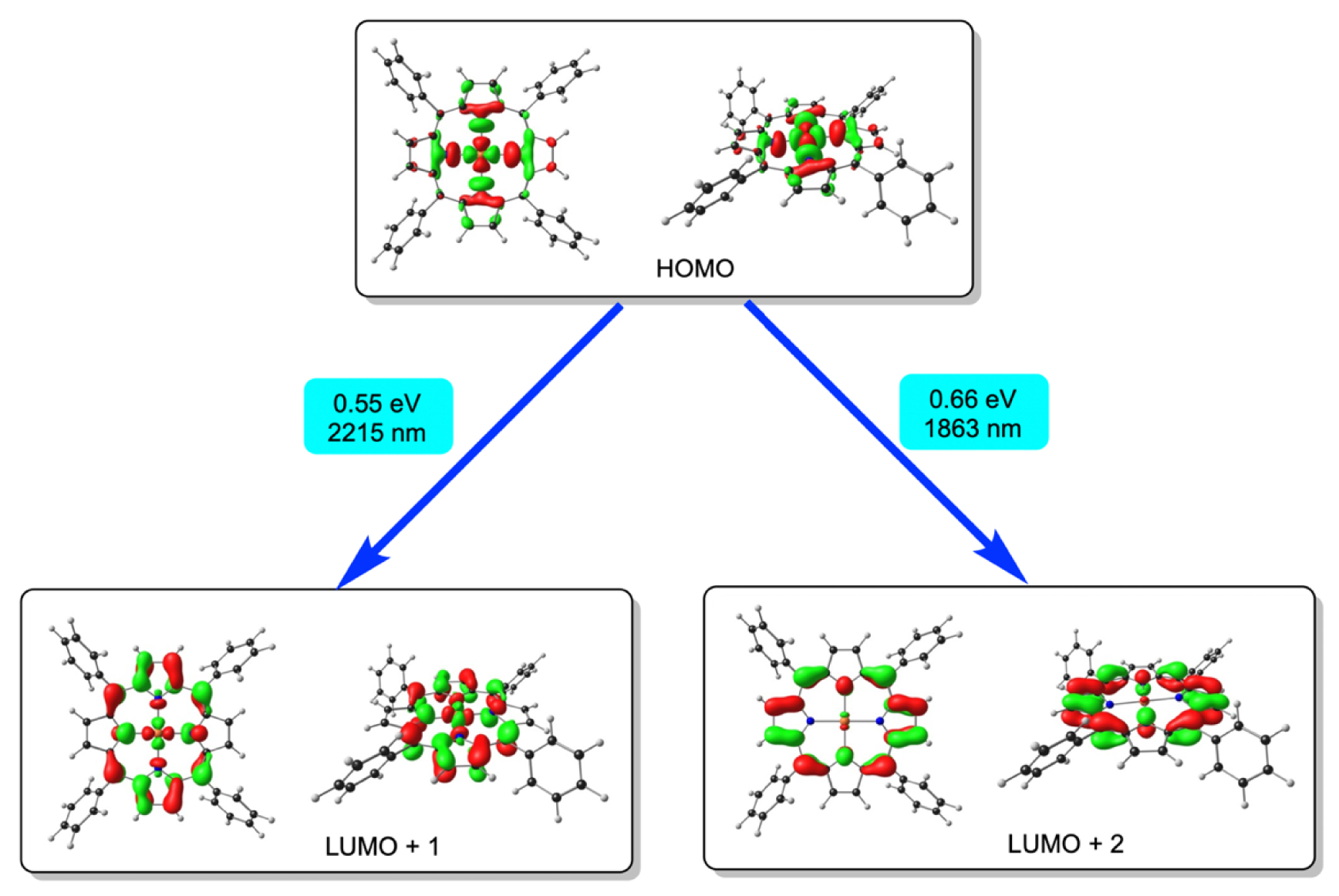
The inherent, electronically driven wave distortion of Au(II) porphyrins is reminiscent of the inherent saddling of copper corroles [42, 43, 44, 45], which is driven by the electronic imperative of the formally empty Cu(3dx2‐y2) orbital to accept electron density from the corrole’s π-HOMO. A similar orbital interaction is less important for silver corroles [46, 47] and not at all important for gold corroles [48, 49, 50, 51, 52]. The reason for the latter has to do with both relativistic destabilization of the Au(5dx2‐y2) orbital and the exceptionally strong σ-ligand field of the corrole [53]. Charge-neutral gold porphyrins and copper corroles provide rare examples where metal(d)–porphyrinoid(π) interactions alone suffice to engender nonplanar distortions of the macrocyclix ligands, even in the absence of sterically hindered, peripheral substituents [54].
3. Computational methods
Each Au(II) porphyrin and its corresponding cation were optimized with scalar-relativistic and two-component spin–orbit DFT (OLYP [55, 56]-D3 [57]) calculations with the ZORA [58] Hamiltonian and ZORA STO-TZ2P basis sets, as well as with nonrelativistic calculations with the same basis sets, all as implemented in the ADF program system [59]. Single-point scalar-relativistic energies were also calculated using the B3LYP∗ [60, 61] functional and found to be in excellent agreement with the OLYP-D3 results. Carefully tested, fine integration grids and tight SCF and geometry optimization criteria were used in all calculations.
4. Conclusion
The present study, in our view, has significantly deepened our electronic-structural understanding of Au(II) porphyrins.
First, the first IPs of Au(II) porphyrins have been found to be unusually low, >1 eV lower than those calculated for Ag(II) porphyrins; this difference is largely attributable to scalar relativistic effects, which are much stronger for gold than for silver. Electron-withdrawing substituents, however, are predicted to yield Au(II) derivatives such as Au[TPFPP] with higher oxidative stability.
Second, our calculations have put a whole new complexion on the experimentally observed structural distortions of Au[TPP]. The primary stereoelectronic effect appears to be a wave distortion driven by an Au(5dx2‐y2)–porphyrin(π) orbital interaction, which allows the formal Au(II) center to assume a pseudo-d10 configuration. The lateral distortion allowing for Au 5dx2‐y2-5dz2-6s mixing appears to be a secondary effect, a consequence of the wave deformation. Tellingly, in computational experiments, absent a wave formation, Au(II) porphyrins do not undergo an in-plane lateral distortion.
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.
Data availability statement
All data generated or analyzed in this study are included in this published article and its supplementary information.
Funding
This work was supported in part by grant no. 324139 of the Research Council of Norway (AG) and grant nos. 129270 and 132504 of South African National Research Foundation (JC).




 CC-BY 4.0
CC-BY 4.0