1. Introduction
Jarosite-type compounds are minerals belonging to the alunite–jarosite group presenting an ideally general formula [AαBβ(CO4)γ(OH)δ]. Several types of jarosites can form depending on the ions occupying the A-, B-, and C-sites in the mineral structure. A-sites are commonly occupied by monovalent (K+, Na+, Ag+, Tl+,
The most important and common jarosite-type mineral found in terrestrial environments is K-jarosite [KFe3(SO4)2(OH)6]. The structure of jarosite is based on linear tetrahedral–octahedral–tetrahedral (T–O–T) sheets, made up from slightly distorted FeO6 octahedra and SO4 tetrahedra [5, 7]. Authors affirm that K-jarosite structure generally contains ferric ion vacancies and “additional water” in the form of hydronium. Therefore, the chemical formula is more correctly written as H3O1−xKxFe3−y[(OH)6−3y(H2O)3y(SO4)2] [3, 4, 7, 8, 9].
According to Alpers et al. [4], any attempt to define the thermodynamic properties of minerals in the alunite–jarosite group must consider issues related to the non-stoichiometry of their structures. Indeed, the values of the (Al + Fe)/SO4 ratio can vary considerably from the ideal stoichiometry of 3/2 (3 moles of Fe3+ to 2 moles of sulfate), as observed in the work of Härtig et al. [8], with ratios ranging from 2.20/2 to 2.52/2, as well as in the research of Ripmeester et al. [9], with a ratio of 2.33/2.
1.1. Jarosite in the environmental context
Jarosite-type compounds are largely found in the terrestrial ecosystem as ferric sulfate salt that often forms in acidic and oxidizing environments enriched in sulfate. Different studies have shown its presence in:
- Acid sulfate soils formed from pyrite sediments [10, 11, 12, 13];
- Acid sulfate waters [14];
- Acid rock drainage (ARD) or acid mine drainage (AMD) [4, 15, 16, 17, 18, 19, 20, 21, 22, 23];
- Weathering residues from sulfide ore deposits [24];
- Alteration of coal from pyritic coal beds [25];
- Clay layers and beds [26, 27];
- Proximity to volcanic fissures [28, 29, 30];
- Oceanic fumaroles [31, 32] and hot springs [33];
- Hydrothermal environments [34, 35], sometimes associated with basalt [36];
- Hypersaline lakes, such as those in Australia and Antarctica [26, 29, 37, 38, 39, 40, 41, 42].
The formation of jarosite and the release of H+ are often attributed to the oxidation of sulfur-bearing minerals such as pyrite (FeS2), which alters groundwater and effluent environments [43, 44]. Ideally, the formation (1) and dissolving (2) equations for K-jarosite are expressed below:
| (1) |
| (2) |
Furthermore, the early 2000s brought the discovery, in situ and from orbiting spacecraft, of jarosite on Martian soil [47, 48, 49, 50, 51, 52, 53, 54, 55]. This observation indicates that oxidizing and acidic fluids were present when jarosite was formed [48, 56, 57], and consequently, suggests the possibility of water existence on Martian soil. Other evidence has shown that hematite found on Mars has also been formed from jarosite [36, 58, 59].
1.2. Jarosite in the hydrometallurgical industrial context
Since the 1960s, the hydrometallurgical industry has been widely using the precipitation of jarosite compounds in industrial processes for separation of zinc from iron [60]. The production of zinc generates a large amount of jarosite-type compounds, which represents a potential environmental problem, since the jarosite scavenger property allows the presence of toxic elements in the iron residues. On the other hand, these residues may present economic value with the recovery of critical and valuable metals from zinc production waste. The study of jarosite leaching conditions constitutes, therefore, an attractive research area to reduce environmental issues and produce new resources [61].
Due to the presence of jarosite in industrial processes, it is of great importance to manage its residues, as its formation and dissolution mechanisms can alter the chemical environmental of rivers and groundwater by releasing the retained acidity, sulfate, hazardous elements, and secondary mineral waste depending on the conditions. Therefore, understanding the immobilization property of jarosite-type compounds is useful in forming stable minerals to reduce their spread in soils and aquifers and to help manage waste materials from mining tailings.
Therefore, having in mind the wide range of applications, rigorously understanding and evaluating jarosite dissolution and stability is important to predict the effect of long-term jarosite behavior on soil, water, and industrial processes, as well as to effectively manage hazardous waste to create potential remediation strategies, diminish environmental impact and improve hydrometallurgical processes to create economic profit [43, 44, 46, 62, 63, 64, 65, 66, 67].
With that aim, the collection and critical assessment of thermodynamic and kinetic data for jarosite dissolution and precipitation processes are necessary. Therefore, numerous scientists and research groups have made efforts to elucidate the behavior of jarosite-type compounds under different conditions over the past decades. Regardless, the results described in the literature concerning the solubility and kinetics of this compound are highly variable [46, 68]. Consequently, this review dedicates the following sections to shedding light on the works conducted up to this date and explaining the potential sources of disagreement among them.
1.3. Jarosite stability and transformations
Ferric phases undergo transformations into alternative phases upon removal from their stability zones. Jarosite-type compounds, for instance, are documented to go through a transformation resulting in the different phases, as illustrated in Figure 1.
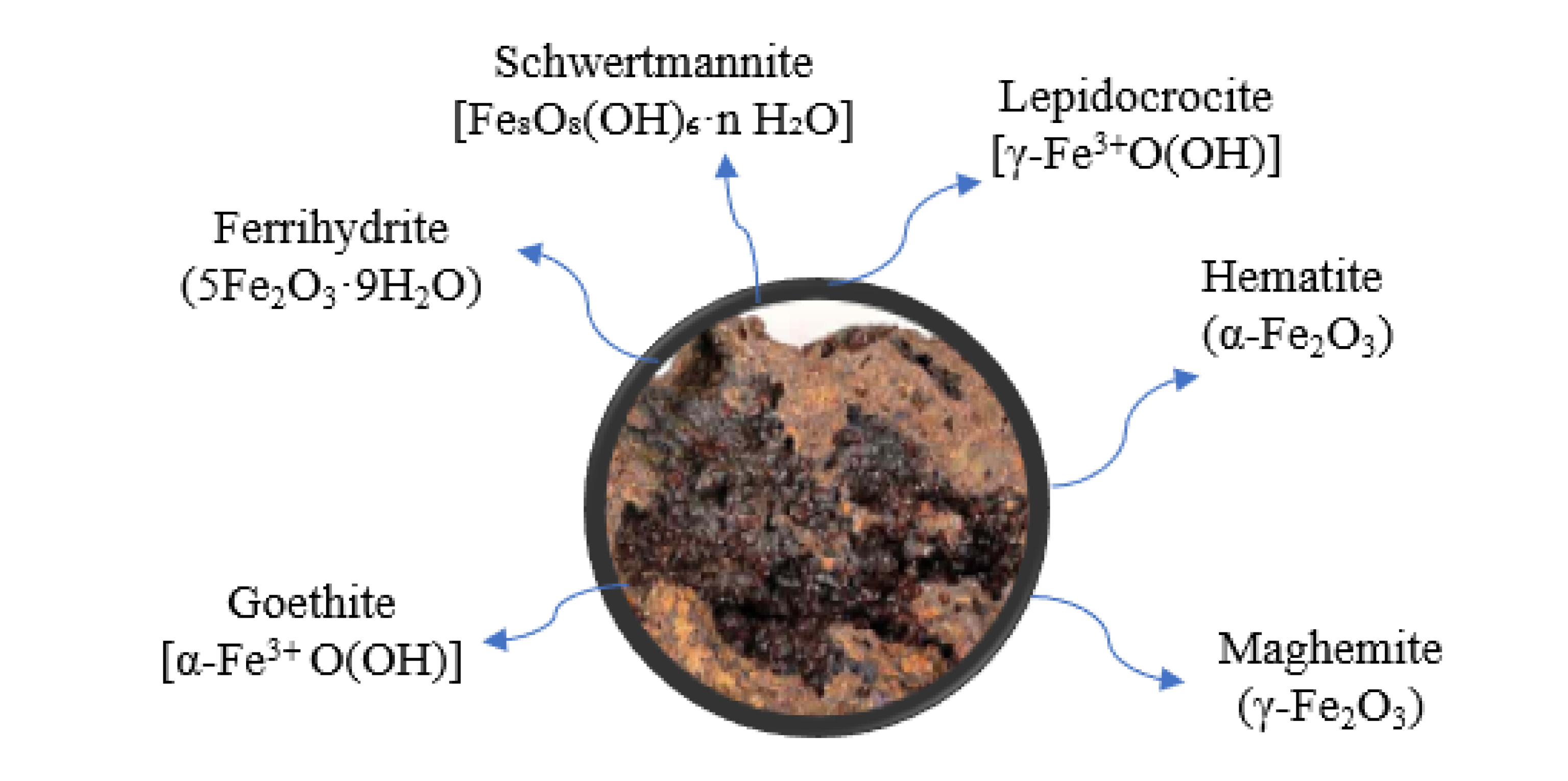
Transformations of jarosite compounds into different ferric phases.
It is established that jarosite can easily decompose when removed from its stability zone, transforming into phases of iron oxide or iron (III) oxyhydroxide [5, 35]. These transformations can also result in the release of acidity. Jarosite is considered a retained acidity (RA) resource in these environments, a form of acidity potentially released through the hydrolysis of poorly soluble and poorly crystalline Al3+ or Fe3+ minerals [46, 65, 66, 69]. According to Stoffregen [70], under surface conditions, jarosite tends to transform into goethite through the following reaction when exposed to diluted water with a higher pH:
| (3) |
However, this reaction can be complicated by the formation of metastable phases such as schwertmannite and ferrihydrite [71]. Ferrihydrite is a well-known hydrated iron oxide with chemical formula 5Fe2O3 ⋅ 9H2O [72], where the hydration level can vary depending on how much water is present within the molecular arrangement [73, 74]. Schwertmannite is an oxyhydroxysulfate with chemical formula Fe8O8(OH)8−2x(SO4)x ⋅ nH2O where 1 ⩽ x ⩽ 1.75.
Above the transition temperatures from goethite to hematite, i.e., at 373.15 K, the transformation reaction of jarosite becomes:
| (4) |
| (5) |
The anhydrous forms of iron oxide can also exhibit different polymorphs, meaning the same chemical structure but different crystalline systems. The most well-known forms are hematite (α-Fe2O3) and maghemite (γ-Fe2O3). Hematite can be formed from magnetite through the following equation:
| (6) |
Like iron oxides, anhydrous iron oxyhydroxides (FeOOH) can exhibit several polymorphs. Goethite (α-FeOOH) is the most well-known compound, but there is also akaganeite (β-FeOOH) and lepidocrocite (γ-FeOOH). Redox-pH potential diagrams have been constructed showing the jarosite–hematite boundary between pH 2 and 4, and jarosite–goethite between pH 2 and 3 [76].
Bigham et al. [77] analyzed ochreous sediments as well as their associated solutions from twenty-eight AMD sites ranging from 279 to 300 K. The results revealed a change in solid composition depending on the pH of the mixture. Precipitates formed above pH 6.5 were mainly composed of ferrihydrite or a mixture of ferrihydrite and goethite. In contrast, precipitates with pH between 2.8 and 4.5 were mainly composed of schwertmannite, with traces of goethite and/or jarosite. Solutions with intermediate pH (between 4.5 and 6.5) produced a mixture of ferrihydrite and schwertmannite. Only the solution at pH 2.6 contained a considerable amount of jarosite. Bigham and his colleagues also developed a revised model for mineral speciation at 298 K and redox potential ranging, according to the pH, from −237 to 947 mV (pH > 6.5), 118 to 1065 mV (2.8 < pH < 4.5), 0 to 1000 mV (4.5 < pH < 6.5) and 592 to 1184 mV (pH < 2.6).
The continuation of this paper is organized as follows: Section 2 presents thermodynamic studies of jarosite, including those using dissolution, precipitation, and calorimetry. Section 3 discusses the kinetic dissolution studies within the environmental and industrial contexts. Section 4 focuses on the kinetic studies of jarosite-type compound precipitation at high and low temperatures, both with and without the presence of microorganisms. Finally, Section 5 highlights the most relevant methods used in the literature to characterize jarosite phases.
2. Thermodynamic studies of jarosite
Several studies have focused extensively on the study of the crystallography and structure of jarosite compounds [78, 79]. The investigations into the structure of jarosite date back to the mid-20th century. Initially, Parker [80] examined alunite minerals containing potassium or sodium. Concurrently, Brophy et al. [81] studied K-jarosite and K-alunite. Kubisz [82] dedicated his research to the study of potassium and hydronium substitution in jarosite, demonstrating the existence of H3O-jarosite.
However, Brophy and Sheridan [2] were the first to investigate the substitution of K–Na–H3O+ mixture in the jarosite structure under terrestrial surface temperature and pressure conditions. Additionally, in their study, they asserted that hydronium substitution by potassium in the jarosite structure is facilitated by an increase in temperature, in line with several studies conducted in the 1950s on the composition of natural and synthetic jarosites. Furthermore, Ross et al. [83] showed that H3O-jarosite can form in the absence of alkalis.
Since the studies on the structure and composition of jarosites, researchers have frequently noted the variability of the solubility product data. Some authors have delved into dissolution and/or precipitation phenomena to obtain thermodynamic data [4, 7, 68, 70, 84, 85, 86], while others have reinterpreted these results by introducing additional thermodynamic data for equilibrium calculations, proposing new values [22, 24, 87, 88, 89, 90].
Nevertheless, the most cited paper and reliable data used nowadays still is Baron and Palmer [68] who studied the thermochemistry and solubility of synthetic K-Jarosite dissolution at different pH and near room temperatures using a stirred batch reactor and were the first to carry out a calorimetric study of K-Jarosite. This study formed a basis for other similar investigations, like the thermodynamic study by Smith et al. [7] who calculated the solubility product constant (Ksp), the ion activity product (IAP) and saturation indices (SI). However, more recently, Lemire et al. [90] from the OECD Nuclear Energy Agency published a book on the chemical thermodynamics of iron re-evaluating the results obtained by Baron and Palmer [68], which will be discussed later in Section 2.1.
Other authors, like Drouet and Navrotsky [76], worked with the calorimetric study of Na-jarosite, while Majzlan et al. [91] studied thermodynamic properties of H3O-jarosite. Other authors studied the thermodynamics of jarosite such as Jamieson et al. [17], Navrotsky et al. [19], Casas et al. [92], and Forray et al. [93].
Hence, Section 2 is divided into two main parts. Section 2.1 presents studies using dissolution and precipitation processes to obtain thermodynamic data, while Section 2.2 focuses on thermodynamic data obtained through calorimetry studies.
2.1. Thermodynamic studies through dissolution and precipitation
Table 1 presents the thermodynamic solubility constants, mostly at 298.15 K, reported in the literature, which vary considerably from one study to another. For example, for K-jarosite, the logarithm of the equilibrium constant ranges from −7.12 to −12.51, a difference of five orders of magnitude. These discrepancies are primarily explained by variations in the methodologies used, which will be described in this section.
Solubility constants of jarosites found in the literature at 298.15 K
| Authors | Jarosite-type | Method | logKsp | Δf G°298.15 (kJ/mol) |
|---|---|---|---|---|
| Brown [84] | K | Prec. and Diss. | −9.65 | −3276 and −3192 |
| Zotov et al. [87] | K | Precipitation | −9.47 | −3305.70 |
| Van Breemen [88] | K | Dissolution recalculated | −9.46 | −3299.00 |
| Vlek et al. [85] | K | Dissolution | −9.86 | −3331.40 |
| Kashkay et al. [86] | K | Precipitation | −9.32 | −3299.67 |
| Lindsay [94] | K | −12.51 | ||
| Hladky and Slansky [89] | K | Calculated | −9.08 | |
| Bladh [24] | K | Dissolution | −7.12 | −3287.60 |
| Chapman et al. [22] | K | Dissolution | −9.21 | |
| Alpers et al. [4] | K | Precipitation | −9.35 | −3300.25 |
| Stoffregen [70] | K | Precipitation | −8.8 | −3416.3a |
| Öborn and Berggren [95] | K | Dissolution | −9.42 to −9.41 | |
| Baron and Palmer [68] | K | Dissolution | −11.0 | −3309.8 |
| Smith et al. [7] | K | Dissolution | −11.3 | |
| Lemire et al. [90] | K | Recalculated | −9.8 | |
| Kashkay et al. [86] | Na | Precipitation | −8.93 | −3256.70 |
| Hladky and Slansky [89] | Na | Calculated | −5.10 | |
| Bladh [24] | Na | Dissolution | −3.60 | |
| Chapman et al. [22] | Na | Dissolution | −5.28 | |
| Alpers et al. [4] | Na | Precipitation | −7.18 | |
| Öborn and Berggren [95] | Na | Dissolution | −9.39 to −9.31 | |
| Hladky and Slansky [89] | Pb | Calculated | −7.89 | |
| Chapman et al. [22] | Pb | Dissolution | −16.28 | |
| Bladh [24] | H3O | Dissolution | −3.57 | |
| Alpers et al. [4] | H3O | Precipitation | −6.04 |
a Values of Δf G° at 473.15 K and 10 MPa.
Brown [84] investigated the precipitation of K-jarosite at 298.15 K and 0.1 MPa over a six-month period. He used K2SO4, hydrated FeSO4, and dissolved Fe2(SO4)3 in known concentrations of H2SO4. Subsequently, he employed a reverse approach (dissolution) using 0.5 g of jarosite in 0.005 M H2SO4 solution for six months. Brown considered the potential presence of additional compounds after precipitation and dissolution experiments. Consequently, X-ray diffraction (XRD) analysis was employed to address this question. However, all the X-ray diffraction patterns could only be identified as jarosite lines. Through the calculations of the free energy of formation, he demonstrated that equilibrium was practically reached by both methods with a slight difference in free energy of formation (−3276 ± 84 and −3192 ± 25 kJ/mol for precipitation and dissolution, respectively). Additionally, he calculated redox potential (Eh), pH, and plotted the activity logarithm diagram for the jarosite–goethite–pyrite system, highlighting the equilibrium of these minerals under ambient conditions.
The Gibbs free energies found by Brown [84] were initially recalculated (−3302 ± 84 and −3300 ± 25 kJ/mol for precipitation and dissolution, respectively) by Zotov et al. [87], who identified an arithmetic error in the calculations. Then, they used different thermodynamic data from Naumov et al. [96]. Furthermore, Zotov et al. [87] conducted precipitation experiments using a natural water sample and found the Gibbs free energy to be −3305.7 kJ/mol. Subsequently, Van Breemen [88] also revised Brown’s [84] values using other thermodynamic data from Robie and Walbaum [97] and found the Gibbs free energy to be equal to −3299 kJ/mol.
Vlek and colleagues [85] determined the solubility product of jarosite using the chelation method. Given that the solubility of Fe (III) compounds was low under their conditions, solubility measurements to detect the presence of iron were limited to highly acidic solutions. They developed a new method involving the use of EDTA as a chelating agent to increase the concentrations of Fe (III) from a natural jarosite sample, taken from a sulfate-acidic soil, in suspension. In this way, dissolution was studied, yielding a Gibbs free energy of −3310.4 kJ/mol and a logarithm of the solubility product constant (logKsp) of −9.86. They acknowledged that the results obtained in their study could be subject to various errors resulting from pH measurements, iron concentrations, as well as incorrect estimations of constants and ionic strength. Moreover, they did not mention the use of XRD to identify the remaining solids after the experiments. Baron and Palmer [68] subsequently recalculated their Gibbs free energy with different free energies for the ions and found a value of −3331.4 kJ/mol.
Kashkay et al. [86] conducted three precipitation experiments from supersaturated solutions of K-jarosite, Na-jarosite, and Pb-jarosite over a 15-month period at room temperature. Additionally, they performed precipitations at 373.15 K. The Gibbs free energy for K-jarosite was −3299.7 ± 4 kJ/mol at 298.15 K and −3184 kJ/mol at 373.15 K. The solubility found at 298.15 K was greater for Na-jarosite than for K-jarosite.
In his thesis, Nordström [21] studied hydrogeochemical and microbiological parameters influencing the chemical speciation of heavy metals in AMD effluents in Northern California. His calculations revealed that the samples were in a state of supersaturation with respect to jarosite.
Hladky and Slansky [89] investigated the stability of minerals in the alunite–jarosite group in aqueous solutions at room temperature and pressure. Stability domains concerning pH were investigated for K-jarosite, Na-jarosite, and Pb-jarosite using Gibbs free energy values. It was revealed that pH constitutes the main control factor for the stability of minerals in the alunite group under the studied conditions.
Bladh [24] simulated the chemical erosion of felsic rocks to study the formation of goethite, jarosite and alunite. He recalculated the thermodynamic data previously obtained by Brown [84], Zotov et al. [87], Vlek et al. [85], and Van Breemen [88]. According to Bladh, the ambiguities present in those studies arose from the varied data regarding the free energies of ions that were utilized in the calculation. He calculated the solubility product (logKsp) to be −7.12, while that of Na-jarosite was −3.60, and H3O-jarosite was −3.57.
The Gibbs free energy determined by Bladh [24] for K-jarosite (−3287.60 kJ/mol, recalculated by Baron and Palmer [68]) from Posnjak and Merwin [75] and Kashkay et al. [86] data is inconsistent with Alpers et al. [4] data. However, values reported by Zotov et al. [87] and Vlek et al. [85] are closer. Despite this, Kashkay et al. [86] were the only ones to provide a set of data for all three substitution ions (K–Na–H3O) in the A-site of jarosite at that time.
Chapman et al. [22] studied two AMD samples to understand the processes controlling the transfer and attenuation of heavy metals. They highlighted the variation in jarosite solubility thermodynamic data, making it difficult to select the necessary thermodynamic parameters (Ksp) to predict the saturation state of a mixture. They claimed that this variation is probably due to the use of different ΔfG° values. They utilized X-ray powder diffraction to identify the solids. However, the results were limited to identifying the mineral phases since most of the precipitates were amorphous.
Several values for the of Fe3+ have already been reported. For example, Chapman and colleagues [22] chose to use the data used by Naumov et al. [96], Kashkay et al. [86], and Zotov [87] because they considered them coherent with each other. The results obtained by Nordström et al. [21] regarding the solubility product varied three to five orders of magnitude below than those found by Chapman et al. [22].
Alpers et al. [4] studied precipitates from AMD solutions in California, USA. In their experiments, seven samples with initial pH between 0.8 and 1.4 were kept for 11 to 13 years at a temperature of 295 ± 3 K. At the time of sampling, they were undersaturated with respect to jarosite. The oxidation of ferrous iron during storage led to saturation and precipitation of the ore. These minerals were characterized by solid analysis techniques such as XRD, scanning electron microscopy (SEM)-energy dispersive X-ray spectroscopy (EDS), and thermogravimetric analysis. The crystals had a diameter between 5 and 10 μm and a rhombohedral shape. The authors state that the well-crystallized nature indicated that the AMD had reached a thermodynamic equilibrium with jarosite. The relationship between crystallinity and equilibrium will be further addressed in Section 4.3.
Thus, Alpers et al. [4] recommended using a Δf G° value of 3293.5 ± 2.1 kJ/mol for a solid with composition K0.77Na0.03(H3O)0.20Fe3(SO4)2(OH)6. The average logKsp of −9.35 showed good agreement with previous results from Chapman et al. [22]. Alpers and colleagues highlighted the need to determine the solubility of jarosite for more varied compositions to quantify the influence on solubility of substitution in the A-site (K, Na, H3O). Despite the lack of data, they observed that the K–H3O substitution approaches the ideal substitution compared to Na–K and Na–H3O substitutions. Alpers et al. [4] estimated that additional experimental work was needed to accurately determine the solubility and free energy of formation of jarosite.
Stoffregen [70] studied the stability relationships between jarosite and Na-jarosite at temperatures ranging from 423.15 to 523.15 K through hydrothermal experiments lasting 1 to 11 weeks. X-ray powder diffraction was used to identify phases present in the products after the experiments. Experimental study of jarosite at high temperatures has advantages: (i) there are only three stable phases at temperatures above 423.15 K, compared to seven phases reported at 298.15 K by Posnjak and Merwin [75], (ii) reaction rates are higher, and (iii) hydronium substitution, which is common in natural jarosites and complicates the determination of terminal member properties, is negligible [4].
The Gibbs free energies were calculated by Stoffregen [70] at 473.15 K and 10 MPa, as presented in Table 1. Furthermore, they suggested that jarosite and Na-jarosite form nearly ideal minerals (A-site substituted only for K or Na) at 473.15 K, and there is complete miscibility between the two types of jarosite at 298.15 K.
Öborn and Berggren [95] studied two types of jarosite (K- and Na-jarosite) from sulfide sedimentary deposits in the Baltic Sea. The jarosites were characterized by XRD after dissolution, and the solubility product was determined from the dissolution of samples that reached equilibrium at different time intervals (from 6 h to 8 days). The solubility constants corresponded to −9.41 to −9.42. Additionally, Bigham et al. [77] reported solubility values for K-jarosite in a range from −9.21 (Kashkay et al. [86]; Chapman et al. [22]) to −12.51 (Lindsay [94]).
Today, the results obtained by Baron and Palmer [68] are most commonly used to predict the dissolution/precipitation of jarosite. Indeed, their work enabled the calculation of Gibbs free energies, enthalpy, entropy, and heat capacity. They were the first researchers to conduct a calorimetric study of the free energy of formation. Dissolution experiments of synthetic K-jarosite were conducted at different pH values (1.5–3.0) and temperatures close to room temperature (277.15–308.15 K) using a batch reactor. Two methodological approaches were considered for dissolution: first, the temperature at 298.15 K was kept constant while the pH varied from 1.5 to 3; second, the temperature varied from 277.15 to 308.15 K with a constant pH of 2. The composition (chemical formula) of jarosite was quasi-ideal, and the solids remained in the reactor for up to six months. XRD analyses were not conducted to characterize the reaction product solids in detail. Their study served as the basis for subsequent similar studies.
They observed that equilibrium was reached after 40 to 125 days of dissolution at pH 2 and 298.15 K, with an initial concentration of 0.2 g of jarosite/L of solution. The results obtained by Baron and Palmer [68] were closer to those of Alpers et al. [4], but one to two orders of magnitude higher compared to the results of Kashkay et al. [86] and Chapman et al. [22]. Ksp decreases as the temperature increases, ranging from −11.06 at 277.15 K to −11.68 at 308.15 K, indicating a negative enthalpy [68]. In other words, the addition of heat does not favor the reaction. However, this dependence in this temperature range is not linear, implying a variation in the enthalpy of reaction as the temperature changes.
According to Baron and Palmer [68], several reasons explain the divergences from previous studies:
- Inconsistency of thermodynamic data and variations in the values used for the calculation of free energies and ion activities;
- Substitution of ions in the jarosite structure;
- Variations introduced by different experimental methodologies;
- Analytical uncertainties.
Arslan and Arslan [60] conducted a review of the stability regions between jarosite and goethite at 298.15 and 368.15 K. They observed that the stability region of jarosite not only shifts toward a more acidic and oxidizing zone as the temperature increases but also becomes more restricted. However, they emphasized that, in addition to these thermodynamic considerations, the reaction kinetics play a significant role in the precipitation of iron compounds.
The work of Baron and Palmer [68] was considered the starting point for more complex structures containing mixtures of Fe3+ and Al3+ in B-sites, as well as the substitution of S6+ and Cr6+ in C-sites. Baron and Palmer [98] also studied the dissolution of analog jarosite with Cr substitution in the sulfur site. These studies were further pursued based on calorimetric investigations.
Thermodynamics was also studied by Smith et al. [7], aiming to monitor the ion release during dissolution and to characterize the newly formed solid phases. They calculated the equilibrium constant (Ksp) and solid saturation ratios (Ω) at pH 2 and 8 and room temperature (293.15 K). The results are close to those of Baron and Palmer [68], with logKsp equal to −11.30. According to these authors, positive saturation ratios for hematite and goethite indicate the likely appearance of these minerals after a prolonged dissolution period. They utilized XRD analysis to identify the solids remaining after dissolution.
The study conducted by Smith and colleagues [7] was significant as it was the first to examine the dissolution of jarosite and the formation of new phases at pH 8, where Fe3+ reprecipitates. This is likely responsible for preventing the continuation of jarosite dissolution and reinforces the incongruence of jarosite dissolution already observed by Baron and Palmer [68]. This incongruence (non-stoichiometry of the solid) is due to the strong stability of the FeO6 octahedron compared to the weak stability of KFe(OH)4.
Smith et al. [99] also investigated the dissolution of Pb-jarosite [(H3O)0.74Pb0.13Fe2.92(SO4)2(OH)5.76] and arsenic-substituted Pb-jarosite [(H3O)0.68Pb0.32Fe2.86(SO4)1.69(AsO4)0.31(OH)5.59] at pH 2 and 8. The logKsp results showed a decrease (−9.35 to −10.65) compared to the standard jarosite structure. Their study demonstrated that, since jarosite dissolution is non-stoichiometric under the conditions studied, it is important to step back from diagrams such as Stoffregen [70] since the solid stability limits assume that the dissolution reaction occurs congruently (stoichiometrically).
Casas et al. [92] studied solubility through the precipitation of Na-jarosite and the speciation of an Fe(III)–Na–H2SO4–H2O system at 343.15 K. They reported a lack of information on Na-jarosite solubility. Solubility data available in the literature up to that point had been obtained at room temperature or above 363.15 K. There was no information in the range 333.15–353.15 K, corresponding to the temperature range in which thermophilic microorganisms are active. The synthesis was carried out in reactors using a mixture of NaOH and FeH(SO4)2. Different mixtures of sulfuric acid and ferric iron were prepared and left to reach equilibrium for 45 days in a rotary oven at 343.15 K. The formation of Na-jarosite was observed at pH above 1.72 with the presence of goethite in the mixture after XRD analysis of the remaining solids. In contrast, for pH below 1.42, Na-jarosite was pure. Research by Casas and colleagues highlighted the dependence of ionic balance on bisulfates and sulfate complexes such as FeH(SO4)2,
As mentioned earlier in this section, Lemire et al. [90] re-evaluated the logKsp value at 298.15 K, revising from −11.0 to −9.8. According to them, uncertainties in the stoichiometry, particle size, crystallinity variation, and the incongruence of dissolution (as reinforced by Smith et al. [7]) render the estimations provided by Baron and Palmer [68] merely speculative.
This detailed section illustrates that estimating the solubility of jarosite-type compounds is a complex task that has been attempted by numerous scientists over the past 50 years. The biggest challenges in estimating this constant are related to the variety of substitutions within the mineral, the variability of experimental methodologies employed, and discrepancies in the thermodynamic data regarding the free energy of ions. Despite the revaluation of Lemire et al. [90], who considered the calculated solubility product constant found by Baron and Palmer as speculative, their study has remained the most widely utilized since due to its detailed methodology and well-explained results. The techniques utilized by Baron and Palmer [68], including the precipitation methodology to obtain the solids used in the dissolution experiments, continue to be employed. The principal trends were also confirmed by Smith et al. [7] and were further corroborated by calorimetric studies described in Section 2.2 which affirmed that Baron and Palmer [68] had achieved equilibrium.
2.2. Thermodynamic studies through calorimetry
Drouet and Navrostky [76] conducted a calorimetric study to obtain formation enthalpies through dissolution calorimetry in molten mixtures at high temperatures. In contrast to Stoffregen [70], who used estimations, the data were obtained directly. However, the results of Stoffregen [70] are not consistent with the equation
| (7) |
Subsequently, Drouet et al. [100] conducted calorimetric studies to determine the enthalpy of jarosite containing chromate (CrO4). Furthermore, Drouet et al. [101] also investigated solid mixtures between Na-jarosite and Na-alunite. From these studies, they determined the enthalpy of formation and were able to recommend values for Gibbs free energy and entropy.
Similar to Drouet and colleagues, Majzlan et al. [91] focused on the thermodynamic properties of H3O-jarosite and obtained data on enthalpy, heat capacity, and entropy. Then, Majzlan et al. [102] continued their research on different jarosite-type compounds (K, Na, Rb, and NH4), reporting their heat capacities and entropies. They calculated entropies from experimentally measured Cp data using an adiabatic calorimeter, unlike Stoffregen [70] who extrapolated data from experiments at high temperatures. Majzlan and collaborators considered their data more reliable. According to them, the significant variations found in the values of thermodynamic properties of jarosite indicated that the study of these properties would need to be addressed more reliably in future work. Additionally, with the data on enthalpy and entropy, it would be possible to calculate phase diagrams for the phase equilibria of this complex and challenging mineralogical group.
Forray et al. [103] studied the formation of yavapaiite KFe(SO4)2 resulting from the heating of K-jarosite at temperatures above 673.15 K to better understand the decomposition of this mineral. Then, in 2010, Forray and colleagues [93] synthesized, characterized, and studied the thermodynamics of Pb-jarosite, providing the enthalpy of formation of the compound and enabling the calculation of Pb–Fe–SO4–H2O diagrams as well as the estimation of the equilibrium constant (logKsp ranging from −24.3 to −26.2). Furthermore, Forray et al. [104] continued their work on the synthesis and thermodynamics of Pb–As, Pb–Cu, and Pb–Zn jarosite mixtures, resulting in the following logKsp values: −13.94 ± 1.89; −4.38 ± 1.81; −3.75 ± 1.80, respectively. They concluded that the transformations and dissolution reactions of arsenic-containing jarosites are much more complex.
3. Kinetic studies of jarosite dissolution processes
The most used tool to model dissolution and precipitation processes in the geochemistry field is thermodynamics. Nonetheless, not every mineral can attain equilibrium in a rapid way, especially when using conditions at low temperatures and neutral pH. These minerals presenting slow reaction rates often keep geochemical processes from reaching equilibrium and this makes geochemical kinetics another essential tool for modeling these situations [105]. Therefore, elucidating the behavior of jarosite dissolution and precipitation can aid in the development of robust models which describe the geochemical cycling of these elements in the environment and in hydrometallurgical processes.
The importance of studying the dissolution kinetics of jarosite compounds gained academic significance after the 1990s. Kinetic data have been found and modeled by several authors. The results generally converge in the same direction; however, differences appear mainly due to the various parameters used in the studies. Three main models have been used to mathematically represent the process and the effects of variables: the derivative kinetic model (DVKM), the Noyes–Whitney kinetic model (NWKM), and the shrinking core kinetic model (SCKM).
The DVKM entails obtaining initial rate constants derived through the fitting of initial kinetic data to a second-order polynomial equation and calculating the slope, considering the beginning of the curve as time zero.
While the NWKM describes dissolution as a diffusion process, proportional to the difference between the solute’s saturation concentration in the solvent (solubility) and the solute’s concentration in the solution. This concentration gradient-based approach is inspired by Fick’s law and has influenced several diffusion-based dissolution models [106]. This equation is widely used in the study of dissolution in the pharmaceutical field.
The SCKM, initially developed by Yagi and Kunii [107] is described by Levenspiel [108]. It considers mass transfer mechanisms in the studies of the dissolution reaction of a solid in a fluid. In this model, particle size decreases over time, and particles eventually disappear as the reaction progresses. During dissolution, two main steps are observed: (i) the induction period, where the reaction front is forming and the concentration increases very slowly, and (ii) the progressive period, where the reaction front is already established and the concentrations increase faster until reaching equilibrium.
In this section, the studies will be divided into two categories: those intended for the study in environmental settings (Section 3.1) and those in the hydrometallurgical industry conditions (Section 3.2). Additionally, Section 3.3 discusses the nature of the jarosite-type compound samples used in the thermodynamic studies of Section 2 and in the kinetic studies of Sections 3.1 and 3.2, whether they are natural or synthetic and how this distinction may influence the outcomes.
3.1. Kinetics of jarosite environmental dissolution
Many researchers started studying jarosite dissolution rates with different conditions and methodologies. The first robust study of the dissolution kinetics of jarosite was conducted by Baron and Palmer [68], focusing on the release of ions in an acidic environmental medium. They used the Noyes–Whitney model to fit the data from dissolution at pH 2 and 298.15 K, resulting in a first-order kinetics and a kinetic constant K equal to 7.9 ± 0.5 × 10−7 s−1. As discussed earlier, in the thermodynamic part studied by these authors, their study served as a basis for subsequent research.
Gasharova et al. [45] investigated the surface behavior of jarosite using Atomic Force Microscopy (AFM) at pH 5.5. The goal was to directly observe morphological changes on the surfaces of jarosite depending on interactions with different aqueous solutions, to study the mechanisms of dissolution and to compare dissolution rates of jarosites containing K+ and H3O+. The kinetic rates found for each jarosite compound were two orders of magnitude higher than those of Baron and Palmer [68] using the DVKM model, −6.84 and −6.35 for K+ and H3O+, respectively.
The dissolution rates of K-jarosite were also studied by Smith et al. [7] to simulate conditions similar to ARD/AMD sites and remediated sites, using pH values of 2 and 8 at 293.15 K. They noticed that Baron and Palmer [68] had studied dissolutions at low temperatures but without characterizing the solids produced at the end of the reaction. Even without investigating temperature and agitation, they suggested that the dissolution was controlled by mass transfer.
In Figure 2, equilibrium was reached by both Baron and Palmer et al. [68] and Smith et al. [7] with the same acid medium (HCl), same pH (2) and initial concentration (0.2 g/L), and similar temperatures (293.15 and 298.15 K, respectively). However, the time required to reach this quasi-equilibrium was approximately 80 days for Smith et al. [7] and 40 days for Baron and Palmer [68]. The concentrations at the end of dissolution were similar for iron (Fe), potassium (K), and sulfate
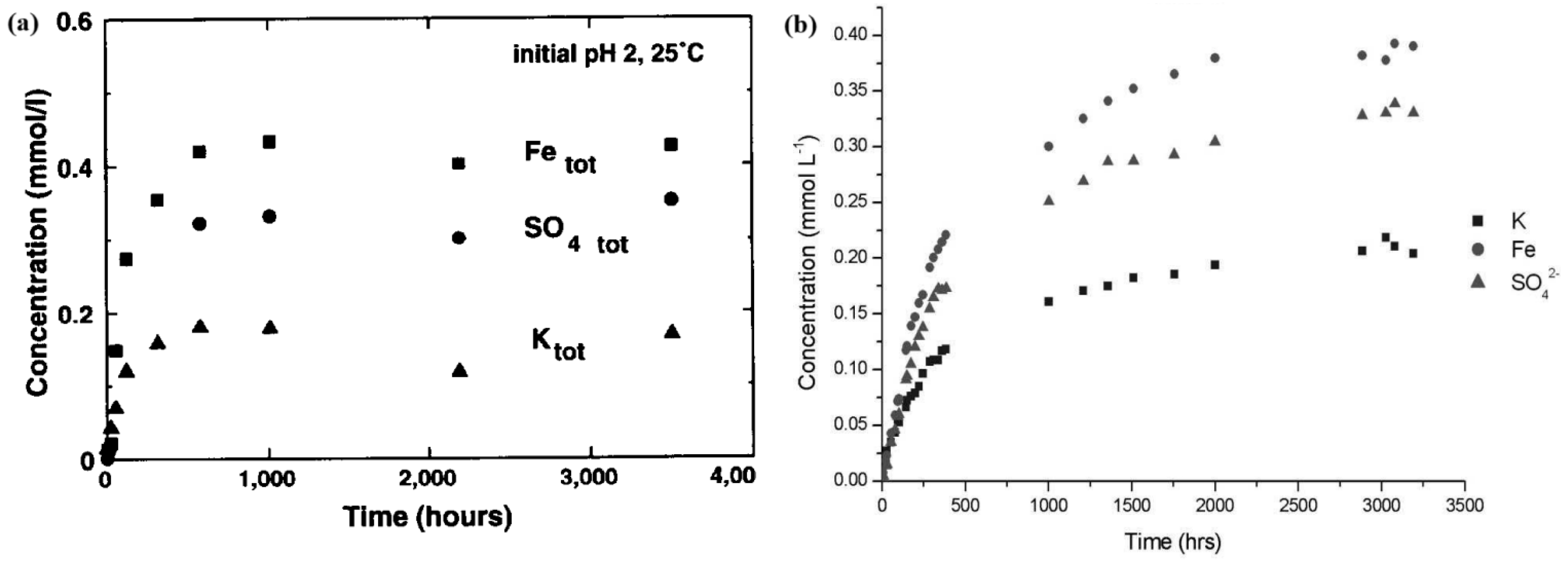
Dissolution curves of K-jarosite for (a) Baron and Palmer [68] and (b) Smith et al. [7] (Figures reprinted with permission from Elsevier).
Welch et al. [43] used higher pH values (3 and 4) to simulate ARD conditions in Australia using a natural sample. According to their observations, equilibrium was not reached after 12 days. Jarosite continued to dissolve for the rest of the year, though at a slower rate. Figure 3 shows dissolution kinetic curves at pH 3. Figure 3(a) shows kinetic data utilizing HCl, which promotes the release of elements in larger quantities, while H2SO4 (Figure 3b) produces a less pronounced release.
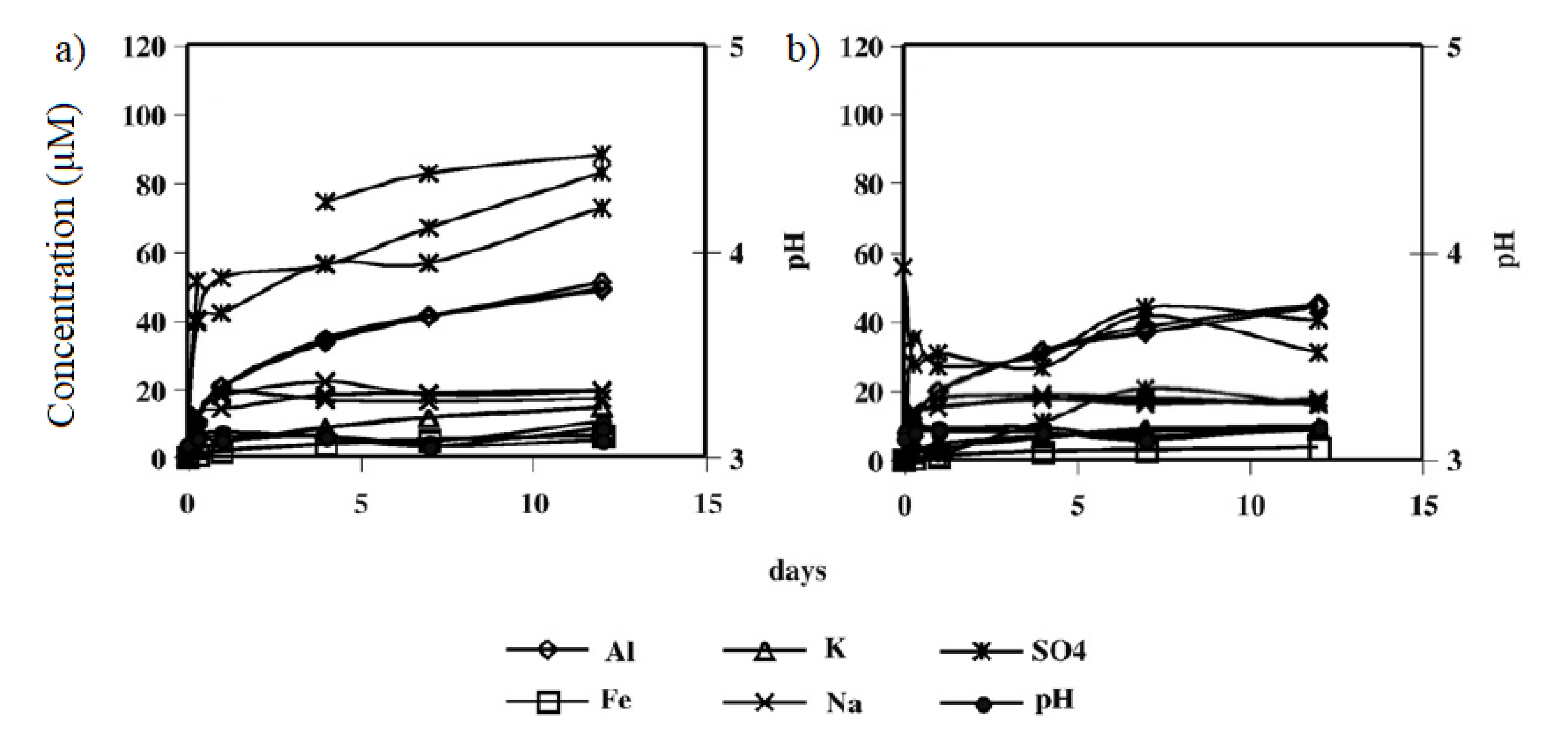
Dissolution curves of K-jarosite according to Welch et al. [43] at pH 3 using (a) HCl and (b) H2SO4 (Figures reprinted with permission from Elsevier).
Elwood Madden et al. [109], Pritchett et al. [110], and Legett et al. [111] simulated conditions closely resembling those found on Mars with different pH, temperatures, and salinities for the dissolution of K-jarosite, and Zahai et al. [112] for Na-jarosite.
Elwood Madden et al. [109] studied the effect of pH (1 to 10) and temperature (277.15 to 323.15 K) on the initial kinetic rates of K-jarosite dissolution. Their objective was also to investigate morphologies and reaction products. Linear regression on rates found from experiments resulted in a value of Ea = 79 kJ/mol, applying the Arrhenius equation. Moreover, a Type V behavior was found where the lowest rate is at pH 3.5, but the rate increases either by increasing aH+ (pH < 3.5) or increasing aOH- (pH > 3.5). A general trend of the Elwood-Madden et al. data [109] can be observed in Figure 4.
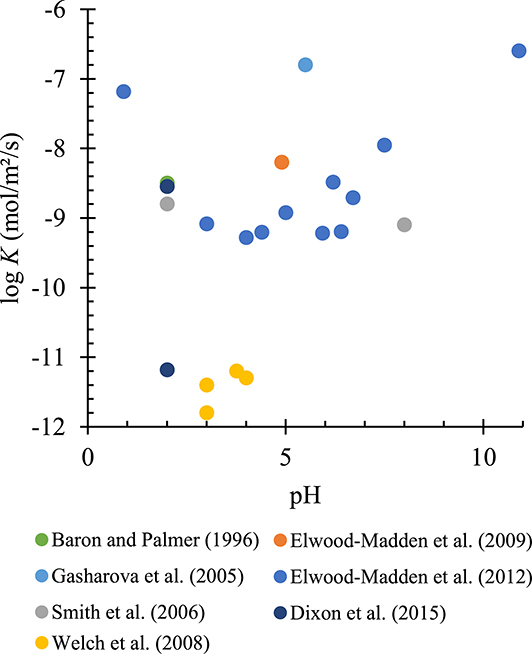
Variation of the dissolution rate (mol/m2/s) of K-jarosite with pH at room temperature (293.15–298.15 K).
Kendall et al. [44] used the same conditions as Smith et al. [7] but added a third scenario in which a sudden input of fresh water (ultrapure water) was considered, using As-jarosite to compare with K-jarosite dissolution in a sulfuric acid medium. They observed a faster release of K+ during the first two hours, followed by a decrease in speed. Regarding Fe3+, its release proved faster after the first day, exceeding the potassium concentration. Despite the effect observed by Welch et al. [43], where dissolution kinetics are faster for chloride environments than for sulfuric environments, Kendall et al. [44] reached equilibrium in 14 days of experimentation, much faster than Baron and Palmer [68] or Smith et al. [7], challenging the accuracy or reliability of the results obtained by Kendall and collaborators.
Similar to Baron and Palmer [68], the dissolution rate studies mentioned above used batch reactors that do not take reactive transport into account, a critical aspect in environmental geochemistry [46, 113]. Therefore, more recent research in this field has studied the dissolution process in continuous flow reactors to consider the effect of liquid flowing.
Dixon et al. [42] studied the dissolution rates of jarosite in circulation reactors, showing that dissolution rates are not affected by the flow rate, but they did not explore the relationship with pH. Meanwhile, Qian et al. [114] studied the dissolution of natural jarosite under quiescent solution conditions using non-stirred batch reactors and column leaching experiments. They reported slower dissolution rates than those observed using dissolution methods in stirred reactors.
However, the use of gravity-driven column leaching experiments, while more realistic, did not allow control over mass transport conditions within the column. Noticing this lack of information, Trueman et al. [46] investigated the dissolution of jarosite in a circulation reactor with a constant flow rate and at various pH levels.
All these studies provided useful insights under a range of different conditions such as pH, temperature, and salinity. However, varying orders of magnitude were found for the dissolution rate because of differing experimental conditions or mineral samples.
As an example, Figure 4 illustrates the variation in dissolution rate values of K-jarosite with pH for reactions in batch reactors at room temperature (293.15–298.15 K).
Figure 4 shows the variation in rate even for similar conditions of pH and temperature, the most important parameters for jarosite dissolution. These variations are likely due to the nature of jarosite (natural or synthetic), its structure and ion substitution, differing solid/liquid ratios, stirring speeds, and the duration of dissolution monitoring (several authors, such as Elwood Madden et al. [109] or Kendall et al. [44], have used only the first two hours, which increases the rate for potassium ions). In Table 2, the different studies in batch reactors (or AFM study, used by Gasharova et al. [45]) are gathered along with their main parameters and results.
Kinetic data (logr) of jarosite dissolution
| aH 2O | Initial pH | T (K) | Solution | logra | Authors | Element |
|---|---|---|---|---|---|---|
| K-jarosite | ||||||
| 1 | 1.97 | 296.15 | H2SO4 | −11.18 | Dixon et al. [42] | K+ |
| 1 | 1.97 | 296.15 | H2SO4 | −11.19 | Dixon et al. [42] | Fe3+ |
| 1 | 8 | 296.15 | Tris | −7.95 (0.13) | Kendall et al. [44] | K+ |
| 1 | 6 | 296.15 | Water | −9.20 (0.05) | Kendall et al. [44] | K+ |
| 1 | 2 | 296.15 | H2SO4 | −9.10 (0.00) | Kendall et al. [44] | Fe3+ |
| 1 | 2 | 296.15 | H2SO4 | −8.42 (0.03) | Kendall et al. [44] | K+ |
| 0.75 | N.D. | 273.15 | NaCl | −9.94(0.09) | Pritchett et al. [110] | K+ |
| 0.35 | N.D. | 273.15 | CaCl2 | −11.51(0.05) | Pritchett et al. [110] | K+ |
| 0.75 | N.D. | 263.15 | NaCl | −11.55(0.00) | Pritchett et al. [110] | K+ |
| 1 | 6.4 | 280.15 | Water | −9.71 (0.16) | Elwood Madden et al. [109] | K+ |
| 1 | 6.8 | 296.15 | Water | −9.2 (0.05) | Elwood Madden et al. [109] | K+ |
| 1 | 5.9 | 313.15 | Water | −8.59 (0.03) | Elwood Madden et al. [109] | K+ |
| 1 | 6.4 | 323.15 | Water | −7.15 (0.08) | Elwood Madden et al. [109] | K+ |
| 1 | 0.9 | 296.15 | H2SO4 | −7.18 (0.06) | Elwood Madden et al. [109] | K+ |
| 1 | 2 | 296.15 | H2SO4 | −8.54 (0.06) | Elwood Madden et al. [109] | K+ |
| 1 | 3 | 296.15 | H2SO4 | −9.08 (0.05) | Elwood Madden et al. [109] | K+ |
| 1 | 4 | 296.15 | H2SO4 | −9.28 (0.02) | Elwood Madden et al. [109] | K+ |
| 1 | 5.9 | 296.15 | NaOH | −9.22 (0.18) | Elwood Madden et al. [109] | K+ |
| 1 | 6.4 | 296.15 | NaOH | −9.20 (0.10) | Elwood Madden et al. [109] | K+ |
| 1 | 7.1 | 296.15 | NaOH | −8.92 (0.05) | Elwood Madden et al. [109] | K+ |
| 1 | 9.6 | 296.15 | NaOH | −8.71 (0.09) | Elwood Madden et al. [109] | K+ |
| 1 | 10.9 | 296.15 | NaOH | −6.60 (0.07) | Elwood Madden et al. [109] | K+ |
| 1 | 6.3 | 296.15 | MES | −8.49 (0.07) | Elwood Madden et al. [109] | K+ |
| 1 | 7.9 | 296.15 | MES | −7.95 (0.13) | Elwood Madden et al. [109] | K+ |
| 1 | 4.3 | 296.15 | Water | −9.1 (0.4) | Elwood Madden et al. [115] | K+ |
| 1 | 4.9 | 296.15 | Water | −8.2 (0.5) | Elwood Madden et al. [115] | K+ |
| 1 | 2 | 293.15 | HClO4 | −8.8 | Smith et al. [7] | K+ |
| 1 | 8 | 293.15 | Ca(OH)2 | −9.1 | Smith et al. [7] | K+ |
| 1 | 3.76 | 298.15 | Water | −11.2 (0.1) | Welch et al. [43] | K+ |
| 1 | 4 | 298.15 | HCl | −11.3 (0.9) | Welch et al. [43] | K+ |
| 1 | 3 | 298.15 | HCl | −11.4 (0.4) | Welch et al. [43] | K+ |
| 1 | 4 | 298.15 | H2SO4 | −11.3 (0.5) | Welch et al. [43] | K+ |
| 1 | 3 | 298.15 | H2SO4 | −11.8 (0.3) | Welch et al. [43] | K+ |
| 1 | 5.5 | 298.15 | Water | −6.8 (0.4) | Gasharova et al. [45] | K+ |
| 1 | 2 | 298.15 | HClO4 | −8.5 (0.03) | Baron and Palmer [68] | K+ |
| Na-jarosite | ||||||
| N.D. | 5.7 | 277.15 | Water | −9.29(0.20) | Zahrai et al. [112] | Na+ |
| N.D. | 8.1 | 295.15 | Water | −8.85(0.06) | Zahrai et al. [112] | Na+ |
| N.D. | 1 | 295.15 | H2SO4 | −6.98(0.06) | Zahrai et al. [112] | Na+ |
| N.D. | 2 | 295.15 | H2SO4 | −6.85(0.35) | Zahrai et al. [112] | Na+ |
| N.D. | 8 | 295.15 | Tris+HCl | −7.22(0.16) | Zahrai et al. [112] | Na+ |
| N.D. | 10 | 295.15 | Tris | −6.93(0.06) | Zahrai et al. [112] | Na+ |
| N.D. | 5.7 | 323.15 | Water | −7.89(0.35) | Zahrai et al. [112] | Na+ |
| 0.75 | N.D. | 273.15 | CaCl2 | −10.58(0.38) | Pritchett et al. [110] | Na+ |
| 0.35 | N.D. | 273.15 | CaCl2 | −11.19(0.17) | Pritchett et al. [110] | Na+ |
aThe values in parentheses represent the standard deviation among repeated experiments.
Buffers: Tris (Tris(Hydroxymethyl)aminomethane) and MES (2-(N-morpholino)ethanesulfonic acid).
3.2. Kinetics of jarosite industrial dissolution
Numerous efforts have been made to examine the impacts of chemical composition, temperature, pH, and particle size on dissolution rates in various reactive industrial environments. Due to the growing interest in the recovery of strategic metals from industrial residues containing Zn, as well as other high-value metals such as Pb, Cu, Ag, Cd, Co [61, 116], several leaching agents have been used as promising alternatives to recovery processes. Meanwhile, others authors have focused on avoiding the release of toxic metals in industrially precipitated jarosite.
The shrinking core kinetic model (SCKM) has been widely utilized over the past thirty years to describe the decomposition kinetics of jarosite-type compounds by evaluating decomposition conditions in order to prevent environmental issues and recover high-value metals such as silver. Primarily, researchers have used an alkaline medium as lixiviant in numerous studies regarding jarosites containing silver [117, 118, 119, 120, 121, 122, 123, 124], prompting many studies in alkaline environments (NaOH/Ca(OH)2). In these dissolutions, jarosite decomposition typically occurs between 323.15 and 363.15 K, and silver is leached with or without cyanide. Other studies have also examined the release of minerals such as rubidium [125], arsenic [126, 127, 128], chromium [129, 130] mercury [131], and thallium [67]. However, in recent years, attention has also been given to the use of various acids as a decomposition medium, as evidenced in Table 3 where conditions are displayed, as well as the activation energies and reaction order for both the induction and progressive periods.
Literature using the shrinking core kinetic model to describe the dissolution of jarosite-type compounds
| Authors using a basic medium | Jarosite type | Leaching medium | T (K) | Ea,pro (kJ/mol) | npro | Ea,ind (kJ/mol) | nind |
|---|---|---|---|---|---|---|---|
| Roca et al. [117] | [Ag0.78(H3O)0.22]Fe3(SO4)2(OH)6 | NaOH | 323.15 | 42.00 | 0.50 | 71.00 | 0.50 |
| Ca(OH)2 | 323.15 | 42.00 | 0.00 | 71.00 | 0.00 | ||
| Patiño et al. [119] | Pb0.32Ag0.011(H3O)0.35]Fe3(SO4)2(OH)6 | NaOH | 323.15 | 53.00 | 1.00 | N.D. | N.D. |
| Ca(OH)2 | 323.15 | 47.00 | 0.00 | N.D. | N.D. | ||
| Patiño et al. [120] | [Na0.675Ag0.005(H3O)0.32]Fe3(SO4)2(OH)6 | NaOH | 308.15 | 96.00 | 0.40 | 84.00 | 0.90 |
| Ca(OH)2 | 308.15 | 47.00 | 0.50 | 84.00 | 0.70 | ||
| Cruells et al. [122] | [K0.91Ag0.007(H3O)0.83]Fe3(SO4)2(OH)6 | NaOH | 303.15 | 43.00 | 0.60 | 86.00 | 0.70 |
| Ca(OH)2 | 303.15 | 80.00 | 0.50 | 36.00 | 0.20 | ||
| Salinas et al. [123] | [Ag0.001Na0.07K0.02Pb0.007(NH4)0.59(H3O)0.31]Fe3(SO4)2(OH)6 | NaOH | 308.15 | 77.00 | 1.10 | 88.00 | 1.40 |
| NaOH/NaCN | 308.15 | 46.00 | 0.80 | 154.00 | 3.20 | ||
| Patiño et al. [121] | [(NH4)0.71Ag0.040(H3O)0.24]Fe2.85(SO4)2(OH)5.50 | Ca(OH)2 | 308.15 | 70.00 | 0.40 | N.D. | N.D. |
| Ca(OH)2/NaCN | 308.15 | 29.00 | 0.65 | N.D. | N.D. | ||
| Roca et al. [118] | [(NH4)0.71Ag0.040(H3O)0.25]Fe2.85(SO4)2(OH)5.50 | NaOH | 303.15/323.15 | 60.00 | 0.60 | 80.00 | 0.75 |
| NaOH/NaCN | 52.00 | 0.00 | 54.00 | 0.50 | |||
| Reyes et al. [132] | [Na0.87(H3O)0.13]Fe2.5(SO4)1.95(AsO4)0.05[(OH)4.45(H2O)1.55] | NaOH | 303.15 | 57.10 | 0.70 | 120.40 | 1.00 |
| Ca(OH)2 | 303.15 | 48.60 | 1.51 | 79.40 | 0/1 | ||
| Perez-Labra et al. [125] | Rb0.9432Fe3(SO4)2.1245(OH)6 | Ca(OH)2 | 298.15 | 98.70 | 0.43 | N.D. | N.D. |
| Flores et al. [126] | [K0.75(H3O)0.25]Fe1.84(SO4)1.82(AsO4)0.18[(OH)2.34(H2O)3.66] | NaOH | 60.30 | 1.86 | 84.70 | 2.65 | |
| Ca(OH)2 | 74.40 | 1.14 | 88.30 | 0.24 | |||
| Patiño et al. [127] | [Na0.87(H3O)0.13]Fe2.50(SO4)1.95(AsO4)0.05[(OH)4.45(H2O)1.55] | NaOH | 303.15 | 57.11 | 0.746/0 | 118.11 | 1.06 |
| Ca(OH)2 | 303.15 | 48.22 | 1.56 | 73.50 | 1.03 | ||
| Patiño et al. [133] | KFe3(SO4)1.82(AsO4)0.18(OH)5.82 | NaOH | 303.15 | 60.30 | 1.86 | 84.60 | 0.23/2.65 |
| Ca(OH)2 | 303.15 | 74.40 | 1.15 | 88.20 | 0.24/0 | ||
| Méndez et al. [128] | [(NH4)0.23K0.77]Fe2.47(SO4)1.69(AsO4)0.31[(OH)4.01(H2O)1.59] | NaOH | N.D. | N.D. | N.D. | N.D. | N.D. |
| Islas et al. [134] | Tl0.86(H3O)0.25Fe3.11(SO4)2.11[(OH)6.11(H2O)0.44] | NaOH | N.D. | N.D. | N.D. | N.D. | N.D. |
| Mireles et al. [129] | [K0.86(H3O)0.14]Fe2.67[(SO4)1.23(CrO4)0.77][(OH)5.01(H2O)0.99] | Ca(OH)2 | 51.56 | 1.99 | 63.75 | 0.67 | |
| González-Ibarra et al. [135] | AgFe3(SO4)2(OH)6 | NaOH | 303.15 | 40.42 | N.D. | N.D. | N.D. |
| Ca(OH)2 | 303.15 | 21.72 | N.D. | N.D. | N.D. | ||
| Reyes et al. [130] | [K. (H3O)]Fe3[(SO4)2−x(CrO4)x][(OH)6(H2O)n] | NaOH | 75.70 | 1.10 | 82.70 | 1.10 | |
| Ordonez et al. [131] | Hg0.39(H3O)0.22Fe2.71(SO4)2.17[(OH)4.79(H2O)2.09] | NaOH | 303.15 | 56.90 | 0.99/0 | 81.70 | 0.52/1.48 |
| Tl0.86(H3O)0.14Fe3.11(SO4)2.11(OH)6.11(H2O)0.44 | NaOH | 303.15 | 91.90 | 1.10 | 101.60 | 1.10 | |
| Islas et al. [67] | Hg0.39(H3O)0.22Fe2.71(SO4)2.17(OH)4.79(H2O)2.09 | NaOH | 303.15 | 56.90 | 0.99 | 81.70 | 1.48 |
| Pb0.48(H3O)0.04Fe2.97(SO4)1.93(OH)6.05(H2O)0.6 | NaOH | 303.15 | 85.20 | 0.74 | 66.40 | 1.19 | |
| Pb0.39(H3O)0.22Fe2.89(S0.92As0.08O4)2(OH)5.51(H2O)0.49 | NaOH | 303.15 | 66.10 | 0.99 | 96.90 | 2.40 | |
| Islas et al. [136] | (Na0.96Ag0.04)Fe2.82(SO4)2.01(OH)5.36(H2O)0.86 | NaOH/CN− | 303.15 | 46.30 | 0.61 | 69.80 | 0.66 |
|
|
303.15 | 53.30 | 0.51 | 70.10 | 0.51 | ||
| NaOH/SCN− | 303.15 | 45.10 | 0.60 | 71.50 | 0.59 | ||
| Flores et al. [137] | [(NH4)0.72Na0.06(H3O)0.21]Fe3(2.52)(SO4)1.85(AsO4)0.15[(OH)4.41(H2O)1.59] | NaOH/CN | 303.15 | 51.60 | 0.94 | 65.00 | 1.22 |
| Authors using an acidic medium | Jarosite type | Leaching medium | T (K) | Ea,pro (kJ/mol) | npro | Ea,ind (kJ/mol) | nind |
| Calla-Choque [138] | Ag/Cu | Thiourea | N.D. | N.D. | N.D. | N.D. | N.D. |
| Reyes et al. [130] | [K. (H3O)]Fe3[(SO4)2−x(CrO4)x][(OH)6(H2O)n] | HCl | 303.15/323.15 | 68.03 | 1.2 | 109.4 | 1.05/0.47 |
| Reyes et al. [61] | [(M. H3O)]Fe3[(S1−xAsxO4)2][(OH)6(H2O)n] | H2SO4 | 303.15/323.15 | 77.9 | 1.2 | 66.8 | 1 |
| Tl0.86(H3O)0.14Fe3.11(SO4)2.11(OH)6.11(H2O)0.44 | H2SO4 | 303.15 | 58.4 | 1.07 | 55.9 | 0.9 | |
| Islas et al. [67] | Hg0.39(H3O)0.22Fe2.71(SO4)2.17(OH)4.79(H2O)2.09 | H2SO4 | 303.15 | 83.5 | 0.98 | 61.2 | 0.98 |
| Pb0.48(H3O)0.04Fe2.97(SO4)1.93(OH)6.05(H2O)0.6 | H2SO4 | 303.15 | 63.3 | 1.01 | 55.9 | 1.1 | |
| Pb0.39(H3O)0.22Fe2.89(S0.92As0.08O4)2(OH)5.51(H2O)0.49 | H2SO4 | 303.15 | 77.3 | 1.05 | 35.1 | 0.99 | |
| Calla-Choque and Lapidus [124] | Ag | Thiourea et Oxalate | N.D. | N.D. | N.D. | N.D. | N.D. |
| Calla-Choque and Lapidus [139] | NaFe3(SO4)2(OH)6, Ag | Thiourea et Oxalate | 303.15 | 44 | N.D. | N.D. | N.D. |
| Nolasco et al. [140] | [Na0.70(H3O)0.30][Fe2.95Cu0.042](SO4)2.25[(OH)5.46(H2O)0.54] | H2SO4 | 323.15 | 57,9 | 1,1 | N.D. | N.D. |
3.2.1. Dissolution through alkaline medium
One of the first team to study this dissolution was Roca et al. [117], who utilized NaOH and Ca(OH)2 as basic medium, temperatures ranging from 298.15 to 333.15 K, and NaCN concentrations from 5 to 30 mM. Subsequently, Patiño et al. [119] investigated the cyanidation–decomposition of Pb-jarosite containing silver, also using both alkaline media because this type of jarosite is commonly found in Nature and industrial processes.
Later, Patiño et al. [120] examined the decomposition of silver-containing Na-jarosite with cyanidation. They obtained activation energies of 96 kJ/mol for the NaOH medium and 39.6 kJ/mol for the Ca(OH)2 medium. Additionally, they found that the addition of salts such as NaCl or Na2SO4 increased the reaction rate for the experimental conditions used.
Cruells et al. [122] studied the decomposition of silver-containing K-jarosite using the same media. They obtained activation energies of 86 kJ/mol for the NaOH medium and 36 kJ/mol for the Ca(OH)2 medium. When coupling with cyanidation (CN−), the activation energy decreased to 43 kJ/mol for NaOH and increased to 80 kJ/mol with Ca(OH)2.
Salinas et al. [123] investigated alkaline (NaOH) decomposition coupled with cyanidation of NH4-jarosites containing silver. When only NaOH was utilized, the activation energy rose to 77 kJ/mol, while coupling with CN− reduced the energy to 46 kJ/mol.
Patiño et al. [121] studied silver-containing NH4-jarosite using Ca(OH)2. They found an activation energy of 70 kJ/mol using only the base and 29 kJ/mol adding CN−. The decomposition rates were higher than those of jarosites produced during the zinc hydrometallurgical process. Roca et al. [118] used the same type of jarosite as Patiño et al. [121] and studied its decomposition in a cyanide and alkaline environment using NaOH instead of Ca(OH)2. The activation energy for the induction period was higher than for the progressive conversion period. The activation energies for the progressive period were 60 kJ/mol without cyanide and 52 kJ/mol with cyanide. They confirmed a trend of reduced activation energy using cyanidation, as already observed by Salinas et al. [123].
González-Ibarra et al. [135] investigated the kinetic decomposition of an industrial jarosite using both NaOH and Ca(OH)2 as well as cyanidation. They succeeded in increasing silver recovery by coupling alkalinity with cyanidation. When using NaOH, kinetics were controlled by the chemical reaction stage, while using Ca(OH)2, diffusion through a passivation layer of CaCO3 played a crucial role, and the activation energies were 40.42 and 21.72 kJ/mol, respectively.
Islas et al. [136] studied the leaching of silver in jarosites using non-cyanide complexing agents such as thiosulfate
Reyes et al. [132] studied the reactivity of Na-jarosites containing arsenic. They found activation energies of 57.11 kJ/mol for NaOH and 48.61 kJ/mol for Ca(OH)2. Flores et al. [126] investigated the decomposition of K-jarosites containing arsenic using NaOH and Ca(OH)2 media, with activation energies of 60.3 kJ/mol and 74.4 kJ/mol, respectively. This difference in activation energy between K- and Na-jarosite may be related to the fact that K-jarosite is more stable during dissolution than Na-jarosite.
Patiño et al. [127, 133] examined the decomposition of Na–As-jarosite in NaOH and Ca(OH)2 media, the former through a design of experiments approach and the latter using only the SCKM.
The first study reported the presence of unreacted As-jarosite and the formation of halos of Fe(OH)3 particles with adsorbed AsO4. Temperature and OH− concentration, as well as their combination, were the most influential parameters on the kinetics. The second study found activation energies of 60.3 kJ/mol and 74.4 kJ/mol for NaOH and Ca(OH)2 media, respectively. This corroborates the claim that activation energies are lower with NaOH than with Ca(OH)2, indicating easier dissolution when NaOH is used.
Méndez et al. [128] studied NH4–K-jarosite containing arsenic, and Flores et al. [137] investigated the decomposition of arsenic-containing NH4–Na-jarosite, both using NaOH medium. The controlling mechanism was the chemical reaction, and there was the formation of Fe(OH)3 with adsorbed arsenate. Flores and collaborators emphasized that using this type of jarosite is an alternative to arsenic removal from water because, even after decomposition, arsenic is retained in the residual solid.
Pérez-Labra et al. [125] synthesized rubidium jarosite and studied its decomposition in an alkaline solution containing five different concentrations of Ca(OH)2. The obtained solid residues incorporated calcium and formed goethite. The kinetic analysis could be modeled by the SCKM with the chemical reaction control stage, with an activation energy of 98.70 kJ/mol.
Islas et al. [134] studied the dissolution of thallium jarosite using NaOH, leading to the formation of an amorphous solid around the particle, likely containing hydroxide and thallium. The decomposition of this type of jarosite seems to be described by a constant particle size model, controlled by the chemical reaction.
Mireles et al. [129] analyzed the decomposition kinetics of chromium-containing jarosite in a Ca(OH)2 medium. Experimental data show that the reaction follows the SCKM with chemical reaction control. The activation energy was 63.75 kJ/mol for the induction period and 51.56 kJ/mol for the progressive period, and the reaction results in the formation of Fe(OH)3 residues.
Ordoñez et al. [131] dedicated their study to the decomposition of mercury jarosite in a NaOH medium. The activation energy was 81.70 kJ/mol for the induction period and 56.90 kJ/mol for the progressive period.
This section illustrates that the dissolution of various types of jarosite has been extensively studied, mainly utilizing NaOH and Ca(OH)2 as basic mediums. A trend was observed where reactions occurring in NaOH medium were less energy-dependent compared to those in Ca(OH)2 medium. Cyanidation was also employed to enhance the dissolution rate in basic medium. Moreover, other complexing agents (such as
3.2.2. Dissolution through acidic medium
More recently, acid dissolution has also attracted attention, given that jarosite is an acidic compound and requires a large amount of base for its dissolution process in a basic environment. Calla Choque et al. [138] were the first researchers to apply the SCKM to the acid decomposition of jarosite, coupling leaching with thiourea as a complexing agent to study the effect of different cations (Cu2+, Fe3+, Zn2+, Fe2+) in this system for silver recovery. They reported that acid decomposition would be an interesting alternative as jarosites are naturally acidic, meaning that process costs would be reduced.
Subsequently, Reyes et al. [130] studied the dissolution rates of K–Cr(VI)-jarosite in acidic (HCl) and basic (NaOH) environments to investigate the mobility of chromium under more extreme conditions (mostly at pH < 1 and T > 303.15 K). They suggested studying reactions at an intermediate pH (2 ⩽ pH ⩽ 10) because unreacted solids remain, and calculations must consider equilibrium.
While Reyes et al. [61] studied the dissolution kinetics of Na–As-, K–As-, and NH4–As-jarosites in sulfuric acid to determine the factors influencing the recovery of high-value metals by varying pH, temperature, particle size, and substitution at A- and C-sites of jarosite-type compounds. Sulfuric acid was chosen due to its lower cost and better compatibility with other reducing agents. Similar to their previous research, Reyes and collaborators used more extreme conditions to calculate condition parameters (mostly pH < 1 and T > 303.15 K) to obtain the final model. For pH < 1, they reported that the decomposition process follows the SCKM controlled by the chemical reaction stage. The authors demonstrated that, for the acidity levels used, ion substitution does not influence the dissolution rate.
Islas et al. [67] studied the dissolution of several jarosites containing potentially hazardous elements (Pb, As, Tl, Cr) in different conditions using the SCKM in basic (NaOH) and acidic (H2SO4) media. They demonstrated that the kinetics-controlling step is the chemical reaction at extreme pH levels (pH < 1), and mass transfer in the liquid phase when pH deviates towards less extreme values (1 < pH < 1.68).
Calla-Choque and Lapidus [139] undertook a study to analyze the effects of pH, temperature, and solid/liquid ratio on silver recovery from jarosite, employing complexing agents such as thiourea and oxalate. Their research highlights the use of oxalate in stabilizing thiourea within an acidic environment. The decomposition of jarosite releases powerful oxidants, mainly iron, inducing chemical instability and thiourea oxidation. Results showed improved recovery with a temperature increase from 323.15 to 333.15 K, pH reduction, and adjusting the solid/liquid ratio. In addition, when oxalate was used, thiourea degradation was minimized, consequently decreasing the temperature required for jarosite dissolution.
Calla-Choque and Lapidus [124] studied the dissolution rate with a non-homogeneous particle size system, unlike the approach in Reyes et al. [61], which used specific particle sizes, in the presence of oxalate and thiourea at different pH and temperatures. They modified the SCKM to account for particle size variation. According to Gbor and Jia [141], particle size distribution is of fundamental importance when evaluating kinetics with the SCKM. However, it is often disregarded, leading to erroneous conclusions about the control regime of the process.
Nolasco et al. [140] conducted jarosite dissolution in acidic conditions and investigated how the incorporation of divalent cations, such as Cu2+ and Fe2+, into jarosite structure affects the reaction rate. The SKCM was able to satisfactorily describe the leaching behavior of Na-jarosite containing copper under acidic conditions. According to authors, the nature of the central atom bonding (Fe–OH) within the jarosite structure plays an important role in acid dissolution. They suggested that the complete replacement of B-site by other trivalent cations could likely alter the dissolution rate.
Studies on dissolution rates in acidic medium are relatively recent in the literature but have reached a higher level of scientific maturity, partly due to the groundwork laid by studies conducted in basic mediums. Temperature, pH, particle size, ion substitution into jarosite structure, utilization of complexing agents, and use of different acids are the main parameters investigated. These studies reveal certain trends, such as the chemical kinetic control of the progressive period when extreme pH levels (<1.5) and temperatures (>323 K) are employed. However, further experiments are required to elucidate the behavior of the SCKM under conditions of less acidic pH (>1.5) and ambient temperature (∼295 K) during the experiments.
3.3. Natural and synthetic jarosites
Based on the kinetic studies previously presented in this section, it is noteworthy that the nature of the jarosite-type compound can impact the results. For this reason, this additional subsection on the dissolution kinetics presents some kinetic studies that synthesized jarosite-type compounds and the methodology used to achieve this synthesis. The use of synthesized methodologies allows other scientists to replicate the experiments and compare them with new dissolution conditions, for example. On the other hand, some authors have preferred the use of natural jarosite samples to replicate processes as they occur in the environment. However, natural jarosite often contains different amounts of other species that will influence the concentration of elements in aqueous solution. Additionally, the effect of the temporal alteration of rocks and minerals can also reduce the dissolution rate of this mineral.
3.3.1. Synthetic jarosites
The article by Driscoll and Leinze [142] is one of the most frequently used as a guideline for the synthesis of different types of jarosites within the scope of their work at the United States Geological Survey (USGS). Their method is based on the synthesis of K-jarosite as proposed by Baron and Palmer [68]. They mix 17.2 g of hydrated ferric sulfate (Fe2(SO4)3 ⋅ nH2O) and 5.6 g of potassium hydroxide (KOH) dissolved in 100 ml of 18 MΩ⋅cm ultrapure water. The solution is prepared on a hot plate at 368.15 K with stirring. Moderate boiling is maintained for 4 h; then, the solution is removed from the hot plate, and after decantation, the liquid phase is rinsed with deionized water. The washings are discarded, and the remaining solid is placed in a drying oven at 383.15 K for 24 h. After drying, the substance is recovered, in the form of a yellow-brown precipitate. Smith et al. [7], Elwood Madden et al. [109], Zahrai et al. [112], Pritchett et al. [110], Kendall et al. [44], and Dixon et al. [42] have used the method validated by Driscoll and Leinze [142].
As explained by Baron and Palmer [68], synthetic jarosite exhibits a potassium deficiency due to the substitution by hydronium ions (H3O+) in the alkali ion position. Various factors control this hydronium substitution, including pH and the activity of K+. To minimize this substitution and synthesize a product with a composition close to the ideal, it is necessary to add an excess amount of KOH, thereby increasing the activity of K+ and simultaneously reducing the concentration of H+.
Other authors have employed different methods for the production of K-jarosite. Gasharova et al. [45] based their synthesis on the one suggested by Fairchild et al. [143], in which crystallization at 423.15 K and 0.5 MPa occurs from an aqueous solution of K2SO4 and Fe2(SO4)3 in 1 N sulfuric acid. Jones et al. [144] synthesized jarosite according to the method of Dutrizac et al. [145], Dutrizac and Jambor [27], and Crabbe et al. [146], dissolving 6.4 g Fe2(SO4)3 ⋅ nH2O and 24 g HNO3 in 800 g deionized water, then adding 0.8 ml H2SO4 and heating at 363.15 K for 24 h. Brand et al. [147] used 1.74 g of Fe2(SO4)3 ⋅ 9H2O and 0.70 g of K2SO4 diluted in deionized water, reacting at 368.15 K for 5 h, then filtering through a syringe filter, obtaining a calculated composition of K0.9(H3O)0.1Fe2.39(SO4)2OH4.17(H2O)1.83. Reyes et al. [61] synthesized K-jarosite using the method of Patiño [127], which was based on that of Dutrizac et al. [148] for Na-jarosite. In this method, 1 L solution was used containing 0.3 mol/L of Fe2(SO4)3 ⋅ nH2O, 0.01 mol/L of H2SO4, 0.027 mol/L of Na2HAsO4 ⋅ 7H2O, and 0.2 mol/L of Z2SO4, where Z represents monovalent alkaline species Na+, K+,
3.3.2. Natural jarosites
Welch et al. [43] used natural jarosite samples [(K, H3O)Fe3(SO4)2(OH)6] from a degraded acidic sulfate soils site on the north coast of New South Wales, Australia, in order to determine experimentally the dissolution kinetics. Similarly, Qian et al. [114] and Trueman et al. [46] also used natural jarosite. Calla-Choque and Lapidus [124] used jarosite from a zinc leaching plant in Mexico.
It was evident that Welch and colleagues’ jarosite dissolved very slowly compared to synthetically prepared material in the study by Smith et al. [7]. Indeed, the solids presented different morphologies: euhedral [45] for natural jarosite or anhedral [7] for synthesized jarosite. The reactivity differences between synthetic mineral and naturally weathered samples have been documented for sulfates [149, 150] and silicate minerals [151, 152, 153], as indicated by Welch et al. [43].
According to White and Brantley [153], when studying silicate dissolution, the time dependency of silicate weathering can be discussed in intrinsic terms, as the surface area increases with the duration of weathering, accumulation of leached layers, and secondary precipitates. Alternatively, it can be discussed in extrinsic terms, as low permeability, high mineral/fluid ratios and increased solute concentrations, produce weathering reactions close to thermodynamic equilibrium under field conditions compared to highly unsaturated conditions during experimental reaction. These factors could explain the differences between dissolution rates of natural and synthesized samples.
4. Precipitation kinetics of jarosite-type compounds
4.1. Studies in abiotic environments at high temperatures
The precipitation of jarosite is of significant industrial interest due to the adoption of the industrial process known as the “Jarosite Process”. This process is employed for controlling hydrometallurgical impurities, primarily in zinc production. During its course, ferric iron precipitates in the form of jarosite, and zinc can be recovered. These processes are known to occur at elevated temperatures exceeding 363.15 K [27].
Dutrizac is one of the authors who has extensively researched the effects of conditions on the precipitation of various jarosite-compounds types in hydrometallurgical processes and their behavior in the presence of other elements in different reaction environments.
Dutrizac and Kaiman [154] initially worked on the synthesis of rubidium and thallium jarosite. Subsequently, Dutrizac et al. [145] investigated the conditions affecting the formation of Pb-jarosite, while Dutrizac [155] studied their formation in hydrochloric acid. Dutrizac and Dinardo [156] examined the coprecipitation of copper and zinc with Pb-jarosite.
Dutrizac and collaborators have also studied the behavior of several elements during the precipitation of jarosite compounds, including: selenate [157], mercury [158], cesium and lithium [159], silver [160], arsenic at 370.15 K from sulfate and hydrochloric acid medium [161] as well as at 423.15 K [148], cadmium [162], thiocyanate and cyanate [163], gallium [164], lanthanides [165], vanadium [166], rare earth elements [167], thallium (III) [168], chromium (III) [169, 170], germanium and tin [171], alkaline-earth elements (beryllium and radium) [172], halides (fluoride, chloride, bromide, and iodide) [173], scandium, yttrium, and uranium [174], selenium (VI) and selenium (IV) [175].
Among Dutrizac’s most important findings, in his study of the effects of alkaline precipitation of Na-jarosite, he demonstrates that alkali substitution in the jarosite structure and solid formation yields increase with an increase in alkali concentration in the precipitation solution. According to the author, seeding and ionic strength had little influence on the yield since for a 24 h reaction the iron-precipitated % remained almost constant. The author established that the stability of different precipitated jarosite types follows the order:
Limpo et al. [176] studied the influence of acidity, Fe3+ concentration, ammonia concentration, and seeding on the precipitation rate of Fe3+ as NH4-jarosite from solutions containing sulfuric acid at temperatures between 363.15 and 373.15 K. These authors observed that the control step was crystal growth, and the nucleation rate was proportional to the surface area of the solids introduced into the system, the ammonia concentration, and the concentration of the
The study of seeding at different temperatures was then undertaken and showed positive effects on precipitation rate. Teixeira and Tavares [177] conducted batch experiments to study the effect of seeding on the initial precipitation rate of NH4-jarosite, noticing a linear increase with the growing quantity of seeds. This trend proved valid for both high and low concentrations of Fe3+,
Dutrizac [178] investigated the effect of seeding on the precipitation of NH4-jarosite and Na-jarosite, connecting it to other factors such as pH, temperature, and concentrations of ferric sulfate. The experiments were conducted with a solution containing 0.30 M Fe(SO4)1.5, 0.30 M Na2SO4, a pH of 1.5, a temperature of 371.15 K, and agitation at 500 rpm, lasting around 8 h. His conclusions indicated that seeding promotes precipitation, where the initial rate increases linearly in the presence of seeds (from 0 to 100 g/L). The presence of seeds also broadens the jarosite precipitation range to lower pH and temperatures, thereby eliminating the induction time.
Among the discoveries he made, he determined that the activation energy of Na-jarosite in the presence of seeds was equal to 106 kJ/mol. The increase in temperature (from 353.15 to 373.15 K) and pH (from 1.10 to 2.00) favors precipitation. In order to calculate the initial kinetic rate, he fitted the data to a second-order polynomial and calculated the slope using the derivative kinetic method (DVKM) as explained in Section 3.
Dutrizac [178] also compiled apparent activation energy data published by different authors [179, 180, 181] up to that year, demonstrating the variety of results for different types of jarosite but always at high temperatures and using restricted temperature ranges.
Dutrizac [182] examined the factors influencing the precipitation of K-jarosite in a hydrochloric and sulfate medium. Subsequently, Dutrizac [183] compared the precipitation rates of NH4-jarosite and Na-jarosite in a ferric sulfate medium (0.30 M Fe(SO4)1.5/sulfuric acid) at a temperature between 343.15 and 373.15 K. The results showed an activation energy of 87 kJ/mol and indicated a faster precipitation of NH4-jarosite compared to Na-jarosite.
In the hydrometallurgical industry, significant efforts have been made to study the precipitation of jarosite at high temperatures in abiotic environments (>363.15 K), given that the majority of microorganisms are not capable of thriving at such high temperatures. However, the development of hydrometallurgy for the recovery of high-value metals has led to the creation of new processes operating at more moderate temperatures due to the use of a biotic medium. In this way, additional research has emerged to consider lower temperatures as can be seen in the next section.
4.2. Studies in biotic environments at low temperatures
Investigations aiming to understand the formation of jarosite under biotic environments and low temperatures, as well as the rate at which this reaction takes place, are necessary. Its precipitation can compromise the performance of recovering high-value metals. Additionally, understanding precipitation is very important since it can lead to the formation of diffusion barriers on mineral surfaces, impacting dissolution rate, reducing the concentration of ferric iron, hindering ore attack, and potentially trapping high-value metals, such as silver.
In this regard, researchers have dedicated their work to study the control of mineral formation, including jarosite, in the presence of microorganisms. The experimental results obtained in sulfate-rich bioleaching systems, studied by Toro [184], suggest the formation of jarosite at a 303.15 K in environments rich in Acidithiobacillus bacteria. In these systems, jarosite precipitation exhibits very favorable and non-selective kinetics regarding pH. This is attributable to the high concentration of iron (III), which promotes the formation of precipitation intermediates of this phase, as well as the presence of bacterial cells serving as surface for crystalline growth.
Wang et al. [185] synthesized schwertmannite and jarosite from solutions containing ferrous iron sulfate, inoculated with Acidithiobacillus ferrooxidans. Schwertmannite transformed into H3O–NH4-jarosite when the reaction time increased from 19 to 40 days, and the reaction temperature from 309.15 to 318.15 K, in acidic medium at pH 2.
Wang et al. [186] synthesized NH4-jarosite in the presence of microorganisms (A. ferrooxidans between 295.15 and 309.15 K, Sulfolobus metallicus at 318.15 K, and Acidithiobacillus caldus and Sulfobacillus spp. at 338.15 K) at temperatures ranging from 295.15 to 338.15 K and ferrous sulfate oxidation in pH ranging from 2 to 3, with varying concentrations of
Egal et al. [187] investigated arsenic trapping during Fe2+ oxidation in a medium containing Acidithiobacillus ferrooxidans. They found that the type of bacteria used favored the formation of tooeleite ore rather than schwertmannite, while jarosite formed without the need for bacteria at the end of the experiments (after 15 days).
Recently, process studies involving the oxidation of iron by archaea at 343.15 K in continuous reactor were undertaken by Kaksonen [188] as well as Kaksonen [189] in a two-stage airlift bioreactor, aiming to assess the performance of these reactors and their ability to separate the jarosite produced during the reaction.
4.3. Studies in abiotic environments at low temperatures
Despite the advancement of research in jarosite precipitation at low temperatures under biotic conditions, little data was found to understand jarosite precipitation at low temperatures without the influence of microorganisms. Consequently, new studies under these conditions have been initiated in the last few years.
Bigham et al. [190] characterized ferric iron precipitates in batch experiments conducted at temperatures ranging from 295.15 to 313.15 K, using ferric sulfate and mineral salts in sulfuric acid. The goal of these experiments was to simulate bioleaching solutions in an oxidizing environment containing K+, Mg2+, Ca2+, NO3−, and
According to Sasaki and Konno [192] and Wang [186], synthesis conditions play a crucial role in the structure and morphology of jarosite samples. They observed a tendency for the formation of more individual particles at higher temperatures. Some particles exhibited needle-shaped surface characteristics, which could be attributed to metavoltine formation.
However, based on the observation of surface morphology, these characteristics also resemble previous descriptions of schwertmannite [Fe8O8(OH)6(SO4)] [185, 186, 193]. The presence of schwertmannite is not observed in the diffractograms because this mineral is poorly crystallized, and its characteristic peaks are broad and masked by the sharper jarosite peaks. Similarly, the background noise in the diffractograms is directly proportional to the amount of poorly crystallized materials, including potentially schwertmannite.
As part of the study on jarosite formation under ambient-like conditions, Kim et al. [194] investigated the effects of the presence of oxyanions (
In jarosite samples with low precipitation rates and low crystallinity, the amorphous phase contained high concentrations of oxyanions, likely due to the rapid precipitation of the amorphous phase of iron oxyanions. The results demonstrated that jarosite coprecipitation could play a more significant role in controlling the behavior of
These studies conducted at low temperatures and in the absence of microorganisms show that the parameters employed during precipitation experiments have an impact not only on the crystallinity and surface characteristics of particles, but also on the formation of additional mineral phases. It indicates the importance of solid analysis to understand the phenomenon and highlights the challenge in characterizing ferric iron phases. Further research is warranted to evaluate the kinetics of jarosite formation and improve the comprehension of its formation reaction.
5. Characterization of the solid phases of jarosite
Solid analyses are crucial in evaluating jarosite-type compounds, given the diversity of jarosites that can exist both in Nature and in industrial processes. This variety leads to complex solid structures, different morphologies, and surfaces. The inherent complexity of these variations makes the identification of these compounds challenging.
Among the commonly employed methods for the identification and assessment of jarosites, scanning electron microscopy (SEM) and X-ray diffraction (XRD) appear indispensable.
The study of the dissolution and precipitation of jarosite-type compounds has resulted in different X-ray diffractograms and varied SEM images. As an example, in Figure 5, two completely different jarosite morphologies are presented.

SEM of synthetic anhedral jarosite (a) by Smith et al. [7] and natural euhedral jarosite (b) by Welch et al. [43] (Figures reprinted with permission from Elsevier).
In Figure 5(a), jarosite exhibits an irregular and globular shape with various grain sizes, most measuring between 1 and 5 μm. Some grains show cleaved sides, which may be signs of mechanical abrasion resulting from agitation during synthesis [7]. Similar particle morphologies for synthetic jarosite have been reported elsewhere [194]. On the other hand, in Figure 5(b), using a natural sample, Welch et al. [43] observed a relatively euhedral shape for jarosite, with a grain size ranging from 0.5 to 5 μm. Qian et al. [114] also used euhedral Na-jarosite, indicating a highly crystalline phase, similar to Gasharova et al. [45].
According to Sasaki and Konno [192], particle morphology is also influenced by cations in the A-site. K-jarosite exhibits a round shape, while NH4-jarosite manifests as an agglomeration of pseudo cubic particles. The anhedral and euhedral natures of different samples can lead to varying dissolution rates. Another example illustrating these differences concerns the evolution of the morphology of jarosites synthesized by Reyes et al. [130] as the amount of chromium in the structure increases. The morphology evolves from Figure 6a/b to Figure 6c/d.
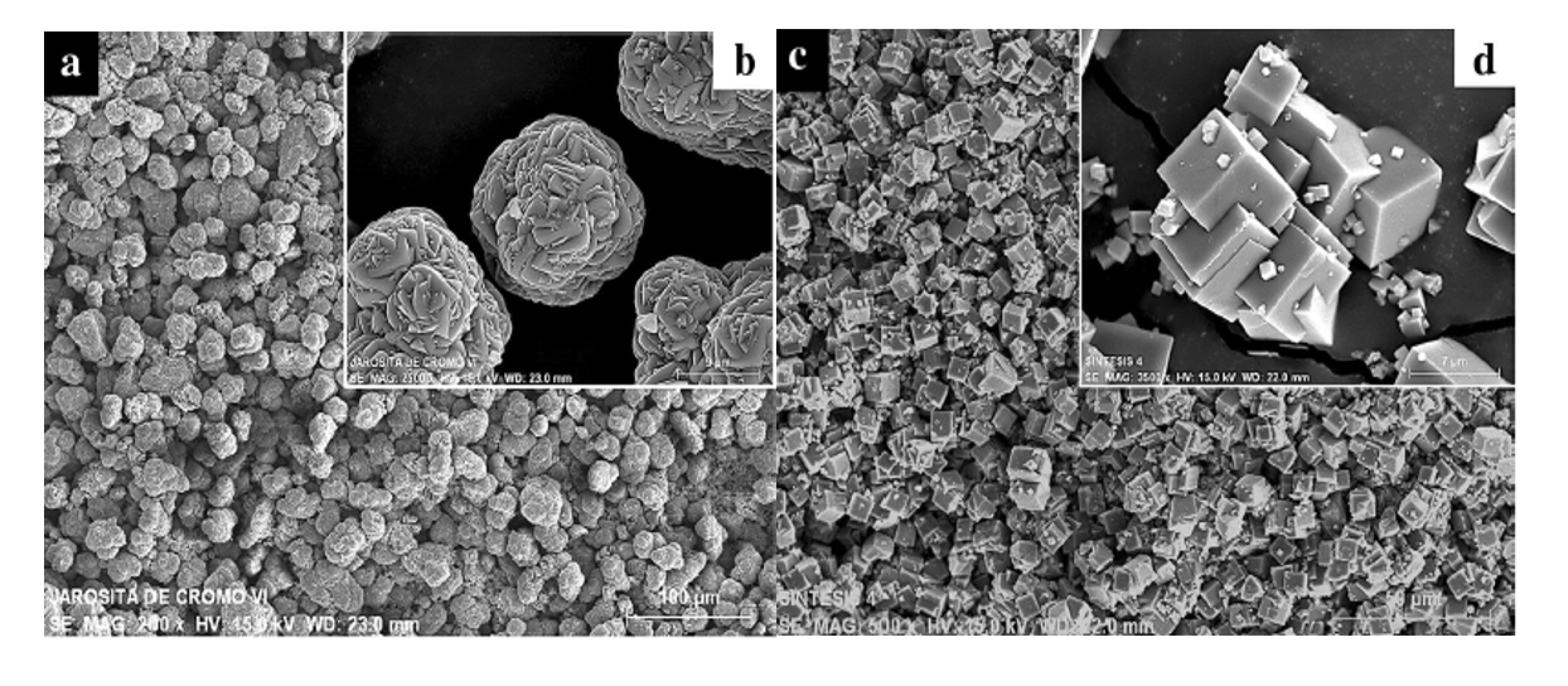
Cr-jarosites synthesized with increasing amounts of chromium by Reyes et al. [130] (Figures reprinted from open access article).
Due to these differences, the use of solid analyses is essential to understand the morphologies and structures of this type of mineral, as well as to assess how they may influence the thermodynamic and kinetic data of precipitation/dissolution of these solids.
6. Conclusion and perspectives
The bibliographic review presented in this article traces the evolution of the existing research on jarosite dissolution and precipitation, initially aimed at understanding the structure of jarosite and its presence in the environment. Subsequently, these studies focused on acquiring thermodynamic and kinetic data related to the formation and dissolution of jarosite compounds.
The entirety of this literature review highlights a marked diversity in existing results. Among these, significant divergences and gaps have been identified:
- A major issue arising from these published data is the difficulty in obtaining thermodynamic and kinetic data due to the time required to reach equilibrium under the conditions used. To circumvent long-duration experiments, a trend has emerged favoring studies under more extreme conditions (high temperature and low pH) that promote faster dissolution or precipitation.
- When less favorable reaction conditions were employed, shortcuts such as using the first few hours of the reaction were employed to describe the kinetics. This time lapse, varying according to the application and conditions, proves insufficient to predict the behavior of jarosite compound kinetics. This is due to both reactions (dissolution and precipitation) requiring extended times, leading to solution evolution, and the transformation of solids in terms of structure and morphology.
- The transformations undergone can result sometimes in poorly crystalline solids with different morphologies, which can influence the data obtained. Therefore, the use of solid analysis methods is crucial for a correct understanding of the results and for comparison with previous findings.
- The disparity in kinetic data highlights that using different precipitation methodologies in order to produce jarosite solids for dissolution studies could introduce errors, as the solids may vary, and complicate the comparison between studies.
- The diversity of jarosite structures observed in the environment and in industry also places constraints on comparisons between experiments, as ions incorporated into their structure can alter kinetics and thermodynamic properties.
- Comparing these results is further complicated by the choice of thermodynamic and kinetic models, along with their inherent limitations in accurately characterizing the intricate reactive mechanisms of jarosite compounds.
However, where difficulties persist, opportunities to discover mechanisms, characterize behaviors, improve existing data, and resolve contradictions emerge.
- The challenge for further kinetic studies of jarosite lies primarily in understanding the dissolution and precipitation reaction mechanisms at temperatures closer to room temperature, conditions under which most jarosites form in the environment and where some industrial processes take place.
- The studies must take into account the evolution of precipitated and dissolved solids over time.
- It seems fundamental to understand how the precipitation methodology can influence the synthesized solid and how morphology can play a significant role in dissolution.
- The use of different models to describe both phenomena (dissolution/precipitation) is important. The use of models that connect the thermodynamic and the kinetic aspects, such as the Transition State Theory, widely used by geochemists, would be of great value to facilitate the control of the kinetics using the thermodynamics of solutions.
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.





 CC-BY 4.0
CC-BY 4.0