Superconductivity has now been seen in a broad range of materials, including many examples of molecular metals. It is useful in trying to understand the origins of the superconductivity in such molecular systems to search for trends that might exist across the broad class of molecular superconductors, independent of the finer details of each system. Such universal trends could present valuable pointers towards the underlying mechanisms responsible for the superconductivity, giving guidance for developing theories of superconductivity and providing a stringent test for ‘good’ theories.
One trend in superconducting properties that was originally identified from μSR studies of high Tc cuprate superconductors is the Uemura law [1] describing a linear scaling between the two primary experimental observables of a superconductor: ρs, the strength of a superconductor against applied magnetic fields (ρs = c2/λ2, where λ is the penetration depth), and Tc, the superconducting transition temperature, which is related to the energy scale of the pairing interactions. This scaling applies in the underdoped region of cuprate superconductors where a local pairing model might be considered more appropriate and one interpretation of the law follows from noting that both the Bose–Einstein Condensation (BEC) temperature of preformed pairs in the 2D layered case and also ρs are proportional to the carrier concentration [2].
Although at first sight the molecular superconductors appeared to be consistent with the linear Uemura scaling [2], closer investigation of μSR data across a wider range of molecular superconductors suggested a scaling law better described as something closer to Tc ∝ ρs3/2 or equivalently Tc ∝ λ−3 (Fig. 1a) [3,4]. The presence of any such Uemura-style scaling law in the molecular systems is actually quite remarkable, since the nominal carrier concentration hardly varies across the family, unlike the case of the high Tc cuprates where carrier doping controls the properties. From consideration of these scaling properties it was concluded that one possible explanation is that the effective superconducting carrier concentration is significantly reduced in the lower Tc molecular systems [4–6]. Departures from the Uemura scaling were also considered in the BEC scenario [2], where dimensionality effects on the carrier dispersion and differences in inter-site hopping between single carriers and carrier pairs in boson-fermion models were identified as possible factors [4].
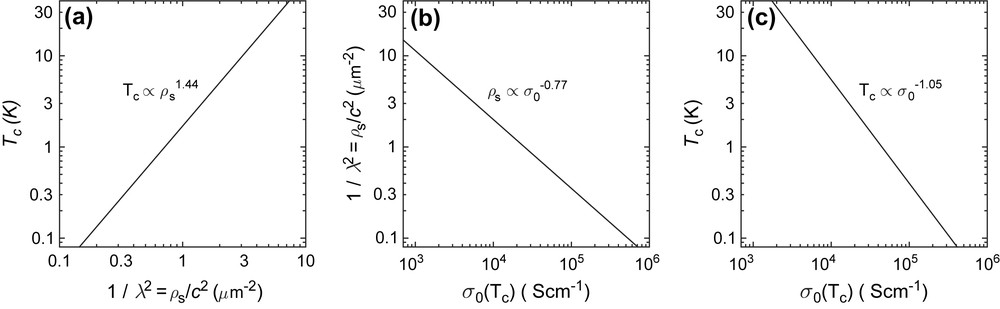
Empirical scaling relations between ρs, Tc and σ0 obtained from data on a range of molecular superconductors [5].
Another type of scaling property is revealed by consideration of the normal state dc conductivity σ0 just above the superconducting transition, measured in the most highly conducting direction. In the case of cuprates, Homes et al. [7] showed that ρs increases with increasing σ0, whereas Tc is not apparently strongly correlated with σ0 and it was found that ρs scales linearly with the product σ0Tc [7] for the full range of doping. In the case of molecular superconductors, a completely different behaviour was observed: both ρs and Tc decrease rather than increasing with increasing σ0 (Fig. 1b,c) and no scaling of ρs with the product σ0Tc was seen [5].
For the molecular superconductors, the dominant control parameter for the scaling was suggested to be U/W, the ratio of the on-site (i.e. molecular) electron correlation energy to the electronic bandwidth [5]. Chemical or physical pressure can be used to tune the value of U/W within a particular subclass of molecular superconductors. For example in the κ-phase ET salts, U/W can be reduced by applying pressure, with a corresponding drop in ρs and Tc and an increase in σ0. Dynamical Mean-Field Theory (DMFT) has emerged in recent years as a powerful way of calculating properties of strongly correlated electronic systems over the full range of U/W, however, both DMFT [8] and Resonating Valence Bond (RVB) theory [9] clearly predict an increase in ρs with pressure, as the system is pulled away from the metal–insulator transition by decreasing U/W. This is completely contrary to experiment (see Fig. 2). Thus current theoretical approaches to the physics of molecular superconductors appear to be missing some important features of their behaviour and this is clearly an area where further theoretical progress is needed.
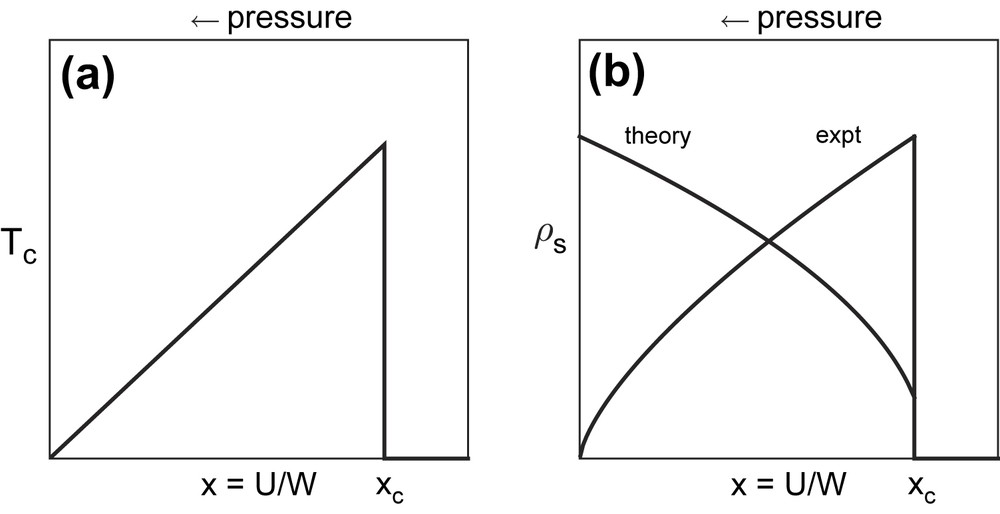
Illustration of the effect of the correlation parameter x = U/W on (a) Tc, where both theory and experiment suggest enhancement as the metal–insulator transition at xc is approached and (b) the behaviour of ρs, where theory and experiment suggest opposite dependences on x.
Acknowledgements
The author has benefited greatly from collaboration and interaction in this work with Steve Blundell, Ben Powell and Ross McKenzie.


