Synthesis of phosphoenol pyruvates. Theoretical and experimental study

Amina Ghomri; Abdelkrim Atmani

doi:10.1016/j.crci.2014.03.005

Synthesis of phosphoenol pyruvates. Theoretical and experimental study
[Synthèse des phosphates d’énols pyruviques. Étude théorique et expérimentale]

Amina Ghomri ^1,² ; Abdelkrim Atmani ³

¹ École préparatoire Sciences et Techniques Tlemcen, BP 165 RP Bel horizon, 13000 Tlemcen, Algeria
² Laboratoire de thermodynamique appliquée et modélisation moléculaire no 53, Département de chimie, Faculté des sciences, Université Abou-Bekr-Belkaid, BP 119, 13000 Tlemcen, Algeria
³ Laboratoire des substances naturelles et bioactives (LASNABIO), Département de chimie, Faculté des sciences, Université Abou-Bekr-Belkaid, BP 119, 13000 Tlemcen, Algeria

Comptes Rendus. Chimie, Volume 17 (2014) no. 12, pp. 1230-1236.

Résumés

Anglais
Français

A theoretical and experimental study of the reaction of α-chloropyruvate with trialkyl phosphites in toluene is reported. The phosphoenol pyruvate obtained was characterized by (¹H, ¹³C and ³¹P) NMR. DFT-based reactivity descriptors are used to explain the main reaction product found experimentally. Global and local reactivity indices, namely global electrophilicity and Parr function, were computed at the B3LYP/6-311(d) level of theory. The solvent's effect on the reactivity indices is elucidated. The computed regioselectivity is in good agreement with experimental outcomes.

Une étude théorique et expérimentale de la réaction des α-chloropyruvates avec les trialkyl phosphites dans le toluène a été réalisée. Les phosphates d’énols obtenues sont caractérisés par RMN (¹H, ¹³C et ³¹P). Les descripteurs de réactivité dérivant de la DFT sont utilisés pour expliquer les produits de réaction obtenus expérimentalement. Les indices globaux et locaux de réactivité, à savoir l’électrophilie globale et la fonction de Parr, sont calculés par la méthode B3LYP/6-311G(d). L’effet du solvant sur les indices de réactivité est élucidé. La régiosélectivité calculée est en bon accord avec les résultats expérimentaux.

Métadonnées

Reçu le : 2013-11-04
Accepté le : 2014-03-03
Publié le : 2014-10-08

DOI : 10.1016/j.crci.2014.03.005

Keywords: α-chloropyruvate, Phosphoenol pyruvate, Electrophilicity index, Regioselectivity, Parr function
Mot clés : α-chloropyruvate, Énol pyruvique, Indice d’électrophilicité, Régioselectivité, Fonction de Parr

Affiliations des auteurs :

Amina Ghomri ^{1, 2} ; Abdelkrim Atmani ³

¹ École préparatoire Sciences et Techniques Tlemcen, BP 165 RP Bel horizon, 13000 Tlemcen, Algeria
² Laboratoire de thermodynamique appliquée et modélisation moléculaire no 53, Département de chimie, Faculté des sciences, Université Abou-Bekr-Belkaid, BP 119, 13000 Tlemcen, Algeria
³ Laboratoire des substances naturelles et bioactives (LASNABIO), Département de chimie, Faculté des sciences, Université Abou-Bekr-Belkaid, BP 119, 13000 Tlemcen, Algeria

@article{CRCHIM_2014__17_12_1230_0,
     author = {Amina Ghomri and Abdelkrim Atmani},
     title = {Synthesis of phosphoenol pyruvates. {Theoretical} and experimental study},
     journal = {Comptes Rendus. Chimie},
     pages = {1230--1236},
     publisher = {Elsevier},
     volume = {17},
     number = {12},
     year = {2014},
     doi = {10.1016/j.crci.2014.03.005},
     language = {en},
}

TY  - JOUR
AU  - Amina Ghomri
AU  - Abdelkrim Atmani
TI  - Synthesis of phosphoenol pyruvates. Theoretical and experimental study
JO  - Comptes Rendus. Chimie
PY  - 2014
SP  - 1230
EP  - 1236
VL  - 17
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crci.2014.03.005
LA  - en
ID  - CRCHIM_2014__17_12_1230_0
ER  -

%0 Journal Article
%A Amina Ghomri
%A Abdelkrim Atmani
%T Synthesis of phosphoenol pyruvates. Theoretical and experimental study
%J Comptes Rendus. Chimie
%D 2014
%P 1230-1236
%V 17
%N 12
%I Elsevier
%R 10.1016/j.crci.2014.03.005
%G en
%F CRCHIM_2014__17_12_1230_0

Amina Ghomri; Abdelkrim Atmani. Synthesis of phosphoenol pyruvates. Theoretical and experimental study. Comptes Rendus. Chimie, Volume 17 (2014) no. 12, pp. 1230-1236. doi : 10.1016/j.crci.2014.03.005. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.1016/j.crci.2014.03.005/

Version originale du texte intégral

1 Introduction

A tremendous amount of experimental work has been devoted to the study of the phosphoenols because of their important biological and pharmacological properties [1–4]. Phosphoenols represent important intermediates in organic chemistry for the synthesis of complex organic molecules [5–8].

The reaction of trialkyl phosphite with α-halogenated ketones [9,10] leads to a competition between the Perkow reaction (phosphoenols formation) and the Arbuzov reaction (β-ketophosphonate) (Fig. 1). However, a great amount of experimental works devoted to the selective syntheses of phosphoenols can be found in the literature [11–21].

Fig. 1
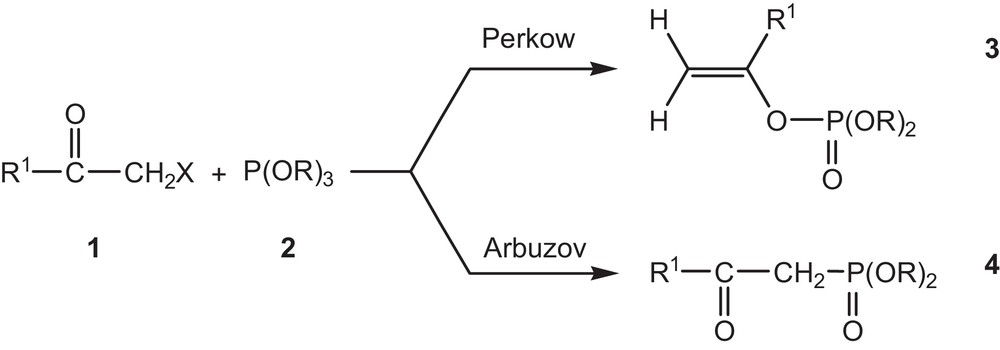
Competition between the Perkow reaction (formation of phosphoenols) and the Arbuzov reaction (β-ketophosphonate).

The aim of this work is first to present a simple and selective method of synthesis of phosphoenol pyruvates (PEP). Based on a preceding work [22], we used the α-chloropyruvates because they present direct precursors of phosphoenol pyruvates and are also easily accessible. We note that, compared with the previous work, our synthesis method has several advantages, such as fairly short reaction times, high yields, mild reaction conditions, absence of catalyst; moreover, it offers ready access to structural variety such as β-substituted phosphoenol pyruvates, not previously available in these series of compounds (Fig. 2).

Fig. 2
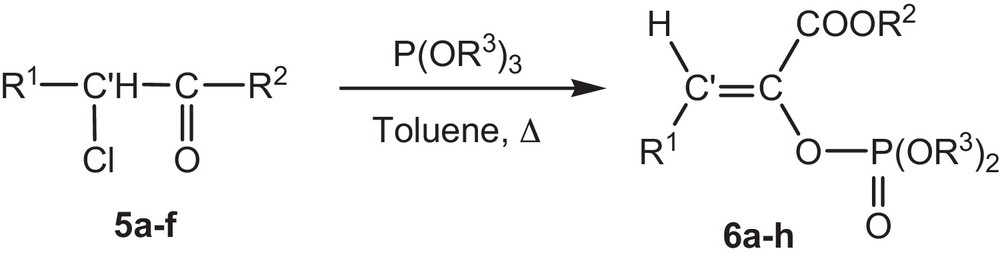
Reaction of α-chloropyruvate **5a-f** with trialkylphosphites in toluene.

The second purpose of this study is to evidence the experimental outcomes that state that, in this reaction, the carbon atom of the carbonyl group (CO) of the α-halogenoketone is preferred for the electrophilic attack of the trialkyl phosphites P(OR)₃ using theoretical descriptors.

Recently, the popularity and success of density functional theory (DFT) has stimulated many groups to use the Hard and Soft Acids and Bases (HSAB) principle, formulated with DFT [23,24], as a qualitative and quantitative treatment to predict reactivity based upon ground-state properties (density). Furthermore, DFT-based reactivity descriptors, such as condensed Fukui functions [25], local softness [26], local hardness [24b,26], electrophilicity [27], and nucleophilicity indices [28], have proven their utility for the analysis of organic reactions [29–31].

Very recently, Domingo et al. introduced the electrophilic and nucleophilic Parr functions as local indices and showed that these new descriptors provide useful clues for the characterization of the most electrophilic and nucleophilic centers of molecules, and for the establishment of the regio- and chemoselectivity in polar reactions [32]. The proposed Parr functions were compared with both, the Parr–Yang Fukui functions [33], based on frontier molecular orbitals, and Yang–Mortier condensed Fukui functions [34] based on Mulliken charges. In the present work, we used the electrophilic Parr function as local reactivity indices to justify our experimental finding. To be in agreement with the experimental procedure, the calculations were done in the gas phase then in toluene; the obtained results allow us to discuss the solvent's effect in the determination of the local reactivity indices.

2 Theoretical background

2.1 Global quantities

Assuming the differentiability of the electronic energy, E, with respect to N and v(r), a series of response functions appear, among which the most important are probably electronegativity (χ) [35] and hardness (η) [23,36], have been provided with rigorous definitions within the purview of conceptual DFT [25,37]. Electronegativity is the negative of the chemical potential, defined by:

χ = - μ = - {(\frac{\partial E}{\partial N})}_{v (r)}

(1)

μ is the Lagrange multiplier associated with the normalization constraint of DFT [25].

Hardness (η) is defined as the corresponding second derivative,

η = {(\frac{\partial^{2} E}{\partial N})}_{v (r)} = {(\frac{\partial μ}{\partial N})}_{v (r)}

(2)

Softness (S) is the reciprocal of hardness; S = 1/η.

Using a finite-difference method, the working equations for the calculation of μ and η may be given as [25]:

μ = - \frac{I + A}{2}

(3)

η = I - A

(4)

where I and A are the ionization potential and electron affinity, respectively. If ɛ_HOMO and ɛ_LUMO are the energies of the highest occupied and lowest unoccupied molecular orbitals, respectively, then the above equations can be rewritten [37], using Koopman's theorem [38], as:

μ \approx \frac{ε_{HOMO} + ε_{LUMO}}{2}

(5)

η \approx ε_{LUMO} - ε_{HOMO}

(6)

The electrophilicity index, as defined by Parr et al. [27], is given by:

ω = \frac{μ^{2}}{2 η}

(7)

2.2 Local quantities

As opposed to the global reactivity descriptors described above, the analysis of site selectivity in a molecule demands the knowledge of local descriptors. Taking into account the observations obtained from the atomic spin density ASD analysis performed in polar reactions, Domingo et al. propose a new local reactivity index, named the Parr function P(r), which is obtained from the ASD at the radical cation and at the radical anion of the corresponding reagents, and is given by the following equations [32]:

P^{+} (r) = ρ_{s}^{ra} (r) for nucleophilic attack

(8a)

P^{-} (r) = ρ_{s}^{rc} (r) for electrophilic attack

(8b)

where

ρ_{s}^{rc} (r)

is the ASD of the radical cation, and

ρ_{s}^{rc} (r)

is the ASD of the radical anion. Each ASD condensed at the different atoms of the radical cation and radical anion provides the local nucleophilic

P_{k}^{-}

and electrophilic

P_{k}^{+}

Parr functions of the neutral system.

The local electrophilicity index [39], ω_k, condensed to atom k, is easily obtained by projecting the global quantity onto any atomic center k in the molecule by using the electrophilic $P_{k}^{+}$ Parr functions, yielding:

ω_{k} = ω P_{k}^{+}

(9)

3 Computational details

The quantum chemistry calculations reported in this work have been performed at the B3LYP/6-311g(d) level of theory using the Gaussian 09 series of programs [40]. All stationary points found were characterized as true minima by frequency calculations. We note that the global indices calculated in this work, namely the chemical potential, μ, the global hardness, η, and the global electrophilicity, ω, are calculated using Eqs. (5), (6), and (7), respectively. The electrophilic Parr function, $P_{k}^{+}$ , was obtained through the analysis of the Mulliken ASD of the radical anion by single-point energy calculations over the optimized neutral geometries, using the unrestricted UB3LYP formalism for radical species. Solvent effects have been considered at the same level of theory by geometry optimization of the gas-phase structures, using a self-consistent reaction field (SCRF) [41] based on the PCM of the Tomasi's group [42].

4 Results and discussion

4.1 Synthesis of β-substituted-phosphoenol pyruvates

In this study, a series of β-substituted phosphoenol pyruvates derivatives 6a–h are obtained by Perkow reaction of the α-trimethyl phosphite with α-chloropyruvates as shown in (Fig. 2).

The reaction yield ranges from 70 to 95%. The obtained results are presented in Table 1.

Product	R¹	R²	R³	Y(%)	Bp/°C/mmHg
6a	H	Et	Me	80	91/1
6b	Me	Me	Me	95	98/0.5
6c	Et	Me	Me	85	110/0.1
6d	i-Pr	Me	Me	85	115/0.5
6e	t-Bu	Me	Me	80	120/0.5
6f	Ph	Me	Me	80	180/0.5
6g	Et	Me	Et	90	117/0.1
6h	t-Bu	Me	Et	70	110/0.3

(¹H,¹³C,³¹P) NMR confirms the structures of the synthesized phosphoenol pyruvates. The reaction products are obtained as mixtures of Z and E isomers, characterized by ¹H NMR, with the proton signal of ethylene. We note that the Z-isomer is obtained mainly in the final mixtures. Our results lead to the same stereoselectivity as that obtained by Gaydou [43].

4.2 Optimized geometries

Optimized geometries are presented in Fig. 3, which shows that for all the optimized systems, the C′C bond lengths range from 1.314 to 1.331 Ǻ and correspond to the double bond (CC) length of ≈1.3 Ǻ. On the other hand, the (R1CCO) dihedral angles D (degree) arise from –5.45 to 1.11°; these results show that, for the studied systems, the equilibrium geometry corresponds to the Z stereoisomer. Our theoretical results are in good agreement with our experimental outcomes.

Fig. 3
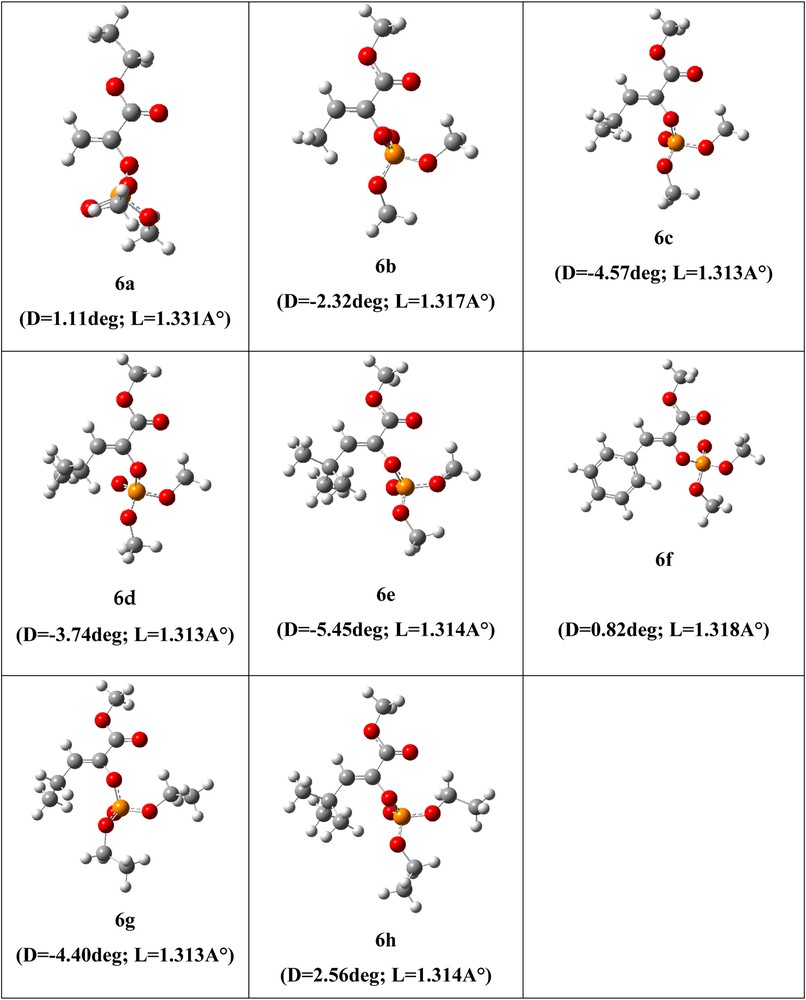
(Color online). Optimized geometries of reaction products (phosphoenol pyruvates) 6a–h, R¹C′CO dihedral angle D and the C′C bond length L are given in° (degrees) and Ǻ, respectively.

4.3 Theoretical prediction of the positional selectivity (CO)/(C′Cl) of the nucleophilic attack on α-halogenoketones derivatives

Our experimental results show that the nucleophilic attack will occur preferentially on the C carbon position of the carbonyl (CO) rather than on the C′ position (C′Cl).

In order to rationalize the experimental regioselectivity of the nucleophilic attack of trialkyl phosphites on the α-halogenoketones 5a–f, we have calculated the global and local electrophilicity indices, ω and $ω_{k}$ , defined in Eq. (7) and Eq. (9), respectively, and the results are reported in Tables 2–4. The local and global indices are calculated in the gas phase and in toluene.

Reactant	HOMO	LUMO	μ(ua)	η(ua)	ω(eV)
5a	–0.2749	–0.0980	–0.1865	0.1769	2.67
5b	–0.2746	–0.0954	–0.1850	0.1792	2.59
5c	–0.2731	–0.0940	–0.1835	0.1791	2.55
5d	–0.2712	–0.0901	–0.1807	0.1811	2.45
5e	–0.2689	–0.0932	–0.1811	0.1757	2.53
5f	–0.2623	–0.0971	–0.1797	0.1652	2.66

Reactant	HOMO	LUMO	μ(ua)	η(ua)	ω(eV)
5a	–0.2662	–0.0890	–0.1776	0.1771	2.42
5b	–0.2659	–0.0864	–0.1761	0.1795	2.35
5c	–0.2645	–0.0851	–0.1748	0.1794	2.31
5d	–0.2626	–0.0811	–0.1719	0.1814	2.21
5e	–0.2603	–0.0842	–0.1723	0.1761	2.29
5f	–0.2538	–0.0882	–0.1710	0.1656	2.40

Reactant	Gas-phase	Toluene
	P_k⁺	ω_k	P_k⁺	ω_k
5a
C′	0.0494	0.1319	0.0354	0.0858
C	0.2894	0.7727	0.3189	0.7717
5b
C′	0.0593	0.1537	0.0422	0.0992
C	0.2978	0.7713	0.3222	0.7520
5c
C′	0.0610	0.1557	0.0423	0.0977
C	0.2987	0.7618	0.3240	0.7485
5d
C′	0.0625	0.1532	0.0415	0.0917
C	0.3208	0.7861	0.3447	0.7618
5e
C′	0.0620	0.1569	0.0441	0.1011
C	0.3150	0.7971	0.3333	0.7634
5f
C′	0.0822	0.2188	0.0696	0.1672
C	0.2320	0.6172	0.2695	0.6469

The analysis of the tabulated values shows that the global electrophilicity indices ω range from 2.42 to 2.21 eV in toluene, and from 2.65 to 2.45 eV in vacuo; this result shows that all α-halogenoketones 5a-f are strong electrophiles [44]. Our results also show that the solvent's effect on the electrophilic character of the molecules is moderate, and that the ordering of the studied molecules according to their electrophilic power is the same in the gas phase and in toluene.

The local electrophilicity indices obtained using the electrophilic Parr function (Table 4) show that the carbon position of the carbonyl C is characterized by the highest value of the local electrophilicity indices. Indeed, in all cases, $ω_{c}$ > $ω_{c'}$ ; this result is found in the gas phase and in the solvent. Consequently, the C position is predicted to be more reactive than the C′ position for all systems 5a–f. Table 4 shows also that taking into account solvation has only little effect on local electrophilicity.

5 Concluding remarks

In this work, we have theoretically and experimentally examined the reaction of a series of α-halogenoketones compounds with trialkyl phosphite. Global and local DFT-based reactivity descriptors of α-halogenoketones have been used to rationalize the experimental data.

Our calculations show that the experimental regioselectivities are correctly reproduced. Indeed, the local electrophilicity index predicts that the C position is more reactive than the C′ one in all systems. Our calculations also show that the new proposed Parr function correctly reproduces the relative reactivities of the C position. Consequently, we can conclude that the local electrophilicity, as deﬁned by Domingo's group using the electrophilic Parr function, is suitable for the prediction of regioselectivity. Finally, we note that the solvent's effect on the reactivity indices is small, even though the electrophilic power decreases moderately.

6 Experimental

6.1 General procedures and materials

¹H NMR and ¹³C NMR spectra were recorded on a PerkinElmer R12 (300 MHz for ¹H NMR and 75 MHz for ¹³C NMR) spectrometer using CCl₄ as the solvent. The chemical shifts (δ) are reported in parts per million (ppm) relative to (TMS) as an internal standard, and coupling constants J are given in Hertz. All the chemicals were obtained from Merck Chemicals and Aldrich, and were used without further purification. FT–IR (KBr) spectra were recorded on a Beckman Acculab 8 spectrophotometer.

6.2 General procedure for the synthesis of compounds 6a–6h

To a solution of the appropriate 3-chloro-2-oxoester (0.1 mol) in dry toluene (20 mL), 0.1 mol of trimethylphosphite was added at 70 °C over a period of 15 min. The mixture was heated at 110 °C for 90 min. After removal of the solvent in vacuo, the distillation of the residue gave the yellow oil 6.

6.3 Spectral data for compounds 6a–6h

6.3.1 Ethyl-2-[(dimethoxyphosphoryl)oxy]prop-2-enoate (6a)

Yellow oil, yield 80%; FTIR (KBr, cm⁻¹): 1720 (CO), 1740 (CC), 1266 (PO); ¹H NMR (CCl₄, 300 MHz): δ_H (ppm) 3.77 (s, 3H, COOCH₃); 3.78 (d, 3H, J = 11.03 Hz, POCH₃); 5.6 (dd, 1H, J = 3 Hz, CH₂C); 5,9 (dd, 1H, 2 Hz, CH₂C); ¹³C NMR (CCl₄, 75 MHz): δ_C (ppm) 13(COOCH₂CH₃), 54(POCH₃), 60.5(COOCH₂CH₃), 109(H₂CC), 143(H₂CC), 160.7(COOC₂H₅); ³¹P NMR (H₃PO₄ 85%) δ = –1.70.

6.3.2 Methyl-2-[(dimethoxyphosphoryl)oxy]but-2-enoate (6b)

Yellow oil, yield95%, FTIR (KBr, cm⁻¹): 1720 (CO), 1740 (CC), 1272 (PO); ¹H NMR (CCl₄, 300 MHz): δ_H (ppm) 1.92(d, 3H, J = 7.28 Hz, CH₃CHC); 3.80 (s, 3H, COOCH₃); 4.09 et 4.12 (2d, 6H, J = 11.03 Hz, POCH₃); 6.20 (q, 1H, J = 7.28 Hz, CH₃CHC); ¹³C NMR (CCl₄, 75 MHz): δ_C (ppm) 14.6(CH₃CHC), 52.2 (COOCH₃), 55(POCH₃), 120(CH₃CHC), 144.8(CH₃CHC), 162.7 (COOCH₃)); ³¹P NMR (H₃PO₄ 85%) δ = –3.21.

6.3.3 Methyl-2-[(dimethoxyphosphoryl)oxy]pent-2-enoate (6c)

Yellow oil, yield 85%, FTIR (KBr, cm⁻¹): 1720 (CO), 1740 (CC), 1270 (PO); ¹H NMR (CCl₄, 300 MHz): δ_H (ppm) 1.1 (t, 3H, J = 7.80 Hz, CH₃CH₂CHC); 2.3 (dq, 2H, J = 7.80 Hz et 8.38 Hz, CH₃CH₂CHC), 3.80 (s, 3H, COOCH₃); 4.08 et 4.12 (2d, 6H, J = 11.03 Hz, POCH₃); 5.85 (t, 1H, J = 8.38, CH₃CH₂CHC); ¹³C NMR (CCl₄, 75 MHz): δ_C (ppm) 11.1 (CH₃CH₂CHC), 17.9 (CH₃CH₂CHC), 50.8(COOCH₃), 53.5(POCH₃), 130.7(CH₃CH₂CHC), 135.7(CH₃CH₂CHC), 161.3(COOCH₃); ³¹P NMR (H₃PO₄ 85%) δ = –3.19.

6.3.4 Methyl-2-[(dimethoxyphosphoryl)oxy]-4-methylpent-2-enoate (6d)

Yellow oil, yield85%, FTIR (KBr, cm⁻¹): 1735 (CO), 1740 (CC), 1265 (PO); ¹H NMR (CCl₄, 300 MHz): δ_H (ppm) 0.98 (d, 6H, J = 6.80 Hz, CH(CH₃)₂); 2,44 (m, 1H, CH(CH₃)₂); 3.79 (s, 3H, COOCH₃); 4.04 et 4.11 (2d, 6H, J = 11.03 Hz, POCH₃); 5.8 (d, 1H, J = 10.50 Hz, iPrCHC); ¹³C NMR (CCl₄, 75 MHz): δ_C (ppm) 22(CH(CH₃)₂), 25.2(CH(CH₃)₂), 52.3(COOCH₃), 55.1(POCH₃), 133.1(iPrCHC), 144.8(iPrCHC), 162.7(COOCH₃), ³¹P NMR (H₃PO₄ 85%) δ = –3.22.

6.3.5 Methyl-2-[(dimethoxyphosphoryl)oxy]-4,4-dimethylpent-2-enoate (6e)

Yellow oil, yield80%, FTIR (KBr, cm⁻¹): 1735 (CO), 1740 (CC), 1266 (PO); ¹H NMR (CCl₄, 300 MHz): δ_H (ppm) 1.20 (s, 9H, C(CH₃)₃); 3.79 (s, 3H, COOCH₃); 4.04 et 4.11 (2d, 6H, J = 11.03 Hz, POCH₃); 5.9 (d, 1H, J_HP = 2.8, J_PH = 0 Hz, tBuCH = C); ¹³C NMR (CCl₄, 75 MHz): δ_C (ppm) 29.8(C(CH₃)₃), 33.2(C(CH₃)₃, 52.4(COOCH₃), 55(POCH₃), 134.7(tBuCHC), 144.8(tBuCHC), 162.6(COOCH₃), ³¹P NMR (H₃PO₄ 85%) δ = –3.20.

6.3.6 Methyl-2-[(dimethoxyphosphoryl)oxy]-3-phenylprop-2-enoate (6f)

Yellow oil, yield 80%, FTIR (KBr, cm⁻¹):1735 (CO), 1740 (CC), 1265 (P–O); ¹H NMR (CCl₄, 300 MHz): δ_H (ppm) 3.77 (s, 3H,COOCH₃); 3.79 et 3.79 (2d, 6H, J = 11.03 Hz, POCH₃); 6.60(m, 1H, C₆H₅CHC); 7 (m, 5H, C₆H₅); ¹³C NMR (CCl₄, 75 MHz): δ_C (ppm) 52.4(COOCH₃), 55(POCH₃), 118(C₆H₅CHC), 128.9(C₆H₅), 129.3(C₆H₅), 129.6(C₆H₅), 130.6(C₆H₅), 144.4(C₆H₅CHC), 162.5(COOCH₃); ³¹P NMR: δ = –3.21.

6.3.7 Methyl-2-[(diethoxyphosphoryl)oxy]pent-2-enoate (6g)

Yellow oil, yield70%, FTIR (KBr, cm⁻¹): 1735 (CO), 1740 (CC), 1260 (PO); ¹H NMR (CCl₄, 300 MHz): δ_H (ppm) 1.06 (t, 3H, J = Hz, CH₃CH₂CHC); 1.20 (t, 3H, J = Hz, POCH₂CH₃), 2.05 (dq, 2H, J = 7.0 Hz, CH₃CH₂CHC); 3.78 (s, 3H, COOCH₃); 4.04 (m, 4H, POCH₂CH₃); 6.1 (t, 1H, J = 7.8 Hz, CH₃CH₂CHC); ¹³C NMR (CCl₄, 75 MHz): δ_C (ppm) 13.2 (CH₃CH₂CHC), 16 (POCH₂CH₃), 19.2 (CH₃CH₂CHC), 52.3 (COOCH₃), 64.7 (POCH₂CH₃), 131.3 (C₂H₅CHC), 144.8 (C₂H₅CHC), 162.1 (COOCH₃);³¹P NMR (H₃PO₄ 85%) δ = –5.24.

6.3.8 Methyl-2-[(diethoxyphosphoryl)oxy]-4,4-dimethylpent-2-enoate(6h)

Yellow oil, yield70%, FTIR (KBr, cm⁻¹): 1720 (CO), 1745 (CC), 1274 (PO); ¹H NMR (CCl₄, 300 MHz): δ_H (ppm) 1.2 (s, 9H, C(CH₃)₃); 1.28 (t,6H, J = Hz, POCH₂CH₃); 3.80 (s, 3H, COOCH₃); 4.04 (m, 4H, POCH₂CH₃); 5.9 (m, 1H); ¹³C NMR (CCl₄, 75 MHz): δ_C (ppm)16 (POCH₂CH₃), 29.8 (C(CH₃)₃), 33.1 (C(CH₃)₃), 52.3 (COOCH₃), 64.7 (POCH₂CH₃), 134.7 (tBuCHC), 144.8 (tBuCHC), 162.6 (COOCH₃); ³¹P NMR (H₃PO₄ 85%) δ = –5.24.

Acknowledgements

We thank Professor J.-C. Combret (Université de Rouen, France) for the leave during which this work was conducted; we also thank Dr. C. Malhiac for the helpful discussions concerning this synthesis. This work was supported by research funds provided by the Ministry of the Higher Education and Scientific Research of the Algerian Government (CNEPRU E02020130167, MESRS-Algeria).

Bibliographie

[1] N.G. Ternan; J.W. McGrath; J.P. Quinn Appl. Environ. Microbiol., 64 (1998), p. 2291

[2] L.F. García-Alles; B. Erni Eur. J. Biochem., 269 (2002), p. 3226

[3] G. Zhang; J. Dai; Z. Lu; D. Dunaway-Mariano J. Biol. Chem., 278 (2003), p. 41302

[4] M. Allison; R.D. Hutton; F.C. Cochrane; J.A. Yeoman; G.B. Jameson; E.J. Parker Biochemistry, 50 (2011), p. 3686

[5] A. Whitehead; J.D. Moore; P.R. Hanson Tetrahedron Lett., 44 (2003), p. 4275

[6] H. Fuwa; M. Sasaki J. Org. Chem., 74 (2009), p. 212

[7] A.B.C. Simas; D.L. de Sales; K.C. Pais Tetrahedron Lett., 50 (2009), p. 6977

[8] E. Krawczyk; G. Mielniczak; K. Owsianik; J. Łuczak Tetrahedron Asym., 23 (2012), p. 1480

[9] P.A. Chopard; V.M. Clark; R.F. Hudson; A.J. Kirby Tetrahedron, 21 (1965), p. 1961

[10] M. Sekine; K. Okimoto; K. Yamada; T. Hata J. Org. Chem., 46 (1981), p. 2097

[11] M. Sekine; K. Okimoto; T. Hata J. Am. Chem. Soc., 100 (1978), p. 1001

[12] K. Takai; K. Oshima; H. Nozaki Tetrahedron Lett., 21 (1980), p. 2531

[13] M. Sekine; T. Futatsugi; K. Yamada; T. Hata J. Chem. Soc. Perkin Trans., 1 (1982), p. 2509

[14] G.B. Hammond; T. Calogeropoulou; D.F. Wiemer Tetrahedron Lett., 27 (1986), p. 4265

[15] G. Blotny; R.M. Pollack Synthesis, 109 (1988)

[16] C. Despax; J. Navech Tetrahedron Lett., 31 (1990), p. 4471

[17] D.H.R. Barton; C.-Y. Chern; J.C.S. Jaszberenyi Tetrahedron, 51 (1995), p. 1867

[18] T. Moriguchi; K. Okada; K. Seio; M. Sekine Lett. Org. Chem., 1 (2004), p. 140

[19] D.S. Ayhan; S. Eymur J. Org. Chem., 72 (2007), p. 8527

[20] P. Beier; R. Pohl; A.V. Alexandrova Synthesis, 957 (2009)

[21] R.-J. Song; Y.-Y. Liu; J.-C. Wu; Y.-X. Xie; G.-B. Deng; X.-H. Yang; Y. Liu; J.-H. Li Synthesis, 1119 (2012)

[22] X.-Y. Zhu; J.-R. Chen; L.-Q. Lu; W.-J. Xiao Tetrahedron, 68 (2012), p. 6032

[23] R.G. Pearson, Wiley-VCH, Weinheim, Germany (1997), p. 3

[24] H. Chermette; P. Geerlings; F. De Proft; W. Langenaeker Chem. Rev., 20 (1999), p. 129

[25] R.G. Parr; W. Yang Density functional theory of atoms and molecules, Oxford University Press, Oxford, 1989

[26] M. Berkowitz; S.K. Ghosh; R.G. Parr; W. Langenaeker; F. De Proft; P. Geerlings; R.K. Roy; S. Krishnamurti; P. Geerlings; S. Pal; R.K. Roy; N. Tajima; K. Hirao J. Phys. Chem. A, 107 (1985), p. 6812

[27] R.G. Parr; L.V. Szentpály; S. Liu J. Am. Chem. Soc., 121 (1999), p. 1922

[28] L.R. Domingo; E. Chamorro; P. Perez J. Org. Chem., 73 (2008), p. 4615

[29] A. Ponti; A. Ponti; G. Molteni; G. Molteni; A. Ponti; A. Ponti; G. Molteni; P. Perez; L.R. Domingo; M.J. Aurell; R. Contreras Tetrahedron, 104 (2000), p. 8843

[30] L.R. Domingo; W. Benchouk; S.M. Mekelleche; P. Merino; T. Tejero; U. Chiacchio; G. Romeo; A. Rescifina; P. Merino; J. Revuelta; T. Tejero; U. Chiacchio; A. Rescifina; G. Romeo; W. Benchouk; S.M. Mekelleche J. Mol. Struct. Theochem., 63 (2007), p. 4464

[31] L.R. Domingo; M.J. Aurell; M. Arno; J.A. Saez; L.R. Domingo; M.J. Aurell; R. Jalal; M.J. Esseffar; M. Bakavoli; F. Moeinpour; A. Davoodnia; A.J. Morsali Mol. Struct. Theochem., 811 (2007), p. 125

[32] L.R. Domingo; P. Pérez; J.A. Saez RSC Adv., 3 (2013), p. 1486

[33] R.G. Parr; W. Yang J. Am. Chem. Soc., 106 (1984), p. 4049

[34] W. Yang; W. Mortier J. Am. Chem. Soc., 108 (1986), p. 5708

[35] L. Pauling; K.D. Sen; C. Jorgenson The nature of the chemical bond, Structure and bonding: electronegativity, Vol. 66, Cornell University Press, Ithaca, New York, 1960

[36] K.D. Sen; D.M.P. Mingos, Structure and bonding: chemical hardness, Vol. 80, Springer, Berlin, 1993

[37] P. Geerlings; F. de Proft; W. Langenaeker; H. Chermette J. Comput. Chem., 103 (2003), p. 1793

[38] R.G. Parr; R.A. Donnelly; M. Levy; W.E. Palke J. Chem. Phys., 68 (1978), p. 3801

[39] L.R. Domingo; M.J. Aurell; P. Pérez; R. Contreras J. Phys. Chem. A, 106 (2002), p. 6871

[40] M.J. Frisch et al. Gaussian 09, revision A.1, Gaussian Inc., Wallingford CT, USA, 2009

[41] J. Tomasi; M. Persico; B.Y. Simkin; I. Sheikhet Chem. Rev., Quantum chemical and statistical theory of solutions – A computational approach, 94, Ellis Horwood, London, 1994, p. 2027

[42] E. Cances; B. Mennucci; J. Tomasi; M. Cossi; V. Barone; R. Cammi; J. Tomasi; V. Barone; M. Cossi; J. Tomasi J. Comput. Chem., 107 (1997), p. 3032

[43] E.M. Gaydou; J.-P. Bianchini Can. J. Chem., 54 (1976), p. 3626

[44] L.R. Domingo; M.J. Aurell; P. Pérez; R. Contreras Tetrahedron, 58 (2002), p. 4417

Commentaires - Politique