1. Introduction
Organometallic chemistry textbooks teach us that metal alkyl compounds are very reactive species, often decomposing upon exposure to the atmosphere (oxygen, moisture) and by a few spontaneous processes (𝛽-H elimination, reductive elimination, etc.). Consequently, they can be maintained as stable species, isolated and characterized only with special precautions (inert atmosphere, choice of R group and ancillary ligand, etc.). At the same time, this high reactivity and the multitude of available reaction pathways make them extremely useful and versatile in catalysis, where they are involved in elementary steps that generally feature 2-electron changes in the metal coordination sphere (migratory insertion, bond metathesis, etc.).
An additional process leading to metal alkyl decomposition is bond homolysis, which is a one-electron process generating an organic radical. As organic radicals are themselves very reactive species and ultimately disappear by irreversible coupling and disproportionation processes, metal alkyl complexes can be isolated or used as catalytic intermediates only if the metal–carbon bond has sufficient homolytic strength. Nevertheless, it has become increasingly apparent that compounds with a weak metal–carbon bond, hence prone to generate transient radical species, are extremely useful. Like for the above-mentioned two-electron reactivity, this one-electron reactivity can be harnessed to promote useful and unique transformations. The importance of metal–carbon bond homolysis has probably been first highlighted in biochemistry, where metal centers in enzymes and cofactors play a crucial role in the physiological regulation of radical reactivity, but has also subsequently been recognized in the areas of polymer chemistry and organic chemistry. In this article, I wish to highlight a few important principles and considerations and provide a few examples from our own work, which is mostly focused on metal-mediated radical polymerization. In this respect, although the standard abbreviation of a generic metal by organometallic chemists is M, I elected to use the alternative abbreviation Mt, to avoid confusion with the same abbreviation used within the polymer community for a generic monomer. A generic formal oxidation state will be indicated by the symbol x (e.g. Mtx, Mtx+1). Again, in order to avoid confusion, one-electron ligands (in most cases a halogen) will be identified by the symbol Y rather than by the more commonly used X. The symbol T will be used when a one-electron species, generally stable in the free form, acts as a radical trap. A generic coordination sphere will be identified as L/ (e.g. L∕Mtx or Mtx∕L) and a generic radical as R. The considerations that I develop in this article are also valid in principle for metal-aryl bonds, though the vast majority of current applications involves alkyls. The Mt–R bond homolysis can be activated either thermally or photochemically. A redox stimulus may also promote bond homolysis, but only via an alteration of the Mt–R bond strength by the oxidation state change, while the bond cleavage process itself remains either thermally or photochemically activated. In this article, I will only focus on the thermal activation method.
2. Energy profile and thermal stability
The key thermodynamic and kinetic parameters of the homolytic bond cleavage, which may be expressed on the enthalpy and/or free energy scales, are shown in Figure 1. The homolytic cleavage process generates two species from a single one, thus entails a very positive entropy term (𝛥S), which is already largely expressed at the transition state level (; however, see further discussion in Section 4.2 below). Consequently, 𝛥G≪𝛥H and , whereas . In the absence of steric impediments, geometrical reorganization, the need of ligand dissociation, or a spin state change, the L∕Mtx-radical coupling proceeds at diffusion-limited rates, namely the barrier to the radical deactivation process is very small (estimated as <2 kcal⋅mol−1) [1, 2, 3, 4]. Therefore, the experimentally more readily accessible activation enthalpy gives a close estimate of the BDE, although this conclusion may be dangerous for systems where Mtx∕L requires dissociation of solvent molecules, e.g. water, see further discussion in Section 4.3.
Energetic profile of a metal–carbon bond cleavage.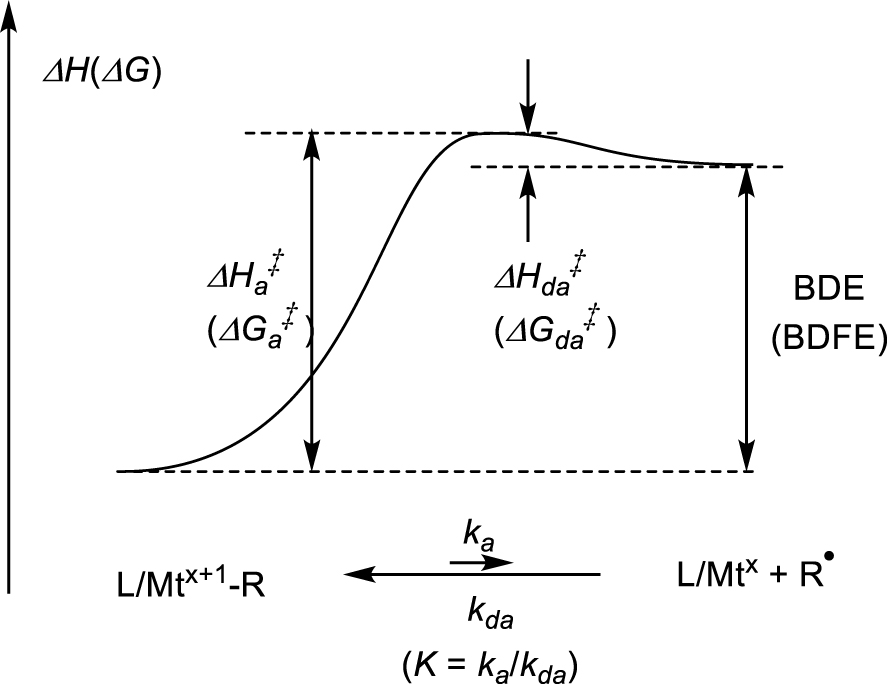
Generation and reactivity of radicals.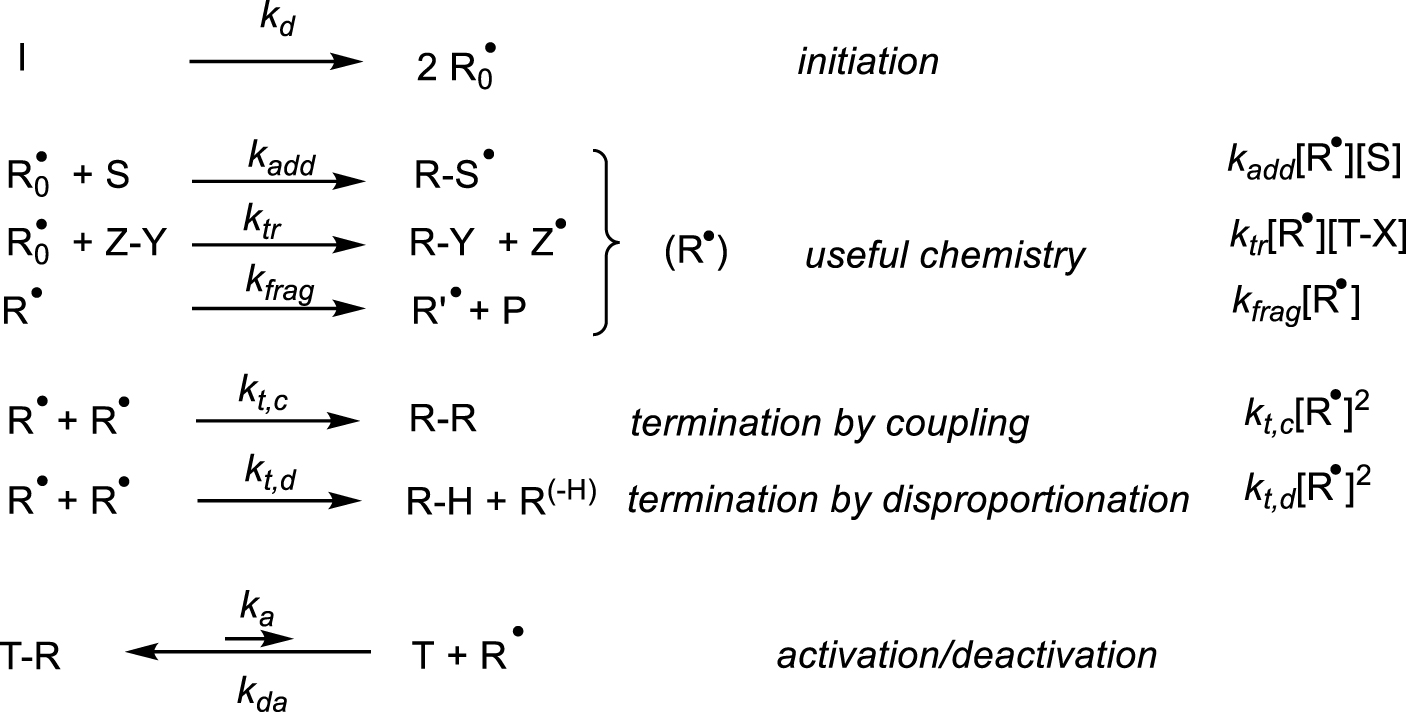
It is important to appreciate the relationship between these parameters and the “stability” or lifetime of the compound. A useful reference point is provided by [(CO)5Mn–CF3], which may be considered as a typical “stable” organometallic compound. Extensive heating of this compound in an inert solvent at 100 °C or above and in the absence of a radical trapping species does not significantly decompose it. However, as shown from recent work in my laboratory, the bond can be broken at measurable rates in the presence of a radical trap (see the details in Section 4.6) [5]. The measured Mn–C bond activation parameters are and . Assuming , the equilibrium constant can be estimated as 3.3 × 10−18 at 100 °C or 4.4 × 10−14 at 150 °C, yielding initial radical concentrations of 2.9 × 10−9 and 2.1 × 10−7 M, respectively, from a standard 1 M solution of the organometallic precursor . These concentrations, though very small, are still suitable to promote radical reactivity. For instance, the radical flux at 100 °C (where ) from a 1 M solution of [Mn(CF3)(CO)5] can be calculated from the Eyring equation as 2.3 × 10−5 mol⋅s−1 (t1∕2 = 3.2 × 104 s or 9 h), which is not unreasonably long for a chemical reaction. However, heating [(CO)5Mn–CF3] alone in an inert solvent at 100 °C for 9 h will not lead to 50% decomposition, not even to a small fraction of it. The reason is the greater efficiency of the back-trapping process from the caged fragment couple relative to cage escape and subsequent irreversible processes leading to decomposition (coupling of two [(CO)5Mn∙] to yield [Mn2(CO)10] and of two to yield C2F6, plus other possible processes involving the solvent). In addition, the back-trapping process is kinetically first-order and the radical coupling processes are second order, hence disfavored at low concentrations. Thus, even compounds with lower BDEs, therefore giving greater radical fluxes and promoting radical reactivity at higher rates, may be “thermally stable” in a practical sense, if kept away from radical trapping species. The low BDE limit that allows isolation and manipulation of a metal alkyl complex under reasonably practical conditions appears to be around 20 kcal⋅mol−1. Examples are certain fragile alkylcobalamins and other related L∕CoIII–R compounds [6, 7]. The point that I wish to stress in this article, however, is that even when the Mt–C bond strength is too small to allow isolation, the organometallic species may still play a role as a transient in a stoichiometric or catalyzed reaction, improving the radical reaction selectivity, through the so-called “persistent radical effect”.
3. The “persistent radical effect”
Radical reactions may be triggered by primary radicals generated from a stable initiator (I) through a suitable stimulus (thermal, irradiation, redox, etc.), Scheme 1. These radicals then engage in a variety of useful transformations, such as additions to unsaturations, atom/group transfer and fragmentations, generating new radicals (R0–S∙, Z∙, R∙, collectively indicated as R∙), which may undergo the same transformations again (chain mechanism) and at some point eliminate a stable product (P) by a fragmentation process. This useful reactivity always competes with the irreversible bimolecular radical terminations by combination and disproportionation. However, the presence of a reversible trapping species (T), able to produce a stable but reactivatable dormant species T–R, reduces the impact of the terminations and improves the performance of the useful radical reactivity. This is known as the “persistent radical effect” and the reversible formation of a metal–carbon bond (i.e. if T = [L∕Mtx]) is only one of many ways in which this effect can be implemented. The origin of this effect is kinetic: the useful processes are all first-order in radical, whereas both types of terminations (combination and disproportionation may be combined into a single rate law with kt = kt,c + kt,d) are second-order. The activation/deactivation equilibrium lowers the active radical concentration under steady-state reaction conditions. Hence, whereas the rate of the sought transformations scales linearly with the radical concentration, the terminations rate scales quadratically. Take an ideal but realistic example where, in the absence of reversible radical trap, the steady-state radical concentration is 10−7 M, the rate constants of the terminations and of the useful transformation are 108 and 102 M−1⋅s−1, respectively, and the substrate concentration is 1 M. The useful chemistry proceeds at a rate of (102 M−1⋅s−1)(10−7 M)(1 M) = 10−5 M⋅s−1 whereas the radicals disappear at a rate of (108 M−1⋅s−1)(10−7 M)2 = 10−6 M⋅s−1, namely 10% of the generated radicals are lost before they can undergo any useful transformations. However, in the presence of a moderating equilibrium with, for the sake of argument, K = 10−9 and [L∕Mtx+1–R] = [L∕Mtx], the steady-state radical concentration becomes 10−9 M, yielding rates of 10−7 M⋅s−1 for the useful transformation and 10−10 M⋅s−1 for the terminations (only 0.1% of the radical are lost). The useful process has become 100 times slower, but the terminations have become 10,000 times slower.
I wish to comment on the use of the “persistent radical effect” (PRE) terminology. This name was coined after the initial investigations of radical reactions where both R∙ and T are radicals, one of which (T) is persistent. This term was introduced by Daikh and Finke (organometallic chemists) in a 1992 investigation of a radical isomerization process occurring in a coenzyme B12 model complex, where the self-coupling of benzyl radicals is suppressed by the presence of the L∕CoII “persistent radical” [8]. The PRE terminology was then popularized by Fischer (who actually inspired the study of Daikh and Finke) with specific application to controlled radical polymerization [9, 10], and has since been extensively used by the polymer chemists working in this area. The PRE terminology has also creeped into the jargon of the organic chemistry community working on radical reactions [11, 12]. There are two different ways to see the meaning of the PRE terminology. On one side, it can be interpreted as a trick that allows to extend the life of the R∙ radicals, hence rendering them more persistent. This is a fine interpretation. It is, however, also prone to be interpreted (as it has been) as the effect provided by the “persistent radical” T. This is not a correct interpretation! As we now know, the same effect can be provided by metal complexes with any spin state, including diamagnetic ones. In addition, work from my laboratory has demonstrated that the same effect can be provided by certain unstable species that slowly decompose themselves bimolecularly [13, 14]. Therefore, the reversible radical trap (T) that ensures the PRE does not need to be a radical and does not need to be persistent! It should rather be identified as a moderating species/agent, since its role is just to moderate the steady-state radical concentration. I reluctantly continue to use the PRE terminology, though within quotes, but suggest to rather use more appropriate and general terminologies such as “moderating effect” or “reversible trapping effect”.
Evolution of the radical and T concentrations following terminations [9, 15, 16, 17].
In order to fully benefit from this moderating effect, if primary radicals are injected into solution from a conventional initiator (as in Scheme 1), the molar amount of the trapping species (T) must be at least as high as the total amount of the radicals produced by the initiator. However, the reaction may also be initiated by a labile T–R compound (e.g. an organometallic compound L∕Mtx+1–R0 with a fragile bond), providing itself the primary radical and the moderating species T, in which case an independent radical initiator (I) is not required. In this case, the moderating equilibrium evolves in a predictable way [9, 15, 16, 17] as a consequence of the inevitable radical terminations (Scheme 2). If T is stable, the R∙ disappearance entails the conversion of the equivalent amount of T–R into T and the [T] monitoring provides a convenient way to assess the fraction of lost radicals. Consequently, the T–R/T ratio decreases, inducing a [R∙] decrease through the equilibrium expression. This evolution further increases the positive effect of the moderating equilibrium.
4. Assessment of the thermodynamic and activation parameters
4.1. Thermodynamic parameters
The thermodynamic Bond Dissociation Enthalpy (BDE) may be obtained from constant pressure calorimetric measurements (combustion calorimetry, photoacoustic calorimetry, etc.), which generally require the application of thermochemical cycles and a number of approximations and assumptions and results in the accumulation of experimental errors [18, 19]. Many BDEs determined by these methods have subsequently been reassessed (one example will be provided below in Section 4.6) and this line of research appears abandoned. Published BDE values obtained by these methods should be taken with extreme care.
The equilibrium constant K gives access to the Bond Dissociation Free Energy (BDFE) and its temperature dependence yields the BDE, as well as the entropy change, through van’t Hoff’s relationship. Direct equilibrium measurements, however, are impossible because of the radical species instability. Hence, indirect methods are necessary. In addition, the solvent must be innocent (i.e. not chemically interact with L∕Mtx and/or T), or the related interaction energies must be known in order to correct the determined enthalpy value. Certain organometallic compounds lead to measurable equilibria involving the metal–carbon bond homolysis to yield stable end-products, which allows to calculate the bond homolysis BDFE through thermochemical cycles. For instance, various [(L)(dmgH)2CoIII–CH(CH3)Ph] compounds (L = pyridine, 4-substituted pyridine, imidazole) decompose to yield [(L)(dmgH)2CoII], styrene and H2 selectively (no radical coupling) via 𝛽-H atom transfer from Ph(CH3)CH∙ to the CoII center followed by bimolecular decomposition of the resulting [(L)(dmgH)2CoIII–H] intermediate [20, 21, 22]. Combination of 𝛥H° from the measured equilibrium in the 10–37 °C temperature range with the heats of formation of styrene and of the Ph(CH3)CH∙ radical has provided the sought CoIII–CH(CH3)Ph BDEs. Another indirect method has consisted in the [L∕Mtx+1–R] and [L∕Mtx] measurement in the presence of a steady-state concentration of continuously generated and terminating R∙, combined with the indirect [R∙] knowledge from the steady-state conditions (Vi = Vt), namely [R∙] = (kd[IN]∕2kt)1∕2 ([IN] = initiatorconcentration). For instance, the steady-state concentration of styryl radicals, obtained from the thermal decomposition of AIBN in the presence of excess styrene, has allowed the K determination for the homolysis of [(TAP)CoIII–CH(CH3Ph)] (TAP = tetra(p‐anisyl)porphyrin) [23, 24].
Time evolution of the T concentration during the T–R decomposition according to Scheme 2 [17].
Kinetics approach for the measurement of the activation rate constant.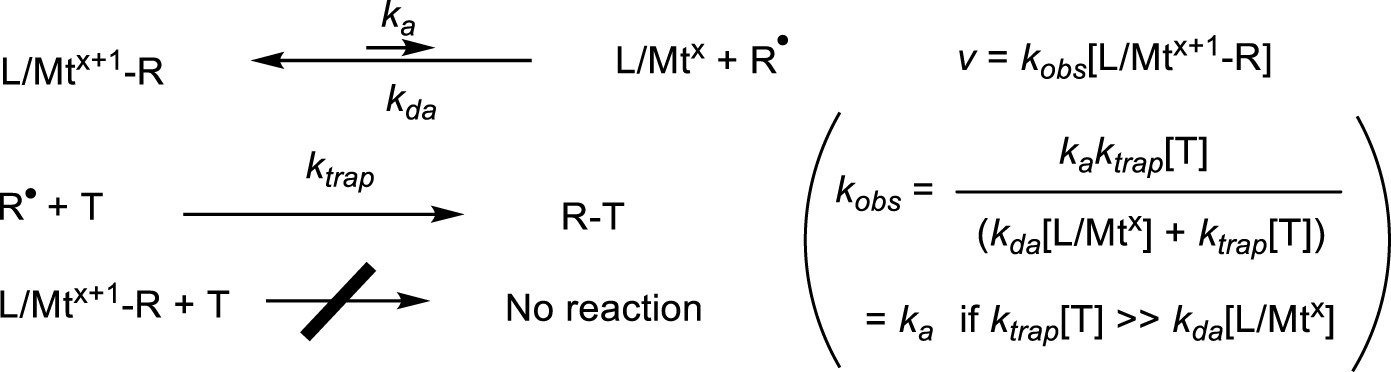
The equilibrium constant (hence the BDFE) can also be derived from the thermal decomposition kinetics according to Scheme 2 (T = L∕Mtx) in the absence of radical traps, monitoring either the L∕Mtx+1–R disappearance or the equivalent L∕Mtx accumulation. Equations describing the time evolution of [T] have been derived (Scheme 3). Under conditions where [T]≪[T–R]0, namely up to small conversions (e.g. ≈10%), the T concentration grows linearly with t1∕3 and the equilibrium constant K can be extracted from the slope of the ([T]–|T]0) versus t1∕3 linear best fit, provided the radical termination rate constant kt is known [9, 15, 16]. For decompositions proceeding to greater conversions, K can be extracted from the slope of the F versus t linear best fit [17]. Extraction of the BDE requires this analysis to be repeated at different temperatures and knowledge of the kt temperature dependence. This method has been used to determine the equilibrium constants of other fragile bond homolyses such as the O–C bond in alkoxylamines [17] and of atom transfer equilibria [25], but not yet of metal–carbon bonds homolyses to the best of our knowledge. However, the method is simple and of potentially wide applicability, provided T (i.e. L∕Mtx) is stable. The T accumulation continuously slows down the decomposition as discussed in the previous section, thus relatively fragile bonds may be conveniently investigated. If L∕Mtx+1–R is not sufficiently stable for isolation, the method can still be applied if the compound can be generated in situ at a known concentration in a shorter timescale than that of its spontaneous decomposition.
In a few special cases, K has also been derived by combining the measured ka and kda values. This has been applied to systems where , generated by pulse radiolysis, reacts with L∕Mtx to form unstable L∕Mtx+1–CH3 transients, which subsequently decompose by rate-limiting homolysis [26, 27].
Kinetics scheme for the bond homolysis of a few L∕CoIII–R compounds in the presence of 𝛽-H atom transfer.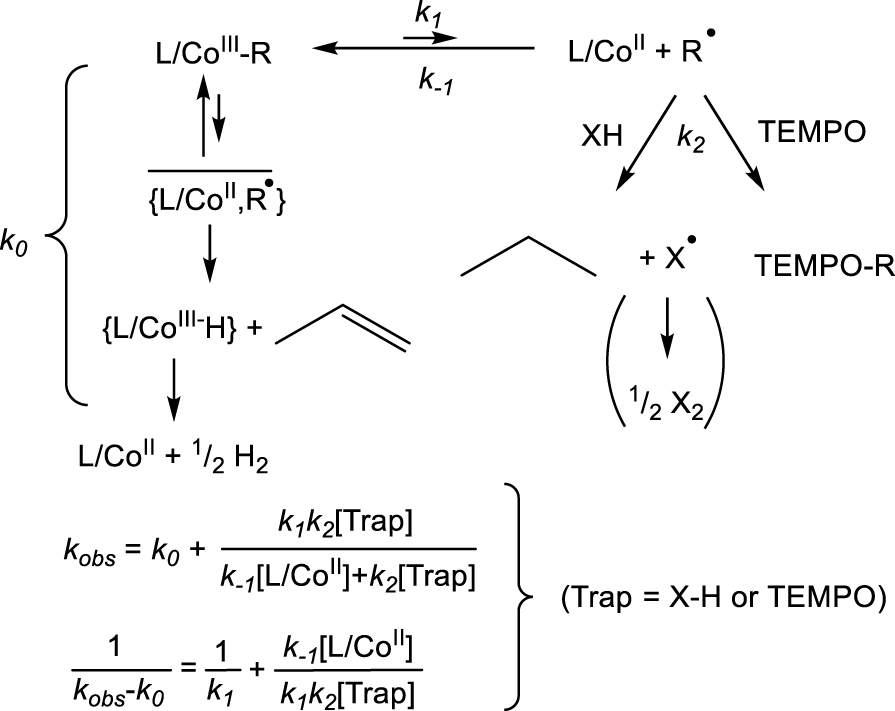
4.2. Bond cleavage barrier
The activation rate constant (ka) is accessible by measuring the rate of the organometallic precursor disappearance under conditions in which the back recombination (radical deactivation) is removed from the kinetics scheme [28]. This approach is easier to implement and has been much more widely used than the BDE or BDFE determination. The key is to add a suitable trapping agent, able to irreversibly capture one or both of the produced fragments competitively with respect to the back reaction (i.e. saturation conditions), Scheme 4. The trapping agent must also be inert with respect to the organometallic precursor. The temperature dependence of ka then provides and from Eyring’s equation. Various radical traps have been used for this purpose, the choice being dictated by the nature of the organometallic system and the need to exclude side reactions such as oxidation or ligand addition or exchange. Examples are (2,2,6,6-tetramethylpiperidin-1-yl)oxyl (TEMPO) [6, 22, 29, 30, 31, 32, 33], H-atom donors (thiols [34], silanes [5, 35], stannanes [36], metal hydrides [37, 38]), O2 [7, 39, 40] or other oxidizing agents (H2O2, aqueous metal ions and complexes) [41, 42, 43, 44] and also other L∕Mtx complexes that form a stronger Mt–R bond than the bond being broken [45, 46]. For certain systems containing 𝛽-H atoms on R, the decomposition could also be kinetically monitored in the absence of a trapping agent (see below) [20, 21, 22, 34, 47, 48]. This kinetic method can be applied to compounds that are sufficiently stable to be isolated in a pure form or that can be generated at known concentration in a shorter timescale than that of the trapping experiment. The lowest reported values appear to be around 17 kcal⋅mol−1 [22, 36]. In a couple of cases, the activation parameters could be extracted from a temperature-dependent 1H NMR line broadening study, with no need of trapping agents or concentration-time measurements [23, 49]. This method may be more widely applicable to thermally “stable” compounds. Most investigations have dealt with complexes of 3d metals, which feature homolytically weaker bonds than their heavier congeners.
The ka measurement is complicated by the presence of a 𝛽-H atom on the alkyl chain. In that case, the decomposition may follow a trap-independent pathway that involves 𝛽-H atom transfer from the alkyl group to the metal center within the caged fragment pair to generate the hydride complex L∕Mtx+1–H and an alkene, as pointed out for a few CoIII complexes (Scheme 5) [20, 21, 22, 34]. The fleeting CoIII hydride intermediate rapidly releases H2. In principle, both the trap-free first-order (k0) and the trap-dependent saturation (k1∕k−1,k2) pathways are initiated by CoIII–C bond homolysis, but the need to encounter the trapping species in the latter affects the transition state structure, the activation enthalpy (in all cases, ), and particularly the activation entropy . The k0 value could be measured in the absence of trapping agent and the k1 value from the intercept of a plot of (kobs − k0)−1 versus [Trap]−1. For those derivatives where R does not contain any 𝛽-H atom, k0 is zero and the decomposition only follows the quenched pathway.
The reported activation enthalpies span a rather wide range (17–54 kcal⋅mol−1), being limited at the lower end by the ability to generate the organometallic precursors L∕Mtx+1–R and at the upper end by the experimental conditions needed for sufficiently high decomposition rates. For a series of compounds with the same L∕Mtx+1, the (and thus presumably the BDEs) qualitatively scales with the homolytic strength of the corresponding R–H bond (e.g. benzyl < secondary alkyl < primary alkyl < Me < Ph). However, steric bulk induces inversions because the crowded L∕Mtx+1 exerts a stronger steric pressure than the simple H atom. The facile activation of the primary neopentyl group is a notable example [36, 46]. The investigation of series of compounds with the same R, on the other hand, illustrates the importance of ligand effects. More electron-donating ligands stabilize L∕Mtx+1–R better than L∕Mtx and thus tend to increase [6, 21, 22]. However, the bond strength has a more pronounced and inverse dependence on the ligand cone angle, generally masking the basicity effect [6, 36, 47]. Ligand addition to convert a 5- to a 6-coordinate system labilizes the Mtx+1–R bond (e.g. for the B12 system on going from the base-off to the base-on form), in line with the predominance of steric over electronic effects. Linear free-energy relationships have been proposed to understand the relative contributions of steric, bond polarity, and product stabilization factors to the homolytic strengths of various bonds [50, 51, 52], though this method has not been applied so far, to the best of my knowledge, to L∕Mtx+1–R bonds.
Like the activation enthalpies, the reported activation entropies , surprisingly, also span a very wide range, up to 66 cal⋅mol−1⋅K−1 for [(CO)5Mn–CF3] [5] and down to negative values, which is not consistent with a bond breaking process. Halpern has commented on this unexpected behavior and highlighted a qualitative relationship between and , which was termed “compensation effect” [28], but a persuasive rationalization of this phenomenon could not be offered. I would like to propose a possible way to interpret this behavior. The bond homolysis produces the {L∕Mtx,R∙} fragment pair in a solvent cage before radical trapping by T. All published activation parameters are based on the kinetic analysis of Scheme 4, in which no consideration is given to the caged intermediate. One contribution pointed out that the caged pair needs to be separated (k2∕k−2 equilibrium in Scheme 6), but that analysis also assumed that the trapping agent does not intervene until after radical escape from the cage (k3) [53]. That revised kinetic scheme proposed a modulation of the bond homolysis activation parameters by the parameters of the caged pair recombination and cage escape: ; , where Fc (fractional cage efficiency) = k−1∕(k−1 + k2). When Fc = 0 (fast caged pair separation relative to recombination) and , whereas when Fc approaches 1 (and thus ), and . However, even this scheme cannot rationalize negative values.
New kinetics scheme for the L∕Mtx+1–R bond homolysis with consideration of a trap-inclusive cage effect.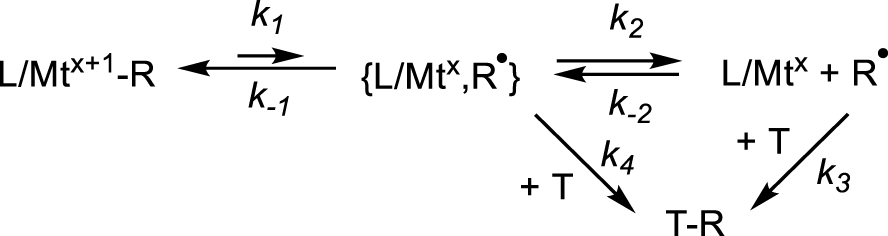
It seems to me quite plausible that the trapping agent may also be part of the cage walls, hence can interact directly with the caged pair, introducing a fourth step in the kinetic scheme (k4 in Scheme 6). The saturation kinetics analysis yields the 1∕k1 value by extrapolation of 1∕kobs to 1∕[T] = 0 (i.e. to very large [T]) rendering the assumption of no trap in the cage rather absurd. This does not amount to saying that the process is associative (such as an SH2 process), for which the rate law would show a first-order dependence on [T] and the extrapolation of 1∕kobs to 1∕[T] = 0 yields zero (no saturation). The mechanism remains of SH1 type, but the transition state “feels” the presence of the trap in the cage (Mt⋯R⋯T), which is expressed in the molecular organization at the transition state level and can account for negative activation entropies. This situation is closely related to the above-mentioned trap-free pathway when R contains 𝛽-H atoms, where the caged pair evolves by H-atom transfer within the cage and indeed the resulting 𝛥Sa value is lower than for the trap-dependent pathway. Certain trapping species have a radical character (e.g. nitroxides, CoII complexes) and thus may favorably interact with the dissociative Mt⋯R transition state because the C atom has developed a large spin density at that level, as suggested by DFT calculations [54, 55]. This idea is also supported by investigations of enzymatic reactions catalyzed by adenosyl cobalamin (AdoCbl), where kinetic coupling between the cobalt-carbon homolysis step and the subsequent radical-substrate reaction was demonstrated by the presence of a deuterium kinetic isotope effect [56, 57, 58]. If the trapping species does not intervene until after the radical cage escape, or at least until after the rate-determining transition state, a very positive activation entropy is anticipated, as is indeed observed for many bond homolyses. Note that the presence of a Mt⋯T interaction at the transition state level may also affect the measured activation enthalpy. In order to evaluate this effect, measurements of the bond homolysis activation parameters for the same L∕Mtx+1–R compound with different traps are necessary. This test was indeed done for the bond cleavage kinetics of several [(H2O)5CrIII–R]2+ [41, 42, 43] and [(H2O)(dmgBF2)2Co–CH2Ph] [44], yielding essentially indistinguishable activation parameters, but additional studies for other L∕Mtx+1–R bonds seem warranted. This “trap-inclusive cage effect”, however, does not predict any specific relationship between and .
Although most investigated L∕Mtx+1–R bond homolyses are indeed consistent with an SH1 mechanism, an SH2 process (Scheme 7) has been documented for the methyl radical transfer in various L∕CoIII–CH3–L′∕CoII systems (L′ = or≠L) with 𝛥H‡ as low as 7.5 kcal⋅mol−1 and very negative 𝛥S‡ (ca. − 20 cal⋅mol−1⋅K−1) [59]. The alkyl and benzyl radical transfer from [(dmgH)2CoIII–R] to another organic radical R′∙, to yield RR′ and [(dmgH)2CoII], also adopts an SH2 mechanism [60], as are other metal–carbon bond homolyses [61]. Thus, the rate law and particularly the presence of the saturation regime should always be carefully checked.
4.3. Bond formation barrier
Direct measurement of the deactivation rate constant (kda) is difficult, as it requires either monitoring the disappearance of L∕Mtx in the presence of a known concentration of radicals (which is possible only in flash photolysis or pulse radiolysis experiments), or the measurement of the kda∕ktrap competition and the separate knowledge of ktrap. These studies have generally been carried out only at one temperature to yield estimated kda values without experimental error [3, 43, 62, 63, 64, 65, 66, 67, 68, 69]. Most reported values are >107 and often >108 L⋅mol−1⋅s−1, i.e. close to the diffusion limit. The addition of the ∙CH2OH radical, produced by radiolysis of N2O-saturated aqueous solutions containing CH3OH, at low pH to complex [CoII(nta)(H2O)2]− (nta = nitrilotriacetate, N(CH2COO−)3) is a rare example of a temperature-dependent investigation. The measured addition rates in the 7–55 °C range are (0.97–4.1) × 108 M−1⋅s−1, yielding 𝛥H‡ = 4.8 ± 0.5 kcal⋅mol−1 and 𝛥S‡ = −4.6 ± 2 cal⋅mol−1⋅K−1 [26]. The relatively high 𝛥H‡ value might be associated to the need to displace a water molecule from the coordination sphere. For solvated cations, particularly in water, dissociation of the coordinated solvent seems indeed an important step during the Mtx+1–R bond formation process, as suggested by the activation volumes measured by pressure-dependent kinetic studies [70, 71]. The kda can also be estimated from the independent knowledge of ka and K. In many contributions discussing the homolytic strength of a L∕Mtx+1–R bond, the BDEs was estimated from the data assuming a diffusion-limited recombination rate ( equal to the 𝛥H‡ of the viscous flow, which is ca. 2 kcal⋅mol−1 for typical low-viscosity solvents) [72]. Indeed, measurements in higher-viscosity solvents such as ethylene glycol have yielded higher values [33]. The most precisely determined kda values appear to be those obtained from electrochemical data (next section).
SH1 versus SH2 processes involving the Mtx+1–R bond homolysis.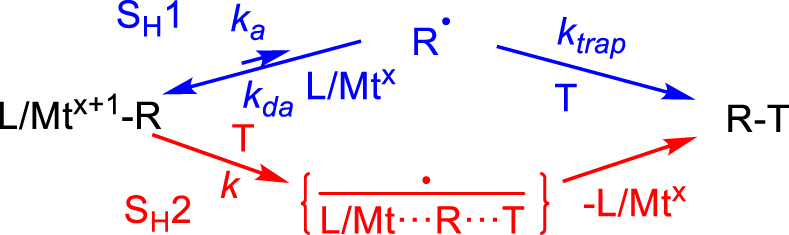
Left: scheme of the cascade processes leading to the generation of L∕Mtx+1–R from L∕Mtx+1–Y and R–Y. Right: cyclic voltammogram of one specific example (the lines are background-subtracted experimental data and the points correspond to the simulation) in the absence (blue) and presence (red) of R–Y at a scan rate of 0.5 V⋅s−1 in CH3CN. The example used L∕Mtx+1–Y = [CuBr(TPMA)]+(1.0 × 10−3 M) made in situ from CuBr2 and tris(pyridylmethyl)amine (TPMA = L) and R–Y = bromoacetonitrile (Br–CH2CN, BAN). The right image is reproduced with permission from Ref. [75]. Copyright 2019 American Chemical Society.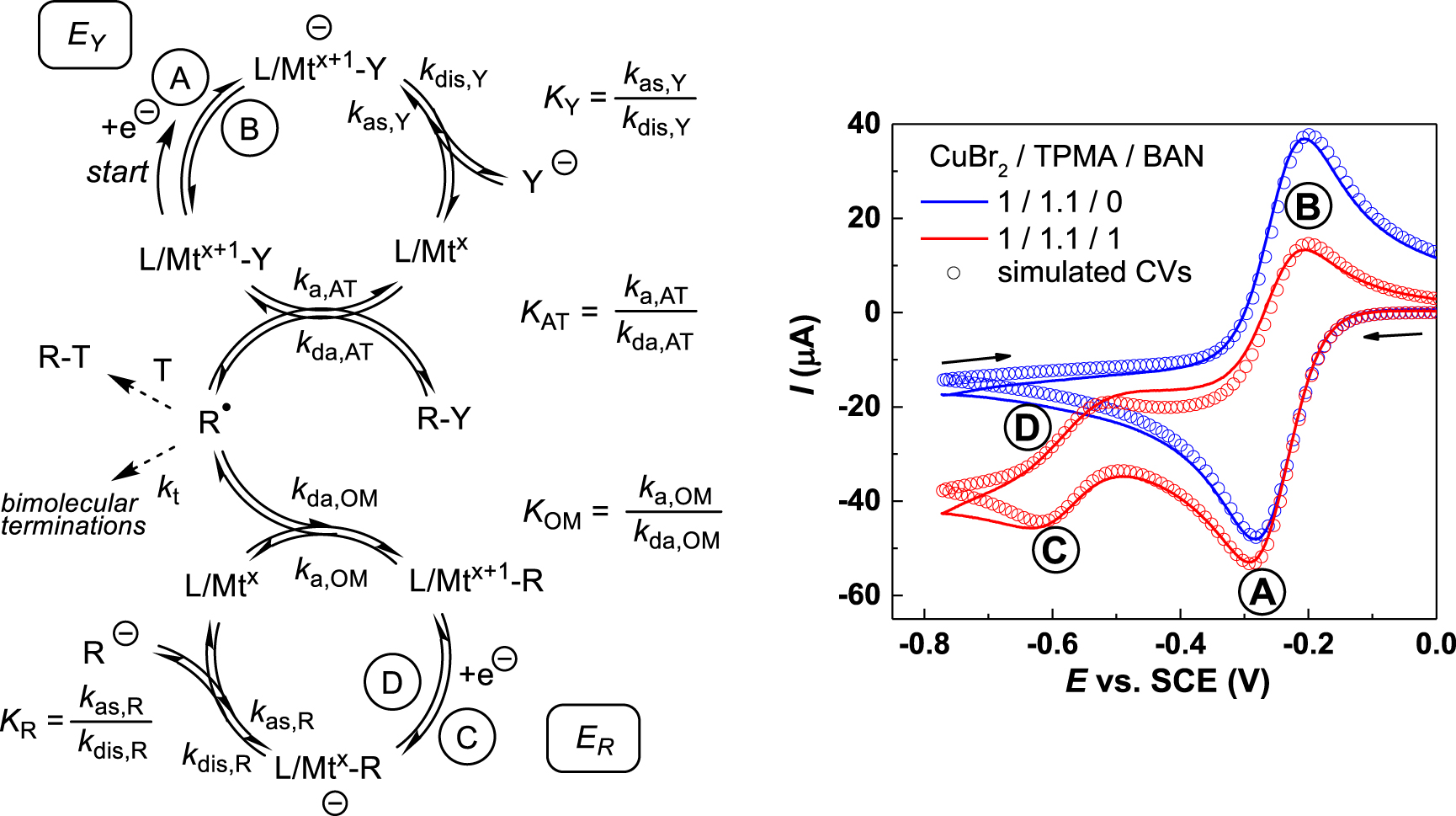
4.4. Electrochemical simulations
The simultaneous experimental determination of the L∕Mtx+1–R bond homolysis thermodynamic and kinetic parameters has been possible for certain copper(II) systems from the simulation of cyclic voltammograms. The method is based on a cascade of events triggered and followed electrochemically, where the L∕Mtx+1–R compound is formed by trapping in situ-generated radicals with in situ-generated L∕Mtx. The sequence of events and a typical electrochemical response are shown in Figure 2 [73, 74, 75]. One-electron reduction of a stable L∕Mtx+1–Y precursor, where Mtx+1 = CuII and Y = Cl or Br, at the EY potential (wave A) yields L∕Mtx and Y− at the electrode surface and is reversible (blue curve) in the absence of R–Y substrate. The EY potential is affected by the rapid Y− dissociation equilibrium (KY, EC process) and is thus [Y−]-dependent. Addition of an alkyl halide substrate (R–Y) alters the voltammetric response (red curve) as a consequence of the following events: the reduced L∕Mtx complex activates R–Y by atom transfer (AT, rate constant ka,AT) to generate R∙ and L∕Mtx+1–Y, decreasing the intensity of the reverse wave B. This R–Y activation is reversible (KAT equilibrium), as exploited in the popular “atom transfer radical polymerization” (ATRP) [76, 77]. At this point, the produced R∙ can either (i) be trapped by L∕Mtx+1–Y (deactivation by atom transfer, rate constant kda,AT); (ii) be trapped (if desired) by an added external trapping agent T; (iii) be trapped by L∕Mtx (deactivation to generate by L∕Mtx+1–R, rate constant kda,OM); or (iv) spontaneously terminate by coupling and/or disproportionation. The L∕Mtx+1–R bond formation is also reversible (KOM equilibrium). This bond formation occurs only if the bond is sufficiently strong (sufficiently small KOM) and is evidenced by the appearance of waves C and D at the ER potential, which is more negative than EY because of the greater donating power of R− relative to Y−. The reversibility of this second electrochemical process depends on the follow-up events of the electrochemically generated [L∕Mtx–R]− (e.g. equilibrated release of the reactive carbanion R−, KR). The simulation of the observed voltammogram depends on many independent parameters (EY, ER, KY, ka,AT, kda,AT, ka,OM, kda,OM, KR, [R–Y], scan rate), but the thorough exploration of the reaction space (variations of the scan rate and [R–Y]) and the independent determination of certain parameters under simplified conditions (for instance, using TEMPO as an irreversible radical trap under saturation conditions) has allowed an improvement of the fit.
In the more accurate investigation [75], the solvent-dependent KOM was found to range from (4.2 ± 1.4) × 10−10 for [(TPMA)CuII–CH2CN]+ (a primary alkyl radical) in DMF to (2.7 ± 1.4) × 10−6 for [(TPMA)CuII–CH(CH3)COOCH3]+ (a secondary alkyl radical) in MeCN, whereas tertiary radicals (e.g. ∙CMe2COOR) are not efficiently trapped for the investigated systems. The corresponding BDFE range is 8.2–13.6 kcal⋅mol−1. The activation rate constant (ka,OM) spans a wide range from (4.6 ± 0.8) × 10−2 s−1 for [(TPMA)CuII–CH2CN]+ in MeCN to (6.4 ± 2.4) × 102 s−1 for [(TPMA)CuII–CH(CH3)COOCH3]+ in DMSO and the deactivation rate constant (kda,OM) is always >107 M−1⋅s−1, ranging from (4.1 ± 0.6) × 107 M−1⋅s−1 for [(TPMA)CuII‐CH2CN]+ in MeCN to (1.4 ± 0.2) × 109 M−1⋅s−1 for [(TPMA)CuII–CH(CH3)CN]+ in DMF. This method, only applied so far to the investigation of organocopper(II) species [73, 74, 75], can potentially be extended to other L∕Mtx+1–R systems with labile Mtx+1–R bonds. The OM equilibrium parameter can be accurately estimated only if ka,OM is sufficiently high to have an impact on the CV shape within the timescale of the measurement, but at the same time the Mtx+1–R bond must be strong enough to allow the generation of observable amounts of the organometallic species in situ. These conditions are associated to systems that are generally not amenable to isolation as pure compounds, at least under standard laboratory conditions.
Reported experimental and computational bond dissociation/activation enthalpies for compounds [(CO)5MnI–RF] (RF = CF3, CHF2).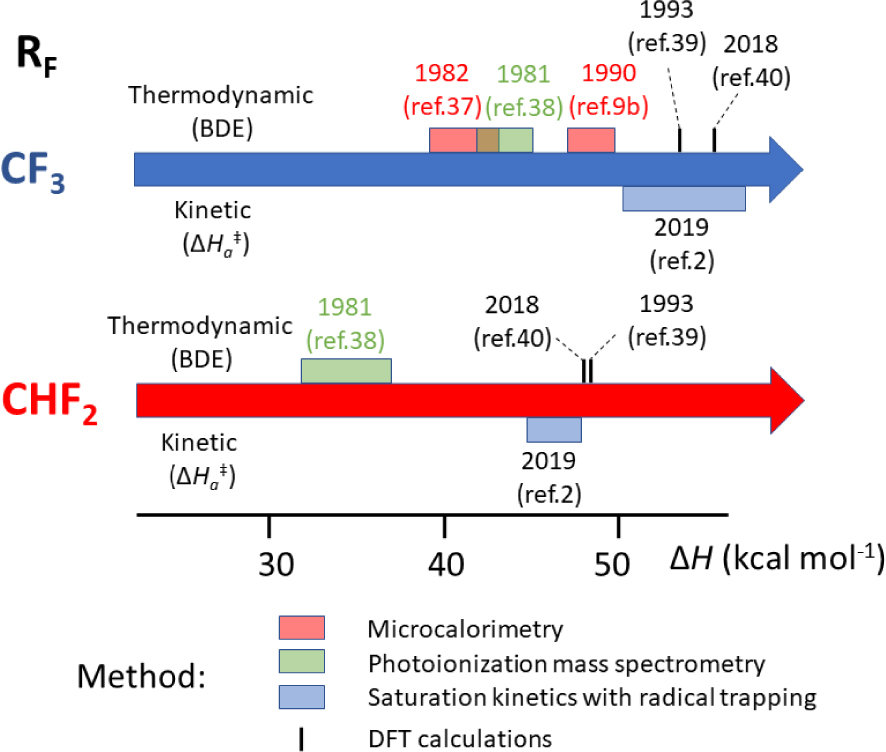
4.5. Computational studies
In addition to all the above-mentioned experimental methods of investigation, the L∕Mtx+1–R bond homolysis, with particular focus on the thermodynamic BDE parameter, has been investigated by theoretical calculations, in most cases using a density functional theory (DFT) approach. The computational error cannot be assessed in DFT methods, making this approach of limited and doubtful value for the quantitative estimation of BDEs. Indeed, values spreading over a very large range have been obtained for the same compound depending on the selected functional. For instance, the intensively investigated coenzyme B12 has afforded BDEs from 29.5 kcal⋅mol−1 (close to the experimentally accepted value) to 15 kcal⋅mol−1 or less [78, 79, 80, 81, 82, 83]. Pure functionals appear to afford better results than hybrid functionals [80, 84, 85] and it is crucial to appropriately consider dispersion forces [80]. Complexes than can adopt two or more different spin configurations introduce additional difficulties because different functionals introduce different relative stabilization effects for spin isomers [86]. Thus, confidence in the relevance of any computed value must be gained from the extensive benchmarking of the computational method against any available (and reliable) experimental value. The most reliable information concerns the enthalpic (BDE, ) parameters, not the free energies. This is related to the difficult transposition of the computed gas phase entropic correction to the condensed phase. In spite of the uncertainties related to the absolute computational error, DFT investigations have proven invaluable to rationalize observed (sometimes unexpected) phenomena, providing useful insight and understanding, and to predict trends when exploring a series of closely related systems, assisting the design and experimental development of new systems capable of achieving a desired performance. A few examples of the contribution of DFT calculations for work carried out in my laboratory and in those of my collaborators will be presented in the remainder of this article.
4.6. Reassessing bond strengths: comparison of calorimetric, kinetic and computational data
As stated in Section 4.1, old thermochemical data have occasionally been shown erroneous. A recent reassessment based on work carried out in my laboratory has concerned the Mn–C BDE in [(CO)5MnI–CF3] and [(CO)5MnI–CHF2]. Figure 3 summarizes the evolution of the experimental and computational efforts to assess the bond strength of these two compounds. For [(CO)5MnI–CF3], the BDE was first evaluated by Connor et al. in 1982 by microcalorimetric determinations of the enthalpies of sublimation, thermal decomposition, bromination and iodination of the compound, yielding its enthalpy of formation through thermochemical cycles. This value could then be combined with the already assessed Mn–Mn BDE in [Mn2(CO)10] (94 kJ⋅mol−1), leading to the estimation, on the basis of additional assumptions, of the Mn–CF3 BDE as 172 ± 7 kJ⋅mol−1 (41.1 ± 1.7 kcal⋅mol−1) [87]. A re-evaluation in a 1990 review article by Martinho Simões and Beauchamp [19], based on a new and perceived more precise Mn–Mn BDE in [Mn2(CO)10] (159 ± 21 kJ⋅mol−1), placed this BDE at 203 ± 6 kJ⋅mol−1 (48.5 ± 1.4 kcal⋅mol−1). However, an independent photoionization mass spectrometric study cited in the same review article [19] and published only in a 1981 Ph.D. thesis [88], which also used thermochemical cycles and assumptions, gave a BDE of 182 ± 11 kJ⋅mol−1 (43.5 ± 2.6 kcal⋅mol−1). The same method also provided a BDE of 144 ± 11 kJ⋅mol−1 (34.4 ± 2.6 kcal⋅mol−1) for the Mn–C bond in [(CO)5MnI–CHF2] [19, 88]. In 1993, however, Folga and Ziegler applied the DFT approach for the computation of BDEs in a number of Mt–H and Mt–C bonds in [(CO)5MnI–R] and [(CO)4CoI–R] compounds, including those with R = CF3 and CHF2, using a local density approximation (LDA) with the optional addition of non-local exchange and correlation corrections (LDA/NL) [89]. The BDE values for these two systems were calculated as 53.5 and 48.4 kcal⋅mol−1 at the more accurate LDA/NL level, respectively (or 72.6 and 66.0 kcal⋅mol−1 at the LDA level) and these authors made the explicit suggestion that the previously published experimental values are too low. However, as mentioned in Section 4.5, the DFT methods are not quantitatively reliable and there may be questions about the suitability of the chosen theory level. No further studies on these bonds have apparently appeared until our own recent experimental and computational reinvestigations [5, 90].
The bonds in question are much stronger than for any of the experimentally investigated compounds reported until then. The highest value available in the literature at that time was apparently 39.5 ± 1.0 kcal⋅mol−1 for compound [(H2O)5CrIII–CH2‐p‐pyH]3+, investigated in the 55–64 °C range [39]. We could find a suitable trapping agent (tris(trimethylsilyl)silane, TTMSS) and experimental conditions (70–100 °C in C6D6 solution, TTMSS∕Mn = 10) yielding saturation kinetics for the [(CO)5MnI–RF] disappearance (RF = CF3, CHF2 and CH2CF3). The resulting bond homolysis activation parameters are 𝛥Ha = 53.8 ± 3.5 (CF3), 46.3 ± 1.6 (CHF2), 50.6 ± 0.8 (CH2CF3) kcal⋅mol−1; and 𝛥Sa = 66.0 ± 9.5 (CF3), 55.8 ± 4.7 (CHF2), 65.4 ± 2.2 (CH2CF3) cal⋅mol−1⋅K−1. In spite of the very strong bonds, the very high activation entropies (higher than for any previously investigated L∕Mtx+1–R bond homolysis) bring the 𝛥Ga values in a suitable range for kinetic monitoring, namely ka in the (0.85–63) × 10−5 s−1 range (half-lives between 23 h and 18 min). On the basis of the usual assumption of diffusion-limited recombination (𝛥Hda ≈ 2 kcal⋅mol−1), the estimated BDEs for the CF3 and CHF2 systems (51.8 and 44.3 kcal⋅mol−1, respectively) are quite close to those calculated by Folga and Ziegler at the LDA/NL level and much higher than those previously obtained by microcalorimetry and by photoionization mass spectrometry. We have further investigated the bond homolysis by the DFT approach [90] using a dispersion-corrected hybrid functional (BPW91*-D3), a functional that gave matching BDE values for several RF-H benchmarks and quite different than that previously used by Folga and Ziegler. This functional yielded BDEs for the [(CO)5Mn–RF] bonds (55.1, CF3; 48.0, CHF2; 50.5, CH2CF3; kcal⋅mol−1) that are rather close to those estimated from the kinetically determined activation parameters and to the LDA/NL values reported by Folga and Ziegler. It was particularly rewarding to observe the same trend from the calculations and the experimental kinetics, with a strojnger bond for the CF3 compound, a weaker one for the CHF2 compound, and an intermediate strength for the CH2CF3 compound.
Incidentally, the DFT investigation was extended to all F-substituted ethyl groups, yielding the results shown in Figure 4 (left). The investigation shows a bond strengthening upon introduction of 𝛼 and 𝛽 F substituents. There is a >3 kcal⋅mol−1 increase from C𝛼H2 to C𝛼F2 with the greater difference being associated to the introduction of the second 𝛼-F substituent and a quantitatively even stronger and continuous BDE increase upon addition of 𝛽-F substituents (>7 kcal⋅mol−1 from C𝛽H3 to C𝛽F3). Another organometallic system, T = [CoII(acac)2], yields a qualitatively identical bond strengthening trend (Figure 4 center), whereas the opposite trend (decreasing BDE by both 𝛼-F and 𝛽-F substitution) occurs for T = I. The reason for the different trends is related to the opposite bond polarity and to the consequently opposite effect of the electronegative F atoms on the energetic cost of the charge reorganization that is associated to the homolytic bond cleavage [90]. I’ll come back to the cobalt system in Section 5.3.
DFT-calculated T‐CFnH2−nCFmH3−m BDEs (kcal/mol) (n = 0, 1, 2; m = 0, 1, 2, 3). T = Mn(CO)5 (left), Co(acac)2 (center), I (right). Reproduced with permission from Ref. [90]. Copyright 2018 Elsevier Science.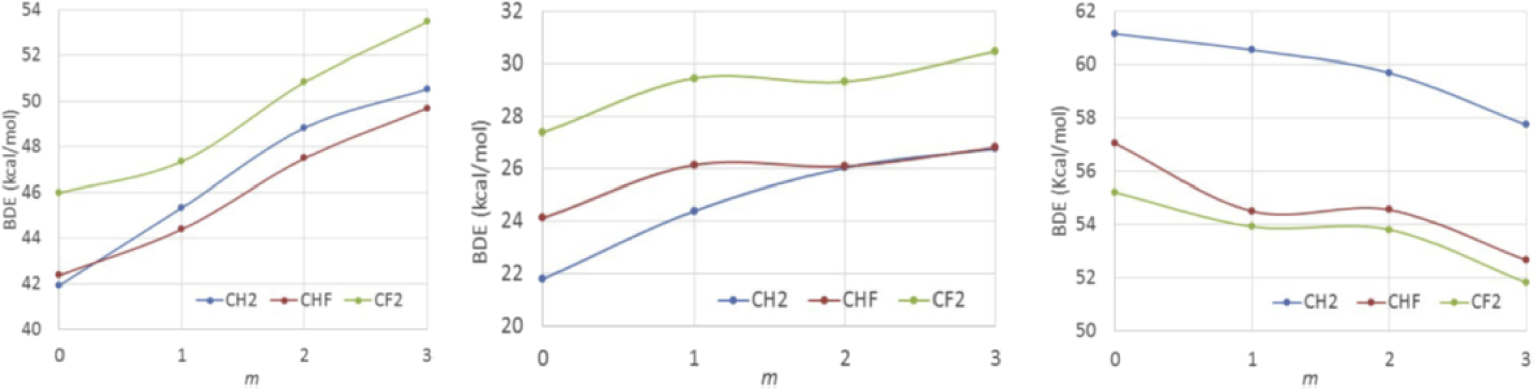
5. A few OMRP tales
I now wish to tell a few short stories on how homolytically weak metal–carbon bonds can aid, or play havoc, in an area of strong interest and research activity for the polymer chemistry community, namely controlled radical polymerization (CRP). This polymerization strategy relies on the reduced impact of terminations relative to propagation, to the point of yielding quasi-living chain-growth. In terms of the general radical reactivity shown in Scheme 1, the useful chemistry is the repetitive addition of the radical polymer chain-end to the monomer . This leads to polymers of controlled R0–Mn-T composition with chain-end functionality (R0 and T) approaching 100% and narrow molar mass dispersities around the average degree of polymerization (n), which is targeted on the basis of the initial molar monomer/initiator ratio. There are several ways to achieve this control, depending on the nature of the selected controlling agent (T) used in combination with a conventional radical source (producing the primary radical) or in a unimolecular R0–T initiator. Two different families of methods can be distinguished on the basis of the Pn–T dormant species activation, i.e. dissociative or associative, named respectively “reversible termination” (or “reversible deactivation”) and “degenerative transfer” [91]. I’ll mostly focus on the dissociative activation method and on the use of a metal complex as the radical concentration moderator (T = L∕Mtx). Reversible trapping by L∕Mtx yields an organometallic dormant species L∕Mtx+1–Pn. For this reason, I have named this approach “organometallic radical polymerization” and gave it the OMRP acronym [92]. In common usage, the method has later become known as “organometallic-mediated radical polymerization” [93, 94, 95, 96, 97, 98], which is not in my mind a completely appropriate name, because the mediating agent is not necessarily organometallic; only the dormant species is. However, the OMRP acronym stuck.
5.1. Steric control and ligand design
It has occurred to me that OMRP has a clear advantage, relative to all other CRP strategies that use small atoms or groups as T (e.g. halogens, ONR2): the steric parameter can be modulated by ligand engineering with a profound effect on the metal–carbon BDE, as already discussed in Section 4.2. Steric labilization of the metal–carbon bond makes the dormant species more easily reactivated, allowing CRP to be extended to less reactive monomers, i.e. associated to more reactive chain-end radicals. An opportunity to test this idea came when Kevin M. Smith, a former post-doc of mine and now Professor at UBC Okanagan, offered to test his half-sandwich CrII complexes as moderators. He had obtained a series or [CpCrII(nacnacAr,Ar′)] complexes (nacnacAr,Ar′ = ArNC(CH3)CHC(CH3)NAr′) [99] and had shown that they could be converted to stable [CpCrIII(nacnacAr,Ar′)(CH3)] complexes by oxidation/alkylation, whereas derivatives with larger alkyl groups only led to decomposition products presumably resulting from CrIII–alkyl bond homolysis and subsequent radical reactivity. Of particular interest was the comparison between the symmetric (Ar = Ar′ = 2,6‐C6H3R2) complexes with R = Me(Xyl) or iPr (Dipp), which yield a quite different steric bulk in the moderating species.
Vinyl acetate (VAc), CH2 = CHOCOCH3, attracts great attention because the corresponding polymer (PVAc) is the precursor of water-soluble poly(vinyl alcohol). Therefore, the incorporation of PVAc blocks in tailored polymer chains opens the way to many useful applications. The radical polymerization of this monomer generates non-stabilized, relatively reactive PVAc–CH2CH∙(OCOCH3) chain ends by the dominant regular (head-tail) monomer additions and even less stabilized, more reactive PVAc– chain ends by the less frequent (ca. 1–2%) [100] inverted or head-head monomer additions. Earlier attempts to control the VAc polymerization with capping halogens (i.e. by ATRP) [101] or nitroxides [102] led to very slow conversions or to inhibition. It was thus of interest to test the half-sandwich CrII complexes as moderators.
Polymerizations initiated by the labile V-70 azo initiator (R0–N = N–R0 with R0 = (CH3)2C(OCH3)CH2C∙(CH3)(CN); t1∕2 = 10 h at 30 °C) in the presence of the less bulky [CpCrII(nacnacXyl,Xyl)] system did not give any evidence of reversible chain trapping of polystyrene radical chains (same polymerization rate as the metal-free control). Conversely, the polymerization of VAc was much slower than the metal-free control, but not fully inhibited. This indicates reversible CrIII–C bond formation with the PVAc∙ chains, whereas the PS chain-end radical does not form a sufficiently strong bond. On the other hand, the bulkier [CpCrII(nacnacDipp,Dipp)] complex allowed a faster VAc polymerization that exhibited the expected traits of CRP, albeit with less than ideal control [103]. Kevin was later able to obtain a well-defined CrIII alkyl compound with a bulky neopentyl group, [CpCrIII(nacnacXyl,Xyl)(CH2 tBu)], which proved an excellent single-molecule initiator for a slow but relatively well-controlled VAc polymerization [54, 104]. Interestingly, an analogous alkylchromium(III) complex with the bulkier nacnacDipp,Dipp could not be obtained. Computational studies of the [CpCrIII(nacnacAr,Ar)‐CH(CH3)OCOCH3] system, where the alkyl group models a poly(vinyl acetate) chain, confirmed the significant steric labilization for the CrIII–C bond homolysis (𝛥E = 25.9, 20.6 and 18.6 kcal⋅mol−1 for Ar = Ph, Xyl and Dipp, respectively) [54]. Even though clearly illustrating the principle of ligand-based steric labilization in OMRP, this study remains of purely academic interest for two reasons. The first one is the elaborate synthesis, fragility (air sensitivity) and toxicity of the moderating agent, which remains as chain end group in the macromolecular product. The second reason is related to a slowdown phenomenon, which results from the inverted monomer additions. I’ll return to this phenomenon in the next section.
Another steric labilization phenomenon was highlighted in my laboratory in the same period for a cobalt bis(𝛽-diketonate) system. Work by Antoine Debuigne et al. had previously shown the excellent performance of a simple and commercially available compound, [CoII(acac)2], as moderating agent for the VAc radical polymerization [105]. This polymerization is not negatively affected by a polymerization slowdown for reasons that will be detailed in the next section. It actually occurs by the associative activation method, whereas the [(acac)2CoIII‐PVAc] bond in the dormant chains is too strong to yield significant polymerization rates by reversible dissociation, but dissociative activation can be promoted by the addition of monodentate donor ligands [106]. This phenomenon is related to the moderator stabilization by coordination, [CoII(acac)2(L)n](n = 1,2), and will not be further detailed here, since it does not involve a steric modulation of the CoIII–C BDE. Of greater interest to the present discussion is the steric modulation of the CoIII–PVAc BDE, in the absence of additional donor ligands, by operating on the 𝛽-diketonate ligand scaffold. Indeed, the related bis(2,2,6,6-hexamethylhepta-3,5-dionate) complex, [Co{tBuC(O)CHC(O)tBu}2], induced a faster VAc polymerization in the dissociative activation regime, while at the same time and for the same reason decreasing the positive acceleration effect of added donor ligands [107].
It is also of interest to point out that the VAc polymerization has also been controlled by porphyrin [108, 109, 110] and Schiff-base [111, 112, 113, 114] cobalt(II) complexes. These polymerizations only occur by degenerative exchange, by photoinduced bond cleavage, or by addition of donor ligands, whereas the dissociative thermal activation of the dormant chains is completely inhibited in spite of the high ligand steric bulk in some cases (e.g. tetramesitylporphyrin). This suggests that the O4 coordination sphere in the bis(𝛽-diketonate) systems labilizes the CoIII–C bond relative to the N4 and N2O2 coordination spheres of porphyrin and Schiff base ligands. Indeed, further playing with electron delocalization in the conjugated O,O-bidentate ligand by switching to the 9-oxyphenalenone (OPN) ligand system, the CoIII–PVAc bond was weakened to such a point where the presence of competitive catalytic chain transfer (CCT) could be highlighted for the first time in VAc polymerization [115] (see Section 5.4 for further details on the CCT phenomenon).
5.2. Effect of the inverted monomer additions for VAc
How could [CoII(acac)2] sustain a well-controlled PVAc∙ chain growth without any slowdown or loss of control? The primary PVAc– chain ends that are occasionally obtained (ca. 1–2%) by inverted monomer addition are expected to yield stronger, hence less easily reactivatable, PVAc–CH(OCOCH3)CH2–Mtx+1∕L bonds relative to the bond established by the regular secondary chain-end radical, PVAc–CH2CH(OCOCH3)–Mtx+1∕L. Such a continuous accumulation of less easily reactivatable dormant chains is anticipated to induce a decrease of polymerization rate in a dissociative activation mode, as indeed observed for L∕Mtx = [CpCrII(nacnacXyl,Xyl)] (previous section) [104], and a loss of control in the degenerative transfer activation mode. There are only two possible explanations: either [CoII(acac)2] is somehow able to reduce the frequency of the head-head additions, or the CoIII–C bond to the primary radical in the dormant species is not significantly stronger (or is weaker) than the bond obtained after trapping the regular secondary chain-end radical. The first possibility would imply a monomer addition to the caged {PVAc∙,CoII(acac)2} fragment pair with an influence of the cobalt complex on the relative addition barriers.
Above: relative enthalpies and optimized geometries of the species implicated in the deactivation process of the tail (left) and head (right) PVAc radical models by [CoII(acac)2] (reproduced with permission from Ref. [116]; copyright 2013 American Chemical Society). Below: activation enthalpies (in kcal⋅mol−1) for the tail and head dormant species, and their difference, obtained with different functionals.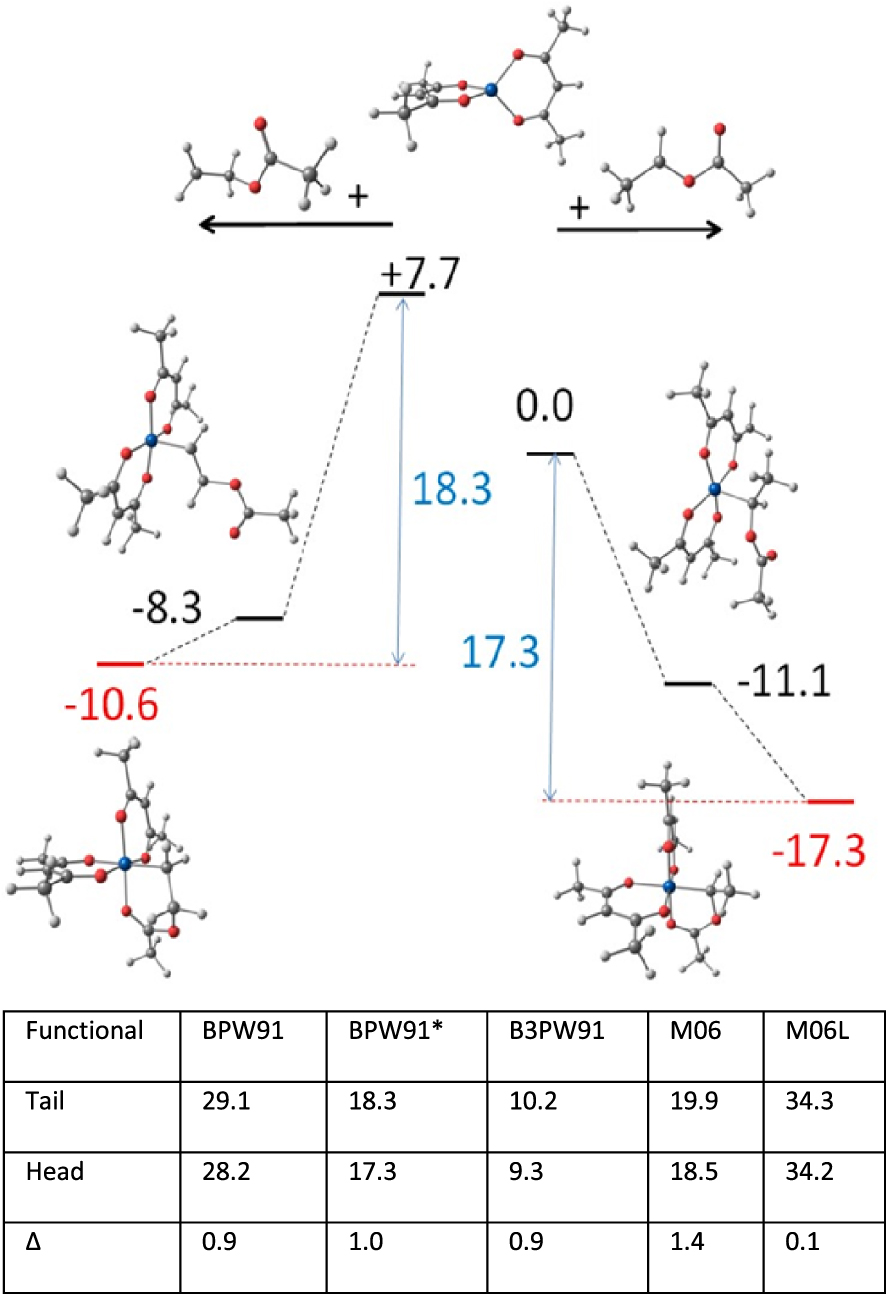
In a collaborative effort with Antoine Debuigne [116], the first option was explored by a thorough NMR investigation of the recovered PVAc–CoIII(acac)2 macromolecules (both in-chain and chain-end monomer configurations), revealing that the inverted monomer frequency is undistinguishable from that of free radical polymerization. Thus, either propagation occurs on the uncaged radical, or the [CoII(acac)2] proximity has no significant effect on the relative monomer addition barriers. The second option was tested by DFT calculations, using five different functionals and the CH3(CH3COO)CH∙ and radicals to model the regular- and inverted-monomer PVAc chain ends. This is a case where the type of functional has a dramatic effect on the BDE, particularly because a spin state change occurs during the bond cleavage process: the diamagnetic [(acac)2CoIII–CH(OOCCH3)CH3] and [(acac)2CoIII–CH2CH2(OOCCH3)] species yield the organic radical (S = 1∕2) and a spin quartet (S = 3∕2)[CoII(acac)2] complex. The [(acac)2CoIII–CH(OOCCH3)CH3] BDE was calculated as low as 9.3 kcal⋅mol−1 with the hybrid B3LYP functional and as high as 34.2 kcal⋅mol−1 with the diffusion-corrected M06L functional, see Figure 5. However, the difference between the two activation enthalpies obtained with all functionals varies in a very narrow range. Furthermore, these differences are very close to zero, suggesting that the two dormant species should be reactivated at nearly equivalent rates. The feature making this [CoII(acac)2] moderating agent “special” is its coordinative unsaturation. Bond formation between [CoII(acac)2] and the radical yields a diamagnetic 5-coordinate complex with a square pyramidal geometry and an axial alkyl group. This 16-electron species can be further stabilized by saturation of the vacant coordination site. In the absence of added donor ligands, chelation by the ester carbonyl function of the Co-bonded monomer unit prevails for entropic reasons over coordination of an external monomer. Thus, the regular (secondary) chain-end model radical (Figure 5, above right) forms a better stabilizing 5-membered chelate ring, whereas the inverted (primary) chain-end model radical (Figure 5, above left), which yields as expected a homolytically stronger bond, forms a poorer stabilizing 6-membered chelate ring. The opposite trends of the CoIII–C BDE and chelate ring stabilization effects re-equilibrate the needed enthalpy cost for the reactivation of the two dormant species. The chelated nature of the PVAc chain end in the dormant species had been experimentally established by a previous NMR and IR investigation of a small [(acac)2CoIII–VAcn–R0] oligomer mixture (n ∼ 4) [117], which can be isolated from the V-70-initiated VAc polymerization in the presence of a large [CoII(acac)2] excess. Incidentally, this product is an excellent unimolecular initiator for the polymerization of VAc and other monomers [117, 118, 119, 120].
5.3. Effect of the inverted monomer additions for VDF
Vinylidene fluoride (VDF), CH2 = CF2, is another less activated monomer of great interest for a variety of high-tech applications and polymerizes only by the radical mechanism [121]. Its polymerization with a high level of control has long been sought but is hampered by the high inverted monomer addition probability. The chain growth mainly involves regular head-tail additions to yield the head PVDF– radical, while the minor (ca. 4–5%) head-head additions lead to the tail PVDF– radical. Both radicals are highly reactive and yield strong PVDF-T bonds in the dormant species. Iodine-transfer polymerization (working through the degenerative transfer principle) was the first methods to produce controlled PVDF chains, though with limited control [122]. The accumulation of the less easily reactivatable tail dormant species, PVDF–CF2CH2–I, was assumed to be responsible for this limitation and higher degrees of polymerization could only be obtained using chemical tricks for this species reactivation [123, 124, 125]. This hypothesis was later validated by DFT calculations on model compounds (Figure 4, right) [90], showing that the associative exchange of PVDF–CF2CH2–I with the dominant PVDF– radical chains is endoergic (non-degenerate) because the PVDF–CF2CH2–I bond is stronger than the PVDF–CH2CF2–I bond.
Bruno Améduri attracted my attention to the VDF CRP problem. With his group at the ICG Montpellier, he had already shown that the VDF polymerization using another degenerate transfer method of control, which uses a xanthate (R0–SC(S)–OEt) as reversible chain transfer agent, yields a similar loss of control beyond relatively small targeted degrees of polymerization [126]. In a first collaborative effort, by performing again DFT calculations on model compounds, we showed that the tail dormant chains, PVDF–CF2CH2–SC(S)OEt, have a homolytically stronger C–S bond than the head ones, PVDF–CH2CF2–SC(S)OEt [127]. Thus, the behavior of the VDF degenerate transfer polymerization with iodoalkanes and xanthate transfer agents is qualitatively the same. The kinetic model indicated that control was lost after all chains are trapped in the tail isomeric form but also suggested that these dormant species are not dead. They can be reactivated, through too slowly to ensure reasonable control. Indeed, the 100% tail PVDF–SC(S)OEt product could be reactivated by chain extension with VAc, yielding well-defined PVDF-b-PVAc diblock copolymers [128]. The DFT study could rationalize this phenomenon. A more interesting question, however, was whether the two types of dormant chains, PVDF–CH2CF2–T and PVDF–CF2CH2–T, could equally well be reactivated through an OMRP approach. The L∕Mtx moderator choice was naturally oriented toward [CoII(acac)2] because of its proven ability to yield homolytically weak bonds with the PVAc radical chains.
As already shown in Figure 4 (center), our DFT calculations led to the prediction of a bond strengthening upon introduction of F atoms on the alkyl ligand, at both the 𝛼 and 𝛽 positions, like for the [(CO)5Mn‐Et] system (Figure 4, left), and opposite to the trend observed for I-Et (Figure 4, left) and EtOC(S)S–Et [90]. In particular, the cost of the reactivation of the tail and head dormant chains is predicted to be quite similar, even slightly in favor of the tail species, 26.0 kcal⋅mol−1 for the [(acac)2Co–CH2CHF2] model, versus 27.4 kcal⋅mol−1 for the head [(acac)2Co–CF2CH3] model. Encouraged by these results and with the help of Debuigne’s oligomeric [(acac)2CoIII–VAc∼4–R0] initiator, we proceeded to experimentally test the [CoII(acac)2]-mediated OMRP of VDF and we were very pleased with the result: the VDF polymerization proceeded with an unprecedented level of control up to high degrees of polymerization (>100; >4 inverted monomer additions) with a linear Mn versus conversion plot and low Mw∕Mn values (<1.3) [129]. Subsequently, we could show similar control for the polymerization initiated by the combination of [CoII(acac)2] and a conventional radical initiator, increasing the practical value of this polymerization process [130].
5.4. Catalytic chain transfer (CCT): 𝛽-H elimination or homolysis/transfer?
Catalytic chain transfer entails transfer of a chain-end 𝛽-H atom to the L∕Mtx catalyst in a first step, yielding a dead chain with an unsaturated 𝜔 end (macromonomer) and a hydride intermediate L∕Mtx+1–H. In the second step, this hydride complex transfers the H atom to the monomer, generating a new growing chain with an H 𝛼 chain end. A chain transfer catalyst operates through the same oxidation state and coordination number changes as an OMRP moderator and an ATRP catalyst. Thus, the same molecule can promote all three processes, as was first observed in my laboratory working with a half-sandwich MoIII system [131, 132, 133, 134]. Therefore, this is an unwanted phenomenon in CRP, although it is of importance in industry, if L∕Mtx has a very high CCT activity, to obtain controlled molar mass macromonomers [135].
[L∕FeII] complexes used as ATRP catalysts for styrene polymerization and proposed interplay of CCT via the OMRP dormant species.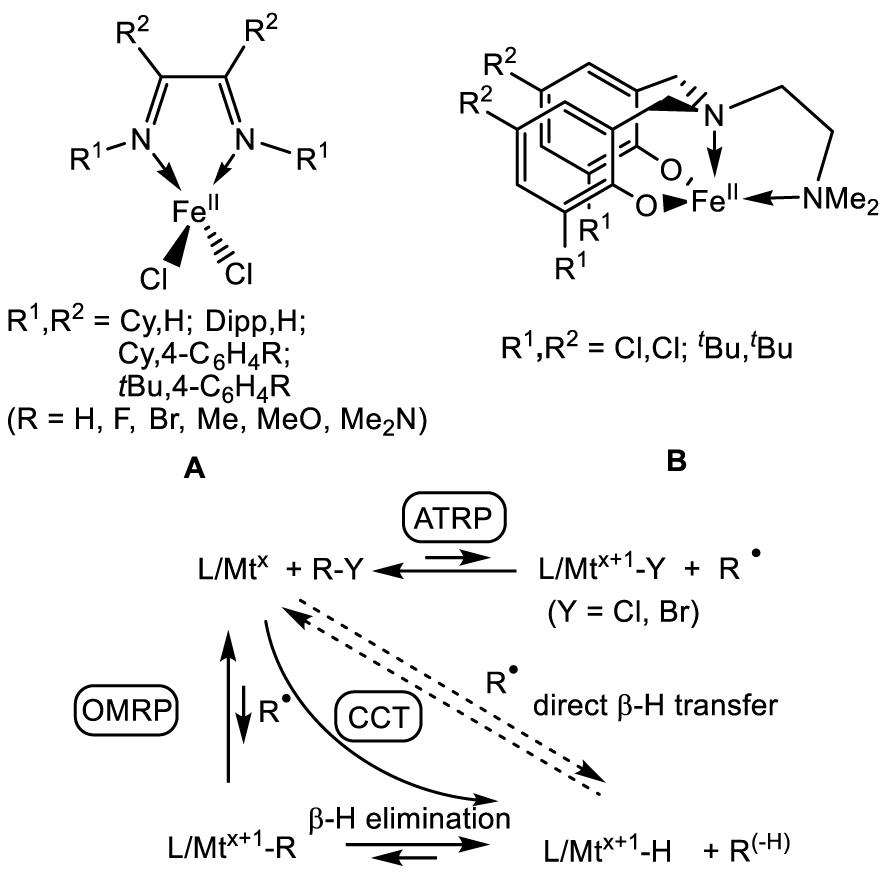
Two pathways for alkene elimination from L∕Mtx+1–R and for the reverse alkene addition to L∕Mtx+1–H.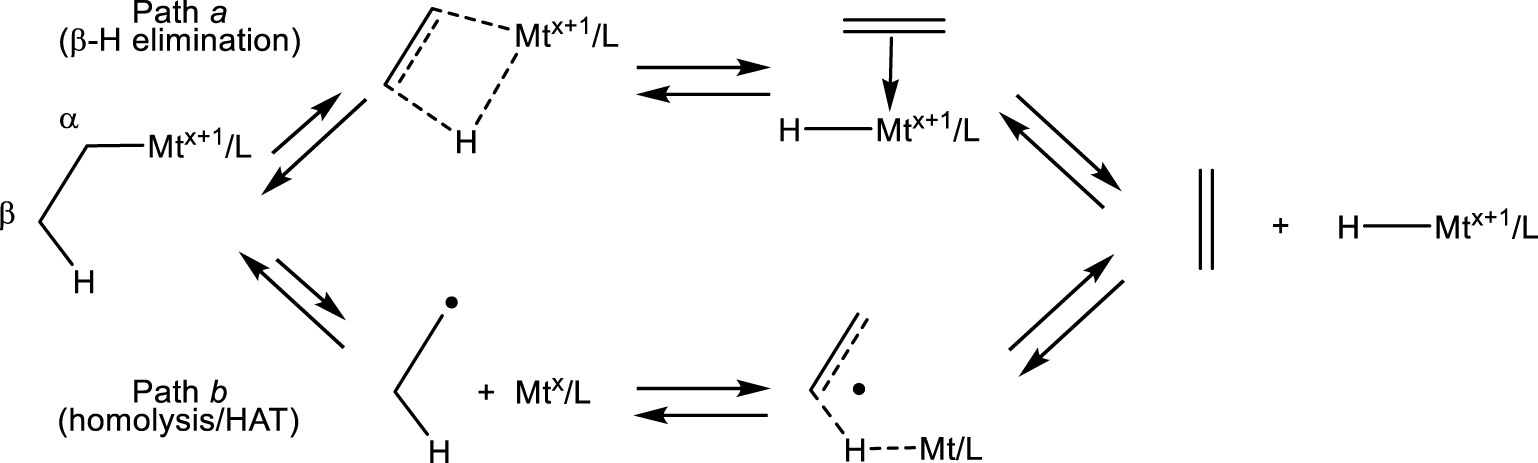
In 2006–2007 [136, 137, 138, 139], Gibson et al. showed that [FeIICl2(𝛼‐diimine)] compounds (A in Scheme 8), in combination with organohalide initiators, catalyze the ATRP of styrene, although the process was affected by variable degrees of CCT depending on the ligand substituents. These authors proposed that the CCT pathway was favored by an increased “carbophilicity” of the ATRP catalyst and that this correlated with the spin state of the [FeIICl3(𝛼‐diimine)] atom transfer product. In their proposed scheme, the increased carbophilicity would promote the direct chain trapping by L∕Mtx to generate the OMRP dormant species, which would then lead to the hydride intermediate by 𝛽-H elimination. These authors did mention that CCT may also occur by direct 𝛽-H atom transfer from the radical chain to the metal center, which was the established dogma until then, but proposed the radical trapping/𝛽-H elimination sequence to rationalize their observations.
A few years later, Michael P. Shaver (who also coauthored the previous contribution with Gibson) and his coworkers demonstrated that an apparently related system supported by a diaminobis(phenolate) ligand (B in Scheme 8) is able to control the polymerization of styrene by both ATRP and OMRP mechanisms, without any significant CCT contribution. These polymerizations were initiated using the stable [L∕FeIII–Cl] complex and a conventional radical initiator (reverse ATRP conditions), generating the [L∕FeII] catalyst in situ [140, 141]. On the basis of this result, if CCT indeed requires 𝛽-H elimination from the OMRP dormant species, it is unclear why A, which is a poorer trapping agent for the polystyrene radical chain, would lead to CCT whereas B, which more favorably leads to the OMRP dormant species, does not.
In collaboration with Shaver, I have therefore carried out a DFT study of these systems. In a first contribution, we could rationalize the better performance of the B system in ATRP/OMRP when R1, R2 = Cl, Cl relative to the tert-butyl-substituted ligand system. This is a consequence of the inductive electron withdrawing effect of the phenolato Cl substituents, leading to minor but determining energy differences that make both the ATRP and the OMRP trapping processes more favorable [55]. In a subsequent contribution, we could show that the organometallic intermediate L∕FeIII–PS, modelled as L∕FeIII–CHMePh in the calculations, has a stronger bond for B because the strain of the tetradentate diaminobis(phenolate) ligand raises the relative energy of the L∕FeII system, whereas A can relax to the preferred tetrahedral coordination environment. The establishment of a FeII⋯CHMePh interactions for A provides an insignificant stabilization (1.0 kcal⋅mol−1, versus 13–15 kcal⋅mol−1 for the BDE in B depending on the L/ substituents). Therefore, the pathway leading to CCT proceeds directly by H-atom transfer. This pathway occurs entirely along the spin quartet surface, since the ground state of the hydride product (S = 3∕2) is equivalent to the antiferromagnetic combination of the [L∕FeII] complex and styryl radical spin states (2 and − 1∕2) [142]. Furthermore, we discovered that, contrary to the earlier proposition [136], there is no spin state control of CCT: the L∕FeII systems are always spin quintets, the L∕FeIII–Cl systems are always spin sextets and the L∕FeIII–CHMePh systems are always spin quartets, independent on the ligand system (Cl2-diimine or diaminobis(phenolate)) and on the ligand substitution pattern. The different aptitude of the 𝛼-diimine systems with different ligands to promote CCT has a simpler explanation. It can be traced to electronic effects that significantly alter the ATRP activation barrier, whereas the H-atom transfer barrier is essentially unaffected. Thus, the more active ATRP catalysts render the background CCT process less significant. In conclusion, the 𝛽-H elimination hypothesis for these organoiron(III) systems has to be abandoned and the homolysis/𝛽-H transfer dogma holds for CCT.
I wish to further comment on the alkene elimination from L∕Mtx+1–R compounds (also named “dehydrometallation”) and its microscopic reverse, the alkene insertion into the L∕Mtx+1–H bond. Several contributions (that I shall not cite) on metal-promoted or catalyzed radical reactions using 3d transition metals (mostly Cr, Mn, Fe, Co, Ni and Cu) invoke the ubiquitous 𝛽-H elimination (path a in Scheme 9) as the dehydrometallation mechanism. However, the L∕Mtx+1–R bonds for those metals, at least in the oxidation states presumed in the proposed mechanisms, are homolytically quite weak and more likely follow the homolysis and 𝛽-H atom transfer pathway (path b), like the organoiron(III) system above. Path a is typically followed by complexes with homolytically strong metal–carbon bonds. Furthermore, path a requires a cis-vacant coordination site, whereas path b does not have this requirement. It only requires a homolytically weak Mt–C bond. Thus, all 𝛽-H elimination claims for 3d-metal L∕Mtx+1–R intermediates in radical processes should be reconsidered. Conversely, the reverse path b process (named “hydrogen atom transfer” or HAT) is consciously and universally invoked by those practicing radical organic chemistry as a way to trigger radical transformations. This chemistry is initiated by reactive metal hydride intermediates with homolytically weak Mt–H bonds, often made in situ from a stable L∕Mtx+1–Y precursor (halide, alkoxide, acetylacetonate, etc.) and a reducing hydride (silane, stannane, borane, etc.) [143]. However, the produced radical is then proposed to pursue its useful chemical transformations, in most cases without consideration of the possible L∕Mtx intervention as a moderating agent. I’ll return to this point in Section 6. Metal hydride complexes with homolytically strong Mt–H bonds, on the other hand, if able to provide facile access to a cis-vacant coordination site, are more likely to adopt path a (coordination/insertion) as is well-established in metal-catalyzed olefin polymerization as the initial step after a chain transfer event by 𝛽-H elimination. As a short summary: the transformation shown in Scheme 9, in both directions, prefers path a for homolytically strong Mt–R/Mt–H bonds and path b for homolytically weak Mt–R/Mt–H bonds.
5.5. Catalyzed radical termination (CRT)
In an ATRP process, the L∕Mtx ATRP catalyst may also form metal–carbon bonds with the growing radical chain, positively contributing to the polymerization control by providing an additional moderating effect. As already stated above, this OMRP/ATRP interplay was first demonstrated for a MoIII system in my laboratory [131], but was also later shown to occur for OsII [144, 145] and for FeII [55, 140, 141].
For a number of years, I have had a most fruitful collaboration with Krzysztof Matyjaszewski (Kris for his friends), who co-discovered ATRP [146] and is one of the main players in this area, mainly working with the L∕CuI–L∕CuII–Y system. The question of whether organocopper(II) species are present in L∕CuI-catalyzed ATRP has intrigued me since the beginning of our collaboration, because the natural homolytic weakness of CuII–C bonds, as suggested by the paucity of stable alkylcopper(II) compounds [147], lends hope for a controlled polymerization of less activated monomers by the OMRP approach using L∕CuI as chain trapping agent. Indeed, Kris had already shown in 1998, through the observation of a retardation effect on the polymerization rate, that L∕CuI complexes interact with propagating poly(methyl acrylate) chains while L∕CuII complexes do not, but the produced polymers did not have the expected characteristics of a controlled process and the nature of this interaction was unclear [148]. We have tested a few polymerizations of VAc in the presence of L∕CuI complexes under OMRP conditions, but the results were not exciting and were not published. Meantime, Kris and his students kept increasing the ATRP catalytic activity of L∕CuI complexes through an increase of the moderating equilibrium constant by ligand engineering. This mostly involved the tris(pyridylmethyl)amine (TPMA) ligand family (Scheme 10) [149]. A donor power increase (TPMA < TPMA∗1 < TPMA∗2 < TPMA∗3 < TPMANMe2) exerts a greater stabilizing effect on L∕CuII–Y than on L∕CuI, as evidenced by the redox potentials, resulting in a KATRP increase by several orders of magnitude. The current champion on the activity scale, [CuI(TPMANMe2)]+, was recently synthesized in a collaborative effort [150].
Ligands of the TPMA family used in ATRP and in the study of CRT.
As already pointed out in Section 4.2, a L∕Mtx+1–R bond strengthening by a greater ligand donor power had been demonstrated by previous investigations on organocobalt(III) compounds. The same phenomenon may therefore be anticipated for L∕CuII–R. However, the lower polarity of CuII–R relative to CuII–Y bonds further suggests that KOMRP should be less affected than KATRP. Indeed, this was demonstrated (see Figure 6) by the already cited electrochemical study [75] (Section 4.4). A deeper investigation of the interaction between growing poly(n-butyl acrylate) radical chains and L∕CuI, using the very active TPMA∗3 ligand, revealed that the observed polymerization rate decrease results from a new phenomenon, not previously witnessed for any other OMRP system, namely the catalytic action of the L∕CuI complex in radical termination. Since then, this phenomenon has also been highlighted for a FeII catalyst [151].
Comparison of ATRP (red) and OMRP (blue) equilibrium constants for different L systems, involving the activation of methyl 2-bromoproprionate in DMF. Reproduced with permission from Ref. [75]. Copyright 2019 American Chemical Society.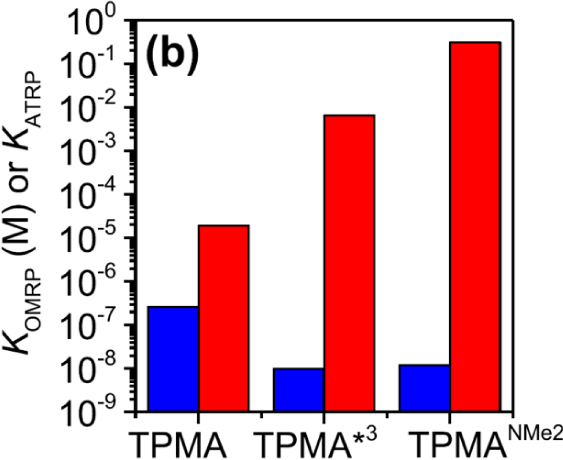
A subsequent study with different ligands has shown that the CRT activity, like the ATRP activity, scales with the ligand donor power and involves the formation of L∕CuII–R, which is then capable of promoting the interaction between the trapped radical and a second radical [152]. The intermediacy of the organometallic complex is also consistent with the absence of CRT for the polymerization of methacrylates, since the tertiary polymethacrylate chain-end radical does not form as strong a bond with the L∕CuI moderator as the secondary polyacrylate chain-end radical. To this day, however, the intimate mechanism of this radical termination process is not fully elucidated. We do not even know, as yet, what fractions of coupling and disproportionation products are produced by the CRT process, since the product distribution is skewed by other competing phenomena (e.g. conventional radical termination, reductive radical terminations) [153, 154, 155]. Further investigations aimed at determining this product distribution are ongoing. The possibility to use a L∕CuI moderator for the OMRP of less activated monomers also remains an open question.
A few of many proposed catalytic cycles for radical cross-coupling processes.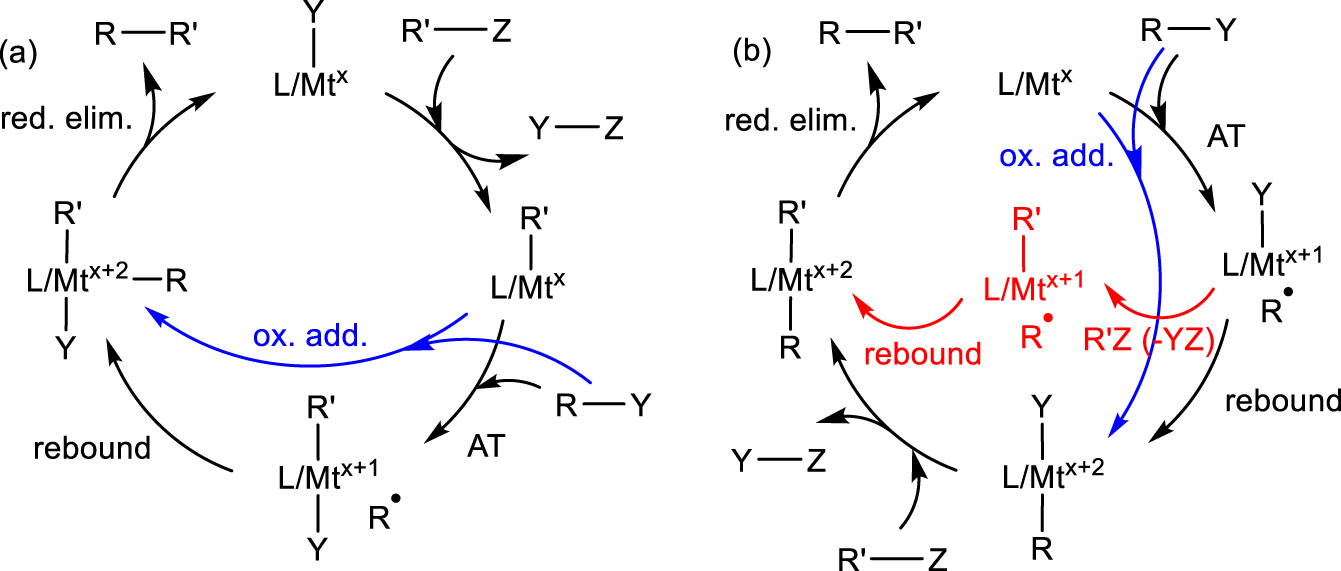
I now wish to draw a parallel between the CRT phenomenon and the C–C bond forming step involved in a family of powerful radical cross coupling processes [156, 157, 158, 159]. Several Fe-, Co-, Ni- and Cu-catalyzed cross-couplings between an alkyl or aryl halide, R–Y, and a nucleophilic coupling partner R′–Z involve radical intermediates and many different catalytic cycles have been proposed, though rarely with sufficient supporting evidence. The most consensual cycles (though not the only ones) involve FeI∕FeII∕FeIII, Co0∕CoI∕CoII, NiI∕NiII∕NiIII, or CuI∕CuII∕CuIII species. In one of many possible variants (Scheme 11a), a L∕Mtx(Y) complex is converted to an L∕Mtx(R′) intermediate by interaction with the nucleophilic reagent R′–Z with elimination of Y–Z (e.g. MgClY in Kumada-type coupling). This intermediate then activates R–Y by either a radical pathway (atom transfer, AT) to generate L∕Mtx+1(R′)(Y) and R∙ followed by radical rebound to yield L∕Mtx+2(R)(R′)(Y), or by standard 2-electron oxidative addition (indicated in blue). The cycle is then completed by the reductive elimination of the cross-coupled product RR′. Alternatively, the activation of the nucleophilic and electrophilic reagents may occur in the reverse order as shown in Scheme 11b. In the latter case, yet another possibility is that the L∕Mtx+1–Y intermediate obtained by AT is first alkylated by R′Z and then R∙ adds to the resulting L∕Mtx+1(R′) (variant indicated in red). Alkyl electrophiles seem to prefer the AT/rebound radical pathway whereas aryl electrophiles undergo 2-electron oxidative addition. Either way, the typically proposed final step is the RR′ reductive elimination, which is also represented in Scheme 12 (path a). Note that the same intermediate, under favorable circumstances, may also evolve by 𝛽-H elimination/reductive R-H elimination (path a′) to yield disproportionation products.
Radical rebound to the metal center versus the metal-bonded R′ ligand in cross-coupling.
It is possible, however, to envisage an alternative way in which the C–C bond forming step takes place. Since metal–carbon bonds are homolytically weak for a 3d metal, it is conceivable that the L∕Mtx+2(R)(R′) intermediate, even if it does form, may preferentially proceed by Mt–R bond homolysis, followed by radical rebound on R′ (Scheme 12, path b). Indeed, a direct radical rebound to the metal-bonded aryl group, without formation of a dialkyl derivative in the Mtx+2 oxidation state, has been proposed for a few Fe-catalyzed Kumada radical cross-couplings involving R–Y and ArMgBr, namely with [FeIICl2{1,2‐[(3,5‐R2C6H3)2P]2C6H4}] (R = tBu,SiMe3) [160, 161], [FeIICl2(IPr)2] [162] and [FeIIPh2(IPr2Me2)2] [163] (IPr2Me2 = 1, 3-diisopropyl-4,5-dimethylimidazol-2-ylidene; IPr = 1, 3-diisopropylimidazol-2-ylidene) pre-catalysts. For these systems, a cycle involving L(Y)∕FeII, L(Ar)FeII and L(Ar)FeIII–Y species (without involvement of an unlikely FeIV species) has been proposed. Of great relevance to this alternative pathway for C–C bond formation, Meyerstein et al. demonstrated the occurrence of path b for the reaction between [(NH3)5CoII(H2O)]2+ and radiolytically produced R∙ (R = CH3, CH2COO−): a first radical adds to generate a [(NH3)5CoIII–R]2+ transient, which then quenches a second R∙ to produce RR [164]. This pathway dominates relatively to the direct bimolecular coupling and to the heterolytic bond cleavage, which yields the alternative RH termination product and [(NH3)5CoIII(H2O)]3+. The possible addition of the second radical to the CoIII center was excluded on the basis of the high rate constant, e.g. (6 ± 3) × 108 M−1⋅s−1 for CH3, whereas addition to the metal would require dissociative replacement of an NH3 ligand, which is known to be slow (1.8 s−1 for the trans labilized ligand in [(NH3)5CoIII(CH3)]2+) [165].
Incidentally, a direct bond formation similar to that shown in Scheme 12 (path b) can also occur when R′ = H. This has been proposed for the [Co2(CO)8]-catalyzed hydrogenation of anthracene and derivatives [166]. In this reaction, [Co2(CO)8] and H2 yield [HCo(CO)4], which transfers the H atom to the substrate to yield and a stabilized anthacenyl radical. The latter is too stabilized and does not form a metal–carbon bond. Rather, it reacts with a second [HCo(CO)4] molecule to yield the hydrogenated product and a second , which combines with the first one to regenerate [Co2(CO)8].
If the alkyl radical R∙ rebounds on a metal-bonded alkyl (rather than aryl) group R′, the possible abstraction of a R′ 𝛽-H atom (path b′), leading to the disproportionation products (R–H and R′(−H)), also seems possible. This radical pathway is an alternative to the 2-electron path a′ from the LMtx+2(R)(R′) intermediate, leading to the same disproportionation products. In this respect, a seminal investigation by Kochi et al. on the effect of the metal oxidation state for the reductive elimination of dialkyliron complexes merits to be highlighted and commented [167]. Compounds [(bipy)2FeIIR2] (R = Et, nPr, among others) were thermally decomposed and the same study was carried out for their 1-electron and 2-electron oxidation products, leading to variable distributions of R–H, R(−H) and R–R. The neutral FeII complexes decompose at 50 °C and yield the disproportionation products selectively, with <0.1% of R–R, which clearly suggests a 2-electron 𝛽-H elimination/R-H reductive elimination pathway (a′ in Scheme 12). The 1-electron oxidation products [FeIII(bipy)2R2]+ are more thermally fragile, but sufficiently stable to be isolated and characterized. They decay by a first-order rate law with k in the (2.0–4.1) × 10−1 s−1 range at 30 °C, leading to mixtures of disproportionation and coupling products, the latter being dominant (75–90%). The investigation elegantly demonstrated that the majority of these products originate from an in-cage radical recombination, with the small fraction of cage escape being assessed by a [FeIII(bipy)2Et2]+∕[FeIII(bipy)2(nPr)2]+ crossover experiment, which leads to the detection of small amounts of pentane. The authors proposed that the first step of this process is bond homolysis to produce a {[(bipy)2FeIIR]+,R∙} caged pair, and stated that “this homolysis may be followed in rapid succession by the cleavage of the second alkyl-iron bond”. However, no further comments or additional experiments were offered to interpret the observed product distribution, except for noting that the [(bipy)2FeIIIEt2]+ decomposition yields a similar product distribution to the photolysis of azoethane, EtN = NEt. Clearly, after homolysis of the first bond, the residual bond in [(bipy)2FeIIR]+ should be homolytically stronger, thus a rebound of the caged radical onto the FeII-bonded alkyl group as shown in paths b and b′ of Scheme 12 is an alternative to be considered. In that case, the minor disproportionation product may indeed result from a direct 𝛽-H atom abstraction. The second oxidation process, generating [(bipy)2FeIVR2]2+, is electrochemically irreversible. Both chemical and electrochemical oxidations selectively yielded R–R with only traces or undetectable amounts of R(−H), which demonstrates a clean 2-electron reductive elimination with no involvement of radicals for the FeIV intermediate.
6. Metal complex moderators in organic radical reactions
In previous sections, I have commented on the lack of the systematic consideration, by those who practice metal-mediated/catalyzed radical reactions, of the possible contribution of reversible metal–carbon bond formation. On the other hand, the involvement of organometallic intermediates is well-recognized for systems leading to sufficiently strong Mt–C bonds, allowing their isolation or spectroscopic observation, notably organocobalt(III) species [168]. However, even bonds that are so weak as to hamper any spectroscopic detection (not to mention their isolation) may contribute to improve a radical reaction selectivity by moderating the radical concentration and consequently reducing the impact of the bimolecular terminations.
I could give a small contribution to this area thanks to the solicitation of Patrick L. Holland. He has previously investigated, in collaboration with Phil S. Baran, the mechanism of a versatile [Fe(acac)3]-catalyzed radical cross-coupling process, the scope of which had already been demonstrated by Baran [169]. The reaction couples an electron-rich alkene, R1CH = CR2R3 (including with heteroatom functionalities) with an electron-poor alkene, R4CH = CR5-EWG (EWG = electron-withdrawing group), in the presence of a silane as hydride donor and ethanol (solvent) as proton donor to produce R1CH2CR2R3–CHR4CR5(EWG)H in high yields and chemoselectivity. The Baran-Holland collaborative efforts led them to propose that the process starts by generation of an active [FeIIIH(acac)2] species, which is able to activate the donor alkene by HAT with generation of [FeII(acac)2] and a tertiary radical, R1CH2C∙R2R3. The latter then adds to the acceptor alkene to yield R1CH2CR2R3–CHR4C∙R5(EWG) and final quenching occurs by capturing a proton from ethanol and an electron from [FeII(acac)2]. This final step produces [FeIII(OEt)(acac)2], which was proposed to be the cycle resting state. Indeed, this compound was independently prepared and characterized as a diethoxo-bridged dimer and found to be catalytically competent. The reaction of [FeIII(OEt)(acac)2] with PhSiH3 then regenerates [FeIIIH(acac)2] to start the next cycle [170]. However, a few points concerning this mechanism and the observed high selectivity remained open: (i) the lack of experimental evidence of the [FeIIIH(acac)2] intermediate; (ii) the preference of the nucleophilic radical for addition to the acceptor alkene over reductive quenching; (iii) the preference of the electrophilic radical for reductive quenching over addition to a second acceptor alkene molecule (oligomerization); (iv) the low impact of bimolecular radical terminations; (v) the intimate mechanism of the reductive quenching step (stepwise outer-sphere electron transfer, OSET, or concerted proton-coupled electron transfer, PCET).
With additional and intertwined experimental and computational mechanistic investigations, the full cycle could be elucidated (Figure 7) [171]. The first part of the free energy profile, calculated using isobutene and methyl acrylate as model donor and acceptor alkenes, is shown in Figure 8. The computed free energy difference between TS1 (turnover-determining transition state, TDTS) and [Fe(acac)2(OEt)]2 (resting state) gave the cycle free energy span as 24.9 kcal⋅mol−1. This value is not far from the number experimentally provided by new kinetics experiments (22.8 ± 0.2 kcal⋅mol−1, from the turnover frequency through the Eyring relationship). A 3.3 kcal⋅mol−1 fraction of this amount is the cost of splitting the dimer into monomeric [FeIII(OEt)(acac)2] (sextet ground state). The unobserved [FeIIIH(acac)2] intermediate is nearly isoenergetic in all possible spin states (doublet, quartet and sextet), the quartet being the ground state, while dimerization is unfavorable. H atom transfer from [FeIIIH(acac)2] to isobutene has a very small barrier of 4.7 kcal⋅mol−1 through TS2, whereas the back reaction has a much higher activation barrier of 16.3 kcal⋅mol−1. It was hard to convince a reviewer, who demanded us to experimentally prove the existence of this hydride intermediate as a condition for our manuscript acceptance, that with such an energy profile the detection of this compound would be impossible: the rate constant for formation of the hydride complex from the ethoxide dimer is k1 = 3.53 × 10−6 s−1⋅M−1; the reverse step occurs with k−1 = 7.07 s−1⋅M−1 and the forward HAT step with k2 = 2.2 × 109 s−1⋅M−1. Using these rate constants and the known reagent concentrations, the upper limit on the hydride intermediate concentration is estimated from the steady-state approximation as 6 × 10−17 M. This is of course a rough approximation, using the standard free energy values calculated at room temperature. It is conceivable that the situation may improve somewhat by lowering the temperature and Holland’s student Dongyoung Kim at Yale redoubled his efforts to detect this species at lower temperatures with a wider variety of solvents, silane donors and Fe starting materials, which delayed the revised manuscript submission by a few months, but no convincing signals could be found. Fortunately, the reviewer and the editor were finally persuaded by our arguments. The reason for the very high reactivity of this [FeIIIH(acac)2] complex is obvious when considering that the calculated Fe–H homolytic BDE is only 17 kcal/mol, whereas the BDE of typical stable (through reactive) metal hydride compounds are in the 55–75 kcal⋅mol−1 range [172, 173].
Mechanism for Fe-catalyzed intermolecular alkene cross-coupling, supported by experiments and computations. Reproduced with permission from Ref. [171]. Copyright 2019 American Chemical Society.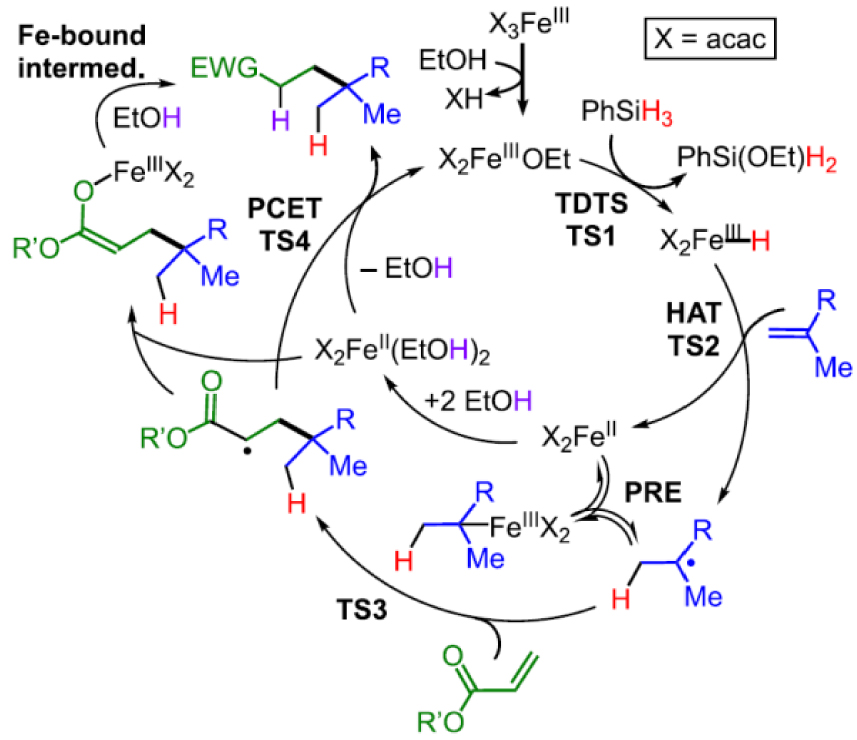
DFT-calculated energy profile of the catalytic cycle in Figure 7 from the [FeIII(acac)2(OEt)]2 resting state to the Me3C∙ radical.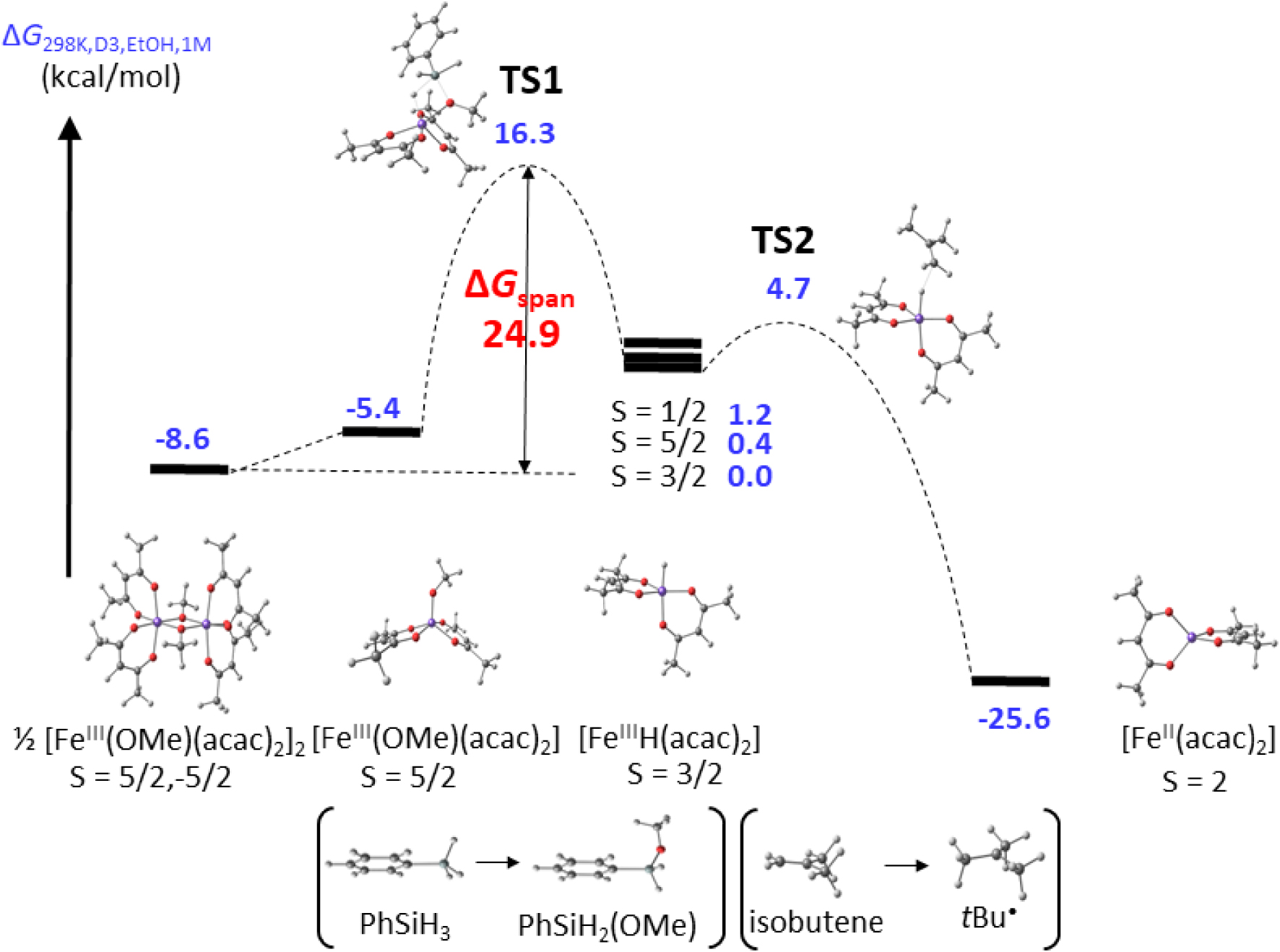
DFT-calculated energy profile of the catalytic cycle in Figure 7: PRE versus cross-coupling (TS3).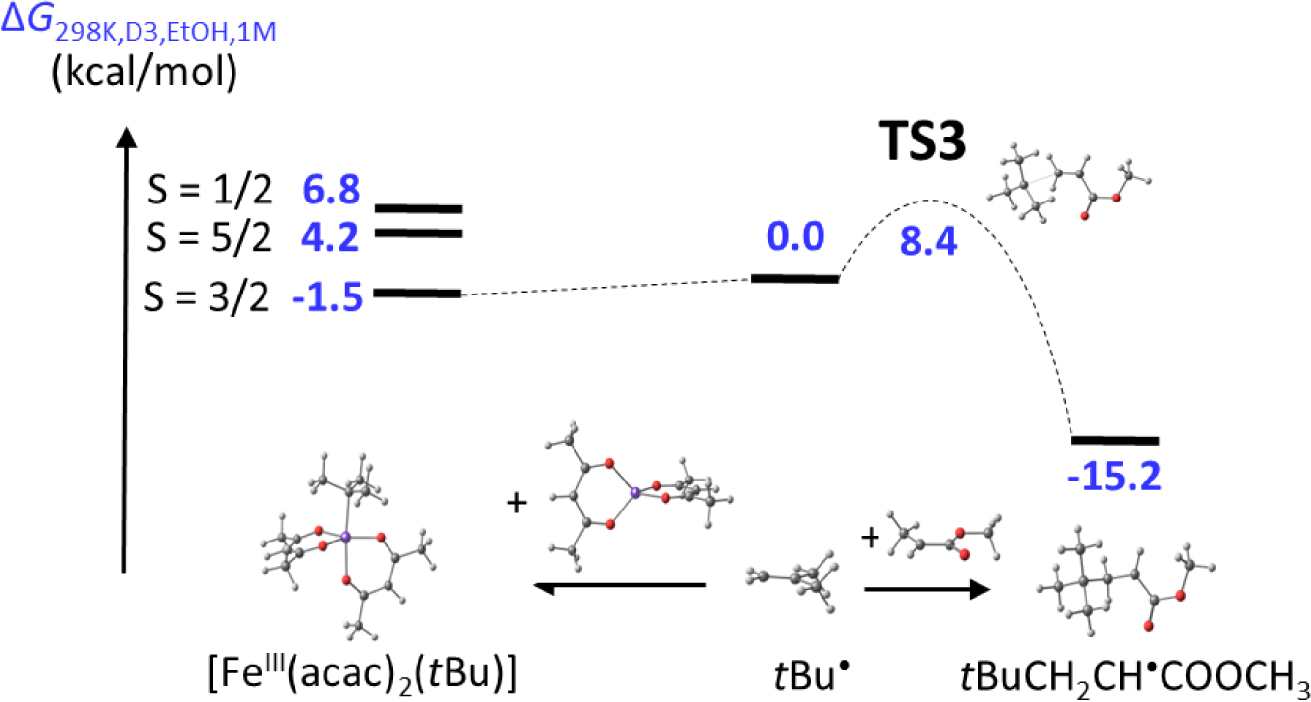
Of greater relevance to this article topic, the produced {[FeII(acac)2,tBu∙} caged pair is predicted to collapse to an organometallic [FeIII(tBu)(acac)2] adduct with a quartet ground state, although the stabilization provided by the “bond” is barely significant (see Figure 9). Still, a slight “persistent radical effect” (PRE) may be expected: from this 𝛥G and the catalyst concentration used in the experiments, ca. 50% of the radicals are predicted to be protected as dormant organometallic species. This improves the efficiency of the subsequent addition to the acceptor olefin, which occurs through a relatively small activation barrier (TS3). With all the caveats outlined in Section 4.5, this value can only be taken as indicative, at best. Calculations with a dispersion-corrected pure functional (BP86-D3) yielded a much stronger BDE (25.1 kcal⋅mol−1). However, the BPW91*-D3 functional selected for this investigation has given, in our hands, more credible results for a number of other previously investigated systems of light transition metals (including those highlighted in the previous sections), as well as satisfactory agreement with three different benchmarks during the present investigation: the first one has already been highlighted above (calculated cycle span versus experimental TOF). The second benchmark was the electrochemical reduction potential of the [FeIII(acac)3]∕[FeII(acac)3]− couple versus the ferrocene/ferricenium standard, measured as − 0.48 V (𝛥G = +11.1 kcal⋅mol−1 from the Nernst equation) and calculated as + 9.6 kcal⋅mol−1. The third benchmark was the EtOH binding equilibrium to [FeII(acac)2] to yield [FeII(acac)2(EtOH)2] with no observable [FeII(acac)2(EtOH)] intermediate, measured as K = 3.2 ± 0.2 M−1 (𝛥G = −0.69 ± 0.95 kcal⋅mol−1) and calculated as − 0.6 kcal⋅mol−1, while the relative G of the [FeII(acac)2(EtOH)] intermediate was calculated as + 1.3 kcal⋅mol−1, in agreement with its non-observation.
Finally, the OSET pathway for the product quenching step, involving sequential tBuCH2CH∙(COOCH3) reduction to enolate by [FeII(acac)2] and protonation, was found too energetically costly. On the other hand, the PCET pathway involving the proton of one of the coordinated ethanol ligands in [FeII(acac)2(EtOH)2] occurs with a low barrier of 9.4 kcal⋅mol−1 (TS4). The DFT exploration also unveiled an unexpected alternative and competitive pathway (barrier of 9.9 kcal⋅mol−1) involving the tBuCH2CH∙(COOCH3) addition to [FeII(acac)2(EtOH)] through the O atom to yield the enolate [FeIII(acac)2{O‐C(OMe) = CHCH2 tBu}(EtOH)] followed by intramolecular proton transfer, whereas the FeIII–C bond formation for this radical is unfavorable. The direct quenching of the tBu∙ radical by CPET is also energetically competitive (and is indeed experimentally observed in the absence of acceptor olefin) but the addition to methyl acrylate is favored by the concentration bias, whereas the barrier to radical propagation with methyl acrylate to make oligomers is slightly higher than for CPET. In conclusion, the high chemoselectivity for this versatile radical reaction involves a delicate balance of the relative barriers and relative concentrations of the reagents involved in the various steps, and might benefit, in addition, from a small moderating action by the [FeII(acac)2] compound generated in the HAT activation to reversibly trap the initial nucleophilic radical. I personally feel that a similar moderating action is present for a great many organic radical reactions involving transition metals, where such a phenomenon has been overlooked.
7. Conclusion
I have presented a general analysis of the radical concentration moderation through the reversible formation of homolytically weak metal–carbon bonds and described how the thermodynamic and kinetic parameters of the bond homolysis equilibrium can be experimentally assessed. I have also mentioned the useful contribution, as well as the caveats, of the computational analysis of the metal–carbon bond homolysis. This survey highlights several opportunities for future investigations. One interesting avenue is the measurement of the homolysis equilibrium constant by the kinetic approach described in Schemes 2 and 3, which is potentially applicable to the very fragile bonds of compounds that cannot be isolated. The measurement of the activation rate constant from the 1H NMR line broadening, used so far only in a few cases, also appears as a method of wider applicability for compounds with relatively strong bonds. It may also be useful to develop linear free-energy relationships for the metal-alkyl BDE to analyze the relative importance of electronic, steric and resonance stabilization factors, similar to those already developed for alkyl-halogen and other alkyl-heteroatom bonds, though such relationships would be metal-specific. In addition, the weird low (even negative in some cases) bond cleavage activation entropies determined in previous studies may be worthy of a re-evaluation on the basis of a new kinetic scheme that considers the direct trapping of the solvent caged fragment pair (k4 in Scheme 6), for instance by performing these investigations again using different trapping agents. The electrochemical study of systems where radicals can be generated in situ and trapped by electroactive L∕Mtx metal complexes to generate electroactive L∕Mtx+1–R species, applied so far only to the investigation of organocopper(II) systems as shown in Section 4.4, might allow the investigation of other compounds with quite thermally fragile metal–carbon bonds. Finally, our recent use of TTMSS as a radical trap for the successful determination of the [(CO)5Mn‐RF] bond activation parameters (the strongest bonds ever measured by this kinetic approach), as shown in Section 4.6, could be extended to the investigation of other strong metal–carbon bonds.
In the second part of this article I have described a few investigations where the synergistic approach of DFT calculations and experiments carried out in my laboratory and in those of my collaborators have provided insight into the contribution of reversible metal–carbon bond homolysis to the areas of organometallic radical polymerization (OMRP) and metal-mediated organic transformations. In particular, we have shown that L∕Mtx moderating species have the advantage of an Mt–C BDE steric modulation through ligand engineering. We have also shown how the simple [CoII(acac)2] moderator, for different and unrelated reasons linked to monomer chelation and bond polarity effects, re-equilibrates the BDEs of the head and tail dormant species obtained in the CRP of two challenging monomers, VAc and VDF. In that respect, homolytically weak metal–carbon bonds make more robust mediating systems for the CRP of challenging asymmetric monomers [174]. We have argued how reversible metal–carbon bond homolysis may be the preferred pathway for dehydrometallation of organometallic intermediates in organic radical transformations and confirmed that catalytic chain transfer polymerization does not require the formation of metal–carbon bonds followed by 𝛽-H elimination. We have also investigated the L∕CuI-catalyzed radical termination (CRT), which may feature the same elementary steps as certain 3d-metal catalyzed radical cross-couplings. The intimate mechanism of this process and the nature of the terminated chains (coupling or disproportionation) remains to be fully elucidated. It is also of interest to understand the origin of the CRT activity and its dependence on the radical nature, in order to engineer new L∕CuI ATRP catalysts that do not promote this unwanted process. Another specific goal is the development of new efficient OMRP moderators for less activated monomers based on L∕CuI systems and other metals. Finally, I have described recent work on the mechanism of a Fe-catalyzed selective and versatile alkene radical cross-coupling, pointing out that the reversible formation of organometallic intermediates needs to be considered, even when the stabilization provided by the metal–carbon bond formation is very low.




 CC-BY 4.0
CC-BY 4.0