Plan
Comptes Rendus
no. 8

Essai
Théorie cinétique de l’équilibre chimique
Mathieu Lazerges1, 2  ; Sylvain Marque3
1 GeoRessources, UMR 7359 CNRS. Université de Lorraine, Faculté des Sciences et Techniques, rue Jacques Callot, 54506 Vandœuvre-lès-Nancy, France
2 Unité de Technologies Chimiques et Biologiques pour la Santé, UMR 8258 CNRS, U 1022 INSERM. Paris Sciences Lettres, Chimie ParisTech, 11 rue Pierre et Marie Curie, 75005 Paris, France. Université de Paris, Faculté de Santé, Faculté de Pharmacie de Paris, 4 avenue de l’Observatoire, 75006 Paris, France
3 Institut Lavoisier de Versailles, UMR 8180 CNRS, Université Paris-Saclay, Université de Versailles Saint Quentin-en-Yvelines, 45 avenue des Etats-Unis, 78035 Versailles, France
Comptes Rendus. Chimie, Volume 23 (2020) no. 8, pp. 445-503.

Résumés

Willard Gibbs formule en 1873 une fonction mathématique, l’énergie de Gibbs, qui gouverne l’évolution du gaz parfait. Ludwig Boltzmann présente en 1895 une description microscopique du gaz parfait concordante avec l’approche phénoménologique de Gibbs. La thermodynamique chimique, qui se développe historiquement dans la continuité du modèle du gaz parfait, est fondée sur le postulat de l’existence du potentiel chimique par Gibbs en 1876. Le potentiel chimique, quantité attribuée à chaque espèce chimique, constitue la force motrice d’une réaction chimique. Les chimistes et physiciens utilisent depuis le début du 20ème siècle le modèle de Gibbs et Boltzmann pour exprimer les lois qui gouvernent l’évolution des systèmes microscopiques, réactions chimiques et transitions de phase. Ce modèle, qui présente une faiblesse pour décrire certains systèmes qualifiés de non idéaux, a été progressivement décliné en une myriade de modèles empiriques de complexités et performances prédictives croissantes mais dont la portée est restreinte à des systèmes particuliers. Un modèle unifié des évolutions microscopiques, fondé sur une description cinétique en rupture avec le modèle thermodynamique actuel, est présenté dans ce manuscrit : l’existence du potentiel chimique est remise en cause, et, l’entropie calorimétrique issue du second principe de la thermodynamique, appropriée pour décrire les échanges de chaleur, n’est pas jugée pertinente pour prévoir l’évolution d’une transformation microscopique. L’entropie cinétique qui émerge de cette étude se substitue à l’entropie calorimétrique dans la fonction qui gouverne l’évolution des réactions chimiques et équilibres de phases.

Compléments :
Des compléments sont fournis pour cet article dans le fichier séparé :

Willard Gibbs formulated in 1873 a mathematical function, the Gibbs energy, whose variation governs the perfect gas evolution. In 1895, Ludwig Boltzmann presented a microscopic description of the perfect gas in concordance with the phenomenological approach of Gibbs. The chemical thermodynamics has been historically developed using the model of the perfect gas from the existence of the chemical potential postulated in 1876 by Gibbs. The chemical potential, a quantity ascribed to every chemical species, represents the driving force of a chemical reaction. Chemists and physicists use since the beginning of the 20th century Gibbs and Boltzmann model to express the evolution laws of chemical reactions and phase transitions. This model, which presents a weakness to describe certain systems so-called as not ideal systems, was gradually declined in numerous successive empirical models of complexities and increasing predictive performances but restricted to particular systems. A unified model of microscopic evolutions based on kinetics is presented in this manuscript which is a clearly-cut breakthrough with thermodynamic chemistry: the existence of the chemical potential is not recognized and the calorimetric entropy from the second law of thermodynamics, which is consistent for heat transfer prediction, is not consistent to predict microscopic evolutions. Kinetic entropy rising from this approach replaces calorimetric entropy in the function that governs chemical reactions and phases equilibria evolutions.

Supplementary Materials:
Supplementary material for this article is supplied as a separate file:

Métadonnées
Reçu le :
Révisé le :
Accepté le :
Publié le :
DOI : 10.5802/crchim.40
Mot clés : Boltzmann, Cinétique, Collision, Entropie, Équilibre, Second principe, Thermodynamique
Keywords: Boltzmann, Kinetics, Collision, Entropy, Equilibrium, Second law, Thermodynamics

Mathieu Lazerges 1, 2 ; Sylvain Marque 3

1 GeoRessources, UMR 7359 CNRS. Université de Lorraine, Faculté des Sciences et Techniques, rue Jacques Callot, 54506 Vandœuvre-lès-Nancy, France
2 Unité de Technologies Chimiques et Biologiques pour la Santé, UMR 8258 CNRS, U 1022 INSERM. Paris Sciences Lettres, Chimie ParisTech, 11 rue Pierre et Marie Curie, 75005 Paris, France. Université de Paris, Faculté de Santé, Faculté de Pharmacie de Paris, 4 avenue de l’Observatoire, 75006 Paris, France
3 Institut Lavoisier de Versailles, UMR 8180 CNRS, Université Paris-Saclay, Université de Versailles Saint Quentin-en-Yvelines, 45 avenue des Etats-Unis, 78035 Versailles, France
Licence : CC-BY 4.0
Droits d'auteur : Les auteurs conservent leurs droits 
@article{CRCHIM_2020__23_8_445_0,
     author = {Mathieu Lazerges and Sylvain Marque},
     title = {Th\'eorie cin\'etique de l{\textquoteright}\'equilibre chimique},
     journal = {Comptes Rendus. Chimie},
     pages = {445--503},
     publisher = {Acad\'emie des sciences, Paris},
     volume = {23},
     number = {8},
     year = {2020},
     doi = {10.5802/crchim.40},
     language = {fr},
}
TY  - JOUR
AU  - Mathieu Lazerges
AU  - Sylvain Marque
TI  - Théorie cinétique de l’équilibre chimique
JO  - Comptes Rendus. Chimie
PY  - 2020
SP  - 445
EP  - 503
VL  - 23
IS  - 8
PB  - Académie des sciences, Paris
DO  - 10.5802/crchim.40
LA  - fr
ID  - CRCHIM_2020__23_8_445_0
ER  - 
%0 Journal Article
%A Mathieu Lazerges
%A Sylvain Marque
%T Théorie cinétique de l’équilibre chimique
%J Comptes Rendus. Chimie
%D 2020
%P 445-503
%V 23
%N 8
%I Académie des sciences, Paris
%R 10.5802/crchim.40
%G fr
%F CRCHIM_2020__23_8_445_0
Mathieu Lazerges; Sylvain Marque. Théorie cinétique de l’équilibre chimique. Comptes Rendus. Chimie, Volume 23 (2020) no. 8, pp. 445-503. doi : 10.5802/crchim.40. https://comptes-rendus.academie-sciences.fr/chimie/articles/10.5802/crchim.40/

Version originale du texte intégral (Proposez une traduction )

Préambule

Ce manuscrit présente une description des transformations microscopiques, réaction chimique et transition de phase, pour laquelle l’équation de l’équilibre est établie à partir d’équations cinétiques. Le modèle élaboré constitue une remise en cause du modèle thermodynamique chimique standard :

  1. L’entropie calorimétrique introduite par Rudolf Clausius en 1855, appropriée pour prévoir les échanges de chaleur et travail, n’est pas jugée adéquate pour prévoir l’évolution des transformations microscopiques, en particulier et non exhaustivement celles de la réaction chimique et de la fusion.
  2. L’existence du potentiel chimique, postulée par Willard Gibbs en 1876, n’est pas reconnue.

Compte tenu de l’importance de la remise en question des fondements de la thermodynamique chimique, le premier chapitre est consacré à l’historique de sa construction. Il se distingue néanmoins d’une revue encyclopédique exhaustive car il ne mentionne ni les théories fondées sur l’existence du potentiel chimique, ni celles qui font usage de l’entropie calorimétrique dans les équations qui gouvernent l’équilibre chimique et l’équilibre de phases puisque ces deux notions sont remises en question.

La construction du modèle cinétique des équilibres fait l’objet du deuxième chapitre pour la réaction chimique et du quatrième chapitre pour la fusion. La description cinétique de l’équilibre n’est pas fondée sur l’existence du potentiel chimique et n’utilise pas l’entropie calorimétrique : elle est fondée sur une formulation cinétique de l’équilibre. L’entropie cinétique qui émerge de cette description se substitue à l’entropie calorimétrique dans les équations qui gouvernent l’évolution des transformations microscopiques, réaction chimique et fusion.

Les troisième et cinquième chapitres sont dédiés à la confrontation des modèles thermodynamique et cinétique des équilibres chimique et de fusion. Il est montré pour des systèmes variés, sièges d’une réaction chimique ou d’une transition de phase liquide–solide, que la description cinétique est soit aussi pertinente, soit plus appropriée, que la description thermodynamique. La description cinétique s’affranchit de l’usage de paramètres d’ajustement de nature empirique indispensables pour décrire des systèmes qualifiés de non idéaux par le modèle thermodynamique. En outre, la description cinétique rationalise des processus variés inexplicables par le modèle classique.

Le sixième et dernier chapitre est dédié au modèle cinétique de l’équilibre des transformations microscopiques dans un cadre théorique général et présente des concepts qui découlent de ce modèle.

1. Introduction historique de la thermodynamique chimique

1.1. Premier principe

Au 19ème siècle, un médecin allemand, Julius Robert von Mayer, énonce clairement le premier principe de la thermodynamique [1]. Il déduit, de l’observation physiologique de marins lors d’expéditions aux antipodes, que la chaleur de combustion de la nourriture sert à la fois à maintenir la température du corps et à fournir un effort physique [2]. Il établit en 1842 la relation entre chaleur et travail et conclut [3] :

« Ex nihilo nihil fit. »

« Rien n’est créé de rien »

Le premier principe s’exprime dans le formalisme actuel par l’existence d’une grandeur extensive conservative de tout système isolé, l’énergie [4] :

E=constante(1)
Un système isolé n’échange ni matière ni énergie avec le milieu extérieur. L’énergie est la somme de l’énergie cinétique macroscopique, de l’énergie potentielle extérieure et de l’énergie interne :
E=EcM+Ep,ext+U(2)
EcM est l’énergie cinétique macroscopique du mouvement du système par rapport à un référentiel galiléen. Ep,ext est l’énergie potentielle des forces extérieures qui s’exercent sur le système. L’énergie interne U est la somme de l’énergie cinétique microscopique Ecm, de l’énergie potentielle des forces intérieures au système Ep,int et de l’énergie de masse m⋅c2 du système :
U=Ecm+Ep,int+m⋅c2(3)
Le premier principe de la thermodynamique énoncé dans le cadre du système isolé est restrictif. En effet, il ne permet pas l’étude de machines thermodynamiques qui échangent chaleur et travail avec le milieu extérieur comme le moteur ou la pompe à chaleur. Le problème est le même pour les transitions de phase et les réactions chimiques, elles sont usuellement utilisées pour fournir chaleur et travail. Une formulation moderne du premier principe de la thermodynamique prend en compte la possibilité d’échanges d’énergie avec le milieu extérieur afin de permettre de telles transformations [5], c’est-à-dire en considérant un système fermé : il n’échange pas de matière mais il peut échanger de l’énergie avec le milieu extérieur. Le système échange de l’énergie avec le milieu extérieur via les forces qui s’exercent sur la surface qui le délimite, cet échange d’énergie correspond au travail W. La chaleur Q correspond à l’échange d’énergie du système avec le milieu extérieur qu’il faut ajouter au travail pour obtenir l’échange total d’énergie :
𝛥E=W+Q(4)
Soit :
𝛥(EcM+Ep,ext+U)=W+Q(5)
Il est usuel en chimie de considérer un système au repos et de négliger les champs de forces extérieures, soit :
𝛥U=W+Q(6)

1.2. Second principe

Figure 1.

Système isolé à pression constante d’une mole de deux solides A et B en contact, de même structure chimique et de températures initiales TA et TB différentes. La capacité calorifique molaire à pression constante et le volume des solides sont supposés indépendants de la température.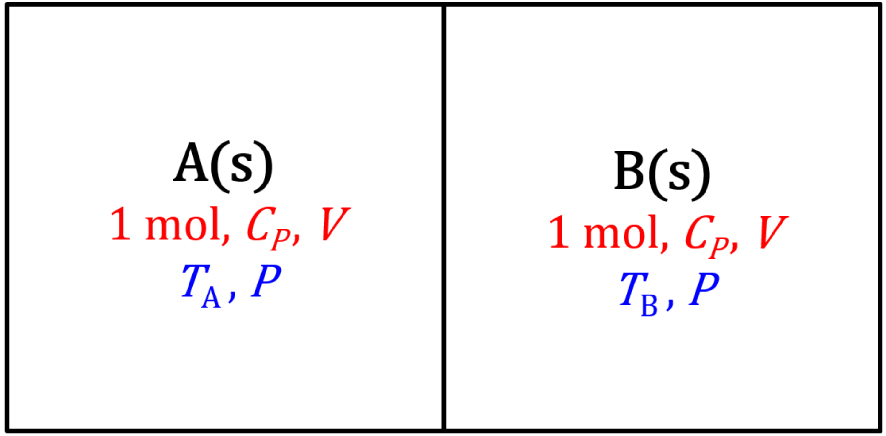

Un ingénieur français, Sadi Carnot, publie en 1824 un ouvrage à frais d’auteur intitulé « Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance » dans lequel il étudie la transformation par les moteurs de la chaleur de combustion en travail mécanique [6]. Il conclut à la fin de son manuscrit que le travail fourni lors de la combustion d’un kilogramme de charbon fournie par les moteurs les plus performants de son époque est très en deçà de la chaleur dégagée par la combustion de la même quantité de combustible :

|W|<|Q|(7)
Cet effet est quantifié par le physicien allemand Rudolf Clausius, il introduit en 1855 l’entropie S d’un système isolé dont la variation lors d’une évolution est la somme d’un terme d’échange Se et d’un terme de création Sc :
𝛥S=Sc+Se(8)
L’entropie d’échange d’une transformation est définie par le rapport entre la chaleur échangée par le système avec le milieu extérieur au travers de la surface qui le délimite et la température thermodynamique de cette surface [7] :
Se=QT(9)
L’apparente simplicité de ce formalisme ne laisse pas présager qu’il définit la flèche du temps. Cette propriété fondamentale sera illustrée dans le cas d’un échange de chaleur entre deux solides (Figure 1).

Les deux solides forment un système isolé du milieu extérieur mais ils constituent chacun un système fermé qui échange de l’énergie avec l’autre. L’énergie du système isolé se conserve :

𝛥U=0(10)
Les solides n’échangent pas de travail car leur volume est supposé indépendant de la température :
WA=WB=0(11)
Dans ces conditions, l’équation de conversion de l’énergie devient :
QA+QB=0(12)
L’expérience montre que les températures des solides A et B, initialement différentes, convergent vers une température d’équilibre intermédiaire Teq. Les chaleurs échangées par une mole de solide A et une mole de solide B, obtenues par intégration de la chaleur élémentaire δQ, sont respectivement égales à :
QA=∫TATeqδQA=CP⋅(Teq−TA)(13)
QB=∫TBTeqδQB=CP⋅(Teq−TB)(14)
La température d’équilibre se déduit des trois équations précédentes :
Teq=TA+TB2(15)
Les variations d’entropie d’échange des solides A et B lors de l’évolution du système sont respectivement égales à :
SAe=∫TATeqδQAT=CP⋅lnTA+TB2⋅TA(16)
SBe=∫TBTeqδQBT=CP⋅lnTA+TB2⋅TB(17)
En postulant l’entropie extensive, il est possible de calculer la variation d’entropie totale du système :
𝛥S=SAe+SBe=CP⋅ln(TA+TB)24⋅TA⋅TB(18)
La variation d’entropie totale du système est positive quelles que soient les températures initiales des deux solides. L’entropie du système augmentera donc toujours lors de l’évolution du système vers l’état d’équilibre thermique. Cette évolution est irréversible. Le processus inverse, l’apparition spontanée d’un gradient de température persistant et de dimension macroscopique dans un solide, n’a jamais été observé. La variation d’entropie totale du système est :
𝛥S=Sc+Se(19)
Puisque le système est isolé :
Se=0(20)
L’entropie créée déduite de ces trois dernières égalités est :
Sc=CP⋅ln(TA+TB)24⋅TA⋅TB(21)
Sc>0(22)
L’augmentation de l’entropie d’un système isolé, jamais mise à défaut par l’expérience, a été érigée en principe :

« Il existe une grandeur extensive et non conservative, l’entropie, qui augmente pour un système isolé avec le temps. »

Au même titre que le premier principe, le deuxième principe de la thermodynamique énoncé dans le cadre du système isolé ne permet pas l’étude de systèmes qui échangent chaleur et travail avec le milieu extérieur. Une formulation moderne du deuxième principe de la thermodynamique [5] prend en compte la possibilité de tels échanges, c’est-à-dire en considérant un système fermé :

« Il existe pour tout système fermé, délimité du milieu extérieur par une surface fermée, une fonction d’état extensive et non conservative, l’entropieS. Sa variation est la somme d’une entropieSc créée à l’intérieur du système et d’une entropieSe échangée avec le milieu extérieur :

𝛥S=Sc+Se(23)
L’entropie créée augmente avec le temps. Elle quantifie le caractère irréversible des évolutions réelles :
Sc⩾0(24)
L’entropie liée aux échanges de chaleur du système avec le milieu extérieur est quantifiée par le rapport entre la chaleur échangée et la températureTS en tout point de la surface fermée qui délimite le système du milieu extérieur.
Se=∫δQTS(25)

1.3. Energie de Gibbs

Willard Gibbs introduit en 1873 une fonction mathématique dont la variation élémentaire à température et pression constantes est nulle à l’équilibre thermodynamique [8]. La formule historique de cette fonction est :

d(U−T⋅S+P⋅V)=0(26)
La fonction différenciée correspondante, notée G, est appelée énergie de Gibbs :
G=U−T⋅S+P⋅V(27)
La différentielle de l’énergie de Gibbs d’une transformation réversible est, en prenant en compte les premier et second principes de la thermodynamique :
dG=−S⋅dT+V⋅dP(28)
Pour une transformation irréversible à température et pression constantes, la différentielle de l’énergie de Gibbs est négative :
dGT,P⩽0(29)
Toute évolution isotherme et isobare d’un système s’accompagne d’une diminution de son énergie de Gibbs jusqu’à un minimum qui constitue l’état d’équilibre :
dGT,P,eq=0(30)

1.4. La thermodynamique chimique, une science fondée sur un postulat

Gibbs postule en 1876 l’existence du potentiel chimique 𝜇 comme force motrice de la réaction chimique, qu’il introduit dans la différentielle de l’énergie interne [9]. La variation élémentaire d’énergie interne d’une réaction qui implique i espèces chimiques est :

dU=T⋅dS−P⋅dV+ ∑i𝜇i⋅dmi(note 1)(31)

Gibbs n’avait pas explicité dans son manuscrit l’expression du potentiel chimique, il en avait postulé l’existence comme force motrice de la réaction chimique qui vient s’additionner à la fonction qui gouverne l’équilibre d’un fluide. Le manuscrit de Gibbs traduit en français par Henry Le Chatelier inclut une note personnelle de ce dernier sur l’introduction du potentiel chimique [10] :

« C’est là en réalité une hypothèse qui revient à attribuer à chaque corps une force chimique définie, comme il possède un poids défini. Cette hypothèse très rationnelle doit être considérée comme un postulatum analogue à ceux qui servent de base à la mécanique rationnelle. »

La différentielle de l’énergie interne n’est pas, d’un point de vue pratique, appropriée pour prévoir l’évolution d’un équilibre chimique. En effet, il n’est pas aisé, lors d’une transformation, de maintenir l’entropie constante. En revanche, la différentielle de l’énergie de Gibbs dépend de celles de la température et de la pression qu’il est aisé de contrôler et s’avère de fait plus pertinente pour l’étude des équilibres chimiques :

dG=−S⋅dT+V⋅dP+ ∑i𝜇i⋅dmi(32)
Pour une transformation à température et pression constantes, l’équilibre est gouverné par le produit du potentiel chimique par la variation de masse des espèces chimiques réactives :
dGT,P= ∑i𝜇i⋅dmi(33)
La quantité de matière de la variation élémentaire d’énergie de Gibbs d’un mélange s’exprime usuellement en mole :
dG=−S⋅dT+V⋅dP+ ∑i𝜇i⋅dni(34)
Le potentiel chimique du constituant i dans une phase homogène est défini par la dérivée partielle de l’énergie de Gibbs à température, pression et compositions des constituants j autres que i constantes :
𝜇i=∂G∂niT,P,j≠i(35)
La thermodynamique chimique est une discipline universelle. Ses lois s’appliquent à une grande variété de transformations microscopiques. Cette richesse s’exprime autant par la diversité des espèces chimiques impliquées (atome, molécule, ion, complexe, polymère, cristal, protéine) que par celle des transformations physiques réalisables (formation et rupture de liaison chimique, transition de phase, transition de phase magnétique, transfert d’électron). L’étude présentée se limite à deux transformations : la réaction chimique en phase homogène et la transition de phase liquide–solide. Ces deux transformations, bien renseignées en termes de données expérimentales, sont à l’origine de la construction de la thermodynamique chimique de l’équilibre au début du 20ème siècle.

1.5. Contenu du potentiel chimique : l’équilibre de fusion

Le premier travail des chimistes et physiciens du début du 20ème siècle, dont l’esprit avait été échauffé par l’éclosion de la thermodynamique chimique, une science nouvelle, fut de trouver l’expression du potentiel chimique dont l’existence avait été postulée par Gibbs. L’effet eutectique, l’abaissement mutuel du point de fusion des constituants d’un mélange lorsque leur proportion diminue, s’observe pour des composés qui forment une phase liquide homogène à chaud et dont les solides sont immiscibles à froid. Le diagramme de phases liquide–solide d’un mélange de deux constituants, notés A et B, est établi par l’observation expérimentale des phases stables du mélange en fonction de sa composition et de la température (Figure 2).

Figure 2.

Topologie du diagramme de phases liquide–solide d’un système binaire à invariant eutectique. Courbes d’équilibre de fusion de la température en fonction de la fraction molaire du constituant A dans la phase liquide : constituant A (trait rouge), constituant B (trait bleu) et palier eutectique (trait noir).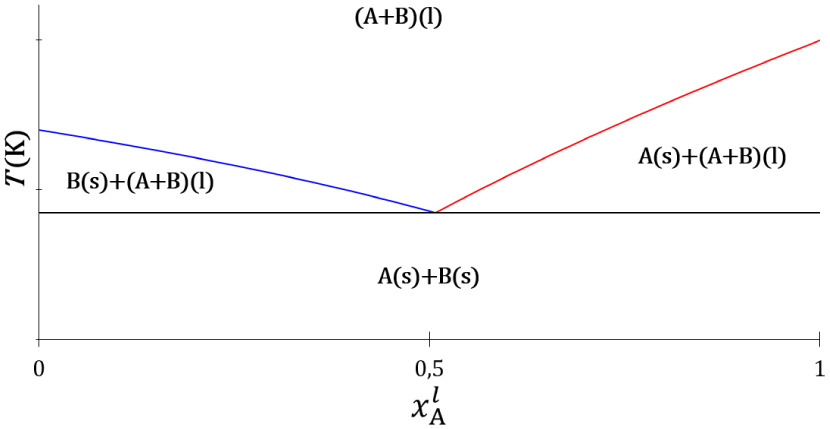

L’étude par Iw. Schröder en 1901 de l’équilibre de fusion du mélange eutectique du naphtalène avec le 1,3-dinitrobenzène est un travail précurseur et fondateur [11] (Figure 3).

Figure 3.

Structures chimiques du naphtalène et du 1,3-dinitrobenzène.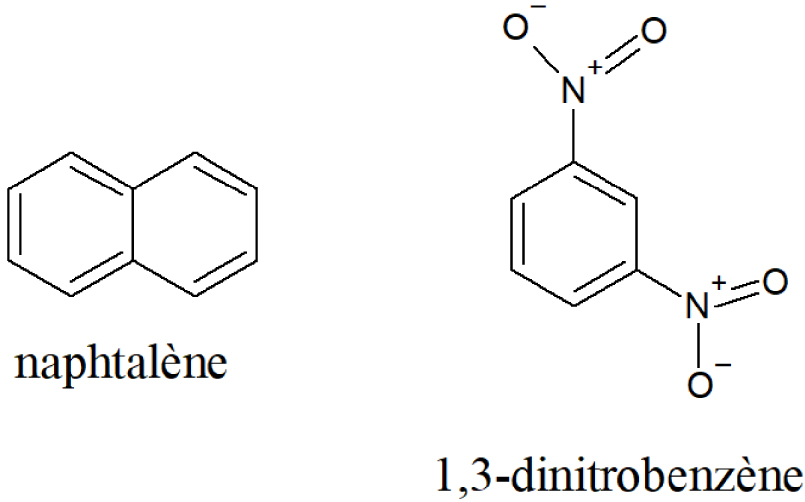

Schröder dégage de l’étude de ce mélange une équation de la courbe d’équilibre de fusion (i.e. liquidus) qui exprime la température de fusion d’un solide en fonction de sa composition dans son liquide. Cette courbe d’équilibre dépend des température Tfus° et chaleur de fusion Qfus° à une pression de 1 bar de l’espèce chimique pure :

ln(xeql)=Qfus(cal∕mol)°2⋅1Tfus°−1Tfus(36)
Cette équation, dans laquelle la chaleur est exprimée en calorie et la température en Kelvin est la forme originale de l’équation actuelle de la courbe idéale de l’équilibre de fusion :
ln(xeql)=𝛥fusH(J∕mol)°R⋅1Tfus°−1Tfus(37)
Le produit de 2 par le nombre de joules dans une calorie (8,37 J⋅K−1⋅mol−1) s’écarte de moins de 1% de la valeur numérique de la constante de l’équation d’état du gaz parfait (8,31 J⋅K−1⋅mol−1) :
P⋅V=n⋅R⋅T(38)
Ce résultat permet d’établir sur une base phénoménologique, c’est-à-dire sans faire appel à la physique statistique, un lien entre la détente isotherme du gaz parfait et la fusion d’un constituant chimique d’un mélange. En effet, la chaleur échangée avec le milieu extérieur d’une enceinte au sein de laquelle s’effectue la détente isotherme d’une mole de gaz parfait entre un volume initial Vi et un volume final Vf se déduit de l’équation :
lnVfVi=QTR⋅T(39)
Les chimistes et physiciens du début du 20ème siècle furent encouragés par cette analogie à construire la thermodynamique chimique, puis la thermodynamique statistique en utilisant le gaz parfait. Il est important de préciser que le liquidus de nombreux mélanges, comme celui du chlorure de sodium avec l’eau [12], s’écarte du liquidus prévu par le modèle. De tels mélanges, gênants, furent naturellement écartés de la construction de la thermodynamique chimique dans un premier temps au profit de ceux qui confortaient le modèle, comme celui du naphtalène avec le 1,3-dinitrobenzène.

1.6. Equilibre de phases liquide–solide d’un système à invariant eutectique

Une description thermodynamique de l’équilibre de fusion est présentée dans ce chapitre. Soit un constituant chimique i dont le solide est en équilibre dans son mélange liquide homogène avec d’autres constituants j immiscibles dans la phase solide de i. L’équilibre de fusion est étudié à pression et température constantes :

i(s)⇌i(l)
Le potentiel chimique du constituant i dans un mélange liquide s’exprime relativement à un état de référence définit par l’utilisateur. Un état de référence utilisé pour l’étude des transitions de phase est le constituant chimique pur à la pression standard :
p°=1bar
Cet état de référence est approprié car il ne fixe pas de contraintes sur la température du système qu’il est nécessaire de faire varier pour établir un diagramme de phases et il fixe la pression à une valeur proche de la pression atmosphérique. Le potentiel chimique du constituant i dans un mélange liquide dépend :
  1. i. du potentiel chimique 𝜇il° du liquide i pur ;
  2. ii. de sa fraction molaire xil dans le mélange liquide.

Soit :

𝜇il=𝜇il°+R⋅T⋅ln(xil)(40)
Dans le cas ou les autres constituants ne sont pas miscibles dans la phase solide de i, le potentiel chimique du solide dans le mélange est égal à celui du solide pur :
𝜇is=𝜇is°(41)
L’équilibre de fusion à une température inférieure à la température de fusion du solide pur se traduit par l’égalité des potentiels chimiques du liquide et du solide :
𝜇i,eql=𝜇i,eqs(42)
D’où :
𝜇il°+R⋅T⋅ln(xi,eql)=𝜇is°(43)
Les potentiels chimiques de i à l’état liquide et solide sont définis par la dérivée partielle de la fonction G à température, pression et compositions des constituants j autres que i constantes :
𝜇il°=∂Hl°∂nT,P,j≠i−T⋅∂Sl°∂nT,P,j≠i(44)
𝜇is°=∂Hs°∂nT,P,j≠i−T⋅∂Ss°∂nT,P,j≠i(45)

L’équation de l’équilibre de fusion est usuellement exprimée avec le formalisme des grandeurs molaires :

𝛥fusHi°−T⋅𝛥fusSi°=−R⋅Tfus⋅ln(xil)(46)
Avec :
𝛥fusHi°=∂Hl°∂nT,P,j−∂Hs°∂nT,P,j(47)
𝛥fusSi°=∂Sl°∂nT,P,j−∂Ss°∂nT,P,j(48)
Les enthalpies et entropies de fusion de l’équation de l’équilibre sont déterminées par des mesures calorimétriques :
𝛥fusH=QP(49)
𝛥fusS=∫0+TδQPT′(note2)(50)

Le comportement de certains mélanges à invariant eutectique est en accord avec ce modèle, l’équation de l’équilibre de fusion déduite de mesures calorimétriques est en accord avec celle du diagramme de phases expérimental :

𝛥fusHi°−Tfus⋅𝛥fusSi°=−R⋅Tfus⋅ln(xeql)(51)
Il existe des systèmes pour lesquels les enthalpie et entropie de fusion ne dépendent pas de la température et de la composition. L’équation de l’équilibre de fusion se déduit dans ce cas particulier des propriétés du corps pur :
ln(xeql)=𝛥fusHi°R⋅1Tfus°−1Tfus(52)
Le système binaire à invariant eutectique entre le naphtalène et le 1,3-dinitrobenzène étudié par Schröder en 1901 présente un tel comportement. Cependant, le comportement d’autres systèmes s’écarte de celui prévu par ce modèle. Le diagramme de phases ne se déduit pas des propriétés calorimétriques :
𝛥fusHi°−Tfus⋅𝛥fusSi°≠−R⋅Tfus⋅ln(xeql)(53)
La concordance numérique de l’équation de l’équilibre a été rétablie en introduisant un paramètre d’ajustement empirique, le coefficient d’activité 𝛾 :
𝛥fusHi°−T⋅𝛥fusSi°=−R⋅Tfus⋅ln(𝛾i⋅xi,eql)(54)
L’activité a d’un constituant dans un mélange liquide a été définie avec le coefficient d’activité et la fraction molaire :
al=𝛾l⋅xl(55)
L’activité est donc la grandeur qui se substitue à la fraction molaire dans l’équation qui exprime l’équilibre d’une transition de phase, et par conséquence dans l’expression du potentiel chimique dans le cas où une divergence du comportement réel avec celui prévu par le modèle thermodynamique est observée :
𝜇l=𝜇l°+R⋅T⋅ln(al)(56)

1.7. Equilibre chimique dans une phase homogène gazeuse ou liquide

Marcellin Berthelot et Louis–Denis Péan de Saint–Gilles établissent en 1863 que diverses réactions d’estérification donnent lieu à l’établissement d’un équilibre, caractérisé par l’invariance de la concentration de chaque espèce réactive engagée. Ils étudièrent en particulier la réaction d’estérification de l’acide éthanoïque par l’éthanol [13] :

 CH3CO2H(l)+CH3CH2OH(l) ⇌CH3CO2CH2CH3(l)+H2O(l)
Ils remarquent en éliminant l’eau du mélange réactionnel qu’un équilibre chimique se déplace systématiquement de manière à compenser la disparition d’un réactif. La rationalisation de l’équilibre chimique en solution, plus tardive que celle de l’équilibre de fusion, est également inspirée du gaz parfait, mais aussi des travaux précurseurs réalisés sur les équilibres de phases par Schröder [11]. En 1923, Gilbert Newton Lewis et Merle Randall expriment la constante thermodynamique d’un équilibre chimique en fonction des activités de chaque réactif et produit de la réaction [14]. L’état de référence classiquement utilisé pour l’étude des réactions chimiques est l’état standard. Le potentiel chimique d’une espèce chimique i dans un mélange gazeux est fonction de son potentiel de référence et de sa pression partielle exprimée en bar :
𝜇ig=𝜇ig°+R⋅T⋅lnpip°(57)
Soit une réaction chimique dans un mélange gazeux à température et pression de 1 bar constantes :
A(g)+B(g)⇌C(g)+D(g)
A l’équilibre chimique, la somme des potentiels chimiques des réactifs est égale à celle des produits :
𝜇A,eqg+𝜇B,eqg=𝜇C,eqg+𝜇D,eqg(58)
Soit, en prenant en compte l’expression du potentiel chimique de chaque réactif et produit :
pC,eq⋅pD,eqpA,eq⋅pB,eq=exp−𝜇Cg°+𝜇Dg°−𝜇Ag°−𝜇Bg°R⋅T(59)
Cette égalité devient, en introduisant la constante d’équilibre et l’énergie de Gibbs molaire standard de réaction :
K=exp−𝛥rG°R⋅T(60)
L’énergie de Gibbs molaire standard de réaction est fonction des enthalpie et entropie molaires de réaction :
𝛥rG°=𝛥rH°−T⋅𝛥rS°(61)
L’enthalpie molaire standard de réaction est la chaleur de réaction à une pression constante de 1 bar :
𝛥rH°=Qp°(62)
L’entropie molaire standard de réaction est une fonction d’état, c’est la somme des entropies standards absolues des produits diminuée de celle des réactifs :
𝛥rS°=SCg°+SDg°−SAg°−SBg°(63)
L’entropie absolue standard est déterminée par l’intégrale du rapport entre la variation élémentaire de chaleur et la température d’une température proche de 0 K et la température T du système :
Sg°=∫0+TδQp°T′(64)
La constante d’équilibre s’exprime en fonction des enthalpie et entropie molaires standards de réaction :
ln(K)=−𝛥rH°R⋅T+𝛥rS°R(65)
La linéarité du logarithme népérien de K en fonction de l’inverse de la température est vérifiée pour de nombreux équilibres chimiques (Figure 4).

Figure 4.

Evolution de ln(K) en fonction de l’inverse de la température d’une réaction chimique.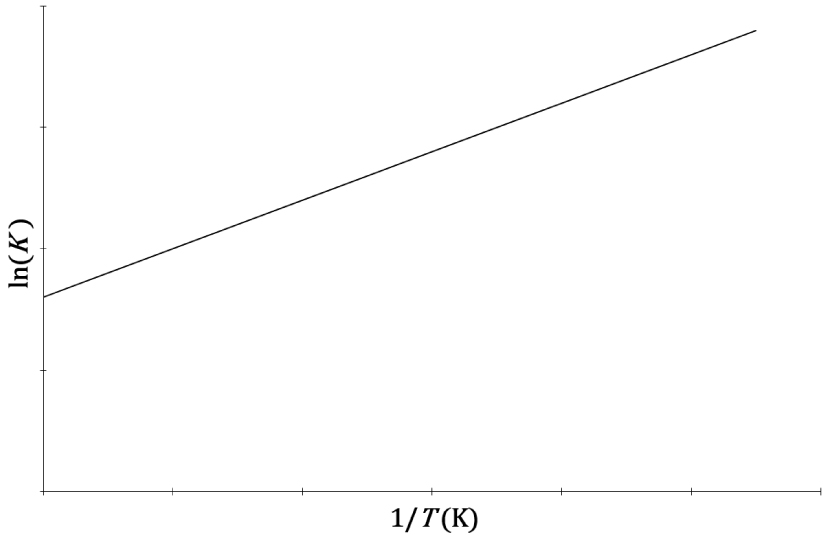

La concordance numérique entre la constante d’équilibre déterminée par le dosage des réactifs et produits d’une réaction à l’équilibre et celle déduite des propriétés calorimétriques est vérifiée pour certains équilibres chimiques, qualifiés d’idéaux :

pC,eq⋅pD,eqpA,eq⋅pB,eq=exp−𝛥rH°−T⋅𝛥rS°R⋅T(66)
C’est le cas de l’équilibre de dissociation du dihydrogène en phase gazeuse entre 2000 K et 3000 K à une pression de 1 bar [15] :
H2(g)⇌2H(g)pH,eq2pH2,eq⋅p°=exp−𝛥rH°R⋅T+𝛥rS°R(67)
Pour d’autres équilibres chimiques, qualifiés de non idéaux, la concordance numérique entre la constante d’équilibre K déterminée par le dosage des réactifs et produits d’une réaction à l’équilibre et celle déduite des propriétés calorimétriques n’est pas vérifiée :
pC,eq⋅pD,eqpA,eq⋅pB,eq≠exp−𝛥rH°−T⋅𝛥rS°R⋅T(68)
L’introduction d’un coefficient d’activité 𝛾ig de nature empirique, pour chaque réactif et produit de l’équilibre chimique, permet de rétablir la concordance numérique de l’équation thermodynamique de l’équilibre :
ag=𝛾g⋅pp°(69)
𝛾Cg⋅pC,eq⋅𝛾Dg⋅pD,eq𝛾Ag⋅pA,eq⋅𝛾Bg⋅pB,eq=exp−𝛥rH°−T⋅𝛥rS°R⋅T(70)
L’équilibre de la synthèse de l’ammoniac présente un caractère non idéal [16] :
12N2(g)+32H2(g)⇌NH3(g)pNH3,eq⋅p°pN2,eq1∕2⋅pH2,eq3∕2≠exp−𝛥rH°−T⋅𝛥rS°R⋅T(71)
La concordance numérique de cette dernière équation est rétablie en introduisant pour chaque espèce chimique un coefficient d’activité :
 𝛾NH3g⋅pNH3,eq⋅p°𝛾N2g1∕2⋅pN2,eq1∕2⋅𝛾H2g3∕2⋅pH2,eq3∕2 =exp−𝛥rH°−T⋅𝛥rS°R⋅T(72)
Le constat est le même que pour les équilibres de fusion : l’activité est la grandeur qui substitue la pression partielle de chaque réactif et produit de la réaction dans l’équation du potentiel chimique dans le cas où une divergence de comportement avec celui prévu par le modèle thermodynamique chimique est observée :
𝜇g=𝜇g°+R⋅T⋅ln(ag)(73)

1.8. Le coefficient d’activité, paramètre empirique de la thermodynamique chimique

Le coefficient d’activité a été introduit dans les équations thermodynamiques de l’équilibre de fusion et de l’équilibre chimique pour décrire certains systèmes dont le comportement s’écartait de celui prévu par le modèle thermodynamique chimique. Le coefficient d’activité ne présente pas dans sa définition de restriction sur les valeurs numériques qu’il peut prendre, il sera donc toujours possible de l’ajuster de manière à corriger n’importe quel écart observé entre le comportement expérimental et celui prévu par le modèle :

𝛾>0(74)
ln(𝛾)∈]−∞;+∞[(75)
Les chimistes et physiciens ont proposé plusieurs modèles de calcul du coefficient d’activité des constituants d’un mélange, de complexité et performance prédictives croissantes. Le modèle de Margules [17], l’un des plus anciens, est fondé sur l’ajustement des paramètres d’une équation de l’équilibre qui approche le comportement observé. Les modèles UNIQUAC [18] et COSMOSPACE [19], plus récents, sont fondés sur l’interaction entre les surfaces des molécules. Ces modèles peuvent être totalement empiriques, comme celui de Margules, ou partiellement empiriques, comme UNIQUAC et COSMOSPACE, remarquables en termes de performances prédictives. La géométrie joue un rôle central dans les modèles thermodynamiques prédictifs les plus aboutis, UNIQUAC et COSMOSPACE.

1.9. Description microscopique du gaz parfait

L’équation d’état du gaz parfait, établie par l’expérience et formulée par Emile Clapeyron en 1833 dans son mémoire sur la puissance motrice de la chaleur, est une équation phénoménologique pour laquelle la température est exprimée en degrés Celsius [20] :

P⋅V=n⋅R⋅(T(°C)+267)(76)
La valeur numérique de la constante du gaz parfait, notée R, a été déterminée par l’expérience. La nature microscopique de la température était à cette époque inconnue. Cette équation d’état, dans laquelle la température est exprimée en degrés Celsius, est proche de l’équation actuelle du gaz parfait renseignée dans le Gold Book de l’International Union of Pure and Applied Chemistry (IUPAC) [21] :
P⋅V=n⋅R⋅(T(°C)+273,15)(77)
La valeur numérique de R référencée par l’IUPAC est [22] :
R=8,314462J⋅K−1⋅mol−1(78)
Ludwig Boltzmann établit à la fin du 19ème siècle, dans une leçon en deux volumes sur la théorie des gaz, une description microscopique du gaz parfait parfaitement cohérente avec la thermodynamique phénoménologique de Gibbs [23, 24, 25]. Il établit la relation entre la température absolue d’un gaz et le mouvement microscopique des particules qui le constituent, atomes ou molécules.
kB=RNA(79)
L’énergie cinétique de translation du gaz parfait est égale à kB⋅T∕2 pour chaque direction x, y et z de l’espace, soit une énergie cinétique de translation totale de 3⋅kB⋅T∕2 dans un espace à trois dimensions. L’énergie moyenne engagée par atome ou molécule de gaz, qui subit une collision sur la paroi d’une enceinte ou avec une autre particule microscopique, est égale à kB⋅T. Cette description mène à une loi de partition de l’énergie. Pour un ensemble de N particules, le nombre de particules Ni,eq qui occupent un des gi états quantiques de niveau d’énergie Ei à l’équilibre est :
Ni,eq=N⋅gi⋅exp−EikB⋅TZ(80)
La grandeur Z est appelée somme d’état :
Z= ∑i=1Ng i⋅exp−EikB⋅T(81)
L’entropie s’exprime en fonction du nombre de combinaisons 𝛺 de l’état du système le plus probable [15] :
S=kB⋅ln(𝛺)(82)
ln(𝛺)=UkB⋅T+N⋅lnZN+N(83)
La thermodynamique développée en physique statistique est parfaitement cohérente avec la thermodynamique phénoménologique de Gibbs mais présente la même faiblesse que celle-ci : elle ne s’affranchit pas de l’usage de coefficients d’activité de nature empirique pour la description de systèmes dont le comportement s’écarte de celui prévu par le modèle.

1.10. Synthèse

La thermodynamique chimique constitue un modèle prédictif puissant et de large portée de l’évolution des transformations microscopiques. Elle est utilisée avec succès depuis plus d’un siècle dans des domaines variés. Elle présente néanmoins des faiblesses et incohérences :

  1. i. la thermodynamique chimique est fondée sur le postulat de Gibbs, l’existence du potentiel chimique;
  2. ii. la thermodynamique chimique est fondée sur l’hypothèse selon laquelle l’entropie d’un équilibre chimique ou de phases s’identifie à l’entropie calorimétrique issue du second principe qui gouverne l’évolution de systèmes qui échangent chaleur et travail ;
  3. iii. la description de systèmes non idéaux ne peut s’affranchir de l’utilisation de coefficients d’activité de nature empirique. Le caractère ajustable du coefficient d’activité ne confère pas à la thermodynamique chimique le statut de théorie scientifique définie en termes de réfutabilité [26] ;
  4. iv. les équations qui permettent le calcul des coefficients d’activité sont de portées restreintes à des systèmes particuliers ;
  5. v. les fonctions thermodynamiques qui gouvernent les équilibres, comme la fonction de Gibbs, s’affranchissent de toute considération géométrique, alors qu’elle joue un rôle primordial dans les modèles thermodynamiques prédictifs les plus performants.

Comme la thermodynamique chimique est perfectible, la question scientifique adressée par cette étude est la suivante :

« Est-il possible de décrire l’équilibre des transformations microscopiques, réaction chimique et transition de phase, sans utiliser l’entropie calorimétrique et le potentiel chimique ? »

2. Théorie cinétique de l’équilibre chimique

2.1. Cadre de l’analyse

Le cadre de la théorie cinétique de l’équilibre chimique est celui du premier principe et celui du second principe restreint aux échanges de travail et chaleur. Ainsi, le potentiel chimique et l’entropie calorimétrique issue du second principe ne seront pas utilisés pour établir la fonction qui gouverne l’équilibre.

2.2. Définition de l’équilibre cinétique d’une réaction chimique

L’équilibre cinétique d’une réaction chimique est défini ainsi :

« L’équilibre chimique d’un système fermé est atteint lorsque la vitesse de formation de chaque constituant chimique est compensée par sa vitesse de disparition. »

Soit une réaction chimique qui se produit dans une phase homogène liquide ou gazeuse (note 3 ) :

A+B⇄C+D
L’équation qui exprime l’équilibre cinétique est l’égalité entre la vitesse de réaction des réactifs (+) et la vitesse de réaction des produits (−) :
veq+=veq−(84)

2.3. Loi de vitesse d’une réaction chimique

Soit une réaction élémentaire entre deux espèces chimiques A et B, dans une phase homogène liquide ou gazeuse, à température T et pression P de 1 bar constantes :

A+B→produit(s)
Le choix de l’expression mathématique de la vitesse de réaction chimique utilisée pour établir l’équation cinétique de l’équilibre est libre. Cette étude utilisera l’expression de la vitesse de réaction chimique, exprimée en mol⋅L−1⋅s−1, ci-après qui est proche de celle recommandée par l’IUPAC [27] :
v=[A]⋅[B]⋅zAB°⋅pAB°⋅exp−𝛥‡H°R⋅T(85)
zAB° est la fréquence de collision indépendante des concentrations entre A et B, exprimée en L⋅mol−1⋅s−1, issue de la théorie cinétique des collisions établie en 1916 par Max Traustz [28] :
zAB°=NA⋅π⋅(rA°+rB°)2⋅8⋅kB⋅Tπ⋅𝜇AB12(86)
𝜇AB est la masse réduite de A et B :
𝜇AB=mA⋅mBmA+mB(87)
𝛥‡H° est la hauteur du col d’enthalpie à franchir pour que la réaction se produise, issue de la théorie de l’état de transition d’Henry Eyring [29] (Figure 5) :
𝛥‡H°=H‡°−HA°−HB°(88)

Figure 5.

Diagramme du col d’enthalpie standard de transition d’une réaction chimique.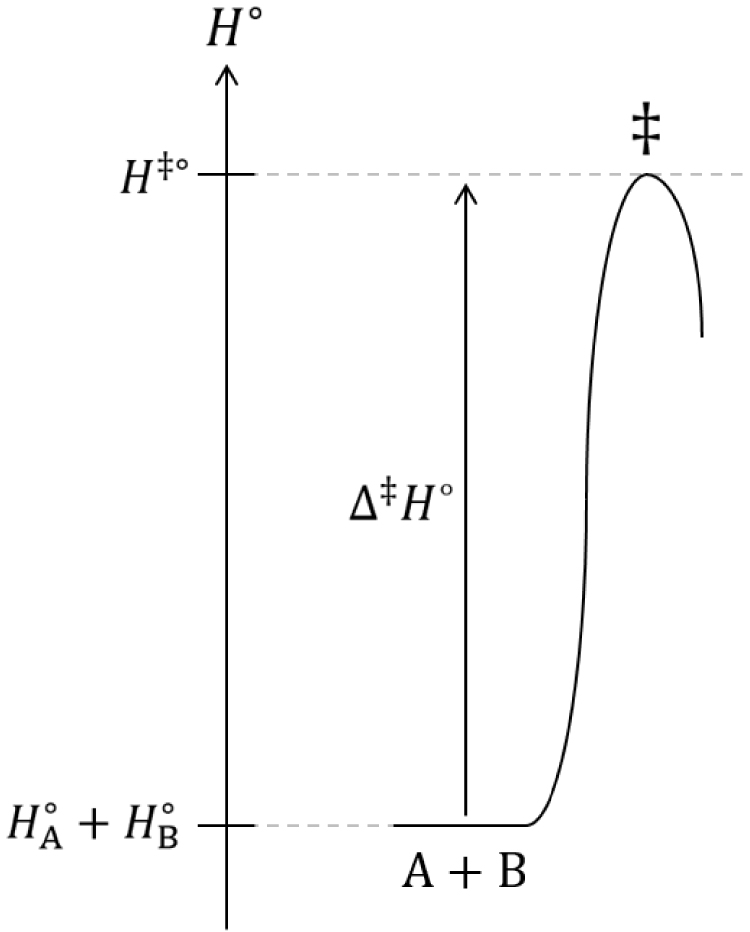

pAB° s’apparente au facteur stérique 𝜌 introduit par Cyril Norman Hinshelwood mais il ne s’identifie pas exactement à ce dernier : contrairement au facteur stérique 𝜌, cette probabilité est inférieure à 1 :

0<pAB°⩽1(89)
𝜌⩾1(90)
Pour certaines réactions, la vitesse de la réaction est supérieure à la fréquence de collision : la réaction se produit à une distance entre les réactifs supérieure à leur distance de contact, le facteur d’Hinshelwood est alors supérieur à 1. Afin de faire coïncider l’équation de vitesse exprimée avec une probabilité pAB° inférieure à 1 avec la vitesse de ces réactions, le terme rA°+rB° de la fréquence de collision n’est pas la somme des rayons de Van der Waals de A et B mais la distance à laquelle la réaction se produit, qui peut être supérieure. pAB° est donc la probabilité que la réaction se produise, à l’instant où les réactifs sont suffisamment proches pour réagir, indépendamment du franchissement du col d’enthalpie d’activation.

2.4. Equation cinétique de l’équilibre chimique

Les grandeurs z±°, p±° et 𝛥‡ H±° utilisées dans cette analyse seront supposées indépendantes de la température et de l’avancement de la réaction. Soit la réaction chimique en phase gazeuse renversable ci-après à température et pression égale à 1 bar constantes :

A+B⇄C+D
Le diagramme enthalpique de cette réaction est présenté sur la Figure 6.

Figure 6.

Diagramme du col d’enthalpie standard de transition d’une réaction chimique.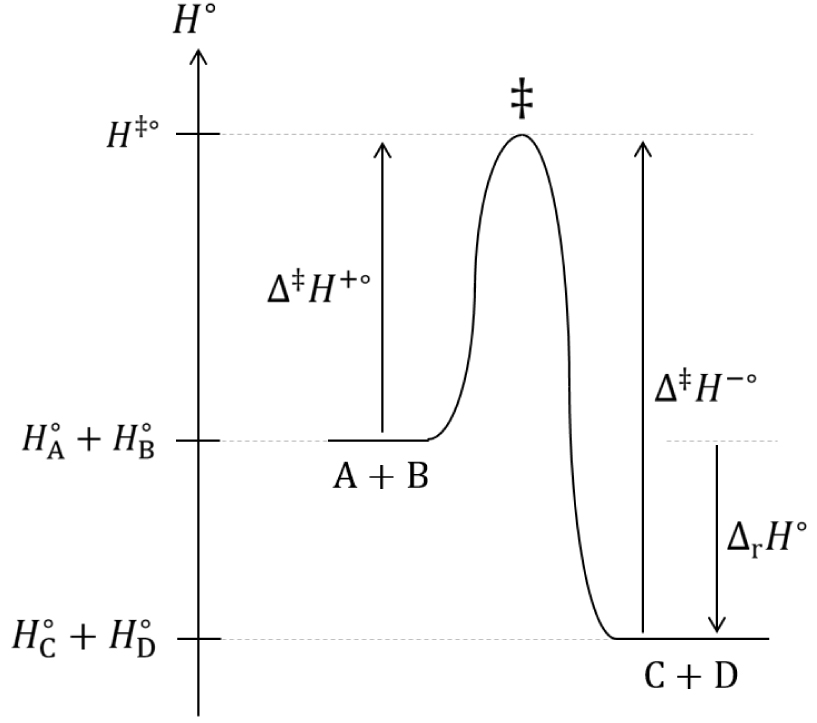

L’enthalpie standard de réaction est :

𝛥rH°=HC°+HD°−HA°−HB°=𝛥‡H+°−𝛥‡H−°(91)
La vitesse de réaction v+ de passage des réactifs (A et B) aux produits (C et D) pour cette réaction est :
v+=[A]⋅[B]⋅z+°⋅p+°⋅exp−𝛥‡H+°R⋅T(92)
Réciproquement, la vitesse de réaction v− de passage des produits C et D aux réactifs A et B est égale à :
v−=[C]⋅[D]⋅z−°⋅p−°⋅exp−𝛥‡H−°R⋅T(93)
A l’équilibre cinétique, les vitesses de réaction v+ et v− sont égales :
veq+=veq−(94)
La constante d’équilibre K déduite de cette dernière égalité est :
K=[C]eq⋅[D]eq[A]eq⋅[B]eq=z+°⋅p+°z−°⋅p−°⋅exp−𝛥rH°R⋅T(95)
Le quotient de réaction Q défini en dehors de l’équilibre est :
Q=[C]⋅[D][A]⋅[B](96)
Soit la fonction enthalpie libre cinétique G qui gouverne l’équilibre à température et pression constantes, choisie de façon à être homogène à une énergie molaire et telle que sa variation soit négative si la réaction chimique évolue dans le sens de formation des produits, positive si la réaction évolue dans le sens de formation des réactifs et égale à 0 à l’équilibre :
𝛥rG=R⋅T⋅lnQK(97)
𝛥rG devient, en prenant en compte les expressions de Q et K :
𝛥rG=𝛥‡H+°−R⋅T⋅ln([A]⋅[B]⋅z+°⋅p+°) −(𝛥‡H−°−R⋅T⋅ln([C]⋅[D]⋅z−°⋅p−°))(98)
L’évolution du système et de 𝛥rG, d’un état initial arbitraire à l’état d’équilibre, est illustrée sur la Figure 7.

Figure 7.

Evolution du système et de l’enthalpie libre cinétique de réaction d’un état initial arbitraire à l’état d’équilibre.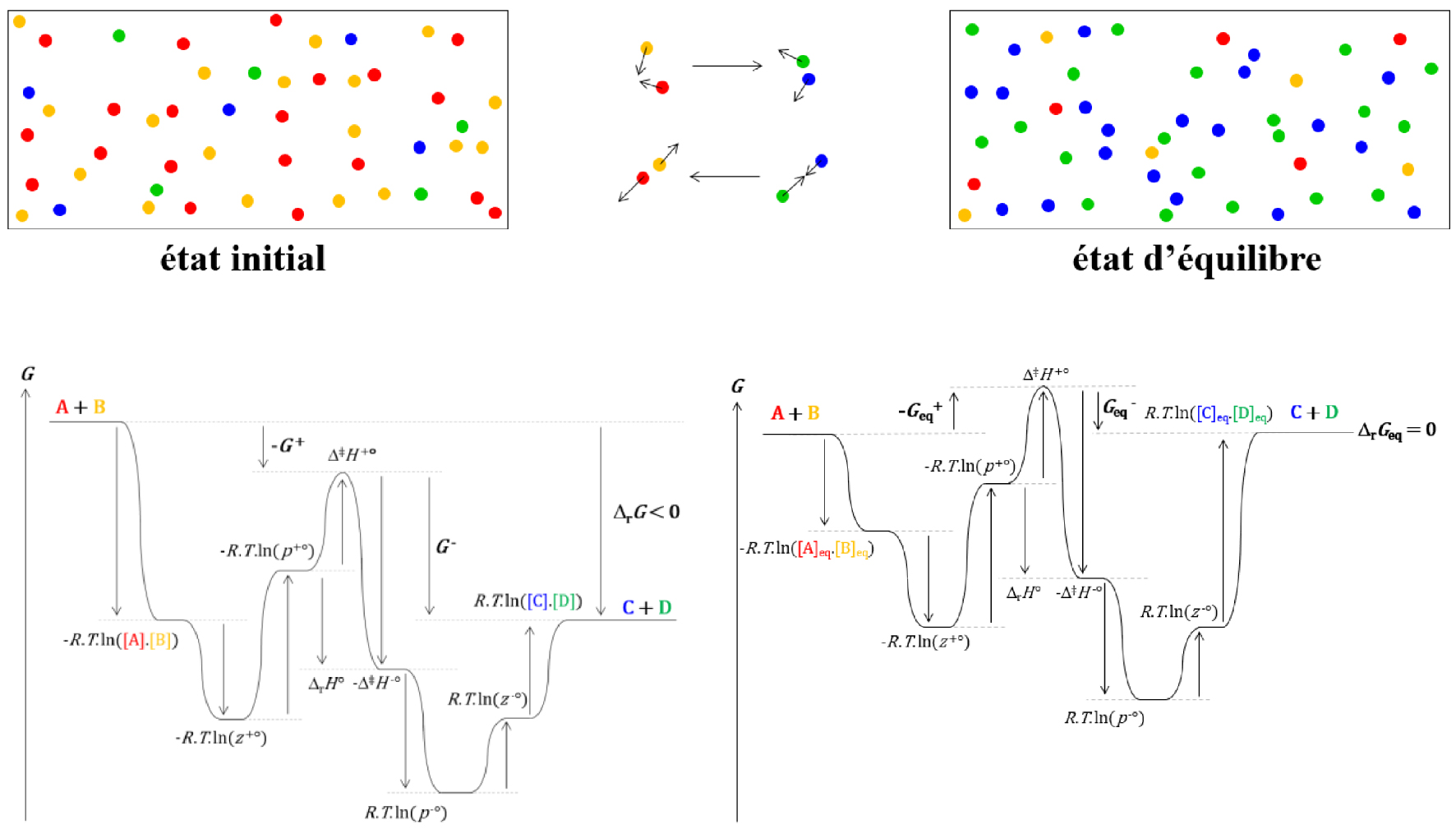

L’enthalpie libre cinétique de réaction 𝛥r G peut se décomposer en deux termes, G+ et G−, qui reflètent respectivement les vitesses de passage des réactifs aux produits et des produits aux réactifs.

𝛥rG=G−−G+(99)
L’équilibre cinétique correspond à l’égalité entre ces deux fonctions :
Geq+=Geq−(100)
Les énergies libres cinétiques G+ et G− peuvent s’exprimer en fonction d’un terme homogène à une énergie et d’un terme homogène à une entropie :
G+=−𝛥‡H+°+T⋅S+(101)
G−=−𝛥‡H−°+T⋅S−(102)
Les entropies cinétiques S+ et S− ainsi définies sont :
S+=R⋅ln([A]⋅[B]⋅z+°⋅p+°)(103)
S−=R⋅ln([C]⋅[D]⋅z−°⋅p−°)(104)
L’entropie cinétique de réaction est définie par la différence entre les entropies de réaction S+ dans le sens direct et S− dans le sens indirect :
𝛥rS=S+−S−(105)
Soit :
𝛥rS=R⋅lnz+°⋅p+°z−°⋅p−°+R⋅ln[A]⋅[B][C]⋅[D](106)
L’entropie de réaction est la somme d’une entropie standard et d’une fonction du quotient de réaction :
𝛥rS=𝛥rS°−R⋅ln(Q)(107)
Avec :
𝛥rS°=R⋅lnz+°⋅p+°z−°⋅p−°(108)
L’expression de l’enthalpie libre cinétique de réaction devient :
𝛥rG=𝛥rH°−T⋅𝛥rS°+R⋅T⋅ln(Q)(109)
Soit :
𝛥rG=𝛥rG°+R⋅T⋅ln(Q)(110)
Avec :
𝛥rG°=𝛥rH°−T⋅𝛥rS°(111)
L’expression de la constante d’équilibre devient :
K=exp−𝛥rG°R⋅T(112)

2.5. Synthèse

L’équation de l’équilibre a été établie en utilisant une loi cinétique issue de mesures expérimentales de vitesse de réaction. L’entropie calorimétrique et le potentiel chimique n’ont pas été utilisés. Les équations de l’énergie de Gibbs de réaction et de l’enthalpie cinétique de réaction sont formellement identiques :

𝛥rG=𝛥rG°+R⋅T⋅ln(Q)(113)
Les grandeurs standards correspondantes sont également identiques :
𝛥rG°=𝛥rH°−T⋅𝛥rS°(114)
Les enthalpies de réaction des approches thermodynamiques et cinétiques sont strictement égales en vertu du premier principe de la thermodynamique.
𝛥rH°=HC°+HD°−HA°−HB°=𝛥‡H+°−𝛥‡H−°(115)
En revanche, les entropies de réaction des approches thermodynamique et cinétique sont formellement différentes.
Thermodynamique :𝛥rS°=SC°+SD°−(SA°+SB°) (116)
Si°=∫0+TδQi°T′(117)
Cinétique :𝛥rS°=R⋅lnz+°⋅p+°z−°⋅p−°(118)
Les entropies de réaction thermodynamique et cinétique ne sont pas de même nature. En effet, l’entropie calorimétrique est définie pour chaque réactif et produit de la réaction chimique alors que l’entropie cinétique est définie pour des couples d’espèces réactives qui entrent en collision. En outre l’entropie calorimétrique est une caractéristique globale des espèces chimiques, puisque toute la matière est impliquée dans les échanges de chaleur, alors que l’entropie cinétique est une caractéristique locale des espèces chimiques, située à la zone de contact des espèces chimiques lors de la collision qui précède la réaction. Il n’y a donc pas lieu que les valeurs numériques de ces deux entropies soient égales. Les expressions des constantes d’équilibre thermodynamique et cinétique sont formellement identiques :
K=exp−𝛥rG°R⋅T(119)
Cependant, la constante d’équilibre thermodynamique ne dépend pas de la vitesse à laquelle s’instaure l’équilibre, alors que la constante d’équilibre cinétique dépend complètement des cinétiques des réactions chimiques impliquées dans l’équilibre.

3. Etude thermodynamique et cinétique d’équilibres chimiques

3.1. Cadre de l’analyse

Ce chapitre confronte les modèles thermodynamique et cinétique aux observations expérimentales d’équilibres chimiques dans les conditions standards. Les enthalpies et entropies standards cinétique et thermodynamique seront considérées indépendantes de la température.

3.2. Formation d’un complexe d’association intermoléculaire

Soit l’équilibre d’association de la β-cyclodextrine avec l’acide salicylique en solution aqueuse (Figure 8).

Figure 8.

Equilibre d’association de la β-cyclodextrine (A) avec l’acide salicylique (B).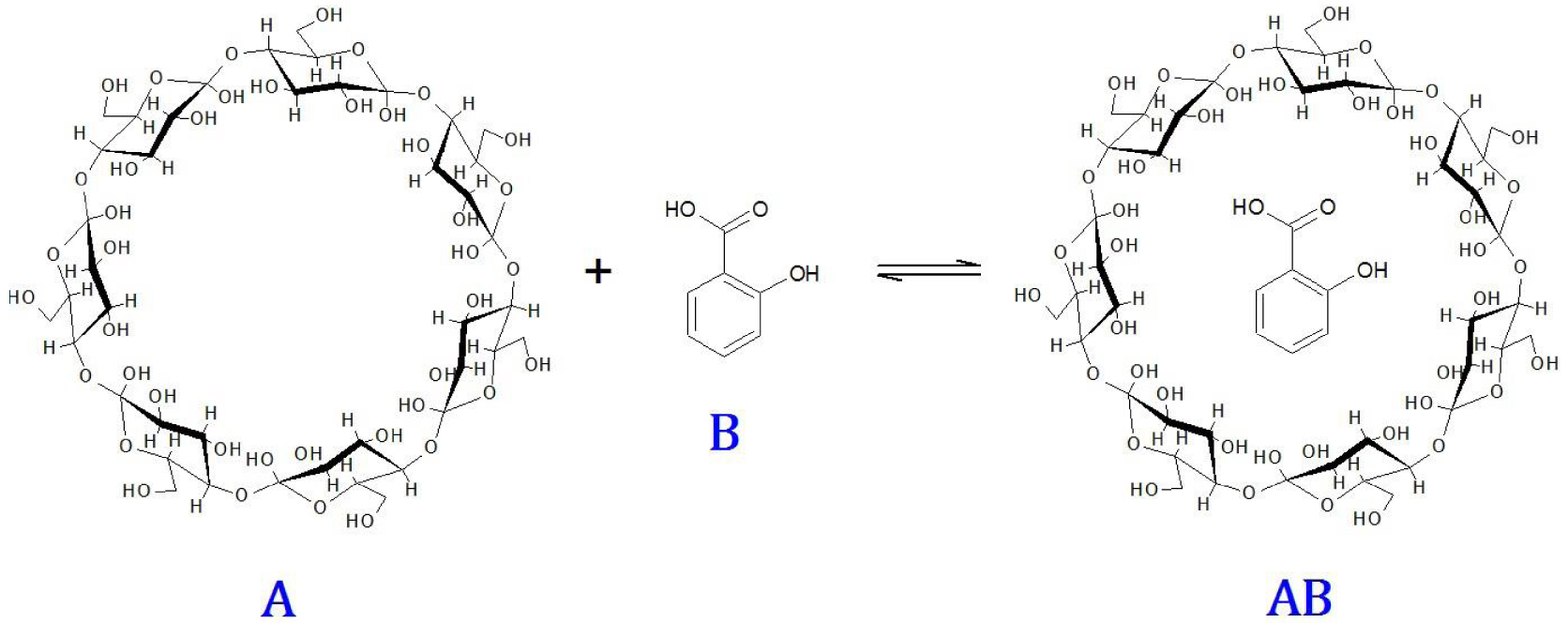

Cette réaction d’association se produit dans le sens direct suite à une collision entre A et B. Dans le sens opposé, le complexe d’association AB est dissocié lors de sa collision avec n’importe quelle molécule X du milieu : A, B, AB ou H2O. L’équation chimique de l’équilibre s’écrit, en indiquant entre crochets les espèces qui entrent en collision :

[A(aq)+B(aq)]+X(l)⇌[AB(aq)+X(l)]
Ce formalisme d’écriture de l’équation chimique respecte la conservation de la matière et le processus collisionnel préalable à la réaction chimique. La réaction se produit dans le sens direct suite à une collision entre A et B, ce qui implique l’utilisation stricte de ces deux espèces en termes de concentrations dans le développement de l’expression de la vitesse de réaction. La collision avec la molécule X n’est pas nécessaire dans cet événement réactionnel. En revanche le rôle de la molécule X est primordial dans le sens indirect, puisque le complexe sera dissocié suite à une collision avec la molécule X qui apporte suffisamment d’énergie cinétique pour que la dissociation du complexe se produise. Si le milieu est suffisamment dilué, X est une molécule du solvant, l’eau. La loi de vitesse dans le sens indirect sera donc exprimée avec le produit de la concentration du complexe d’association avec la concentration de X. L’équilibre cinétique se traduit par l’égalité entre la vitesse de la réaction d’association et la vitesse de la réaction inverse, de dissociation :
veq+=veq−(120)
D’où :
 [A]eq⋅[B]eq⋅z+°⋅p+°⋅exp−𝛥‡H+°R⋅T =[AB]eq⋅[X]eq⋅z−°⋅p−°⋅exp−𝛥‡H−°R⋅T(121)
Avec :
[X]eq=[A]eq+[B]eq+[AB]eq+[H2O]eq(122)
Les concentrations en β-cyclodextrine, acide salicylique et en complexe d’association, qui ne dépassent pas 10−2 M, sont négligeables devant la concentration de l’eau, de l’ordre de 56 M :
[X]eq≅56M(123)
La constante d’équilibre cinétique est :
K≅56.[AB]eq[A]eq⋅[B]eq≅exp−𝛥rH°−T⋅𝛥rS°R⋅T(124)
Avec :
𝛥rH°=HAB°−HA°−HB°(125)
𝛥rS°=R⋅lnz+°⋅p+°z−°⋅p−°(126)
La constante d’équilibre thermodynamique est :
K=[AB]eq[A]eq⋅[B]eq=exp−𝛥rH°−T⋅𝛥rS°R⋅T(127)
Avec :
𝛥rH°=HAB°−HA°−HB°(128)
𝛥rS°=SAB°−SA°−SB°(129)
L’évolution du logarithme népérien de la constante d’équilibre déterminée par l’expérience [30] avec l’inverse de la température de cette réaction d’association est linéaire pour les deux modèles (Figure 9).

Figure 9.

Evolution de la constante d’équilibre cinétique (bleu) et calorimétrique (rouge) avec l’inverse de la température de l’association entre la β-cyclodextrine et l’acide salicylique.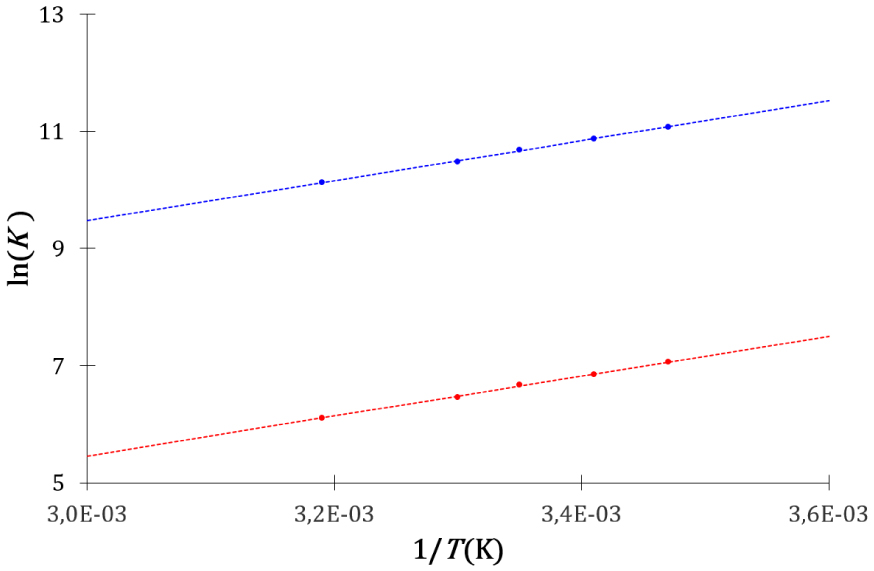

La manière différente de définir les constantes d’équilibre cinétique et thermodynamique est arbitraire, elle ne constitue pas un critère pour comparer leurs performances prédictives. Les descriptions cinétique et thermodynamique conduisent à des équations concordantes avec la dépendance en température de la constante d’équilibre établie par l’expérience.

3.3. Estérification de Fischer

Soit l’équilibre de l’estérification de Fischer entre un acide carboxylique, l’acide lévulinique, et le n-butanol, un alcool d’alkyle primaire (Figure 10).

Figure 10.

Equation de l’équilibre de l’estérification de Fischer entre l’acide lévulinique et le n-butanol.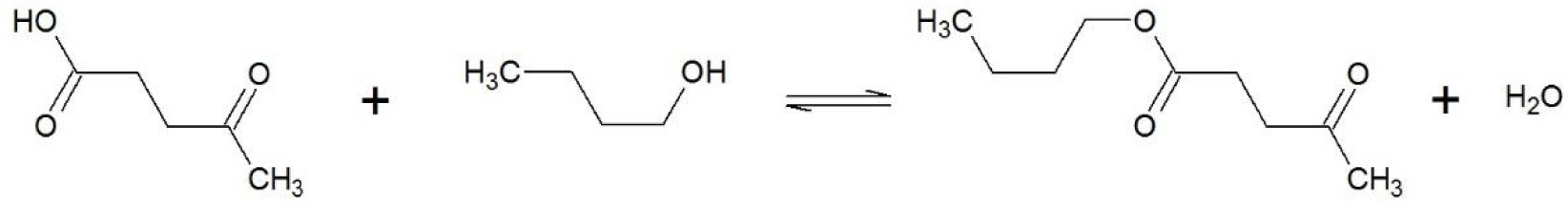

Cette réaction est catalysée par un acide de Bronsted qui est soit un acide ajouté au milieu réactionnel, soit présent dans le milieu. En effet, cette réaction est connue pour être catalysée par un de ses réactifs, l’acide carboxylique. Le mécanisme de l’estérification de Fischer se décompose en cinq étapes élémentaires (Figure 11). Les espèces qui entrent en collision préalablement à chaque réaction sont indiquées entre crochets. L’espèce chimique X se rapporte à n’importe quelle espèce chimique présente dans le milieu réactionnel : réactif, produit ou solvant.

Figure 11.

Mécanisme réactionnel de l’estérification de Fischer, les mouvements électroniques ont été omis par souci de clarté.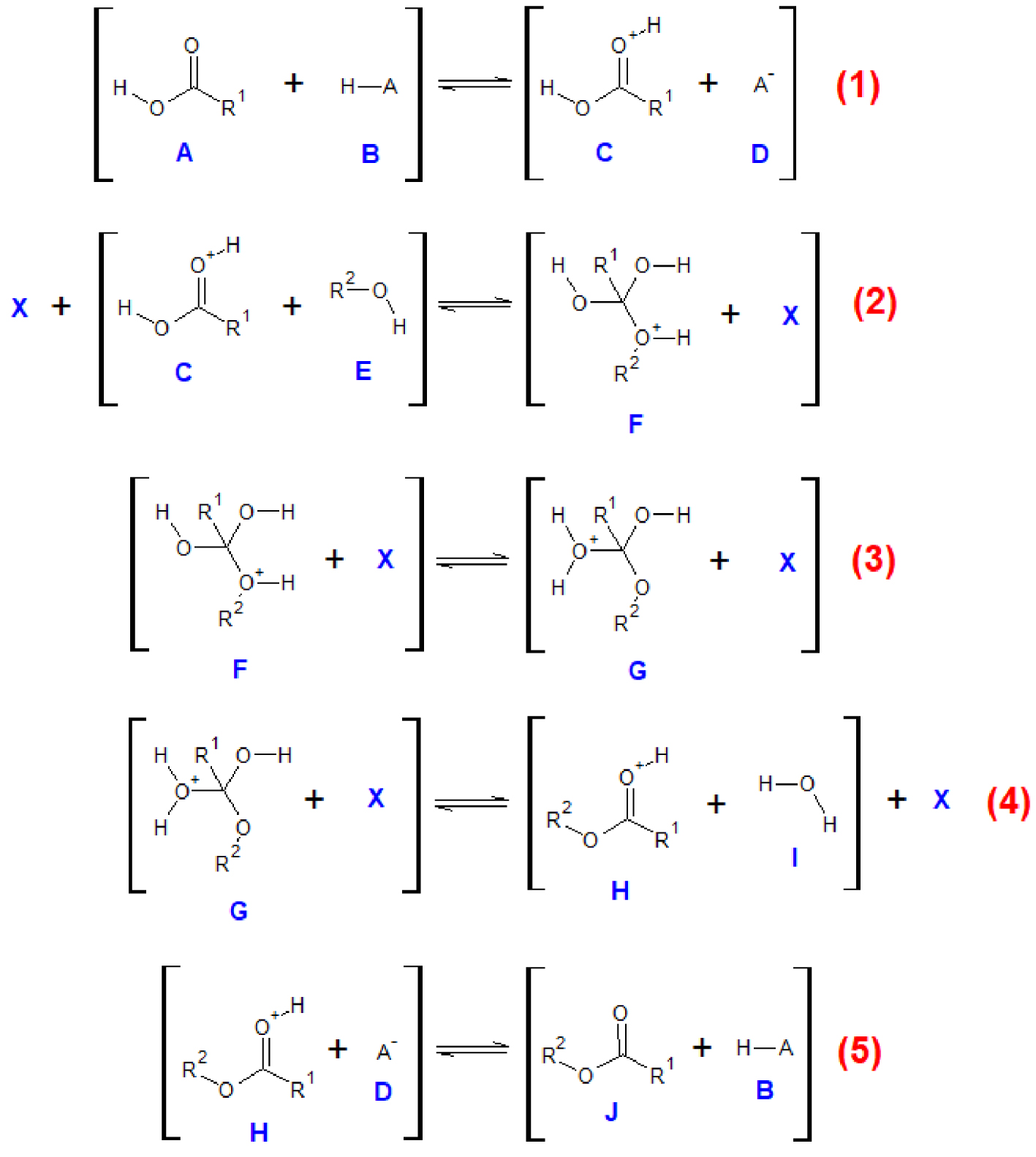

Les équations de l’équilibre cinétique sont :

{vi,eq+°=vi,eq−°}i∈[1;5](130)
Soient :
 [A]eq⋅[B]eq⋅z1+°⋅p1+°⋅exp−𝛥‡H1#+°R⋅T =[C]eq⋅[D]eq⋅z1−°⋅p1−°⋅exp−𝛥‡H1#−°R⋅T(131)
 [C]eq⋅[E]eq⋅z2+°⋅p2+°⋅exp−𝛥‡H2+°R⋅T =[F]eq⋅[X]eq⋅z2−°⋅p2−°⋅exp−𝛥‡H2−°R⋅T(132)
 [F]eq⋅[X]eq⋅z3+°⋅p3+°⋅exp−𝛥‡H3+°R⋅T =[G]eq⋅[X]eq⋅z3−°⋅p3−°⋅exp−𝛥‡H3−°R⋅T(133)
 [G]eq⋅[X]eq⋅z4+°⋅p4+°⋅exp−𝛥‡H4+°R⋅T =[H]eq⋅[I]eq⋅z4−°⋅p4−°⋅exp−𝛥‡H4−°R⋅T(134)
 [H]eq⋅[D]eq⋅z5+°⋅p5+°⋅exp−𝛥‡H5+°R⋅T =[J]eq⋅[B]eq⋅z5−°⋅p5−°⋅exp−𝛥‡H5−°R⋅T(135)
La conservation de l’énergie implique :
𝛥rH°= ∑i=15(𝛥‡Hi+°−𝛥‡Hi−°)(136)
La constante d’équilibre cinétique se déduit de ce système d’équations :
K=[J]eq⋅[I]eq[A]eq⋅[E]eq=∏i=15zi+°⋅pi+°zi−°⋅pi−°⋅exp−𝛥rH°R⋅T(137)
Soit :
K=[J]eq⋅[I]eq[A]eq⋅[E]eq=exp−𝛥rH°−T⋅𝛥rS°R⋅T(138)
Avec :
𝛥rS°=R⋅ln∏i=15zi+°⋅pi+°zi−°⋅pi−°(139)
Soit, en regroupant les termes de même nature :
𝛥rS°=S+°−S−°(140)
Avec :
S+°=∏i=15zi+°⋅pi+°(141)
S−°=∏i=15zi−°⋅pi−°(142)
La constante d’équilibre et l’entropie de réaction thermodynamiques sont respectivement :
K=[J]eq⋅[I]eq[A]eq⋅[E]eq=exp−𝛥rH°−T⋅𝛥rS°R⋅T(143)
𝛥rS°=SJ°+SI°−SA°−SE°(144)
Les constantes d’équilibre cinétique et thermodynamique sont formellement identiques même si leur terme entropique ne s’explicite pas de la même manière. L’évolution du logarithme népérien de la constante d’équilibre déterminée par l’expérience [31] avec l’inverse de la température de cette réaction d’estérification est linéaire (Figure 12).

Figure 12.

Evolution du logarithme népérien de la constante d’équilibre avec l’inverse de la température de la réaction d’estérification de l’acide lévulinique par le n-butanol.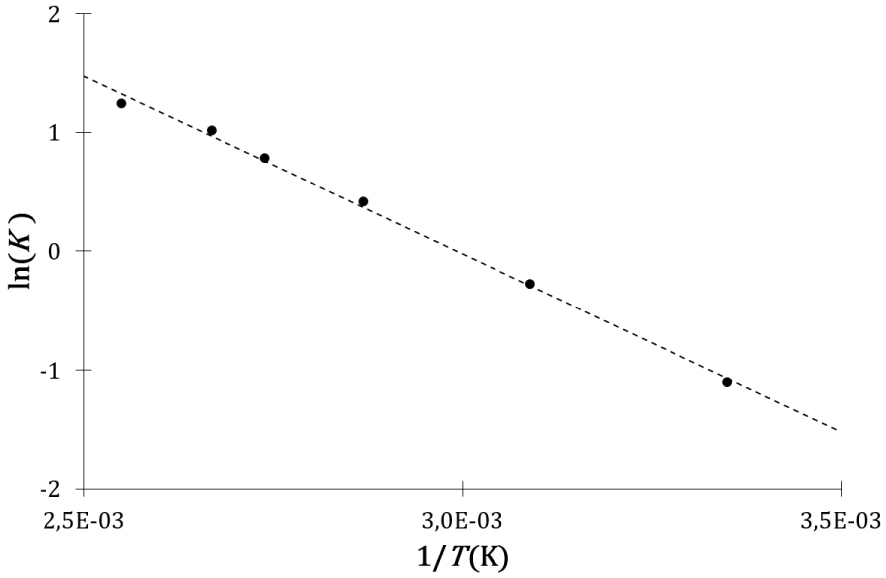

Une fois encore, même si l’interprétation de l’entropie des descriptions cinétique et calorimétrique est différente, les expressions mathématiques des constantes d’équilibre cinétique et thermodynamique sont formellement identiques et en accord avec l’expérience, c’est-à-dire avec une évolution linéaire du logarithme népérien de la constante d’équilibre avec l’inverse de la température.

3.4. Catalyse de l’estérification de Fischer par un acide fort

Soit l’équilibre d’estérification de l’acide éthanoïque par l’éthanol :

 CH3COOH(l)+CH3CH2OH(l) ⇌CH3COOCH2CH3(l)+H2O(l)
Les constantes de cet équilibre, avec et sans ajout d’un acide fort (RSO3H), sont reportées dans le Tableau 1 :

Tableau 1.

Constantes et temps d’établissement de l’équilibre d’estérification de l’acide éthanoïque par l’éthanol

TKCatalyseurteqRéférence
323 K3,4 Aucun22 joursCalvar et al. [32]
323 K4,6RSO3H 0,2 M3 heuresHe et al. [33 ]

L’ajout d’une faible quantité de l’hydrogénosulfate de 1-sulfobutyl-3-méthylimidazolium (RSO3H) ne modifie pas significativement la constante de l’équilibre mais accélère dans des proportions considérables la vitesse avec laquelle il s’établit. Les expressions de la constante d’équilibre et de l’entropie standard de réaction cinétiques de l’estérification de Fischer, établies dans le chapitre précédent, sont respectivement :

K=[ester]eq⋅[eau]eq[acide]eq⋅[alcool]eq=exp−𝛥rH°−T⋅𝛥rS°R⋅T (145)
𝛥rS°=S+°−S−°(146)
Il a de même été établi que les expressions de la constante d’équilibre et de l’entropie standard de réaction thermodynamiques sont respectivement :
K=[ester]eq⋅[eau]eq[acide]eq⋅[alcool]eq=exp−𝛥rH°−T⋅𝛥rS°R⋅T (147)
𝛥rS°=Sester°+Seau°−Sacide°−Salcool°(148)
La diminution du temps d’établissement de l’équilibre s’explique pour les deux modèles par la diminution de l’enthalpie de l’état de transition (Figure 13) :
Hcat‡°<H‡°(149)

Figure 13.

Diagrammes réactionnels cinétique (gauche) et thermodynamique (droite) de l’estérification de Fischer.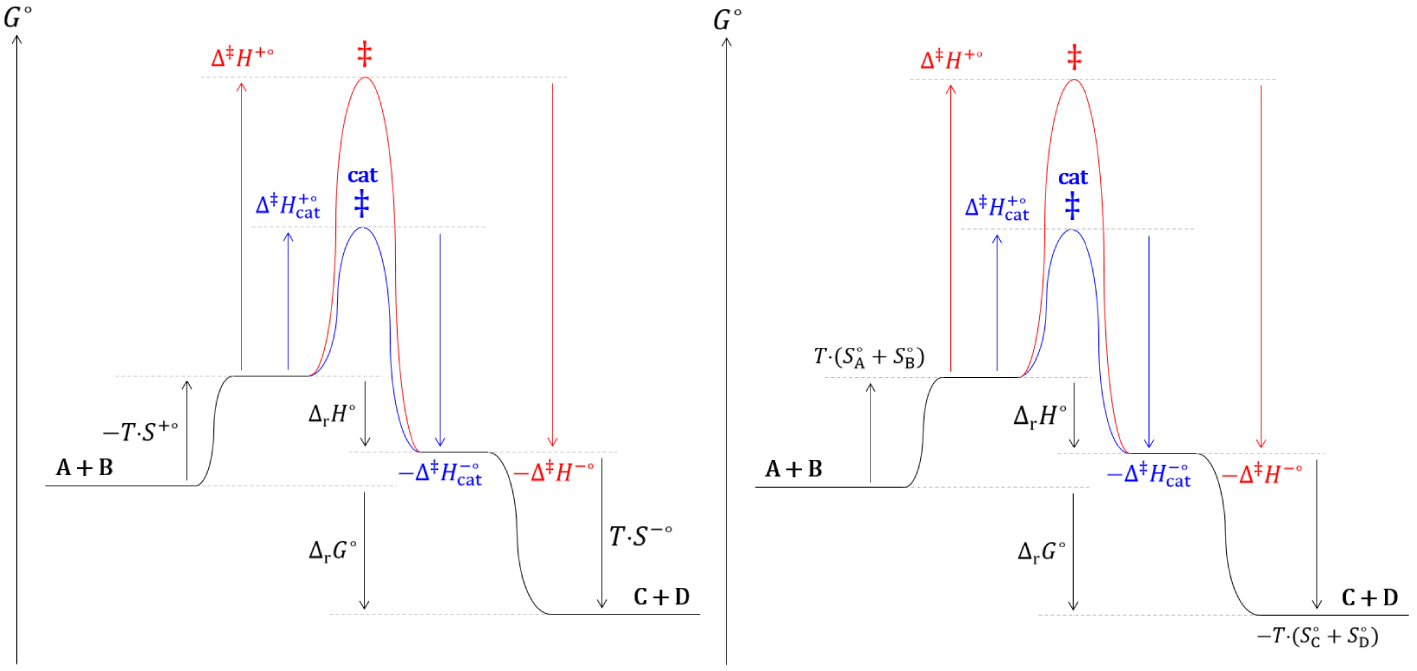

Les analyses thermodynamique et cinétique d’une réaction chimique catalysée prévoient un comportement identique et en accord avec les observations expérimentales.

3.5. Catalyse enzymatique d’une transestérification

Les énantiomères réactifs engagés dans certaines réactions catalysées par une molécule chirale sont synthétisés en produits énantiomères dans des proportions différentes. L’équilibre de la transestérification du butanoate de 2,2,2-trifluoroéthyle par les énantiomères du 3-fluoro-1-phénoxypropan-2-ol (Figure 14), dont la transformation est catalysée par l’enzyme Candida Antartica [34], présente ce caractère.

Figure 14.

Equilibres de transestérification du butanoate de 2,2,2-trifluoroéthyle par les énantiomères R et S du 3-fluoro-1-phénoxypropan-2-ol.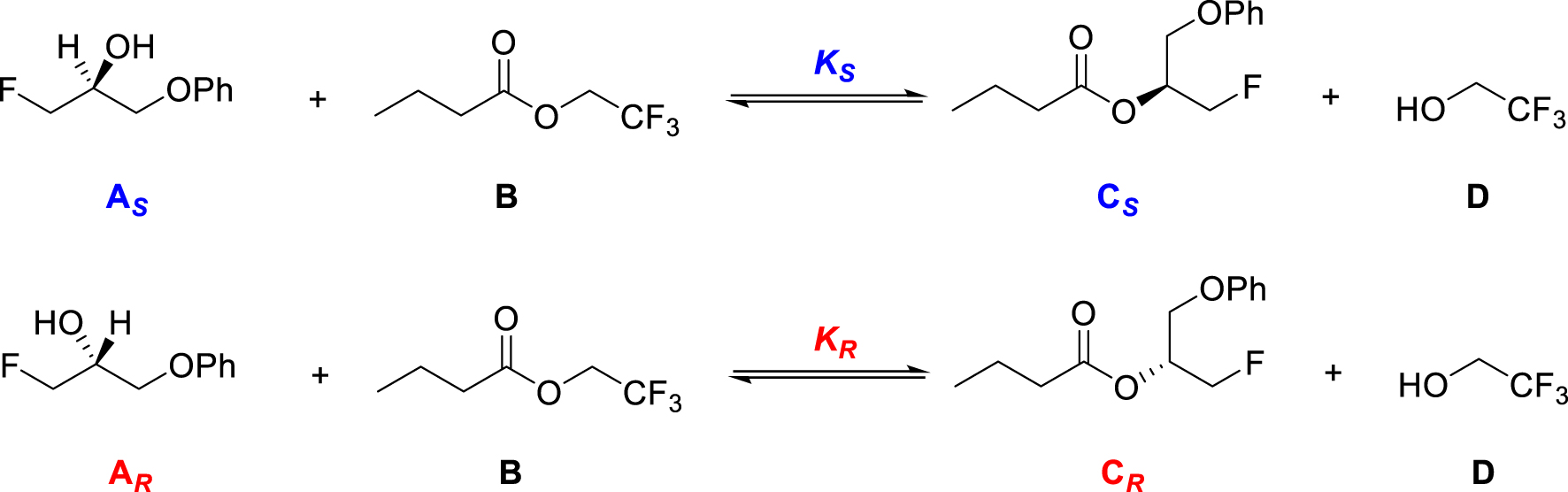

A l’équilibre, le facteur d’énantiosélectivité de cette transestérification, de 490, est supérieur à 1, ce qui signifie que la constante d’équilibre de la réaction avec l’énantiomère S est supérieure à celle de la réaction avec l’énantiomère R :

[CS]eq[CR]eq=490(150)
KS>KR(151)

Le mécanisme de transestérification résulte d’une succession de réactions élémentaires consécutives, que la réaction soit catalysée ou non (cf. estérification de Fischer), il est donc possible d’exprimer les constantes d’équilibre cinétique ainsi :

KS=[CS]eq⋅[D]eq[AS]eq⋅[B]eq=exp−𝛥rHS°−T⋅𝛥rSS°R⋅T(152)
𝛥rSS°=SS+°−SS−°(153)
KR=[CR]eq⋅[D]eq[AR]eq⋅[B]eq=exp−𝛥rHR°−T⋅𝛥rSR°R⋅T(154)
𝛥rSR°=SR+°−SR−°(155)

Les enthalpies de transestérification S et R sont égales car les enthalpies de formation de deux énantiomères sont égales.

HS°=HR°(156)
𝛥rHS°=𝛥rHR°(157)

La séquence peptidique du domaine catalytique de l’enzyme Candida Antartica (Trp104, His224, Ser105) permet d’établir avec l’énantiomère S et l’ester B achiral un réseau de liaisons hydrogènes et d’interactions de Van der Waals qui augmente la vitesse de formation de l’énantiomère S, ce qui se traduit par une valeur plus élevée du rapport des probabilités de la transestérification S :

pS+°pS−°>pR+°pR−°(158)
Or :
𝛥rS°=R⋅lnz+°⋅p+°z−°⋅p−°(159)
Donc :
𝛥rSS°>𝛥rSR°(160)
Le rapport d’équilibre cinétique de la transestérification S est en conséquence supérieur à celui de la transestérification R :
KS>KR(161)
Les diagrammes réactionnels cinétiques de ces transestérifications sont présentés sur la Figure 15.

Figure 15.

Diagramme réactionnel cinétique des transestérifications du butanoate de 2,2,2-trifluoroéthyle par les énantiomères R et S du 3-fluoro-1-phénoxypropan-2-ol.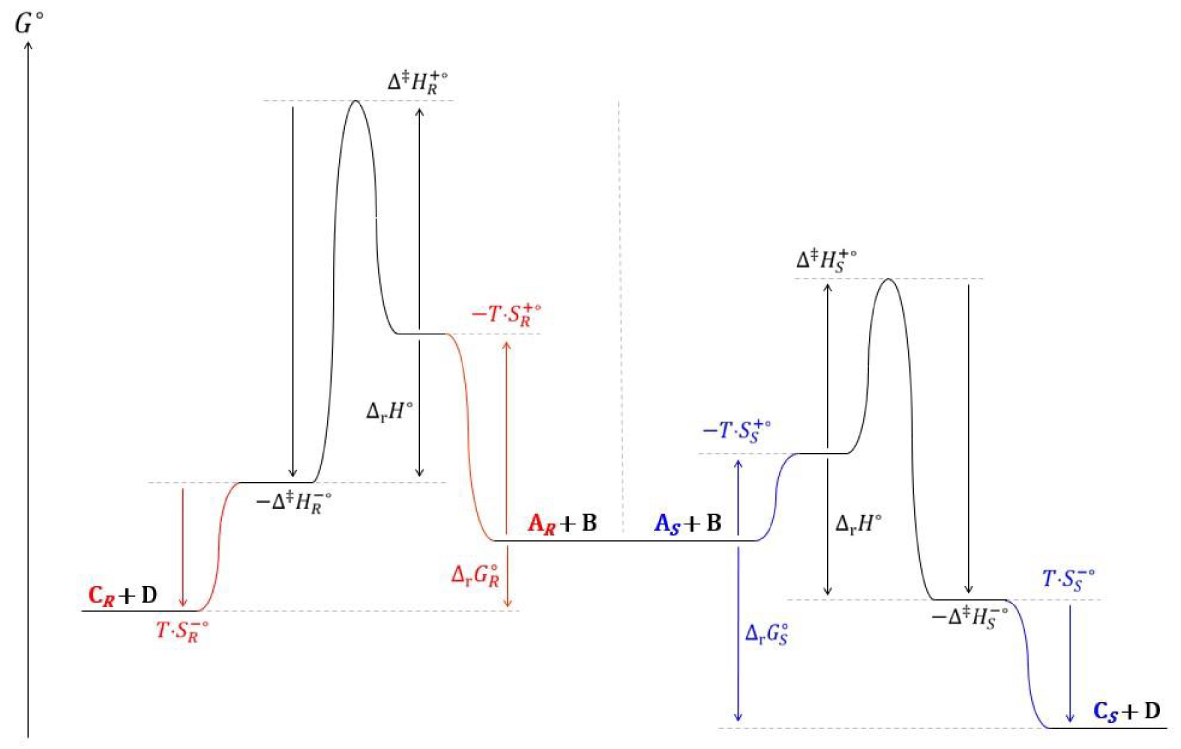

La description cinétique de cet équilibre est satisfaisante. Pour le modèle thermodynamique, les enthalpies et capacités calorifiques standards de deux énantiomères sont égales :

HS°=HR°(162)
Cp,S°=Cp,R°(163)

Ces deux égalités induisent l’égalité entre les enthalpies de transestérifications des énantiomères d’une part et de leurs entropies d’autre part, soient respectivement :

𝛥rHS°=𝛥rHR°(164)
𝛥rSS°=𝛥rSR°=SC°+SD°−SA°−SB°(165)
Ce qui conduit de facto à l’égalité entre les enthalpies libres de transestérification et in fine des rapports d’équilibres :
𝛥rGS°=𝛥rGR°(166)
KS=KR(167)
La catalyse d’une réaction chimique dans le contexte de l’existence du potentiel chimique présente l’inconvénient d’accélérer aussi bien la vitesse de la réaction dans le sens inverse que dans le sens direct, la conséquence en est que la catalyse ne modifie pas le rapport d’équilibre. Le diagramme réactionnel thermodynamique de la catalyse illustre ce propos (Figure 16).

Figure 16.

Diagramme réactionnel thermodynamique des transestérifications du butanoate de 2,2,2-trifluoroéthyle par les énantiomères R et S du 3-fluoro-1-phénoxypropan-2-ol.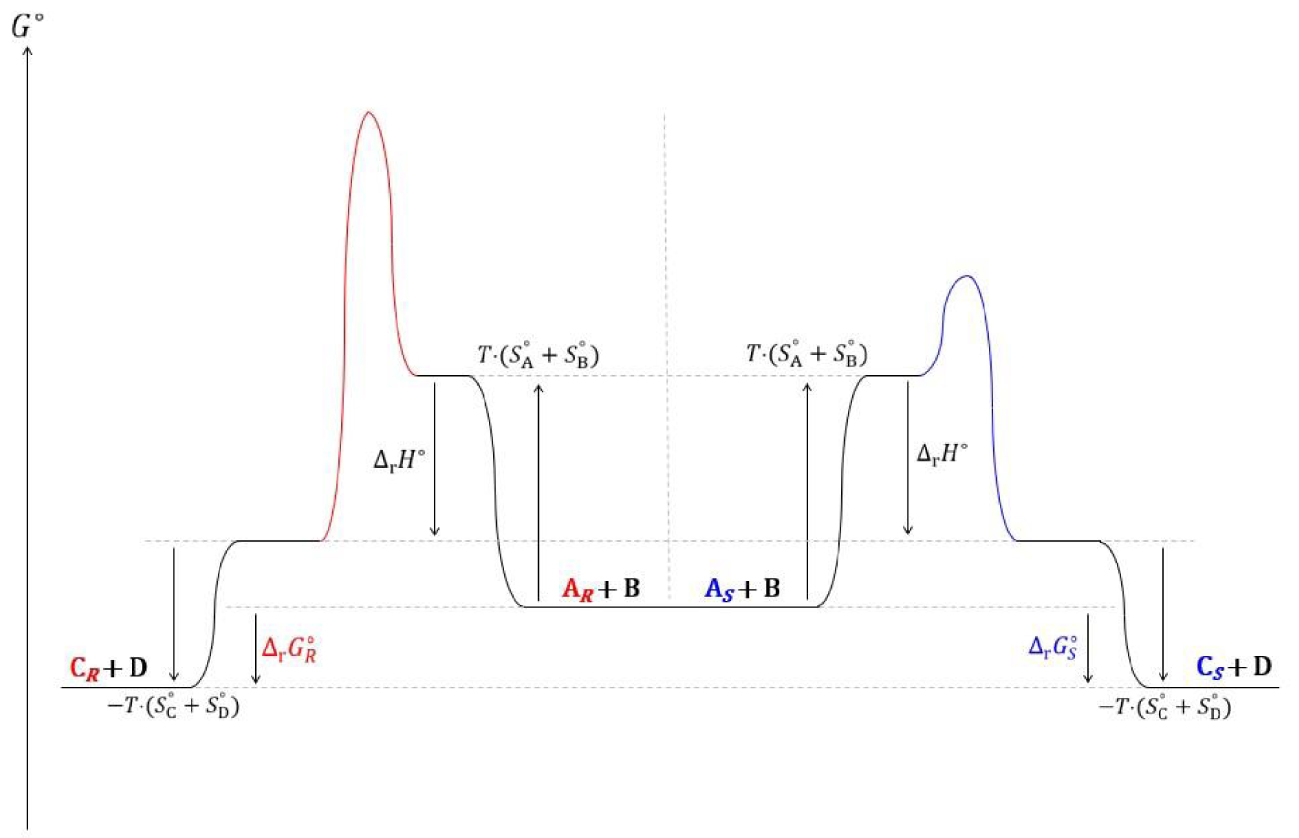

Le modèle cinétique de l’équilibre offre une description plus cohérente de l’équilibre de transestérification enzymatique que le modèle thermodynamique. Il conviendrait à la lumière de cette description de nuancer deux types de catalyse. La première, qui ne modifie pas la valeur de la constante d’équilibre (i.e. estérification de Fischer), est de nature enthalpique, la deuxième, qui peut drastiquement l’affecter (i.e. transestérification énantiosélective), est de nature entropique.

3.6. Dissociation de mono- et di-acides faibles

Les mono- et di-acides carboxyliques, solubles dans l’eau à basse concentration, présentent un caractère acide (Figure 17).

Figure 17.

Equilibres de dissociation de première acidité de mono- et di-acides carboxyliques linéaires en solution aqueuse.

La constante d’acidité est définie par le produit de la constante d’équilibre d’une réaction acide-base avec la concentration de l’eau, supposée constante en solution diluée :

Ka=K⋅[H2O](168)
Les constantes expérimentales de première acidité des équilibres de dissociation des mono- et di-acides carboxyliques reportés dans la littérature sont renseignées dans le Tableau 2 en échelle logarithmique :
pKa=−log(Ka)(169)

Tableau 2.

Constantes de première acidité exprimées en échelle logarithmique de réactions de dissociation de mono- et di-acides carboxyliques issues de la littérature

Monoacide (M) pKaRéférence   Diacide (D)pKaRéférence
HCO2H3,76Kim et al. [35 ]   HO2CCO2H1,32Mateus et al. [36 ]
Dasgupta et al. [37]  1,27 Lugo et al. [38]
H(CH3)1CO2H4,74Espinoza et al. [39 ]  HO2C(CH2)1CO2H2,83Khalil et al. [40 ]
H(CH3)2CO2H4,876Lomas et al. [41 ]   2,86Gelles et al. [42 ]
Körtum et al. [43]  HO2C(CH2)2CO2H4,19Khalil et al. [40 ]
Mansfield et al. [44]  HO2C(CH2)3CO2H4,34German et al. [45 ]
4,81 Chen et al. [46]   HO2C(CH2)4CO2H4,46Radalla et al. [47 ]
H(CH3)3CO2H4,86Headley et al. [48 ]   Jeffery et al. [49 ]
   Gane et al. [50]
  HO2C(CH2)5CO2H4,51Radalla et al. [47 ]
   Jeffery et al. [49]
   Gane et al. [50]
  HO2C(CH2)6CO2H4,52Jeffery et al. [49 ]

Le pKa de première acidité des mono- et di-acides carboxyliques augmente avec la longueur de la chaîne hydrocarbonée, il atteint une valeur limite pour des longueurs élevées de la chaîne hydrocarbonée (Figure 18).

Figure 18.

Evolution du pKa de première acidité de mono- et di-acides carboxyliques avec la longueur de la chaîne hydrocarbonée.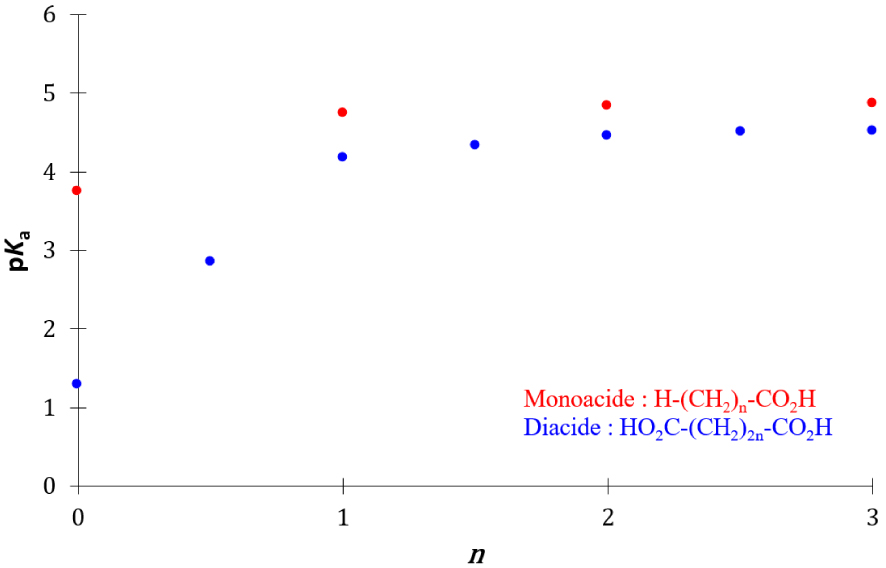

Cet effet d’atténuation du pKa est en accord avec celui de l’atténuation des effets inductifs avec la longueur de la chaîne aliphatique. Les vitesses des réactions directe et inverse des monoacides carboxyliques sont respectivement :

vM+=[MH]⋅[H2O]⋅zM+°⋅pM+°⋅exp−𝛥‡HM+°R⋅T(170)
vM−=[M−]⋅[H3O+]⋅zM−°⋅pM−°⋅exp−𝛥‡HM−°R⋅T(171)
Ces vitesses sont égales à l’équilibre :
vM,eq+=vM,eq−(172)
La constante de dissociation de monoacides carboxyliques se déduit de cette dernière égalité :
KM=zM+°⋅pM+°zM−°⋅pM−°⋅exp−𝛥rHM°R⋅T(173)
La constante de première acidité de la dissociation de diacides carboxyliques déduite par un raisonnement analogue est :
KD=zD+°⋅pD+°zD−°⋅pD−°⋅exp−𝛥rHD°R⋅T(174)
Si la longueur de chaîne est élevée, l’environnement électronique de la fonction acide carboxylique des mono- et di-acides engagée dans la réaction acide-base est semblable. Il est donc légitime de supposer que leurs variations d’enthalpies et probabilités de réaction sont voisines :
𝛥rHM°=𝛥rHD°(175)
pM°=pD°(176)
Les fréquences de collision des réactions inverses de dissociation des mono- et di-acides sont voisines car ils présentent un seul groupe carboxylate réactif :
zM−°=zD−°(177)
La fréquence de collision de la réaction directe de dissociation du diacide est le double de celle du monoacide car il présente deux groupes réactifs acide carboxylique contre un seul pour le monoacide :
2⋅zM+°=zD+°(178)
La valeur du rapport entre les constantes d’équilibre est donc, dans le cadre de ces hypothèses :
KDKM=2(179)
Le rapport déduit des mesures expérimentales issues de la littérature est :
KDKM=2,19(180)
La description cinétique de l’équilibre concorde quantitativement avec les mesures expérimentales. Le modèle thermodynamique ne permet pas de prévoir quantitativement un tel écart. En effet, les variations de capacité calorifique lors de la réaction pour des longueurs de chaîne hydrocarbonées élevées devraient être égales pour les mono- et di-acides puisque les modifications de l’environnement électronique résultant des deux réactions sont équivalentes. La Figure 19 permet de visualiser clairement l’effet cinétique sur la topologie du diagramme réactionnel.

Figure 19.

Diagramme réactionnel cinétique de la dissociation d’acides mono- et di-carboxyliques.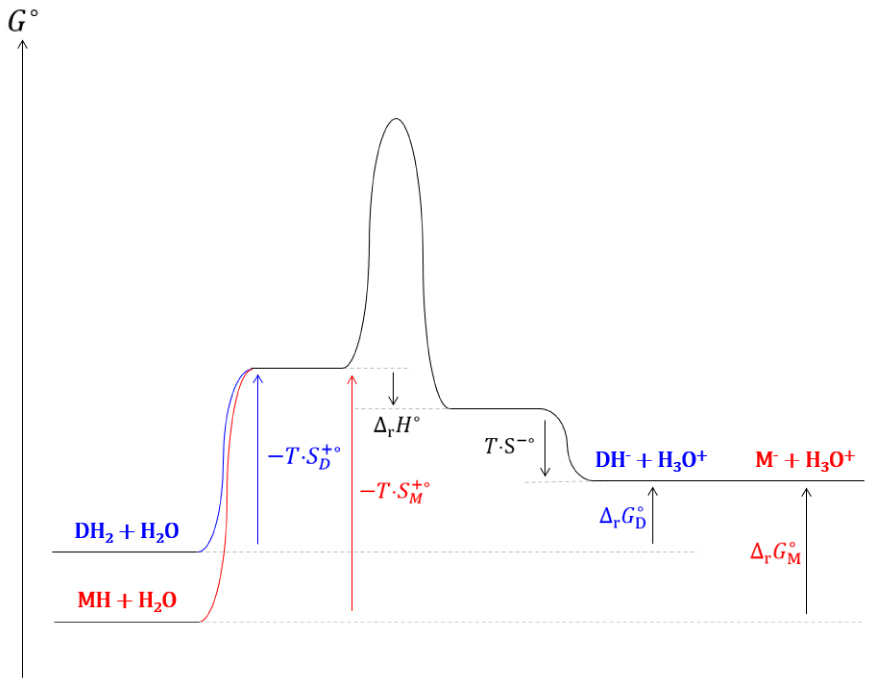

3.7. Synthèse

Les modèles thermodynamique et cinétique de l’équilibre chimique prévoient une évolution linéaire du logarithme népérien de la constante d’équilibre avec l’inverse de la température, en accord avec le comportement de nombreuses réactions. Les deux approches donnent une explication satisfaisante de la catalyse de certaines réactions. En revanche, le modèle cinétique est plus approprié que le modèle thermodynamique pour comprendre un équilibre chimique où la géométrie des réactifs lors de leur collision favorise sélectivement une des réactions possibles, la transestérification enzymatique. L’analyse cinétique de l’équilibre permet de distinguer deux types de catalyse : la catalyse enthalpique pour laquelle l’enthalpie de l’état de transition diminue et la catalyse entropique pour laquelle la probabilité de réaction suite à une collision augmente indépendamment de l’enthalpie. Le modèle cinétique de l’équilibre permet également de quantifier l’écart entre les constantes d’acidité de mono- et di-acides carboxyliques linéaires sur la base du mécanisme collisionnel en amont de la réaction chimique.

4. Théorie cinétique de l’équilibre de fusion

4.1. Cadre de l’analyse

Le cadre de la théorie cinétique de l’équilibre de fusion est le même que celui de la théorie cinétique de l’équilibre chimique présentée dans le troisième chapitre, à savoir celui du premier principe et celui du second principe restreint aux échanges de travail et chaleur. Ainsi, le potentiel chimique et l’entropie calorimétrique issue du second principe ne seront pas utilisés pour établir la fonction qui gouverne l’équilibre de fusion.

4.2. Equilibre cinétique d’une fusion

L’équilibre cinétique d’une fusion est défini de manière analogue à l’équilibre cinétique d’une réaction chimique (note 4 ) :

« L’équilibre de fusion d’un constituant chimique d’un système fermé est atteint lorsque la vitesse de sa fusion est compensée par sa vitesse de solidification. »

Soit l’équilibre de fusion de l’espèce chimique A pure ou dans un mélange liquide homogène avec d’autres espèces chimiques immiscibles dans la phase solide de A :

A(s)⇄A(l)
L’équation qui exprime l’équilibre cinétique de cette fusion est :
vfusion=vsolidification(181)

4.3. Lois de vitesse d’une fusion et d’une solidification

La fusion est la transformation d’une espèce chimique A (atome, molécule, paire d’ions, complexe d’association) de l’état solide à l’état liquide. Réciproquement, la solidification est la transformation d’une espèce chimique A de l’état liquide à l’état solide. L’interface (σ) de l’équilibre de fusion est constituée du domaine de contact entre le solide et le liquide où les propriétés de l’espèce chimique A sont différentes du cœur du solide (s) et du cœur du liquide (l) (Figure 20).

Figure 20.

Schéma de l’équilibre de fusion.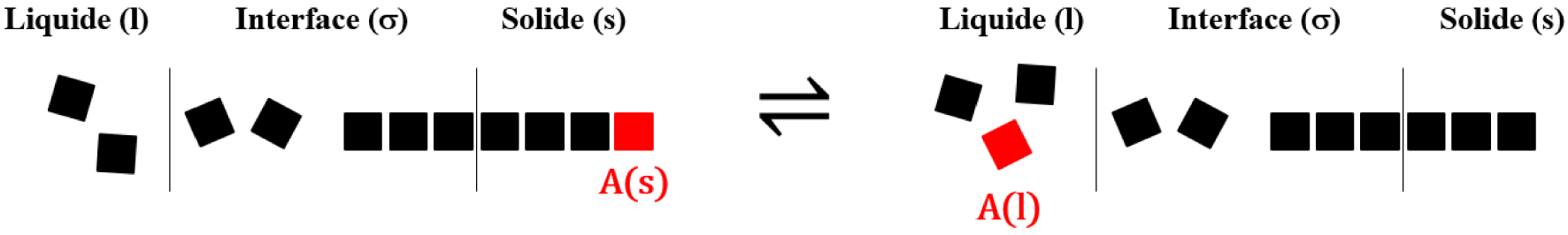

Il est important de préciser afin d’éviter toute confusion que les segments verticaux entre (l) et (σ) d’une part, et entre (σ) et (s) d’autre part, ne constituent pas des interfaces. Ces segments verticaux sont les lignes de démarcation de l’interface (σ) avec le liquide (l) et le solide (s). Dans cette description, l’interface (σ) est un volume. Un état de transition, de même nature que celui existant pour les réactions chimiques en phase homogène, est franchi lors de la fusion et de la solidification (Figure 21).

Figure 21.

Diagramme du col d’enthalpie standard de transition d’une fusion.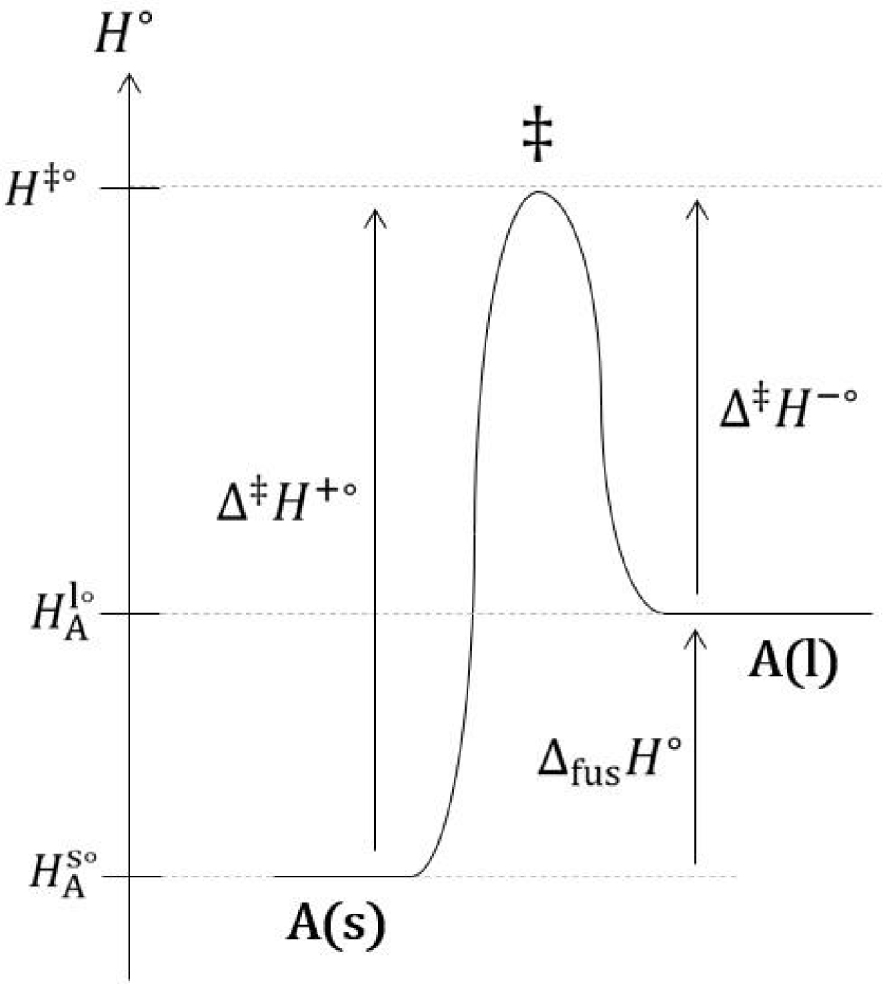

L’expression de l’enthalpie standard de fusion est :

𝛥fusH°=HAl°−HAs°=𝛥‡H+°−𝛥‡H−°(182)
Les vitesses de fusion v+ et de solidification v− seront exprimées avec un formalisme analogue à celui de la réaction chimique en phase homogène mais dans une unité différente : mol⋅m−2⋅s−1. La vitesse de fusion est proportionnelle à la concentration surfacique 𝛤A° du solide A pur :
v+°=𝛤A°⋅z+°⋅p+°⋅exp−𝛥‡H+°R⋅T(183)
z+° est la fréquence de collision exprimée en s−1 des espèces microscopiques des phases liquide et solide avec les espèces chimiques de la surface du solide indépendante de la concentration surfacique 𝛤A°. p+° est la probabilité que la fusion se produise lorsque l’énergie cinétique de la collision est supérieure à la hauteur du col d’enthalpie de fusion. La vitesse de solidification est proportionnelle à la concentration surfacique 𝛤A° et à la concentration [A]° de A dans le liquide pur :
v−°=𝛤A°⋅[A]°⋅z−°⋅p−°⋅exp−𝛥‡H−°R⋅T(184)
z−° est la fréquence de collision exprimée en L⋅mol−1⋅s−1 des espèces A dans la phase liquide avec la surface du solide A indépendante de la concentration surfacique 𝛤A° et de la concentration en solution [A]°. p−° est la probabilité que la solidification se produise lorsque l’énergie cinétique de la collision est supérieure à la hauteur du col d’enthalpie de solidification.

4.4. Equation cinétique d’évolution d’une fusion

L’équilibre de fusion s’exprime par l’égalité entre les vitesses de fusion et solidification :

veq+°=veq−°(185)
Soit :
 𝛤A°⋅z+°⋅p+°⋅exp−𝛥‡H+°R⋅Tfus° =𝛤A°⋅[A]°⋅z−°⋅p−°⋅exp−𝛥‡H−°R⋅Tfus°(186)
La seule variable de cette équation de l’équilibre est la température, il n’existe donc pour un corps pur soumis à une pression constante qu’une seule température solution de l’équation de l’équilibre :
T=Tfus°(187)
La fusion d’un corps pur dans cette description est isotherme, ce qui est en accord avec l’observation expérimentale. L’entropie cinétique standard de fusion déduite de l’équation de l’équilibre cinétique est :
𝛥fusS°=S+°−S−°(188)
Avec :
S+°=R⋅ln(𝛤A°⋅z+°⋅p+°)(189)
S−°=R⋅ln([A]°⋅𝛤A°⋅z−°⋅p−°)(190)

L’enthalpie libre cinétique standard de fusion déduite de l’équation de l’équilibre est nulle :

𝛥fusG°=𝛥fusH°−Tfus°⋅𝛥fusS°=0(191)
Cette dernière équation permet d’exprimer l’entropie cinétique de fusion en fonction de l’enthalpie de fusion :
𝛥fusS°=𝛥fusH°Tfus°(192)
Comme une fusion est endothermique, une entropie cinétique de fusion sera toujours positive. Cette condition est toujours vérifiée car si l’entropie cinétique de fusion était négative, cela signifierait que la fusion de la forme solide de A est plus rapide que sa solidification et par conséquence que cette forme n’est pas stable. Le diagramme réactionnel de l’équilibre cinétique de fusion du corps pur est présenté sur la Figure 22.

Figure 22.

Diagramme réactionnel cinétique de l’équilibre de fusion d’un corps pur soumis à une pression de 1 bar.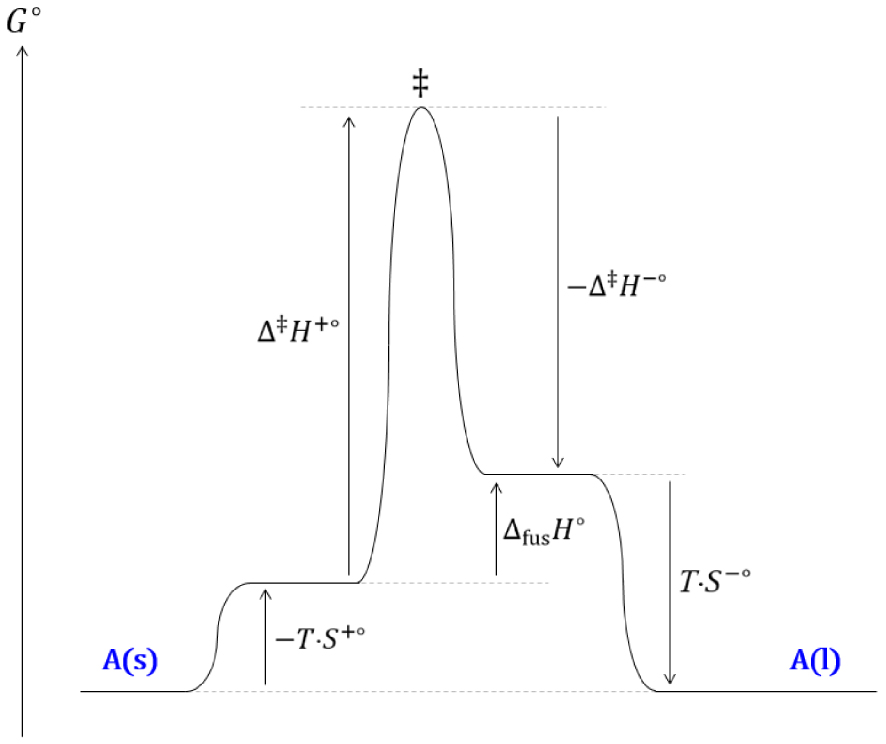

Dans le cas d’un mélange de A avec d’autres espèces qui forment une phase liquide homogène avec la phase liquide de A mais qui sont immiscibles dans la phase solide de A, les vitesses de fusion et solidification sont respectivement :

v+=𝛤A°⋅z+°⋅p+°⋅exp−𝛥‡H+°R⋅T(193)
v−=[A]⋅𝛤A°⋅z−°⋅p−°⋅exp−𝛥‡H−°R⋅T(194)

L’équilibre de fusion s’exprime par l’égalité entre les vitesses de fusion et solidification :

 𝛤A°⋅z+°⋅p+°⋅exp−𝛥‡H+°R⋅Tfus =[A]eq⋅𝛤A°⋅z−°⋅p−°⋅exp−𝛥‡H−°R⋅Tfus(195)
La division terme à terme de cette équation de l’équilibre avec celle obtenue précédemment pour A pur mène à :
ln[A]eq[A]°=𝛥fusH°R⋅1Tfus°−1Tfus(196)
Soit y la fraction de concentration de A dans un mélange liquide par rapport à A dans les conditions standards (i.e. liquide pur à une pression de 1 bar) :
y=[A][A]°(197)
L’équation de l’équilibre de fusion de A dans un mélange devient :
ln(yeq)=𝛥fusH°R⋅1Tfus°−1Tfus(198)
Cette équation indique que la température de fusion d’un solide dans un mélange diminue avec sa concentration dans la phase liquide, ce qui est en accord avec l’expérience. L’équation cinétique de l’équilibre est proche de l’équation thermodynamique de l’équilibre de fusion établie par Schröder [11] :
ln(xeq)=𝛥fusH°R⋅1Tfus°−1Tfus(199)

4.5. Synthèse

L’équation de l’équilibre de fusion a été établie en utilisant des lois cinétiques. De manière analogue à l’étude cinétique de l’équilibre chimique, l’entropie calorimétrique et le potentiel chimique n’ont pas été utilisés pour établir l’équation de l’équilibre de fusion. Les équations thermodynamique et cinétique de l’équilibre de fusion sont formellement très proches, respectivement :

ln(xeq)=𝛥fusH°R⋅1Tfus°−1Tfus(200)
ln(yeq)=𝛥fusH°R⋅1Tfus°−1Tfus(201)

Les enthalpies de fusion thermodynamique et cinétique sont, en vertu du premier principe de la thermodynamique, strictement égales :

𝛥fusH°=HAl°−HAs°=𝛥‡H+°−𝛥‡H−°(202)
Les entropies de fusion thermodynamique et cinétique sont égales mais de nature différente car la première est indépendante de la vitesse d’établissement de l’équilibre de fusion alors que la deuxième est complètement dépendante de celle-ci :
𝛥fusS°=SAl°−SAs°(203)
𝛥fusS°=S+°−S−°(204)

5. Etude thermodynamique et cinétique d’équilibres de fusion

5.1. Cadre de l’analyse

Ce chapitre confronte les modèles thermodynamique et cinétique aux observations expérimentales d’équilibres de fusion à la pression standard. Les enthalpies et entropies standards cinétique et thermodynamique seront considérées indépendantes de la température. Pour le modèle cinétique, la dilution d’une espèce chimique dans sa phase liquide est quantifiée par le rapport entre sa concentration [A] dans le mélange liquide et sa concentration [A]° dans sa phase liquide lorsqu’il est pur :

y=[A][A]°(205)
La relation entre la fraction de concentration y d’une espèce chimique A et sa fraction molaire x dans un mélange avec une autre espèce chimique B est (Annexe 1) :
y=xx+𝜌Al°⋅MB𝜌Bl°⋅MA⋅(1−x)(206)
Les enthalpies de mélange des liquides seront négligées. Il est plus approprié, pour des raisons pratiques, de représenter les diagrammes de phases de manière classique, c’est-à-dire en utilisant la fraction molaire x plutôt que la fraction de concentration y, même si cette dernière est utilisée dans le calcul du liquidus cinétique. En effet, les utilisateurs des diagrammes de phases souhaitent disposer d’un outil pratique pour déterminer la phase d’un constituant d’un mélange de composition et température données et il est plus simple de calculer la fraction molaire que la fraction de concentration.

Tableau 3.

Propriétés physiques de NaCl et RbCl

ComposéM (g∕mol)𝜌Tfusl°(g∕cm3)Tfus°(K)𝛥fus H° (kJ∕mol)
NaCl 58,4 1,56 1072 28,0
IUPAC [61] Janz [51]Pelton et al. [53]Kubaschewski et al. [54]
Nasch et al. [52]
RbCl 120,9 2,25 993 18,4
IUPAC [61] Janz [51]Pelton et al. [53] Sternberg et al. [55]
Nasch et al. [52]

5.2. Mélange binaire idéal de sels ioniques

Soient les équilibres de fusion du système binaire à invariant eutectique du mélange entre le chlorure de sodium et le chlorure de rubidium :

NaCl(s)⇌NaCl(l)RbCl(s)⇌RbCl(l)

Les équations cinétiques de ces équilibres de fusion sont respectivement :

ln(yNaCl,eq)=𝛥fusHNaCl°R⋅1Tfus,NaCl°−1Tfus,NaCl (207)
ln(yRbCl,eq)=𝛥fusHRbCl°R⋅1Tfus,RbCl°−1Tfus,RbCl (208)

Avec :

yNaCl=xNaClxNaCl+𝜌NaCll°⋅MRbCl𝜌RbCll°⋅MNaCl⋅(1−xNaCl)(209)
yRbCl=xRbClxRbCl+𝜌RbCll°⋅MNaCl𝜌NaCll°⋅MRbCl⋅(1−xRbCl)(210)
xNaCl+xRbCl=1(211)

Les propriétés physiques issues de la littérature du chlorure de sodium, du chlorure de rubidium et de leur mélange, sont renseignées dans les Tableaux 3 et 4.

Tableau 4.

Propriétés physiques du mélange NaCl/RbCl

Teut(K)𝜌Tfus,NaCl,eutl°(g∕cm3)𝜌Tfus,RbCl,eutl°(g∕cm3)
823 1,69 2,39
Pelton et al. [53] Janz [51] Janz [51]
Nasch et al. [52]Nasch et al. [52]

Le diagramme de phases expérimental du mélange entre le chlorure de sodium et le chlorure de rubidium [53] et les diagrammes de phases théoriques issus des modèles thermodynamique (Annexe 2) et cinétique (Annexe 3), calculés avec les valeurs physiques des Tableaux 3 et 4, sont tracés sur la Figure 23.

Figure 23.

Diagrammes de phases liquide–solide composition-température du mélange NaCl–RbCl : expérimental (disques noirs), théorique thermodynamique (traits rouges) et théorique cinétique (traits bleus).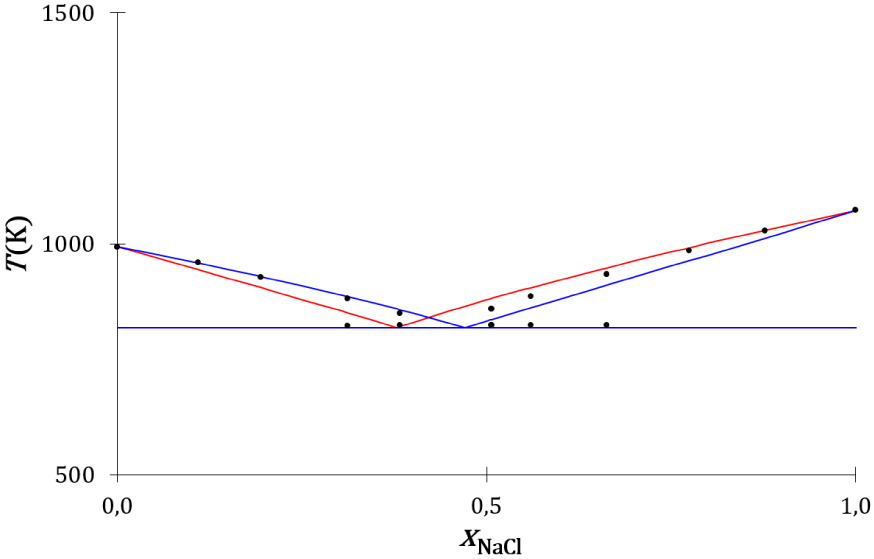

Les liquidus du chlorure de sodium et du chlorure de rubidium déduits du modèle thermodynamique, sont :

ln(xNaCl,eq)=𝛥fusHNaCl°R⋅1Tfus,NaCl°−1Tfus(212)
ln(xRbCl,eq)=𝛥fusHRbCl°R⋅1Tfus,RbCl°−1Tfus(213)
xNaCl+xRbCl=1(214)

Les équations cinétique et thermodynamique de l’équilibre de fusion sont proches. Elles ne se différencient que par la variable de composition du mélange : la fraction de concentration pour le modèle cinétique et la fraction molaire pour le modèle thermodynamique. Les liquidus thermodynamiques sont présentés sur la Figure 23, ils sont proches des liquidus cinétiques et proches des liquidus expérimentaux.

5.3. Mélange binaire non idéal de sels ioniques

Soient les équilibres de fusion du mélange du chlorure de sodium avec l’eau :

NaCl(s)⇌NaCl(l)H2O(s)⇌H2O(l)

Les équations cinétiques de l’équilibre de fusion du chlorure de sodium et de l’eau dans le mélange sont :

ln(yNaCl,eq)=𝛥fusHNaCl°R⋅1Tfus,NaCl°−1Tfus,NaCl (215)
ln(yH2O,eq)=𝛥fusHH2O°R⋅1Tfus,H2O°−1Tfus,H2O (216)

Avec :

yNaCl=xNaClxNaCl+𝜌NaCll°⋅MH2O𝜌H2Ol°⋅MNaCl⋅(1−xNaCl)(217)
yH2O=xH2OxH2O+𝜌H2Ol°⋅MNaCl𝜌NaCll°⋅MH2O⋅(1−xH2O)(218)
xNaCl+xH2O=1(219)

Les liquidus thermodynamique (Annexe 4) et cinétique (Annexe 5), déterminés avec les propriétés des corps purs renseignées dans le Tableau 5, sont comparés aux liquidus expérimentaux [54] (Figure 24) : le diagramme de phases expérimental présenté ne prend pas en compte la formation de l’hydrate du chlorure de sodium qui se forme à basse température, il utilise le point de fusion eutectique expérimental métastable du mélange entre NaCl et H2O reporté dans la littérature (Tableau 6).

Tableau 5.

Propriétés physiques de NaCl et H2O

ComposéM(g∕mol)𝜌Tfusl°(g∕cm3)Tfus°(K)𝛥fus H° (kJ∕mol)
NaCl 58,4 1,56 1072 28,0
IUPAC [61] Janz [51] Pelton et al. [53]Kubaschewski et al. [54]
Nasch et al. [52]
H2O 18,0 1,00 273,2 6,0
IUPAC [61]Wagner et al. [57] Giauque et al. [58]

Tableau 6.

Propriétés physiques du mélange eutectique NaCl–H2O

Teut (K)𝜌Tfus,NaCl,eutl°(g∕cm3)𝜌Tfus,RbCl,eutl°(g∕cm3)
249 2,001,00
Li et al. [56] Janz [51]
Nasch et al. [52]

Figure 24.

Diagrammes de phases liquide–solide composition-température du mélange NaCl–H2O expérimental (disques noirs) et calculés avec les modèles thermodynamique (traits rouges), cinétique (traits bleus) et cinétique avec prise en compte de la formation de la première sphère de solvatation de la paire d’ions Na+, Cl- (courbes vertes).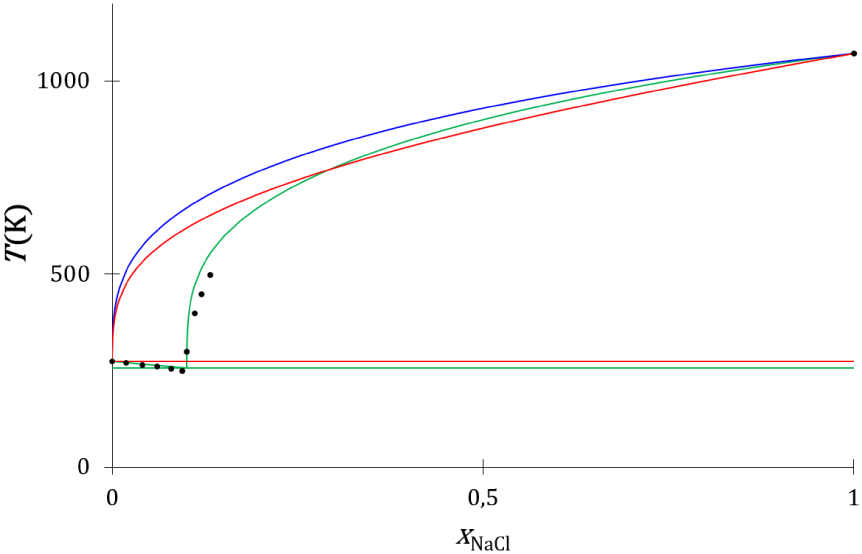

Les liquidus du chlorure de sodium déterminés par les modèles thermodynamique (courbe rouge) et cinétique (courbe bleu) s’écartent fortement du liquidus expérimental (disques noirs). En effet, à la composition eutectique, la température de fusion expérimentale est de 249,5 K, celle du liquidus thermodynamique est de 607 K, et celle du liquidus cinétique de 658 K.

Le chlorure de sodium en solution dans l’eau à haute concentration est une paire d’ions solvatée par des molécules d’eau. Le nombre de molécules d’eau de la première sphère de solvatation déterminée par des modèles théoriques est compris entre 8 et 10 (Tableau 7).

Tableau 7.

Nombre de molécules d’eau de la première sphère de solvatation du chlorure de sodium déterminée par modélisation

NH 2OModèleRéférence
8Dynamique moléculaire (SHAKE) Belch et al. [59]
10Ab initio (Hartree–Fock)Petersen et al. [60]

Tableau 8.

Tableau d’avancement de formation de la première sphère de solvatation du chlorure de sodium dans son mélange avec l’eau

Espèce Na+Cl− (aq)9H2O(l)Na+Cl−(H2O)9(aq)
Etat initialxNaCl1 − xNaCl0
Etat final10⋅xNaCl−1901−xNaCl9

Soit la réaction de formation de la première sphère de solvatation de la paire d’ions du chlorure de sodium, pour un nombre de molécules d’eau de 9, intermédiaire entre les deux valeurs issues de la littérature :

Na+Cl−(aq)+9H2O(l)⇌Na+Cl−(H2O)9(aq)
La paire d’ions solvatée est très stable. La collision d’une paire d’ions avec la surface d’un cristal de chlorure de sodium défavorise la solidification du chlorure de sodium car les molécules d’eau de la première sphère de solvatation empêchent le contact entre la paire d’ions et la surface cristalline du chlorure de sodium lors de leur collision (Figure 25).

Figure 25.

La collision d’une paire d’ions du chlorure de sodium solvatée avec la surface d’un cristal de glace provoque la solidification (haut) tandis que la collision d’une paire d’ions avec la surface d’un cristal de chlorure de sodium non (bas).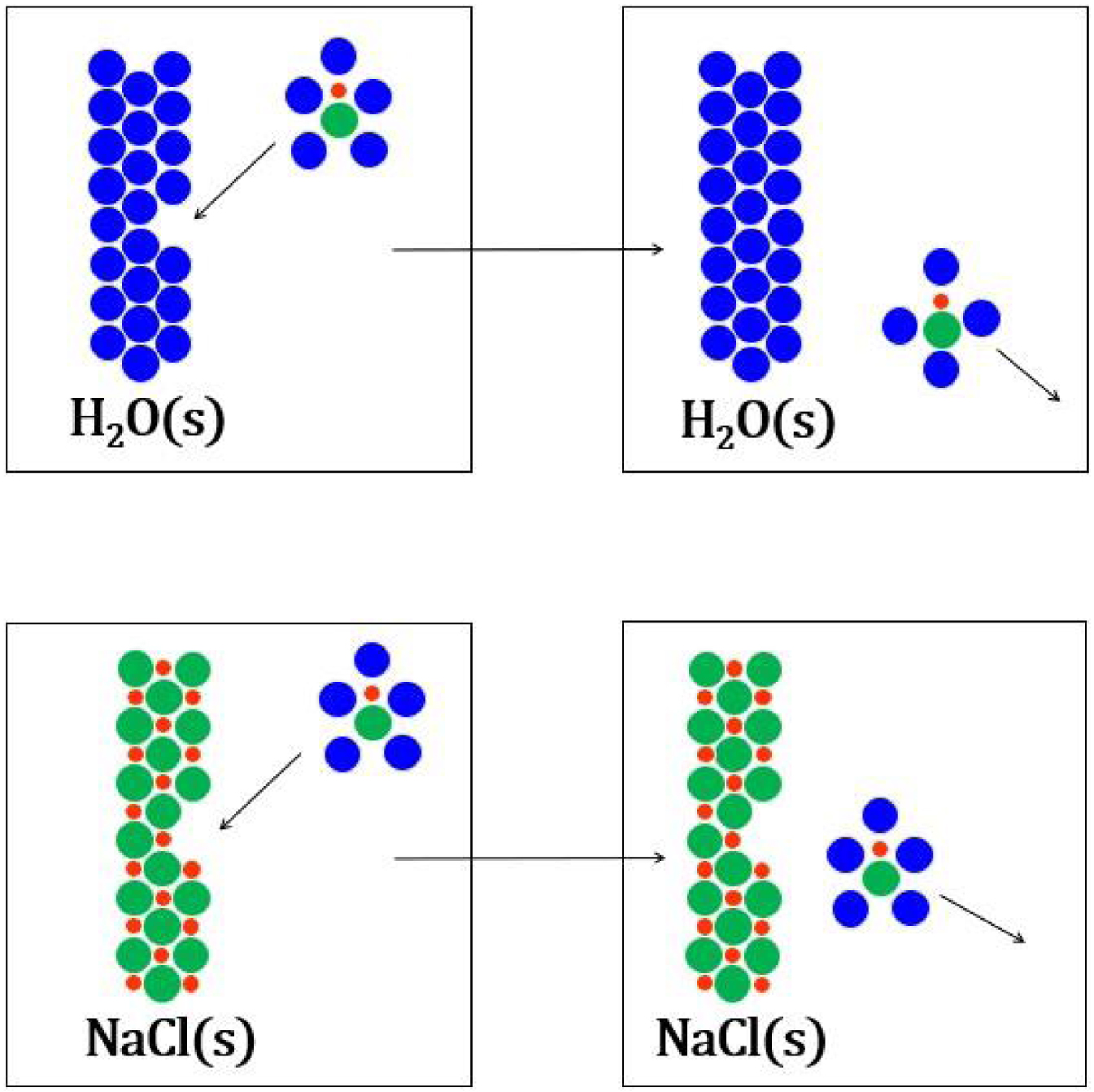

La situation est différente pour la solidification de l’eau car les molécules d’eau de la première sphère de solvatation sont au contact de la surface des cristaux de glace lors d’une collision (Figure 25). D’après ce qui précède, la solidification de l’eau devrait être faiblement affectée dans le mélange, l’équation cinétique du liquidus de l’eau n’est donc pas modifiée :

ln(yH2O,eq)=𝛥fusHH2O°R⋅1Tfus,H2O°−1Tfus,H2O(220)
La composition statistique en paires d’ions non solvatées, pour le domaine de composition riche en NaCl, est calculée avec le tableau d’avancement 8 en considérant que la réaction de formation de la première sphère de solvatation est totale.

Le liquidus cinétique du chlorure de sodium calculé en prenant en compte la composition statistique de paires d’ions libres, c’est-à-dire non solvatées (Annexe 6) est :

ln(yNaCl,eq)=𝛥fusHNaCl°R⋅1Tfus,NaCl°−1Tfus,NaCl (221)
yNaCl=xNaCl,librexNaCl,libre+𝜌NaCll°⋅MH2O𝜌H2Ol°⋅MNaCl⋅(1−xNaCl,libre) (222)
xNaCl,libre=10⋅xNaCl−19(223)

Le diagramme de phases construit avec les liquidus cinétiques de l’eau et du chlorure de sodium qui prennent en considération la formation de la première sphère de solvatation est proche du diagramme de phases expérimental (Figure 24, traits verts). Cette description cinétique de l’équilibre ne fait pas appel à un coefficient d’activité de nature empirique, elle utilise une caractéristique du système, le nombre de molécules d’eau par paire d’ions solvatée issu de mesure expérimentales, et prend en compte la dynamique collisionnelle de la solidification. Cet effet entropique de nature cinétique est à l’origine de la grande différence de température de fusion eutectique des mélanges du chlorure de sodium avec le chlorure de rubidium et l’eau en particulier, et des sels ioniques en solution aqueuse en général. La description thermodynamique du système à invariant eutectique chlorure de sodium-eau ne peut pas s’affranchir de l’utilisation d’un coefficient d’activité de nature empirique [12].

5.4. Mélange binaire idéal de molécules organiques

Soient les équilibres de fusion du système binaire de l’acide laurique avec l’acide oléique (Figure 26) :

LA(s)⇌LA(l)OL(s)⇌OL(l)

Figure 26.

Structures de l’acide laurique (LA) et de l’acide oléique (OL).

Les équations cinétiques de ces équilibres de fusion sont respectivement :

ln(yLA,eq)=𝛥fusHLA°R⋅1Tfus,LA°−1Tfus,LA(224)
ln(yOL,eq)=𝛥fusHOL°R⋅1Tfus,OL°−1Tfus,OL(225)

Avec :

yLA=xLAxLA+𝜌LAl°⋅MOL𝜌OLl°⋅MLA⋅(1−xLA)(226)
yOL=xOLxOL+𝜌OLl°⋅MLA𝜌LAl°⋅MOL⋅(1−xOL)(227)
xLA+xOL=1(228)

Les masses molaires, densités, températures et enthalpies de fusion de l’acide laurique et de l’acide oléique issues de la littérature sont renseignées dans le Tableau 9.

Tableau 9.

Propriétés physiques de l’acide laurique et de l’acide oléique

ComposéM(g∕mol)𝜌Tfusl°(g∕cm3)Tfus°(K)𝛥fus H° (kJ∕mol)
Acide laurique 200,3 0,87 317,4 36,6
IUPAC [61]Hossein et al. [62]Tohru et al. [63]Tohru et al. [63]
Acide oléique 282,5 0,89 286,5 39,6
IUPAC [61]Hossein et al. [62]Tohru et al. [63]Tohru et al. [63]

Le diagramme de phases expérimental du mélange entre l’acide laurique et l’acide oléique [63] et les diagrammes de phases théoriques thermodynamique (Annexe 7) et cinétique (Annexe 8) calculés avec les valeurs du Tableau 9 sont présentés sur la Figure 27.

Figure 27.

Diagrammes de phases liquide–solide composition-température du mélange acide laurique-acide oléique expérimental (disques noirs), thermodynamique (traits rouges) et cinétique (traits bleus).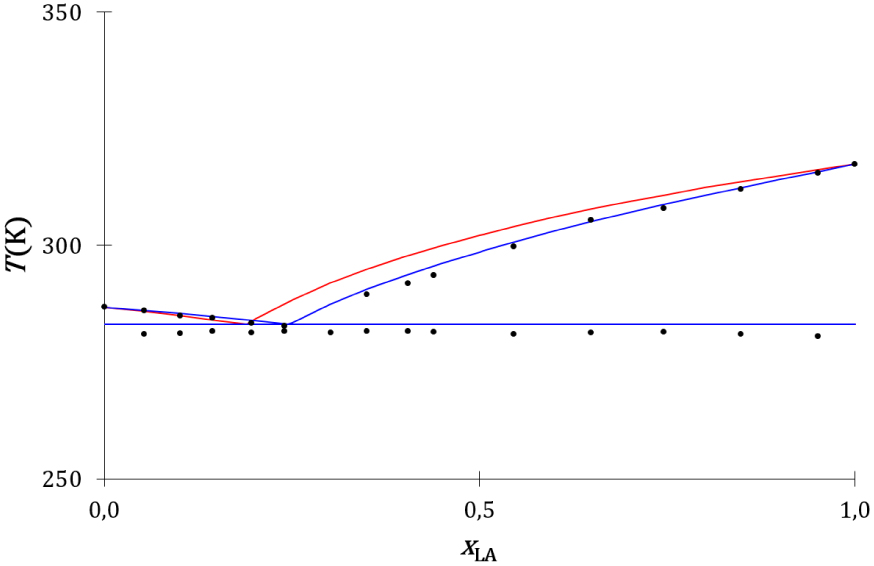

Les liquidus cinétique et thermodynamique sont proches l’un de l’autre et proches des liquidus expérimentaux. Leurs équations ne se différencient que faiblement : la fraction de concentration est utilisée pour le modèle cinétique et la fraction molaire pour le modèle thermodynamique. Aucune différence significative n’est observée entre les descriptions cinétique et thermodynamique de l’équilibre de fusion du mélange binaire à invariant eutectique entre l’acide laurique et l’acide oléique.

Tableau 10.

Propriétés physiques de l’acide laurique et de la lidocaïne

ComposéM (g∕mol)𝜌Tfusl°(g∕cm3)Tfus°(K)𝛥fus H° (kJ∕mol)
Acide laurique 200,3 0,87 317,4 36,6
IUPAC [61] Hossein et al. [62] Tohru et al. [63] Tohru et al. [63]
Lidocaïne 234,3 1,04 340,7 16,4
IUPAC [61]Lazerges et al. [65]Lazerges et al. [66]Lazerges et al. [66]

5.5. Mélange binaire non idéal de molécules organiques

Soient les équilibres de fusion du mélange de l’acide laurique (LA) avec la lidocaïne (LC) :

LA(s)⇌LA(l)LC(s)⇌LC(l)

Les équations du liquidus de l’acide laurique et de la lidocaïne issues de la description cinétique, obtenues par une analyse analogue à celle du mélange de l’acide laurique avec l’acide oléique, sont :

ln(yLA,eq)=𝛥fusHLA°R⋅1Tfus,LA°−1Tfus,LA(229)
ln(yLC,eq)=𝛥fusHLC°R⋅1Tfus,LC°−1Tfus,LC(230)

Avec :

yLA=xLAxLA+𝜌LAl°⋅MLC𝜌LCl°⋅MLA⋅(1−xLA)(231)
yLC=xLCxLC+𝜌LCl°⋅MLA𝜌LAl°⋅MLC⋅(1−xLC)(232)
xLA+xLC=1(233)

Les liquidus thermodynamique (Annexe 9) et cinétique (Annexe 10) sont calculés avec les propriétés des corps purs renseignées dans le Tableau 10 afin d’être comparés aux liquidus expérimentaux [64].

Le diagramme de phases expérimental et les diagrammes de phases théoriques du mélange acide laurique-lidocaïne sont présentés sur la Figure 28 : les liquidus thermodynamique et cinétique de l’acide laurique s’écartent fortement du liquidus expérimental. L’acide laurique, à l’état solide comme à l’état liquide, est sous forme de dimère associé par une double liaison hydrogène [67], mais ce dimère peut se dissocier dans le mélange liquide de l’acide laurique avec la lidocaïne [64] (Figure 29) :

(LA−LA)(l)+2 LC(l)⇌2(LA−LC)(l)

Une double liaison hydrogène se forme entre la fonction acide carboxylique de l’acide laurique et la fonction amide de la lidocaïne. La lidocaïne à l’état solide n’établit pas avec elle-même de double liaison hydrogène [68]. La solidification de la lidocaïne se produit lors de la collision du complexe d’association avec la surface d’un cristal de lidocaïne (Figure 30).

Figure 28.

Diagrammes de phases liquide–solide composition-température du mélange lidocaïne-acide laurique expérimental (disques noirs), thermodynamique (traits rouges) et cinétiques sans (traits bleus) et avec prise en compte de la formation d’un complexe d’association entre l’acide laurique et la lidocaïne (traits verts).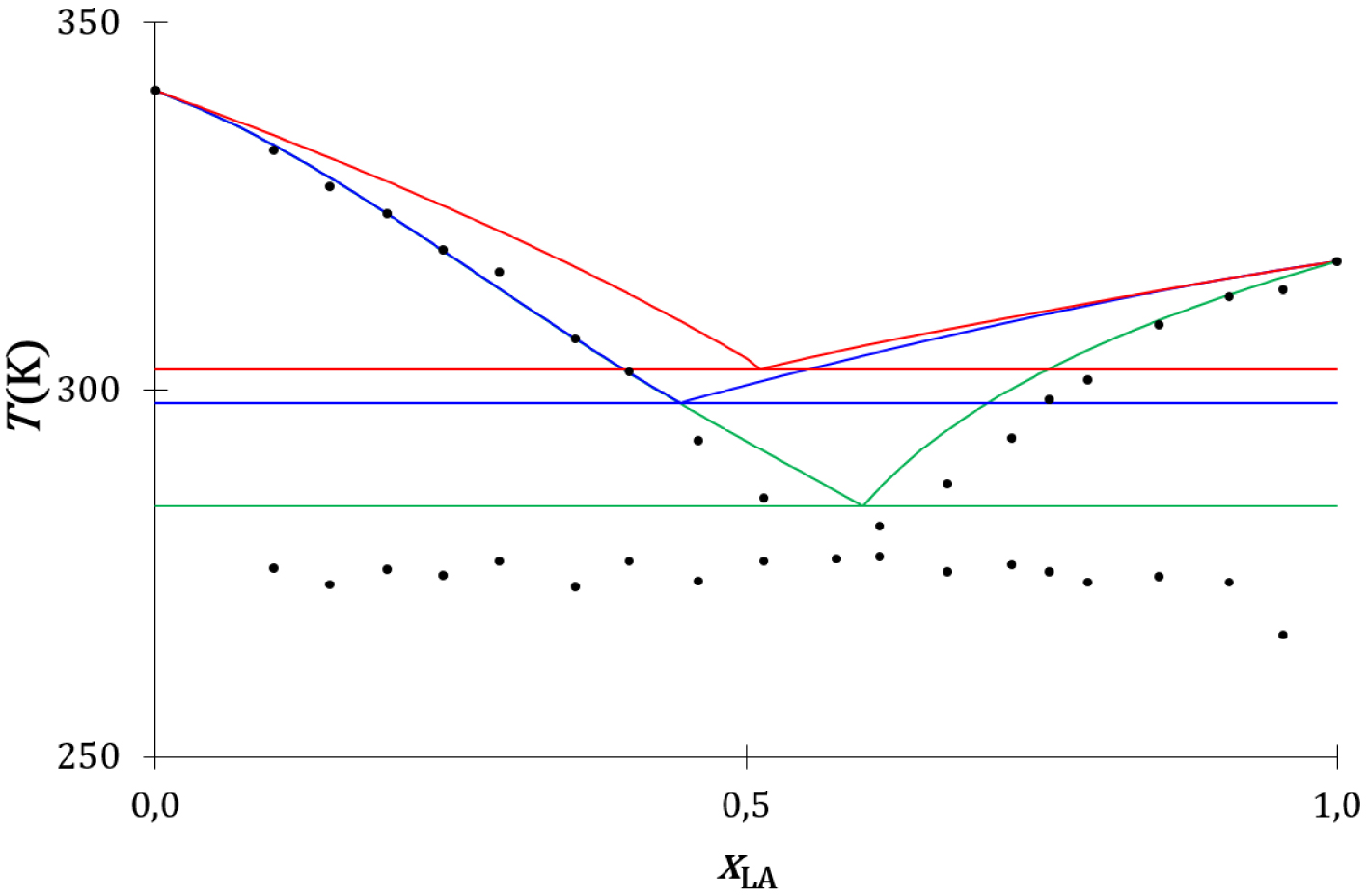

En revanche, la solidification de l’acide laurique ne peut pas se produire lors de la collision du complexe d’association avec la surface du cristal d’acide laurique, puisque le complexe d’association n’inclut pas le motif du cristal (Figure 30). Il convient donc de ne considérer que la fraction molaire d’acide laurique associé à lui-même dans l’équation du liquidus.

(LA−LA)(l)⇌(LA−LA)(s)
La fraction molaire en acide laurique qui prend part à la solidification est calculée avec le tableau d’avancement de formation du complexe d’association acide laurique-lidocaïne (Tableau 11).

Le liquidus de l’acide laurique avec prise en considération de la formation du complexe acide laurique-lidocaïne est :

ln(yLA,eq)=𝛥fusHLA°R⋅1Tfus,LA°−1Tfus,LA(234)
yLA=xLAxLA+𝜌LAl°⋅MLC𝜌LCl°⋅MLA⋅(1−xLA)(235)
xLA,libre=2⋅xLA−1(236)

Le liquidus cinétique (traits verts) (Annexe 11) est proche du liquidus expérimental (disques noirs) (Figure 28). La description cinétique de l’équilibre de fusion de l’acide laurique dans son mélange avec la lidocaïne est concordante avec l’observation expérimentale.

Figure 29.

Structure chimique des complexes d’association acide laurique-acide laurique (gauche) et acide laurique-lidocaïne (droite).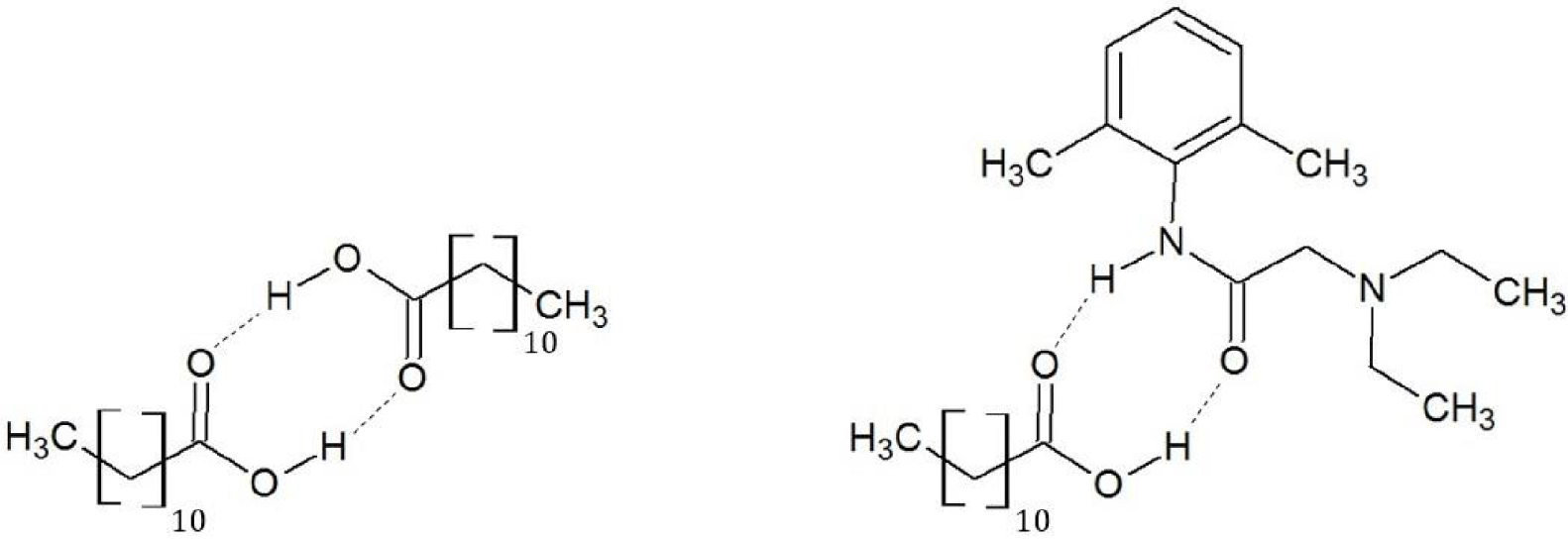

5.6. Entropie cinétique de mélanges binaires

La description cinétique des mélanges du chlorure de sodium avec la chlorure de rubidium ou l’eau d’une part, et des mélanges de l’acide laurique avec l’acide oléique ou la lidocaïne d’autre part, montre qu’il est possible d’établir une fonction analytique des courbes d’équilibre de fusion fondées sur le mécanisme collisionnel entre l’espèce chimique et la surface du cristal qui se produit en amont de la solidification. Ces fonctions cinétiques des courbes d’équilibre sont établies en substituant les fractions molaires des espèces par les fractions molaires des espèces qui entrent en collision avec la surface du cristal. Ainsi les fractions molaires du chlorure de sodium dans son mélange avec l’eau et de l’acide laurique dans son mélange avec la lidocaïne deviennent :

xNaCl→10⋅xNaCl−19(237)
xLA→2⋅xLA−1(238)

Tableau 11.

Tableau d’avancement de formation du complexe d’association acide laurique-lidocaïne

EspèceLA(l)LC(l)(LA − LC)(l)
Etat initialxLA1 − xLA0
Etat final 2⋅xLA − 101 − xLA

Dans les deux cas, la fraction molaire de l’espèce chimique considérée diminue, ce qui induit une diminution de l’entropie de solidification. Ainsi, le chlorure de sodium dans son mélange avec l’eau est liquide dans un domaine de composition et de température, et solide dans ce même domaine dans son mélange avec le chlorure de rubidium. De manière analogue, l’acide laurique dans son mélange avec la lidocaïne est liquide dans un domaine de composition et de température, et solide dans ce même domaine dans son mélange avec l’acide oléique. Ces comportements sont illustrés sur les diagrammes cinétiques de fusion de la Figure 31.

Figure 30.

Collision du complexe d’association entre l’acide laurique et la lidocaïne avec la surface d’un cristal de lidocaïne (haut) et d’acide laurique (bas).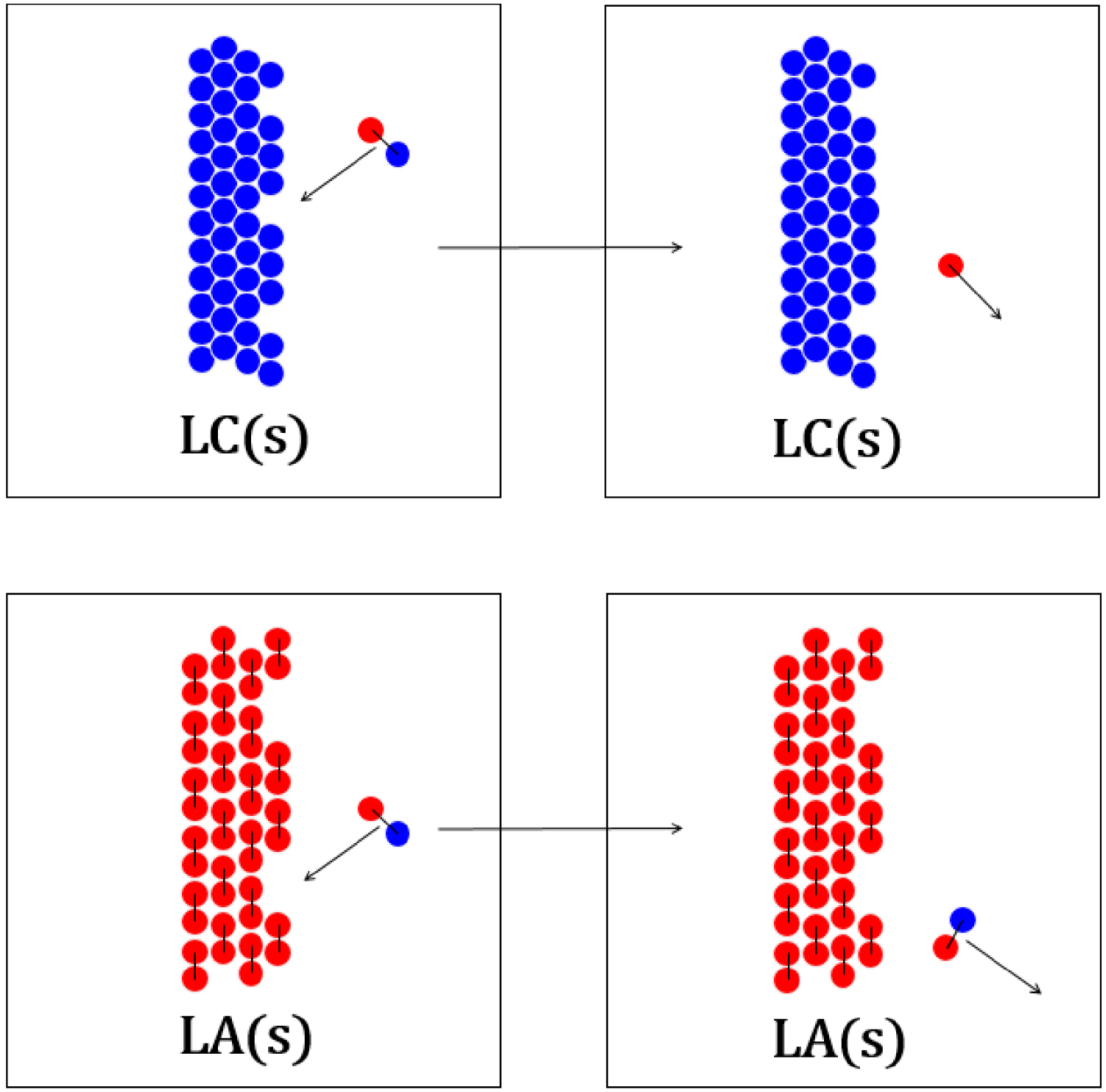

Figure 31.

Diagrammes réactionnels cinétiques de l’équilibre de fusion du chlorure de sodium (gauche) et de l’acide laurique (droite) dans leurs mélanges.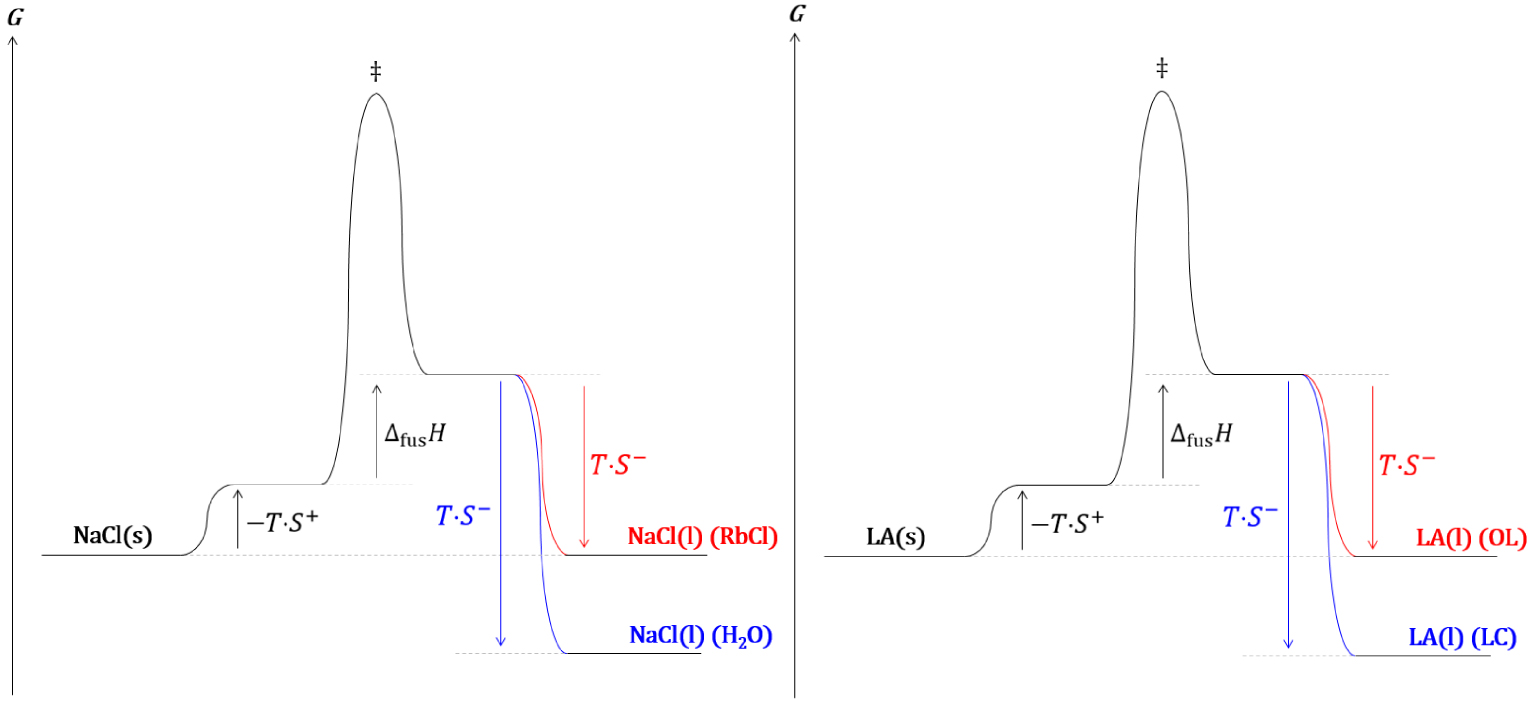

5.7. Mélange binaire de molécules chirales

Le mélange de certains couples d’énantiomères donne lieu à la formation d’un cocristal racémique plus stable que les cristaux de chaque énantiomère :

A(s)+A_(s)⇌AA_(s)
La topologie du diagramme de phases liquide–solide d’un système à invariant eutectique du mélange d’un couple d’énantiomères avec son racémique est présentée sur la Figure 32 :

Figure 32.

Topologie du diagramme de phases liquide–solide composition-température expérimental d’un système à invariant eutectique d’un couple d’énantiomères (A et A) avec son racémique (AA).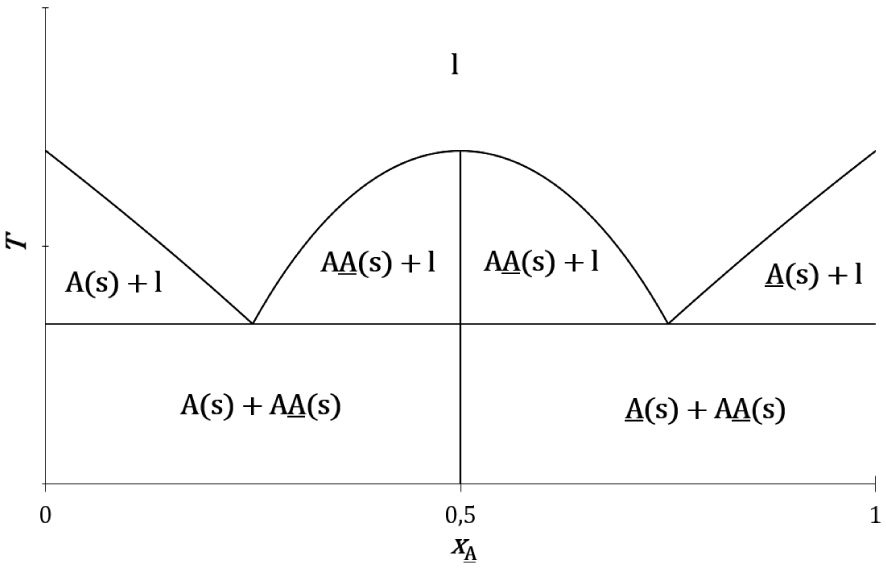

Trois équilibres de fusion sont impliqués :

A(s)⇌A(l)A_(s)⇌A_(l)AA_(s)⇌A(l)+A_(l)

Les équations cinétiques qui expriment ces trois équilibres de fusion sont :

vA,eq+=vA,eq−(239)
vA_,eq+=vA_,eq−(240)
vAA_,eq+=vAA_,eq−(241)

Les deux premières égalités, qui concernent l’équilibre de fusion de A et A, mènent à :

ln(yA,eq)=𝛥fusHA°R⋅1Tfus,A°−1Tfus,A(242)
ln(yA_,eq)=𝛥fusHA_°R⋅1Tfus,A_°−1Tfus,A_(243)

Avec :

Tfus,A°=Tfus,A_°(244)
𝛥fusHA°=𝛥fusHA_°(245)
yA=xA(246)
yA_=xA_(247)
xA+xA_=1(248)

Les énantiomères A et A qui constituent le cocristal AA conservent leur structure moléculaire, il est donc possible d’exprimer l’équilibre de fusion du cocristal par deux équations cinétiques : une équation pour la fusion/solidification de A au sein du cocristal et une équation pour celle de A :

vAA_,A,eq+=vAA_,A,eq−(249)
vAA_,A_,eq+=vAA_,A_,eq−(250)

Donc :

 𝛤A°⋅zAA_+°⋅pAA_+°⋅exp−𝛥‡HAA_+°2⋅R⋅Tfus,AA_ =[A]eq⋅𝛤A°⋅zAA_−°⋅pAA_−°⋅exp−𝛥‡HAA_−°2⋅R⋅Tfus,AA_(251)
 𝛤A°⋅zAA_+°⋅pAA_+°⋅exp−𝛥‡HAA_+°2⋅R⋅Tfus,AA_ =[A_]eq⋅𝛤A°⋅zAA_−°⋅pAA_−°⋅exp−𝛥‡HAA_−°2⋅R⋅Tfus,AA_(252)

Tableau 12.

Propriétés calorimétriques des formes cristallines des acides tartrique et mandélique

Acide tartriqueAcide mandélique
Tfus°(K)𝛥fus H° (kJ∕mol)Tfus°(K)𝛥fus H° (kJ∕mol)
Enantiomère (+)∕(−)443,436,3404,825,5
Racémate (+−)479,272,6393,425,8

Le produit de ces équations de l’équilibre de fusion mène à :

[A]eq⋅[A_]eq=zAA_+°⋅pAA_+°zAA_−°⋅pAA_−°2⋅exp−𝛥fusHAA_°R⋅Tfus,AA_(253)
Pour le cocristal AA pur, les concentrations en A et A sont moitié moindres que celles des cristaux A et A purs, le produit des équations de l’équilibre de fusion mène dans ce cas à :
[A]°⋅[A_]°4=zAA_+°⋅pAA_+°zAA_−°⋅pAA_−°2⋅exp−𝛥fusHAA_°R⋅Tfus,AA_°(254)
Le rapport des équations de l’équilibre de fusion du cocristal en mélange et pur mène à l’équation cinétique de l’équilibre de fusion :
ln(4.xeq.(1−xeq))=𝛥fusHAA_°R⋅1Tfus,AA_°−1Tfus,AA_(255)
Cette équation de l’équilibre cinétique de fusion est identique à l’équation thermodynamique de l’équilibre de fusion de Prigogine–Defay [69]. Les couples d’énantiomères de l’acide tartrique et de l’acide mandélique (Figure 33) donnent chacun lieu à la formation d’un cocristal racémique.

Figure 33.

Structure chimique de couples d’énantiomères de l’acide tartrique et de l’acide mandélique.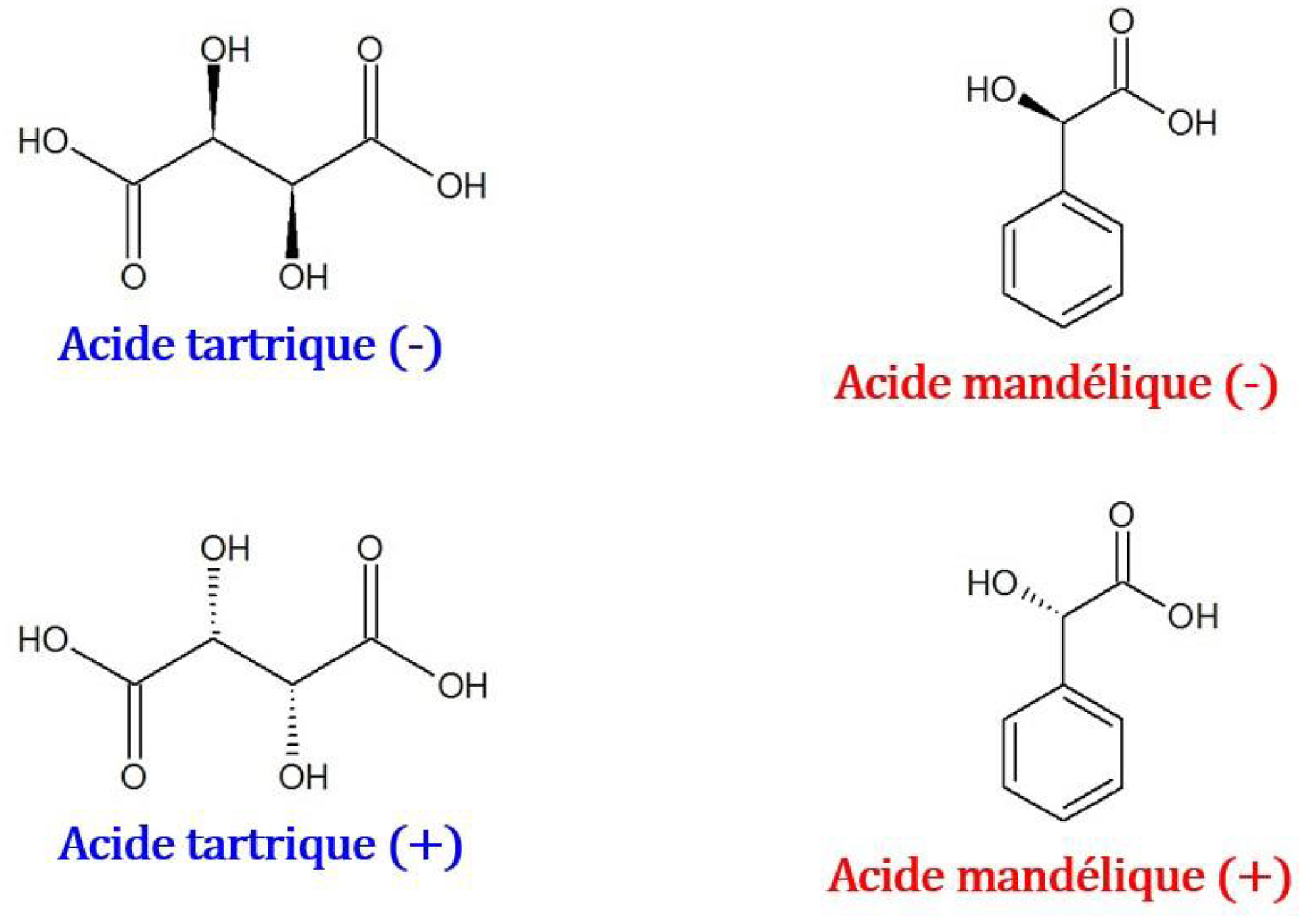

Les températures et enthalpies de fusion des énantiomères et racémates des acides tartrique [70] et mandélique [71] sont consignées dans le Tableau 12.

Les diagrammes de phases expérimentaux de ces deux systèmes concordent avec ceux déduits des analyses thermodynamique et cinétique (Figure 34, Annexes 12 et 13).

Figure 34.

Diagrammes de phases liquide–solide composition-température des énantiomères de l’acide tartrique (gauche) et de l’acide mandélique (droite), expérimentaux (disques noirs) et déterminés par les modèles cinétique et thermodynamique : liquidus du cocristal (traits rouges) et liquidus de l’énantiomère (traits bleus).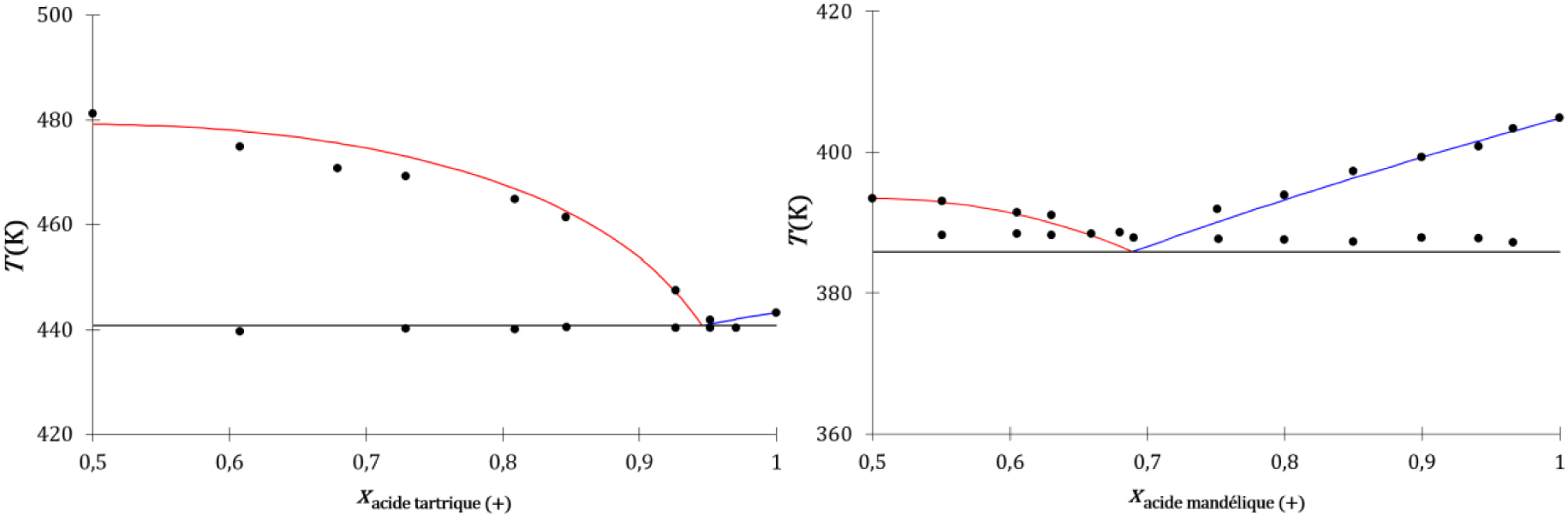

Les descriptions thermodynamique et cinétique de l’équilibre de fusion de systèmes à invariant eutectique à liquide idéal de mélanges d’énantiomères avec leur racémate sont équivalentes. Elles concordent entre elles et concordent avec le comportement expérimental de tels systèmes.

5.8. Cristaux atomiques et moléculaires

Les évolutions avec la masse molaire des températures et entropies de fusion standards des éléments de la classification périodique [72, 73, 74] qui cristallisent dans une structure compacte et des alcanes linéaires [75] sont présentées sur la Figure 35.

Figure 35.

Températures et entropies de fusion standards des éléments de la classification périodique qui cristallisent dans des empilements compacts (hexagonal compact ou cubique à faces centrées) (bleu) et des alcanes linéaires de 2 à 22 atomes de carbones (rouge).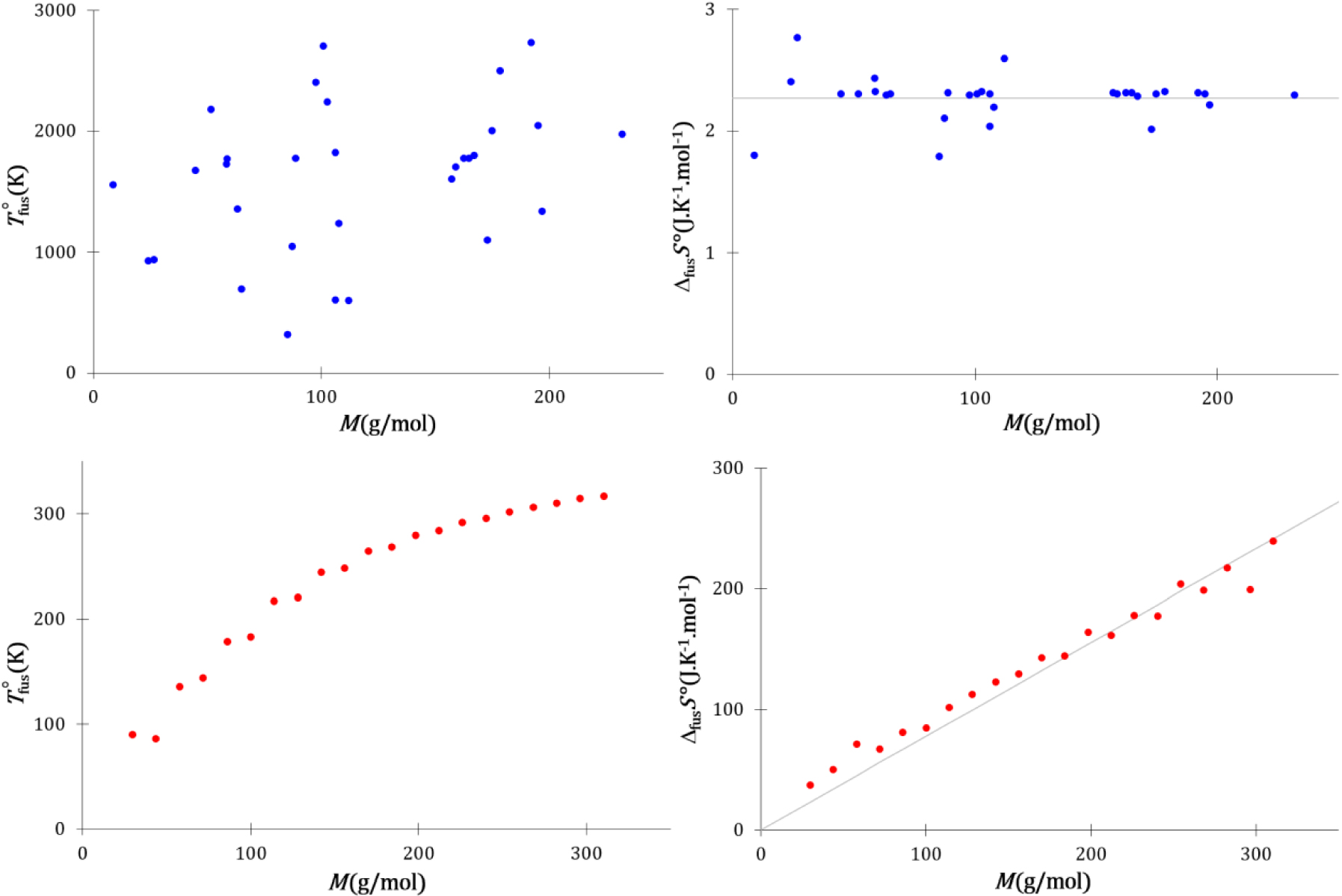

L’entropie de fusion des corps simples ne dépend pas de leur masse molaire, contrairement à celle des alcanes linéaires qui est proportionnelle à cette dernière. En thermodynamique statistique, l’entropie est liée au nombre d’états microscopiques :

S=kB⋅ln(𝛺)(256)
L’entropie de fusion des corps simples ne dépend pas de leur masse molaire car la fusion procède toujours du passage d’un état initial solide de même nature, un empilement cristallin compact, à un état final également de même nature, un liquide isotrope ou les atomes, assimilables à des sphères, disposent de trois degrés de liberté de translation. En revanche, l’entropie de fusion augmente avec la taille des alcanes linéaires car le nombre de conformations, et donc d’états microscopiques, augmente avec le nombre d’atomes qui les constituent. La description thermodynamique est donc en accord avec les observations expérimentales. L’expression de l’entropie cinétique de fusion est :
𝛥fusS=R⋅ln𝛤A∗⋅z+⋅p+[A]⋅z−⋅p−(257)
Pour les éléments, le rapport 𝛤A*∕[A] est indépendant de la masse molaire puisque les deux concentrations de ce rapport diminuent lorsque la masse molaire augmente. De la même manière le rapport z+∕z− ne dépend ni de la température, ni de la masse molaire, puisque ces fréquences de collision augmentent identiquement lorsque la température augmente et diminuent pareillement lorsque la masse molaire augmente. Le rapport p+∕p− dépend de la nature du mécanisme, mais ce dernier ne change pas avec la nature de l’élément considéré : p+ est la probabilité qu’un atome à la surface du cristal qui subit une collision passe dans la phase liquide et p− est la probabilité qu’un atome qui entre en collision avec la surface du solide s’associe au cristal, ceci indépendamment des énergies cinétiques de collisions (Figure 36).

Figure 36.

Fusion et solidification d’un corps simple.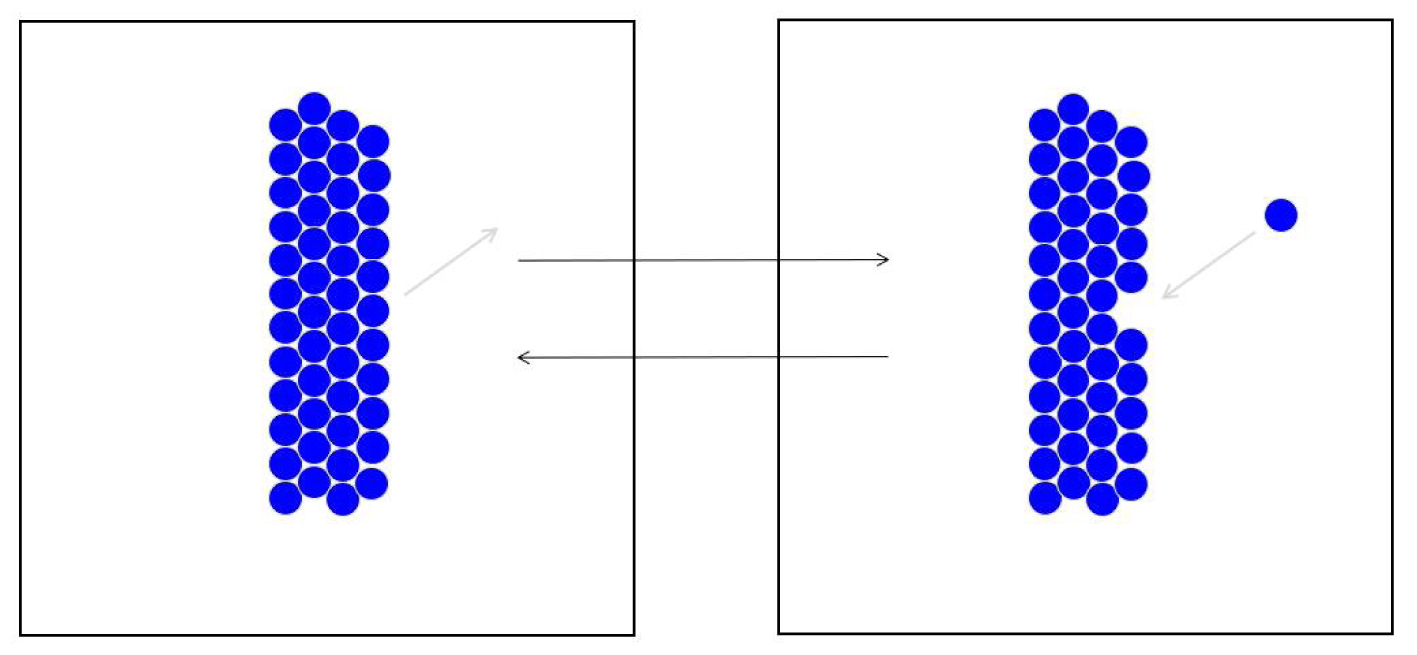

Pour les alcanes linéaires, la probabilité p− qu’une molécule qui entre en collision avec la surface du solide s’associe au solide est d’autant plus faible que la taille de l’alcane est élevée. En effet, il faut à la fois que la conformation, la position et l’orientation de la molécule au moment de la collision soient favorables à la cristallisation (Figure 37).

Tableau 13.

Températures de fusion et solidification de corps purs

Corps purAcide laurique Bi Sn Pb
Tfus°(K)315,4544,6505,1429,8
Tsol°(K)304,6516,4480,6429,1
Référence Cette étudeKano [76]

Tableau 14.

Effet de la vitesse de refroidissement sur la température de solidification de l’eau liquide

vrefroidissement (K∕min)−0,3−0,5−1
Tsol°(K)265,3264,1262,2

Tableau 15.

Températures de fusion et solidification standards de l’acide laurique

Tmoyenne°(K)Tmin°(K)Tmax°(K)Ecart type (K)
Fusion315,3314,6316,1 0,5
Solidification304,6301,7307,2 2,0

Tableau 16.

Temps de solidification d’échantillons du même lot de salicylate de phényle

Echantillonn°1n°2n°3n°4n°5n°6n°7n°8n°9n°10
t (h)4,81,01,650,422,71,04,65,44,65,0

Par contre, la taille n’altère pas la probabilité p+ puisque la conformation, la position et l’orientation d’une molécule à la surface du cristal sont déjà définies. La probabilité de cristallisation d’une molécule lors d’une collision diminuera donc avec sa taille ce qui induit une augmentation de l’entropie cinétique de fusion avec la masse molaire. Les descriptions thermodynamique et cinétique de l’équilibre de fusion sont concordantes et en accord avec les observations expérimentales.

5.9. Hystérésis de la fusion et caractère métastable des nanocristaux

La température de solidification d’un corps pur est en général inférieure à sa température de fusion (Tableau 13).

La température de solidification d’un corps pur dépend en général de la vitesse de refroidissement [77] (Tableau 14).

Les températures de fusion puis de solidification de l’acide laurique ont été mesurées à 10 reprises dans le cadre de cette étude afin d’illustrer le caractère partiellement aléatoire de la solidification. En effet, celle-ci se produit dans un intervalle de température plus large que la fusion (Tableau 15).

Figure 37.

Fusion et solidification d’un alcane linéaire : la collision d’une molécule d’alcane avec la surface du cristal ne mène pas à la solidification si la conformation de l’alcane (I) ou la position de la collision (II) sont défavorables. La solidification ne peut se produire que si ces deux conditions sont favorables (III).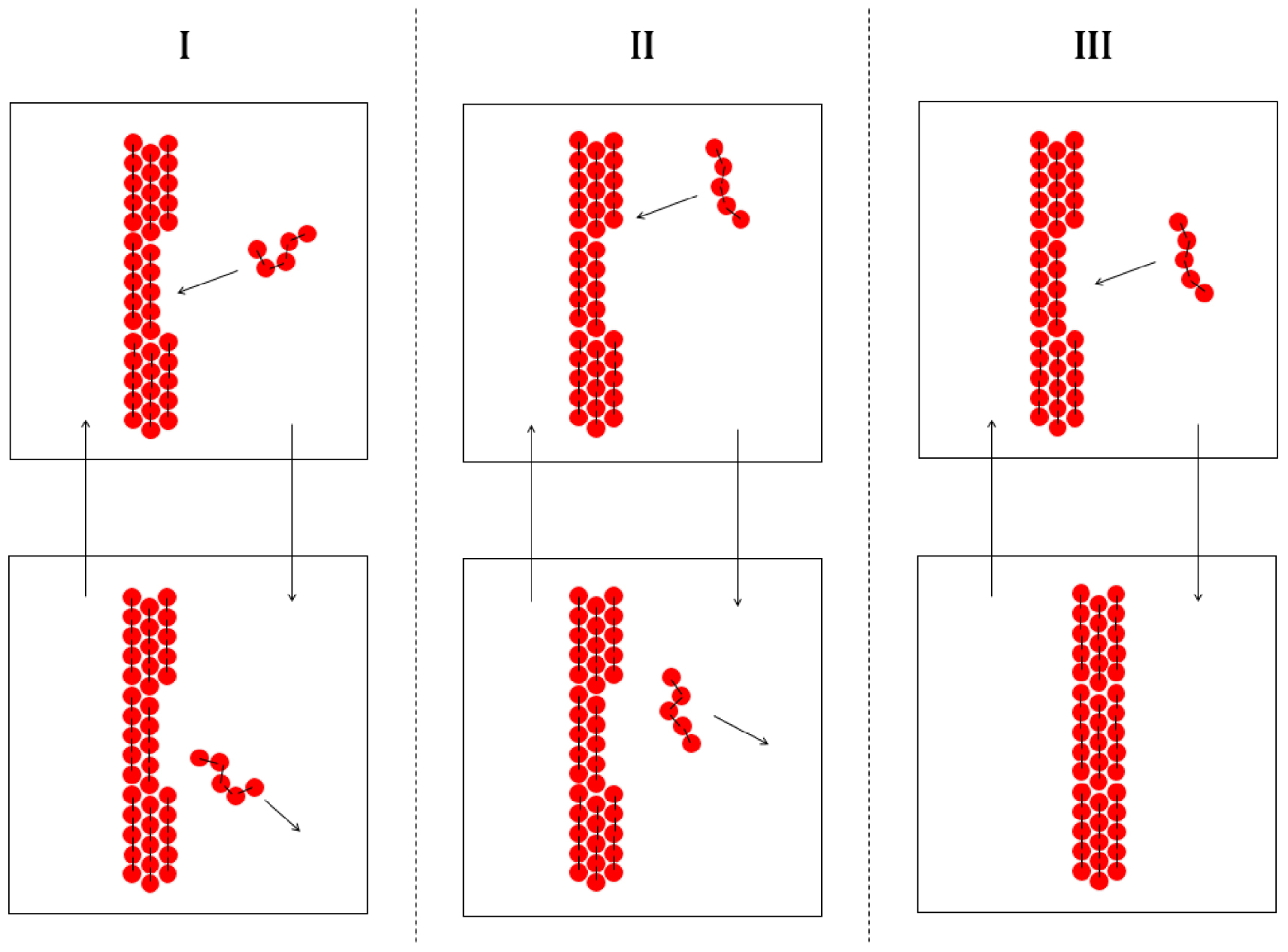

Une autre expérience qui illustre le caractère stochastique de la solidification de manière encore plus probante a également été menée dans le cadre de cette étude : 10 échantillons du même lot de salicylate de phényle ont été fondus. Les temps de solidification des échantillons présentent une dispersion importante (Tableau 16).

La solidification commence par la croissance d’un germe cristallin de dimensions nanométriques. La température de fusion d’un cristal nanométrique (nc) est inférieure à celle d’un cristal (c) (Tableau 17).

Tableau 17.

Températures de fusion de cristaux (c) et nanocristaux (nc) de corps purs

Sn Pb Benzène Naphtalène
Tfusc°(K)506,1600,6280,8356,1
Karmakar et al. [78]Qi [79]Zhang et al. [80]Zhang et al. [80]
Tfusnc°(K)427,5438,6253,9341,3
Qi [79]Qi [79]Zhang et al. [80]Zhang et al. [80]
Taille (nm) 5,3 4,7 1,9 1,9

La température de fusion d’un nanocristal d’une espèce chimique diminue avec sa taille [80] (Tableau 18).

Tableau 18.

Température de fusion de cristaux de chlorobenzène de différentes tailles

Taille>1 μm13,0 nm7,8 nm4,3 nm1,9 nm
Tfusnc°(K)229,1225,7222,2216,1201,2

L’enthalpie de fusion d’un nanocristal diminue de manière encore plus marquée avec sa taille que sa température de fusion [80] (Tableau 19).

Tableau 19.

Enthalpie de fusion de cristaux de chlorobenzène de différentes tailles

Taille>1 μm21,9 nm10,9 nm5,6 nm
𝛥fusnc°H°(kJ∕mol)9,86,353,6

Soit la fusion d’un cristal (c) de grande taille (i.e. >1 μm) d’un corps pur A dans son liquide :

A(c)⇌A(l)
Dans la description thermodynamique, les énergies de Gibbs standards du cristal et du liquide sont égales à l’équilibre :
Gc°=Gl°(258)
Soit :
𝛥fusGeqc°=Geql°−Geqs°=0(259)
La description cinétique est fondée sur les vitesses de fusion et solidification du cristal, respectivement :
v+c°=𝛤c°⋅z+c°⋅p+c°⋅exp−𝛥‡H+c°R⋅T(260)
v−c°=𝛤c°⋅z−c°⋅p−c°⋅exp−𝛥‡H−c°R⋅T(261)

A la température de fusion, ces vitesses sont égales :

T=Tfusc°(262)
veq+c°=veq−c°(263)

D’où :

𝛥fusGeq°c=Geq−°−Geq+°=0(264)
Les diagrammes réactionnels thermodynamique et cinétique de l’équilibre de fusion d’un cristal (c) sont présentés sur la Figure 38.

Figure 38.

Diagramme réactionnel thermodynamique (gauche) et cinétique (droite) de l’équilibre de fusion d’un cristal (c) d’un corps pur dans les conditions standards.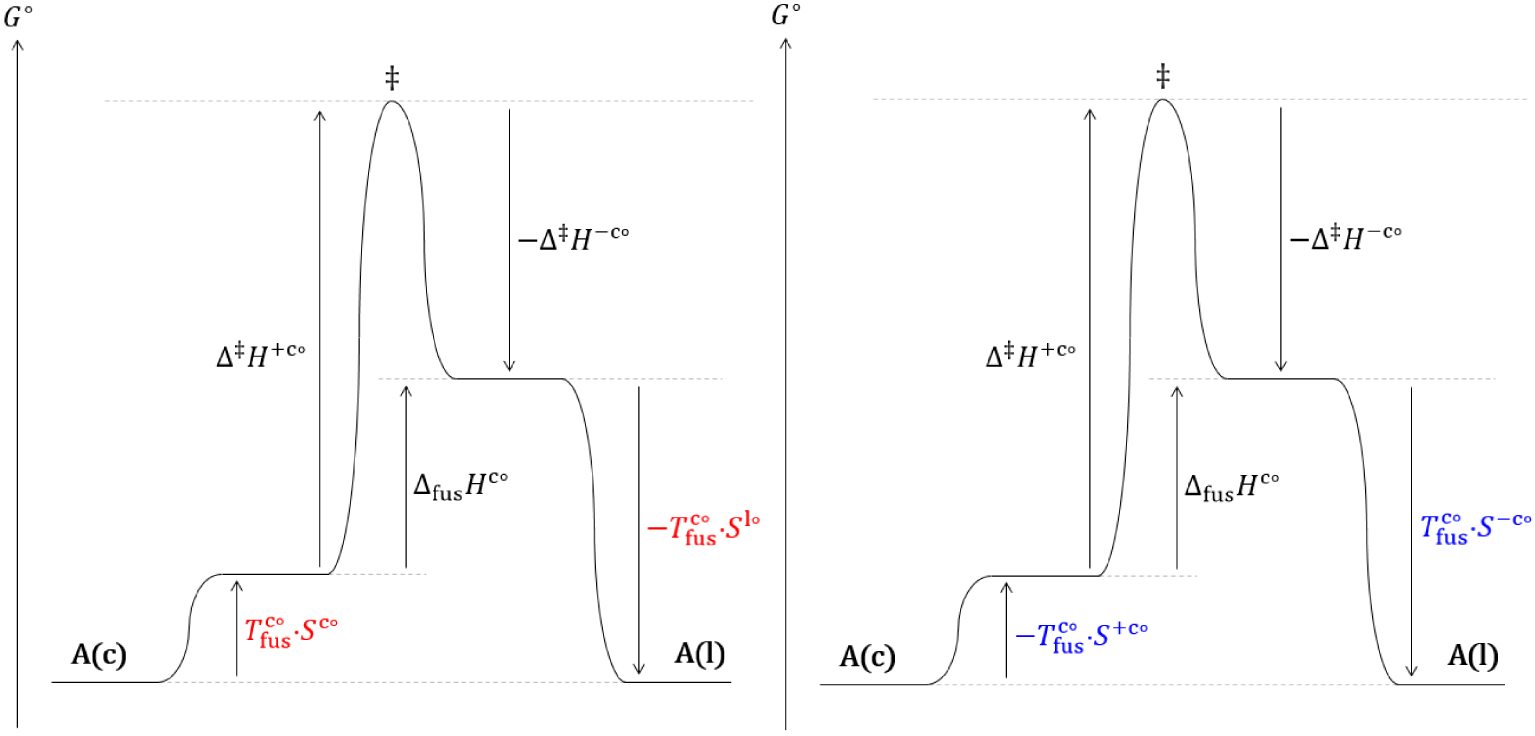

A une température inférieure à la température de fusion, la solidification est spontanée :

T<Tfusc°(265)
Dans la description thermodynamique, l’énergie de Gibbs du cristal (c) est inférieure à celle du liquide :
Gc°<Gl°(266)
Soit :
𝛥fusGc°=Gl°−Gc°>0(267)
Dans la description cinétique, la vitesse de solidification d’un cristal (c) est supérieure à sa vitesse de fusion :
v+c°<v−c°(268)
Soit :
𝛥fusGc°=G−°−G+°>0(269)
Les diagrammes réactionnels thermodynamique et cinétique hors équilibre de la solidification d’un cristal (c) à une température inférieure à sa température de fusion sont présentés sur la Figure 39.

Figure 39.

Diagrammes réactionnels thermodynamique (gauche) et cinétique (droite) hors équilibre de la solidification du cristal (c) d’un corps pur à une température inférieure à sa température de fusion.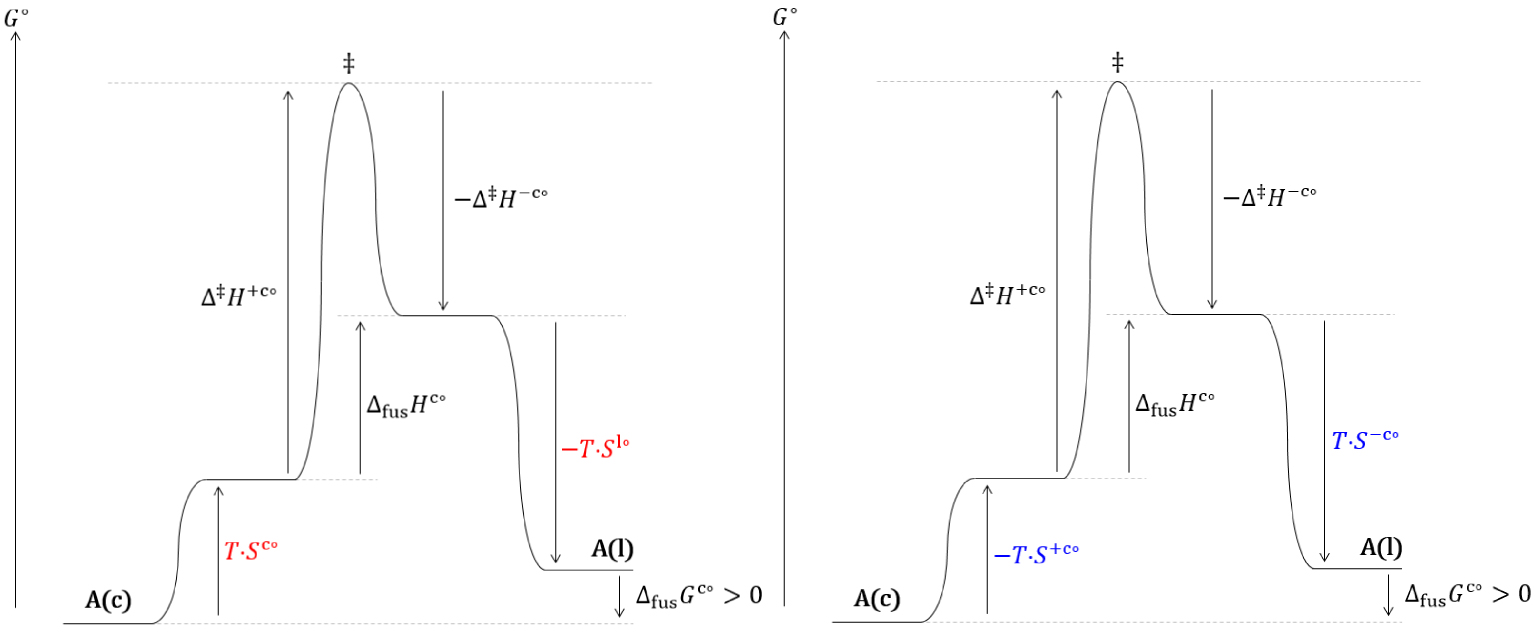

La cristallisation d’un corps pur débute par la formation d’un germe nanocristallin (nc) :

A(nc)⇄A(l)
La température de fusion d’un nanocristal est inférieure à la température de fusion d’un cristal :
Tfusnc°<Tfusc°(270)
Il existe donc un domaine de température pour lequel un nanocristal est instable et le cristal est stable :
Tfusnc°<T<Tfusc°(271)
Cette situation est représentée sur les diagrammes thermodynamique et cinétique de la Figure 40.

Figure 40.

Diagrammes réactionnels thermodynamique (gauche) et cinétique (droite) hors équilibre de la fusion d’un nanocristal dans un domaine de température où le cristal est stable.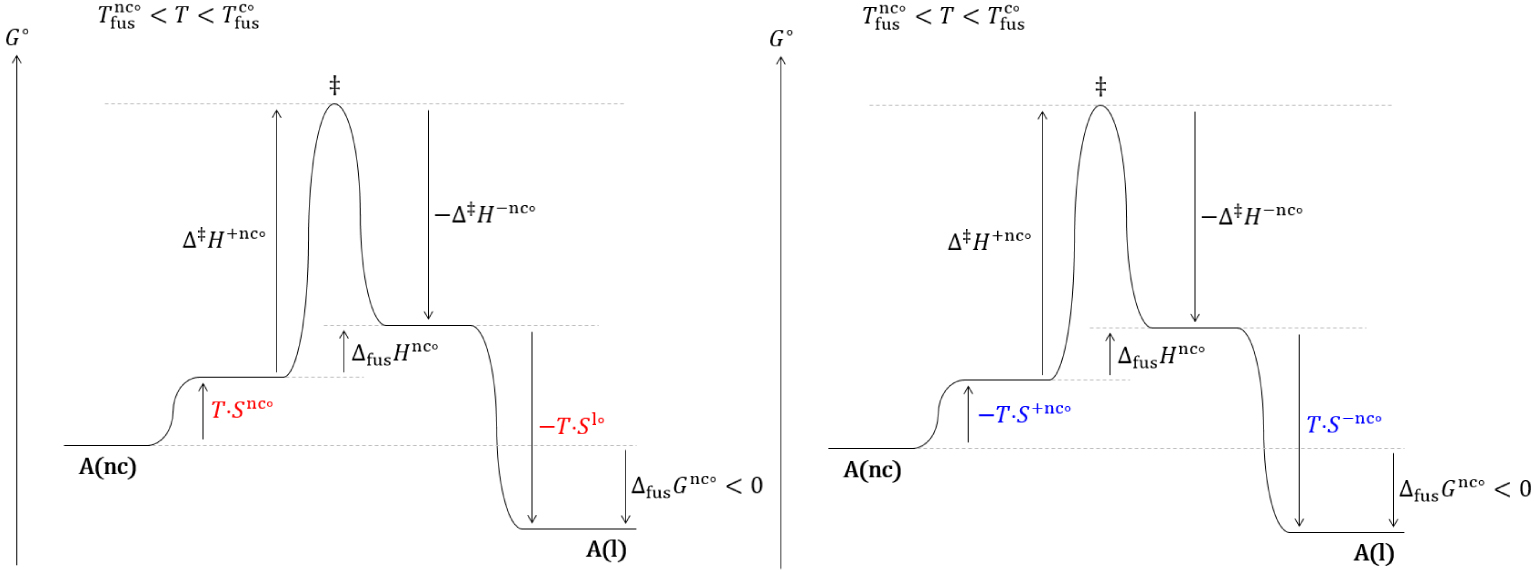

Les descriptions thermodynamique et cinétique des fusions d’un cristal et d’un nanocristal mènent aux mêmes conclusions pour le signe de 𝛥fusG°, la suite de l’analyse est donc valable pour les deux descriptions. La taille, et par conséquence la valeur de 𝛥fus G° d’un germe nanocristallin dans le domaine métastable est fluctuante (Figure 41-I). Ce nanocristal peut atteindre, par ce jeu de fluctuations, une taille critique à partir de laquelle la solidification est spontanée. La valeur de 𝛥fus G° de ce nanocristal augmente alors et ne fluctue plus de manière significative (Figure 41-II). Le nanocristal continue à croitre jusqu’à ce qu’il devienne un cristal, c’est-à-dire lorsque sa croissance n’affecte plus sa température de fusion, 𝛥fus G° atteint alors une valeur maximale. Comme la température du milieu est inférieure à la température de fusion d’un cristal de grande taille, le processus de solidification se poursuit jusqu’à la solidification totale de la phase liquide (Figure 41-III).

Les modèles thermodynamique et cinétique hors équilibre offrent une description cohérente de la solidification, de la naissance du premier germe cristallin nanométrique à la croissance spontanée d’un cristal de taille plus importante. La métastabilité des nanocristaux est à l’origine de l’hystérésis de la fusion-solidification et de la dispersion des températures de solidification : en effet, les fluctuations de la taille du nanocristal à l’origine de la cristallisation sont de nature stochastique.

Figure 41.

Evolution conceptuelle de 𝛥fus G° du cristal d’un corps pur à une température inférieure à sa température de fusion : fluctuation de la taille d’un germe nanocristallin instable (I), croissance spontanée d’un germe cristallin stable de taille intermédiaire (II) et croissance d’un cristal de grande taille (III) jusqu’à la solidification totale (IV).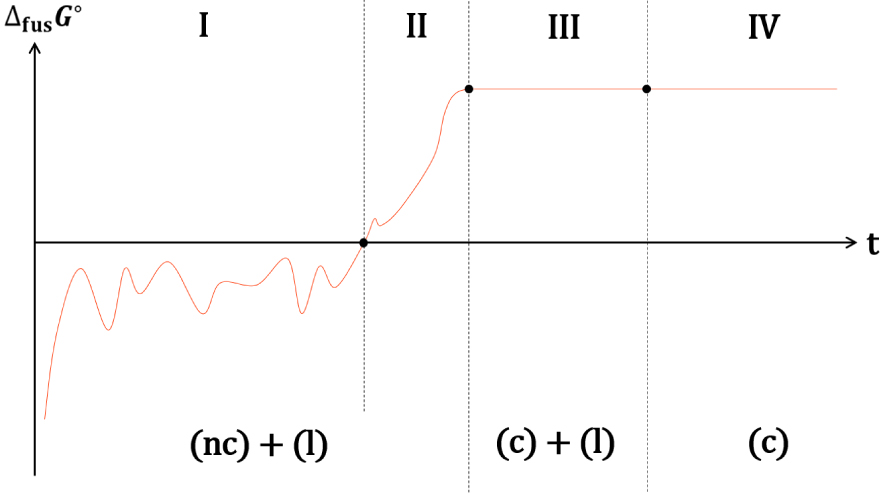

5.10. Formation de cristaux chiraux de sels ioniques

L’analyse présentée dans ce chapitre utilise les résultats obtenus dans le chapitre précédent sur la croissance cristalline d’un germe nanocristallin à un cristal de grande taille : les deux modèles, thermodynamique et cinétique, sont utilisables puisqu’ils mènent aux mêmes évolutions de la fonction 𝛥fus G. La cristallisation des chlorate (NaClO3) ou bromate (NaBrO3) de sodium en solution aqueuse présente un comportement singulier : alors que les cations en solution de ces sels sont achiraux, les cristaux présentent une chiralité [81]. Les formes chirales sont formées en proportions égales en absence d’agitation [82] :

2A(aq)⇌A(s)+A_(s)
En revanche, des cristaux d’une seule forme chirale, A ou A, sont obtenus sous agitation. L’obtention des formes A ou A est équiprobable :
A(aq)⇌A(s)A(aq)⇌A_(s)

Soit une solution sursaturée de chlorate ou bromate de sodium. La taille des premiers germes nanocristallins (A et A) fluctue (Figure 42-I) jusqu’à l’instant où un cristal d’une des formes chirales (A) atteint une taille critique à partir de laquelle sa croissance est spontanée (Figure 42-II). A partir de cet instant, la taille de ce cristal (A) croît de manière continue. La concentration de la solution sursaturée décroît de manière continue et homogène dans toute la solution en raison de l’agitation, ce qui défavorise la solidification des cristaux de l’autre forme chirale (A), qui vont progressivement se dissoudre jusqu’à disparaitre. La croissance du cristal (A) consomme les ions de la solution (Figure 42-III) jusqu’à établissement de l’équilibre (Figure 42-IV) : le solide d’une des deux formes chirales dans la solution aqueuse saturée. Un tel phénomène, pour lequel un changement mineur (formation d’un nanocristal de taille critique) entraîne la totalité du système à évoluer dans une des deux voies qui lui sont offertes (solidification de A ou A) est appelé en physique une bifurcation.

Figure 42.

Evolution conceptuelle de 𝛥fusG et de la concentration en A en solution : fluctuation de la taille de germes nanocristallins (A et A) (I) ; formation d’un cristal de taille critique d’une forme chirale (A) et solubilisation de la forme chirale énantiomère (A) (II) ; diminution de la concentration de la solution sursaturée (III) jusqu’à saturation (IV).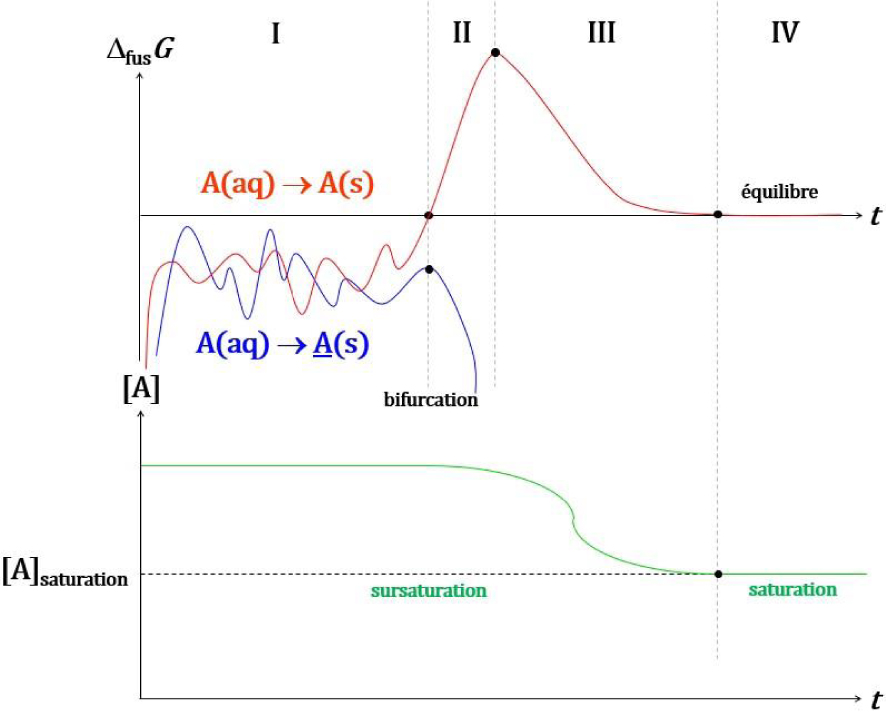

Si la solution n’est pas agitée, la modification de concentration induite par la croissance des germes cristallins ne se répercute pas sur celles des autres rapidement, ce qui laisse le temps aux germes cristallins des deux formes chirales d’atteindre la taille critique à partir de laquelle la cristallisation devient spontanée. Les modèles thermodynamique et cinétique hors équilibre permettent de comprendre pourquoi une seule forme chirale des cristaux de chlorate ou bromate de sodium se forme lorsque la solution est agitée et une seule lorsqu’elle ne l’est pas.

5.11. Synthèse

Les modèles thermodynamique et cinétique à l’équilibre et hors équilibre permettent de comprendre et quantifier la fusion de nombreux systèmes :

  1. i. mélanges binaires de sels ioniques et molécules organiques (NaCl–RbCl et acide laurique-acide oléique) ;
  2. ii. mélanges binaires de molécules chirales (acide tartrique et acide mandélique) ;
  3. iii. évolution de l’entropie de fusion de cristaux atomiques compacts et d’alcanes linéaires avec la masse molaire ;
  4. iv. lien entre le caractère métastable des nanocristaux et l’hystérésis de la fusion ;
  5. v. effet des conditions rhéologiques sur la formation de cristaux chiraux.

Pour d’autres systèmes, qui présentent un écart à l’idéalité selon le modèle thermodynamique, le modèle cinétique s’avère plus pertinent :

  1. i. mélange binaire du chlorure de sodium avec l’eau ;
  2. ii. mélange binaire de l’acide laurique avec l’acide oléique.

Alors que le modèle thermodynamique de tels systèmes ne peut s’affranchir de paramètres d’ajustement de nature empirique, le modèle cinétique permet de construire des fonctions analytiques des courbes de l’équilibre de fusion en se fondant sur la nature du processus collisionnel qui se produit en amont de la solidification. L’étude de ces deux systèmes, comparés à des systèmes qui partagent une des deux espèces chimiques du mélange, montre que l’entropie cinétique est totalement dépendante des espèces chimiques associées. Ainsi la solidification du chlorure de sodium dépend drastiquement de son partenaire, le chlorure de rubidium ou l’eau. De la même manière, la solidification de l’acide laurique en mélange avec l’acide oléique se distingue de celle en mélange avec la lidocaïne.

6. Théorie cinétique de l’équilibre

L’étude de systèmes réels des chapitres précédents, réactions chimiques et équilibres de fusion, corrobore le modèle cinétique de l’équilibre. Ce dernier chapitre présente le modèle cinétique de l’équilibre des transformations microscopiques dans un cadre théorique général.

6.1. Fonction cinétique d’évolution

Dans cette première partie, la fonction cinétique d’évolution d’une réaction chimique est établie. Il est important de préciser que cette fonction d’évolution est utilisable strictement dans le cas d’une seule transformation microscopique. Le cas de transformations microscopiques couplées sera traité dans le chapitre suivant. Soient deux molécules de gaz A et B qui peuvent réagir pour donner un ou plusieurs produit(s).

A(g)+B(g)→produit(s)
Ces deux molécules sont contenues dans une enceinte (Figure 43).

Figure 43.

Système fermé constitué de deux molécules réactives A et B en mouvement dans une enceinte de volume V, de pression P° constante égale à 1 bar et dont les parois sont thermostatées à une température T constante.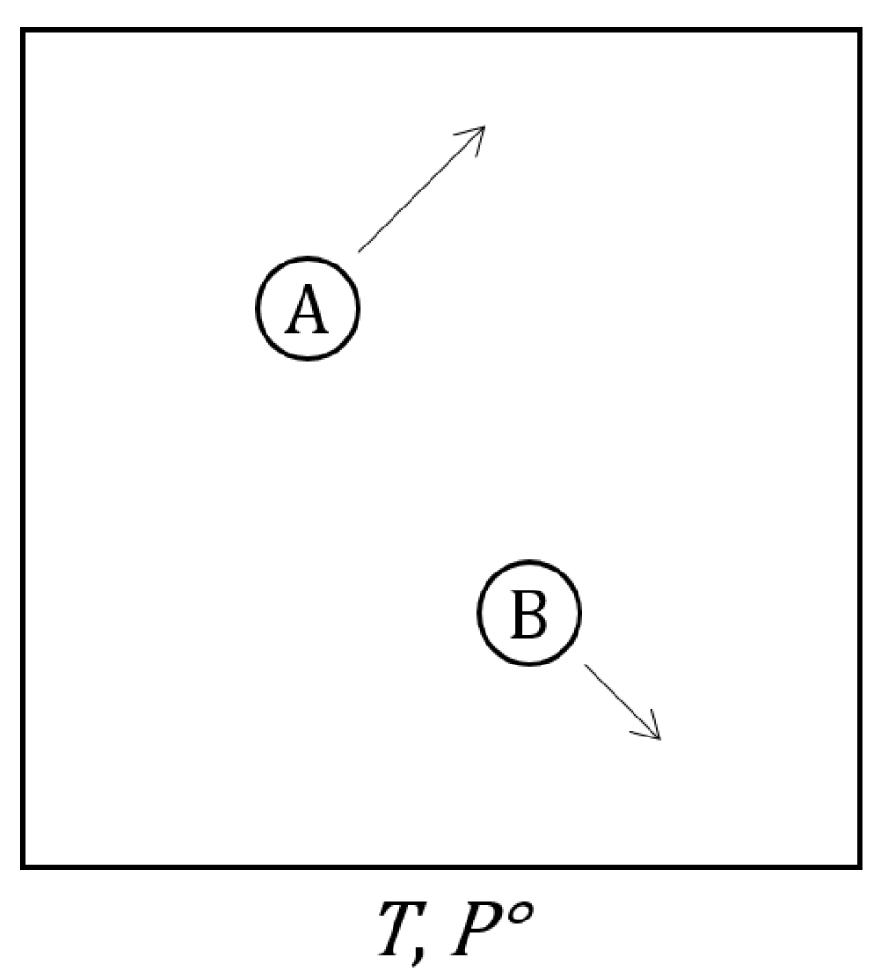

La pression de la boîte thermostatée est choisie suffisamment faible pour que la collision entre A et B ne se produise pas avant que l’énergie cinétique des molécules soit indépendante des conditions initiales. Autrement formulé, le nombre de collisions de A et B avec les parois de l’enceinte avant leur collision est grand devant 1. Dans ces conditions, la densité de probabilité de la norme de la vitesse des molécules A et B suit la loi de distribution de Maxwell–Boltzmann[83] :

pA(vA)=mA2⋅π⋅kB⋅T12⋅4⋅π⋅vA2 ⋅exp−mA⋅vA2kB⋅T(272)
pB(vB)=mB2⋅π⋅kB⋅T12⋅4⋅π⋅vB2 ⋅exp−mB⋅vB2kB⋅T(273)
Soit h¯ l’enthalpie microscopique, définie comme la valeur moyenne de l’enthalpie d’une molécule :
h¯=HNA(274)
𝛥h‡°¯ est l’énergie d’activation microscopique :
𝛥h‡°¯=𝛥H‡°NA(275)
Cette énergie d’activation microscopique est la différence entre l’enthalpie microscopique h‡°¯ du col à franchir pour que la réaction se produise et les enthalpies microscopiques hA(g)°¯ et hB(g)°¯ des molécules réactives :
𝛥h‡°¯=h‡°¯−(hA(g)°¯+hB(g)°¯)(276)
La vitesse de réaction v(1) de ce couple d’espèces réactives, exprimée par unité de volume et de temps (L−1⋅s−1), est calculée en prenant en compte le mouvement dans l’espace des molécules A et B et en considérant le cas où la collision qui précède la réaction est parfaitement inélastique (Annexe 14) :
v(1)=z(1)°⋅p°⋅exp−𝛥h‡°¯𝜒°⋅kB⋅T(277)
p° est la probabilité que la réaction se produise au moment de la collision indépendamment du franchissement du col d’enthalpie d’activation. z(1) est la fréquence de collision d’un couple de molécules :
z(1)°=𝜋⋅kB⋅TmA12⋅mB1212⋅π⋅(rA°2+rB°2)V2(278)
𝜒° est un coefficient qui dépend du rapport 𝛥h‡°¯∕(kB⋅T) entre l’enthalpie microscopique de transition et l’énergie cinétique de collision (Figure 44).

Figure 44.

Evolution de 𝜒° avec 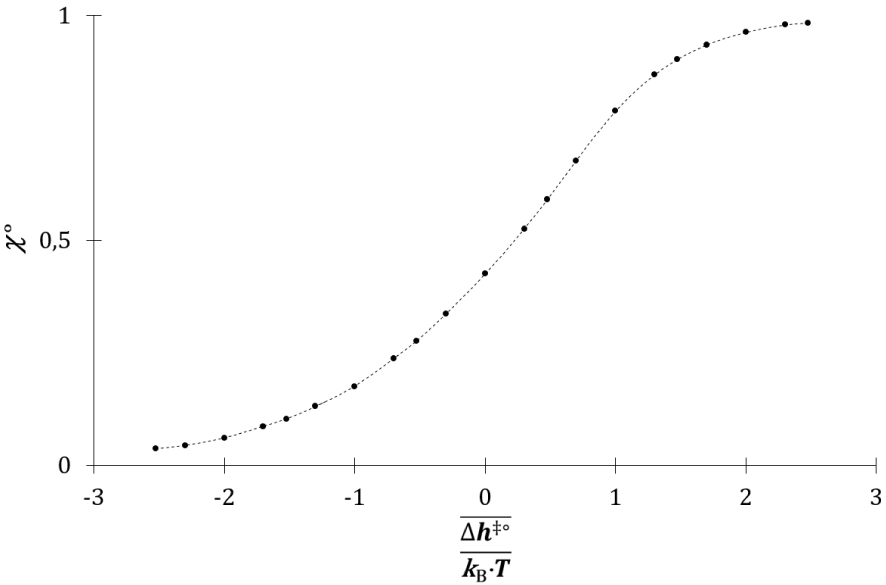𝛥h‡°¯∕(kB⋅T).

Il augmente avec le rapport 𝛥h‡°¯∕(kB⋅T), il tend vers 0 pour une valeur faible de ce rapport et vers 1 pour une valeur élevée de celui-ci. Le coefficient 𝜒° représente la fraction de l’énergie cinétique des molécules A et B engagées dans la collision. En effet, même lors d’une collision totalement inélastique, la variation d’énergie cinétique des molécules est inférieure à l’énergie cinétique totale. La vitesse v de la réaction chimique entre Ni molécules de A et Nj molécules de B, avec Ni et Nj grands devant 1, se déduit de la vitesse de réaction v(1) pour un couple d’espèces réactives : chacune des Ni molécules de A peut entrer en collision avec chacune des Nj molécules de B.

v=Ni⋅Nj⋅v(1)(279)
Soit, en exprimant la vitesse en mol⋅L−1⋅s−1 :
v=[A]⋅[B]⋅zAB°⋅pAB°⋅exp−𝛥‡H°𝜒°⋅R⋅T(280)
Avec :
zAB°=NA⋅π⋅(rA°2+rB°2)⋅𝜋⋅kB⋅TmA12⋅mB1212(281)
Cette fréquence de collision est proche de celle de la loi cinétique classique dérivée de la loi d’Eyring utilisée dans le chapitre 2.3 :
vclassique=[A]⋅[B]⋅zAB,classique°⋅pAB°⋅exp−𝛥‡H°R⋅T (282)
zAB,classique°=NA⋅π⋅(rA°+rB°)2⋅8⋅kB⋅Tπ⋅𝜇AB12(283)
Les valeurs des constantes de proportionnalité de ces deux modèles, pour deux molécules identiques, sont du même ordre de grandeur :
zAB°≅11,1⋅NA⋅(kB⋅T)12⋅r°2(284)
zAB,classique°≅40,1⋅NA⋅(kB⋅T)12⋅r°2(285)
La constante de proportionnalité de la fréquence de collision du modèle classique est supérieure car sa section de collision est surestimée (Annexe 14). Cette différence est sans conséquence pour l’étude d’équilibres car les constantes de proportionnalité sont éliminées dans le calcul de la constante d’équilibre qui est un rapport de constantes cinétiques. Soit la réaction renversable ci-après :
A(g)+B(g)⇄C(g)+D(g)
NA molécules A et NB molécules B sont introduites dans une enceinte de volume V, de pression P° constante égale à 1 bar et dont les parois sont thermostatées à une température T constante :
NA≫1(286)
NB≫1(287)
Les vitesses de réaction entre A et B, d’une part, et C et D, d’autre part, sont respectivement :
v+=[A]⋅[B]⋅zAB°⋅pAB°⋅exp−𝛥‡H+°𝜒+°⋅R⋅T(288)
v−=[C]⋅[D]⋅zCD°⋅pCD°⋅exp−𝛥‡H−°𝜒−°⋅R⋅T(289)
Avec :
𝛥rH°=𝛥‡H+°−𝛥‡H−°(290)
Les vitesses sont égales à l’équilibre cinétique :
veq+=veq−(291)
Soit :
K=[C]eq⋅[D]eq[A]eq⋅[B]eq=zAB°⋅pAB°zCD°⋅pCD° ⋅exp−1R⋅T𝛥‡H+°𝜒+°−𝛥‡H−°𝜒−°(292)
Cette équation peut s’écrire :
K=zAB°⋅pAB°zCD°⋅pCD°⋅exp−𝛥rH°𝜒°⋅R⋅T(293)
La grandeur 𝜒° dépend de 𝜒+° et 𝜒−°, elle dépend donc de 𝛥‡ H+°∕(R⋅T) et de 𝛥‡ H−°∕(R⋅T). L’évolution de ce paramètre est représentée sur la Figure 45 en fonction de 𝛥‡ H+°∕(R⋅T) et de 𝛥r H°∕(R⋅T) (Annexe 15).

Figure 45.

Evolution de 𝜒° avec 𝛥‡ H+°∕(R⋅T) et 𝛥r H°∕(R⋅T).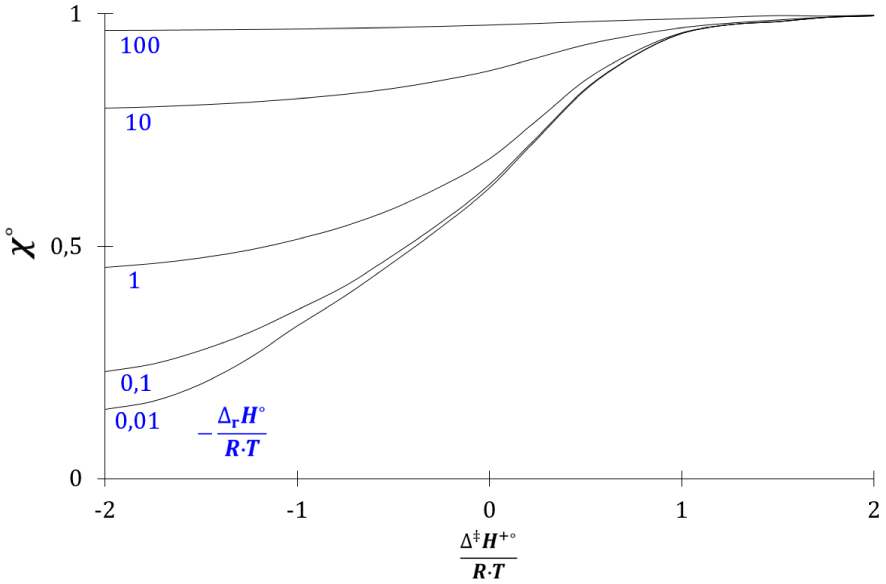

La grandeur 𝜒°, comprise entre 0 et 1, augmente avec les rapports 𝛥‡ H+°∕(R⋅T) et 𝛥r H°∕(R⋅T). L’enthalpie libre cinétique standard dépend donc de la grandeur 𝜒° :

𝛥rG°=−R⋅T⋅ln(K)(294)
Soit :
𝛥rG°=𝛥rH°𝜒°−T⋅𝛥rS°(295)
Avec :
𝛥rS°=S+°−S−°=R⋅ln(zAB°⋅pAB°)−R⋅ln(zCD°⋅pCD°)(296)
Dans le cas général, lorsque la transformation microscopique n’est pas à l’équilibre, il convient de considérer l’enthalpie libre cinétique :
𝛥rG=𝛥rG°+R⋅T⋅ln(Q)(297)
Soit :
𝛥rG=𝛥rH°𝜒°−T⋅𝛥rS(298)
Avec :
𝛥rS=S+−S−=R⋅ln(zAB°⋅pAB°⋅[A]⋅[B]) −R⋅ln(zCD°⋅pCD°⋅[C]⋅D)(299)
L’enthalpie libre cinétique a été formulée dans cette analyse de manière analogue à l’enthalpie libre thermodynamique de manière à comparer les deux modèles. Dans l’absolu, cette formulation de l’enthalpie est arbitraire. De manière analogue, l’entropie cinétique a été introduite dans la fonction enthalpie libre cinétique de la même manière que l’entropie calorimétrique a été introduite dans la fonction enthalpie libre par Gibbs, c’est-à-dire par son produit avec la température thermodynamique. Ce choix est également arbitraire. Il est donc possible de définir le terme entropique autrement :
𝛥rG=𝛥rH°−𝜒°⋅32⋅R⋅T⋅𝛥rS(300)
Le terme (3⋅R⋅T)∕2 est l’énergie cinétique de translation Ec des molécules, le terme 𝜒° est la fraction de l’énergie cinétique Ec engagée dans l’évolution du système (note 5 ) et 𝛥r S la variation d’entropie de réaction sans dimension. Soit :
𝛥rG=𝛥rH°−𝜒°⋅Ec⋅𝛥rS(301)
Toute transformation microscopique à température et pression constantes évolue donc jusqu’à ce que la fonction ci-après soit nulle :
𝛥rH°−𝜒°⋅Ec⋅𝛥rS(302)
Á l’équilibre :
𝛥rSeq=𝛥rH°𝜒°⋅Ec(303)
L’entropie cinétique d’une transition microscopique à l’équilibre est donc égale au rapport entre l’enthalpie de la transition et la fraction d’énergie cinétique engagée dans la transition.

De la même manière qu’aucun gradient de température macroscopique n’a jamais été observé dans un échantillon de matière à l’équilibre thermique, une réaction chimique parvenue à l’équilibre n’a jamais évolué spontanément et significativement vers la formation persistante d’un de ses réactifs. Comme l’entropie cinétique de réaction 𝛥rS évolue vers la grandeur 𝛥r H°∕𝜒°⋅Ec, le caractère irréversible des transformations microscopiques peut se corréler à la diminution avec le temps de la fonction :

d𝛥rS−𝛥rH°𝜒°⋅Ecdt<0(304)

6.2. Couplage des équilibres thermique et cinétique

Soit un système constitué d’un nombre N grand devant 1 de particules sphériques, contenues dans une enceinte thermostatée, qui peuvent occuper deux états A et B d’énergies respectives eA et eB :

N≫1(305)
A⇌B 
𝛥eAB=eB−eA(306)
Le nombre de particules se conserve :
NA+NB=N(307)
Soit e‡ le maximum du col d’énergie à franchir pour que les transitions entre A et B se produisent :
𝛥eAB‡=e‡−eA(308)
𝛥eBA‡=e‡−eB(309)
𝛥eAB=𝛥eAB‡−𝛥eBA‡(310)
Les lois des vitesses de transition entre les deux états utilisées dans cette analyse sont :
vAB=NA⋅pAB⋅zAB⋅exp−𝛥eAB‡𝜒AB⋅kB⋅T(311)
vBA=NB⋅pBA⋅zBA⋅exp−𝛥eBA‡𝜒BA⋅kB⋅T(312)
z est la fréquence de collision, p la probabilité que la transition se produise suite à une collision indépendamment de l’énergie cinétique et 𝜒 la fraction de l’énergie cinétique kB⋅T engagée dans la transition (cf. chapitre précédent). Ces vitesses sont égales à l’équilibre :
vAB=vBA(313)
Donc :
NBNA=pAB⋅zABpBA⋅zBA⋅exp−𝛥eAB𝜒⋅kB⋅T(314)
Les populations des particules dans les états A et B à l’équilibre cinétique se déduisent de l’équation précédente et de celle de la conservation du nombre de particules :
NA=N1+pAB⋅zABpBA⋅zBA⋅exp−𝛥eAB𝜒⋅kB⋅T(315)
NB=N1+pBA⋅zBApAB⋅zAB⋅exp−𝛥eBA𝜒⋅kB⋅T(316)
Les lois de distribution de Maxwell des densités de probabilité des normes des vitesses A et B peuvent s’exprimer en fonction de l’énergie cinétique des particules :
pA(ec,A)=8⋅π⋅mAkB3⋅T31∕2⋅ec,A⋅exp−ec,AkB⋅T(317)
pB(ec,B)=8⋅π⋅mBkB3⋅T31∕2⋅ec,B⋅exp−ec,BkB⋅T(318)
Avec :
ec,A=mA⋅v22(319)
ec,B=mB⋅v22(320)
Les énergies de particules de A et B choisies au hasard sont respectivement :
e(ec,A)=eA+ec,A−ec,A¯(321)
e(ec,B)=eB+ec,B−ec,B¯(322)
L’énergie cinétique moyenne des particules sphériques A et B est :
ec,A¯=ec,B¯=4⋅kB⋅Tπ(323)
Les densités de probabilité d’énergie nA et nB des états A et B dépendent à la fois des distributions entre les états A et B et des distributions de leurs énergies cinétiques :
nA=pA(ec,A)⋅NAN(324)
nB=pB(ec,B)⋅NBN(325)
D’où :
nA=8⋅π⋅mAkB3⋅T31∕2⋅ec,A⋅exp−ec,AkB⋅T1+pAB⋅zApBA⋅zB⋅exp−𝛥eAB𝜒⋅kB⋅T(326)
nB=8⋅π⋅mBkB3⋅T31∕2⋅ec,B⋅exp−ec,BkB⋅T1+pBA⋅zBpAB⋅zA⋅exp−𝛥eBA𝜒⋅kB⋅T(327)
Les équations sont paramétrées :
kB⋅T=1(328)
8⋅π⋅mA=8⋅π⋅mB=1(329)
𝜒=1(330)
Soit :
nA=ec,A⋅exp(−ec,A)1+pAB⋅zApBA⋅zB⋅exp(−𝛥eAB)(331)
nB=ec,B⋅exp(−ec,B)1+pBA⋅zBpAB⋅zA⋅exp(−𝛥eBA)(332)
Avec :
e(ec,A)=eA+ec,A−4π(333)
e(ec,B)=eB+ec,B−4π(334)

Les courbes de densités de probabilité d’énergie des états A et B sont présentées sur la Figure 46 pour quelques cas particuliers.

Figure 46.

Courbes de quelques densités de probabilité d’énergie particulières des particules A et B.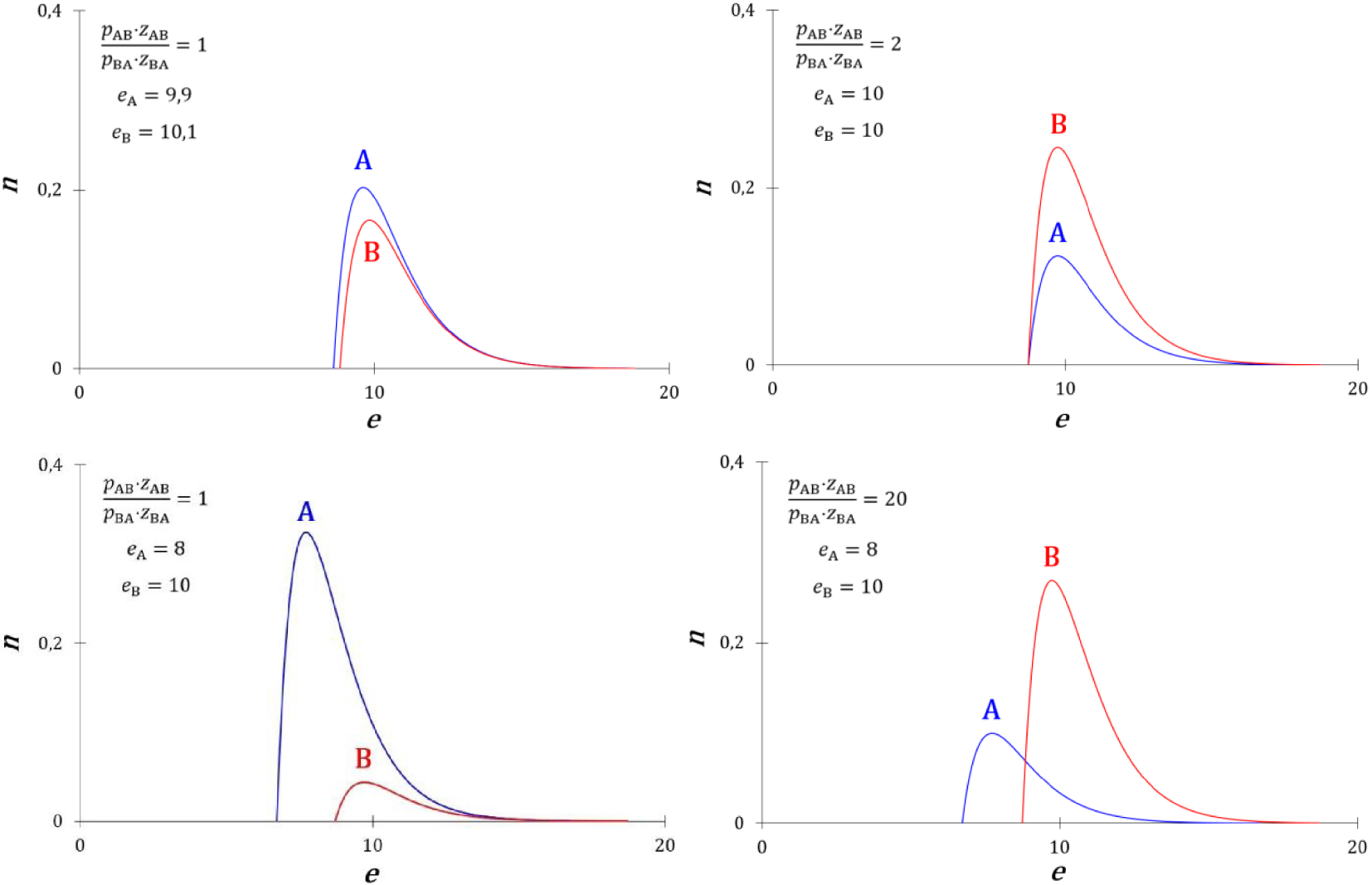

6.3. Equilibres couplés

Soit un système fermé délimité par une surface fermée, thermostaté à température T constante et de pression P ou volume V constant. Ce système est constitué de p états impliqués dans q transformations élémentaires :

∑i=1pnij+⋅Ai⇌∑i=1pnij−⋅Aijϵ[1;q](335)
Ai est l’état i et nij est le nombre d’états Ai engagés dans la transformation microscopique j. L’état est défini par la nature du système, ainsi pour une réaction chimique et une transition de phase, l’état peut être défini par une espèce chimique dans une phase définie. NAi est le nombre de particules dans l’état Ai. L’équilibre cinétique s’exprime par l’invariance du nombre de particules dans le temps pour chaque état :
dNAidteq=0iϵ[1;p](336)
Soit, en exprimant la variation du nombre de particules dans le temps en fonction des vitesses de réaction vij+ des réactifs et vij− :
∑j=1qvij,eq−−vij,eq+=0iϵ[1;p](337)
Les vitesses sont exprimées par rapport au réactif i, ainsi, les relations ci-après entre les vitesses des différents réactifs d’une même transformation sont vérifiées :
vj=vij±nij±iϵ[1;p](338)
Soit, à titre d’exemple, le système d’équilibres chimiques et de phases couplés ci-après :
A(s)⇌B(l)(1)
B(l)+C(g)⇌D(l)(2)(1)
D(l)⇌E(g)(3)(2)
2E(g)⇌F(g)(4)(3)
Le modèle cinétique distingue une espèce chimique dans deux phases de la même manière que deux espèces chimiques différentes de la même phase, il est donc possible d’écrire formellement le système précédent de la façon suivante :
A1⇌A2(1)
A2+A3⇌A4(2)(1)
A4⇌A5(3)(2)
2A5⇌A6(4)(3)
A l’équilibre :
dNA1dteq=v11,eq−−v11,eq+=0(339)
dNA2dteq=v12,eq+−v12,eq−+v22,eq−−v22,eq+=0(340)
dNA3dteq=v23,eq−−v23,eq+=0(341)
dNA4dteq=v24,eq+−v24,eq−+v34,eq−−v34,eq+=0(342)
dNA5dteq=v35,eq+−v35,eq−+v45,eq−−v45,eq+=0(343)
dNA6dteq=v46,eq+−v46,eq−=0(344)
Avec :
vij±=nij±⋅vj(345)
Les équations qui expriment l’équilibre cinétique sont indépendantes des lois cinétiques utilisées pour exprimer les vitesses de réaction. Dans les chapitres précédents, des lois cinétiques proches de la loi d’Eyring ont été utilisées pour exprimer les vitesses de la réaction chimique, de la fusion et de la solidification. Il est néanmoins possible d’utiliser d’autres lois cinétiques. Par ailleurs, la notion d’état dans cette description n’est pas exclusivement une espèce chimique dans une phase définie. Deux isomères de conformations AI et AII d’une molécule peuvent constituer deux états :
AI(g)⇌AII(g)
Soit :
A1⇌A2
De manière analogue, deux états quantiques d’un atome ou d’une molécule A𝛹I(g) et A𝛹II(g) peuvent constituer deux états :
A𝛹I(g)⇌A𝛹II(g)
Soit :
A1⇌A2
La vitesse de formation d’un produit peut dépendre de la conformation des molécules réactives :
AI(g)+B(g)⇌C(g)(1)
AII(g)+B(g)⇌C(g)(2)(1)
Soit :
A1+A3⇌A4(1)
A2+A3⇌A4(2)(1)
La vitesse d’une réaction chimique peut également dépendre de l’état quantique des molécules :
A𝛹I(g)⇌B𝛹I(g)(1)
A𝛹I(g)⇌B𝛹II(g)(2)(1)
A𝛹II(g)⇌B𝛹I(g)(3)(2)
A𝛹II(g)⇌B𝛹II(g)(4)(3)
Soit :
A1⇌A3A1⇌A4A2⇌A3A2⇌A4

Le formalisme d’écriture des équilibres cinétiques présenté dans ce chapitre n’est en pratique pas intéressant, il est en effet inconfortable pour un utilisateur de devoir consulter un tableau de correspondance des états Ai de chaque transformation du système : le dessein de ce chapitre était de montrer qu’il existe un système d’équations cinétiques adéquat pour étudier l’évolution de n’importe quel système de transformations.

6.4. Equilibres couplés cyclique et linéaire

Soit un système fermé délimité par une surface fermée, thermostaté à température T constante et de pression P ou volume V constant, constitué de N particules microscopiques qui peuvent occuper trois états. Les transitions des particules entre ces trois états sont permises (Figure 47) :

A⇌B(1)
B⇌C(2)(1)
C⇌A(3)(2)

Figure 47.

Système cyclique à trois états.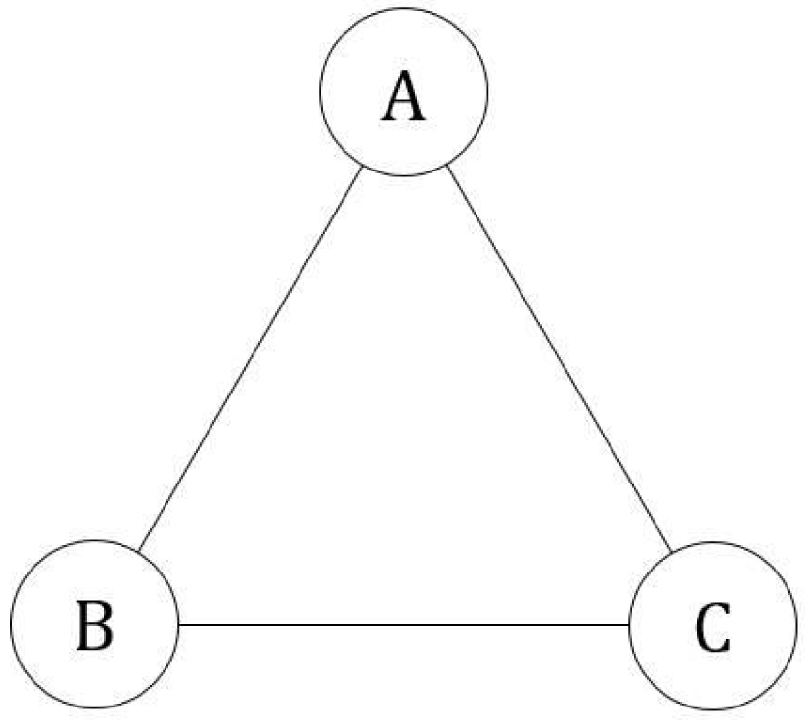

Le nombre de particules se conserve :

N=NA+NB+NC(346)
Les équations qui expriment l’équilibre cinétique sont :
dNAdteq=v1,eq−−v1,eq++v3,eq+−v3,eq−=0(347)
dNBdteq=v2,eq−−v2,eq++v1,eq+−v1,eq−=0(348)
dNCdteq=v3,eq−−v3,eq++v2,eq+−v2,eq−=0(349)
Les vitesses de transition obéissent à la loi cinétique :
v=k⋅N(350)
Soit :
k1−⋅NB,eq−k1+⋅NA,eq+k3+⋅NC,eq−k3−⋅NA,eq=0 (351)
k2−⋅NC,eq−k2+⋅NB,eq+k1+⋅NA,eq−k1−⋅NB,eq=0 (352)
k3−⋅NA,eq−k3+⋅NC,eq+k2+⋅NB,eq−k2−⋅NC,eq=0 (353)
La résolution de ce système d’équations permet de déterminer les constantes d’équilibre des trois transitions :
K1=NB,eqNA,eq=k1+⋅k2−+k1+⋅k3−+k2−⋅k3+k1−⋅k3−+k2+⋅k3−+k1−⋅k2−(354)
K2=NC,eqNB,eq=k2+⋅k3++k1+⋅k2++k1−⋅k3+k1+⋅k2−+k1+⋅k3−+k2−⋅k3+(355)
K3=NC,eqNA,eq=k2+⋅k3++k1+⋅k2++k1−⋅k3+k1−⋅k3−+k2+⋅k3−+k1−⋅k2−(356)
La constante de chaque équilibre d’un système cyclique dépend des constantes cinétiques des deux autres équilibres. Soit le cas particulier d’un système linéaire pour lequel la transition entre les états A et C est interdite (Figure 48).

Figure 48.

Système linéaire à trois états.

Ce système est le cas particulier du système cyclique à trois états lorsque k3+ et k3− sont nuls :

k3+=0(357)
k3−=0(358)
Les constantes d’équilibre de ce système sont :
K1=NB,eqNA,eq=k1+k1−(359)
K2=NC,eqNB,eq=k2+k2−(360)
La constante d’équilibre de chaque réaction du système linéaire ne dépend pas des constantes cinétiques de l’autre réaction. La connaissance de la constante d’équilibre d’une réaction chimique isolée ne peut pas être utilisée pour prédire celle de cette même réaction lorsqu’elle est impliquée dans un mécanisme réactionnel cyclique :
Kisolée≠Kcycle(361)
En revanche, la connaissance des constantes cinétiques des réactions isolées permet de déterminer les constantes d’équilibre de ces réactions lorsqu’elles sont engagées dans un mécanisme réactionnel cyclique. Par ailleurs, l’enthalpie libre cinétique définie précédemment dans cette étude pour des réactions chimiques et transitions de phase isolées ou engagées dans un mécanisme réactionnel linéaire, ne peut plus s’exprimer dans le cas d’un mécanisme cyclique par la différence entre une énergie et le produit d’une différence d’entropie cinétique avec la température :
Gcycle≠H−𝜒⋅T⋅𝛥S(362)
En effet, il n’est pas possible de factoriser par une seule fonction exponentielle les expressions des constantes d’équilibre du système réactionnel cyclique précédent. La notion d’entropie en qualité de grandeur physique que l’on pourrait isoler de l’énergie dans l’équation qui gouverne l’équilibre d’un système s’efface, il convient donc dans le cas général de renoncer à un critère d’évolution fondé sur l’entropie et d’utiliser un système d’équations cinétiques (Chapitre 6.3).

6.5. Entropie cinétique et évolution

Soit une transformation renversable entre deux états microscopiques :

X⇌Y
N particules microscopiques peuvent occuper ces états :
N=NX+NY(363)
Les vitesses de cette transformation sont :
v+=NX⋅z+⋅p+(364)
v−=NY⋅z−⋅p−(365)
z est la fréquence de collision et p la probabilité que la transformation se produise suite à une collision. A l’équilibre, ces vitesses sont égales :
veq+=veq−(366)
La constante d’équilibre se déduit de cette égalité :
K=NY,eqNX,eq=z+⋅p+z−⋅p−(367)
Soit un catalyseur C qui altère la cinétique de cette transformation dans un seul sens, comme l’enzyme qui catalyse la transestérification de Fischer (Chapitre 3.5) :
zC+>z+(368)
zC−=z−(369)
La constante d’équilibre de la transformation catalysée est donc plus élevée :
KC>K(370)
Cette transformation microscopique catalysée est schématisée sur la Figure 49.

Figure 49.

Schéma d’une transformation microscopique catalysée.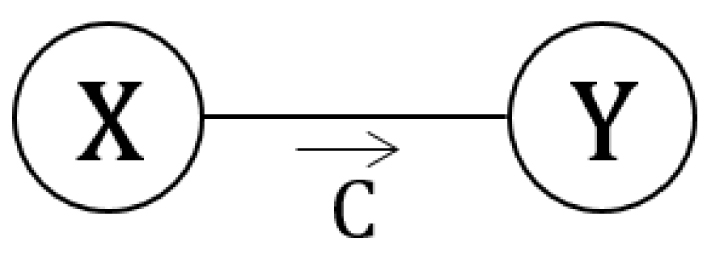

Soit un système constitué de particules engagées dans des transformations couplées dont certaines sont catalysées, les particules sont initialement dans l’état A (Figure 50).

Figure 50.

Système de transformations couplées dont certaines sont catalysées (flèches).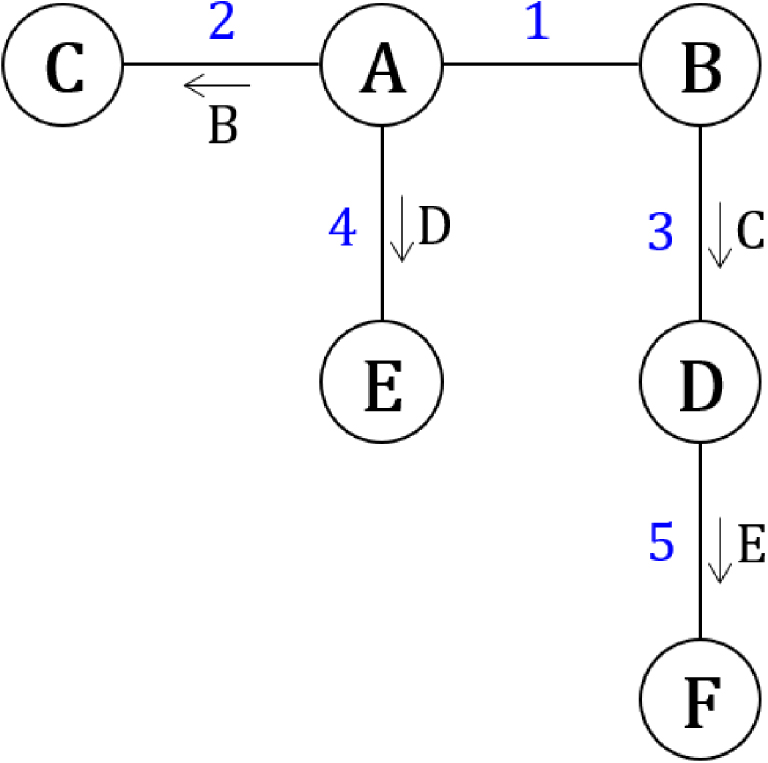

Si les constantes des équilibres avec catalyseur sont grandes devant celles des équilibres sans catalyseur, ce système évoluera de manière privilégiée en suivant l’ordre indiqué par les chiffres bleus. Le système ne pourra pas évoluer de A à C sans passer par B (étape 1), il ne pourra pas non plus évoluer de B à D sans passer par C (étape 2), et ainsi de suite. Dans le cas où un état est engagé dans deux transformations catalysées par des particules qui occupent un été particulier, le système évoluera de manière privilégiée vers la transformation dont l’espèce catalytique est apparue en premier (Figure 51), comme dans le cas de la cristallisation d’une seule des deux formes chirales de sels à partir du premier germe cristallin (Chapitre 5.9).

Figure 51.

Evolution irréversible d’une transformation vers l’état occupé en premier.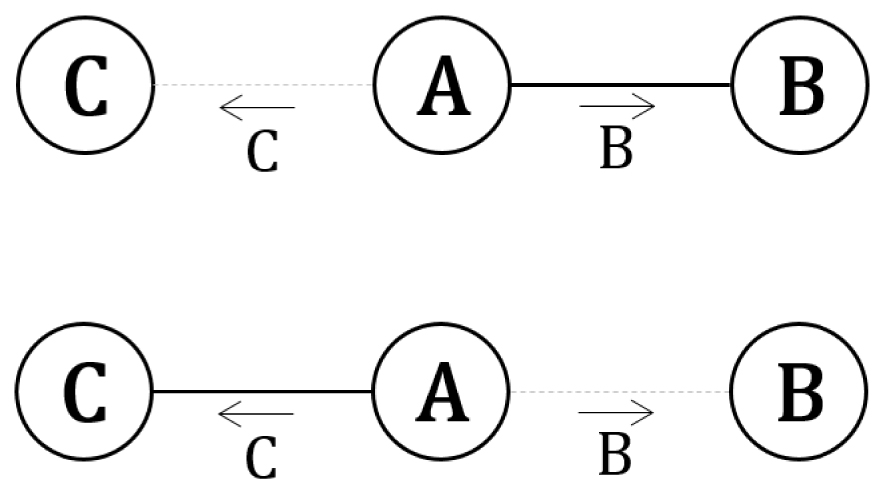

Un tel phénomène constitue une bifurcation chimique.

6.6. Synthèse

La nature de l’entropie cinétique a été précisée dans ce dernier chapitre :

« Soit un système constitué de N particules engagées dans une transformation entre deux états, à pression (ou volume) et température constantes :

A⇌B
𝛥rE=𝛥rU(T,V)=𝛥rH(T,P)(371)
Il existe une grandeur𝛥rSsans dimension, appelée entropie cinétique de réaction, telle que le système évoluera jusqu’à ce que la fonction ci-après soit nulle :
𝛥rE−𝜒⋅Ec⋅𝛥rS(372)
𝜒est la fraction de l’énergie cinétique de translation des particules engagée dans la transformation. L’entropie cinétique de la transformation à l’équilibre est le rapport entre l’énergie 𝛥r Ede la transformation et l’énergie cinétique 𝜒⋅Ec engagée dans la transformation :
𝛥rSeq=𝛥rE𝜒⋅Ec(373)
0<𝜒⩽1(374)
Le caractère irréversible d’une transformation est corrélé à la variation de son entropie cinétique :
d𝛥rS−𝛥rE𝜒⋅Ecdt<0 »(375)

Une loi de Boltzmann thermique et cinétique a été établie :

« Soit un système constitué de N particules sphériques engagées dans une transformation entre deux états, à pression (ou volume) et température constantes :

A⇌B
Les densités d’énergie des particules dans les états A et B sont respectivement :
nA=8⋅π⋅mAkB3⋅T31∕2⋅ec,A⋅exp−ec,AkB⋅T1+pAB⋅zApBA⋅zB⋅exp−𝛥eAB𝜒⋅kB⋅T(376)
nB=8⋅π⋅mBkB3⋅T31∕2⋅ec,B⋅exp−ec,BkB⋅T1+pBA⋅zBpAB⋅zA⋅exp−𝛥eBA𝜒⋅kB⋅T(377)
z est la fréquence de collision et p la probabilité que la transition d’une particule entre les deux états suite à une collision se produise indépendamment de l’énergie engagée dans la transition. »

Un système d’équations cinétiques permettant l’analyse de n’importe quel système de transformations couplées a été établi :

« Soit un système fermé délimité par une surface fermée, thermostaté à température T constante et de pression P ou volume V constant. Ce système est constitué depétats impliqués dansqtransformations élémentaires :

∑i=1pnij+⋅Ai⇌∑i=1pnij−⋅Aijϵ[1;q](378)
Aiest l’étatietnijest le nombre d’états Ai engagés dans la transformation microscopiquej. NAi est le nombre de particules dans l’état Ai. L’équilibre cinétique s’exprime par l’invariance du nombre de particules dans le temps pour chaque état :
dNAidteq=0iϵ[1;p](379)
Soit, en exprimant la variation du nombre de particules dans le temps en fonction des vitesses de réactionvij+ des réactifs etvij− :
∑j=1q(vij,eq−−vij,eq+)=0iϵ[1;p](380)
Les vitesses sont exprimées par rapport au réactif i, ainsi, les relations ci-après entre les vitesses des différents réactifs d’une même transformation sont vérifiées :
vj=vij±nij±iϵ[1;p]»(381)

L’étude de systèmes de transformations couplées linéaire et cyclique montre que la connaissance de la constante d’équilibre d’une transformation isolée ne peut pas être utilisée pour déterminer la constante d’équilibre de cette transformation dans le cas général lorsque celle-ci est couplée à d’autres transformations. En revanche, la connaissance des constantes cinétiques est utilisable pour ce dessein. L’entropie d’un système de réactions couplées ne peut pas être isolée de l’énergie dans l’équation qui gouverne l’équilibre. L’existence d’une grandeur physique unique de nature entropique dont le sens de variation gouverne l’évolution d’un système est remise en cause par la description cinétique des équilibres.

Enfin, le modèle cinétique constitue un outil analytique permettant d’appréhender l’évolution de systèmes complexes incluant des bifurcations.

7. Conclusions et perspectives

7.1. L’erreur historique de Gibbs

Les différences entre le modèle cinétique de l’équilibre chimique présenté dans cette étude et le modèle thermodynamique sont colossales. En effet, les deux descriptions ne sont pas compatibles car les propriétés d’une des deux grandeurs fondamentales qui gouverne l’évolution, l’entropie, est fondamentalement différente. Le premier grand succès de Williard Gibbs, en 1873, fut l’étude de l’évolution de fluides avec une fonction mathématique de l’énergie et de l’entropie découverte quelques décades auparavant par Rudolph Clausius. Après le succès éclatant de ses travaux sur les fluides, en 1876, la tentation de Williard Gibbs fut d’utiliser l’entropie, de nature calorimétrique, pour prévoir l’évolution des réactions chimiques et transformation de phases, puisque ces transformations s’accompagnent dans le cas général d’échanges de chaleur. La question qui se pose est :

« Pourquoi l’entropie calorimétrique ne serait-elle pas appropriée pour décrire l’évolution de transformations microscopiques ? »

Autrement formulée :

« Pourquoi l’entropie cinétique serait plus appropriée que l’entropie calorimétrique pour décrire l’évolution de transformations microscopiques ? »

Un échange de chaleur se distingue fondamentalement d’une réaction chimique à l’échelle microscopique. En effet, lors de la collision de deux molécules ou atomes réactifs, l’échange d’énergie thermique (i.e. énergie cinétique) est un évènement certain alors que la réaction chimique est un évènement probable (Figure 52).

Figure 52.

L’échange d’énergie des atomes ou molécules réactives A et B lors d’une collision est certain alors que la réaction est seulement probable.

Le modèle thermodynamique physique statistique ne prend pas plus en compte que la thermodynamique de Gibbs cette différence fondamentale : les fonctions d’état F et G sont établies en physique statistique pour le gaz parfait, puis extrapolées aux réactions chimiques et équilibres de phases. A contrario, le modèle cinétique de l’équilibre chimique est construit en introduisant un terme probabiliste dans l’équation élémentaire de l’équilibre : la réaction suite à une collision entre les atomes ou molécules A et B n’est pas certaine. L’équation de l’équilibre cinétique pour un nombre élevé de particules est fondée sur le comportement de ce système élémentaire et prend donc intrinsèquement en compte la différence fondamentale entre échange de chaleur et réaction chimique à l’échelle microscopique en termes de probabilités.

7.2. Les états inaccessibles

Au-delà des performances prédictives satisfaisantes de systèmes réels, la description cinétique des évolutions ouvre de nouvelles frontières. En effet, elle offre un degré de liberté de plus que l’approche thermodynamique chimique, celui de considérer que les produits d’une réaction chimique ne dépendent pas des stabilités intrinsèques des réactifs et produits, mais des vitesses à laquelle ils se forment et disparaissent, elles-mêmes dépendantes de l’environnement.

« Dis-moi à quelle vitesse tu te formes, je te dirais si tu es. »

« Dis-moi où tu te formes, je te dirais qui tu es. »

De ce fait, la description cinétique de l’équilibre chimique permet d’atteindre des états (molécule, polymorphe d’un cristal, conformation d’une molécule) qui sont inaccessibles, d’un point de vue conceptuel, à la thermodynamique, qui statue qu’une espèce chimique ou une phase est intrinsèquement stable ou instable.

7.3. Entropie cinétique et évolution

Un aspect intéressant qui émerge de la description cinétique des transformations microscopiques est la catalyse entropique, qui permet d’appréhender rationnellement le phénomène de bifurcation chimique d’un système de transformations microscopiques couplées : l’évolution d’un système vers une des voies qui s’offrent à lui est gouvernée par la nature de l’environnement chimique à l’instant où ces possibilités se présentent.

Remerciements

Les fondements utilisés dans le modèle cinétique de l’équilibre microscopique présenté dans cette étude sont issus de deux ouvrages de thermodynamique écrits en langue française : Eléments de thermodynamique statistiques [15] (1963), d’Adolphe Pacault et Thermodynamique, fondements et applications [4, 5, 83] (2001) de José-Philippe Pérez. La très grande clarté de ces deux ouvrages permet d’accéder sûrement à la connaissance des fondements de la thermodynamique à l’équilibre et de la physique statistique.

L’accès à des ouvrages récents et anciens et à des données expérimentales thermodynamiques a été possible grâce à l’accès ouvert de ressources numériques du World Wide Web, nous remercions le National Institute of Standards and Technology, la Dortmund Data Bank, la Bibliothèque Nationale de France pour l’accès Gallica aux fonds anciens et Ressource Canada.

Nous remercions les nombreuses personnes qui ont participé à l’éclosion de ce modèle. Nos collègues chercheurs pour leur écoute et leurs critiques constructives. Sophie Griveau, Virginie Lair et Gérard Côte de Chimie ParisTech, Jean-Christophe Lacroix, François Maurel et Michel Petitjean de l’Université Paris Diderot et Bernard Roques de l’Université Paris Descartes. Nos collègues du service de Technologies de l’Information et de la Communication pour l’Enseignement de la Faculté de Pharmacie de Paris qui ont réalisé le film de la première conférence de la description cinétique des équilibres le 12 janvier 2017[84], Stéphane Carraz, Alexandre Lacroix et Damien Renouf. Nos collègues des services de communication pour en avoir assuré sa diffusion, Samantha Conti de la Faculté de Pharmacie de Paris, Gwenaëlle Hennequin de Chimie ParisTech et Myriam Denis Ledru de l’Université de Versailles Saint-Quentin-en-Yvelines. Les documentalistes associés à nos établissements pour leur pugnacité et leur infatigabilité à localiser éditions rares et ouvrages anciens, Didier Partouche, Alain Delaforge et Eric Varon de la Bibliothèque Universitaire de Santé de Faculté de Pharmacie de Paris, Pascale Boi-Cuzin, Amélie Dessens et Sandrine Mouret de Mines ParisTech et Nathalie Queyroux de la Bibliothèque de Sciences Expérimentales de l’Ecole Normale Supérieure de Paris. Dominique Vichard, de l’Université de Versailles Saint-Quentin-en-Yvelines pour son soutien et Isabelle Gonne pour la relecture consciencieuse de ce manuscrit.

Annexes

Supporting information for this article is available on the journal’s website under https://doi.org/10.5802/crchim.40.

1L’énergie interne est notée E dans la formulation historique du potentiel chimique.

2La notation T′ permet de distinguer la température du terme intégré de celle de la borne supérieure de l’intégrale.

3La nature de la phase ne sera pas précisée dans ce chapitre, afin de ne pas alourdir le formalisme des équations, puisqu’il n’y a qu’une seule phase.

4Les équilibres de fusion entre un polymorphe métastable et un liquide peuvent être décrits par l’approche cinétique présentée dans ce chapitre, en revanche la description cinétique de la transition solide–solide entre un polymorphe métastable et un polymorphe stable n’est pas abordée.

5La constante de proportionnalité du terme 𝜒 de cette équation, comparativement à celui de l’équilibre chimique précédent, a été modifiée de manière à exprimer l’équation d’évolution cinétique en fonction d’une fraction de l’énergie cinétique.

Bibliographie

[1] C. Gregory Encyclopædia Universalis, 19 (1975), pp. 1235-1236

[2] C. Gregory Encyclopædia Universalis, 16 (1973), pp. 29-31

[3] J. R. Mayer Annalen der Chemie und Pharmazie (1842), pp. 233-240

[4] J. P. Pérez Thermodynamique, fondements et applications, Dunod, Paris, 2011 (89-102)

[5] J. P. Pérez Thermodynamique, fondements et applications, Dunod, France, 2011 (103-126)

[6] S. Carnot Réflexions sur la puissance motrice du feu et sur les machines propres à développer cette puissance, Chez Bachelier, Paris, France, 1824 | Zbl

[7] C. Gregory Encyclopædia Universalis, 6 (1972), pp. 308-311

[8] W. Gibbs Trans. Connecticut Acad., 2 (1873), pp. 382-404

[9] W. Gibbs Trans. Connecticut Acad., 3 (1876), pp. 198-524

[10] W. Gibbs Equilibre des systèmes chimiques, Georges Carré et C. Naud, Paris, 1899

[11] I. Schröder Z. Phys. Chem., 11 (1893), pp. 449-465

[12] H. Han; D. Li; L. Guo; Y. Yao; H. Yang; D. Zeng J. Chem. Eng. Data, 60 (2015), pp. 1139-1145

[13] M. Berthelot; L. D. Péan de Saint-Gilles C. R. Acad. Sci., Paris, 56 (1863), pp. 393-397

[14] G. N. Lewis; M. Randall Thermodynamics and the free energy of chemical substances, McGraw Hill Book Company, New York, 1923

[15] A. Pacault Eléments de thermodynamique statistique, Masson, Paris, 1963 (190-193) | Zbl

[16] F. G. Keyes J. Am. Chem. Soc., 49 (1927), pp. 1393-1403

[17] M. Margules Sitz.ber., Kaiserl. Akad. Wiss. Wien, Math. Nat.wiss. Kl. 2a, 104 (1895), pp. 1243-1278

[18] D. S. Abrams; J. M. Prausnitz AIChE J., 21 (1975), pp. 116-128

[19] A. Klamt; J. P. G. Krooshof; R. Taylor Ross AIChE J., 48 (2002), pp. 2332-2349

[20] E. Clapeyron (Mémoire sur la puissance motrice de la chaleur, Journal de l’école royale polytechnique, vingt-deuxième cahier, tome XIV, Paris, 1833)

[21] J. G. Calvert Pure Appl. Chem. (1990), pp. 2167-2219 (2196)

[22] (The International System of Units, 9 ème éd., Bureau International des Poids et Mesures, France, 2019)

[23] L. Boltzmann Vorlesugen über gastheorie part I, J. A. Barth, Leipzig, 1895

[24] L. Boltzmann Vorlesugen über gastheorie part II, J. A. Barth, Leipzig, 1898

[25] L. Boltzmann Leçons sur la théorie des gaz, Imprimerie Gauthier-Villars, Paris, 1903

[26] K. R. Popper Conjectures and Refutations, The growth of scientific knowledge, Basic Books, New York, London, 1962 | MR

[27] K. J. Laidler PAC, 68 (1996), pp. 149-192

[28] M. Trautz Z. Anorg. Allg. Chem., 96 (1916), pp. 1-28

[29] H. Eyring J. Chem. Phys., 3 (1935), p. 107

[30] E. Junquera; E. Aicart J. Chem. Ed., 77 (2000), pp. 1215-1217

[31] H. J. Bart; J. Reidetschláger; K. Schatka; A. Lehmann Ind. Eng. Chem. Res., 33 (1994), pp. 21-25

[32] N. Calvar; B. González; A. Dominguez Chem. Eng. Process., 46 (2007), pp. 1317-1323

[33] R. He; Y. Zou; Y. Dong; Y. Muhammad; S. Subhan; Z. Tong Chem. Eng. Res. Des., 137 (2018), pp. 235-245

[34] B. Helge Hoff; L. Ljones; A. Rønstad; T. Anthonsen J. Mol. Catal., B, 8 (2000), pp. 51-60

[35] M. H. Kim; C. S. Kim; H. W. Lee; K. Kim J. Chem. Soc. Faraday Trans., 92 (1996), pp. 4951-4956

[36] P. Mateus; R. Delgado; P. Brandão; V. Felix J. Org. Chem., 77 (2012), pp. 4611-4622

[37] P. K. Dasgupta; O. Nara Anal. Chem., 62 (1990), pp. 1117-1122

[38] M. L. Lugo; V. R. Lubes J. Chem. Eng. Data, 52 (2007), pp. 1217-1222

[39] S. Espinosa; E. Bosch; M. Rosés Anal. Chem., 74 (2002), pp. 3809-3818

[40] M. M. Khalil; A. M. Radalla; N. M. Abd Elnaby J. Solut. Chem., 42 (2013), pp. 1123-1145

[41] J. S. Lomas J. Phys. Org. Chem., 25 (2012), pp. 620-627

[42] E. Gelles; G. H. Nancollas Trans. Faraday Soc., 52 (1956), pp. 680-685

[43] G. Körtum; W. Vogel; K. Andrussow Dissociation Constants of Organic Acids in Aqueous Solution, Butterworths, London, 1961

[44] G. H. Mansfield; M. C. Whiting J. Chem. Soc., 1956, pp. 4761-4764

[45] W. L. German; A. I. Vogel J. Am. Chem. Soc., 58 (1936), pp. 1546-1549

[46] Y. Chen; H. Wang; J. Wang J. Phys. Chem. B, 118 (2014), pp. 4630-4635

[47] A. M. Radalla J. Solut. Chem., 39 (2010), pp. 1394-1407

[48] A. D. Headley; S. D. Starnes; L. Y. Wilson; G. R. Famini J. Org. Chem., 59 (1994), pp. 8040-8046

[49] G. H. Jeffery; A. I. Vogel J. Chem. Soc., 1935, pp. 21-30

[50] R. Gane; C. K. Ingold J. Chem. Soc. (1931), pp. 2153-2169

[51] IUPAC (28/11/2016) Periodic table of the elements ; https://iupac.org/wp-content/uploads/2015/07/IUPAC_Periodic_Table-28Nov16.pdf

[52] G. J. Janz J. Phys. Chem. Ref. Data, 17 (1988), pp. 1-309

[53] A. D. Pelton; S. N. Fleng Can. J. Chem., 48 (1970), pp. 3483-3486

[54] O. Kubaschewski; E. L. Evans Metallurgical Thermochemistry, Pergamon, London, 1974

[55] P. M. Nasch; S. G. Steinemann Phys. Chem. Liq., 29 (1995), pp. 43-58

[56] S. Sternberg; L. Bejan J. Chem. Thermodyn., 2 (1970), pp. 341-349

[57] W. Wagner; A. Pruß J. Phys. Chem. Ref. Data, 31 (2002), pp. 387-535

[58] W. F. Giauque; J. W. Stout J. Am. Soc., 58 (1936), pp. 1144-1150

[59] D. Li; D. Zeng; X. Yin; H. Han; L. Guo; Y. Yao CALPHAD, Comput. Coupling Phase Diagr. Thermochem., 53 (2016), pp. 78-89

[60] A. C. Belch; M. Berkowitz; J. A. McCammon J. Am. Chem. Soc., 108 (1986), pp. 1755-1761

[61] C. P. Petersen; M. S. Gordon J. Phys. Chem. A, 103 (1999), pp. 4162-4166

[62] N. Hossein; B. C. Teoh; L. Davis Clements J. Am. Oil Chem. Soc., 69 (1992), pp. 1184-1188

[63] I. Tohru; H. Yusuke; I. Ruri; S. Masao Chem. Phys. Lipids, 127 (2004), pp. 161-173

[64] M. Lazerges; Y. Corvis; E. Pardieu; L. Bouteiller; P. Espeau Fluid Phase Equilib., 315 (2011), pp. 107-112

[65] M. Lazerges; I. Rietveld; Y. Corvis; R. Ceolin; P. Espeau Thermochim. Acta, 497 (2010), pp. 124-128

[66] M. Lazerges; P. Espeau; S. Crauste-Manciet; D. Brossard; Y. Corvis; N. Huang; F. Agnely, 2013 (WO2013083910 A)

[67] R. J. Jakobsen; Y. Mikawa; J. W. Brasch Spectrochim. Acta A, 23 (1967), pp. 2199-2209

[68] M. Bambagiotti-Alberti; B. Bruni; M. Di Vaira; V. Giannellini; A. Guerric Acta Cryst. E, 63 (2007), pp. 768-770

[69] I. Prigogine; R. Defay Thermodynamique chimique, Editions Desoer, Liège, 1950 (397-398)

[70] X. Wang; X. Zhang; S. Black; L. Dang; H. Wei J. Chem. Eng. Data, 57 (2012), pp. 1779-1786

[71] H. Lorenz; D. Sapoundjiev; A. Seidel-Morgenstern J. Chem. Eng. Data, 47 (2002), pp. 1280-1284

[72] H. Sawamura Trans. Jpn. Inst. Met., 13 (1972), pp. 225-230

[73] F. D. Rossini; D. D. Wagman; W. H. Evans; S. Levine; I. Jaffe Selected Values of Chemical Thermodynamic Properties, Circular of the National Bureau of Standards, United State Printing Office, Washington, 1952 (500)

[74] K. K. Kelley Contributions to the Data on Theoretical Metallurgy, Bureau of Mines, United States Printing Office, Washington, 1960 (584)

[75] J. C. S. Costa; A. Mendes; L. M. N. B. F. Santos J. Chem. Eng. Data, 63 (2018), pp. 1-20

[76] M. Kano Netsu Sokutei, 18 (1990), pp. 64-70

[77] N. R. Gokhale J. Atmos. Sci., 22 (1963), pp. 212-216

[78] L. Karmakar; D. Das J. Alloys Compd., 767 (2018), pp. 642-650

[79] W. H. Qi Physica B, 368 (2005), pp. 46-50

[80] Z. Zhang; X. X. Lu; K. Q. Jiang Physica B, 270 (1999), pp. 249-254

[81] S. C. Abrahams; J. L. Bernstein Acta Crystallogr. B, 33 (1977), pp. 3601-3604

[82] D. K. Kondepudi; R. J. Kaufman; N. Singh Science, 250 (1990), pp. 975-976

[83] J. P. Pérez Thermodynamique, fondements et applications, Dunod, France, 2011 (25-41)

[84] S. Marque; M. Lazerges Théorie interfaciale collisionnelle, Chimie Paristech, Paris (12/01/2017) : https://mediasd.parisdescartes.fr/#/collection?id=TJ3-aRhkkXQx_

Commentaires - Politique

Ces articles pourraient vous intéresser

Effect of diffusional bridging in multicapillary packing

François Parmentier

C. R. Chim (2020)

Bregman divergences for physically informed discrepancy measures for learning and computation in thermomechanics

Stéphane Andrieux

C. R. Méca (2023)

Risk-averse estimates of effective properties in heterogeneous elasticity

Jeremy Bleyer

C. R. Méca (2023)