1 Introduction
For approximately ten years, the numerical models of convection have shown the importance of the main mantle phase transitions for global convection studies. The olivine-spinel phase change at 400 km depth is exothermic, which facilitates convection through upper mantle. On the contrary, the spinel–perovskite phase change at 660 km is endothermic, which can slow down or even stop the rising and the sinking convection currents at the discontinuity level [15].
The numerical models, which have taken these phase changes into account, agree to depict intermittent pattern of mantle convection according to the level of endothermicity of the spinel → perovskite phase change. Such a regime, which has been found with independent 2D, spherical [15,16], 3D, spherical [14,22], and 2D and 3D Cartesian geometry [8,25], is very robust, since it has been encountered with internal heating rates varying from 0 to chondritic, viscosity stratification and pressure and temperature dependence of viscosity [2]. Within a 2D or 3D spherical, inelastic framework, whole mantle convection is prevailing for a Clapeyron slope lower than . Conversely, it is two-layered for more endothermic reaction. Thus, for a sinking (resp. rising) convection current, the density jump at 660 km resists to flow penetration. Indeed, as the Clapeyron's pressure, necessary to complete the phase change, corresponds, at this colder (resp. higher) temperature, to a depth deeper (resp. shallower) than the actual surrounding density jump, the density contrast may block convection that may spread horizontally.
The agreement between these numerical models does not mean that the answer about the mantle structure is definitively known, but that all these models give a coherent representation of the phase-change effects in terms of physic of fluid. The geoid retrieving by circulation models [23] and the tomographic imaging of deep slabs plunging into the lower mantle argue in favour of a present one- or partially-layered mantle structure [18,24]. This present state results from the long process that has been acting since the early Earth. At this epoch, the huge quantity of heat accumulated during the accretion and the higher radioactive release of energy were heating the mantle, which was necessarily hotter and less viscous than today. Then, the Rayleigh number of this primitive earth was therefore higher than the present one, which has been shown to induce layering of convection [20,21,27,28]. A continuous evolution, from early layered mantle convection to whole mantle, or partly layered mantle structure, implies that we are presently in an avalanche-like regime or, at least, that it has been encountered during the past.
2 Mechanism of the mantle avalanches
The resolution of the full set of convection equations, including the Navier–Stokes equation, but also the non-linear energy equation, is very expensive in terms of computer time and generates huge quantities of data, which cannot be recorded in details. In order to deepen the preliminary results obtained during previous studies [2,3], a new series of axisymmetrical, spherical convection models have been computed to quantify the potential effects of mantle avalanches on the global thermal and dynamical states of the mantle. The numerical code takes into account an exothermic phase change at 400 km, an endothermic phase change at 660 km, a temperature- and pressure-dependent viscosity and a viscosity jump of 30 between the upper and lower mantle. A more detailed description of the physical hypothesis and of the numerical method can be found in our previous work [2].
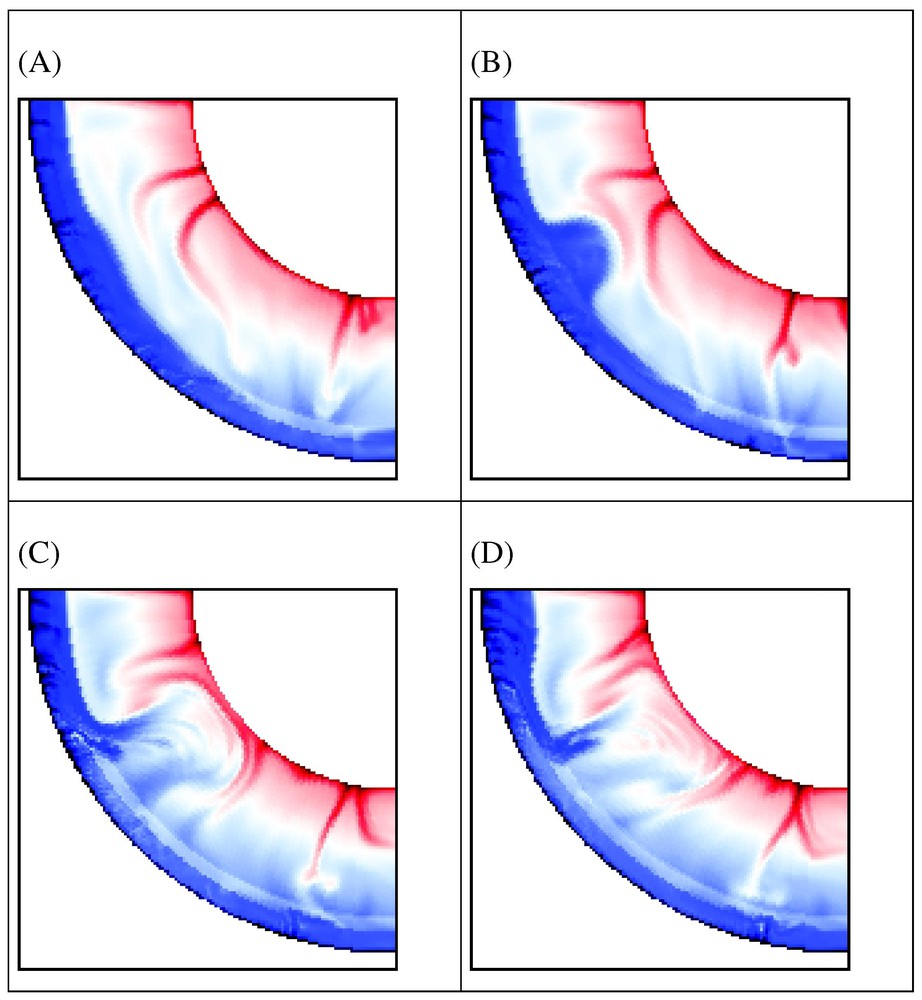
Fig. 1 displays the various types of avalanches that have been encountered during the computation. An animated sequence can be found at the web address: http://www.isteem.univ-montp2.fr/PERSO/machetel/anim.html. The occurrence of the avalanches is a temporally chaotic process, which illustrates the compromise between a global thermal state of the mantle and its local recent history. Fig. 1 (and animation) shows that an avalanche may occur at a fixed location (Fig. 1a), cease and reappear at almost the same place (Fig. 1b). However, it also can start as an unexpected event over a weak zone created by plumes rising from lower mantle (Fig. 1c).

Computed temperature field at 210 Myr (computation time) (panel a), 624 Myr (panel b) and 810 Myr (panel c). Computation has been restarted from (time arbitrary set to 0) after the occurrence of a first very powerful avalanche. The theoretical model includes compressibility; internal and basal heating; a viscosity jump of 30 between the upper and lower mantle; pressure and temperature dependent viscosity; an endothermic phase change at 660 km and an exothermic phase change at 400 km. Panel a shows that an avalanche may occur at a fix location, cease and reappear at an almost contiguous place (panel b). It also can also start, as an unexpected event, over a weak zone destabilized by a hot lower mantle rising plume (panel c).
Champ de température obtenu après 210 Ma (a), 624 Ma (b) et 810 Ma (c). Le calcul a été réinitialisé (origine arbitraire du temps) après une première avalanche très puissante. Le modèle numérique prend en compte la compressibilité du manteau, un mode de chauffage mixte radioactif et basal, un contraste de viscosité de 30 entre le manteau supérieur et le manteau inférieur, un changement de phase endothermique à 660 km de profondeur et un changement de phase exothermique à 400 km de profondeur. La partie (a) montre que les avalanches peuvent survenir de manière répétitive au même emplacement, cesser, puis réapparaı̂tre presque au même endroit (b). Elles peuvent également démarrer de manière inattendue à partir d'une zone de faiblesse, rendue instable par la présence d'un panache chaud du manteau inférieur (c).
In all the cases, the mantle avalanches follow cycles based on four main phases.
1. A local layering of convection occurs, which is illustrated by the stopping of the upper mantle sinking currents. Simultaneously, the insulation due to the layering prevents the heat from escaping, which induces a warming and a softening of the lower mantle. Simultaneously, convection cools and hardens the upper mantle. Both effects result in the growing of a thermal layer at the 660-km level. A new avalanche will shortly be generated by this increasingly unstable evolution (Fig. 2A) [4].
The global sequence that characterizes the avalanche phenomena is: (A) local layering of convection; (B) destabilization of the 670 boundary and brutal advection of cold upper mantle convective structure (the avalanche itself); (C) spreading of the avalanche on the core and surface arrival of return flows; (D) restoration of local layering which marks the end of the avalanche.
Les événements qui caractérisent le phénomène d'avalanche se déroulent ainsi : (A) mise en couches partielle de la convection entre manteau supérieur et manteau inférieur ; (B) déstabilisation de la couche limite thermique à 670 km et advection brutale dans le manteau inférieur de matière froide en provenance du manteau supérieur ; (C) arrivée de l'avalanche au niveau du noyau et des courants de retour au niveau de la surface ; (D) le retour d'une mise en couche partielle marque la fin de l'avalanche.
2. The destabilization of the 660-km thermal layer, which has occurred, is now accelerated by the brutal advection of cold upper mantle material (the avalanche itself). The surrounding upper mantle is drawn toward the avalanche epicentre, while hot rising currents, originating from lower mantle, cross upward the 660-km discontinuity to compensate the effect of the avalanche (Fig. 2B). This mechanism generates violent, rising widely distributed plumes, originating just below the 660-km phase-change level.
3. The sinking avalanche travels the lower mantle and, after a few tens of million years, spreads on the core by sweeping the (softer) CMB boundary layer. Conversely, the return flows provoke the re-heating of the upper mantle and local decreases of the viscosity, which amplify the viscosity contrasts through the 660-km phase change. The approximate synchronization of the avalanche spreading onto the core and of the return flow emergence at the surface is due to a focalization of the sinking avalanche, while the return flows are diffuse over all the 660-km phase-change spherical surface (Fig. 2C).
4. The local layering reappears, while no more upper mantle material sinks into the lower mantle (or at low rate), which also stops (or reduces) the return flows. As the avalanche is no longer fed by cold upper-mantle cold matter, the internal heating and the core heat reheat the lower mantle and reduce the CMB thermal gradient (Fig. 2D). A new cycle is ready to start.
3 Thermal consequences of the avalanche
In a recent work, we have monitored in details the evolution of the mantle temperature during an avalanche. The return flows rise the upper mantle temperature by about 50 to 70 °C, while the lower mantle is simultaneously cooled by the avalanche [12]. It is interesting to note that this process has probably acted as a regulator for the global mantle temperature through the long-term history of the Earth. Indeed, it is probable that as early as the avalanche regime has been established in the past, the thermal layer at the 660-km phase-change level has been recursively destroyed as soon as it was becoming unstable. Within this context, the mantle convection is characterized by quiet periods of partial layering embedded in catastrophic events. Fig. 3 (top) displays the flux of matter that has crossed the 660-km phase change (solid line), and the bottom heat flux versus time (dashed line). During the avalanche, the bottom heat flux remains strong, as a consequence of steep thermal gradient at the CMB level [2]. However, it decreases to reach a low level during the quiet period. Bottom panel of Fig. 3 allows comparing the heat fluxes that simultaneously cross the upper surface and the bottom. Both heat fluxes display the same decreasing trend during the quiet period, but their global shapes are very different, since the signal seems smoother for the bottom heat flux than for the surface heat flux. The bottom heat flux varies in response to the arrival of the cold material of the avalanche, which lowers mantle temperature, and consequently increases the heat flux through the bottom surface. The upper surface heat flux displays a more complex behaviour, because two different kinds of lower mantle return flows act to reheat the upper mantle. Those of the first type start, from the 660-km phase-change level, simultaneously with the beginning of the avalanche, for mass conservation reasons. This can be deciphered on the bottom part of Fig. 3, around time 600 Myr, when the surface heat flux increases in response to the starting of a new avalanche. The delay between the surface heat flow and the flux through the 660-km phase change corresponds to the transfer time of return flow from 660 km to the surface. The explanation of the increase of heat flux around 350 Myr is less obvious. It is due to the arrival at the surface of plumes created at the CMB by the sweeping effect of the sinking avalanche. Indeed, when the cold material of the avalanche arrives on the CMB surface, it creates a strong temperature gradient that results in violent plume rising from the CMB. We are going to verify this hypothesis on a longer computation time, in order to check this behaviour of the surface heat flux for several avalanches. The geomagnetic field reversal stopping during the superchron periods may probably be explained by the temperature perturbations of the CMB, occurring with the spreading of the avalanche onto the core [7]. This event may be embedded by superplume activity, which is due to return flows starting from transition zone. Then, the plumes reach the surface just before the beginning of the superchron. Conversely, the superplume activity, due to the spreading of the avalanche on the CMB thermal layer, reaches the surface after the end of the superchron.
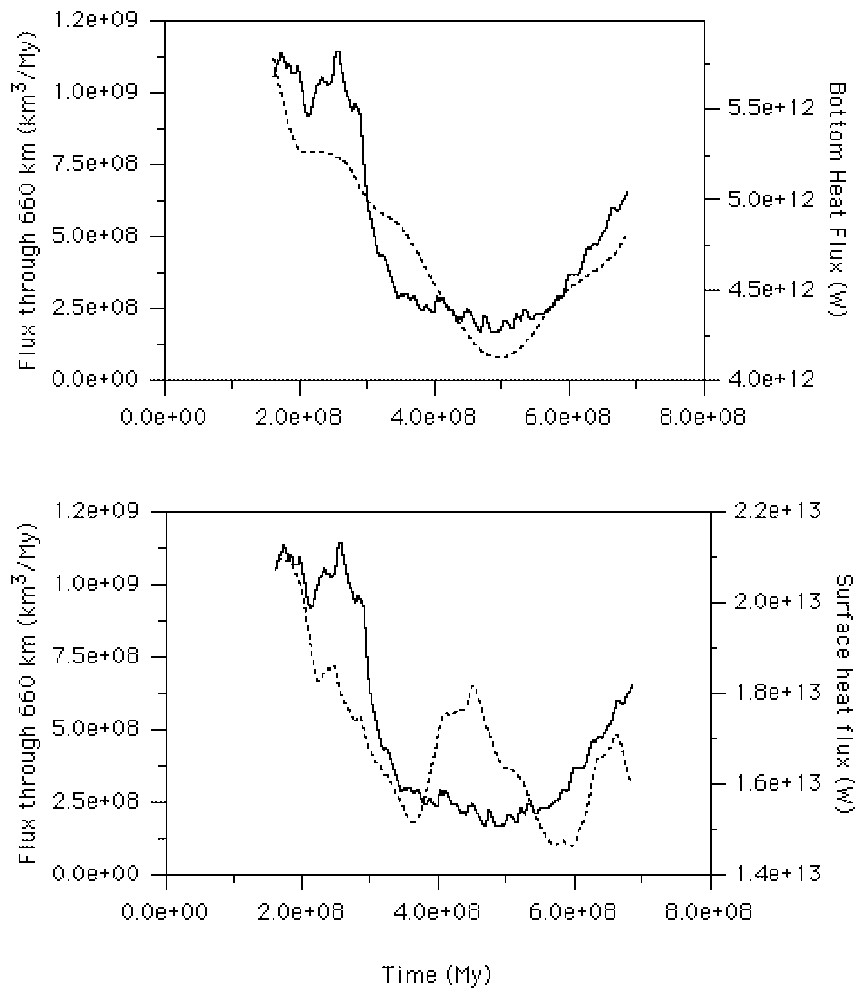
Top: flux of matter through the 660-km phase change (solid line) and heat flux through the bottom surface (dashed line); bottom: comparison between the bottom and surface heat fluxes.
Haut : flux de matière au travers du changement de phase des 660 km (ligne continue) et flux de chaleur à travers la surface inférieure. Bas : comparaison des flux de chaleur au travers de la surface supérieure et de la surface inférieure.
4 Effects of the avalanches on surface velocity
The physical principles that govern convection rely on energy conservation, but also on mass conservation. This implies that avalanches have not only thermal, but also dynamical consequences, which can be seen in Fig. 4. In order to monitor this effect, the maximum of the horizontal velocity at the surface and the mean value of the amplitude of the velocity on the sphere have been computed and drawn versus time. The surface horizontal velocity is very sensitive to the avalanche occurrence. Indeed, its amplitude is twice during the paroxysmal phase. Furthermore, Fig. 4 shows that it is not a local effect, but a global one, since, even after an averaging over the spherical surface, the mean value of the module of the horizontal velocity displays the same trend. Finally, there is an almost perfect synchronization between the evolution of the velocity surface and the mass transfer through the 660-km phase change. This is an important result, since it implies that an avalanche, when it occurs, must go with a simultaneously enhanced plate-tectonic and ridge activity.
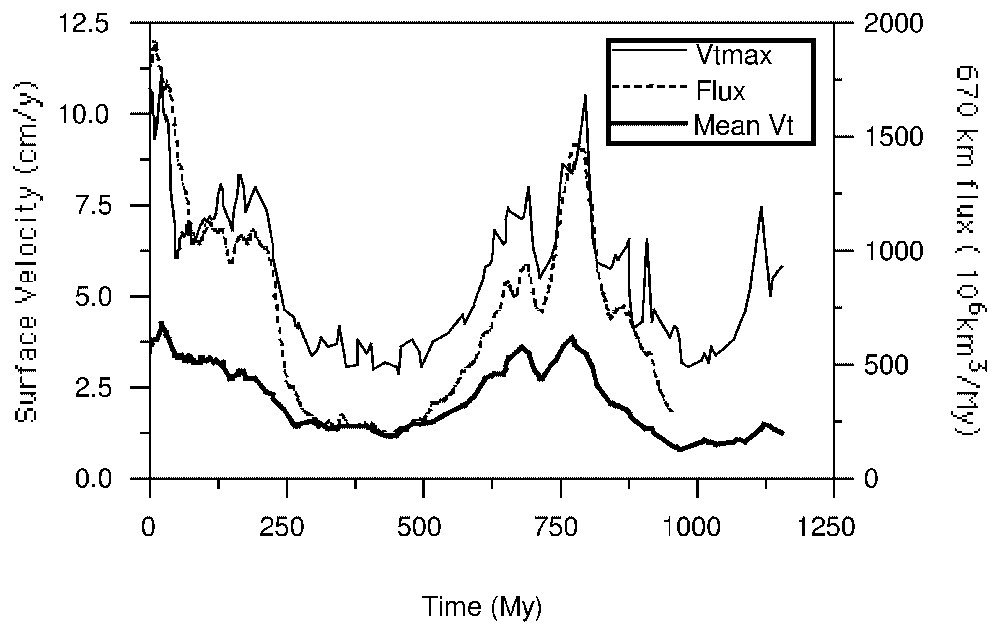
Time evolution of the maximum of surface velocity Vtmax (thin solid line), flux of matter crossing the 660-km phase change (dotted line) and evolution of the mean value of the surface velocity (heavy solid line).
Évolution temporelle de la vitesse horizontale de surface (ligne fine continue), flux de matière au travers du changement de phase des 660 km (ligne pointillée) et évolution de la vitesse moyenne de surface (ligne continue épaisse).
5 Summary and discussion
During our previous studies [12], we have concluded that a high mantle temperature during the Cretaceous was compatible with the global thermal effect of an avalanche. This results was deduced from isostasy considerations and from ODP-sample Na8/Fe8 temperature geochemistry, which both support independently evidence for a mantle thermal high around 125 Myr with amplitude (50 °C) and duration (30 Myr) comparable to those obtained from theoretical convection models.
Furthermore, the potential impact of global thermal anomalies due to an avalanche has also been discussed in term of ability to accelerate the Earth rotation, since the global thermal fluctuations change the depth of the phase changes through the Clapeyron pressure–temperature relationship [13].
These two results have been widely discussed within the context of the large-scale events that have occurred during the Cretaceous: Strong True Polar Wander event [1,17], superchron occurrence and magnetic field reversal perturbations [6], possible earth rotation acceleration [26], enhanced large scale tectonic and ridge activity [5], lower mantle contaminations of Pacific and Atlantic MORB [10,11], evidence for anomalous temperature in hot spots and MORB [9,19].
Within this context, the mantle avalanches offer a coherent explanation for both CMB and transition zone origins for plumes. Such a phenomenon would also be coherent with a global increase of the plate tectonic activity (ridge accretion and continental tearing) as a direct consequence of the surface velocity during the avalanche.
A more philosophical result of this work could be to emphasize the richness of the mantle behaviours, which would consist in alternating quiet periods of partial layering and catastrophic avalanche events. The coupling of the surface and bottom heat fluxes, the thermal regime of the mantle, the origin of plumes, and the surface activity would obviously depend on the instantaneous style of regime with long-term cycles through the Earth's history. We have to keep in mind that this richness has been obtained by including the phase change physics within the convection but without ad-hoc assumptions. On the other hand, the real Earth displays such (and may be worse) complexities that are surprisingly matched by the consequences of mantle avalanches.
Acknowledgements
The author thanks René Guiraud, Vincent Courtillot, and Jean Besse for useful comments and discussions. This work was supported by the CNRS/INSU programme ‘Intérieur de la Terre’.


