1 Introduction
Among planets, the terrestrial bodies are very similar in bulk properties [5,11,22]. They have mantles composed of magnesium-rich silicates and oxides, and they have iron-rich cores that are at least partially liquid because of the presence of sulfur and other alloying constituents. The bodies in this category are Mercury, Venus, Earth, Moon, Mars, Io, and the silicate/iron components of many icy bodies (Europa, Ganymede, Titan, Triton, Pluto). Mercury is iron-rich and the Moon is iron-poor relative to the average composition, but the bulk similarities among these bodies suggest that we should be able to organize our understanding of how they evolve, using physical scaling arguments. These scalings would encompass the two orders of magnitude or so in mass (a factor of five or so in linear size). However, one of the revelations of planetary exploration is that planets, unlike stars, resist this attempt at simple low dimensional characterization. Many factors other than size seem to play a role. The main reason for this failure is that planets are made from complex materials. Planetary materials have complex thermodynamics (e.g., complicated melting behavior) and complex rheologies (faulting and viscous flow). This complexity leads to a rich phenomenology of planetary evolutions. My goal here is to describe what simple scaling arguments suggest and the ways in which these arguments often fail. This is partly a review of our applications of mantle convection to terrestrial bodies, but partly a new attempt to organize our still limited understanding. In the existing literature, Sleep [18] comes closest to what is discussed here, but his emphasis is different.
I begin with a discussion of what simple scaling laws predict, and then proceed to an analysis of how they come to be violated, with a particular emphasis on the puzzle that plate tectonics presents. I then discuss how the various possible behaviors express themselves in the planets we observe.
2 Scaling laws for planetary evolution
Planets start hot, because of the gravitational energy of formation, and this heating is further augmented by the decay of the long-lived radioisotopes, primarily 40K, 238U and 232Th. For Earth-sized planets, the heat of formation is about an order of magnitude larger than the integrated effect of radioactivity, but most of this energy is lost early [21]. However, this early heating sets the initial condition for a subsequent cooling dictated by the gradual decay of radioactivity over geological time.
If conductive equilibrium applied, then the temperature difference ΔT between the surface and center would be about , where Q is the heat production per unit volume, R is the radius and k is the thermal conductivity (assumed constant). For the present-day heating rate of chondritic chondrites, about 3×10−8 W m−3, and for k=4 W m K−1 (appropriate to silicates), this yields ΔT=1500 (R/1000 km)2, which is more than enough for melting in bodies of Moon size or larger. However, conductive equilibration takes a time scale of order R2/κ∼(3×1010 yr) (R/1000 km)2, where the thermal diffusivity , ρ is the density and Cp is the specific heat. In bodies with radii of order 1000 km or larger, the deeply buried sources of heat cannot equilibrate by conductive loss in the age of the solar system and the heat generated would simply accumulate. This corresponds to several thousand degrees temperature rise. In the absence of any other process, the interior would begin to melt. However, mantle minerals can flow even before the melting begins, so convection is a possibility.
The relevant dimensionless number for determining the onset of convection is the Rayleigh number [16], and is defined as
| (1) |
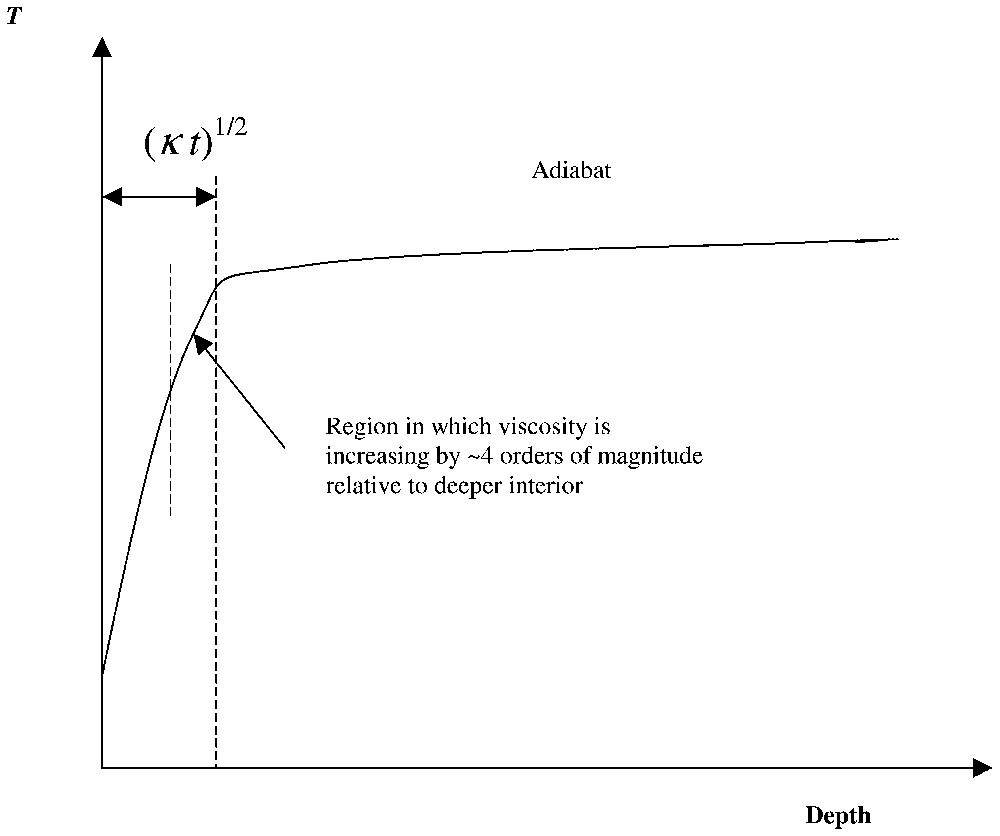
The temperature structure of a planet after elapsed time t, assuming the initial structure is a step function (uniform T or uniform entropy at time t=0). The surface temperature is fixed by the planet's atmosphere and distance from the Sun and is of no importance, because it is much smaller then the interior T(true even for Venus). Conduction along the adiabat is negligible, so it does not matter much whether the deep interior is isothermal or adiabatic. This picture can either represent the initiation of convection (where t is the time elapsed since the planet was assembled) or it can represent the steady state boundary layer (in which case t is the diffusion time through the thermal lithosphere.) In stagnant lid convection, only the region between the two dashed lines participates in convective overturn, and the cooler regions are immobile. In plate tectonics, the entire layer participates. In both cases, the source of the convective instability lies in the region of large temperature gradient and does not depend on the depth of the entire fluid.
Structure de température d'une planète au temps t, supposant que la structure initiale est en marche d'escalier (T uniforme ou entropie uniforme à t=0). La température de surface est fixée par l'atmosphère de la planète et sa distance au Soleil, et peut être négligée parce qu'elle est très inférieure à la température interne (ceci est vrai même pour Vénus). La conduction le long de l'adiabate est négligeable, et il n'importe donc guère de savoir si l'intérieur profond est adiabatique ou isotherme. Cette figure peut représenter le début de la convection (où t est le temps écoulé depuis l'accrétion de la planète) ou la couche limite à l'équilibre (dans ce cas, t est le temps de diffusion à travers la lithosphère thermique). Dans la convection à couvercle stagnant, seule la région entre les deux lignes en tireté participe au retournement convectif, et les régions plus froides sont immobiles. Dans le cas de la tectonique des plaques, la couche entière est impliquée. Dans les deux cas, la source d'instabilité convective est située dans la région de gradient thermique fort et ne dépend pas de la profondeur totale du fluide.
The surface of the planet is cold (excepting a possible, very short lived ‘naked magma ocean’ epoch). This means that the temperature difference is not the total difference between the surface and interior, but rather a much smaller difference, corresponding to the region in which the material in the convecting region is all sufficiently hot to flow viscously. Even a change of 200 K is sufficient to produce two orders of magnitude change in viscosity. This regime is called stagnant lid and it is observed experimentally and in numerical experiments whenever the surface is more viscous than the interior by more than about four orders of magnitude (this regime is violated in the plate tectonic regime, treated separately below). With , α∼2×10−5 K−1, ΔT∼200 K, ν in units of 1016 m2 s−1, and , we get:
| (2) |
| (3) |
| (4) |
It is common practice to talk about convection in planets in terms of the value of the Rayleigh number for the planet as a whole, i.e. d in Eq. (1) becomes the thickness of the mantle. Notice, however, that Eq. (3) for the heat flow has no explicit size dependence on the right-hand side, except through g. This is approximately true because the thickness of the boundary layer that goes unstable is internally determined (cf. Eq. (2)) and not dependent on d (in the language of Nusselt number–Rayleigh number relationships [6], Nu∼Raβ, and the extent to which this simple scaling is incorrect is expressed in the extent to which the exponent β is not 1/3). Large planets in steady state really do have much larger values of Rayleigh number but this is not what matters most (provided Ra⪢103): The heat flow and available buoyancy for that heat flow are determined by the boundary layer properties, and are independent of the depth of the convecting layer. By contrast, Ra has a strong dependence on depth (i.e. radius). There are some secondary issues, such as the vigor of the flow or whether it is chaotic, where Ra is indeed important.
In the stagnant lid regime, the convective heat flow scales as ν−1/3, where ν is the mantle viscosity (evaluated at the top of the adiabatic region of the mantle). Everything else in the formula for heat flow is constant or nearly so. We can therefore write dlnF/dt=−(dlnν/dt)/3. We can further assume (as a first approximation) that F∝Q(t), the time-dependent heat generation in the planet (this neglects for the moment the contribution to surface heat flow arising from the net cooling of the planet). It follows that:
| (5) |
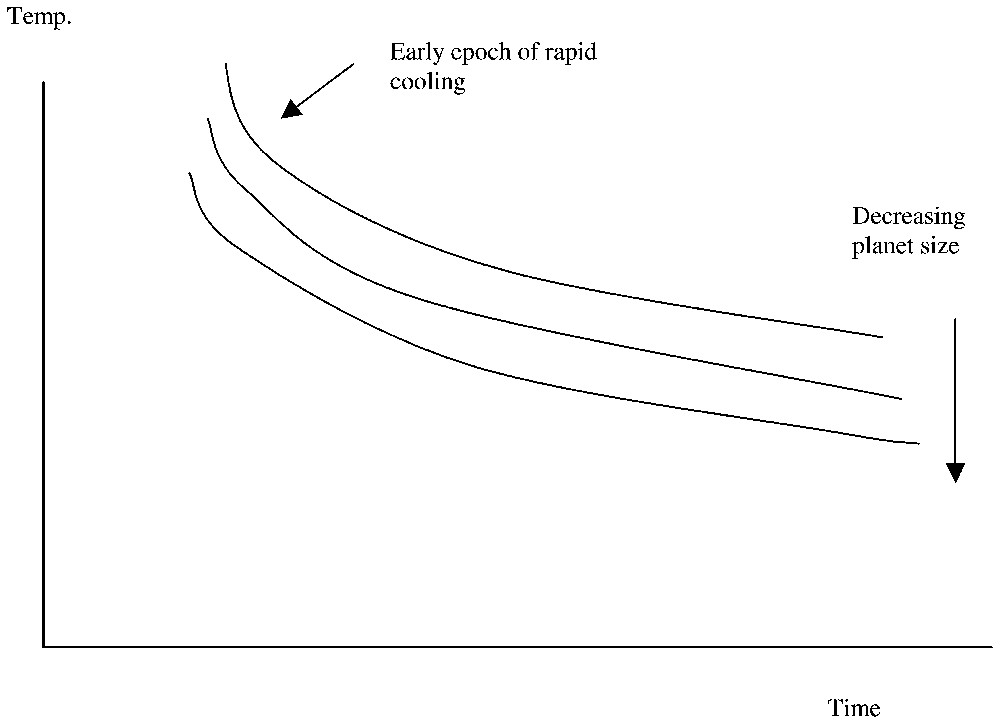
The thermal evolution of planets of differing sizes. The curves are parallel (with lower temperatures corresponding to smaller planets) and the curvature arises from the gradual change in dominant heat source half-lives, as explained in the text (Eq. (5)).
Évolution thermique de planètes de tailles différentes. Les courbes sont parallèles (avec les températures les plus basses qui correspondent aux planètes les plus petites) et la courbure vient du changement progressif des durées de demi-vie des sources de chaleur dominantes, comme expliqué dans le texte (Éq. (5)).
Any initial high temperature of the planet is forgotten (i.e. if the planet starts out hotter than its equilibrium, the most likely case, then it will cool quickly down to the equilibrium cooling curve). This happens because of the very strong temperature dependence of the viscosity.
Typically, γ−1∼50–100 K and is independent of time, because T does not change a lot. However, λ is not constant! In the early history of a planet, it is dominated by the decay of 40K (λ∼0.5/Ga), and later it is dominated by 238U (λ∼0.16 Ga−1) and then 232Th (λ∼0.05 Ga−1). This corresponds to the range of cooling that is as high as 150 K Ga−1 to as low as ∼10 K yr−1. We can then slightly correct the above model by asking what fraction of the heat flow arises from planet cooling. This is usually measured by the Urey number U, defined as the ratio of instantaneous total heat generation by radioactivity, to the total heat output by the planet at that time [16]. Since the cooling rate is independent of planet size it follows that U is also independent of planet size. Both the cooling rate and heat production decline through time but in different ways, so U is not a constant, but the predicted variation is not large. Simple models typically give U∼0.85, though values as low as 0.7 or as high as 0.95 are possible. The fact that the model gives a small 1−U means that the assumptions leading to Eq. (5) are approximately self-consistent. However, present Earth may have U∼0.5, which is probably incompatible with these models, for reasons discussed later.
The cooling has major implications for the existence of a core dynamo, since it is likely that the ability to have a core dynamo is directly connected to the rate at which the core is cooling [20,23]. The core started hot because of heat deposited during the giant impacts that lead to Earth and Moon formation, so there may be an early epoch in which the core loses some of this initial heat. After this, the core cannot cool unless the overlying mantle cools. Although there is a thermal boundary layer at the base of the mantle, the core-cooling rate is about the same as the mantle-cooling rate. If the cooling rate is sufficiently low then the heat flow from the core can be handled by core conduction and core convection will turn off. The dynamo will also turn off at that time. The situation is more complicated (but conceptually the same) if the inner core is growing and providing energy for the dynamo.
Predicted cooling by less than 100 K per billion years (perhaps only 40 K Ga−1 at present) may seem small, but this is enough to suggest much more melting and volcanism in the early history of a planet. The models also predict much more mixing of the mantle in the past than at present. To see this, note that the temperature drop driving convection does not change much through geologic time but the viscosity changes by a large factor. The convection scaling laws indicate that F∝ν−1/3 and convective velocity u∝ν−2/3, so it follows that u∝F2. This is a strong dependence; it means that convective velocities (and plate velocities?) may have been an order of magnitude larger at 3.5 Ga. This means that the preservation of isotopic anomalies is much harder than people often assume, since they tend to base those arguments of preservation on present-day estimates of convective circulation. More happened in mantle dynamics in the first billion years than during all subsequent geological time.
Systems heated from within differ significantly from systems heated from below. When the fluid is heated from below, it has localized thermal anomalies in upwellings as well as downwellings. When the fluid is heated only from within, it has only the localized downwellings, since there is no heat flow and therefore no thermal boundary layer at the base. The scaling laws above assume that the convection is driven from within (or, to be more precise, from the near-surface temperature difference created by the efficient surface cooling of a body uniformly heated from within). Since the effect of secular cooling (the deviation from U=1) is small, it follows the heat from the core is also small, typically only a third to a half of 1−U, in units of total surface heat flow. This assumes that the heat flow into the bottom of the mantle arises merely from cooling. The formation of a bottom boundary layer in the mantle is accordingly a small effect, at least from the point of view of the total energy budget, even though it is presumably the reason for plumes. As a consequence, plumes are a relatively unimportant part of the convecting system. They may have an importance for volcanism (e.g., Hawaii, Olympus Mons), which is out of proportion with their importance for cooling, however. Large-scale upwelling will also have a greater importance in a layered system, as discussed in Sections 4 and 5.
Since F∝x, it follows that the temperature gradient in the outermost region (conductive layer and thermal boundary layer) ∝x also. But g∝x, from which it follows from hydrostatic equilibrium that the pressure gradient ∝x. In other words, dT/dP is roughly constant and independent of the planet size. If we compare two planets of different sizes, but of the same epoch, then they will have roughly similar T(P) curves, differing only deep down (large P) where the smaller planet necessarily asymptotes to a smaller operating temperature. We can then compare this ‘universal’ T(P) with the thermodynamically determined Tsol(P) describing the onset of melting. This latter curve for basalt generation will apply to all epochs and all planets, to the extent the same composition applies.
Consider the hypothetical melting column that is available to the mantle material that ascends adiabatically to a near surface location (Fig. 3). This is conceptually what happens beneath mid-ocean ridges on Earth, or more generally in a rifting environment. To a good approximation, the same pressure range is available for melting in planets of differing size. However, the actual thickness of this column is greater on small (low gravity) bodies. Indeed, the column thickness ∝x−1. Ignoring other factors, small planets can make thicker crust than large planets. Notice that it is not merely proportionately thicker but actually thicker. For example, a situation that would produce a 10-km crustal thickness on Earth could produce a 25-km crust on Mars; this corresponds to a factor ∝x−2 variation in the fractional volume of crust.
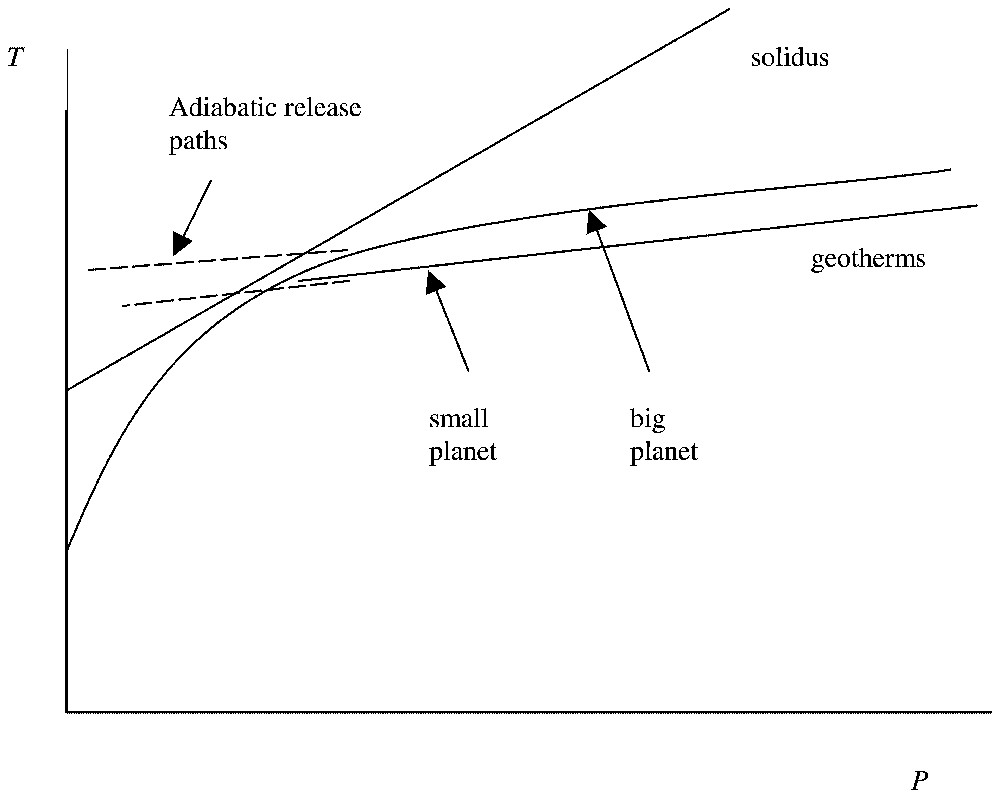
Temperature–pressure profiles are almost the same for different sized planets. The dashed lines are adiabatic release paths for the two cases, showing that about the same pressure interval is involved in each case. However, a small planet has a larger thickness involved (because g is smaller), so small planets produce thicker crust.
Les profils température–pression sont pratiquement les mêmes pour des planètes de tailles différentes. Les lignes en tireté sont les chemins de décompression adiabatique dans les deux cas, montrant que l'intervalle de pression impliqué est sensiblement le même dans chaque cas. Cependant, dans une petite planète, l'épaisseur relative impliquée est plus grande (parce que g est plus petit), donc les petites planètes forment une croûte plus épaisse.
3 Plate tectonics
Somehow, the Earth manages to involve the surface layer despite the enormous viscosity contrast. This is not well understood. It is almost as if the Earth had constant viscosity convection! Indeed, many numerical simulations have had partial success describing mantle convection using this approach. The correct scaling law that would apply for constant viscosity convection is:
| (6) |
If we apply Eq. (6) to present-day Earth, using ΔT∼1200 K, we find that the observed heat flow is compatible with ν∼1017 to 1018 m2 s−1, which is higher than the lowest (asthenospheric) viscosities observed beneath plates but compatible with the average viscosity that a subducting plate might see, based on viscosity estimates from postglacial rebound data. This may be somewhat fortuitous, as the following argument suggests. One way to think about plate tectonics is to ask where is the greatest impedance to motion? It might be at subduction zones. But the remarkable fact is that plates seem to sink at roughly the velocity you would predict if subduction zones were weak. In this sense, the fluid dynamical predictions above may have merit (i.e. some applicability). However, it is true that plates tend on average to be larger than you might have expected based on convection scaling, suggesting that there is indeed some inhibition to convection that ‘looks like’ constant viscosity convection. Increased aspect ratio is normally disadvantageous. One way to think about this is to look at convection from the point of view of its energy budget:
| (7) |
It is remarkable that current Earth just happens to reside at a temperature so close to the solidus at shallow mantle depths. According to the scaling above, this could only be a coincidence, since the mantle temperature is determined by the mantle viscosity law, which is not directly dependent on whether there is melting. However, it is possible that this is not a coincidence but part of how plate tectonics functions. This may be related to the role of water because the extraction of water in partial melting causes the plates to be stiff, while the presence of water in the underlying asthenosphere allows the plates to be lubricated [8].
4 Solid–solid phase transitions
Large density differences can occur because of solid–solid phase transitions in the silicates. The most important are those corresponding to the structural change in olivine at pressures corresponding to ∼400-km depth in Earth's mantle and the disproportionation to perovskite and magnesiowustite at a pressure corresponding to ∼660-km depth in Earth's mantle. This latter transition, which defines the upper-mantle lower mantle boundary in Earth, is barely reached at the base of the Martian mantle and not present in even smaller bodies. Since these phase change density differences are far larger than those thermal density differences driving convection, it is natural to suppose that they play a major role in convection [16]. In reality, the effect is often modest compared to the other complications addressed below. The reason is that the effect depends on the temperature dependence of the phase transition pressure, (dP/dT)ph, and is confined to a small depth region in the flowing fluid in which the material is in the ‘wrong’ phase by virtue of being hotter or colder than the mean at that level. For example, a downwelling, cold limb of convecting material will cause a downward deflection of the lower mantle-upper mantle boundary, because this phase transition is endothermic, i.e. has a negative value of (dP/dT)ph. This leads to more of the lower density (upper mantle) material in that region, thus inhibiting convection. The effect is dependent on Rayleigh number and strongest when the Rayleigh number is very large (e.g., earlier in the planet's history). Despite the large amount of effort and attention paid to this effect (which has the inevitable effect of promoting its importance), there is no evidence of a major inhibition of flow through the upper-lower mantle interface of Earth because of this effect alone, at least at the present day. It may, however, have a substantial effect on the form convection takes, since it tends to lead to larger scales (fewer convective cells) and tends to lead to larger temporal fluctuations of convective vigor [25]. In the earlier history of Earth or Venus, layered convection may have occurred because of this phase transition [4]. The hotter, early core may complicate this by providing more plume activity than now. Weaker or distributed phase transitions at lower or higher pressure might also play a role. Exothermic phase transitions are less important because they enhance rather than hinder convection.
5 Differentiation
Thermal convection is a special case of gravitational energy release, in which the system is kept out of equilibrium by the continued creation of new buoyant material (negatively buoyant material near the surface and/or positively buoyant material at depth). Moreover, the potential for overturn is mediated by the elimination of density differences because of thermal diffusion. When we speak of differentiation, we usually mean a one-way transport of light material up or heavy material down. It is ‘one way’ to the extent that compositional differences (unlike thermal differences) do not usually have a continuous source. It may not be ‘one way’ if the planet can continually recycle. Of course, this only happens when the thermal convective heat engine can do the work required to overwhelm the compositional density differences.
Unlike solid–solid phase transitions, melting usually leads to irreversible differentiation because the liquid and solid have different composition, and because the melt can migrate through the solid (two-phase flow). If some fraction ξ of a planet (radius R, mass M) settles to the bottom and is a factor (1+γ) more dense than the mean density, then you might expect the total energy release to be . Averaged over 4.5×109 yr, one then gets an energy production of relative to radioactivity. A good example of ‘one-way’ differentiation is the formation of the core of a terrestrial planet. In this case, the energy available exceeds that associated with radioactivity for Earth-sized planets. However, this energy was provided very early in the planet's history and thus has no important long-term effect. Formation of the lunar crust or terrestrial continents is also thought to be mostly ‘one way’. Basaltic oceanic crust on Earth is recycled (though its fate is controversial; we do not really know what fraction of it finds its way ‘back up’). Thick layers of basaltic crust are difficult to subduct because of compositional buoyancy. Another complicated case is Earth's water cycle (water can outgas from Earth but also be carried back down at subduction zones).
Although the total energy available from differentiation is potentially very important for large planets, we know of no ongoing source of differentiation (ξ) that affects the overall energetics of any planet (in the sense of competing with radioactivity). Nonetheless, differentiation can greatly affect planetary evolution in at least three ways:
- (1) it can redistribute the radioactive heat sources, for example by placing a potentially large fraction in the crust;
- (2) it can create layers that have density differences exceeding those arising from thermal effects, thus causing layered convection;
- (3) it can actually turn off convection in some large region, should differentiation lead to distributed density differences that oppose the destabilizing effects of temperature.
The most obvious effect of heat source redistribution is that it can cool the interior. To a first approximation, a planet with half of its heat sources in the crust will have an internal temperature like a homogeneously heated planet of half the radius (because heat flux is linear in planet radius). This assumes that all the crust is in the conductive layer and has a basal temperature less than that expected for the convecting interior. More significantly, it also assumes that the crust does not intrude into the depth region that would normally be expected to participate in convection. This is only possible if the crust is far more enriched in radioactive elements than a typical basalt derived from, say, 10 or 20% partial melting. It requires either low degree of melting for a large volume or (more probably) secondary processing and remelting (cf. continents on Earth).
Layered convection has profound effects on planetary thermal structure and thermal evolution. During an early epoch of extensive partial melting, major redistribution of elements could occur, with the natural trend being towards more dense material at depth. There is no reason to expect that the interface between two layers will reside at a phase transition (e.g., the 660 km discontinuity in Earth). At such an interface, the heat generation from the deeper layer must be carried by conduction into the shallower layer; this causes two additional thermal boundary layers, one just above and one just below the interface. The deeper layer is thus substantially hotter than the usual mantle estimate based on the scaling laws provided earlier. The thermal boundary layer at the base of the top convecting layer will also be the source of plumes which could carry much more heat and buoyancy than plumes derived from core heat alone.
The least well understood and perhaps most important consequence of melting arises from the density of the residue (the mantle material left over when basaltic melt is extracted). This residue is less dense than unmelted (fertile) peridotite at the same pressure and temperature. On Earth, this may matter rather little, since the entire assemblage of crust and residue is recycled in the plate tectonic process, but even so it may inhibit subduction. In stagnant lid planets, the effect is potentially far more severe, since the residue forms part of the layer that is expected to undergo convection and the temperature difference of this layer is small relative to deeper mantle [7]. As a consequence, it seems relatively easy to restrict convection in any thermal regime where the heat flow requires large amounts of melt generation. Convection can still continue at greater depths. Since small planets have a larger depth range of melting, it is possible that the convection will be prevented and heat delivery will be by melt transport and conduction alone. This may happen for all or part of the history of the Moon.
6 Comments on the planets
Mercury has a high mean density, suggesting a large iron core and relatively thin mantle. In the standard models for Mercury evolution [15,24], the mantle is convective and the planet cools sufficiently to produce a large inner core and thin liquid outer core. This may allow Mercury to sustain core convection and perhaps a dynamo. However, an early partially molten Mercury and a thin mantle are ideal situations to set up a thick crust and stable interior so it cannot be stated with certainty that Mercury is convective. Future missions, especially Messenger [6], will help resolve this.
Venus lacks large-scale plate tectonics, although there are some features that suggest a role for lithospheric foundering. The mean surface age of ∼700 Ma suggests that there may have extensive resurfacing of Venus prior to that epoch. One possibility is that the Venus lithosphere foundered catastrophically ∼700 Ma ago and that the current regime is closer to stagnant lid [26]. Another interpretation is that Venus is undergoing a gradual transition from mobile lithosphere (e.g., plate tectonics) to stagnant lid [14]. In either case, the scaling laws require that Venus is heating up (or has recently been heating up), implying U∼1 or even larger than unity. This is consistent with the estimates of lithospheric thickness. It would also mean that Venus does not have a dynamo at present because the core is not cooling [20]. This evolution from ‘plate tectonics’ to stagnant lid may have occurred on several bodies and is described in Fig. 4.

Stagnant lid evolution is monotonic and ‘hot’; plate tectonic convection gives monotonic cooling but at a cooler temperature. If the planet transitions from one to the other, then the evolution is non-monotonic. This is suggested for both Mars and Venus (see text).
L'évolution du couvercle stagnant est monotone et « chaude » ; la convection de la tectonique des plaques donne un refroidissement monotone, mais une température plus basse. Si la planète passe d'un mode à l'autre, alors l'évolution n'est plus monotone. C'est ce qui peut s'être passé pour Mars et Vénus (cf. texte).
Earth has much more data to constrain our ideas of mantle convection and evolution. However, it is also an anomalous planet since it is the only current example of plate tectonics. The long-lived preservation of isotopic anomalies, including high 3He/4He in ocean island basalts, and the small value of U∼0.5 are most easily understood if the mantle has some degree of layering. Current models favor a much deeper location than the upper mantle-lower mantle boundary (∼660 km) for the layering interface (see, for example, [1,9]). If the compositional density difference is small then this interface may undergo large vertical excursions and be difficult to identify seismologically. The recent evidence of ‘superplumes’ may be an indication of the compositional effects and the failure of simple thermal convection pictures.
Standard models of the Moon predict a convective mantle, even after extensive extraction of radioactive elements into the crust. However, preservation of isotopic anomalies in lunar rocks suggests imperfect mixing of the interior and this is easier to understand if the Moon lost heat by a combination of conduction and melt migration instead of large scale mantle overturn [10]. Models designed to test the convective stability of the lunar mantle through time show that there are parameter choices for which convection is absent or weak [13]. Resolution of this issue would be aided by more regional and global seismological data.
Mars may have undergone a ‘normal’ cooling history for a stagnant lid body, with mantle temperatures easily sufficient to generate melt throughout a substantial portion of its history. An attractive alternative assumes that Mars had plate tectonics in its early history, cooling the planet efficiently [17]. This then ceased, leading to a heating episode that would have turned off the dynamo responsible for the Martian crustal magnetism [12]. However, there are many additional complications that may have arisen. The very early transport of a large fraction of the radioactive elements into the crust and the development of a stably stratified residue from melting beneath the lithosphere may inhibit convection or lead to layered mantle convection. The loss of water from the mantle may stiffen the rheology and also require mantle heating. Unlike Earth, water may not be recycled back into the mantle because there is no plate tectonics.
Io is of special interest because it is the only body that currently derives most of its heat transport from melt migration. The large mountains and extremely high heat flow permit no alternative explanation. The source of heating in Io is tidal flexing but the specific way in which this is accomplished remains mysterious. It is unlikely that Io can be described using any of the scaling arguments or standard convective approaches common to other terrestrial planets.
7 Conclusion
In one sense, the synthesis offered here is unsatisfying. The planets resist generalization. Nevertheless, simple scaling laws can guide our interpretations even when we know that they fail more often than not. Perhaps the main lesson of this paper is one of optimistic caution: Be suspicious of simple models, but understand them before doing something complicated. We know they do not work for Earth and we see many ways in which they are unlikely to work for other planets.
Acknowledgements
Thanks to reviewers A. Davaille and N. Sleep for useful comments. Work supported by NASA Geology and Geophysics program.


