Experimental characterization of the thermo-poro-mechanical properties of the Aegion Fault gouge

Jean Sulem; Ioannis Vardoulakis; Hichem Ouffroukh; Marc Boulon; Julien Hans

doi:10.1016/j.crte.2003.12.009

Résumés

Anglais
Français

The experimental characterization of the thermo-poro-mechanical behaviour of Aegion Fault drilling cores is presented. The heart of the fault is met at a depth of 760 m and consists of clay-rich material on a length of about 1 m. This zone is surrounded by a cataclastic one. Here the thermo-poro-mechanical behaviour of the clayey core is investigated by means of oedometer and triaxial compression experiments. It is shown that softening behaviour under thermal loading is possible. Thermal collapse of the material may thus activate fluid pressurisation inside the fault and trigger fault slip. In addition, the behaviour of the interface between the intact rock and the cataclastic zone is studied by direct shear tests.

On présente une étude expérimentale du comportement thermo-poro-mécanique des carottes extraites de la faille d'Aegion. Le cœur de la faille, rencontré à 760 m de profondeur, est constitué de matériaux argileux sur une épaisseur d'environ 1 m. Cette zone est entourée d'une zone cataclastique. Le comportement thermo-poro-mécanique du noyau argileux est étudié à partir d'essais de compression oedométrique et de compression triaxiale. On montre qu'un comportement radoucissant sous chargement thermique est possible. Cet effondrement thermique du matériau peut conduire à une pressurisation du fluide de la faille et à une réduction de sa résistance au cisaillement. De plus, le comportement de l'interface entre la zone intacte et la zone cataclastique est étudié à partir d'essais de cisaillement direct.

Version française abrégée

Nous présentons dans cet article les résultats de travaux expérimentaux portant sur le comportement thermo-poro-mécanique de matériaux prélevés dans la faille active d'Aegion, dans le golfe de Corinthe. Le noyau de la faille, rencontré à une profondeur de 760 m, est constitué d'une zone riche en matériaux argileux sur une longueur d'un mètre environ (Fig. 1). Cette zone est entourée d'une zone de brèche calcaire d'une épaisseur de 3 m, au-dessus, et d'une brèche de radiolarites de 9 m d'épaisseur, au-dessous. L'analyse minéralogique des échantillons a été effectuée par diffraction des rayons X et a montré que, dans la zone de gouge argileuse, les fragments de radiolarites et la matrice argileuse avaient une composition semblable (Tableau 1), à base essentiellement de quartz (74 %), de chlorite (3 %), d'illite (10 %), d'albite (9 %) et d'hématite (3 %).

Fig. 1
Box 49 containing the core at depth 759.70 m, characterised as the ‘Aegion fault’ core [5].
Boı̂te 49, contenant la carotte prélevée à 759,70 m, caractérisée comme la carotte « faille d'Aegion » [5].

Sample	Quartz (%)	Chlorite (%)	Illite (%)	Albite (%)	Hematite (%)
Clay particles<80 μm	74	3	10	9	3
Clay matrix<400 μm	66	2	15	13	3.5
Fragments and gravels	73	2	9	8	2.5

Une attention particulière a été portée à la caractérisation du comportement du noyau argileux. En effet, la présence d'argile dans une gouge de faille affecte de manière sensible le comportement de la faille en termes de perméabilité, de réponse mécanique et de réponse thermique, dans la mesure où cette argile, qui est généralement dans un état normalement consolidé, montre une réponse volumique contractante lorsqu'on la chauffe. La courbe granulométrique de la gouge argileuse montre que la proportion des particules fines (de taille inférieure à 80 μm) est de 32 %, tandis que le pourcentage des particules d'argile (fraction de taille inférieure à 2 μm) est de 15 %. Les limites d'Atterberg de ce matériau sont : limite de liquidité, w_L=29 %, limite de plasticité, w_P=17 %, indice de plasticité, PI=12 %.

Le comportement poro-mécanique est étudié à partir d'essais oedométriques à fortes contraintes (Fig. 3) et d'essais de compression triaxiale à différentes pressions de confinement et différentes températures (Figs. 5 et 6). L'essai oedométrique, largement utilisé en mécanique des sols, permet de caractériser le comportement sur une large gamme de contraintes à l'aide de deux paramètres, l'indice de compressibilité pour la charge et l'indice de gonflement pour la décharge. Il permet aussi une évaluation de l'évolution de la perméabilité en fonction de la contrainte appliquée. Le comportement thermique est étudié à partir d'essais de chauffage sous contrainte isotrope en conditions drainées. Ces essais ont montré qu'une augmentation de la température conduisait à une déformation volumique contractante du matériau (Fig. 7). Ce phénomène d'effondrement, dû au comportement thermique radoucissant de la gouge argileuse, peut conduire à une augmentation de la pression interstitielle, et donc à une diminution de la résistance au cisaillement à l'intérieur de la faille lors d'un cisaillement rapide. Les paramètres thermo-poro-mécaniques déterminés en laboratoire sont résumés dans le Tableau 2.

Fig. 3
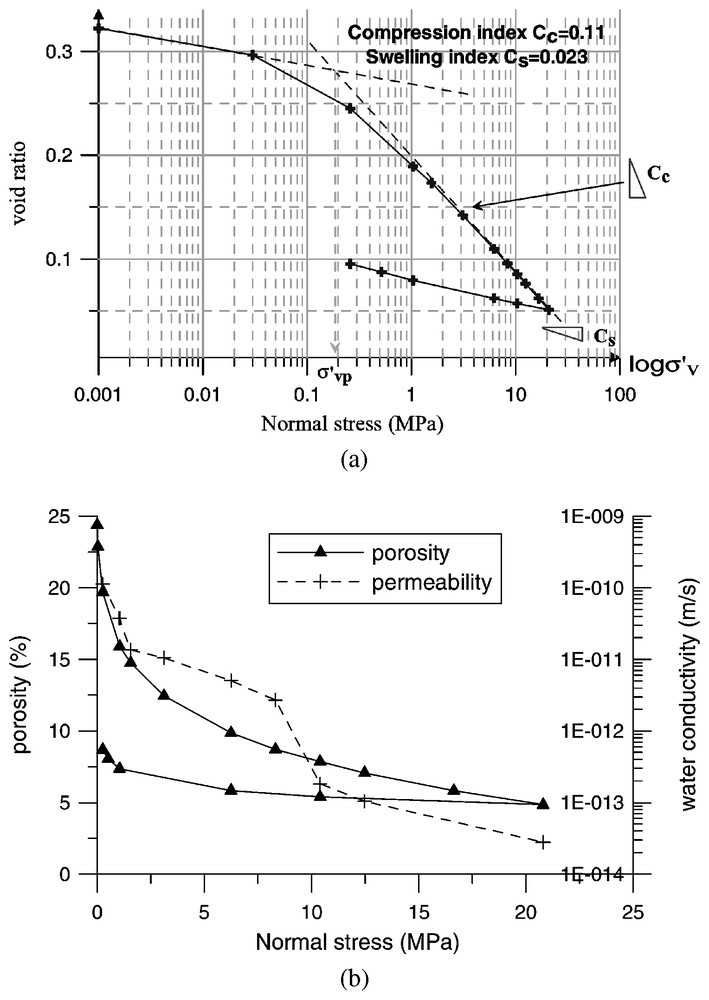
Oedometric compression tests: (a) oedometric curve; (b) porosity and permeability evolution.
Essais de compression oedométrique : (a) courbe oedométrique ; (b) évolution de la porosité et de la perméabilité.

Fig. 5
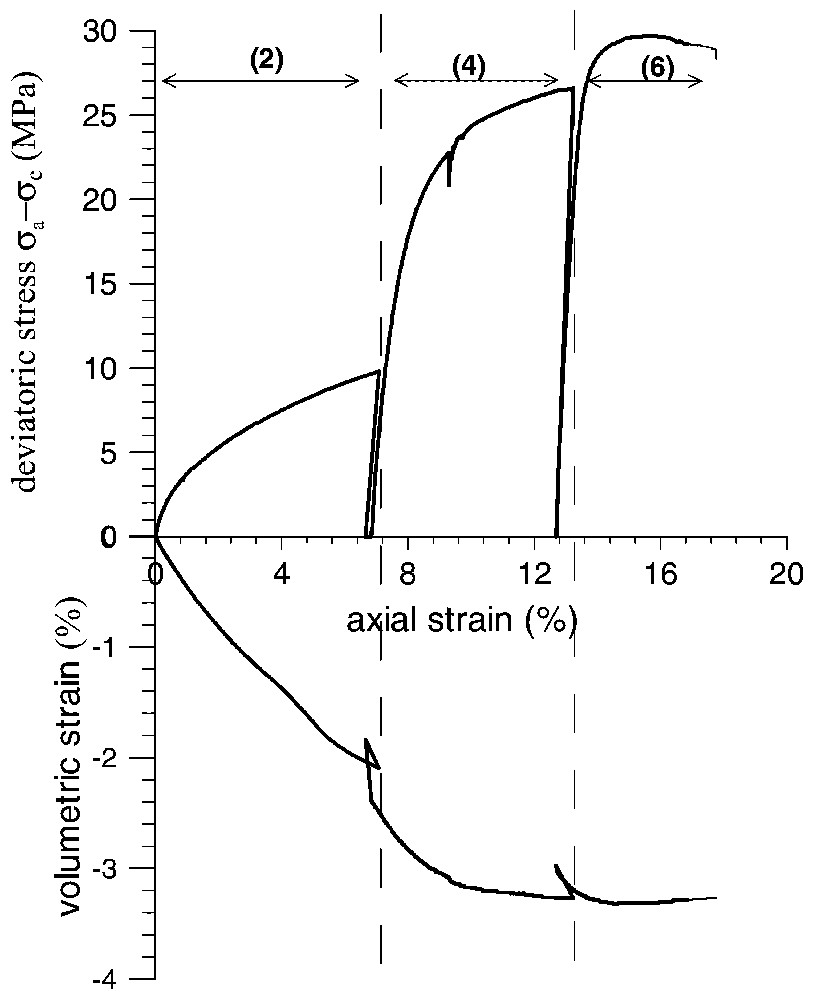
Drained triaxial test performed on the first specimen at room temperature (numbers indicate the loading phases according to Fig. 4).
Essais triaxiaux drainés à température ambiante (les nombres indiquent les phases de chargement, conformément à la Fig. 4).

Fig. 6
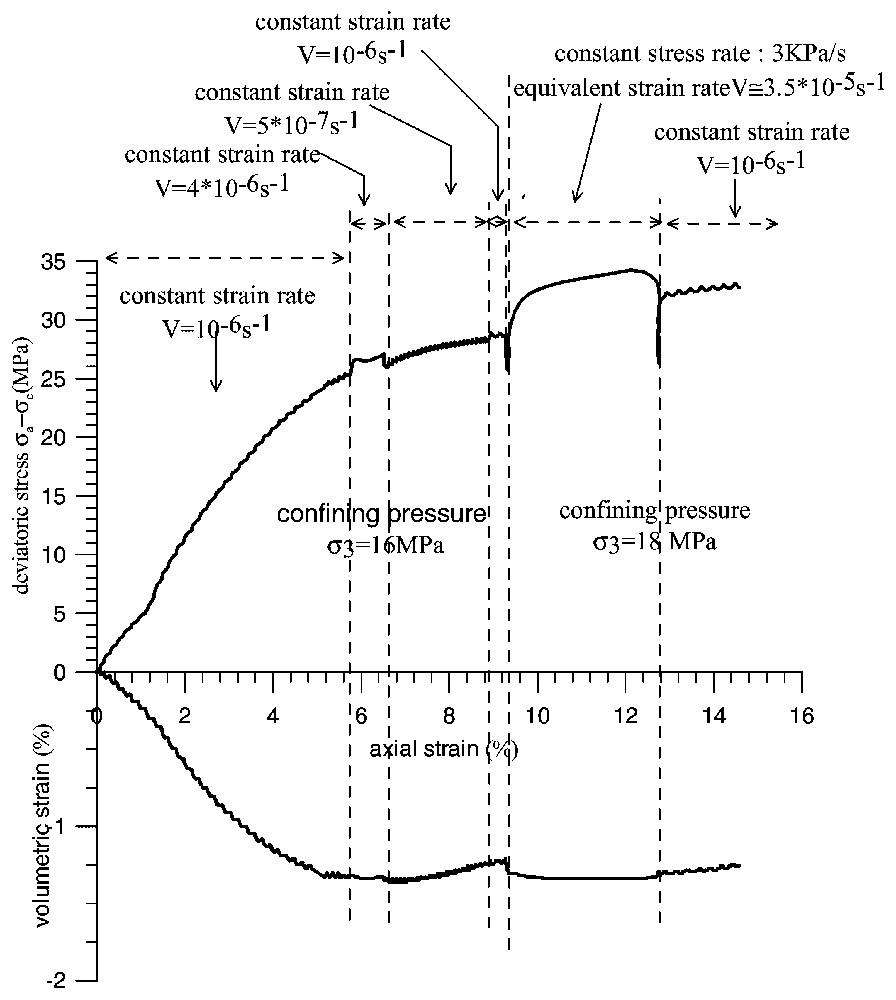
Drained triaxial test performed on the second specimen at 70 °C.
Essais triaxiaux drainés à 70 °C.

Fig. 7
Drained heating tests under isotropic state of stress.
Essais de chauffage drainés sous contrainte isotrope.

Permeability k	7×10⁻²¹ m²
Compression index C_c	0.11
Swelling index C_s	0.023
Consolidation coefficient c_v	2.42×10⁻⁹ m² s⁻¹
Compressibility coefficient c	0.0028 MPa⁻¹
Thermal pressurization coefficient λ	136 kPa °C⁻¹
Friction angle at critical state ϕ_cs	28°–29°

Les conclusions de cette étude sont les suivantes.

– Le noyau argileux de la faille a une perméabilité très faible (∼10⁻²⁰ m²) et présente un comportement volumique contractant lors d'une augmentation de la température (radoucissement thermique) ; ainsi, un cisaillement rapide peut conduire à une pressurisation du fluide de la faille.
– Lors d'essais triaxiaux en conditions drainées à température et confinement constants, le matériau atteint l'état critique (écoulement plastique à volume constant sous déviateur constant) sous compaction monotone.
– La résistance au frottement du matériau argileux augmente légèrement avec la température et la vitesse de déformation (écrouissage positif en température et vitesse de sollicitation).
– Le joint entre la zone des calcaires fracturés et les bandes cataclastiques, étudié à l'aide d'essais de cisaillement direct, montre un comportement fragile et contractant, avec un angle de frottement résiduel d'environ 32°, soit 3° de plus que celui de la gouge argileuse.

1 Introduction

Within the frame of the European projects DG-Lab Corinth and 3F-Corinth, fault zone cores from the active Aegion Fault in the Gulf of Corinth in Greece have been collected continuously from depths between 708 to 782 m [5]. At depth 760 m the Aegion Fault was intercepted, dipping at an angle of about 60°. The heart of the fault is a zone of clay-rich material on a length of about 1 m. This zone is surrounded by a damage zone of highly fractured rock (breccia). The fault material is embedded between limestone cataclasite on top with a thickness of about 3 m and radiolarite cataclasite below with a thickness of about 9 m and is characterized as gouge clayey matrix and radiolarite fragments (Fig. 1) [5].

The mineralogical analysis of the samples was carried out by X-ray diffraction techniques. The radiolarites fragments as well as the clay matrix have been studied. Similar mineral composition was found for the fragments and for the clay particles as shown on Table 1 [7]. On this table the mineral composition is normalized to 100%. The amorphous content is about 20%.

In this paper we present results from rock-mechanical laboratory analyses on specimens taken from the Aegion Fault core. Special attention is paid on temperature effects on the behaviour of the clayey core of the lower part of Aegion Fault drilling core. This zone corresponds to the weakest gouge clayey matrix and radiolarite fragments material encountered in this sequence and is recognisable from its red-brown coloration. In addition, results are presented from direct shear tests performed along the interface between the limestone and the cataclastic bands as encountered at depth 744 m.

2 The role of clay minerals in fault zones

The observations from the active fault drilling operation of the Geological Survey of Japan at Nojima Hirabayashi after the 1995 Hyogoken-nanbu (Kobe) Earthquake and the following analysis by Otsuki et al. [6] renewed the interest of the geophysics community on the role of temperature and fluids in active faulting [2,4]. Shear heating tends to increase pore pressure and to decrease the effective compressive stress and the shearing resistance of the fault material. On the other hand, dilatancy tends to decrease pore pressure. Such couplings have been studied thoroughly in a recent paper of Garagash and Rudnicki [1].

Fault zones are often characterized by large amounts of clay minerals, which form well-defined structures within the fault zone. The total concentration of the clay minerals in the fault zone is usually larger than in the host rock. These clay minerals inside the fault gouge are widely believed to affect significantly the mechanical behaviour of faults, since, as is the case for normally consolidated clays, they tend to contract when heated.

Based on the above-mentioned literature and the recent experimental work by Sultan et al. [9], Vardoulakis has demonstrated [12,13] the importance of thermally collapsible and thermally softening clay on the overall dynamic thermo-poro-mechanical behaviour of clay-rich gouges. Accordingly, conditions for possible softening behaviour of the clay under thermal loading are investigated. The sensitive parameter for the description of the thermo-poro-mechanical coupling is the thermal expansion coefficient of the material. Possible collapse of the clay under thermal loading may activate fluid pressurization inside the fault and lead to substantial reduction of the apparent friction.

3 Thermo-poro-mechanical properties of the red Aegion Fault clay

3.1 Samples preparation and in situ stress

In geotechnical engineering special techniques exist to obtain high-quality undisturbed soil samples and try to prevent alteration of soil structure. It is however very difficult to obtain undisturbed samples from great depths. Unfortunately within the frame of DG-Lab project no resources could be made available to use these techniques and the cores have been disturbed to some degree during sampling and transportation. However this is not so detrimental for the type of gouge material that was recovered as it can be with cemented sands or with soft clays.

As the first reports from the drilling site confirm, the clayey gouge that was extracted from Aegion Fault was a remarkably soft material, Fig. 1. Most probably, this is because this material was continuously stressed due to the aseismic and seismic movements of the fault. Thus, it is expected that the effect of remoulding be of lesser importance, as long as the density and the water content of the samples are preserved for testing.

The in situ density of the material is reasonably retrieved by applying the in situ stresses onto the sample. Notice that it is programmed within the DGLab project to perform direct stress measurements inside the borehole. The data are not available at present. Thus the in situ state of stress has to be estimated. Assuming that the density of the overburden is about 2.5 g cm⁻³, we estimate a total vertical stress of about 19 MPa, which in turn is corresponding to an effective vertical stress of 11.4 MPa.

Once the Aegion Fault core was taken from the borehole, it was stored for a few days on site and then it was transported to the Soil Mechanics Laboratory of ‘École nationale des ponts et chaussées’, Paris, France, where it was stored in a room with controlled temperature and humidity. Obviously, it was not possible to avoid partial drying of the core during extraction, storage and transportation, but then it was regularly wetted as soon as it was stored in good conditions. As it was not possible to use in the experiments the same saturation fluid as in situ, we have used demineralised water in which a certain amount of particles from the sample have been placed during 24 h. The mixture has been then filtered and the resulting fluid has been used for the saturation of the tested samples. This technique is commonly used in soil testing to avoid any chemical influence of the saturation fluid on the mechanical properties of the tested material.

3.2 Particle size characteristics and Atterberg limits of the material

Fig. 2 shows the grain-size distribution curve for the red Aegion Fault clay material. The coarse fraction corresponds to radiolarite fragments. The percentage of fines (fraction smaller than 80 μm sieve size) is 32% and the percentage of clay particles (mass fraction smaller than 2 μm) is about 15%.

Fig. 2
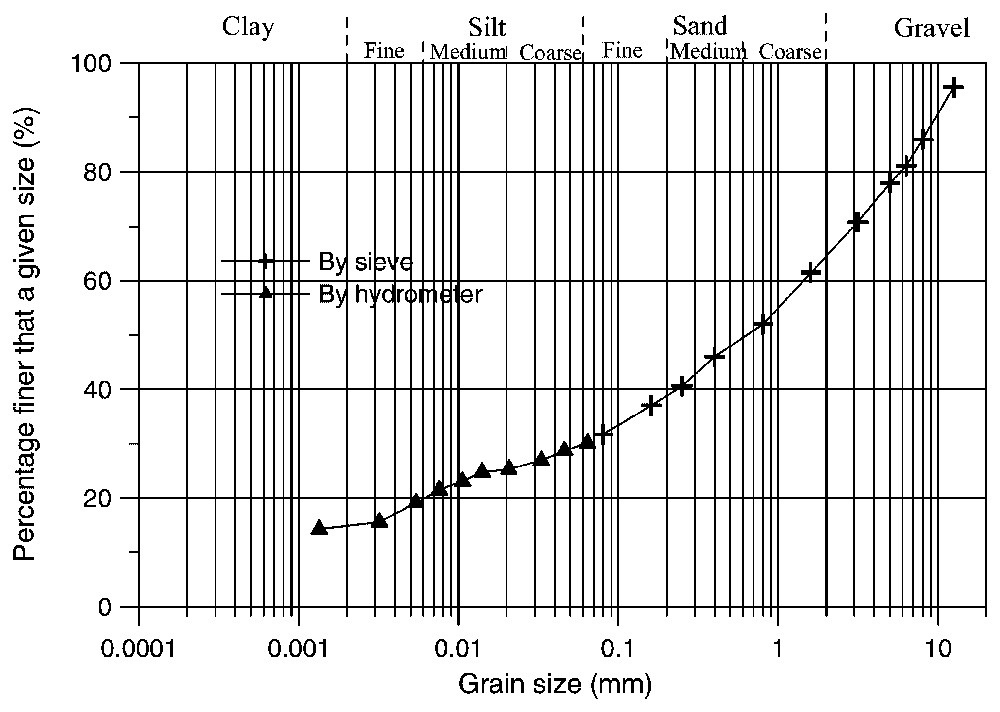
Grain size distribution of the red Aegion fault clayey gouge.
Courbe granulométrique de la gouge argileuse rouge de la faille d'Aegion.

The corresponding Atterberg limits are: liquid limit w_L=29%, plastic limit w_P=17%, which correspond to a relatively low plasticity index (PI=12%). According to the USC system, the material is classified as a ‘clayey sand’.

3.3 Oedometric compression test

The oedometer test is commonly used in soil mechanics practice to measure compressibility. Here for completeness, we outline the basic concepts of this test: a fluid-saturated cylindrical specimen is confined latterly by a stiff metal ring and the specimen is stressed along the vertical axis. Due to the lateral rigid confinement of the specimen, the strains in horizontal directions are suppressed. Porous stones are employed on the top and bottom of the specimen in order to permit the free drainage of the pore-fluid in or out of the specimen. During the test the vertical load is applied in small increments. For each load increment, the vertical deformation of the specimen is monitored using displacement gauges. Assuming that the grains of the solid constituent are incompressible, all volume changes are attributed to changes in the voids ratio of the specimen and are directly linked with the extrusion of the pore-fluid from the pore-space. Thus we relate the change in the void ratio of the specimen Δe with the volumetric strain ε_v:

ϵ_{v} = \frac{Δ e}{1 + e_{0}}

(1)

where e₀ is the initial void ratio.

The commonly observed non-linear stress-strain response of a soft geomaterial in oedometric compression makes it more convenient to plot the void ratio versus the effective vertical stress σ′_v in a logarithmic scale, because, as was first observed by Terzaghi [11], at large stresses the corresponding curve becomes a straight line, so that a unique parameter, the so-called compression index:

C_{c} = - \frac{Δ e}{Δ (\log σ'_{v})}

(2)

is sufficient to characterise the compressibility of the material over a wide range of stresses. Similarly one is defining upon unloading the so-called swelling index C_s.

In Fig. 3 are displayed the results from oedometric compression test performed on a saturated sample using a high-pressure oedometer [3]. A system of double cantilever beam allows a maximum vertical load of 12 t corresponding to a maximum stress of about 31 MPa on a cylindrical sample with a diameter of 70 mm. The curve can be divided into two parts. The first part, starting at the beginning of the curve, represents the reconsolidation phase. At the end of the reconsolidation, the curve shows a sharp bend and becomes a straight line, which corresponds to the primary consolidation line of a normally consolidated sample. The vertical stress σ′_vp, which corresponds to the elbow of the consolidation curve, marks the point where the sample starts to present large irreversible deformation when loaded. After Casagrande, this stress is identified with the so-called pre-consolidation stress. The small value of the pre-consolidation stress obtained here shows that the material has been remoulded during the coring process and has lost the memory of its past loading history. The measured compression index C_c=0.11 is typical of a sandy clay.

The evolution in time of the compression of a fluid-saturated, fluid-permeable porous material is described by Terzaghi's (1925) consolidation theory. According to it, the compaction of the material is associated with the extrusion of the pore-fluid through the permeable boundaries of the specimen. In the considered one-dimensional setting of a specimen compressed vertically in an oedometer, this theory results into the following equation for the dissipation of excess pore pressure:

\frac{\partial u}{\partial t} = c_{v} \frac{\partial^{2} u}{\partial z^{2}}

(3)

where u is the excess pore pressure, z is the coordinate in vertical direction, t is the time and c_v is the consolidation coefficient:

c_{v} = \frac{k_{f} (1 + e)}{γ_{f} a_{v}}

(4)

In this equation, k_f is the hydraulic conductivity of the material with respect to a given fluid, and

a_{v} = - \frac{Δ e}{Δ σ'_{v}} \approx 0.434 \frac{C_{c}}{σ'_{v}}

(5)

is the compression modulus of the material; e is the actual voids ratio and γ_f is the unit weight of the pore-fluid.

By using the Casagrande method [10], it is possible to estimate the consolidation coefficient c_v directly from oedometer test results and thus, from Eq. (4), to evaluate the hydraulic conductivity of the gouge as a function of the applied oedometric pressure (Fig. 3). Notice that the physical or Muskat permeability k of the material, with dimension of square length, is related to the hydraulic conductivity k_f by:

k = \frac{η_{f}}{γ_{f}} k_{f}

(6)

where η_f is the viscosity of the pore fluid.

The oedometer tests have yielded the following values for the consolidation coefficient and the permeability of the tested fault gouge material at σ′_v=15 MPa: c_v≈2.42×10–9 m² s⁻¹, k=7×10⁻²¹ m².

After the last stage of the loading process at σ′_v=21 MPa, the sample was unloaded. The corresponding swelling index is C_s=0.023. The specimen was then removed from the oedometric cell, weighted and then dried in an oven at 105 °C for 24 h. The porosity of the specimen at the end of the test was found to be 8.7%. The evolution of the porosity with axial stress was back calculated from the axial strain measurements, as is shown in Fig. 3b. Thus the back-calculated initial porosity of the material is 19.7% and the porosity of the sample loaded in oedometric compression at σ′_v=16.6 MPa is 5.8%.

We notice finally that the oedometer tests allow the determination of the isothermal compressibility coefficient

c \equiv m_{v} = \frac{Δ ϵ_{v}}{Δ σ'_{v}} = \frac{a_{v}}{1 + e}

(7)

which is directly linked to the aforementioned compression modulus and compression index; cf. Eqs. (2) and (5). At σ′_v=16 MPa, the isothermal, compressibility coefficient of the tested fault gouge is c=0.0028 MPa⁻¹.

3.4 Strength parameters from drained triaxial compression tests

Due to the small amount of material available for experimental studies, only two specimens could be used. The first specimen was tested at room temperature (θ=22 °C) and the second at an elevated temperature (θ=70 °C). For the same reason, ‘stepped’ triaxial testing programmes were imposed, following the stress paths shown in Fig. 4.

Fig. 4
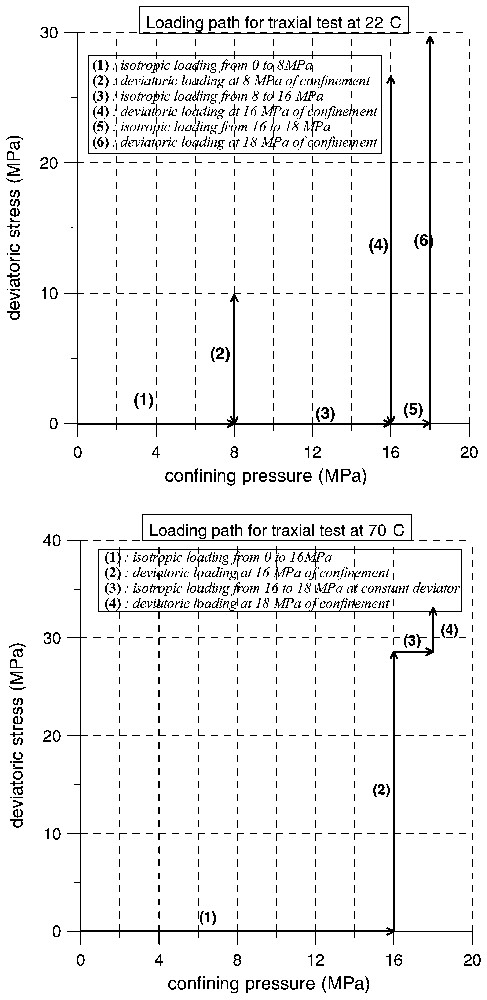
Stress paths followed in the triaxial compression tests.
Chemins de contraintes pour les essais de compression triaxiale.

The first specimen was sheared sequentially at confining pressures σ_c=8 MPa, σ_c=16 MPa and σ_c=18 MPa. At the end of each shearing phase at constant confining pressure, the specimen was unloaded axially and the confining pressure was augmented to reach the next prescribed level. For the second specimen, the axial load was kept constant during the augmentation of the confining pressure from σ_c=16 MPa to σ_c=18 MPa. As we are interested here in the response of the material during the shearing phase and considering that the volumetric strains are not significant during the unloading phases (the material is practically rigid upon unloading), the stress paths followed in the triaxial tests of the first and the second specimen do not differ significantly. The corresponding stress–strain curves are shown in Figs. 5 and 6, respectively. Axial and volumetric strains are measured with respect to an initial state, corresponding to the beginning of the first deviatoric phase of the test.

For the 1st specimen, tested at θ=22 °C and σ_c=8 MPa, the loading phase was interrupted at an axial strain, ε_a=7.2% corresponding to a deviatoric stress q=σ_a−σ_c=9.9 MPa. Since this value of the deviatoric stress is actually smaller than the value, q_f, at which failure occurs, the specimen remained homogeneous. This justifies the loading strategy applied here, according to which the same specimen could be used for a different higher pressure. Using a hyperbolic fitting of the data we could estimate that, at σ_c=8 MPa, q_f≈14 MPa. For the shearing phases at σ_c=16 MPa and at σ_c=18 MPa, the material was compacting and it reached the critical state of maximum compaction at a mobilized friction angle of φ_cs=27.9°. For both tested specimens the critical state was reached for large strains. For the first specimen, the maximum volumetric strain (respectively, axial strain) was ε_v,max≈3.3% (respectively, ε_a,max≈17.8%). The corresponding values for the second specimen are ε_v,max≈1.3% (ε_a,max≈14.5%). We notice that the dilatant behaviour, which is observed at the end of the test, is attributed to the occurrence of shear banding in the sample.

The frictional resistance of the material at critical state increases slightly with the temperature and with the strain rate. The influence of temperature on the friction angle can be judged by comparing the value of maximum friction angle φ_cs=29°, for second specimen and for a strain rate, ${\dot{ϵ}}_{a} = 10^{- 6}$ s⁻¹, with the aforementioned value φ_cs=27.9°, holding for the first specimen, tested at the same strain rate. Thus, a temperature difference of Δθ=48 °C results into an increase of maximum friction angle of Δφ_cs≈1°.

As is shown in Fig. 6, changes in the strain rate during the test indicate also some rate sensitivity. Here we evaluate the rate sensitivity of the tested material in terms of the mobilized-friction coefficient f:

f = \frac{2 \sqrt{3} \sin ϕ_{m}}{3 - \sin ϕ_{m}}

(8)

where φ_m is of the corresponding mobilized friction angle. Thus assuming an exponential law of the form [8]:

f = f_{ref} \exp (S_{f} \frac{{\dot{ϵ}}_{a}}{{\dot{ϵ}}_{a, ref}})

(9)

the frictional rate-sensitivity is estimated from the test data by using the following formula,

S_{f} = \frac{Δ f / ((f^{+} + f^{-}) / 2)}{\ln ({\dot{ϵ}}_{a}^{+} / {\dot{ϵ}}_{a}^{-})}

(10)

For the rest of the tested red clay, we found that S_f≈0.01.

3.5 Drained thermal loading of the clayey gouge

In order to study the effect of temperature on the volumetric behaviour of the material, two tests of drained heating have been performed in isotropic stress conditions. The first test was run with an isotropic effective stress of p′=16 MPa and the second test with p′=12 MPa. For each test, the specimen was first loaded isotropically to its final stress in drained conditions and at constant room temperature. Then by keeping the isotropic stress constant, the specimen was heated in drained conditions at a rate, $\dot{θ} = 0.02$ °C min⁻¹. The experimental results are shown in Fig. 7. The two tests show a good reproducibility and show also that the final state of isotropic stress is not influencing the response. The important result from these experiments is that the clay-rich material is contracting, when heated. This phenomenon represents a thermo-plastic or structural collapse. The corresponding elasto-plastic contraction coefficient is negative:

α_{c}^{ep} = - 2.4 \times 10^{- 4} ° C^{- 1}

(11)

During the cooling phase thermo-elastic contraction is occurring with a rate of

α_{c}^{e} = 1.4 \times 10^{- 4} ° C^{- 1}

(12)

Thus the resulting isobaric thermo-plastic contraction coefficient is:

α_{c}^{p} = α_{c}^{ep} - α_{c}^{e} = - 3.8 \times 10^{- 4} ° C^{- 1}

(13)

Following Vardoulakis [12], the coefficient of thermal pressurization λ can be estimated from the above results:

λ = \frac{- α_{c}^{p}}{c}

(14)

where the compressibility coefficient is given by Eq. (7). The thermal pressurization coefficient of the tested fault gauge is λ≈136 kPa °C⁻¹.

3.6 Summary

The Aegion Fault gouge is a clay-rock mixture. The above results have shown that although the clay fraction is relatively small, it has a significant influence on the thermo-mechanical properties of the material. The thermo-poro-mechanical constants of the water saturated red clayey gouge at a nominal axial effective stress of 16 MPa are summarized in Table 2.

4 Mechanical properties of the joint between the fractured limestone and the breccias zone

It is of interest to study the behaviour of the interface between fractured limestone and cataclastic bands as found above the clayey core of the faults (Fig. 8). One sample has been tested in the direct shear box of Laboratory 3S (Soils, Solids, Structures) in Grenoble, France. The orientation of the joint with respect to the axis of the core is 112°. On the side of the vein wall of the fault, the material is a fissured limestone with open fractures often filled with calcite. On the side of the breccia, it is a crushed, relatively porous material with recent cementing. Voids of several millimetres of diameter and geodes with calcite filling are visible inside the calcite where the crystallization is uncompleted.

Fig. 8
Interface between the fractured limestone and a cataclastic band (Box 33 – Core 13-2) at depth 744 m: (a) core sample; (b) unfolded picture of the core surface.
Interface entre le calcaire fracturé et une bande cataclastique (boı̂te 33 – carotte 13-2) à 744 m de profondeur : (a) échantillon ; (b) développée de la surface.

During the direct shear experiments, the displacement was applied on the joint in a direction that corresponds to the relative movement observed in the Corinth Gulf, i.e., from south to north. The stress path chosen is as follows:

– first an increasing normal stress was applied with two unloading and reloading cycles at 5 MPa and 10 Pa;
– then at a nominal normal stress of 12.20 MPa, a shear displacement was applied up to relative tangential displacement Δu_t=40 mm;
– then the tangential displacement was reversed to zero relative tangential displacement.

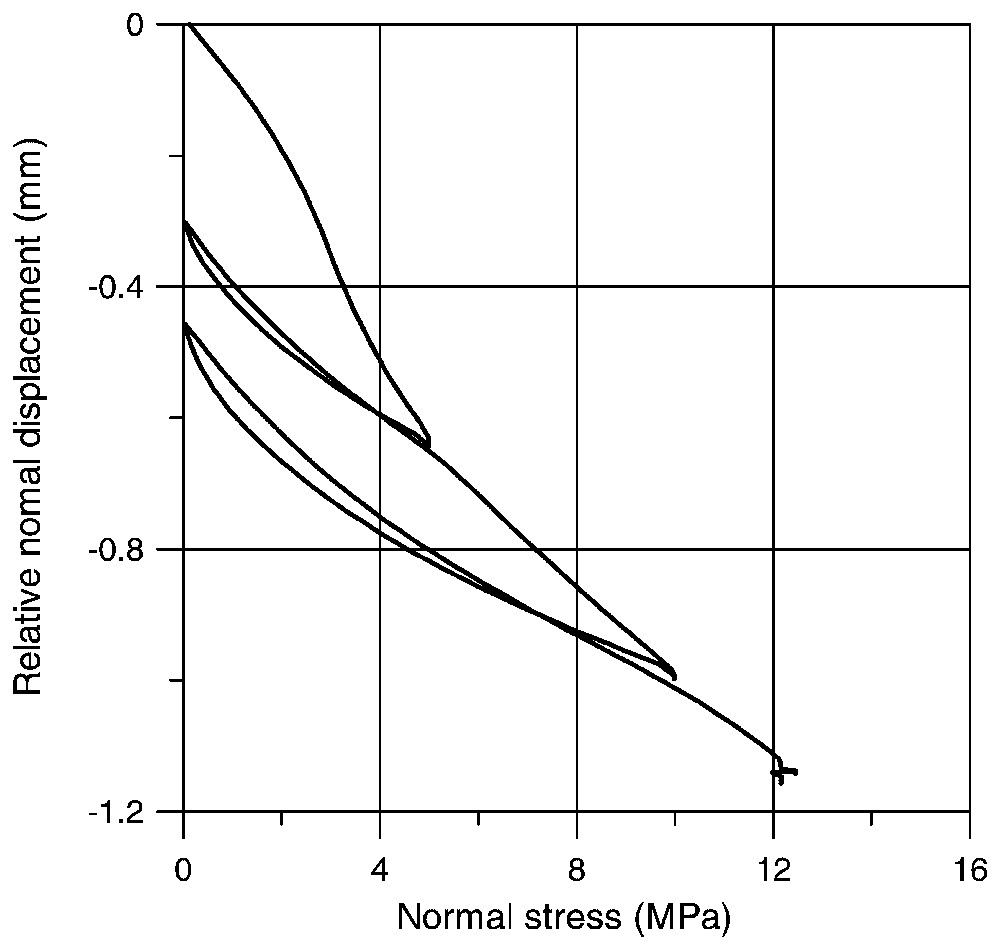
The tangential stiffness of the joint is estimated as k_t=13.9 MPa mm⁻¹. The response to normal loading is shown in Fig. 9. Notice that under constant normal force, the normal stress was increasing with increasing tangential relative displacement (due to cross-section reduction) and reached a value σ≈15 MPa (Fig. 10a). The normal stiffness of the joint was increasing with normal stress from about k_n=10.8 MPa mm⁻¹ at low normal stress, to k_n=17.7 MPa mm⁻¹ at normal stress σ=12 MPa.

Fig. 9
Cyclic normal loading.
Chargement normal cyclique.

Fig. 10
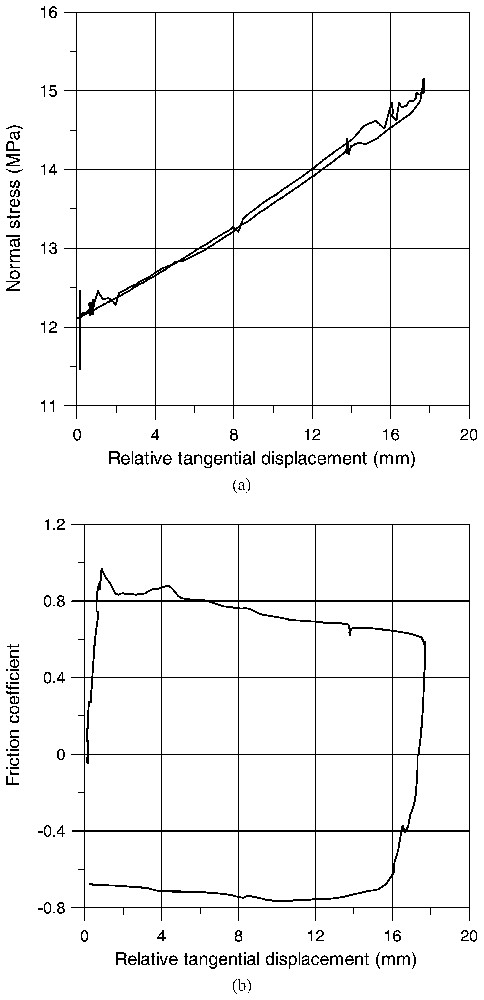
Direct shear experiment under constant normal force: (a) evolution of normal stress; (b) friction coefficient.
Essai de cisaillement direct sous force normale constante : (a) évolution de la contrainte normale ; (b) coefficient de frottement.

The friction coefficient, defined as the ratio between shear stress and normal stress

\tan ϕ = \frac{τ}{σ}

(15)

is plotted in Fig. 10(b) versus the relative tangential displacement. It shows a sharp peak, which corresponds to the rupture of the contact between the limestone and the breccia. The peak corresponds to a friction angle of φ_p=44°, which is close to the internal friction angle of the intact limestone. The residual friction angle of the joint is almost the same in loading and unloading and is φ_r≈32°. It is observed that the peak is not so sharp when the direction of the shear is inverted, which reflects the rapid wear of the contact surface of the joint.

Important porosity reduction is observed for the first cycle. Notice that pore closure is frequently observed in uniaxial testing of highly porous rocks. The contractant character of the interface, when sheared is shown in Fig. 11. The corresponding dilatancy angle is negative, ψ=−7°, during the loading phase and positive, ψ=5°, during the unloading phase.

Fig. 11
Direct shear experiment under constant normal force: contractancy of the joint during shear.
Essai de cisaillement direct sous force normale constante : contractance du joint sous cisaillement.

The mineralogical composition of the crushed material exactly at the contact between the limestone and the breccia (Fig. 12) after the shear test has been analysed using X-ray diffraction and was found as follows.

Calcite : 77 % . Chlorite : 1.5 % . Quartz : 7 % .

Illite : 4.5 % . Albite : 1.5 % . Amorphous : 8.5 % .

The presence of quartz can be related to the close formation of radiolarites. The presence of clay minerals such as illite and chlorite is quite common in fault zones. At this stage of the study, it is not clear whether albite was pre-existent or is an indication of a first stage of metamorphism at a temperature of the order of one hundred degrees Celsius.

Fig. 12
The contact zone between the limestone and the breccia tested in direct shear.
Zone de contact entre le calcaire et la brèche, testée en cisaillement simple.

5 Conclusions

Preliminary results of the experimental characterisation program performed on fault zone cores from Aegion Fault have showed that:

– the clayey core of the fault has a very low fluid permeability and exhibits contractant volumetric behaviour when heated; thus rapid shear deformation may lead to fluid pressurisation inside the fault;
– during drained triaxial tests at constant temperature and confinement, the material is reaching under continuous compaction the critical state (i.e., the state of constant volume and constant deviator);
– the frictional resistance of the material increases slightly with temperature and strain rate;
– the joint between the carbonate zone and the cataclastic bands shows a brittle and contractant behaviour with a residual friction angle of about 32°, which is higher by 3° than the friction angle at critical state of the clay core.

Further experimental studies including the complete mechanical characterisation of the breccia zone and of the interface between this zone and the clayey gouge will be presented in a near future.

Acknowledgements

The authors wish to acknowledge the EU project ‘DG-Lab Corinth’ (EVR1-CT-2000-40005) for supporting this research. They also wish to thank Prof. V. Perdikatsis (Technical University of Crete, Greece), Dr. E. Carrio and Dr. A. Giraud (University Joseph-Fourier, Grenoble, France), Dr. S. Guedon-Dubied and F. Martineau (‘Laboratoire central des ponts et chaussées’, Paris, France) for their contributions in the X-ray petrographic analysis and geological interpretation of the samples.