Abridged English version
Groundwater pollutions by Dense Non-Aqueous Phase Liquids (DNAPL) such as chlorinated solvents constitute a large and serious environmental problem. Identification of the pollution sources is uneasy due to the fact that the chlorinated solvents can rapidly migrate down to the bottom of the aquifer or along different paths than the water [1]. Moreover, they are often present at residual saturation in the aquifer and thus not easy to detect in water or soil samples [5,10].
The Partitioning Interwell Tracer Test (PITT) consists in injecting tracers in the aquifer to detect and quantify pollution sources. The experimental and theoretical basis for the retention of dissolved tracers by the immobile organic phase and the impact on their transport are given by [6] and [11]. The organic fluid phase retains reversibly the reactive tracer, involving a retardation in comparison with the non-reactive or conservative tracer. The assessment of the partitioning between the tracers and the organic phase is thus essential to successfully apply the PITT.
The partitioning coefficient, defined as the concentration ratio of the reactive tracer in the organic phase and in the aqueous phase at equilibrium, can be determined by batch (static) or column (dynamic) experiments. In our study, both types of experiments have been conducted. The batch experiments undertaken consist in mixing during 15 to 120 min a volume of 28 ml of trichlorethylene (TCE) and a volume of 28 ml of an aqueous solution containing the ideal tracer isopropanol and the reactive tracer 4-methyl 2-pentanol (4m2p) at concentrations ranging from 400 to 800 mg l−1. Chromatographic analysis of the aqueous phase allows us to quantify the mass of tracer that has been transferred to the organic phase and to calculate the static partitioning coefficient Kn,w (4). The obtained partitioning coefficient for the reactive tracer with TCE is about 8 (Fig. 1).

Coefficient de partage statique du 4m2p en fonction de la durée d'agitation.
Static partitioning coefficient of 4m2p as a function of the mixing time.
Column experiments have been undertaken with a known volume of TCE. The glass columns, height 100 cm and diameter 9 cm, are water saturated and filled with a medium-size homogeneous sand, described in [1]. The TCE is injected under water into the column to limit its volatilisation. The tracer solution is then injected in the lower part of the column and samples are taken at the upper part before and during all the experiments. Three column tracer tests are undertaken at a room temperature of 15 °C and one at a temperature of 20 °C, with tracer flow velocities of 10, 9.4, 4.9, and 0.25 m d−1. The measured tracers breakthrough curves are then used to calculate the dynamic partitioning coefficient with (6), deduced from (3).
Comparison of the static and dynamic experiments allowed us to suggest a partitioning kinetics between the reactive tracer 4m2p and TCE, as a function of the tracer flow velocity through the porous medium (Fig. 2).
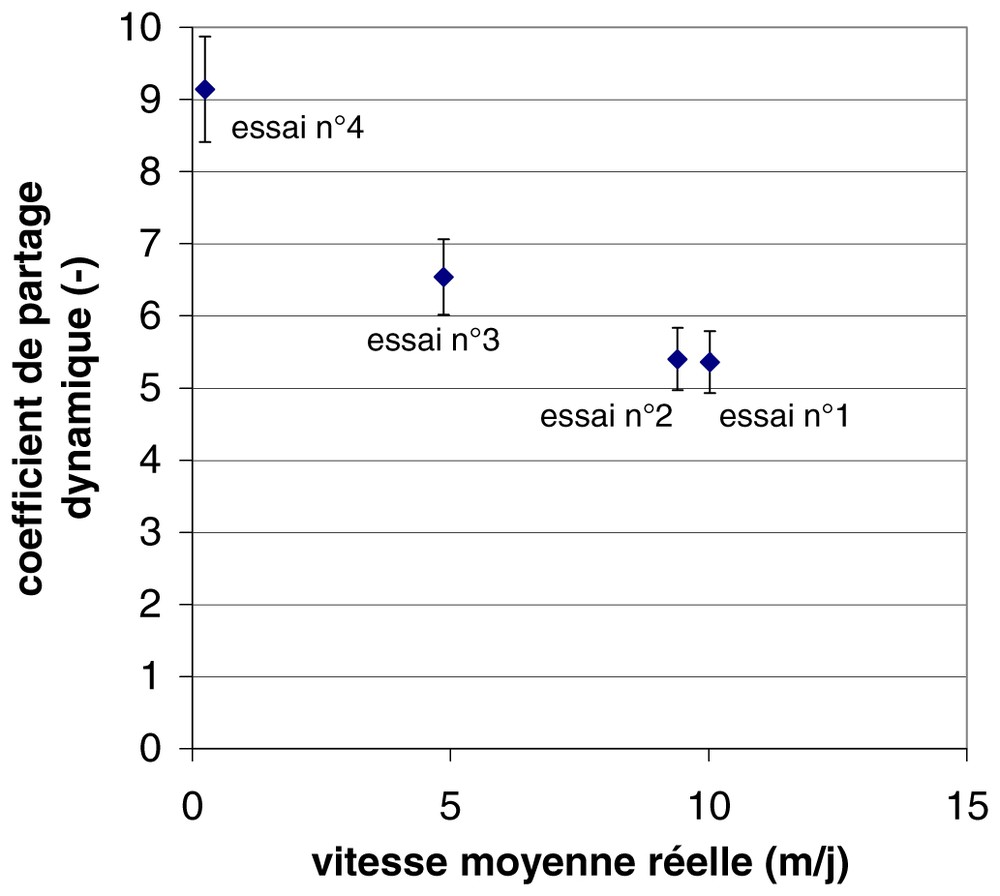
Coefficient de partage dynamique du 4m2p en fonction de la vitesse réelle moyenne.
Dynamic partitioning coefficient of 4m2p as a function of the mean flow velocity.
One of the main hypotheses of the PITT method is an instantaneous partitioning equilibrium [11]. Here we suppose that the tracer concentrations in the organic and aqueous phases can be described by a first-order kinetics introducing a transfer coefficient α (7). To describe the transport of the partitioning tracer in the porous medium, we applied the concept of mobile/immobile zones [4] and introduced an extended transport model similar to the one suggested by Herr et al. [8]. Interpretation of the measured breakthrough curves with the first order kinetic model (8) is shown in Figs. 3–5. In our numerical simulations, α was the only fitted transport parameter. Its value is the same for the three first experiments, which underscores the existence of a partitioning kinetics between the reactive tracer and the organic phase. In the case of the 4th experiment, α was about two orders of magnitude lower. However, the interpretation of this result is partly uncertain due to an incomplete experimental mass recovery of the partitioning tracer, a different temperature and a much longer injection time.
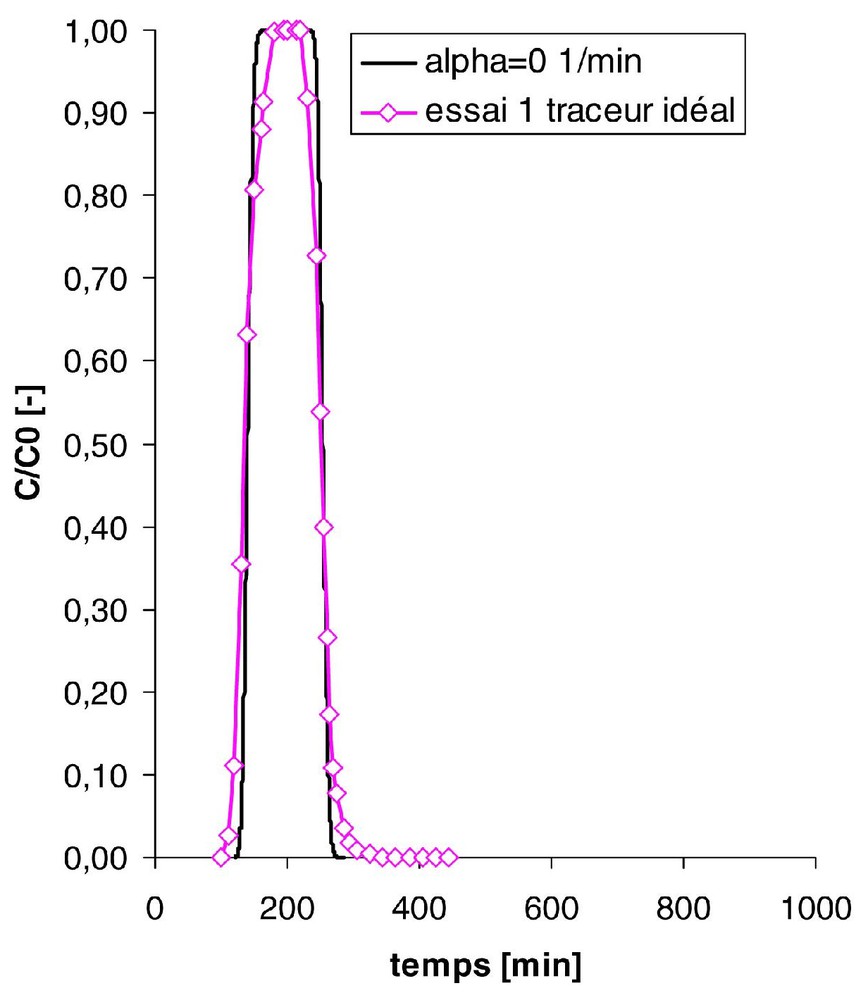
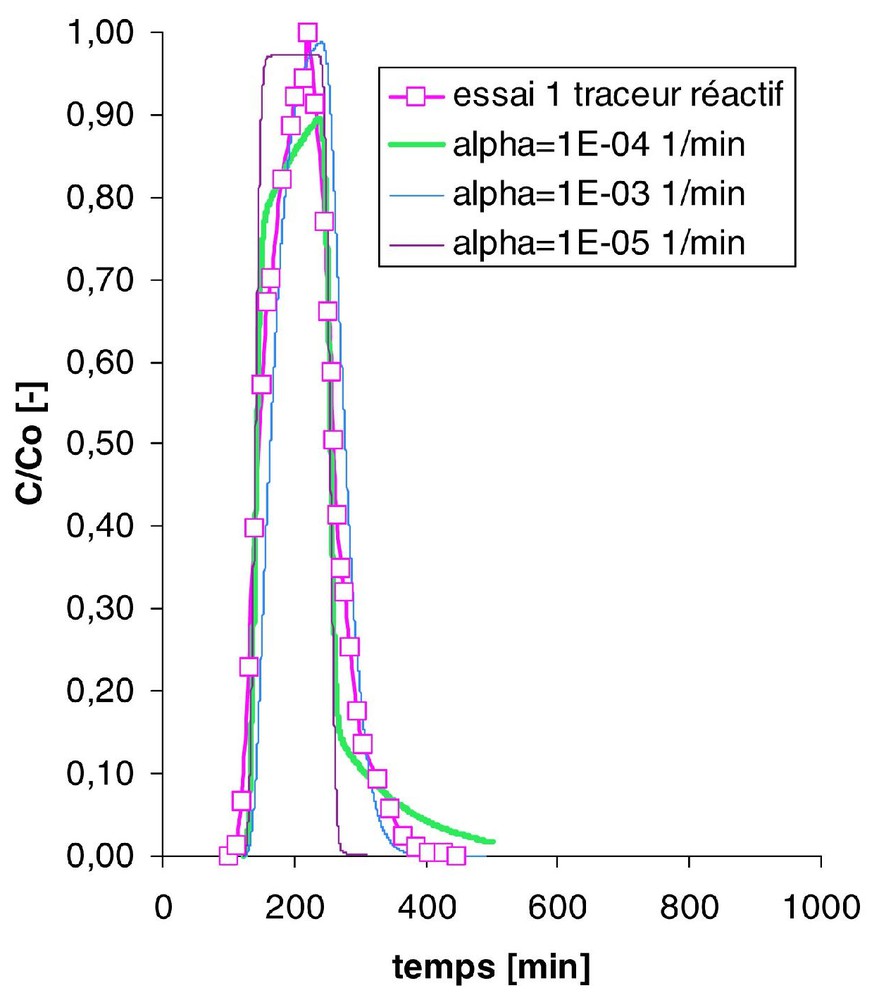
Ajustement des courbes de sortie des traceurs idéal (ipa) et réactif (4m2p) de l'essai 1 à l'aide du modèle d'échange cinétique (les concentrations du traceur C sont normalisées par rapport à la concentration initiale C0).
Fit of the measured breakthrough curves of the ideal (ipa) and partitioning (4m2p) tracers of run 1 using the kinetic transfer model (tracer concentrations C are normalised to the initial concentration C0).
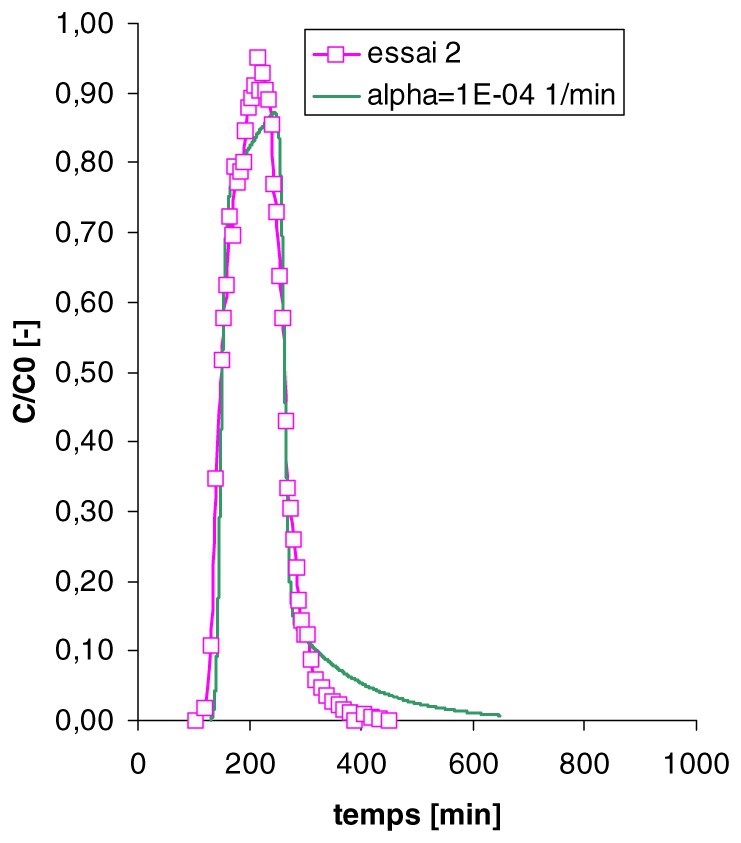
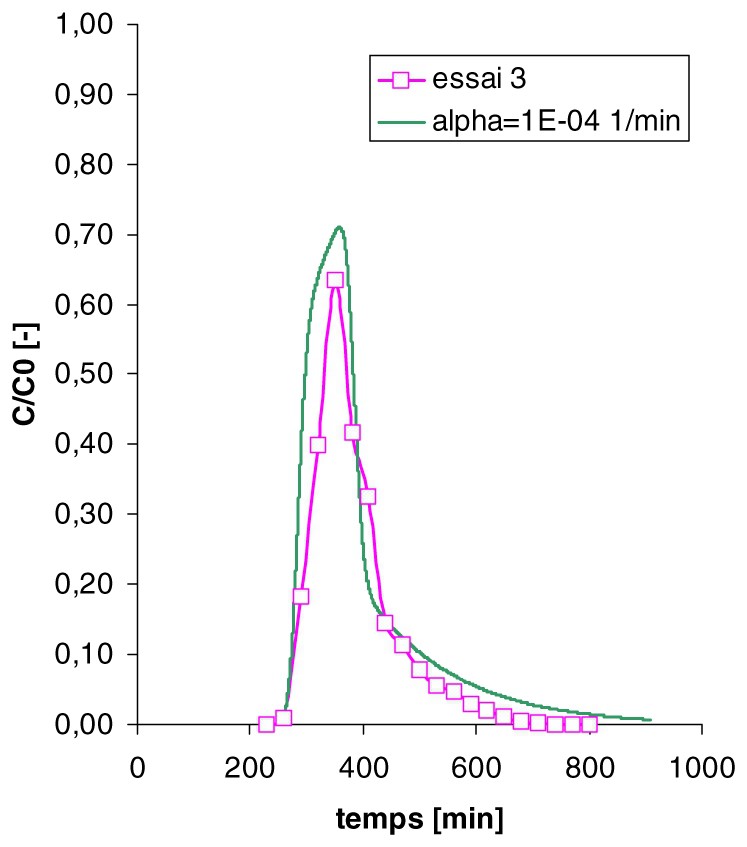
Simulation des courbes de sortie des traceurs réactifs (4m2p) des essais 2 et 3 à l'aide du modèle d'échange cinétique.
Modelling of the breakthrough curves of the partitioning tracer (4m2p) in run 2 and 3 based on the kinetic transfer model.
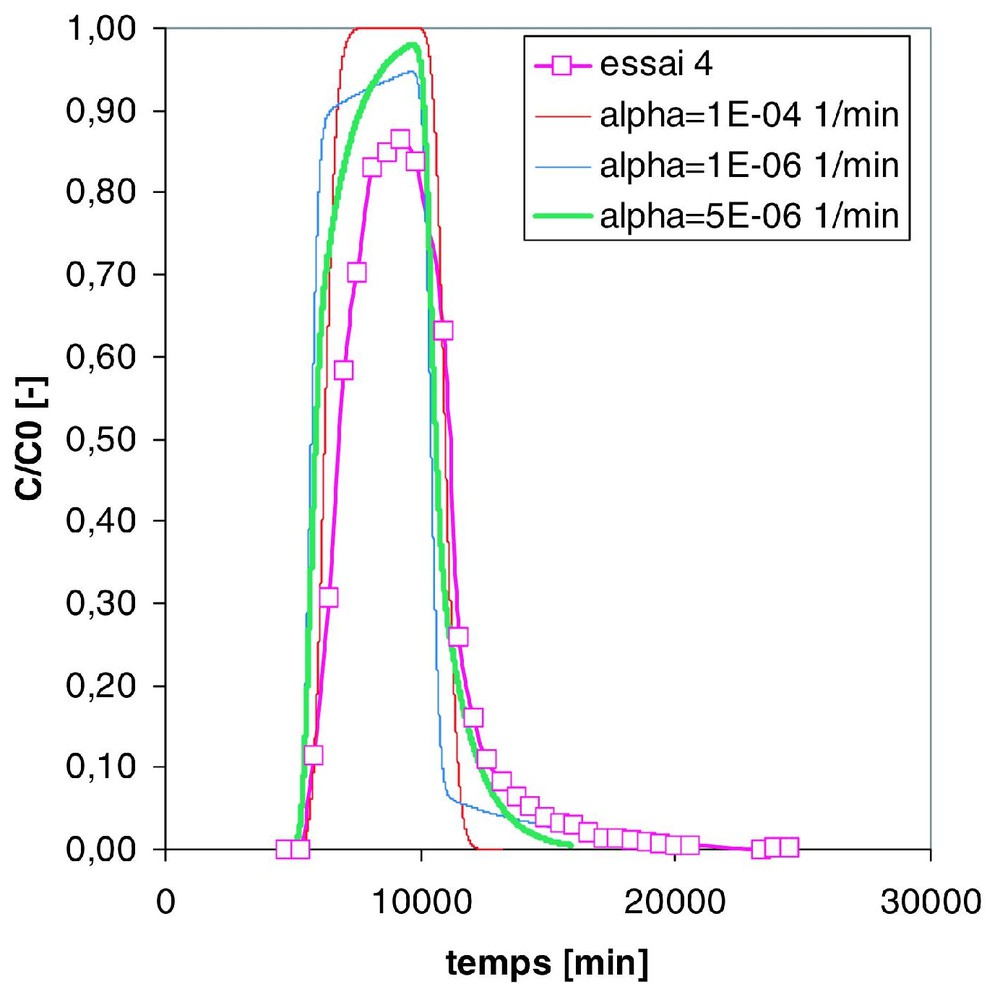
Simulation de la courbe de sortie du traceur réactif de l'essai 4 à l'aide du modèle d'échange cinétique en faisant varier le coefficient de cinétique d'échange α.
Modelling of the breakthrough curves of the partitioning tracer (4m2p) in run 4 based on the kinetic transfer model, with changes of the kinetic transfer coefficient α.
1 Introduction
La contamination d'aquifères par des solvants chlorés comme le trichloréthylène (TCE), est un problème environnemental sérieux et étendu. Il est difficile d'identifier ces sources de pollution du fait de leur forte densité, de leur forte volatilité et du fait qu'ils peuvent avancer le long de chemins qui peuvent être différents de ceux qu'emprunte l'eau [1]. De plus, ils sont souvent présents à saturation résiduelle, il est donc difficile de les observer dans de simples échantillons de sol ou d'eau [5,10].
Le test de traçage (Partitioning Interwell Tracer Test), adaptation et extension de plusieurs méthodes existantes relevant de l'hydrogéologie et de l'ingénierie pétrolière, est une technique de caractérisation des zones sources de pollution de NAPL (Non-Aqueous Phase Liquids), qui consiste à injecter des traceurs devant permettre de détecter et de caractériser la distribution d'une contamination par solvants chlorés dans les environnements souterrains [11]. Son principal avantage est que le volume de milieu poreux traversé et pris en compte pour déterminer la saturation en polluant est beaucoup plus grand que celui qui est pris en compte dans les échantillons de sol ou les mesures géophysiques. Le mélange de traceurs injectés contient un traceur idéal et au moins un traceur réactif. Le traceur idéal n'est pas affecté par la présence de la phase organique (solvant), tandis que le traceur réactif est distribué entre les phases aqueuse et organique, lorsqu'il se déplace le long des lignes de courant, et sera retardé du fait de son partage réversible avec la phase organique immobile. Une comparaison des courbes de sortie du traceur idéal et du traceur réactif peut fournir une information quantitative sur la ou les phase(s) organique(s) présente(s) dans le milieu poreux [11], car l'étendue de la séparation des deux courbes de sortie dépend notamment de la saturation en solvant et du coefficient de partage des traceurs.
La distribution des traceurs entre phases est fonction à la fois de la relation d'équilibre de partage et de limitations provenant des hétérogénéités et/ou de la géométrie du déversement ainsi que de facteurs en relation avec le dimensionnement et la mise en œuvre du test. Une hypothèse commune à la majorité des études rapportées est cependant que les traceurs réactifs se distribuent de manière linéaire entre phase aqueuse et phase organique, sous conditions d'équilibre local de partage qui, s'il n'est pas atteint, rend difficile l'analyse des données des traceurs et soumet le résultat du traçage à de larges erreurs et incertitudes [9].
Le propos de cette étude est d'abord la détermination du coefficient de partage des traceurs isopropanol (ipa) et 4-méthyl 2-pentanol (4m2p) avec le trichloréthylène (TCE), en essais statiques et dynamiques, ensuite la mise en évidence d'une cinétique de partage de ces traceurs avec le TCE lors d'essais en colonne et, enfin, l'interprétation de ces derniers à l'aide d'un modèle de cinétique d'échange.
2 Théorie
Les bases expérimentales et théoriques de la rétention de traceurs par les phases organiques immobiles non miscibles et son impact sur le transport d'un soluté ont été décrites par [3] et [11]. La saturation en polluant Snr dans le milieu poreux est calculée par la relation (1) :
| (1) |
| (2) |
Puis le volume du polluant organique Vn en contact avec le traceur réactif [L3] est donné par (3) :
| (3) |
| (4) |
Ce coefficient de partage peut être mesuré en réalisant des essais statiques en réacteur fermé [11] et/ou des essais sur colonnes de milieu poreux [7].
3 Quantification du coefficient de partage
3.1 Essais statiques en réacteurs fermés
Pour la détermination du coefficient de partage statique des traceurs isopropanol et 4-méthyl 2-pentanol avec le TCE, un volume de 28 ml d'une solution aqueuse contenant des concentrations de 400 à 800 mg l−1 de chacun des traceurs a été mis en contact par agitation magnétique avec 28 ml de TCE, pendant 15, 60 et 120 min à des températures de 15 et 20 °C (Fig. 1). Après agitation, les échantillons sont laissés au repos pendant plusieurs minutes à plusieurs heures afin de laisser aux deux phases le temps de se séparer. Puis 20 ml sont prélevés dans la phase aqueuse et placés dans un tube à essai avec 8 μl d'un étalon interne (isobutanol). Après agitation sur le vortex, 0,5 μl de cette solution sont prélevés et analysés par chromatographie en phase gazeuse, puis la concentration du traceur dans le TCE est calculée à partir de la relation (5) :
| (5) |
La concentration du traceur dans le solvant chloré peut ensuite être tracée en fonction de sa concentration dans l'eau ; en répétant ainsi l'essai en conditions isothermes, la pente de la droite est le coefficient de partage statique.
3.2 Essais dynamiques en colonne
Une seconde manière de mesurer le coefficient de partage des traceurs avec le TCE est de réaliser un test de traçage en colonne, avec un volume connu de TCE.
Les colonnes utilisées, en verre avec embouts en aluminium, d'une hauteur de 100 cm et d'un diamètre intérieur de 9 cm, sont remplies d'eau, puis de sable moyen homogène (d50≈0,45 mm, porosité de 0.4) [1,2]. Afin d'éviter la perte de solvant par volatilisation lors de sa mise en place dans le milieu poreux, le TCE est injecté sous une lame d'eau de 1 à 2 cm. Une fois le TCE stabilisé dans le milieu poreux, la solution de traceurs idéal et réactif (ipa et 4m2p, de concentration initiale de l'ordre de 800 mg l−1) est injectée par le bas de la colonne à l'aide d'une pompe péristaltique et de tuyaux en téflon, inertes aux solvants et alcools. Des prélèvements de solution et des mesures du débit d'injection sont effectués à l'entrée et à la sortie de la colonne, avant et pendant toute la durée des essais (de 7 h à 24 jours ; Figs. 3–5). Les trois premiers essais ont été réalisés à 15 °C et le quatrième à 20 °C.
Les temps moyens de sortie des traceurs peuvent être utilisés pour calculer le coefficient de partage dynamique avec l'équation (6), déduite de la relation (3) :
| (6) |
4 Discussion des résultats expérimentaux
4.1 Détermination du coefficient de partage statique
Pour la gamme de concentrations testées (entre 400 et 800 mg l−1), les coefficients de partage statiques des deux traceurs sont constants [2]. L'équilibre de partage avec le TCE est atteint dès 15 min : le temps d'agitation n'a plus d'influence sur les valeurs du coefficient de partage des traceurs avec le TCE au-delà de 15 min. En revanche, la Fig. 1 montre bien l'effet éventuel de la température sur la valeur du coefficient de partage du traceur réactif. L'isopropanol a un coefficient de partage de 0,1 (±2 %) à 15 et 20 °C. Le 4-méthyl 2-pentanol a un coefficient de partage de 8 (±2 %) à 15 °C et de 8.5 (±2 %) à 20 °C (Fig. 1).
4.2 Détermination du coefficient de partage dynamique
Quatre essais en colonne ont été effectués à des vitesses d'écoulement différentes (Tableau 1). En utilisant le coefficient de partage statique déterminé en réacteur fermé, pour des vitesses d'écoulement des traceurs dans la colonne de l'ordre de 10 m j−1, l'erreur relative sur l'estimation du volume est de −33 % environ. Pour une vitesse de 0,25 m j−1, le volume n'est plus sous-estimé mais approché, avec un écart relatif de 7 %. Le volume de TCE mis en place dans la colonne est donc d'autant mieux estimé que la vitesse est diminuée, c'est-à-dire que le temps de contact entre les traceurs et le solvant est augmenté.
Estimation du volume de TCE par la méthode du traceur bisoluble
Estimation of the TCE volume with the PITT method
| Essai | Vitesse moyenne réelle [m j−1] | Température [°C] | Volume de TCE mis en place [ml] | Volume de TCE estimé avec statique [ml] | Écart relatif % |
| 1 | 10 | 15 | 60 | 40,20 | −33 |
| 2 | 9,4 | 15 | 70 | 47,27 | −32 |
| 3 | 4,9 | 15 | 70 | 57,19 | −18 |
| 4 | 0,25 | 20 | 30 | 32,24 | 7 |
Sur la base de ces essais en colonne, nous avons ensuite calculé le coefficient de partage dynamique du traceur réactif 4m2p selon l'équation (6), que nous avons représenté sur la Fig. 2 en fonction de la vitesse réelle moyenne d'écoulement (la température de l'eau est de 15 °C pour les trois premiers essais et de 20 °C pour l'essai n∘4). Les coefficients de partage dynamiques obtenus ne sont pas constants, mais indiquent une cinétique de partage entre le traceur 4m2p et le TCE qui est fonction de la vitesse d'écoulement du traceur. Pour les vitesses de 5 et 10 m j−1, les coefficients de partage dynamiques sont très inférieurs au coefficient de partage mesuré par la méthode statique, ce qui peut être une indication de non-équilibre d'échange entre le traceur et le TCE lors de ces essais en colonne. À une vitesse d'écoulement de 0,25 m j−1, en revanche, les conditions dans la colonne permettent d'atteindre l'équilibre de partage : le coefficient de partage dynamique (erreur de 7 %) est proche du coefficient de partage statique.
4.3 Interprétation des essais en colonne à l'aide d'un modèle d'échange cinétique
La théorie de la méthode du traceur bisoluble se base sur l'hypothèse de l'équilibre instantané entre les concentrations de la phase aqueuse et de la phase organique en place, exprimé par la relation (4).
L'existence d'un coefficient de partage dynamique discutée dans la Section 3.2 soutient fortement l'hypothèse d'un non-équilibre local entre les deux concentrations, qui pourrait être approché de façon classique par une cinétique d'échange du premier ordre :
| (7) |
En se basant sur le modèle mathématique de transport convectif-dispersif, avec échange dans un milieu poreux composé de zones mobile et immobile introduit par [4] et en suivant la nomenclature choisie par [8], nous réécrivons l'équation de transport mono-dimensionnel pour la phase aqueuse avec la cinétique d'échange selon l'équation (7) de la façon suivante :
| (8a) |
| (8b) |
| (9) |
Dans notre étude, nous avons résolu numériquement le système d'équations (8) avec un schéma de différences finies, proposé par [12]. L'interprétation des courbes de sortie du traceur réactif mesurées a été effectuée au moyen du modèle numérique développé pour des conditions expérimentales données. Le Tableau 2 résume les paramètres du modèle choisis. La colonne de milieu poreux a été discrétisée avec des mailles de 1 mm de longueur. Le coefficient de cinétique d'échange α est le seul paramètre qui a été ajusté lors de la simulation numérique. Le coefficient obtenu par calage pour l'essai 1 (Fig. 3) a été ensuite utilisé dans les simulations des courbes de sortie du traceur réactif des essais 2 et 3 (Fig. 4). Les courbes de concentration mesurées et simulées sont en bon accord, ce qui confirme l'existence d'une cinétique de partage du premier ordre entre le traceur réactif et le polluant mis en place. En revanche, la simulation de l'essai 4 avec ce même coefficient de cinétique d'échange résulte en une courbe de concentration très différente de celle observée. La modélisation de cet essai a nécessité la diminution du coefficient α de près de deux ordres de grandeur (Fig. 5, Tableau 2). L'interprétation de ce dernier essai reste cependant délicate, dans la mesure où la masse récupérée en fin d'expérimentation est de 15 % inférieure à la masse de traceurs injectée dans la colonne. De plus, l'essai a été mené à 20 °C et la durée d'injection des traceurs est bien plus élevée que pour les autres essais.
Paramètres du modèle d'échange cinétique
Parameters of the kinetic transfer model
| Unité | Essai 1 | Essai 2 | Essai 3 | Essai 4 | |
| – | 0,39056 | 0,38896 | 0,38896 | 0,39528 | |
| – | 0,00944 | 0,01104 | 0,01104 | 0,00472 | |
| cm min−1 | 0,71265 | 0,67131 | 0,34994 | 0,01757 | |
| Durée d'injection des traceurs | min | 114 | 114 | 100 | 4728 |
| Coefficient de partage | – | 8 | 8 | 8 | 8,5 |
| Coefficient de cinétique d'échange | 1 min−1 | 1×10−4 | 1×10−4 | 1×10−4 | 5×10−6 |
| Dispersivité longitudinale | cm | 0,1 | 0,1 | 0,1 | 0,1 |
5 Conclusions et perspectives
La détermination des coefficients de partage dynamiques en colonne de milieu poreux nous a permis de mettre en évidence une cinétique de partage du traceur bisoluble avec le TCE, liée à la vitesse d'écoulement du traceur, confirmée par un modèle mathématique de transport à cinétique d'échange. À la théorie de quantification des sources de pollution [11] pourrait ainsi être intégré un modèle simple de cinétique d'échange, avec calage du coefficient de cinétique d'échange et de la saturation résiduelle en polluant.
Remerciements
Ces études ont bénéficié d'une bourse de thèse co-financée par la région Alsace et d'un soutien financier dans le cadre du contrat de plan État-région Alsace, du PPF « IFARE », du contrat quadriennal 2001–2004, du PNRH de l'INSU/CNRS, de conventions Agences de l'Eau (Inter-Agences, AERM) et de l'ADEME.


