Abridged English version
The aim of the present paper is to improve the understanding of the effect of hydrodynamical factors on the morphological behaviour of intertidal mudflats. The hydrodynamical forcing on mudflats can be divided into three main types: surface gravity waves, tide (and the associated flow) and the wind-induced flows. Our study is limited to the action of a cross-shore tidal current, with or without waves. Such a forcing is representative of what we observe on particular mudflats located in semi-enclosed bays.
The tool for numerical experiments is a hydrodynamical model coupled with a sediment transport model (SiAM [2]) in a 1DH configuration. The hydrodynamical model solves the so-called ‘depth-averaged shallow water equations’. The sediment transport model solves an advection/dispersion equation for the suspended matter. Bottom exchanges are formulated according to Partheniades' formula for erosion and to Krone's for deposition. A constant concentration Clim is fixed at the open boundary during the flood.
Wave heights are calculated using the conservation equation for gravity waves' energy (Eq. (1)). Maximum (τmax) and mean (τm) values of the effective bottom shear stress resulting from current and waves interactions over one period are expressed following Soulsby et al.'s procedure [12]. Based on numerical simulations performed by Huynh-Thanh [6], a sinusoidal variation of the instantaneous bottom shear stress τinst is formulated (Eq. (4)). Deposition is calculated according to Krone's formula using only the maximum value of the bottom shear stress τmax (Eq. (5)). On the other hand, it is suggested that the erosion rate respects the evolution of the effective bottom shear stress during the wave period. Partheniades' formulation is thus adapted to the presence of waves (Eq. (6)), by means of time integration over the wave period.
The first numerical experiment was performed with a semi-diurnal tide only (tidal range: 4 m). After more than 90 years of simulation, the mudflat is still accumulating sediment and prograding (advancing seaward). Furthermore, the mudflat profile reaches equilibrium after about 60 years of simulation. The shape of this profile is convex. This convexity as well as the tendency to prograde is in agreement with the results of numerical simulations performed by Pritchard et al. [10]. They are also in agreement with the observations showing that accreting mudflats are convex (e.g., [7]). The shape of this equilibrium profile is independent of the initial profile, but not the time which it takes to reach equilibrium: for an initial slope of the mudflat close to the equilibrium profile (see Fig. 3), equilibrium appears before 13 years. The equilibrium profile seems to be determined by the hydrodynamical forcing, the sediment supply and the type of sediment. The shape of the equilibrium profile is such that the deposition/erosion balance is uniform along the mudflat. If the mudflat slope were uniform, the upper part would experience relatively weak flow and stresses, because this section is wet only around the high tide slack; then, deposition would be favoured. On the other hand, when the upper part becomes less steep (i.e., the profile becomes convex), the tidal flow increases, which reduces the deposition. Thus the deposition/erosion balance during the tidal period is of the same order as over the lower flat and the equilibrium profile can be preserved.

Évolution du profil de l'estran sous l'action d'un courant cross-shore et de vagues de hauteur 0,05 m à la limite aval ; en tiretés, le profil après 13 ans sans vagues : la pente moyenne est analogue à celle de la Fig. 1.
Evolution of the mudflat profile under the action of a cross-shore current and 0.05-m waves at the open boundary; in dotted line, the profile after 13 years without waves: the average slope is similar to that in Fig. 1.
Adding small (locally wind-generated) waves to the tidal forcing notably changes the morphological behaviour of the mudflat. Fig. 3 represents the evolution of the profile over 13 years, with permanent waves (5 cm high) at the open boundary, and shows the profile (shape and location) after 13 years of simulation without waves for the same initial profile. First, the total quantity of sediment deposited on the flat is smaller for the simulation with waves. Additional energy is provided by the waves to erode the muddy bed or to avoid deposition. As previously, the mudflat progrades, keeping an equilibrium profile. The characteristic feature of this profile is that it is steeper at the top, where the erosive action of waves can offset the deposition around slack water, without needing a stronger current. For higher waves (10 cm high at the open boundary; Fig. 4), the equilibrium profile is strongly concave at the top and at the bottom. This results from an increase of the waves' erosive action at high and low water tidal slacks in places where the water depth remains low for a long time. The main result of this simulation is that the mudflat itself reaches a steady equilibrium, i.e. after a few years the mudflat position is stationary. In that case, the energy produced by waves is high enough (in terms of erosion) to exactly offset the sediment input at the open boundary.

Évolution du profil de l'estran sous l'action d'un courant cross-shore et de vagues de hauteur 0,1 m à la limite aval.
Evolution of the mudflat profile under the action of a cross-shore current and 0.1-m waves at the open boundary.
Numerical experiments performed with a 1DH morphodynamical model show that under the action of a cross-shore current and providing a sediment input at the sea boundary, an intertidal mudflat progrades with an equilibrium profile. When waves are added to the tidal forcing, the upper profile is more concave and the mudflat can reach a steady position.
1 Introduction
L'objectif de ce travail est d'essayer de mieux comprendre l'effet de facteurs hydrodynamiques sur le comportement sédimentaire d'estrans vaseux. Il s'agit aussi d'établir comment un forçage donné agit pour modeler le profil général d'un estran sur des échelles de temps allant jusqu'à quelques dizaines d'années. Le forçage hydrodynamique sur une vasière peut être subdivisé en trois types principaux : les vagues, la marée (et le courant associé) et le courant induit par le vent. Les vasières intertidales sont soumises simultanément à ces trois types de forçages, mais à des degrés divers suivant leur localisation et la variabilité saisonnière des forçages. On peut décomposer le courant de marée en composantes parallèle et perpendiculaire au rivage, l'une d'elles pouvant dominer selon la configuration du secteur côtier [8].
La présente étude se limite à l'action d'un courant de marée cross-shore, avec ou sans vagues, ce qui autorise l'usage d'un modèle unidimensionnel cross-shore. Un tel forçage peut être représentatif de ce que l'on observe sur certaines vasières dans des baies semi-fermées (par exemple, la vasière de Brouage, à l'est de la baie de Marennes-Oléron [1]). Comprendre les effets d'un forçage simple sur la morphologie sera également utile pour appréhender ce qui se passe dans le cas d'un forçage plus complexe.
Cette étude s'appuie sur l'utilisation d'un modèle mathématique courantologique couplé à un modèle de transport sédimentaire : le modèle SiAM-2DH [2], qui a été adapté aux simulations morphodynamiques cross-shore. Roberts et al. [11] avaient déjà recherché le profil d'équilibre d'un estran vaseux en utilisant deux modèles numériques, dont l'un d'eux est celui utilisé ici. Les résultats de ces simulations montrent que, pour un forçage de marée seule, le profil à l'équilibre est convexe dans sa partie haute et que la largeur de l'estran est indépendante du marnage ; lorsqu'elles sont prises en compte, les vagues ont pour effet de rendre le profil concave. Pritchard et al. [10], ainsi que Waeles [13], mais indépendamment, ont établi que, sous l'action d'un courant cross-shore sans vagues, l'estran prograde continuellement lorsque le signal de marée imposé à la limite marine est purement sinusoı̈dal.
L'objet est ici d'étudier, avec un modèle de propagation de vagues plus complet que celui de Roberts et al. [11], l'effet des vagues, d'une part, sur le profil d'équilibre d'un estran vaseux et, d'autre part, sur sa progradation. Cependant, les forçages et les matériaux restent schématiques, de telle sorte qu'on ne cherche pas à simuler un estran réaliste, mais seulement à comprendre les mécanismes de son évolution.
2 Description du modèle
2.1 Principe général du modèle
Le modèle intégré selon la dimension verticale est configuré en 1DH. Sur l'estran, l'hydrodynamique est contrôlée par une bathymétrie susceptible d'évoluer de façon importante, ce qui nécessite un couplage morphodynamique (par exemple, [3,4]) : la bathymétrie est réactualisée périodiquement en fonction des érosions/dépôts. Le modèle est constitué d'un module de calcul du courant, d'un module de calcul de vagues ainsi que d'un module calculant le transport de sédiment en suspension. Les échelles de temps associées à l'évolution du fond sédimentaire étant nettement plus longues que celles des processus hydrodynamiques, les bilans de dépôt et d'érosion qui servent à réactualiser la bathymétrie ne sont calculés qu'à intervalles de temps supérieurs au pas de temps hydrodynamique.
2.2 Le modèle courantologique
Le modèle hydrodynamique est un modèle intégré sur la verticale ; la dynamique du fluide est décrite par une formulation unidimensionnelle des équations de St Venant [11]. Les variations de la cote de la surface libre sont imposées à la limite marine du domaine. Les équations sont résolues en chaque maille du domaine selon une méthode implicite en différences finies issue du modèle SiAM-2DH [2], dégénéré ici pour une modélisation 1DH.
2.3 Calcul de vagues
Les hauteurs de vagues sont calculées en utilisant la conservation de la densité d'action étant l'énergie des ondes de gravité. La fréquence relative des ondes de gravité σ étant supposée constante, le calcul s'effectue en considérant la conservation de l'énergie. On peut considérer, en première approximation, qu'une vague se propageant à travers l'estran ne voit pas les variations du niveau de l'eau liées à la marée. En effet, le temps de propagation d'une vague en travers de l'estran est de quelques minutes, tandis que la période de marée dépasse une dizaine d'heures. Ainsi, pour un état stationnaire et dans le cas d'une onde monochromatique (représentation la plus simple d'un régime de vagues), l'équation de conservation (cross-shore) de l'énergie s'écrit :
| (1) |
| (2) |
La vitesse de groupe relative vaut : ∂σ/∂k=(c/2)(1+2kh/sh(2kh)), où est la vitesse de phase de l'onde de gravité. Pour chaque maille, le nombre d'onde k est calculé à partir de la relation de dispersion : k=σ2/(gth(kh)), qui est résolue de manière itérative en prenant pour valeur initiale le nombre d'onde en profondeur infinie, c'est-à-dire σ2/g. Pour les simulations présentées ici, il a été vérifié que le critère de déferlement (H/h>0,8) n'est jamais atteint, ce qui permet de faire l'hypothèse que la théorie linéaire reste acceptable.
2.4 Modèle sédimentaire
2.4.1 Frottement induit par l'interaction non linéaire houle–courant
Les contraintes de cisaillement sur le fond susceptibles d'éroder ou d'empêcher le dépôt de sédiment sont calculées à partir des tensions dues à un courant seul ou à des vagues seules. La contrainte de cisaillement liée au courant seul peut être calculée en fonction du courant cross-shore u selon la formulation quadratique : τc=ρCDu|u|, où . z0 est la longueur de rugosité et e vaut 2,718.
La contrainte de cisaillement maximale générée par la houle seule est donnée par :
| (3) |
| (4) |
2.4.2 Transport, dépôt et érosion en présence de vagues
Le transport de la concentration de matières en suspension C est simulé par une équation classique d'advection–dispersion. Une concentration de matière en suspension Clim est imposée à la limite marine en période de flot. Cette condition en limite marine représente l'apport externe de sédiment à la vasière. Les flux d'échange entre l'eau et le fond sédimentaire, par érosion ou dépôt, constituent des termes sources ou puits de l'équation d'advection–dispersion. Pour le dépôt, la loi de Krone est utilisée en calculant la probabilité de dépôt en fonction de la seule valeur maximale de la contrainte de cisaillement, considérant que la période de vague est très courte devant le temps nécessaire à un tassement éventuel (au moins quelques dizaines de minutes) : le dépôt ne pourra pas avoir lieu dès lors que la tension critique de dépôt τd est dépassée pendant la période de vague. Le flux de dépôt Qd vaut donc :
| (5) |
| (6) |
Par souci de simplification, le phénomène de tassement n'est pas pris en compte. Cependant, une valeur de τd plus faible que celle de τe permet de distinguer les dépôts frais des sédiments moyennement consolidés. Pour des contraintes modérées (τd<τc<τe), tous les dépôts susceptibles de se produire sont remis instantanément en suspension ; lorsque τc>τe, la contrainte est suffisamment forte pour que les sédiments consolidés soient également remis en suspension.
2.4.3 Réactualisation de la bathymétrie
La réactualisation de la bathymétrie résulte directement du bilan net Qd−Qe à chaque pas de temps morphodynamique.
2.5 Paramétrage général du modèle d'estran
Le pas d'espace est de 100 m, les pas de temps morphodynamique et hydrodynamique sont respectivement de 1800 et 60 s.
Paramètres sédimentaires : Clim (concentration en limite marine en flot) : 0,1 g l−1, Ws : 1 mm s−1, τd:0,1 N m−2, τe:0,2 N m−2, me:0,2 kg m−2 s−1.
La valeur retenue pour τe est une valeur moyenne pour un fond purement vaseux (par exemple, [9]). Des tests de sensibilité concernant la vitesse de chute, l'apport de matières en suspension ainsi que l'érodabilité du sédiment seront présentés dans un article en préparation. Initialement, le fond sédimentaire est constitué de 4 m de vase érodable.
Le courant cross-shore résulte d'un signal de marée semi-diurne (marnage : 4 m) à la limite aval ; l'origine de l'axe z est telle que la basse mer (BM) est à +1 m et la pleine mer (PM) à +5 m.
Deux configurations ont été adoptées, qui se distinguent par la pente du fond initiale : (a) la pente du fond est de 2,95×10−3 sur 5 km et se prolonge horizontalement vers le large (Fig. 1) : pour permettre des simulations sur le long terme, la longueur du domaine est de 20 km ; (b) la pente du fond est uniforme (10−3) et la longueur du domaine est de 10 km (Fig. 3) : le calcul est donc plus rapide.
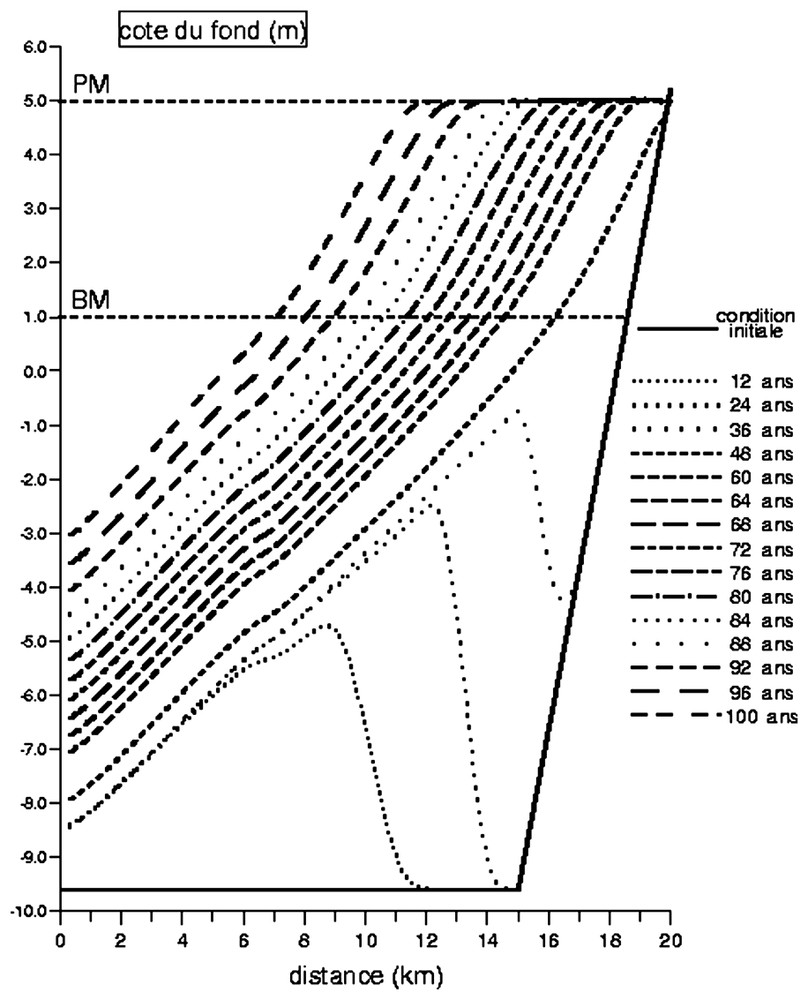
Évolution du profil de l'estran sous l'action d'un courant cross-shore.
Evolution of the mudflat profile under the action of a cross-shore current.
3 Résultats et discussion
3.1 Évolution du profil de l'estran sous l'action d'un courant cross-shore, sans vagues
Un calcul effectué sur une centaine d'années montre que l'estran vaseux prograde continuellement au cours de la simulation (Fig. 1). Le forçage hydrodynamique et la condition en limite marine sur la concentration sont tels que l'estran est toujours en accrétion. On observe que, après un certain temps (60 ans environ), la forme du profil de l'estran tend vers un équilibre, avec une pente moyenne de 7,3×10−4 ; la forme convexe de ce profil est indépendante du profil initial. Ce n'est pas le cas du temps nécessaire pour atteindre ce profil : on observe sur la Fig. 1, pendant les premières années, la formation d'une banquette de vase qui rejoint progressivement la côte. En revanche, sur la Fig. 3 (cas « sans vagues », en tiretés) on voit qu'après 13 ans, le profil d'équilibre était déjà atteint lorsque l'estran initial avait une pente plus proche de ce profil. Cette forme convexe ainsi que la tendance de l'estran à la progradation sont en accord avec les résultats des simulations numériques de Pritchard et al. [10]. Ils le sont aussi avec les observations, qui montrent que les estrans en accrétion ont une forme convexe (par exemple, [7]).
Il semble que le profil d'équilibre soit déterminé par le forçage hydrodynamique appliqué, l'apport de matière en suspension et le type de sédiment. La forme du profil d'équilibre est telle, que le bilan dépôt/érosion est uniforme le long de l'estran. La vitesse du courant de marée cross-shore résulte principalement de la continuité (∂ζ/∂t=−(h∂u/∂x+u∂h/∂x), ζ étant l'élévation de la surface libre) et dépend donc de la pente du fond et du rythme de variation du niveau de la surface libre. Le haut d'estran est atteint uniquement autour de l'étale de pleine mer, lorsque la surface libre varie peu. Ainsi, si la pente y était la même que sur le reste de l'estran, les vitesses y seraient comparativement plus faibles. Ces faibles vitesses seraient susceptibles de favoriser des dépôts, générant alors un profil convexe. Cette convexité a pour effet de réduire la pente en haut d'estran (soit ∂h/∂x, puisque la surface libre reste quasiment horizontale [8], et donc d'augmenter les vitesses et ainsi, à l'équilibre, d'y réduire les dépôts. Le bilan de dépôt/érosion pendant une période de marée peut alors être du même ordre que plus au large.
Il apparaı̂t effectivement que les variations, de bas en haut de l'estran, des maxima de contraintes de cisaillement au cours de la marée sont plus importantes pour un profil de pente uniforme que pour le profil à l'équilibre (Fig. 2). Cela confirme l'approche théorique de Friedrichs et Aubrey [5], selon laquelle une morphologie stable résulte d'une distribution uniforme de la contrainte maximale de cisaillement. Les simulations numériques de Pritchard et al. [10] montrent une tendance identique pour les vitesses maximales, ce qui est équivalent.
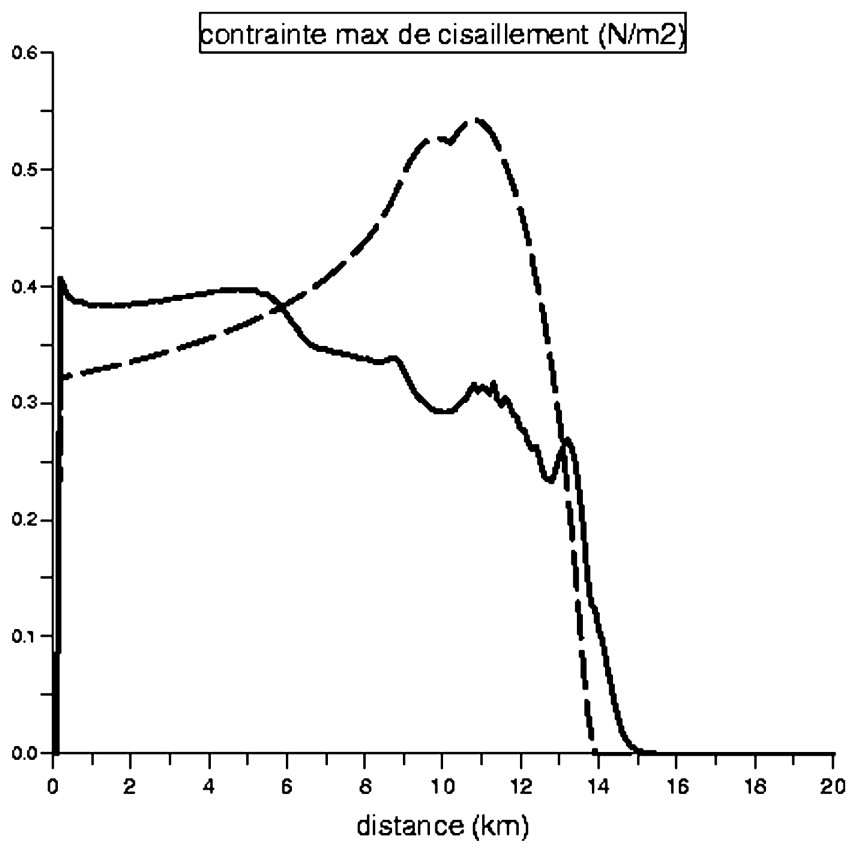
Contrainte maximale de cisaillement sur le fond pendant une période de marée, après 90 ans de simulation (trait continu) et au-dessus d'un estran de même pente moyenne, mais uniforme (pointillés).
Maximum bed shear stress during a tidal period, after 90 years of simulation (full line) and over a mudflat with the same average slope but uniform (dotted line).
3.2 Évolution du profil de l'estran sous l'action simultanée d'un courant cross-shore et des vagues
Les simulations ont été réalisées pour des vagues de faible amplitude, ces conditions étant représentatives de ce qui est observé au-dessus de la plupart des estrans vaseux où domine un courant de marée cross-shore. Les vagues sont souvent générées à proximité immédiate de l'estran ; la zone de fetch y est limitée, les vagues ne dépassent alors pas quelques dizaines de centimètres et les périodes sont courtes. En outre, les conditions de vagues peuvent changer en quelques heures, notamment en raison de l'allongement de la longueur de fetch pendant le flot [11]. Pour simplifier, nous avons considéré deux forçages permanents schématiques : des vagues de 0,05 m (Fig. 3) ou de 0,1 m (Fig. 4) à la limite aval du domaine, avec une période de 3 s. Une telle simplification peut nous aider à comprendre ce qui se passe du point de vue morphodynamique dans le cas d'un forçage de vagues plus réaliste. Des scénarios différents seront présentés dans un article à venir.
La Fig. 3 montre l'évolution du profil de l'estran pendant 13 ans avec des vagues de 0,05 m, ainsi que le profil après 13 ans que l'on aurait eu sans vagues (mêmes conditions de marée que précédemment). En premier lieu, on note que la quantité totale de sédiment déposée le long de l'estran est plus faible que pour la simulation sans vagues. De l'énergie supplémentaire est apportée par les vagues pour empêcher un éventuel dépôt ou pour éroder le fond sédimentaire. L'apport externe de matière en suspension étant le même, la vasière prograde moins rapidement et le flux particulaire sortant pendant le jusant est donc supérieur. Comme pour l'expérience avec un courant cross-shore seul, l'estran prograde de façon quasi continue avec une pente d'équilibre. Cette pente est cependant différente, exprimant le fait que le profil de l'estran s'adapte au forçage hydrodynamique. Pendant toute l'étale de pleine mer, la partie haute de l'estran est recouverte par des hauteurs d'eau suffisamment faibles pour permettre l'action érosive des vagues. Il n'est alors pas nécessaire, comme c'était le cas précédemment, que la pente soit faible en haut d'estran pour induire des vitesses fortes afin de compenser le dépôt autour de l'étale de pleine mer. La partie haute de l'estran est donc plus pentue et le bilan dépôt/érosion peut s'équilibrer le long du profil.
Pour une hauteur de vague plus importante (c'est-à-dire 0,1 m à la limite marine), le profil du haut de la vasière est encore plus concave (Fig. 4). De même, le pied d'estran présente une pente relativement forte induisant des courants plus faibles, équilibrant ainsi l'action érosive des vagues à l'étale de basse mer. Il faut cependant relativiser ces fortes concavités en haut et en pied d'estran, qui sont ici amplifiées en raison du forçage de marée monochromatique. Pour cette simulation, un résultat important est que la vasière elle-même tend vers un équilibre figé. C'est-à-dire qu'après quelques années, la vasière ne prograde plus. L'énergie supplémentaire apportée par les vagues est dans ce cas suffisante en termes d'érosion pour compenser l'apport de sédiment à la limite marine.
Roberts et al. [5] ont simulé l'évolution d'un estran vaseux sous l'action d'un courant cross-shore et de vagues comprises entre 10 et 40 cm ; le modèle hydrodynamique ainsi que le calcul des hauteurs de vagues et des contraintes sur le fond qui en résultent sont cependant différents. De plus, le facteur de frottement de houle fw n'étant pas précisé (la valeur du frottement lié aux vagues dépend fortement de ce paramètre), il n'est pas possible de comparer minutieusement leurs simulations aux nôtres pour un même régime de vagues. En outre, la notion de progradation ou de régression n'est pas précisée dans leur étude, qui porte sur l'allure du profil d'équilibre. Toutefois, les résultats des expériences présentent des similitudes : on retrouve une concavité plus ou moins prononcée en pied et en haut d'estran.
Par ailleurs, nous avons relevé que, pour la simulation avec des vagues de 10 cm à la limite marine, les concentrations de matières en suspension sont fortes (jusqu'à quelques dizaines de grammes par litre) sur l'estran, révélant une érodabilité trop grande du sédiment si celui-ci devait être soumis en permanence à des vagues : une simulation plus réaliste devrait donc tenir compte des variations de résistance au cisaillement du sédiment et des processus de tassement.
4 Conclusion
Sous l'effet d'un seul courant de marée cross-shore, nous avons pu voir que le profil de l'estran tend vers un équilibre, mais que l'estran ne cesse de prograder vers le large au cours du temps. Conformément aux observations, la forme du profil à l'équilibre est convexe en haut d'estran. L'effet des vagues est important vis-à-vis de l'érosion de la vasière lorsque les hauteurs d'eau sont faibles, en particulier à basse mer en pied d'estran et à pleine mer en haut d'estran. Dans le cas d'un forçage associant courant cross-shore et vagues, l'estran vaseux peut tendre vers un état d'équilibre figé, c'est-à-dire que la position de l'estran se fixe après quelques années de simulation, la présence des vagues pouvant être vue alors comme l'action érosive nécessaire pour compenser les dépôts de vase générés par les apports externes. Cet équilibre et sa possibilité d'être figé dépendent non seulement du régime de vagues mais aussi du flux particulaire entrant par le large.
Que ce soit pour la configuration cross-shore de cette étude ou pour une configuration réelle plus complexe, le rôle des vagues, même petites, apparaı̂t essentiel pour la notion d'équilibre morphodynamique. Une étude de sensibilité reste à faire, notamment avec des hauteurs de vagues plus importantes ou même avec un forçage de vagues réaliste (par exemple issu de mesures en zone d'estran). De même, une simulation plus réaliste impose de prendre en compte le cycle vive eau/morte eau ainsi que le processus de tassement de manière explicite ; ces effets seront présentés dans un article en préparation, en même temps qu'une sensibilité au paramétrage sédimentologique.


