Abridged English version
Data assimilation has been conducted in a one-dimensional, coupled physical–ecosystem model of the upper ocean in order to improve the realism of the simulations and to predict the biogeochemical state of the ocean in a realistic way.
The coupled model (Modèle d'ÉCOsystème du GHER et du LOV – MODECOGeL) simulates the primary production in a coastal zone of the Ligurian Sea in the northwestern Mediterranean Sea, where oligotrophic conditions prevail. The ecosystem dynamics is represented by twelve compartments expressed in nitrogen units. The model takes into account nitrate and ammonium to distinguish new production from regenerated production, three compartments of phytoplankton (pico-, nano- and micro-phytoplankton) and three compartments of zooplankton (nano-, micro- and mesozooplankton), two types of particulate organic nitrogen, dissolved organic nitrogen and bacteria for a representation of the microbial loop. The coupling with a hydrodynamic model determines the physical constraints associated to the development of a seasonal mixed layer. The stratification of the water column and the associated vertical turbulent diffusivities, are key parameters of the evolution of the marine ecosystem. The model is constrained by heat fluxes and wind stress at the air–sea interface according to real meteorological data. The coupled system has been developed and validated on the basis of field data collected during the FRONTAL campaigns between 1984 and 1988 at two stations located along a transect between Nice and Calvi.
The assimilation method is based on the Singular Evolutive Extended Kalman (SEEK) filter, which is a reduced-order assimilation scheme. The error sub-space is decomposed into multivariate Empirical Orthogonal Functions (EOFs) of the system's variability. The SEEK filter computes sequential corrections of the model trajectories, taking into account the balance between the confidence of the model prediction and the accuracy of the observed quantities. The experiment presented here concerns nitrate and chlorophyll a profiles assimilation. In the usual case, the error subspace EOFs are evaluated using the model variability as a proxy of the system variability. But in this work, the originality is to use EOFs deduced from observations. This approach permits to introduce processes that could not be represented by a vertical 1D model alone.
1 Introduction
Le modèle MODECOGeL (MODèle d'ÉCOsystème du GHER et du LOV) [10] a été développé en vue de représenter l'écosystème marin de la mer Ligure, située en Méditerranée occidentale. Il s'agit d'un modèle unidimensionnel vertical de production primaire, couplé à un modèle de couche de mélange océanique. Ce dernier a fait l'objet d'une validation détaillée [10,12] à partir de données prélevées le long d'une radiale reliant Nice à Calvi au cours des différentes missions FRONTAL [16] réalisées entre le 12 mars 1984 et le 19 décembre 1988. Des conditions de vent et de flux de chaleur, évaluées sur la base de données météorologiques réelles, sont imposées au modèle hydrodynamique. Le modèle biologique est, quant à lui, basé sur le cycle de l'azote, décrit par douze variables d'état, incluant plusieurs classes de taille planctoniques et une description explicite de la boucle microbienne.
Bien que le modèle MODECOGeL simule de façon satisfaisante l'écosystème de la mer Ligure, ce dernier présente un certain nombre de limitations, résultant de l'hypothèse d'homogénéité horizontale, de l'usage de forçages atmosphériques imparfaits ou encore de paramétrisations approximatives des processus dynamiques. Ainsi, Lacroix [10] a pu identifier une tendance généralisée au réchauffement ainsi qu'une dérive en sel sur cinq années consécutives de simulation, une sous-estimation des concentrations en nitrate, ou encore des maxima chlorophylliens trop élevés. Lacroix et Grégoire [12] mettent également en évidence une surestimation de la profondeur de la nitracline dans les simulations, probablement due à l'absence de processus d'advection verticale dans le modèle 1D.
Une piste pour corriger ces tendances consiste à appliquer, parallèlement au modèle, une méthode d'assimilation de données qui a pour objectif de fournir une représentation plus réaliste du système, en utilisant de manière optimale toutes les informations provenant du modèle et des observations. L'assimilation de données est réalisée au moyen du filtre SEEK (Singular Evolutive Extended Kalman filter) [17], méthode dérivée du filtre de Kalman, qui utilise un principe de réduction d'ordre afin de rendre l'algorithme praticable sur le plan numérique. Dans nos expériences, la matrice de covariance des erreurs du premier estimé est calculée à partir d'une décomposition en fonctions empiriques orthogonales (EOFs) multivariées issues de la variabilité des observations utilisées pour l'assimilation [14]. Contrairement à une approche plus classique qui consiste à prendre en compte la variabilité du modèle pour une représentation des EOFs, cette approche originale permet d'introduire des informations complémentaires sur les processus qui ne peuvent pas être représentés par une modélisation unidimensionnelle verticale, et ainsi de rendre les simulations plus réalistes.
L'expérience présentée par la suite concerne l'assimilation conjointe de profils de nitrate et de chlorophylle a. L'année 1986 a été choisie, car il s'agit de la période annuelle la mieux couverte par les données biologiques acquises au cours des campagnes FRONTAL.
2 Le modèle MODECOGeL
L'étude s'appuie sur le modèle MODECOGeL, un modèle d'écosystème marin couplé à un modèle de couche de mélange océanique de la mer Ligure. C'est un modèle unidimensionnel vertical, développé dans le but d'étudier les processus biologiques le long de la colonne d'eau et de quantifier les flux biogéochimiques en fonction des conditions météorologiques et hydrodynamiques du milieu. Il a été calibré et validé sur base des données FRONTAL prélevées entre 1984 et 1988 en deux stations sur les six réparties selon un transect reliant Nice à Calvi, ces deux stations étant situées de part et d'autre du front liguro-provençal. Elles correspondent respectivement à la station 1, site des programmes DyFAMeD et JGOFS-France, située au large à 28 milles nautiques du cap Ferrat, et la station 6, station côtière à 3 milles nautiques du cap Ferrat. Pour notre part, la zone d'étude correspond à la station 6, les forçages atmosphériques y étant plus réalistes par rapport à la station du large et le jeu de données plus important.
2.1 Le modèle hydrodynamique
Le modèle MODECOGeL est un modèle de couche de mélange multi-niveaux, non linéaire, avec une fermeture turbulente de type k–l. Le modèle hydrodynamique prend en compte cinq variables d'état, à savoir, la température, la salinité, les deux composantes horizontales de la vitesse u et v, ainsi que l'énergie cinétique turbulente, cette dernière variable permettant la fermeture du schéma de turbulence. Les conditions aux limites à l'interface air–mer du modèle hydrodynamique sont imposées sous forme de flux de chaleur, d'eau douce et de quantité de mouvement, estimés à partir de données météorologiques mesurées toutes les 3 h aux stations du cap Ferrat et de l'aéroport de Nice [11]. Ces conditions aux limites déterminent au premier ordre l'activité turbulente dans la couche mélangée, la diffusion turbulente conditionnant très fortement la répartition spatiale des composantes biologiques dans la colonne d'eau, surtout dans le cadre d'un modèle unidimensionnel vertical. L'importance du pilotage du modèle biologique à partir des informations fournies par le modèle hydrodynamique se situe donc principalement au niveau de la prise en compte des variations spatio-temporelles du coefficient de diffusion turbulente.
2.2 Le modèle biologique
Comme le modèle biologique a été développé dans le but d'étudier le rôle de la dynamique sur la répartition verticale des nutriments et de la production primaire, seuls les premiers niveaux trophiques de la chaîne alimentaire sont modélisés. Il prend ainsi en compte 12 variables d'état, à savoir le nitrate et l'ammonium, afin de distinguer la production nouvelle de la production régénérée, trois classes de taille phytoplanctoniques (pico-, nano- et microphytoplancton), trois classes de taille zooplanctoniques (nano-, micro- et mésozooplancton), la matière organique particulaire de taille 1 et 2, l'azote organique dissous et les bactéries. C'est un modèle relativement simple, inspiré du modèle de Fasham et al. [5], avec en plus la prise en compte d'une boucle microbienne afin d'être représentatif de la zone d'étude. La Fig. 1 illustre les processus biologiques régissant les flux de matière entre les différents compartiments du modèle.
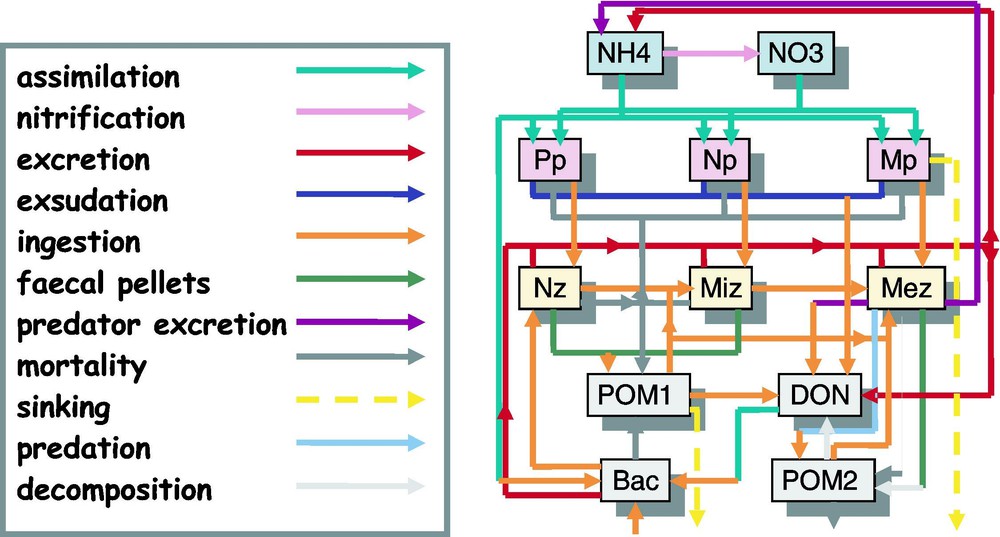
Représentation schématique du modèle biologique MODEDOGeL utilisé dans les simulations couplées ; les 12 compartiments représentent les variables d'état biologiques suivantes : nitrate et ammonium (NO3, NH4) ; pico- (Pp), nano- (Np) et micro-phytoplancton (Mp) ; nano- (Nz), micro- (Miz) et méso-zooplancton (Mez) ; matière organique particulaire (POM1, POM2) ; azote organique dissout (DON) ; bactéries (Bac). Les processus biologiques responsables des flux entre les compartiments sont décrits à gauche.
Schematic representation of the MODEDOGeL biological model used in the coupled simulations; the 12 compartments represent the biological state variables: nitrate and ammonium (NO3, NH4); pico- (Pp), nano- (Np) and micro-phytoplankton (Mp); nano- (Nz), micro- (Miz) and meso-zooplankton (Mez); particulate organic matter (POM1, POM2); disolved organic nitrogen (DON); bacteria (Bac). The biological processes responsible for the fluxes between the compartments are described on the left.
En ce qui concerne les conditions aux limites, le flux en surface de toutes les variables biologiques est nul. À la base de la colonne d'eau modélisée, un flux nul est imposé à toutes les variables du modèle couplé (hydrodynamique et biologique). Les équations aux dérivées partielles sont résolues par une méthode aux différences finies sur une grille décalée. Le pas de temps est de 10 min et la discrétisation verticale est de 1 m entre la surface et une profondeur de 200 m.
3 L'assimilation de données
Le problème de base que nous cherchons à résoudre par l'assimilation de données est une meilleure estimation spatio-temporelle de certaines propriétés de l'océan, en combinant de façon optimale les solutions d'un modèle numérique et des observations.
3.1 Méthodes d'assimilation en biologie marine
Deux principales approches sont possibles, afin de résoudre le problème d'estimation optimale par l'assimilation de données : l'approche variationnelle et l'approche séquentielle [1]. Celle utilisée dans le cadre de ce travail est de type séquentiel, dérivée de la théorie de l'estimation statistique optimale. Elle consiste à fournir un estimé de l'état du système, en corrigeant séquentiellement la prévision du modèle, chaque fois que des observations sont disponibles. L'approche statistique séquentielle fait appel à une connaissance des erreurs correspondant au modèle et aux observations, afin de minimiser l'incertitude sur la solution estimée au sens des moindres carrés.
Kalman [9] a proposé un schéma statistique séquentiel optimal, afin de résoudre les problèmes inverses linéaires. La particularité du filtre de Kalman est de propager dans le temps une estimation statistique des covariances d'erreurs pour des systèmes dynamiques linéaires. Evensen [4] a quant à lui développé un filtre de Kalman d'ensemble s'appliquant à des modèles dynamiques non linéaires comportant de très nombreux degrés de liberté. Une autre approche, mise en place par Pham et al. [17], concerne le filtre SEEK, méthode utilisée dans le cadre de ce travail et plus longuement développée par la suite. Très peu d'études concernant l'utilisation d'une approche séquentielle avec des modèles couplés physiques–biogéochimiques ont été menées jusqu'à présent. Nous pouvons cependant citer les travaux de Eknes et Evensen [3], qui utilisent un filtre de Kalman d'ensemble dans un modèle unidimensionnel à trois composantes biologiques, ou le projet européen DIADEM (Development of Advanced Data Assimilation Systems for Operational Monitoring and Forecasting of the North Atlantic and Nordic Seas), où le filtre SEEK et le filtre de Kalman d'ensemble ont été implémentés dans un modèle tridimensionnel couplé, l'objectif étant de contrôler l'ensemble des variables biologiques au moyen d'observations SeaWIFs de la couleur de l'eau [2,15].
L'approche variationnelle, que nous n'utiliserons pas dans le cadre de ce travail, est dérivée de la théorie du contrôle optimal [13]. Le principe repose sur la minimisation d'une fonction coût, dépendant d'un certain nombre de paramètres qui contrôlent la trajectoire du modèle. Cette fonction coût mesure les écarts quadratiques entre un jeu de données et une solution du modèle. Les paramètres de contrôle peuvent correspondre aux paramétrisations qui caractérisent les processus du modèle, ou à des conditions limites ou initiales par exemple. Cette approche est celle qui est le plus souvent utilisée dans les modèles couplés physiques–biogéochimiques [6–8,18–21]. En effet, la détermination des paramètres qui interviennent dans la paramétrisation des processus biologiques est un problème récurrent en modélisation.
3.2 Le filtre SEEK
Le filtre SEEK [17] est un filtre de Kalman simplifié, dans lequel l'espace d'état complet est projeté dans un espace d'état réduit. La matrice de covariance des erreurs au temps initial est représentée par un nombre limité de fonctions empiriques orthogonales (EOFs) multivariées, décrivant les modes dominants de la variabilité du système et définissant de cette façon la structure de l'espace réduit au temps initial. L'approche multivariée est utile afin de propager l'information depuis les quantités observées vers les quantités non observées. En effet, les observations ne correspondent qu'à un nombre limité de variables du modèle. À travers la représentation multivariée des covariances d'erreurs, les corrections affectent non seulement les variables observées, mais également l'ensemble des variables du modèle.
Le filtre SEEK repose sur un algorithme qui enchaîne une étape d'analyse et une étape de prévision. L'étape d'analyse corrige l'état du système, en intégrant les observations disponibles à l'instant où la correction est effectuée, dans le but de réduire les écarts entre les observations et les prédictions du modèle, en fonction de leurs erreurs respectives. Une covariance des erreurs d'analyse est diagnostiquée. On effectue ensuite une étape de prévision, qui consiste en l'intégration de l'état du système par le modèle, à partir des corrections effectuées au préalable. En parallèle, la covariance des erreurs de prévision est calculée par intégration de la covariance des erreurs de l'analyse précédente, via la dynamique du modèle. Successivement sont appliquées une étape d'analyse, puis une étape de prévision, d'où le caractère récurrent de la méthode.
4 Assimilation des données biologiques FRONTAL
La validation du modèle couplé avait, en effet, fait ressortir quatre principales limitations, touchant aussi bien la partie hydrodynamique que la partie biologique du modèle. Il s'agit d'une tendance généralisée au réchauffement et d'une dérive en sel au cours du temps, d'une sous-estimation des concentrations en nitrate et de maxima chlorophylliens trop élevés [10]. Nous allons explorer ici la question de l'assimilation conjointe de profils verticaux de nitrate et de chlorophylle a, le modèle hydrodynamique n'étant pas contrôlé par des observations de nature physique (température et salinité).
4.1 Les difficultés rencontrées
Les données FRONTAL utilisées ont été échantillonnées à certaines profondeurs : 0, 5, 10, 20, 30, 50, 75, 100, 150 et 200 m. Pour mener à bien l'assimilation, la répartition spatiale des mesures doit, en principe, tenir compte de la variabilité verticale des quantités observées. Or, des expériences préliminaires ont montré que l'échantillonnage spatial choisi lors des missions FRONTAL n'était pas optimum par rapport à la variable ‘nitrate’ et, dans une moindre mesure, à la chlorophylle a [14]. En outre, la répartition des données dans le temps doit aussi pouvoir décrire la variabilité temporelle avec suffisamment de précision. Or, nous ne disposons d'aucun prélèvement de nitrate entre le 8 juillet et le 2 septembre 1986 et de chlorophylle a entre le 18 juin et le 2 septembre 1986, bien que cette année ait été choisie car elle comptabilise le plus de profils sur les cinq années de campagne. Ce déficit au niveau de l'échantillonnage temporel rend a priori l'assimilation plus délicate.
Une difficulté supplémentaire apparaît lors de l'assimilation de données concernant la chlorophylle a. En effet, cette quantité représente une agrégation entre plusieurs compartiments du modèle, à savoir les trois catégories phytoplanctoniques, et il nous est impossible de connaître directement les proportions relatives de chacune de ces catégories à partir d'une simple donnée de chlorophylle a. Cette difficulté est résolue dans l'algorithme SEEK, grâce à une représentation de l'opérateur d'observation H, qui permet de relier les données de chlorophylle a aux concentrations des trois variables phytoplanctoniques, au prorata de leur répartition statistique moyenne, estimée à partir de la variabilité naturelle du modèle libre. La variabilité du rapport Chl/Phy est donc prise en compte au travers de l'importance relative des trois catégories phytoplanctoniques représentées dans le modèle.
Notons enfin que les données dont nous disposons ne représentent qu'une partie des variables d'état biologiques. Il nous est donc impossible de valider le modèle biologique dans son ensemble, et notamment le zooplancton et la matière organique, sachant que nous ne disposons pas de données relatives à ces variables.
4.2 Protocole des expériences d'assimilation
La version du filtre SEEK utilisée pour les expériences d'assimilation est dite « fixe », c'est-à-dire que la statistique d'erreur n'évolue pas d'une étape d'analyse à la suivante selon la dynamique du modèle, mais est simplement amplifiée au moyen d'un facteur constant fixé à la valeur 2. Cette amplification de l'erreur au cours de l'étape de prévision est une paramétrisation qui globalise à la fois les effets de croissance dynamique de l'erreur d'analyse résiduelle et l'incrément d'erreur de simulation lié aux imperfections du modèle [17]. La durée d'un cycle d'assimilation varie en fonction de la distribution temporelle des observations, qui est d'une quinzaine de jours en moyenne. L'erreur d'observation est supposée non corrélée spatialement et son écart-type est fixé à de 0,3 mmol N m−3 pour le nitrate, et à 0,2 mmol N m−3 pour la chlorophylle (après conversion des unités). À noter cependant que ces valeurs ont été fixées par ajustement, de façon à tenir compte à la fois de l'erreur de mesure et de l'erreur de représentativité des données assimilées (qui dépend notamment de la « richesse » de la base réduite utilisée dans le filtre SEEK). Seules les variables biologiques définissant le vecteur d'estimation sont corrigées statistiquement à chaque cycle, vu la difficulté de spécifier des covariances d'erreur suffisamment robustes entre toutes les variables du modèle couplé. Le vecteur d'estimation considéré ici prend en compte les deux catégories de nutriment et les trois classes phytoplanctoniques.
Dans les simulations examinées ici, les conditions initiales en température, salinité, azote et phytoplancton sont imposées au 1er janvier 1986 sous forme d'un profil vertical moyen, calculé à partir des données FRONTAL représentatives de la période hivernale. Les autres variables d'état sont initialisées à une valeur constante sur la verticale, selon la procédure décrite dans [12].
4.3 Assimilation de données de nitrate et de chlorophylle a
La Fig. 2 montre une représentation d'une moyenne annuelle ainsi que des EOFs calculées, d'une part, à partir de la variabilité du modèle et, d'autre part, à partir de la variabilité des données FRONTAL de l'année 1986, entre 0 et 200 m de profondeur. Les sorties du modèle MODECOGeL ont été prises en fonction de l'échantillonnage spatio-temporel des données FRONTAL. Les trois premiers modes de variabilité représentent 93,03 % de la variance correspondant à la variabilité issue des simulations du modèle libre, et 97,15 % de la variance représentée dans les données FRONTAL. La valeur du pourcentage indiqué correspond à la somme des valeurs propres des EOFs retenues, divisée par la somme de toutes les valeurs propres des EOFs issues du jeu de données de départ.
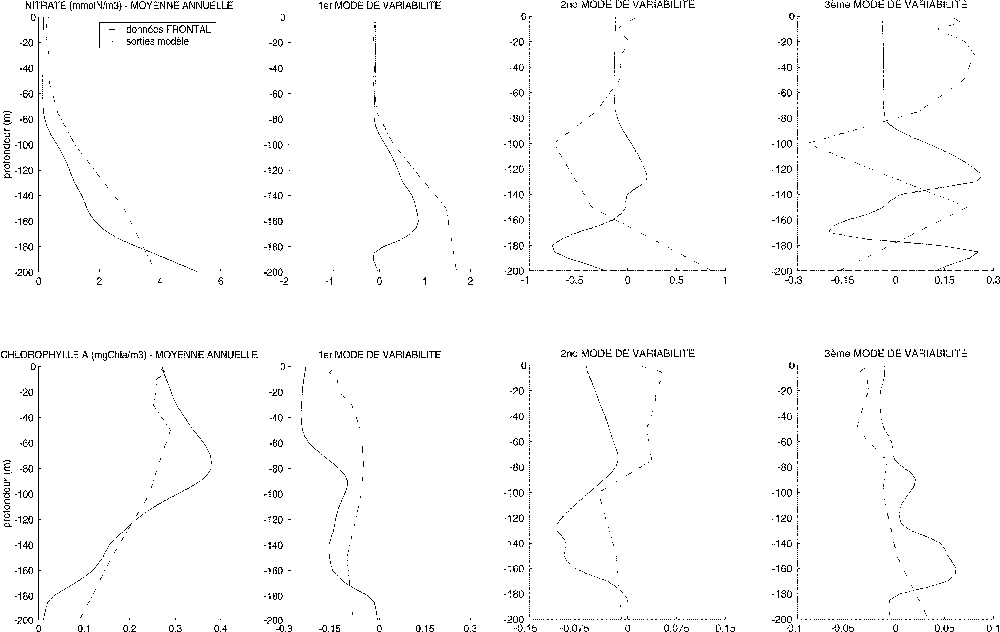
Représentation, en fonction de la profondeur (mètres), d'une moyenne annuelle et des trois premiers modes de variabilité concernant la variable nitrate et la chlorophylle a.
Representation, according to the depth (metres), of an annual average and the first three modes of variability of nitrate and chlorophyll a.
Au regard des profils présentant une moyenne annuelle, on note une augmentation des concentrations en nitrates avec la profondeur, avec cependant une sous-estimation des valeurs simulées. Quant à la chlorophylle a, le modèle simule un pic de concentration vers 80 m de profondeur, non visible d'après les données FRONTAL. Par ailleurs, en dessous de 120 m de profondeur, les simulations tendent à sous-estimer les concentrations. Les modes calculés via le modèle montrent une faible variation en nitrate entre la surface et 80 m de profondeur, contrairement aux second et troisième modes résultant des données FRONTAL. Le premier mode présente des profils similaires, excepté en dessous de 160 m de profondeur. Pour ce qui est de la chlorophylle a, la première EOF calculée via les données FRONTAL montre une certaine homogénéité le long de la colonne d'eau, contrairement à l'EOF calculée à partir du modèle. Cependant, d'après l'étude de la fonction temporelle associée au premier mode de variabilité [14], la variabilité saisonnière est relativement bien représentée. En revanche, les second et troisième modes ont des signaux plus complexes à interpréter, et on ne trouve pas de concordance prononcée entre les deux types de mode, ce qui confirme une certaine divergence entre les données réelles et les résultats du modèle.
La Fig. 3 montre une représentation des écarts RMS entre les simulations assimilées (étape de prévision = « xf » ; étape d'analyse = « xa ») et les données FRONTAL, d'une part, et les simulations sans assimilation (libre) et les données FRONTAL, d'autre part, selon la profondeur et le temps. Les expériences sont initialisées au 1er janvier 1986. Les corrections sur le nitrate sont très marquées, et les écarts RMS en dessous de 100 m de profondeur sont fortement atténués grâce à l'assimilation. En effet, à 200 m de profondeur, les écarts RMS entre la simulation sans assimilation et les observations sont de l'ordre de 2,5 mmol N m−3, alors qu'ils ne sont plus que de 0,5 mmol N m−3 lors de l'analyse. Au cours du temps, ces mêmes écarts ne dépassent pas 0,5 mmol N m−3. Le niveau d'erreur associé à l'étape de prévision se situe entre l'analyse et la simulation libre, ce qui indique que les corrections effectuées durant l'étape d'analyse ne sont pas totalement dégradées lors de l'étape de prévision, et que l'échantillonnage temporel des données ne semble pas être si insuffisant. Les corrections sur la chlorophylle a sont moins marquées, bien que significatives, notamment entre la surface et 80 m de profondeur. Au cours du temps, on note la présence d'un certain nombre d'anomalies (matérialisées par des pics) générées par la simulation libre ; ces dernières sont atténuées grâce à l'assimilation.
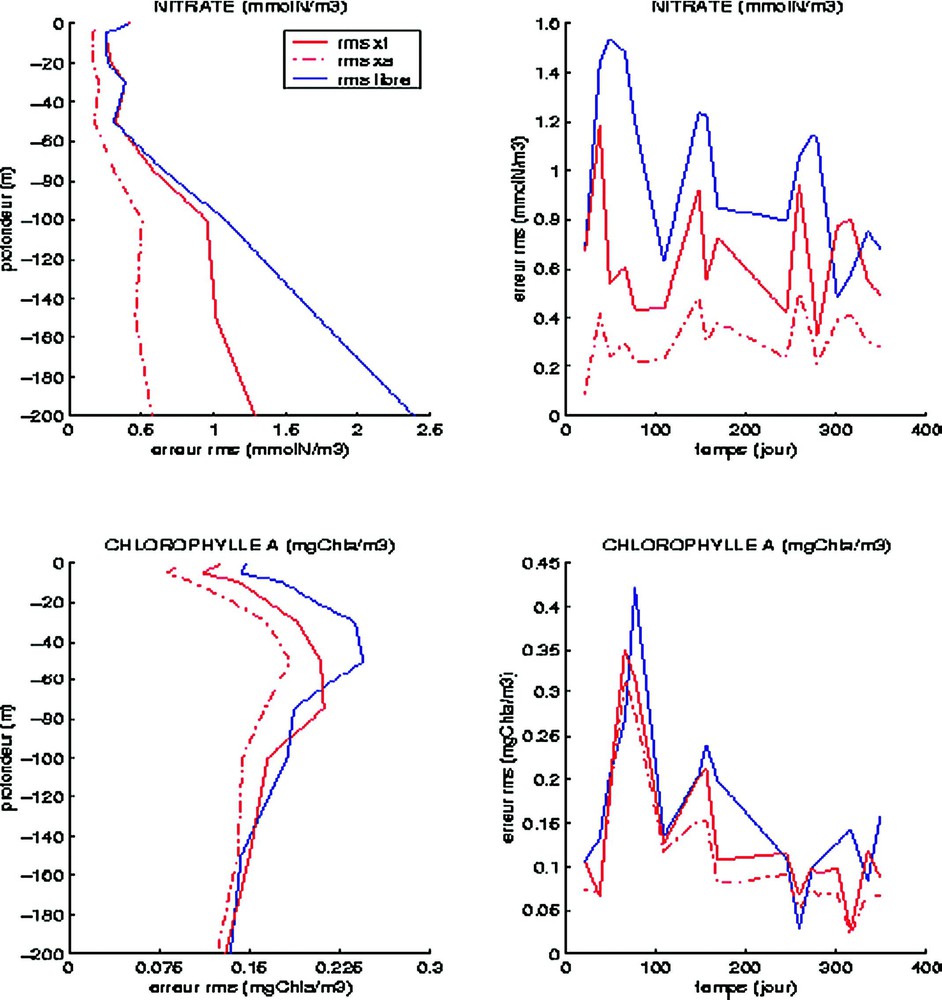
Écarts RMS, en fonction de la profondeur (mètres) et du temps (jours), de la variable nitrate (mmol N m−3) et de la chlorophylle a (mg Chl m−3). Courbe bleue : simulation sans assimilation. Courbes rouges : prévision (trait continu) et analyse (pointillés).
RMS error, according to the depth (meters) and the time (days), of nitrate (mmol N m−3) and chlorophyll a (mg Chl m−3). Blue curve: simulation without assimilation. Red curves: forecast (continue line) and analysis (dotted line).
D'après les données FRONTAL (Fig. 4), on assiste en février à des remontées en nitrate dont les concentrations oscillent entre 0,50 et 0,75 mmol N m−3. Le modèle libre simule également ces remontées, mais les concentrations n'atteignent pas celles prédites par les observations. De plus, entre 150 et 200 m de profondeur, les valeurs en nitrate sont sous-estimées. La simulation assimilée tend à corriger ces anomalies, et on peut noter une évolution spatio-temporelle plus conforme à la réalité, avec des concentrations corrigées entre 150 et 200 m de profondeur, même si les concentrations en début d'année sont encore sous-évaluées. Quant à la chlorophylle a (Fig. 5), les données FRONTAL indiquent une floraison entre 0 et 50 m de profondeur en mars et en avril, dont le maximum de concentration atteint 0,70 mg Chl m−3. A contrario, malgré des quantités de nitrate moins importantes début février dans la simulation libre, on assiste à une poussée de plus grande envergure par rapport aux observations. Les maxima chlorophylliens dans ce cas de figure peuvent alors atteindre 1,13 mg Chl m−3. L'assimilation atténue ce phénomène et permet une meilleure représentation spatio-temporelle de la chlorophylle a, notamment à compter du mois de septembre.
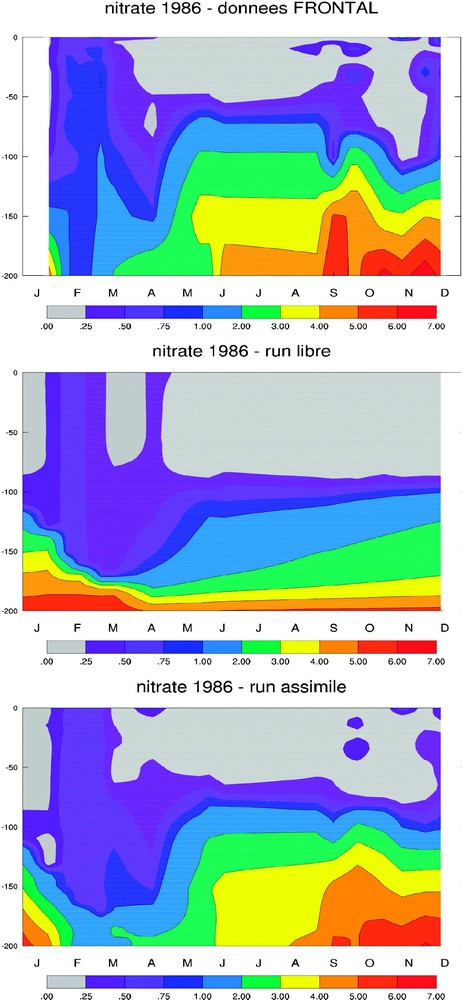
Évolution spatio-temporelle de la variable nitrate (mmol N m−3). Figure du haut : données FRONTAL. Figure du milieu : simulation libre. Figure du bas : simulation assimilée.
Spatiotemporal evolution of the nitrate (mmol N m−3). Top panel: FRONTAL data. Middle panel: free model run. Bottom panel: simulation with assimilation.
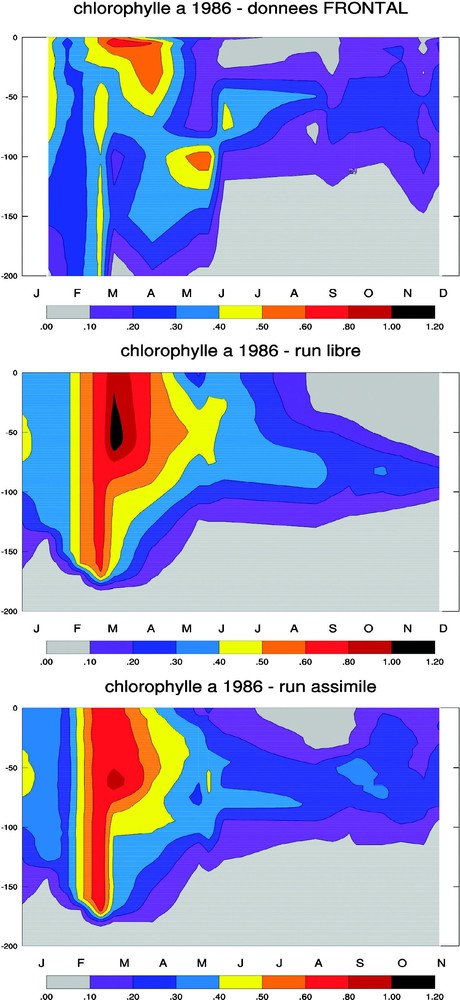
Évolution spatio-temporelle de la chlorophylle a (mg Chl m−3). Figure du haut : données FRONTAL. Figure du milieu : simulation libre. Figure du bas : simulation assimilée.
Spatiotemporal evolution of the chlorophyll a (mg Chl m−3). Top panel: FRONTAL data. Middle panel: free model run. Bottom panel: simulation with assimilation.
5 Conclusion
Au vu des résultats de l'expérience décrite, nous pouvons affirmer que l'assimilation conjointe de profils biologiques de nitrate et de chlorophylle a conduit à des améliorations significatives. Les corrections se sont avérées assez sensibles à la manière dont est construite la matrice de covariance des erreurs initiale. L'approche présentée ici fut d'initialiser le sous-espace d'erreurs au moyen d'EOFs représentatives de la variabilité décrite par des observations réelles, ce qui permet d'obtenir des résultats plus satisfaisants qu'en utilisant des EOFs calculés à partir de la variabilité naturelle du modèle [10]. Cette approche à l'avantage d'intégrer, via les différents modes d'erreurs, des processus non représentés par la modélisation unidimensionnelle verticale. Ceci suppose des stratégies d'observation adéquates, qui donnent accès à l'information multivariée relative à cette variabilité. Dans notre cas, si de futurs prélèvements étaient à effectuer, il serait intéressant d'effectuer davantage de prélèvements en dessous de 100 m de profondeur, afin d'obtenir de plus amples informations sur la variabilité en nitrate, notamment durant les remontées de nutriments, depuis les couches profondes vers la couche superficielle au cours des trois premiers mois de l'année, ainsi qu'au printemps et en automne dans les 100 premiers mètres, à plus haute fréquence temporelle durant les floraisons phytoplanctoniques.


