Sur l'assimilation variationnelle de données par un modèle d'écosystème marin de type NPZ

Yann Leredde; Christine Lauer-Leredde; Frédéric Diaz

doi:10.1016/j.crte.2005.05.003

Océanographie

Sur l'assimilation variationnelle de données par un modèle d'écosystème marin de type NPZ

Présenté par : Jean-François Minster

Yann Leredde ^1,² ; Christine Lauer-Leredde ¹ ; Frédéric Diaz ²

¹ Laboratoire de dynamique de la lithosphère, université Montpellier-2, place Eugène-Bataillon, 34095 Montpellier cedex 5, France
² Laboratoire d'océanographie et de biogéochimie, centre d'océanologie de Marseille, université de la Méditerranée, campus de Luminy, case 901, 13288 Marseille cedex 9, France

Comptes Rendus. Géoscience, Volume 337 (2005) no. 12, pp. 1055-1064.

Résumés

Français
Anglais

Une méthode d'assimilation variationnelle de données est appliquée à un modèle simplifié d'écosystème marin de type NPZ (Nutriment Phytoplancton Zooplancton) impliquant cinq paramètres. Cette méthode permet d'optimiser ces paramètres par un processus itératif de minimisation d'une fonction de coût quantifiant l'écart quadratique entre observations et résultats de simulation. La première partie de cette note décrit comment obtenir le modèle adjoint du modèle NPZ permettant de calculer le gradient de cette fonction de coût vis-à-vis des paramètres. Deux expériences d'assimilation de données artificielles permettent ensuite d'illustrer l'efficacité de cette méthode, mais aussi ses limitations, dues aux non-linéarités et aux problèmes de sensibilité du modèle aux paramètres.

A variational data assimilation method is applied to a simplified marine ecosystem model of NPZ (Nutrient Phytoplankton Zooplankton) type, which implies five parameters. The method allows us to optimise these parameters by an iterative process of minimisation of a cost function which quantifies the quadratic discrepancy between observations and simulation results. The first part of this note describes how to obtain the adjoint model of the NPZ model allowing us to compute the gradient of the cost function relative to the parameters. Two experiments of artificial data assimilation then show the efficiency of this method, but also its limitations because of non-linearities and sensitivity problems of the model relative to the parameters.

Métadonnées

Reçu le : 2004-05-24
Accepté le : 2005-04-05
Publié le : 2005-07-01

DOI : 10.1016/j.crte.2005.05.003

Mot clés : Contrôle optimal, Modèle NPZ, Écosystème marin, Identification de paramètres, Modèle adjoint
Keywords: Optimal control, NPZ model, Marine ecosystem, Identification of parameters, Adjoint model

Affiliations des auteurs :

Yann Leredde ^{1, 2} ; Christine Lauer-Leredde ¹ ; Frédéric Diaz ²

¹ Laboratoire de dynamique de la lithosphère, université Montpellier-2, place Eugène-Bataillon, 34095 Montpellier cedex 5, France
² Laboratoire d'océanographie et de biogéochimie, centre d'océanologie de Marseille, université de la Méditerranée, campus de Luminy, case 901, 13288 Marseille cedex 9, France

@article{CRGEOS_2005__337_12_1055_0,
     author = {Yann Leredde and Christine Lauer-Leredde and Fr\'ed\'eric Diaz},
     title = {Sur l'assimilation variationnelle de donn\'ees par un mod\`ele d'\'ecosyst\`eme marin de type {NPZ}},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {1055--1064},
     publisher = {Elsevier},
     volume = {337},
     number = {12},
     year = {2005},
     doi = {10.1016/j.crte.2005.05.003},
     language = {fr},
}

TY  - JOUR
AU  - Yann Leredde
AU  - Christine Lauer-Leredde
AU  - Frédéric Diaz
TI  - Sur l'assimilation variationnelle de données par un modèle d'écosystème marin de type NPZ
JO  - Comptes Rendus. Géoscience
PY  - 2005
SP  - 1055
EP  - 1064
VL  - 337
IS  - 12
PB  - Elsevier
DO  - 10.1016/j.crte.2005.05.003
LA  - fr
ID  - CRGEOS_2005__337_12_1055_0
ER  -

%0 Journal Article
%A Yann Leredde
%A Christine Lauer-Leredde
%A Frédéric Diaz
%T Sur l'assimilation variationnelle de données par un modèle d'écosystème marin de type NPZ
%J Comptes Rendus. Géoscience
%D 2005
%P 1055-1064
%V 337
%N 12
%I Elsevier
%R 10.1016/j.crte.2005.05.003
%G fr
%F CRGEOS_2005__337_12_1055_0

Yann Leredde; Christine Lauer-Leredde; Frédéric Diaz. Sur l'assimilation variationnelle de données par un modèle d'écosystème marin de type NPZ. Comptes Rendus. Géoscience, Volume 337 (2005) no. 12, pp. 1055-1064. doi : 10.1016/j.crte.2005.05.003. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2005.05.003/

Version originale du texte intégral

Abridged English version

1 Introduction

The marine pelagic ecosystem models of NPZ (Nutriment Phytoplankton Zooplankton) type have been strongly popular since Fasham et al. [7] and are widely used today [6]. One of the main characteristics of these models is the uncertainty of the value of some parameters to which these models are very sensitive.

Various methods, called data-assimilation methods, can then be implemented for the estimation of these parameters. The method used here, following the optimal control theory [15], mainly used in physical oceanography [2,5,18] and meteorology [4,13], consists in computing the discrepancies between the model results and the observations by means of a cost function. As the model results are directly linked to the model inputs (or controls), the minimum of the cost function will correspond to the best adapted controls, called the optimal controls. The minimisation of the cost function is performed by an iterative algorithm involving the computation by an adjoint model of the gradient of the cost function relative to the controls. At the end, a so-called optimal simulation, corresponding to the optimal control, is obtained.

In this note, we first explain how to obtain the adjoint model of a prototype NPZ model. Two academic numerical experiments are then performed to show the validity of the method, but also its difficulties and its limitations.

2 Numerical tools

The selected prototype model presents a structure similar to that of a NPZ model [6,7]. It is very simple, but it uses parameterisations usually met in the literature, such as those of Michaelis and Menten [17].

Three variables, only time-dependent, are used, N playing the role of a nutriment, P, the role of phytoplankton, and Z, the role of zooplankton. These three variables are expressed in terms of nitrogen concentration (mmol N m⁻³). The model is given by Eqs. (1), (2) and (3). Considering that the initial conditions are known, five parameters are the controls. These equations can be differentiated (e.g., (1)^′) to obtain the linear tangent model. A cunning way of obtaining its adjoint model consists in calculating (6) and organising the terms following (7). By integrating by parts (7), and introducing the adjoint equations (1)^*, (2)^*, (3)^*, the general form of the gradient of the cost function is obtained. The cost function can then be minimised in the direction of its gradient using a quasi-Newton algorithm [11]. Iterating the computations of (1) the direct model, (2) the cost function, (3) the adjoint model, (4) the gradient of the cost function, and then (5), a new set of parameters, an optimal set of parameters, corresponding to a so-called optimal simulation, is obtained.

3 Numerical experiments

Following a classical procedure of twin-experiments [4], the observations (Nobs1, Pobs1, Zobs1 on Fig. 1) are simulated first by the direct model. The experiment reproduces qualitatively a phenomenon of phytoplankton bloom, characterized by a fast and sudden growth, consuming the nutrient. The phytoplankton is then quickly grazed by the zooplankton before a slower excretion/remineralisation.

Fig. 1
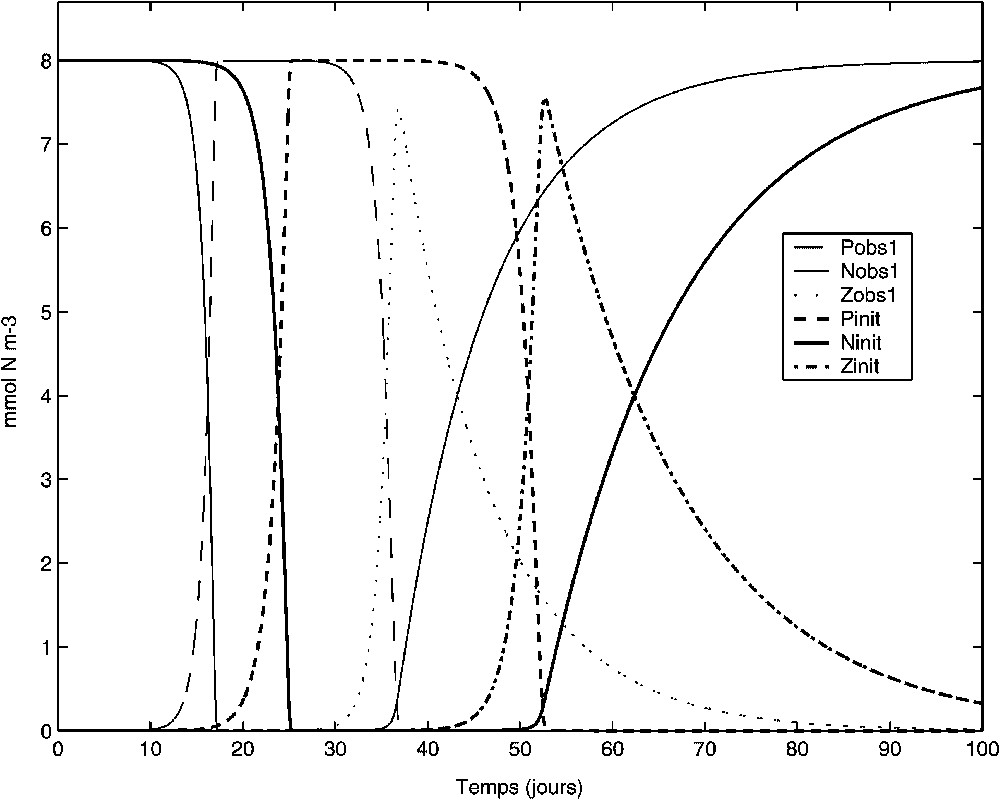
Résultats de la simulation servant à construire les observations de l'expérience 1 (Nobs1, Pobs1, Zobs1). Résultats de la simulation initiale (Ninit, Pinit, Zinit). Les résultats de la simulation optimale obtenue lors de l'expérience 1 sont confondus avec les observations (Nobs1, Pobs1, Zobs1).
Simulation results used to construct the observations of experiment 1 (Nobs1, Pobs1, Zobs1). Initial simulation results (Ninit, Pinit, Zinit). The optimal simulation results obtained for experiment 1 superimpose the observations (Nobs1, Pobs1, Zobs1).

The twin-experiments exercise consists then in assuming the values of the controls (the five parameters) unknown. The initial values, called the first guess of the optimisation exercise, are arbitrarily chosen in a usually admitted range. This choice is a real difficulty for some badly known parameters. Furthermore, contrary to algorithms of global optimisation, such as annealing or genetic algorithms [1], the first guess governs the success of the adjoint method. This last one has, indeed, all the chances to supply a local minimum close to the first guess, instead of the global minimum.

The initial simulation results (Ninit, Pinit, Zinit on Fig. 1) are the starting points of the two following experiments.

3.1 Experiment 1

This experiment consists in assimilating all the data (Nobs1, Pobs1, Zobs1) at all the time steps attributing the same weight to all the observations. The efficiency of the method is demonstrated: the cost function is minimised to 0 ( $\pm 10^{−9}$ ) (Fig. 2). The optimal parameters values are equal ( $\pm 10^{−4}$ ) to those used to simulate the observations.

Fig. 2
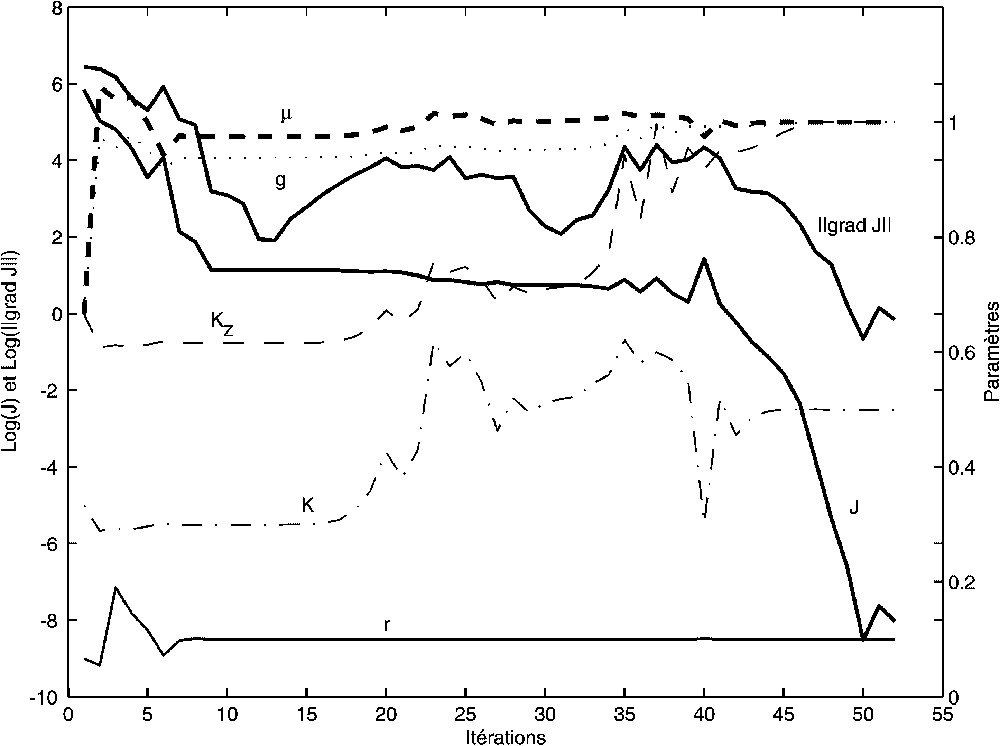
Résultats de l'expérience 1. Fonction de coût (J), norme du gradient de la fonction de coût ‖∇J‖ (représentation suivant une échelle logarithmique sur l'axe de gauche) et valeurs des paramètres à optimiser (axe de droite) en fonction du nombre d'itérations de la méthode.
Results of experiment 1. Cost function, norm of the gradient of the cost function ‖∇J‖ (representation following a logarithm scale on the left axis) and values of the parameters to optimise (right axis) as functions of the number of iterations of the method.

Fifty-two iterations were necessary for this degree of precision. This great number of iterations relative to the number of degrees of freedom of the model (five parameters) is a consequence of the great precision reached in the minimisation of the cost function. In reality, this minimisation is quickly performed (see the eight iterations on Fig. 2), while it is much longer to refind the values of the parameters used to simulate the observations.

3.2 Experiment 2

The experiment 2 aims to investigate the limits of the method. The assimilated observations are restricted to 10 values of phytoplankton (noted Pobs2 on Fig. 3), distributed every 10 days, noised with a threshold to 0. Because of this noise, the cost function cannot be reduced to 0, but is minimised in 53 iterations (Fig. 4). The optimal simulation results (Nopt2, Popt2, Zopt2 on Fig. 3) are those with the minimum discrepancies between the curve Popt2 and the points Pobs2. Fig. 3 shows a good global agreement.

Fig. 3
Résultats de la simulation servant à construire les observations de l'expérience 1 (Nobs1, Pobs1, Zobs1). Observations de l'expérience 2 (Pobs2) obtenues par bruitage de Pobs1. Résultats de la simulation optimale obtenue lors de l'expérience 2 (Nopt2, Popt2, Zopt2).
Simulation results used to construct the observations (Nobs1, Pobs1, Zobs1). Observations of experiment 2 (Pobs2) obtained by the noising of Pobs1. Optimal simulation results obtained for experiment 2 (Nopt2, Popt2, Zopt2).

Fig. 4
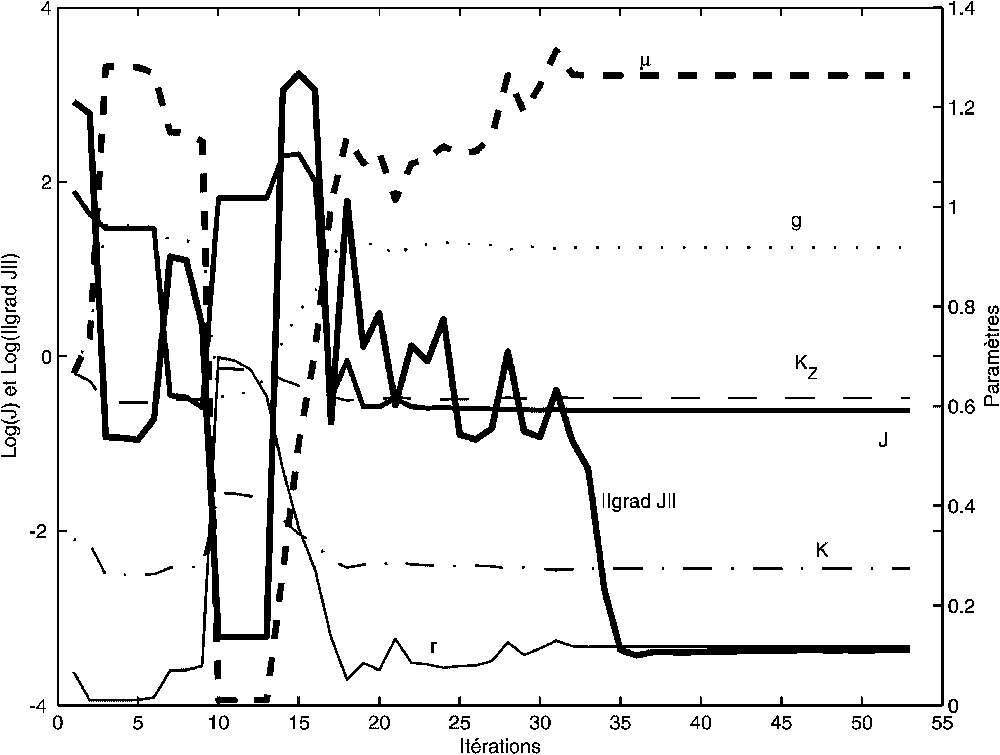
Résultats de l'expérience 2. Même légende que la Fig. 2.
Results of the experiment 1. Same caption as Fig. 2.

The results of this optimal simulation (Nopt2, Popt2, Zopt2) are slightly different from those (Nobs1, Pobs1, Zobs1) used to construct the observations Pobs2. In fact, Popt2 is closer to Pobs2 ( $J = 0.2$ ) than Pobs1 to Pobs2 ( $J = 0.4$ ). Looking only at the assimilated observations, the obtained set of parameters is better than that used to construct the observation.

Fig. 5 allows us to deepen this analysis. The shape of J is caricatural: the global minimum is in a very flat valley where any set of parameters could be considered as optimal control. We also realise that an unfortunate choice of first guess could lead to a divergence of the method or, at least, to a convergence towards a local minimum (it is potentially the case for a first guess of $μ = 2$ day⁻¹).

Fig. 5
Analyse de l'expérience 2. Coupes de la fonction de coût J (axe de gauche) en fonction des valeurs des paramètres μ, K et g. Coupe de $\frac{\partial J}{\partial μ}$ (axe de droite) en fonction des valeurs du paramètre μ.
Analysis of experiment 2. Cross-section of the cost J (left axis) as a function of the parameter values μ, K et g. Cross-section of $\frac{\partial J}{\partial μ}$ (right axis) as a function of the parameter value μ.

4 Conclusion

The implemented numerical tools allow us to show the possibilities of the adjoint method. If observations consistent with the model are available, the adjoint method allows us to determine the optimal controls (parameters or other inputs), defining the closest solution of the model to the observations.

By reducing the number of observations and introducing noise, experiment 2 shows also the limitations of the method. The problems of convergence due to the flatness of the cost function are often solved by the addition of a term of recall to the first guess in the cost function.

1 Introduction

Depuis Fasham et al. [7], les modèles d'écosystème pélagique marin de type NPZ (Nutriment Phytoplancton Zooplancton) connaissent une forte popularité et sont aujourd'hui largement utilisés [6]. Une des caractéristiques de ces modèles est l'incertitude de la valeur de certains paramètres auxquels ces modèles sont très sensibles. Cela rend souvent compte de faiblesses conceptuelles, et les paramétrisations qui en dépendent restent donc en pleine évolution.

Ces modèles ont pour objectif de reproduire au mieux les stocks et flux biogéochimiques des premiers maillons trophiques qui sont observés, soit par satellite (par exemple, projet Seawifs), soit par des stations instrumentées, telles que Dyfamed [16], soit enfin lors de campagnes océanographiques, telles que celles entreprises dans le golfe du Lion [20]. Le but principal des modèles reste donc la confrontation de leurs résultats aux observations. Deux démarches sont alors envisageables. La première consiste à estimer un état dit « analysé » réalisant des corrections séquentielles des états du modèle [3]. La seconde consiste à estimer des paramètres du modèle (au sens large, y compris les conditions initiales et limites), en cherchant à réduire les écarts entre états simulés et observés [19]. Diverses méthodes, dites méthodes d'assimilation de données, peuvent alors être mises en œuvre. Issues de travaux en mathématiques appliquées, ayant souvent transité par les domaines de la météorologie et de l'océanographie physique, ces méthodes commencent à être utilisées dans le domaine de la biogéochimie marine. Dans cette note, nous nous plaçons résolument dans la seconde démarche d'estimation de paramètres, par la mise en œuvre d'une méthode variationnelle d'assimilation de données utilisant un modèle adjoint.

Cette méthode, issue de la théorie du contrôle optimal [15], principalement appliquée en océanographie physique [2,5,18] et en météorologie [4,13], consiste à quantifier l'écart entre résultats du modèle et observations, au moyen d'une fonctionnelle de coût, dont la valeur est d'autant plus petite que la simulation s'ajuste aux observations. Les résultats du modèle étant directement reliés aux valeurs de ses entrées (ou contrôles), le minimum de la fonctionnelle de coût correspondra au contrôle le mieux adapté, dit « contrôle optimal ». La minimisation de cette fonctionnelle de coût ne pouvant le plus souvent pas se faire directement, une méthode itérative est mise en œuvre. Celle-ci utilise un modèle adjoint permettant de calculer le gradient de la fonctionnelle de coût vis-à-vis du contrôle. Le gradient ainsi déterminé, un algorithme de descente, permet de minimiser de proche en proche la fonctionnelle de coût. On obtient ainsi une simulation, dite optimale, correspondant au contrôle optimal.

La nature des modèles d'écologie pélagique, avec de nombreux paramètres dont la valeur est incertaine, rend l'utilisation de cette méthode séduisante. Les précurseurs [9,10,12,21] ont réalisé des expériences numériques réalistes, assimilant de véritables observations et/ou traitant de problèmes concrets. Ils démontrent ainsi l'intérêt de la méthode de l'adjoint, tout en faisant transparaître un certain nombre de difficultés, notamment d'écriture du modèle adjoint et de minimisation de la fonction de coût.

Dans cette note, nous montrons, dans un premier temps, comment obtenir le modèle adjoint d'un modèle NPZ prototype. Cela complète le travail de Faugeras [8], qui aurait pu être agrémenté de l'écriture de ces équations adjointes ou, tout au moins, comme cela est fait dans cet article, en montrer le principe sur un modèle simplifié. Nous réalisons ensuite deux expériences numériques académiques ayant pour but de montrer la validité de la méthode, mais aussi ses difficultés et ses limites. Ces résultats sont ensuite discutés et transposés à des cas d'utilisations moins académiques et plus réalistes.

2 Outils numériques

Le modèle prototype adopté présente une structure analogue à celle d'un modèle NPZ [6,7]. Il est d'une extrême simplicité, mais utilise des paramétrisations couramment rencontrées dans la littérature, telles que celles de Michaelis et Menten [17]. De même que le modèle simplifié utilisé pour étudier les contrôles d'un modèle de turbulence [14], il est mis en œuvre à des fins purement prospectives pour étudier la faisabilité et le comportement de la méthode. De formulation simple, il ne peut être considéré comme un modèle réaliste d'écosystème marin.

Trois variables ne dépendant que du temps t sont utilisées, N jouant le rôle de nutriment, P celui du phytoplancton et Z celui de zooplancton. Ces trois variables sont exprimées en terme de concentration en azote (mmol N m⁻³). Le modèle NPZ considéré prend la forme suivante :

\frac{d P}{d t} = μ \frac{N}{K + N} P - g \frac{P}{K_{Z} + P} Z

(1)

\frac{d N}{d t} = - μ \frac{N}{K + N} P + r Z

(2)

\frac{d Z}{d t} = g \frac{P}{K_{Z} + P} Z - r Z

(3)

où μ, K, g,

K_{Z}

et r sont respectivement le taux de croissance du phytoplancton, la constante de demi-saturation de la prise de nutriment, le taux de broutage, la constante de demi-saturation de ce broutage et le taux d'excrétion du zooplancton. Les trois équations différentielles couplées (1), (2) et (3) représentent le modèle direct et sont intégrées par méthode d'Euler sur l'intervalle

[0, T]

. T, la durée de simulation, sera fixée à 100 jours.

Soit Ψ un contrôle quelconque du modèle direct. En pratique, Ψ est l'un des paramètres μ, K, g, $K_{Z}$ , r ou une condition initiale $N (0)$ , $P (0)$ , $Z (0)$ . On note $\hat{P}, \hat{N}, \hat{Z}$ les observations du système. On définit la fonction de coût J par :

J = \frac{1}{2} \int_{0}^{T} [{(\frac{P - \hat{P}}{σ_{\hat{P}}})}^{2} + {(\frac{N - \hat{N}}{σ_{\hat{N}}})}^{2} + {(\frac{Z - \hat{Z}}{σ_{\hat{Z}}})}^{2}] d t

(4)

où

σ_{\hat{P}}^{2}

,

σ_{\hat{N}}^{2}

et

σ_{\hat{Z}}^{2}

sont les variances d'observations correspondant à l'inverse du poids donné à chacune dans la constitution de la fonction de coût. S'il n'existe pas d'observation pour une variable et un temps donnés, on considère son poids comme nul et sa variance comme infinie. Par simplification, et pour ne pas alourdir les écritures, les observations et les résultats de simulations sont supposés faire partie du même espace. Dans le cas contraire, un opérateur de passage pourrait être ajouté. En notant les dérivées partielles par rapport à Ψ par ′, on écrit les composantes du gradient de la fonction de coût ainsi :

\frac{\partial J}{\partial Ψ} = J^{'} = \int_{0}^{T} [\frac{P - \hat{P}}{σ_{\hat{P}}^{2}} P^{'} + \frac{N - \hat{N}}{σ_{\hat{N}}^{2}} N^{'} + \frac{Z - \hat{Z}}{σ_{\hat{Z}}^{2}} Z^{'}] d t

(5)

Le modèle linéaire tangent à Ψ s'écrit en différenciant les équations (1) à (3). À titre d'exemple, la première équation du modèle linéaire tangent est la suivante :

\frac{d P^{'}}{d t} = μ^{'} \frac{N}{K + N} P - K^{'} μ \frac{N}{{(K + N)}^{2}} P + μ \frac{N}{K + N} P^{'} + μ \frac{K}{{(K + N)}^{2}} P N^{'} - g^{'} \frac{P}{K_{Z} + P} Z + K_{Z}^{'} g \frac{P}{{(K_{Z} + P)}^{2}} Z - g \frac{P}{K_{Z} + P} Z^{'} - g \frac{K_{Z}}{{(K_{Z} + P)}^{2}} Z P^{'}

(1)′

Notons (1)′ cette équation et (2)′ et (3)′, les équations que l'on obtient de la même manière pour

N^{'}

et

Z^{'}

. Les équations (1)′, (2)′ et (3)′ forment le modèle linéaire tangent. Nous proposons ici une manière d'écrire son modèle adjoint vérifié par les variables adjointes notées

P^{*}

,

N^{*}

et

Z^{*}

et les composantes du gradient de la fonction de coût, notées

J^{'}

. En réalisant l'opération :

\int_{0}^{T} [{(1)}^{'} P^{*} + {(2)}^{'} N^{*} + {(3)}^{'} Z^{*}] d t

(6)

où les variables adjointes

P^{*}

,

N^{*}

,

Z^{*}

sont encore indéfinies et en réorganisant les différents termes, on obtient :

\int_{0}^{T} \frac{d P^{'}}{d t} P^{*} + \frac{d N^{'}}{d t} N^{*} + \frac{d Z^{'}}{d t} Z^{*} d t = \int_{0}^{T} [μ^{'} \frac{N}{K + N} P (P^{*} - N^{*}) + K^{'} μ \frac{N}{{(K + N)}^{2}} P (N^{*} - P^{*}) + g^{'} \frac{P}{K_{Z} + P} Z (Z^{*} - P^{*}) + K_{Z}^{'} g \frac{P}{{(K_{Z} + P)}^{2}} Z (P^{*} - Z^{*}) + r^{'} Z (N^{*} - Z^{*}) + P^{'} (μ \frac{N}{K + N} (P^{*} - N^{*}) + g \frac{K_{Z}}{{(K_{Z} + P)}^{2}} Z (Z^{*} - P^{*})) + N^{'} μ \frac{K}{{(K + N)}^{2}} P (P^{*} - N^{*}) + Z^{'} (g \frac{P}{K_{Z} + P} (Z^{*} - P^{*}) + r (N^{*} - Z^{*}))] d t

(7)

Les termes du membre de gauche sont ensuite intégrés par partie :

\int_{0}^{T} \frac{d P^{'}}{d t} P^{*} d t = P^{*} (T) P^{'} (T) - P^{*} (0) P^{'} (0) - \int_{0}^{T} P^{'} \frac{d P^{*}}{d t} d t

(8)

On cherche à faire apparaître l'expression de

J^{'}

dans l'équation (7). À cette fin, on impose aux variables adjointes

P^{*}

,

N^{*}

,

Z^{*}

de vérifier les équations suivantes, dites équations adjointes :

\frac{d P^{*}}{d t} + μ \frac{N}{K + N} (P^{*} - N^{*}) + g \frac{K_{Z}}{{(K_{Z} + P)}^{2}} Z (Z^{*} - P^{*}) = \frac{P - \hat{P}}{σ_{\hat{P}}^{2}}

(1)

\frac{d N^{*}}{d t} + μ \frac{K}{{(K + N)}^{2}} P (P^{*} - N^{*}) = \frac{N - \hat{N}}{σ_{\hat{N}}^{2}}

(2)

\frac{d Z^{*}}{d t} + g \frac{P}{K_{Z} + P} (Z^{*} - P^{*}) + r (N^{*} - Z^{*}) = \frac{Z - \hat{Z}}{σ_{\hat{Z}}^{2}}

(3)

ainsi que les conditions finales

P^{*} (T) = N^{*} (T) = Z^{*} (T) = 0

. En combinant les équations (5) et (7) et en utilisant les équations (1)^*–(3)^*, on obtient la forme générale de

J^{'}

:

J^{'} = P^{*} (0) P^{'} (0) + N^{*} (0) N^{'} (0) + Z^{*} (0) Z^{'} (0) + μ^{'} \int_{0}^{T} \frac{N}{K + N} P (P^{*} - N^{*}) d t + K^{'} \int_{0}^{T} μ \frac{N}{{(K + N)}^{2}} P (N^{*} - P^{*}) d t + g^{'} \int_{0}^{T} \frac{P}{K_{Z} + P} Z (Z^{*} - P^{*}) d t + K_{Z}^{'} \int_{0}^{T} g \frac{P}{{(K_{Z} + P)}^{2}} Z (P^{*} - Z^{*}) d t + r^{'} \int_{0}^{T} Z (N^{*} - Z^{*}) d t

(9)

En supposant l'indépendance des contrôles les uns par rapport aux autres (par exemple, la valeur de r ne dépend pas de l'état initial ou des valeurs des autres paramètres et réciproquement), l'équation (9) nous donne toutes les composantes du gradient (par exemple

\frac{\partial J}{\partial P (0)} = P^{*} (0)

ou

\frac{\partial J}{\partial r} = \int_{0}^{T} Z (N^{*} - Z^{*}) d t

). Dans la suite, on ne s'intéressera qu'au contrôle par les cinq paramètres μ, K, g,

K_{Z}

et r, les conditions initiales étant supposées parfaitement connues. Le modèle adjoint est intégré de l'état final à

t = T

à l'état initial à

t = 0

et les intégrales formant les composantes du gradient de la fonction de coût sont sommées. La fonction de coût peut ainsi être minimisée dans la direction du gradient suivant un algorithme de quasi-Newton [11]. En itérant modèle direct, modèle adjoint, calcul du gradient et recherche d'un nouveau jeu de paramètres, on s'approche d'un jeu de paramètres optimaux permettant une simulation dite optimale.

3 Expériences numériques

Suivant une procédure classique [4], dite d'expériences jumelles, les observations sont tout d'abord simulées par le modèle direct. La simulation de référence servant à construire des observations (Nobs1, Pobs1, Zobs1 sur la Fig. 1) est réalisée avec les valeurs de paramètres suivants : $μ = 1 {jour}^{−1}$ , $K = 0, 5 mmol N m^{−3}$ , $g = 1 {jour}^{−1}$ , $K_{Z} = 1 mmol N m^{−3}$ et $r = 0, 1 {jour}^{−1}$ , et les valeurs initiales suivantes : $N (0) = 8 mmol N m^{−3}$ , $P (0) = 10^{−6} mmol N m^{−3}$ et $Z (0) = 10^{−6} mmol N m^{−3}$ , ces valeurs correspondant à celles couramment rencontrées en Méditerranée nord-occidentale en période hivernale.

Compte tenu du modèle prototype utilisé, on n'accordera aucune interprétation quantitative aux résultats obtenus. Néanmoins, l'expérience reproduit qualitativement un phénomène d'efflorescence phytoplanctonique, caractérisé par une croissance rapide et soudaine du phytoplancton consommant le nutriment (entre les jours 12 et 17). Celui-ci est ensuite brouté par le zooplancton suivant un processus également rapide (jours 36 et 37). Une excrétion/reminéralisation plus lente intervient ensuite. Les valeurs de paramètres utilisées ne permettent pas de provoquer un nouveau cycle de ce type durant les 100 jours de simulation. Avec d'autres valeurs, comme un taux d'excrétion plus rapide, on pourrait très bien obtenir cet autre cycle durant ces 100 jours. La présence d'un compartiment détritus, souvent introduit dans ce type de modèles, rendrait également plus réaliste cette simulation.

L'exercice d'expériences jumelles consiste ensuite à supposer les valeurs de contrôles (les cinq paramètres) inconnues. Les valeurs initiales, point de départ de l'exercice d'optimisation, sont choisies arbitrairement dans une gamme de valeurs couramment admises. Cette difficulté est réelle pour certains paramètres mal connus. De plus, contrairement à des algorithmes d'optimisation globale, tels que le recuit-simulé ou les algorithmes génétiques [1], le point de départ conditionne la réussite de la méthode d'adjoint, puisque celle-ci a toutes les chances de fournir un minimum local proche et non le minimum global. Une bonne connaissance des gammes de valeurs acceptables des paramètres est donc nécessaire. Dans notre cas, un choix complètement fantaisiste de point de départ pourrait conduire à des valeurs physiquement absurdes de ces paramètres.

On choisit ici de partir de valeurs relativement proches de celles des paramètres ayant servi à fabriquer les observations, à savoir $μ = 0, 667 {jour}^{−1}$ , $K = 0, 333 mmol N m^{−3}$ , $g = 0, 667 {jour}^{−1}$ , $K_{Z} = 0, 667 mmol N m^{−3}$ et $r = 0, 067 {jour}^{−1}$ . Les résultats de cette simulation initiale (Ninit, Pinit, Zinit sur la Fig. 1) montrent une croissance phytoplanctonique plus tardive et moins rapide (jours 17 à 26), suivie d'une croissance zooplanctonique, également plus tardive et moins rapide (jours 41 à 52). Le processus de recyclage est également plus lent. Ces résultats sont le point de départ des deux expériences d'assimilation.

3.1 Expérience 1

Cette expérience consiste à assimiler toutes les données (Nobs1, Pobs1, Zobs1) à tous les pas de temps, en accordant un poids unitaire à toutes les observations. L'efficacité de la méthode est démontrée. On réduit la fonction de coût à 0 (à 10⁻⁹ près) (Fig. 2) ; les résultats de simulation optimale sont confondus avec les données (Nobs1, Pobs1, Zobs1) et ne sont donc pas représentés sur la Fig. 1. On identifie aussi des paramètres optimaux dont les valeurs sont égales (à 10⁻⁴ près) aux valeurs ayant servi à simuler les observations (voir Fig. 2).

Pour ce degré de précision, 52 itérations ont été nécessaires. Ce grand nombre d'itérations par rapport au nombre de degrés de liberté du modèle (cinq paramètres) peut paraître surprenant. De même, les quelque 5000 itérations réalisées par Spitz et al. [21] pour optimiser 29 paramètres peuvent paraître excessives. L'argument d'un nombre réduit d'itérations a pourtant été avancé [8] pour favoriser les algorithmes de descentes à gradient, tels que celui proposé dans cette note, par rapport aux algorithmes d'optimisation globale. À première vue, cet argument semble injustifié, mais l'analyse de la Fig. 2 nous montre que tout dépend, en fait, de la précision voulue et/ou atteinte dans la minimisation de la fonction de coût et dans l'identification des paramètres. La fonction de coût, représentée suivant une échelle logarithme à base 10, est en fait très rapidement (en huit itérations) minimisée à des valeurs suffisamment petites pour que l'œil ne distingue plus les écarts entre observations et résultats de simulation (superposition des courbes sur la Fig. 1). Certains paramètres auxquels le modèle est plus sensible sont déjà optimisés, alors que d'autres vont s'ajuster lors des itérations suivantes, au fur et à mesure que la fonction de coût tend vers 0. En réalité, tout dépend de l'objectif fixé. S'il s'agit de réduire l'écart des résultats de simulation aux observations, l'objectif est très rapidement atteint. S'il s'agit de retrouver les paramètres ayant servi à simuler les observations, cela peut se révéler beaucoup plus long.

Au passage, on s'aperçoit que les paramètres μ, g et r sont beaucoup plus rapidement optimisés que les constantes de demi-saturation K et $K_{Z}$ . Ce fait est révélateur d'une plus faible sensibilité du modèle à ces deux derniers paramètres. Cette question de la sensibilité du modèle aux paramètres reste très importante. Dans des versions plus sophistiquées de modèle NPZ, avec des paramètres plus nombreux, on s'aperçoit aussi de la prépondérance de certains paramètres et du lien intrinsèque qu'il peut y avoir entre eux. Des analyses de sensibilité telles que celles mises en oeuvre par Prunet et al. [19] ou Faugeras et al. [9] permettent de faire un premier tri.

3.2 Expérience 2

L'expérience 1 a essentiellement permis de s'assurer du bon fonctionnement numérique de la méthode. L'expérience 2 a pour but d'en explorer les limites. Les observations assimilées ne sont plus que 10 valeurs de phytoplancton (notées Pobs2 sur la Fig. 3), réparties tous les 10 jours, bruitées, mais seuillées à 0. Les conditions initiales sont supposées connues. Le bruitage (gaussien de moyenne 0 et d'écart-type 0,3) donne des observations qui ne sont plus complètement cohérentes avec le modèle. La fonction de coût ne peut donc pas être réduite à 0, mais elle est minimisée en 53 itérations (dont les 15 dernières sont inutiles) (Fig. 4). Les résultats de la simulation optimale (Nopt2, Popt2, Zopt2 sur la Fig. 3) sont ceux qui minimisent l'écart quadratique entre la courbe Popt2 et les points Pobs2. La Fig. 3 montre un bon ajustement général. Celui-ci est parfait pour les jours 10 et 30. La valeur du jour 20 ne pouvant dépasser 8 mmol N m⁻³, quantité totale initiale, la valeur simulée est donc optimale. Aux jours 40 à 100, les valeurs simulées sont nulles, alors que seul le bruitage rend les observations non nulles.

Les résultats (Nopt2, Popt2, Zopt2) de cette simulation optimale (vis-à-vis des seules observations assimilées) sont légèrement différents des résultats (Nobs1, Pobs1, Zobs1) ayant servi à construire les observations Pobs2. Les développements planctoniques sont en fait un peu moins tardifs (2 à 3 jours). Il est à noter que Popt2 est en fait plus proche de Pobs2 ( $J = 0, 2$ ) que ne l'est Pobs1 de Pobs2 ( $J = 0, 4$ ). Au regard des seules observations assimilées, le jeu de paramètres optimaux obtenus ( $μ = 1, 27 {jour}^{−1}$ , $K = 0, 28 mmol N m^{−3}$ , $g = 0, 91 {jour}^{−1}$ , $K_{Z} = 0, 61 mmol N m^{−3}$ et $r = 0, 12 {jour}^{−1}$ ) est donc meilleur que celui ayant servi à construire les observations.

La Fig. 5 permet d'approfondir cette analyse. On y représente des coupes de la fonction de coût, en ne faisant varier qu'un seul des cinq paramètres et en laissant les quatre autres constants et égaux aux valeurs ayant servi à construire les observations. Cette exploration systématique n'est bien sûr envisageable que dans un cas aussi académique que celui-ci, où de très nombreux lancements du modèle direct sont possibles à moindre coût numérique. Par souci de clarté, la fonction de coût J n'est représentée, sur la Fig. 5, qu'en fonction des trois paramètres μ, K et g. La forme de J est caricaturale : son minimum global se trouve d'abord dans une vallée très plate ( $0, 9 < μ < 1, 3, 0, 9 < g < 1, 2$ et $0 < K < 1, 5$ ), où tout jeu de paramètres pourrait convenir comme contrôle optimal. En poussant l'optimisation sur de nombreuses itérations, on obtient toutefois des valeurs de J très petites ( $J = 0, 2$ ) correspondant aux valeurs de paramètres $μ = 1, 27 {jour}^{−1}$ , $K = 0, 28 mmol N m^{−3}$ , $g = 0, 91 {jour}^{−1}$ , $K_{Z} = 0, 61 mmol N m^{−3}$ et $r = 0, 12 {jour}^{−1}$ . On comprend ici pourquoi un nombre important d'itérations est le plus souvent utilisé dans ce type d'expérience d'optimisation. Grâce à la Fig. 5, on réalise aussi qu'un choix malheureux de point de départ pourrait conduire à une non-convergence de la méthode ou en tout cas à la convergence vers un minimum local (c'est potentiellement le cas pour un point de départ de $μ = 2 {jour}^{−1}$ ). La représentation du gradient de J dans la direction μ (Fig. 5, axe de droite) montre l'exactitude de son calcul par le modèle adjoint, mais on voit qu'un algorithme classique de descente par gradient [11] ne pourra se sortir du piège des nombreux minima locaux et des plateaux.

4 Conclusion

Les outils numériques mis en oeuvre permettent de montrer les possibilités de la méthode de l'adjoint. Ces outils restent simples, et même sans avoir recours aux prises automatiques d'adjoint, la Section 2 montre comment écrire le modèle adjoint d'un modèle d'écosystème marin de type NPZ. Si un certain nombre d'observations cohérentes avec le modèle sont disponibles, la méthode d'adjoint permet de déterminer les contrôles (paramètres ou autres entrées) optimaux, c'est-à-dire ceux qui définissent la solution du modèle la plus proche des observations.

Les expériences numériques menées montrent aussi les limitations de la méthode. L'analyse des dysfonctionnements de certaines expériences non montrées permet également de progresser quant à l'utilisation d'une telle méthode numérique.

Par exemple, en augmentant l'écart entre les observations de 10 jours (expérience 2) à 20 jours, la méthode ne converge plus. Dans ce cas, seulement cinq données sont assimilées et le problème est proche de la sous-détermination. On voit ici l'intérêt de la méthode pour déterminer la cadence d'acquisition nécessaire. Une des applications d'une telle méthode est sans aucun doute la mise au point de stratégie d'observations. Quelles données et quelles précisions dans ces données sont-elles nécessaires pour contraindre le modèle ?

Un autre exemple d'expérience malheureuse consisterait à prendre un point de départ qui conduirait la minimisation vers un minimum local. Les conditions extrêmes de l'expérience 2, induites par le très faible nombre de données assimilées, favorisent de telles difficultés. En outre, les problèmes de convergence dus à la platitude de la fonction de coût près du minimum global sont souvent résolus par l'ajout d'un terme de rappel aux valeurs d'une ébauche dans la fonction de coût. Ce degré 0 de la régularisation est un bon moyen d'améliorer la convergence, mais il reste à régler le poids accordé à ces termes de rappel, en fonction du degré d'incertitude sur la connaissance a priori des valeurs de l'ébauche. Quand le choix d'une ébauche est impossible, certains auteurs [1] préconisent un algorithme d'optimisation global. D'autres auteurs [21] proposent d'essayer différents points de départ de la minimisation, espérant ainsi mieux explorer l'espace des paramètres. Tout dépend certainement du problème posé, du nombre de paramètres à optimiser et du nombre de lancements autorisé par les coûts numériques. Une prochaine étude consisterait à explorer la voix intermédiaire qui associerait les deux approches de descente par gradient et de sauts probabilistes afin d'éviter les minima locaux.

Bibliographie

[1] V. Athias; P. Mazzega; C. Jeandel Selecting a global optimization method to estimate the oceanic particle cycling rate constants, J. Mar. Res., Volume 58 (2000), pp. 675-707

[2] D. Begis; M. Crepon On the generation of currents by winds: An identification method to determine oceanic parameters, Lect. Notes Phys., Volume 58 (1975)

[3] V. Carmillet; J.-M. Brankart; P. Brasseur; H. Drange; G. Evensen A singular evolutive extended Kalman filter to assimilate ocean color data in a coupled physical–biogeochemical model of the North Atlantic, Ocean Model, Volume 3 (2001), pp. 167-192

[4] P. Courtier; O. Talagrand Variational assimilation of meteorological observations with the direct and adjoint shallow-water equations, Tellus, Volume 42A (1990), pp. 531-549

[5] J.L. Devenon Optimal control theory applied to an objective analysis of a tidal current mapping by HF radar, J. Atmos. Ocean. Technol., Volume 7 (1990), pp. 269-284

[6] F. Diaz, Évolution saisonnière de la production primaire et des processus d'assimilation/régénération de l'azote dans le golfe du Lion. Estimation d'un bilan de carbone. Approches in situ et modélisation, thèse, université Aix–Marseille-II, Marseille, France, 2000, 351 p

[7] M.J.R. Fasham; H.W. Ducklow; S.M. McKelvie A nitrogen-based model of plankton dynamics in the oceanic mixed layer, J. Mar. Res., Volume 48 (1990), pp. 591-639

[8] B. Faugeras, Assimilation variationnelle de données dans un modèle couplé océan-biogéochimie, thèse, Université Grenoble-I, 2002, 199 p

[9] B. Faugeras; M. Lévy; L. Mémery; J. Verron; J. Blum; I. Charpentier Can biogeochemical fluxes be recovered from nitrate and chlorophyll data ? A case study assimilating data in the Northwestern Mediterranean Sea at the JGOFS-DYFAMED station, J. Mar. Syst., Volume 40–41 (2003), pp. 99-125

[10] M.A.M. Friedrichs A data assimilative marine ecosystem model of the central equatorial Pacific: Numerical twin experiments, J. Mar. Res., Volume 59 (2001), pp. 859-894

[11] J.C. Gilbert; C. et Lemarechal Some numerical experiments with variable-storage quasi-Newton algorithms, Math. Programming, Volume 45 (1989), pp. 407-435

[12] J. Gunson; A. Oschlies; V. Garçon Sensitivity of ecosystem parameters to simulated satellite ocean color data using a coupled physical–biogeochemical model of the North Atlantic, J. Mar. Res., Volume 57 (1999), pp. 613-639

[13] F.-X. Le Dimet; O. Talagrand Variational algorithms for analysis and assimilation of meteorological observations: theoretical aspects, Tellus, Volume 38A (1986), pp. 97-110

[14] Y. Leredde; J.L. Devenon; I. Dekeyser Peut-on identifier les constantes d'un modèle de turbulence par assimilation d'observations ?, C. R. Acad. Sci. Paris, Ser. IIa, Volume 331 (2000), pp. 405-412

[15] J.-L. Lions Contrôle optimal de systèmes gouvernés par des opérateurs aux dérivées partielles, Dunod, Paris, 1968 (426 p)

[16] J.C. Marty; J. Chiavérini; M-D. Pizay; B. Avril Seasonal and interannual dynamics of nutrients and phytoplankton pigments in the western Mediterranean Sea at the DYFAMED time-series station (1991–1999), Deep-Sea Res. II, Volume 49 (2002), pp. 1965-1985

[17] L. Michaelis; M.I. Menten Die Kinetik der Invertinwirkung, Biochem. Z., Volume 49 (1913), pp. 333-369

[18] A.M. Moore Data assimilation in a quasi-geostrophic open-ocean model of the Gulf Stream region using the adjoint method, J. Phys. Ocean., Volume 21 (1991), pp. 398-427

[19] P. Prunet; J.-F. Minster; D. Ruiz-Pino; I. Dadou Assimilation of surface data in a one-dimensional physical–biogeochemical model of the surface ocean. 1. Method and preliminary results, Global Biogeochem. Cycles, Volume 10 (1996) no. 1, pp. 111-138

[20] P. Raimbault; X. Durrieu de Madron Responsables de la publication. Research activities in the Gulf of Lion (NW Mediterranean) within the 1997–2001 PNEC project, Oceanol. Acta, Volume 26 (2003) no. 4

[21] Y.H. Spitz; J.R. Moisan; M.R. Abbott; J.G. Richman Data assimilation and a pelagic ecosystem model: parameterization using time series observations, J. Mar. Syst., Volume 16 (1998), pp. 51-68

Commentaires - Politique