Abridged English version
1 Introduction
The precipitations in Congo-Brazzaville (Fig. 1), as everywhere in the Congolese forested basin, result from several types of mechanisms of different scales, which imply a low coherence of the structures of rainfall variability. The distribution of the sequences of non-rainy days within a rainy season was never thoroughly analysed in Congo-Brazzaville. The previous works [3,13,16] were devoted to large spatiotemporal scales. From the agronomic point of view, the persistence of dry spells during the rainy season is an essential factor for starting cultivation, depending on the soil humidity. The use of daily precipitations data allowed identification of the beginning and of the end of the rainy season on the plateaus Cataractes and Bateke [22].
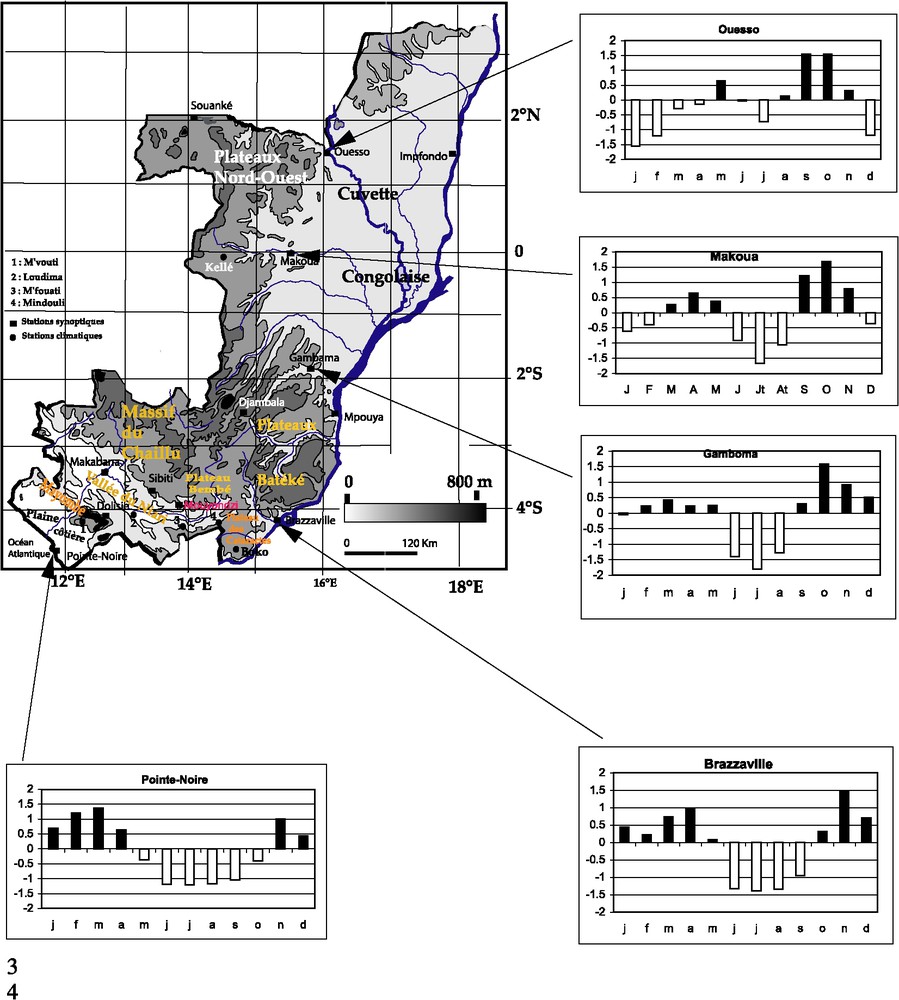
Carte du Congo avec les différentes stations utilisées et les principaux régimes pluviométriques.
Congo map with the various used stations and the main rainfall regimes.
Various models are proposed to adjust the daily rainfall sequences, according to their class, i.e. non-rainy or rainy: they are the Markov chain [18], the Polya law [17] and the Truncated Negative Binomial law [2,8].
We chose the Markov chain in our work for its robustness and because it directly takes into account the influence of the closest last day on the next immediate day. The Markov-chain probability model was widely used for modelling the occurrence of the sequences of days with or without rain. Gabriel and Neuman [7], Caskey [5], Weiss [26] gave the best example of the use of this model. The Markov-chain model for the occurrence of the daily precipitations was generalized by Todorovic and Woolhier [24], Kantz [11], Lestienne [15], Arruda and Pinto [2]. Galloy et al. [24], Moon et al. [18] and Gómez Navaro [9] showed the efficiency of the Markovian model from two states of occurrence of the daily rains. Also, the Markovian model efficiently estimates dryness persistence. This short contribution allows illustrating the successes and the limits of such an approach in Congo-Brazzaville.
2 Data and methods
The data used originate from the archives of the Direction of the National Meteorology of Congo-Brazzaville, and were processed by the ‘Centre de recherches sur les tropiques humides’ (CRTH) of the Marien Ngouabi University in Brazzaville, for the period 1950–1994. For each series, all the values were classified into two states: state 0 (non-rainy day: dry or very dry) and state 1 (rainy day: normal, rainy, very rainy). It was considered that a day is not rainy when it receives less than 1 mm of precipitation. Fig. 1 shows that all the stations situated in the South of Congo display rainfall maxima centred over March or April, then over November, while stations situated in the North have to maxima centred over April or May, then in October. The analysis will thus concern the daily precipitation during the main rainy seasons (in September–November in the North and in October–December in the South, and in March–May), which bring more than 70% of the annual rainfall over the Congolese territory, and during which the main part of the agricultural activities takes place, as defined previously by Samba et al. [22]. The order of the Markov chain to retain in the analysis of the daily precipitations series was determined from the procedure called AIC (Akaike information criterion), proposed by Akaike [1], validated by Thong [25] and summarized by Katz [12] (see Section 2 of the French text).
The test of was applied between both series (observations and models) to evaluate the 95% significance of the results and thus to determine if the model is applicable or not. Every time the calculated value (c2) is superior to the theoretical value (), the model fit is considered plausible.
3 Results and discussion
The results (Tables 1 and 2) oppose two main domains: the southern wet tropical domain, represented by the stations of Pointe-Noire, Dolisie, Makabana, Mouyondzi, Brazzaville, M'Pouya, Djambala, Loudima, Boko, Mindouli and M'fouati, with a strong probability of sequences of two days without rains, and the northern equatorial domain, represented by the stations of Ouesso, Impfondo, Gamboma, Souanké, with a low probability of occurrence of sequences of two days without rain. More, the results, for the majority of the stations in Congo, show that the model predicts relatively well the sequences of days without rain (Fig. 2). The validation based on the test comparing the values calculated from the Markovian model and the frequencies observed is significant for the majority of stations.
Taille des plus longues séquences sans pluie (en nombre de jours)
Size of the longest sequences without rain (in number of days)
| MAM | SON ou OND | |
| Impfondo | 16 | 11 |
| Ouesso | 15 | 18 |
| Souanké | 21 | 28 |
| Makoua | 25 | 26 |
| Gamboroa | 37 | 30 |
| Djambala | 14 | 14 |
| M ou a | 13 | 16 |
| Brazzaville | 40 | 20 |
| Boko | 25 | 21 |
| Mouyondzi | 42 | 52 |
| Loudima | 27 | 25 |
| Sibiti | 30 | 22 |
| Dolisie | 20 | 23 |
| Makabana | 32 | 36 |
| Pointe-Noire | 55 | 32 |
| Mindouli | 41 | 39 |
| M'Fouati | 31 | 50 |
| M'Vouti | 22 | 23 |
Probabilité d'occurrence des précipitations journalières et de transitions (1950–1994). P(0) : Probabilité d'avoir un jour sans pluie et P(1) d'avoir un jour pluvieux ; P(00) probabilité d'avoir une séquence de deux jours non pluvieux et P(11) de deux jours pluvieux
Probability of daily precipitation occurrences and transitions (1950–1994). P(0): Probability to have a dry day and P(1) to have a rainy day; P(00) probability to have a sequence of two dry days and P(11) of two rainy days
| NUM | SON ou OND | |||||||
| P(0) | P(1) | P(00) | P(11) | P(0) | P(1) | P(00) | P(11) | |
| Impfondo | 0,57 | 0,43 | 0,56 | 0,44 | 0,47 | 0,53 | 0,42 | 0,58 |
| Ouesso | 0,59 | 0,41 | 0,60 | 0,40 | 0,45 | 0,55 | 0,44 | 0,56 |
| Souanké | 0,42 | 0,52 | 0,51 | 0,49 | 0,42 | 0,58 | 0,48 | 0,52 |
| Makoua | 0,32 | 0,68 | 0,53 | 0,47 | 0,47 | 0,53 | 0,45 | 0,55 |
| Cmmboma | 0,62 | 0,38 | 0,63 | 0,37 | 0,48 | 0,52 | 0,49 | 0,51 |
| Djambala | 0,50 | 0,50 | 0,51 | 0,49 | 0,64 | 0,36 | 0,53 | 0,47 |
| M'Pouya | 0,54 | 0,46 | 0,58 | 0,42 | 0,55 | 0,45 | 0,55 | 0,45 |
| Brazzaville | 0,64 | 0,36 | 0,68 | 0,32 | 0,59 | 0,41 | 0,63 | 0,37 |
| Boko | 0,51 | 0,49 | 0,69 | 0,31 | 0,47 | 0,53 | 0,69 | 0,31 |
| Mouyondzi | 0,51 | 0,49 | 0,63 | 0,37 | 0,47 | 0,53 | 0,71 | 0,31 |
| Loudima | 0,59 | 0,41 | 0,67 | 0,33 | 0,39 | 0,68 | 0,32 | 0,68 |
| Sibiti | 0,57 | 0,43 | 0,57 | 0,43 | 0,47 | 0,54 | 0,60 | 0,40 |
| Dolisie | 0,45 | 0,55 | 0,52 | 0,48 | 0,45 | 0,55 | 0,57 | 0,43 |
| Makabaaa | 0,58 | 0,42 | 0,65 | 0,35 | 0,42 | 0,58 | 0,67 | 0,33 |
| Pointe-Noire | 0,66 | 0,44 | 0,74 | 0,26 | 0,49 | 0,51 | 0,60 | 0,40 |
| Mindouli | 0,60 | 0,40 | 0,70 | 0,30 | 0,48 | 0,52 | 0,72 | 0,28 |
| M'Fouati | 0,33 | 0,67 | 0,70 | 0,30 | 0,42 | 0,58 | 0,76 | 0,33 |
| M'Vouti | 0,28 | 0,72 | 0,32 | 0,68 | 0,30 | 0,70 | 0,70 | 0,30 |
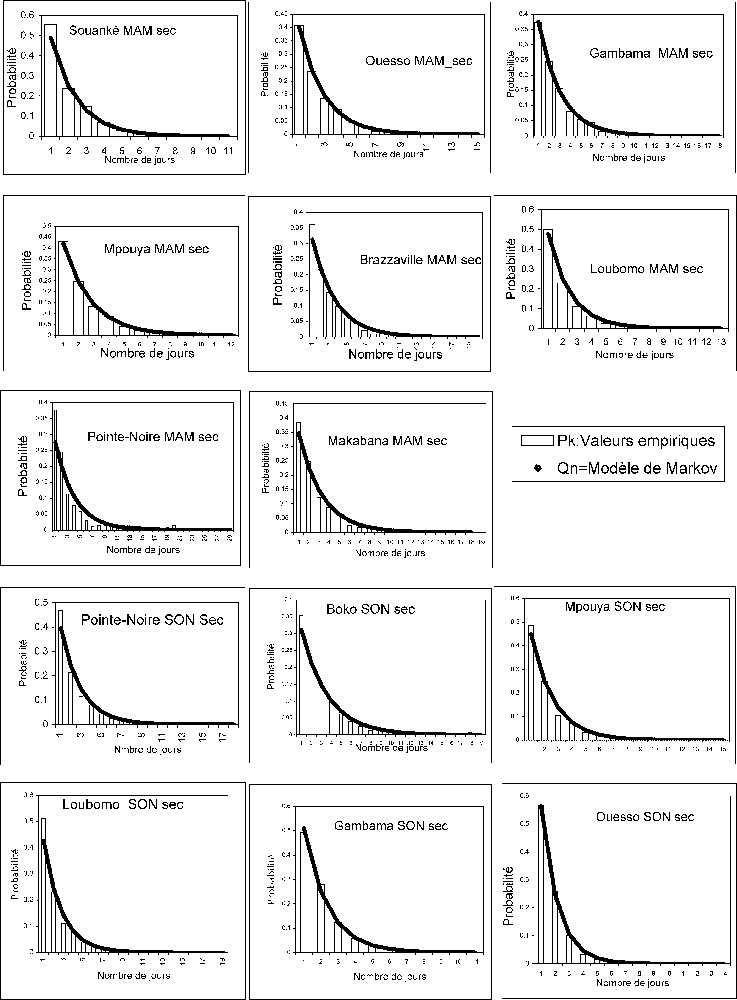
Probabilités empiriques (histogramme) et estimées par la chaîne de Markov de premier ordre (courbe) des différentes stations.
Empirical (histogram) and estimated probabilities by the first-order Markov chain (curve) of the various stations.
These characteristics of the occurrences of daily precipitation call for several remarks about the complexity of rainfall processes and the climate dynamics. The coexistence of convective, orographic rains and disturbances or squall lines complicates the distribution patterns of the daily rains. The air stream stemming from the St. Helena high and which affects southern Congo possesses in fact the character of a trade wind. It then penetrates into the Basin of Congo. Suchel [23] calls this stream ‘pseudo-monsoon’, although it is for Leroux [14] only a trade wind deviated from its trajectory, by the attraction of the Congo low (Fig. 3). This trade wind, which is diverted eastward, is originally stable or dry on the coastal plain, represented by the Pointe-Noire station, with long sequences without rains of 32 or 55 days. It gradually becomes unstable only when it becomes integrated into the cyclonic circulation associated to the Congo Basin depression. This party explains that the Bateke plateau, with the station of Djambala, has the advantage of a better exposure in the humidity issue to Congo low. The Niari Valley (Dolisie) and both plateaus Bembe (Mouyondzi) and Cataractes (Boko) are characterized by long sequences without rains from 20 to 52 days (Table 2), with a strong probability of two days without rain (Table 1). Thus if there was no redistribution of the precipitations by the east disturbances, the South of the Congo would know more intense climatic aridities.
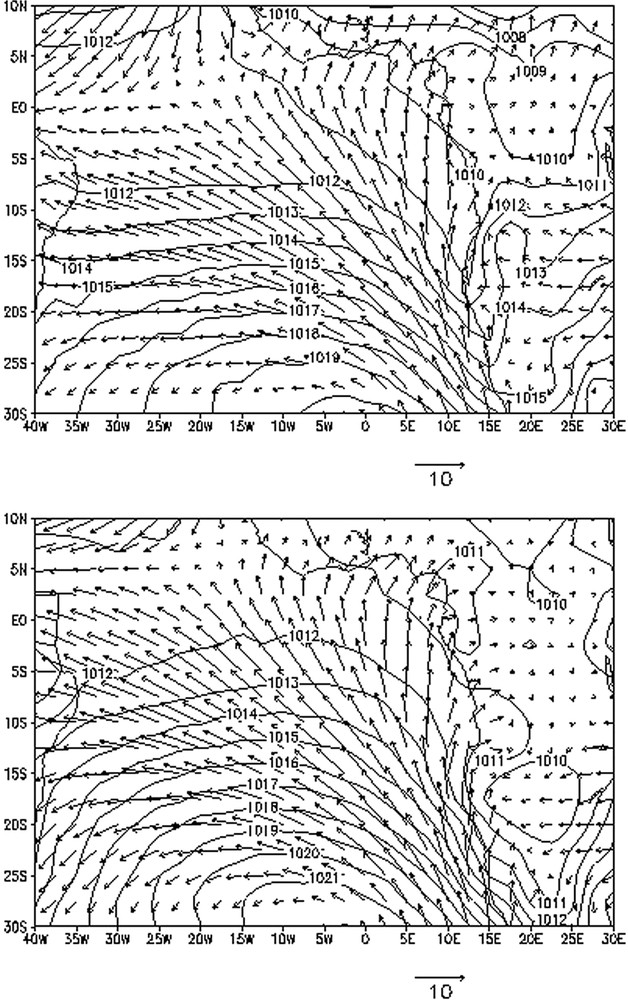
Champs de pression au niveau de la mer (isobares) et flux moyen des vents au sol (flèches noires) : (A) saison mars–mai ; (B) saison septembre–novembre ; Sainte-Hélène : anticyclone de Sainte-Hélène.
Sea-level pressure (isobars) and the average surface wind flow (black arrows): (A) season March–May; (B) season September–November.
With these elements of synoptic scale, it is necessary to associate the important weight of local factors (state of surface) in the daily distribution of the precipitation, which notably modulates the intense thermo-convective activity. They are these aerologic and orographic factors that contribute to the complexity of distribution of days without rain in Congo, complexity that leads to a weak coherence of the spatial structures of the daily rains.
The works of Nicholson [20], Janicot and Fontaine [10], Fontaine et al. [6] on the rainfall of western Africa showed the existence of a strong meridian pressure gradient of the precipitations. The seasonal meridian movement of the ITF (Intertropical Front) or the ITCZ (Intertropical Zone Convergence) as well as its structure indeed leads to a quasi-zonal distribution of the annual isohyets, with a strong diminution of the precipitations to the north [10]. Moron [19] showed a good coherence of the spatiotemporal structures of the precipitations of the space. Eastern Africa also remains a region marked by the homogeneity with regard to the rainfall behaviour [4]. On the other hand, a strong variety of the rainfall regimes characterizes this part of the African continent. We note a very strong pressure gradient NW–NE [21], with a spatial coherence of the distribution of the precipitations. On the other hand, Congo presents a very low spatial coherence of the precipitations.
4 Conclusion
The application of the first order of the chain of Markov on occurrences of the precipitation in the Congo-Brazzaville confirms the existence of two climates domains: tropical wet in the South and equatorial in the North, and the stability of the stream of oceanic trade wind in the South, which becomes unstable on the western margins of the Congolese basin. The distribution of the lengths of dry sequences and the probability of occurrence of two consecutive days without rain in the seasonal scale increase by the North Southward. The orographic effects (coastal plain, mountain range of Mayombe, Valley of Niari and Cataracts plateau) and the role of the disturbances in the spatial rainfall distribution of the precipitation are indirectly highlighted. This analysis is a first approach to the understanding of the daily rains in the Congo-Brazzaville and in the Congo Basin. In perspective, the analysis of the general circulation in this region deserves a deepening with dynamic climatic models.
1 Introduction
Ce travail constitue une analyse d'occurrence des précipitations journalières au Congo-Brazzaville, pour tenter leur ajustement par le premier ordre de la chaîne de Markov en zone intertropicale humide. Le Congo-Brazzaville (Fig. 1), situé en Afrique équatoriale atlantique (AEA), s'étend de part et d'autre de l'équateur, entre les latitudes 4°N et 5°S et entre les méridiens 11°18′ et 18°E, avec une superficie de 342 000 km2 et une densité de population de 7 hab/km2. Cette région est une des moins connues d'Afrique sur le plan climatologique, car elle est sous la domination d'un flux appelé pseudo-mousson, qui présente les caractéristiques d'un alizé. C'est une des zones climatiques les plus complexes, sauf en ce qui concerne la cuvette congolaise, qui a une uniformité géographique et topographique, à laquelle s'opposent les autres unités : la plaine côtière, les plateaux Batéké, le plateau Bembé, le plateau des Cataractes, la vallée du Niari, le massif du Chaillu et la chaîne de montagnes du Mayombe. L'objet de cette étude est donc de comparer entre elles les régions du Congo par rapport aux événements pluvieux consécutifs.
Situé sur les marges occidentales du bassin forestier congolais, le territoire du Congo-Brazzaville a une organisation pluviométrique complexe, en partie liée à la variété des états de surface qui influent sur les masses d'air d'origine océanique (anticyclones de Sainte-Hélène et des Mascareignes) via leurs effets locaux (zone de dépression, forêt, relief). Au Congo-Brazzaville, comme partout dans le bassin forestier congolais, les précipitations résultent de plusieurs types de mécanismes d'échelles différentes, ce qui implique une faible cohérence des structures de variabilité pluviométrique. Les occurrences des précipitations journalières représentent donc un élément pertinent dans la description des caractéristiques climatiques du bassin forestier et du Congo-Brazzaville en particulier. Le dénombrement des séquences des jours non pluvieux au sein d'une saison pluvieuse n'a jamais fait l'objet d'une analyse approfondie au Congo-Brazzaville. Les précédents travaux [3,13,16] ont été consacrés aux grandes échelles spatio-temporelles. Du point de vue agronomique, la persistance des épisodes sans pluie pendant la saison pluvieuse est déterminante pour le démarrage des cultures pluviales. L'analyse des occurrences des précipitations journalières peut aussi aider à la planification des activités agricoles. Les séquences de jours non pluvieux, même courtes, ont un effet important, compte tenu des conditions édaphiques et du régime climatique du Congo-Brazzaville. Le Congo-Brazzaville a pu connaître, dans les dernières décennies du XXe siècle, des sécheresses agricoles très sévères dans la vallée du Niari et sur le plateau des Cataractes. L'utilisation des données journalières des précipitations a, par ailleurs, permis de détecter le début et la fin de la saison des pluies sur le plateau des Cataractes et le plateau Batéké [22].
Gabriel et Neuman [7], Caskey [5], Weiss [26] ont donné les meilleurs exemples de l'utilisation du modèle markovien. La chaîne de Markov a été généralisée, pour l'occurrence des précipitations journalières, par Todorovic et Woolhier [24], Kantz [11], Lestienne [15], et Arruda et Pinto [2]. Galloy et al. [8], Moon et al. [18] et Gómez Navaro [9] ont montré l'efficacité du modèle markovien à partir de deux états d'occurrence des pluies journalières. En effet, différents modèles ont été proposés pour ajuster les séquences climatiques, selon leur classe d'appartenance, par exemple, non pluvieuses ou pluvieuses. On peut citer : la chaîne de Markov [18], la loi de Polya [17] et/ou la loi binomiale négative translatée [2,8]. Nous avons choisi de travailler sur la chaîne de Markov pour sa robustesse et parce qu'elle prend directement en compte l'influence du jour passé le plus proche sur le jour suivant immédiat. Cette chaîne est un modèle stochastique, itératif, qui met en relation des probabilités de passage ou de transition d'un état à un autre, ou de persistance d'un état d'un système. La modélisation des séquences de jours consécutifs sans pluie constitue une contribution à la caractérisation climatologique d'une station ou d'une région. Le modèle probabiliste de la chaîne de Markov a été largement utilisé pour l'occurrence des séquences des jours sans pluie ou pluvieux. De même, le modèle markovien estime avec efficacité la persistance du degré de sécheresse. Cette courte contribution permet d'illustrer les succès et les limites d'une telle approche au Congo-Brazzaville.
2 Données et méthodes
Les données utilisées sont issues des archives de la Direction de la météorologie nationale du Congo-Brazzaville et mises en forme par le Centre de recherches sur les tropiques humides (CRTH) de l'université Marien-Ngouabi de Brazzaville. Ce sont les précipitations journalières des treize stations synoptiques du Congo et des six stations climatiques (Fig. 1), pour la période 1950–1994. Le réseau d'observations utilisé est caractérisé par l'inégale répartition des stations, avec une densité moyenne d'une station synoptique pour 26 308 km2 et par l'hétérogénéité des séries, surtout due à des lacunes. C'est pourquoi les six stations non synoptiques, bien qu'ayant des séries lacunaires, ont été intégrées dans l'étude pour optimiser la représentativité spatiale. Pour l'ensemble des stations, les valeurs journalières manquantes sont de l'ordre de 10%. Pour chaque série, toutes les valeurs ont été ramenées à deux états : un état 0 (jour non pluvieux) et un état 1 (jour pluvieux). Il a été considéré qu'un jour est non pluvieux lorsqu'il reçoit moins de 1 mm de précipitations. Une séquence climatique est dite non pluvieuse (pluvieuse) lorsqu'une suite de jours non pluvieux (pluvieux) consécutifs sépare deux jours pluvieux (non pluvieux).
La Fig. 1 montre que les stations situées dans le Sud du Congo sont associées à des maxima centrés en mars sur Pointe-Noire ou en avril sur Brazzaville, puis en novembre sur ces deux stations, alors que les stations situées dans le Nord le sont en avril ou mai, puis en octobre pour la station de Ouesso. L'analyse concernera les précipitations journalières au cours des grandes saisons des pluies (septembre–novembre au nord et octobre–décembre au sud, et mars–mai), qui apportent plus de 70% de la pluviométrie annuelle sur le territoire congolais, et durant lesquelles se réalise l'essentiel des activités agricoles. Ces deux saisons, mars/avril/mai (MAM) et septembre/octobre/novembre ou décembre (SON ou OND), ont été définies précédemment par Samba et al. [22] comme des SPPU (saisons de pluies potentiellement utiles).
3 La chaîne de Markov
L'ordre de la chaîne de Markov à retenir dans l'analyse des séries de données de précipitations journalières a été déterminé à partir de la procédure dite de l'AIC (Akaike Information Criterion) de Akaike [1], validée par Tong [25] et reprise par Katz [12].
Procédure de choix de l'ordre de la chaîne de Markov
L'AIC estimateur pour l'ordre d'une chaîne de Markov est défini par certaines de ses propriétés [12]. Formellement, l'ordre de la chaîne de Markov est caractérisé par des probabilités de transition , où les indices de rang portent sur les s états possibles.
Soit un échantillon de n observations de la chaîne de Markov , la procédure AIC nécessite le calcul de la fonction maximisée de la probabilité pour un ordre de la chaîne , qui est (en ignorant les premiers termes) :
Une formulation commode de la procédure Akaike de sélection dans le cas de l'ordre de la chaîne de Markov est, en termes de statistiques de rapport de probabilité pour l'ordre () contre l'ordre de la chaîne , avec :
La procédure AIC appliquée aux séries « stationnelles » du Congo permet de retenir l'ordre 1 pour l'estimation des probabilités de passage d'un état à l'autre. Cela signifie que l'état du jour k ne dépend que de l'état . La probabilité d'occurrence d'un jour non pluvieux est estimée par sa fréquence relative , où M est le nombre total des jours secs :
Le test de a été appliqué entre les deux séries (observations et modèle) pour juger de la significativité à 95% des résultats et donc déterminer si le modèle est applicable ou non. Chaque fois que la valeur calculée () est supérieure à la valeur théorique (), le modèle d'ajustement est jugé plausible.
4 Résultats et discussion
Le Tableau 1 indique la durée maximale des séquences de jours secs. Dans l'ensemble, les plus longues séquences non pluvieuses sont observées dans le Sud du Congo. La plus longue séquence de jours sans pluie, pour la saison MAM, est observée à Pointe-Noire, avec 55 jours, et à Mouyondzi, avec 52 jours pour la saison SON ou OND. Le Tableau 2 résume les différentes probabilités d'occurrence des jours sans pluie pour chaque station et pour les deux principales saisons des pluies MAM et SON. Pour la saison MAM, les probabilités, dans les différentes stations, de deux jours consécutifs sans pluie sont plus élevées (0,51 à 0,70) que celles des séquences de deux jours pluvieux (0,26–0,49). Les plus fortes probabilités () de deux jours sans pluie sont observées dans le Sud du Congo (Mindouli, Pointe-Noire, Boko, M'Fouati), ce qui signifie que, dans ces stations, un jour sans pluie a de fortes chances d'être suivi d'un jour sans pluie. La saison SON met en évidence deux zones : une zone dite sud (au sud de Gamboma), avec des probabilités > 0,50, et une zone nord (probabilité < 0,50). Les probabilités assez fortes de deux jours consécutifs pluvieux de la zone nord montrent qu'un jour pluvieux a tendance à favoriser la pluie du lendemain, alors qu'au sud, c'est le caractère non pluvieux d'un jour qui tend à persister le plus. Ces résultats opposent deux domaines principaux : le domaine sud, tropical humide, représenté par les stations de Pointe-Noire, Dolisie, Makabana, Mouyondzi, Brazzaville, M'pouya, Djambala, Loudima, Boko, Mindouli et M'Fouati, avec de fortes probabilités des séquences de deux jours sans pluies, et le domaine nord, équatorial, représenté par les stations de Ouesso, Impfondo, Gamboma, Souanké, avec de faibles probabilités d'occurrence des séquences de deux jours sans pluie.
La Fig. 2 montre les courbes des probabilités de jours sans pluie et les ajustements du modèle markovien. Les résultats, pour la majorité des stations du Congo, montrent que le modèle prédit relativement bien les séquences de jours sans pluie. La validation faite avec le test de entre les valeurs calculées à partir du modèle markovien et les fréquences observées s'avère significative (à ) pour la majorité des stations.
Ces caractéristiques des occurrences de précipitations journalières génèrent plusieurs remarques au niveau de la complexité pluviogénique et de la dynamique climatique. La coexistence des pluies convectives, orographiques et de perturbations ou lignes de grains complique le schéma de la distribution des pluies journalières. Les résultats des Tableaux 1 et 2 montrent, par exemple, que la station de Pointe-Noire sur la plaine côtière (avec de longues séquences de jours sans pluie ou de fortes probabilités de deux jours sans pluie), la station de Mvouti sur le côté au vent de la chaîne de montagne du Mayombe (de courtes longueurs maximales de jours sans pluie et de faibles probabilités de deux jours sans pluie), et celle de Dolisie sous le vent (avec de longues séquences et de fortes probabilités) signent respectivement le caractère stable de l'alizé dans le Sud du Congo et l'effet orographique de la chaîne de montagnes du Mayombe. En effet, le flux de masse d'air issu de l'anticyclone de Sainte-Hélène (Fig. 3), qui baigne le Sud du Congo, possède, en fait, un caractère d'alizé. Il pénètre ensuite sur le bassin du Congo. Suchel [23] qualifie ce flux de « pseudo-mousson », bien qu'il ne soit, pour Leroux [14], qu'un alizé dévié de sa trajectoire par l'attraction de la dépression du bassin du Congo. Cette « pseudo-mousson » (Fig. 3) est originellement stable ou sèche sur la plaine côtière (station de Pointe-Noire, avec de longues séquences sans pluie de 32 ou 55 jours). Ce flux se recharge en humidité sur le continent et ne devient progressivement instable que lorsqu'il s'intègre dans la circulation liée à la dépression du bassin du Congo. C'est pourquoi les plateaux Batéké (station de Djambala), bénéficient d'une meilleure exposition à l'humidité amenée, d'une part, par ce flux de « pseudo-mousson » et, d'autre part, par des apports de perturbations venant de l'est. Le plateau Bembé (station de Mouyondzi) et le plateau des Cataractes (stations de Boko), bien qu'ayant des altitudes relativement aussi élevées, sont traversés par des masses d'air (flux de pseudo-mousson) encore stables (Fig. 3). Ainsi donc, s'il n'y avait pas de redistribution des précipitations par les perturbations d'est, le Sud du Congo connaîtrait des sécheresses climatiques plus intenses. En effet, les pluies thermo-convectives ne suffiraient pas à compenser les pluies. La cuvette congolaise, quant à elle, se trouvant dans un marais barométrique (Fig. 3), bénéficie d'importants effets locaux de la pluviogenèse. Ce qui a pour corollaire des précipitations de faibles hauteurs, mais relativement régulières.
À ces éléments d'échelle synoptique, il faut associer le poids important des facteurs locaux (états de surface : par exemple, l'opposition de la forêt de la Cuvette congolaise et du massif du Chaillu avec la savane des plateaux Batéké), distribution journalière des précipitations qui modulent notamment l'intense activité thermo-convective.
Les travaux de Nicholson [20], Janicot et Fontaine [10], Fontaine et al. [6] sur la pluviométrie de l'Afrique occidentale ont montré l'existence de forts gradients méridiens des précipitations. Cette distribution des précipitations est assurée par un flux de mousson qui présente une bonne cohérence spatio-temporelle [19]. Le mouvement méridien saisonnier du FIT (front intertropical) ainsi que sa structure conduisent, en effet, à une distribution quasi-zonale des isohyètes annuelles, avec une forte décroissance des précipitations vers le nord. L'Afrique orientale, malgré la diversité de ses régimes pluviométriques, est aussi marquée par une homogénéité de la variabilité pluviométrique [4]. La zonalité climatique en Afrique australe est perturbée par l'opposition entre flux atlantique sec et flux humide de l'océan Indien. On note un gradient NW–NE très fort [21], avec une cohérence spatiale de la distribution des précipitations. En revanche, le Congo présente une très faible cohérence spatiale des précipitations. Le flux de l'océan Atlantique, à cause de sa courte trajectoire océan/continent, et aussi de la subsidence dans l'alizé, reste stable. La majeure partie des précipitations est d'origine convective. Les amas nuageux ou ondes d'est sont les perturbations qui apportent des pluies à l'échelle synoptique ou à méso-échelle.
Ce sont ces facteurs aérologiques et orographiques, illustrés par les cas des stations de Pointe-Noire (sur la plaine côtière), de M'Vouti (côté au vent du Mayombe) et de Dolisie (sous le vent) et de Djambala (sur les plateau Batéké) et d'Impfondo (dans la cuvette congolaise), qui concourent à la complexité de la répartition spatiale des jours sans pluie au niveau du Congo, complexité qui conduit à une faible cohérence des structures spatiales des pluies journalières.
5 Conclusion
L'application du premier ordre de la chaîne de Markov sur les occurrences des précipitations au Congo-Brazzaville confirme l'existence des deux domaines climatiques : tropical humide au sud et équatorial au nord et la stabilité du flux d'alizé océanique dans le sud, qui devient instable sur les marges occidentales de la cuvette congolaise. La distribution des longueurs des séquences des jours sans pluie et les probabilités d'occurrence de deux jours consécutifs sans pluie à l'échelle saisonnière augmentent du nord vers le sud. Les effets de l'orographie (plaine côtière, chaîne de montagnes du Mayombe, vallée du Niari et plateau des Cataractes) et le rôle des perturbations d'est dans la distribution spatiale des précipitations sont indirectement mis en évidence. Cette analyse est une première approche pour la compréhension des pluies journalières au Congo-Brazzaville et par là même, dans le bassin du Congo. En perspective, l'analyse de la circulation générale dans cette région mérite un approfondissement avec des modèles climatiques dynamiques.
Remerciements
Les auteurs tiennent à remercier Monsieur Bernard Fontaine, du Centre de recherches de climatologie, CNRS, UMR 5080, de l'université de Bourgogne (Dijon, France), pour ses orientations et corrections.


