Pétrofabrique et propriétés mécaniques des argilites

Françoise Homand; Jian-Fu Shao; Albert Giraud; Christophe Auvray; Dashnor Hoxha

doi:10.1016/j.crte.2006.03.009

Géomatériaux (Minéralogie)

Pétrofabrique et propriétés mécaniques des argilites

Françoise Homand ¹ ; Jian-Fu Shao ² ; Albert Giraud ¹ ; Christophe Auvray ¹ ; Dashnor Hoxha ²

¹ LAEGO–ENSG–INPL, bât. E, rue du Doyen-Marcel-Roubault, 54501 Vandœuvre-les-Nancy cedex, France
² LML UMR CNRS, 1441, bd Paul-Langevin, 59655 Villeneuve-d'Ascq cedex, France

Comptes Rendus. Géoscience, Volume 338 (2006) no. 12-13, pp. 882-891.

Résumés

Français
Anglais

La pétrofabrique des argilites influence leurs propriétés thermiques, hydrauliques et mécaniques. Des mesures de diffusivité, perméabilité et vitesse des ondes montrent que l'anisotropie de ces propriétés dans les argilites du Callovo-Oxfordien est assez faible. Le coefficient de Biot caractérisant le couplage hydromécanique a été déterminé, sa diminution avec la contrainte axiale ne peut pas être expliquée uniquement par la diminution de porosité, même en considérant qu'une matrice incompressible correspond à 1% pour une contrainte axiale variant de 8 à 24 MPa. L'origine de la diminution du coefficient de Biot s'explique par la perte de connexion d'une partie du réseau poreux, jusqu'alors connectée, sous l'effet de l'augmentation de la contrainte axiale. Un modèle élastoplastique isotrope est une approche raisonnable pour la description du comportement mécanique de l'argilite. Cependant, pour une modélisation plus avancée, il est utile de prendre en compte l'endommagement par microfissuration, qui est un mécanisme de dissipation non négligeable et couplé avec la plasticité.

The petrofabric of mudstones influences their thermal, hydraulic and mechanical properties. Measurements of thermal diffusivity, permeability and velocity of ultrasonic waves show that the anisotropy of these properties in this rock is rather low. The diminution of Biot coefficient with axial stress cannot be explained only by the diminution of porosity even by considering an incompressible matrix to 1% for an axial stress varying from 8 to 24 MPa corresponds. The origin of the diminution could be explained by the loss of connection of part of the porous system, hitherto connected, under the effect of an increasing axial stress. An isotropic elastoplastic model is a reasonable approach for the description of the mechanical behaviour of mudstone. However, it is useful to take into account the damage by microfissuring, which could not be neglected and must be considered coupled with plasticity.

Métadonnées

Reçu le : 2005-07-05
Accepté le : 2006-03-28
Publié le : 2006-06-09

DOI : 10.1016/j.crte.2006.03.009

Mot clés : Argilites, Propriétés thermo-hydro-mécaniques, Coefficient de Biot, Modèle de comportement
Keywords: Mudstones, Thermo-hydro-mechanical properties, Biot coefficient, Constitutive model

Affiliations des auteurs :

Françoise Homand ¹ ; Jian-Fu Shao ² ; Albert Giraud ¹ ; Christophe Auvray ¹ ; Dashnor Hoxha ²

¹ LAEGO–ENSG–INPL, bât. E, rue du Doyen-Marcel-Roubault, 54501 Vandœuvre-les-Nancy cedex, France
² LML UMR CNRS, 1441, bd Paul-Langevin, 59655 Villeneuve-d'Ascq cedex, France

@article{CRGEOS_2006__338_12-13_882_0,
     author = {Fran\c{c}oise Homand and Jian-Fu Shao and Albert Giraud and Christophe Auvray and Dashnor Hoxha},
     title = {P\'etrofabrique et propri\'et\'es m\'ecaniques des argilites},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {882--891},
     publisher = {Elsevier},
     volume = {338},
     number = {12-13},
     year = {2006},
     doi = {10.1016/j.crte.2006.03.009},
     language = {fr},
}

TY  - JOUR
AU  - Françoise Homand
AU  - Jian-Fu Shao
AU  - Albert Giraud
AU  - Christophe Auvray
AU  - Dashnor Hoxha
TI  - Pétrofabrique et propriétés mécaniques des argilites
JO  - Comptes Rendus. Géoscience
PY  - 2006
SP  - 882
EP  - 891
VL  - 338
IS  - 12-13
PB  - Elsevier
DO  - 10.1016/j.crte.2006.03.009
LA  - fr
ID  - CRGEOS_2006__338_12-13_882_0
ER  -

%0 Journal Article
%A Françoise Homand
%A Jian-Fu Shao
%A Albert Giraud
%A Christophe Auvray
%A Dashnor Hoxha
%T Pétrofabrique et propriétés mécaniques des argilites
%J Comptes Rendus. Géoscience
%D 2006
%P 882-891
%V 338
%N 12-13
%I Elsevier
%R 10.1016/j.crte.2006.03.009
%G fr
%F CRGEOS_2006__338_12-13_882_0

Françoise Homand; Jian-Fu Shao; Albert Giraud; Christophe Auvray; Dashnor Hoxha. Pétrofabrique et propriétés mécaniques des argilites. Comptes Rendus. Géoscience, Volume 338 (2006) no. 12-13, pp. 882-891. doi : 10.1016/j.crte.2006.03.009. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2006.03.009/

Version originale du texte intégral

Abridged English version

This paper is devoted to the study of petrofabric structure and mechanical properties of the Callovo-Oxfordian argillite. This material is extensively investigated in the framework of scientific research programs to study the possibility of high-level or long-lived radioactive waste deep geological disposal, conducted by ANDRA in France. The term petrofabric is used here to include mineralogical composition, pores distribution and textural organization. A particular emphasis is put on the structural anisotropy regarding variations of permeability, heat diffusivity, mechanical strength and elastic properties, with the orientation of measurement.

The total volumetric fraction of clay element of these argillites is about 50% [21]. The total porosity, estimated from volumetric mass measurement, is between 10 and 17%. The connected porosity should be lower than this value.

The anisotropy is an important element of petrofabric structure in rocks. For sedimentary rocks like argillite, the anisotropy is generally of transversely isotropic type. This particular structural anisotropy can be associated to bedding plane and oriented cracks [12]. In Tables 1 and 2, we present a series of typical values for various physical properties, measured on the argillite samples from the depth of 460 to 505 m.

	0°	90°	Commentaire
Diffusivité thermique (m² s⁻¹)	9,2×10⁻⁷	7,4×10⁻⁷	Moyenne 5 éprouvettes (EST104, −450 ; −530 m)
Perméabilité (m²)	6×10⁻²⁰	4,7×10⁻²⁰	2 éprouvettes (EST204, −480 m)
	5,6×10⁻²⁰	4,3×10⁻²⁰	2 éprouvettes (PEP2001, −500 m)
Résistance (MPa)	43,2	48,9	Essai triaxial ( $σ_{3} = 12 MPa$ ) moyenne 4 éprouvettes cylindriques
			(EST361, −500 m)

	$V_{p}$ (m/s)	$V_{s_{\max}}$ (m/s)	$V_{s_{\min}}$ (m/s)	$I_{b}$ (%)	ΔM (–)	Δm (–)	$E_{1}$ (GPa)	$E_{2}$ (GPa)	$ν_{12}$	$ν_{21}$	$ν_{23}$	$G_{12}$ (GPa)	$G_{23}$ (GPa)	$ν_{12} / E_{1}$	$ν_{21} / E_{2}$
0°3	4050	2000	1900	5	52	1	21	22	0,35	0,37	0,29	9	7,9	0,017	0,017
0°2	4000
90°1	3850	1910	1900	1
45°	3960	1910	1800	6

An extensive series of measurements have been performed for thermal diffusivity [11], with various hydric conditions and along different orientations with respect to the stratification. The thermal diffusivity of saturated rock varies from 5 to $11 \times 10^{−7} m^{2} s^{−1}$ . The anisotropy of thermal diffusivity between the two principal orientations is about 1.24 (see Table 1), which seems to be quite small.

The permeability of argillite is very low and the determination is generally difficult. The pulse test is usually used to estimate low permeability of rocks [10,11,17,19]. According to a few successful tests, the order of magnitude of permeability of argillite is of 10⁻²⁰ m². The anisotropy is also quite small and around 1.27. Therefore, there is a concordance between the anisotropy of permeability and thermal diffusivity.

The mechanical strength of argillite in a triaxial compression test with 12 MPa confining pressure is shown in Table 1. We can see that the anisotropy of mechanical strength is about 1.13, which is smaller that in permeability and thermal diffusivity.

The elastic properties of argillite are shown on Table 2. Static and dynamic methods have been used. Various anisotropy index, as defined by the relations (1), (2) and (3), have been calculated. The obtained results have confirmed a transversely isotropic behaviour of the argillite. However, the anisotropy of elastic properties is also very small. Further, there are no preferentially oriented linear elements in the bedding plane.

Extensive investigations have also been conducted on the determination of Biot coefficient, which is a key parameter in poromechanical coupling. Specific oedometric tests have been performed by using two loading phases [24]. In the first phase, axial stress is increased with constant pore pressure, and the stress-strain relation is given by Eq. (5). In the second phase, pore pressure is increased while the axial stress is hold to be constant and the corresponding pressure–strain curve is described by Eq. (6). The Biot coefficient is then determined by comparing the strain curves from the two phases. The typical results from Vincké et al. [26] and Escoffier [11] are shown in Fig. 2. We can see that the Biot coefficient significantly decreases when the axial stress is higher. According to the theoretical definition of Biot coefficient (7), such a diminution can be attributed to an increase of the drained bulk modulus. From the view point of microstructure, under higher axial stress, an undrained zone can be generated around quartz grains. The undrained modulus is higher than drained one. On the macroscopic scale, the initially drained modulus is progressively replaced by an overall partially drained modulus, which is defined by (9). For instance, the value of the partially drained bulk modulus changes from 1448 to 6000 MPa when the axial stress increases from the range between 8 and 2 MPa to the range between 24 and 18 MPa. 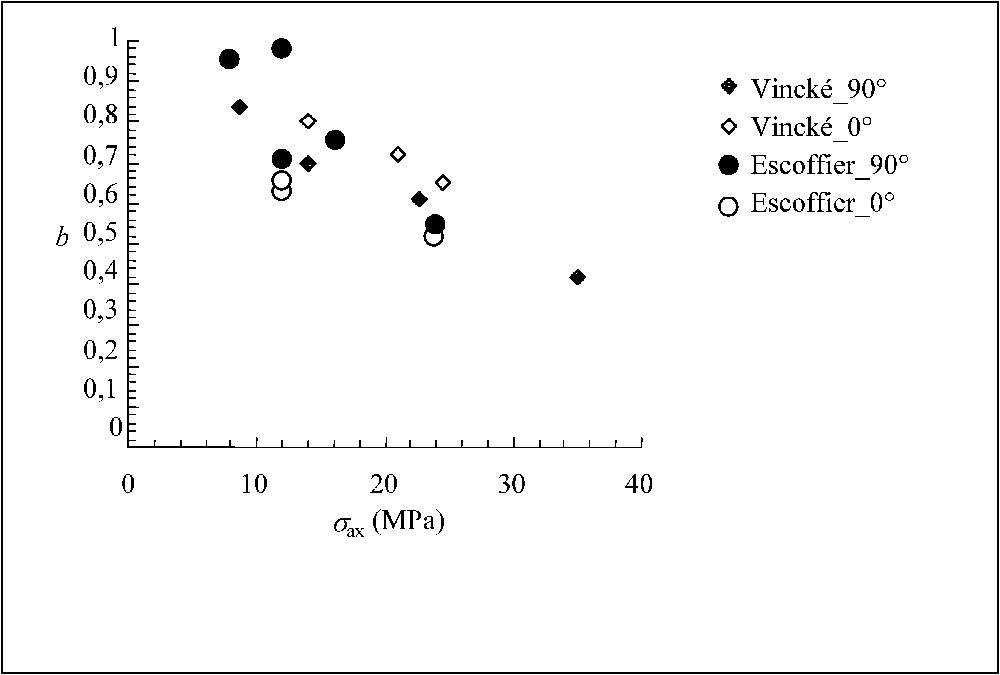Detailed analyses are also presented on the variations of the oedometric modulus, E, and the compressibility of solid grains, $K_{s}$ . However, the anisotropy remains negligible for the Biot coefficient.

Fig. 2
Résultats obtenus comparés à ceux de Vincké et al. [26].
Experimental results compared to Vincké et al. [26].

According to extensive experimental data, the mechanical behaviour of argillite can be described by an elastoplastic model coupled with isotropic damage. The general theoretical framework is provided in Section 4. Plastic flow and induced damage are coupled. Elastic properties are affected by material damage due to microcracks. A non-associated flow rule and isotropic hardening law are used to characterize plastic flow. An example of simulation is presented in Fig. 3. This general framework can be extended to saturated and unsaturated materials by taking into account influence of pore pressure and capillary effect.

Fig. 3
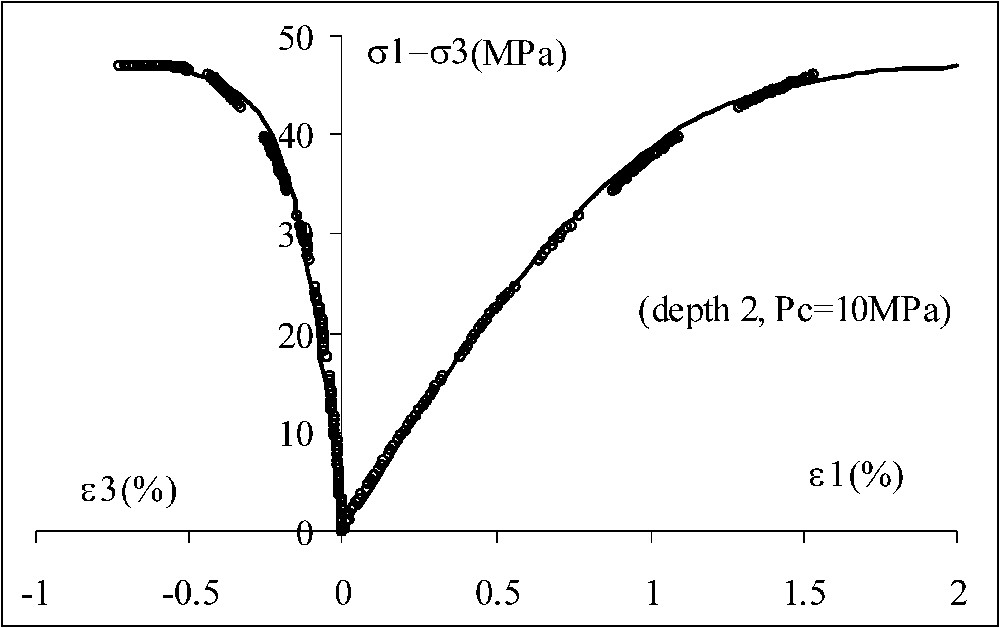
Simulation d'un essai de compression triaxiale avec un confinement de 10 MPa.
Simulation of a triaxial test (confining pressure = 10 MPa).

1 Introduction

Un des objectifs des recherches entreprises sur les argilites du Callovo-Oxfordien est d'identifier les facteurs lithologiques et texturaux à l'origine de la variabilité spatiale des propriétés de diffusion, de transport et de comportement mécanique. Dans cet article, nous nous intéresserons essentiellement au comportement hydromécanique, au coefficient de Biot et à la loi de comportement, ainsi qu'à l'influence de certains éléments de la pétrofabrique de ces roches, en particulier l'anisotropie sur ce comportement.

2 Pétrofabrique des argilites

Sous le terme « pétrofabrique » sont englobés minéralogie, espace poreux et organisation texturale. La question de l'anisotropie de l'argilite sera évoquée en regard de la variation de propriétés comme la perméabilité, la diffusivité thermique, la résistance, le module d'Young, en fonction de la direction de mesure.

2.1 Minéralogie

La composition minéralogique semi-quantitative moyenne peut être exprimée en quatre groupes principaux [3,24] :

– les tectosilicates : quartz principalement (20%), feldspaths ;
– les carbonates : calcite (30%) et un peu de dolomite ;
– les phyllosilicates non gonflants : micas, illite, chlorite, kaolinite ;
– les phyllosilicates gonflants : interstratifiés, illite/smectites, désordonnés ou ordonnés.

La totalité de la fraction argileuse est estimée à environ 50%. Le détail de la composition minéralogique des argiles, ainsi que leur répartition spatiale, sont présentés dans [21].

2.2 Porosité et modèle textural

Plusieurs types de porosité peuvent être définis en fonction du phénomène étudié [19,20] : porosité physique, porosité associée au transport (convection, diffusion), porosité associée aux interactions géochimiques. La porosité physique s'exprime comme le volume des vides, rapporté au volume total de l'échantillon. Cette porosité peut être déterminée à l'aide des masses volumiques ou par porosimétrie au mercure. Cette porosité varie entre 10 et 17% [15]. La porosité au mercure est naturellement plus faible puisqu'il s'agit de la mesure de la porosité connectée.

Les travaux de Sammartino et al. [22–24] conduisent à proposer un modèle conceptuel de l'organisation de l'argilite. La roche est composée de deux ensembles de minéraux formant deux structures opposées : la charge en clastes (tectosilicates et carbonates) et la matrice argileuse (phyllosilicates non gonflants et interstratifiés illite/smectite). Elles sont différentes par :

– leur classe granulométrique ;
– leur porosité (nature et distribution des dimensions) ;
– les effets de surface associés ;
– leur degré de connexion dans la roche ;
– leur propriété d'échange.

Les minéraux détritiques sont de taille micrométrique ou plus, pouvant aller jusqu'à quelques centaines de micromètres pour les bioclastes. Les particules d'argile sont micrométriques. La roche comporte deux types de porosité :

– la porosité interne à la matrice argileuse (autour des agrégats et des particules d'argiles), qui concerne les tailles de pores inframicrométriques (90% du volume poreux). Cette porosité est le lieu des effets de surface et des goulots associés. L'intégralité de la capacité d'échange de la roche y est contenue ;
– la porosité à l'interface entre la matrice argileuse et les clastes, qui concerne les tailles de pores micrométriques (pour les tectosilicates) et des tailles de pores infra-micrométriques (pour les carbonates mieux scellés à la matrice argileuse).

Les minéraux détritiques ont une faible connectivité dans le volume de la roche, à l'échelle macroscopique de l'échantillon, alors que la matrice argileuse est toujours connectée. Les tectosilicates bordent la macroporosité. Les carbonates diminuent le volume poreux accessible à la diffusion et la connexion globale des chemins de diffusion dans la matrice argileuse.

2.3 Anisotropie

Un élément important de la pétrofabrique d'une roche est son anisotropie. L'origine de l'anisotropie, en se limitant à une anisotropie de type isotrope transverse, peut être le litage sédimentaire ou la fissuration. Dans le cas des roches sédimentaires, ces deux phénomènes peuvent être associés. Les Tableaux 1 et 2 donnent quelques valeurs considérées comme représentatives des mesures effectuées sur des roches provenant de la couche au voisinage du laboratoire (entre 460 et 505 m). La valeur de 0° est relative à des éprouvettes dont l'axe correspond à la stratification. Il n'y a aucune prétention à l'exhaustivité dans les valeurs indiquées dans les Tableaux 1 et 2. Il ne s'agit que de donner des valeurs illustratives qui correspondent à des essais de très bonne qualité. Les roches sont naturellement parfaitement saturées lorsqu'il s'agit de la mesure de perméabilité. Elles sont à l'état quasi saturé (replacées dans une enceinte sous humidité relative de 100% après carottage) pour les autres grandeurs physiques mesurées.

2.3.1 Diffusivité thermique

De nombreuses meures de diffusivité thermique ont été effectuées [14] sur les argilites dans diverses conditions hydriques et suivant des orientations différentes par rapport à la stratification. La méthode employée est une mesure transitoire par pulse (méthode Flash [1]), réalisée sur des éprouvettes de 38 mm de diamètre et 10 mm d'épaisseur.

Les diffusivités calculées en interprétant le thermogramme sur roche saturée varient globalement entre 5 et $11 \times 10^{−7} m^{2} s^{−1}$ (Tableau 1). La diffusivité thermique mesurée suivant la direction parallèle à la stratification est toujours plus élevée (moyenne 9,2–10⁻⁷ m² s⁻¹) que celle mesurée dans la direction perpendiculaire (moyenne 7,4–10⁻⁷ m² s⁻¹). Le rapport d'anisotropie est donc de 1,24.

2.3.2 Perméabilité

Avant de répondre à une question sur l'existence d'une anisotropie de la perméabilité, il faut être conscient de la qualité des mesures expérimentales (qualité de l'éprouvette, étanchéité du dispositif, régulation de la température, qualité du pulse), et également de la méthode d'interprétation. En effet, dans le domaine des faibles perméabilités, il faut rester très critique. Les méthodes de mesure et d'interprétation ont été mises au point par Escoffier [11] d'après [18]. Deux essais de perméabilité, de très bonne qualité [19], sont disponibles suivant les deux directions principales d'anisotropie sur des échantillons très voisins, pour s'affranchir le mieux possible des différences de lithologie (Tableau 1). Pour les deux couples d'essais répondant à toutes ces conditions, la perméabilité moyenne suivant la direction de la stratification est de $4, 5 \times 10^{−20} m^{2}$ , alors que perpendiculairement à la stratification, elle est de $5, 8 \times 10^{−20} m^{2}$ , soit un rapport d'anisotropie de 1,29. Ces valeurs sont issues d'une interprétation en méthode directe. L'utilisation de méthodes inverses peut encore améliorer l'interprétation et permettre de qualifier de manière plus objective les résultats expérimentaux [17].

2.3.3 Résistance

Des essais triaxiaux ont été réalisés sur des éprouvettes quasi saturées, sous un confinement de 12 MPa correspondant approximativement à l'état de contraintes in situ aux profondeurs considérées (Tableau 1). Les valeurs de contrainte à la rupture sont tout à fait normalement plus élevées pour les éprouvettes dont l'axe correspond à la stratification. Le rapport d'anisotropie de la résistance est alors de 1,13.

2.3.4 Propriétés élastiques

Les recherches effectuées sur les argilites du Callovo-Oxfordien ont mis immédiatement en évidence cette anisotropie par mesure des vitesses de propagation des ondes ultrasonores [15]. Des travaux récents de David et al. [9] confirment cette anisotropie de vitesse de propagation des ondes et mettent aussi en évidence l'anisotropie des propriétés de susceptibilité magnétique [12]. L'écart des vitesses est cependant assez faible. Plutôt que des moyennes assez peu justifiées dans ce cas, nous préférons donner en exemple les valeurs obtenues sur un cube tronqué (EST361, −500 m). Les mesures ont été réalisées sous une faible contrainte, nécessaire pour assurer un bon couplage de l'échantillon avec les transducteurs [2]. Les notations de ce tableau sont conformes à [16] et aux normes Afnor. La direction 1 est celle perpendiculaire au plan de stratification. La vitesse des ondes P a été mesurée suivant les directions 1 et 2 (directions parallèles à la stratification).

Cet essai est particulièrement de bonne qualité, dans la mesure où la symétrie du tenseur élastique d'isotropie transverse est assurée grâce à l'égalité des rapports $ν_{12} / E_{1}$ et $ν_{21} / E_{2}$ . Dans le Tableau 2, $V_{p}$ et $V_{s}$ désignent les vitesses de propagation des ondes ultrasonores P et S et $I_{b}$ , l'indice de biréfringence (Éq. (1)) égal à :

I_{b} = \frac{V_{s_{\max}} - V_{s_{\min}}}{V_{s_{\max}}} \times 100

(1)

Cet indice qualifie l'anisotropie dans le plan considéré et montre que, dans le plan de stratification, il ne doit pas y avoir d'orientation préférentielle. D'autres indices (Éqs. (2) et (3)) permettent d'évaluer l'anisotropie de structure :

Δ M % = 100 \times [1 - \frac{2 (V_{1})}{V_{2} + V_{3}}]

(2)

Δ m % = 100 \times [1 - \frac{2 (V_{3} - V_{2})}{V_{2} + V_{3}}] avec V_{1} < V_{2} < V_{3}

(3)

L'indice d'anisotropie majeure ΔM traduit la présence d'un plan de stratification, tandis que l'indice Δm traduirait éventuellement la présence d'un alignement dans ce plan. Δm et $I_{b}$ dans le plan 1 sont dans la limite des erreurs de mesure sur les vitesses (50 m s⁻¹), donc il y n'y a pas d'orientation préférentielle mise en évidence dans ce plan avec la méthode considérée. En revanche, le plan de stratification est bien marqué. Le matériau devrait donc être considéré comme isotrope transverse. Cependant, avant de conclure, il est nécessaire de considérer les valeurs des modules d'Young (E), des coefficients de Poisson (ν) et des modules de cisaillement (G). Les modules d'Young principaux sont très voisins. D'autres mesures effectuées conduisent à des modules dynamiques dont le degré d'anisotropie peut être plus élevé. Il est donc difficile de conclure sur l'isotropie ou l'anisotropie de la déformabilité.

3 Évolution du coefficient de Biot en fonction des contraintes et de l'anisotropie

Un des paramètres de couplage intervenant dans les lois de comportement poromécaniques est le coefficient de Biot b. Des expérimentations ont été réalisées par Vincké et al. [26] et Escoffier [11] afin de déterminer ce coefficient fortement lié à la structure du réseau poreux.

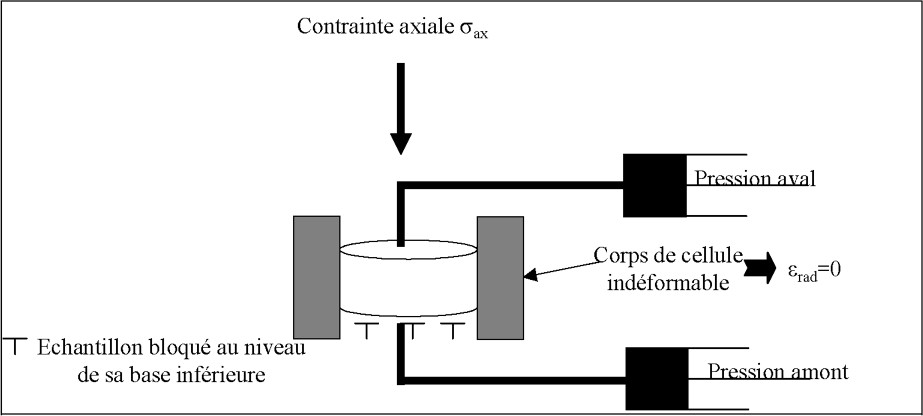
Ces essais ont été réalisés en appliquant un chargement œdométrique sur un échantillon (Fig. 1). L'essai consiste à appliquer une contrainte axiale sur un échantillon cylindrique de faible épaisseur, placé dans un corps de cellule indéformable ( $ε_{rad} = 0$ ). Des générateurs de pression permettent d'appliquer la pression interstitielle de part et d'autre de l'échantillon. Le chargement axial (ou en pression interstitielle) est appliqué par palier et chaque palier est maintenu constant jusqu'à stabilisation de la déformation axiale qu'il a entraînée. La valeur stabilisée de la déformation axiale est reportée sur un graphique, en fonction du logarithme de la contrainte axiale correspondante. Ces essais sont délicats et très longs à réaliser, de l'ordre de 1 à 2 mois pour retrouver un état initial et ensuite 2 à 3 mois par palier.

Fig. 1
Schéma de principe d'un essai en cellule œdométrique.
Mechanical test in oedometric conditions.

Le principe de détermination du coefficient de Biot en cellule œdométrique s'appuie sur la réalisation successive d'un cycle de déchargement en contrainte axiale, à pression interstitielle constante, et d'un cycle de chargement en pression interstitielle, à contrainte axiale constante. Dans le cadre de la mécanique des milieux poreux [8], l'Éq. (4) reliant l'état de contrainte, $\underset{̲}{\underset{̲}{σ}}$ , aux déformations, $\underset{̲}{\underset{̲}{ε}}$ , permet de déterminer le coefficient de Biot, b, à partir de la réalisation en cellule œdométrique ( $ε_{rad} = 0$ ) d'un déchargement en contrainte axiale à pression interstitielle constante (Éq. (5)) et d'un chargement en pression interstitielle à contrainte axiale constante (Éq. (6)) :

\underset{̲}{\underset{̲}{σ}} = \underset{̲}{\underset{̲}{σ^{0}}} + (K_{0} - \frac{2 μ}{3}) tr (\underset{̲}{\underset{̲}{ε}}) \underset{̲}{\underset{̲}{1}} - 2 μ \underset{̲}{\underset{̲}{ε}} - b (P - P^{0}) \underset{̲}{\underset{̲}{1}}

(4)

\frac{σ_{ax} - σ_{ax}^{0}}{ε_{ax}} = \frac{K_{0} - 4 μ}{3} = P_{1}

(5)

\frac{P - P_{0}}{ε_{ax}} = \frac{(K_{0} - \frac{4 μ}{3})}{b} = P_{2}

(6)

avec

\underset{̲}{\underset{̲}{σ^{0}}}

le tenseur des contraintes initiales,

σ_{ax}

et

σ_{ax}^{0}

respectivement la contrainte axiale finale et initiale, P et

P^{0}

respectivement la pression interstitielle finale et initiale,

ε_{ax}

la déformation axiale,

K_{0}

le module d'incompressibilité drainé et μ le module de cisaillement.

Le rapport des pentes des droites, obtenues dans les phases de déchargement en contrainte axiale et de chargement en pression interstitielle, donne le coefficient de Biot. On notera que cette méthode est également applicable dans le cas d'une roche à anisotropie transverse. Le coefficient de Biot a donc été mesuré sur une éprouvette cylindrique d'argilite de 38 mm de diamètre pour 20 mm de hauteur, carottée perpendiculairement aux plans de stratification (90°) ou parallèlement aux plans de stratification (0°). Lors des cycles de déchargement en contrainte axiale, la pression interstitielle a été maintenue constante à 1 MPa. La Fig. 2 présente les résultats obtenus lors de cet essai, ainsi que les résultats de Vincké et al. [26] sur une argilite semblable.

Le coefficient de Biot évolue de 0,95 à 0,55 pour une contrainte axiale qui passe de 8 à 24 MPa. Les valeurs proches de 1 sont considérées comme élevées pour cette roche, mais nous avons préféré ne pas les éliminer.

Boutéca [4] a proposé une explication fondée sur la prise en compte d'une évolution de la microstructure des argilites au cours d'un chargement œdométrique. En reprenant les équations reliant les paramètres poroélastiques aux caractéristiques des composants, il rappelle que l'écart à l'unité du coefficient de Biot est lié à l'évolution du rapport $K_{0} / K_{s}$ (Éq. (7)) :

b = 1 - \frac{K_{0}}{K_{s}}

(7)

L'augmentation du module œdométrique avec la contrainte axiale, traduisant un raidissement du matériau, correspond selon eux à une augmentation du module de compressibilité drainé entraînant ainsi, selon la relation (7), une diminution du coefficient de Biot. La notion de « non drainé » s'associe ici à des temps de diffusion très faible, dans les zones ayant subi des phénomènes de poinçonnement, par rapport au temps de diffusion au sein de l'éprouvette considérée dans son ensemble.

D'un point de vue microscopique, Boutéca [4] explique cette augmentation du module de compressibilité drainé par une évolution du réseau poreux connecté au cours du chargement. Il considère en effet qu'au cours du chargement plastique, une partie du réseau poreux connecté va se déconnecter créant ainsi des zones non drainées au sein de l'échantillon. Localement, certains pores connectés vont perdre leur connexion lors de l'augmentation de la contrainte axiale, qui va créer un poinçonnement au niveau des grains de quartz ou de calcite. Un modèle micromécanique récemment développé montre l'influence de la fermeture de certains goulots sous l'effet des contraintes [13].

Les paramètres poroélastiques marquent l'apparition de zones non drainées par une évolution du module de compressibilité drainé, $K_{0}$ , vers un module de compressibilité drainé global, ${\tilde{K}}_{0}$ . L'expression (7) prend alors la forme (8) :

b = 1 - \frac{{\tilde{K}}_{0}}{K_{s}}

(8)

En considérant que la valeur du module de compressibilité drainé global est la moyenne arithmétique des compressibilités drainée et non drainée et en notant α la fraction de volume non drainé, ils expriment le module de compressibilité globale sous la forme (9) :

{\tilde{K}}_{0} = α K + (1 - α) K_{0}

(9)

Nous avons développé une approche avec prise en compte de l'évolution de la compressibilité de la matrice. Le module de compressibilité drainé global (10) des éprouvettes peut être déterminé à partir du module œdométrique mesuré dans les phases de déchargement en contrainte axiale (ou de chargement en pression interstitielle) :

E^{'} = K_{0} + \frac{4}{3} μ = K_{0} [1 + \frac{4}{3} (\frac{3}{2} \frac{1 - 2 ν}{1 + ν})]

(10)

En considérant la valeur du coefficient de Poisson de 0,3, on obtient

E^{'} = 1, 615 K_{0}

; le Tableau 3 donne les valeurs du module de compressibilité global ainsi déterminées.

Eprouvettes	Orientation	$Δ σ_{ax}$ (MPa)	$K_{0}$ (MPa)
EST02159-2	90°	8 à 2 (P= 1 MPa)	1448
		16 à 10 (P= 1 MPa)	4881
		24 à 18 (P= 1 MPa)	5916

EST05581-3	90°	12 à 6 (P= 1 MPa)	2647
		24 à 18 (P= 1 MPa)	–

EST05581-4	0°	12 à 6 (P= 1 MPa)	2252
		24 à 18 (P= 1 MPa)	4773

EST05752-3	90°	12 à 96 (P= 1 MPa)	5770

EST05752-4	0°	12 à 6 (P= 1 MPa)	3234

On constate une nette évolution du module de compressibilité drainé global, qui passe de 1448 MPa pour une contrainte axiale totale comprise entre 8 et 2 MPa, à quasiment 6000 MPa pour une contrainte axiale totale comprise entre 24 et 18 MPa. De même que pour le module œdométrique, le module de compressibilité drainé global déterminé sur des éprouvettes carottées parallèlement aux plans de stratification est plus faible que celui déterminé sur des éprouvettes carottées perpendiculairement aux plans de stratification.

Contrairement à Boutéca [4], on considère ici que le module de compressibilité de la matrice évolue, de même que le module de compressibilité drainé global, avec la contrainte axiale. En effet, si l'on considère que lors du chargement axial, une partie du réseau poreux connecté va se déconnecter, notamment sous l'effet de phénomènes de poinçonnement, cette porosité devient par définition une porosité occluse. Ainsi, dans certaines zones de l'éprouvette, on peut considérer que la compressibilité de la matrice va diminuer, du fait de l'augmentation du pourcentage de porosité occluse la composant. Bien que les valeurs du module de compressibilité de la matrice puissent être obtenues à partir de l'Éq. (11), les valeurs ainsi calculées sont entachées de l'accumulation des erreurs sur les valeurs du coefficient de Biot, du module œdométrique et du choix de considérer un coefficient de Poisson constant de 0,3 :

K_{s} = \frac{E^{'} [1 + \frac{4}{3} (\frac{3}{2} \frac{1 - 2 ν}{1 + ν})]}{1 - b}

(11)

Dans le Tableau 4, on donne les valeurs de la compressibilité du squelette ainsi calculées. Ces valeurs du module de compressibilité de la matrice, données à titre indicatif, fournissent des tendances sur l'évolution du module de compressibilité du squelette.

Éprouvettes	Orientation	$Δ σ_{ax}$ (MPa)	$K_{s}$ (MPa)
EST02159-2	90°	8 à 2 (P= 1 MPa)	35840
		16 à 0 (P= 1 MPa)	20697
		24 à 18 (P= 1 MPa)	13069

EST05581-3	90°	12 à 6 (P= 1 MPa)	14307
		24 à 18 (P= 1 MPa)	–

EST05581-4	0°	12 à 6 (P= 1 MPa)	6798
		24 à 18 (P= 1 MPa)	9633

EST05752-3	90°	12 à 96 (P= 1 MPa)	57695

EST05752-4	0°	12 à 6 (P= 1 MPa)	9239

Dans le cas de l'éprouvette EST02159-2, le module de compressibilité diminue logiquement avec l'augmentation de la contrainte axiale. Cette tendance se retrouve en réinterprétant les essais de Vincké et al. [26] sur l'éprouvette EST00437 carottée, comme dans le cas de l'éprouvette EST02159-2, perpendiculairement aux plans de stratification.

Seul l'essai réalisé sur l'éprouvette EST05581-4 (éprouvette carottée parallèlement aux plans de stratification) montre une augmentation de la compressibilité de la matrice avec le chargement. Vu les incertitudes sur les valeurs du module de compressibilité de la matrice, on ne peut conclure à une réelle augmentation de celle-ci avec la contrainte axiale.

On notera également que les valeurs du module œdométrique obtenues par Vincké et al. [26] sont plus faibles. Un début d'explication pourrait être trouvé dans les différences entre les dispositifs expérimentaux, les protocoles expérimentaux (mise en place des éprouvettes) ou encore d'échantillonnage à la maille des cellules, en particulier pour les échantillons prélevés dans l'horizon supérieur du Callovo-Oxfordien, qui présente une dispersion assez importante des caractéristiques, notamment minéralogiques.

4 Un modèle élastoplastique

Selon les données expérimentales obtenues par [5], le comportement mécanique de l'argilite est dominé par des déformations plastiques. Il y a une forte dépendance du comportement mécanique de la pression de confinement, marquée par une transition d'un comportement fragile vers un comportement ductile. Un modèle élastoplastique peut donc être considéré comme loi de comportement de base pour l'argilite étudiée. Selon les analyses de la pétrofabrique présentées dans les sections précédentes, l'argilite étudiée présente une anisotropie structurale de type d'isotropie transverse liée au plan de stratification. Cependant, il semble que les conséquences de cette anisotropie sur le comportement mécanique sont assez faibles. Un modèle élastoplastique isotrope est une approche raisonnable pour la description du comportement mécanique de l'argilite. Cependant, pour une modélisation plus avancée, il est utile de prendre en compte l'endommagement par microfissuration, qui est un mécanisme de dissipation non négligeable et couplé avec la plasticité. L'endommagement est d'autant plus important quand la pression de confinement est faible et quand l'argilite est soumise à un processus de désaturation. Par conséquent, nous proposons de développer un modèle élastoplastique couplé à l'endommagement isotrope pour décrire le comportement mécanique de l'argilite. En se basant sur les travaux du LML et du LAEGO [5–7,25], qui ont formulé diverses versions du modèle, on trace ici les grandes lignes du modèle de comportement proposé.

Dans le cadre de la thermodynamique des processus irréversibles, pour un matériau isotrope, l'énergie libre, utilisée comme le potentiel thermodynamique, peut être exprimée sous la forme suivante (12) :

Ψ = \frac{1}{2} (ε - ε^{p}) : C (d) : (ε - ε^{p}) + Ψ_{p} (γ_{p}, d)

(12)

Les variables d'état utilisées sont le tenseur des déformations ε, la variable d'endommagement isotrope d, le tenseur des déformations plastiques $ε^{p}$ et la variable interne pour l'écrouissage plastique $γ^{p}$ . La fonction $Ψ_{p}$ représente l'énergie bloquée pour l'écrouissage plastique. L'équation d'état (13) est ensuite déduite du potentiel thermodynamique :

(13)

k (d)

et

μ (d)

sont respectivement le module de compressibilité et le module de cisaillement du matériau endommagé. Les deux tenseurs d'ordre 4, J et K, permettent de définir les parties sphérique et déviatorique du tenseur des déformations. La force thermodynamique associée à l'endommagement est également déduite du potentiel (14) :

(14)

On constate que la force associée à l'endommagement est directement couplée au mécanisme de plasticité. Le second principe (15) assurant la non-négativité de la dissipation intrinsèque s'écrit alors :

σ : {\dot{ε}}^{p} + Y_{d} \dot{d} ⩾ 0

(15)

Dans le cadre des dissipations non visqueuses, l'évolution de l'endommagement est déterminée par l'identification d'un critère d'endommagement (16) :

f_{d} (Y_{d}, d) = Y_{d} - r (d) ⩽ 0

(16)

La fonction

r (d)

définit le seuil du taux de restitution d'énergie d'endommagement pour une valeur d'endommagement donnée. Le taux d'endommagement peut ensuite être déterminé par la condition de cohérence et la règle de normalité.

Le comportement plastique est décrit par la détermination d'une fonction de charge, d'un potentiel plastique et d'une loi d'écrouissage ((17) à (19)) :

f_{p} (σ, α_{p}, d) ⩽ 0

(17)

g (σ, α_{p}, d) ⩽ 0

(18)

α_{p} (γ_{p}, d) = \frac{\partial Ψ (ε, d, γ_{p})}{\partial γ_{p}}

(19)

Le cadre général du modèle de comportement élastoplastique est ainsi clairement défini. Selon le choix des formes particulières des différentes fonctions, différentes versions du modèle peuvent être obtenues. On donnera ici un exemple de modèle particulier.

En se basant sur des analyses micromécaniques et des données expérimentales, les propriétés élastiques effectives du matériau endommagé peuvent être exprimées en fonction de l'endommagement (20) :

k (d) = k_{0} (1 - α d), μ (d) = μ_{0} (1 - β d)

(20)

Les deux paramètres peuvent être identifiés, soit à partir des mesures expérimentales, soit en utilisant des estimations issues de la micromécanique. Un critère d'endommagement linéaire fournit une approche simple pour l'évolution de l'endommagement (21) :

f_{d} (Y_{d}, d) = Y_{d} - (Y_{d}^{0} + m d) = 0

(21)

Afin de mieux décrire l'influence de la contrainte hydrostatique sur l'écoulement plastique, il est généralement préférable d'utiliser une surface de charge non linéaire, par exemple quadratique (22) :

f_{p} (σ, γ_{p}, d) = q^{2} h^{2} (θ) + α_{p} (p - C) = 0

(22)

où p est la contrainte hydrostatique, q la contrainte déviatorique et θ l'angle de Lode. La fonction

h (θ)

est introduite pour décrire l'influence du troisième invariant de contrainte sur l'écoulement plastique. L'écrouissage plastique est décrit par l'augmentation du coefficient de frottement interne (23) :

α_{p} = \frac{\partial Ψ}{\partial γ_{p}} = (1 - χ d) [α_{p}^{0} + (α_{p}^{m} - α_{p}^{0}) \frac{γ_{p}}{B + γ_{p}}]

(23)

où

α_{p}^{0}

est le seuil initial de plasticité,

α_{p}^{m}

la valeur ultime de l'écrouissage plastique, et B est un paramètre déterminant la cinétique de l'écrouissage. Le paramètre

χ \in [0, 1]

est utilisé pour le couplage entre l'endommagement et la plasticité. Enfin, le potentiel plastique est proposé pour décrire la direction de l'écoulement plastique (24) :

g = q h (θ) + η (1 - χ d) (p - C) \ln (\frac{p - C}{I_{0}}) = 0

(24)

Le paramètre η définit la frontière entre la contractance et la dilatance plastiques. Un exemple de simulation d'un essai de compression triaxiale est montré sur la Fig. 3.

Le cadre de modélisation ainsi proposé peut être étendu au matériau saturé et non saturé, en prenant en compte des influences de la pression interstitielle et des effets capillaires.

5 Conclusion

L'anisotropie des propriétés thermiques, hydrauliques et mécaniques est relativement faible pour les essais sur les argilites présentés. On pourra vraisemblablement interpréter la plupart des expérimentations réalisées dans le laboratoire souterrain en considérant un milieu isotrope, ce qui n'est pas le cas, par exemple, pour les formations du laboratoire du mont Terri, qui sont beaucoup plus fortement anisotropes.

La diminution du coefficient de Biot avec la contrainte axiale ne peut pas être expliquée que par la diminution de porosité qui, même en considérant une matrice incompressible, correspond à 1% pour une contrainte axiale variant de 8 à 24 MPa. L'origine de la diminution du coefficient de Biot s'explique par la perte de connexion d'une partie du réseau poreux, jusqu'alors connectée, sous l'effet de l'augmentation de la contrainte axiale. L'apparition de zones non drainées se traduit par une augmentation du module de compressibilité drainé global de l'éprouvette. Dans le cas des éprouvettes carottées perpendiculairement aux plans de stratification, l'apparition de zones non drainées se traduit également par une diminution du module de compressibilité de la matrice ; néanmoins, étant donné les incertitudes sur les valeurs de la compressibilité de la matrice, les valeurs déterminées restent indicatives.

Un modèle élastoplastique isotrope est une approche raisonnable pour la description du comportement mécanique de l'argilite. Cependant, pour une modélisation plus avancée, il est utile de prendre en compte l'endommagement par microfissuration, qui est un mécanisme de dissipation non négligeable et couplé avec la plasticité. Le cadre de modélisation ainsi proposé peut être étendu au matériau saturé et non saturé, en prenant en compte des influences de la pression interstitielle et des effets capillaires.

Bibliographie

[1] S. André; A. Degiovanni A theoretical study of the transient coupled conduction and radiation heat transfer in glass: phonic diffusivity measurements by the flash technique, Int. J. Heat Mass Transfer, Volume 38 (1995), pp. 3401-3412

[2] C. Auvray, D. Grgic, F. Homand, Caractéristiques géomécaniques – Sondage EST361, rapport Andra CRPOENG04-0500, 2004

[3] C. Bauer-Plaindoux; D. Tessier; M. Ghoreychi Propriétés mécaniques des roches argileuses carbonatées : importance de la relation calcite-argile, C. R. Acad. Sci. Paris, Ser. IIa, Volume 326 (1998), pp. 231-237

[4] M. Boutéca, Réflexion sur l'origine de l'évolution du coefficient de Biot des argilites au cours d'un chargement mécanique, in : Actes des journées scientifiques de l'Andra, Nancy, 1999

[5] A.S. Chiarelli, Étude expérimentale et modélisation du comportement mécanique de l'argilite de l'Est, Influence de la profondeur et de la teneur en eau, thèse de doctorat, université Lille-1, 2000

[6] A.S. Chiarelli; J.F. Shao; N. Hoteit Modelling of elastoplastic damage behaviour of a claystone, Int. J. Plast., Volume 19 (2003), pp. 23-45

[7] A.S. Chiarelli; B. Ledesert; M. Sibai; M. Karami; N. Hoteit Influence of mineralogy and moisture content on plasticity and induced anisotropic damage of a claystone: application to nuclear waste disposals, Bull. Soc. géol. France, Volume 171 (2000)

[8] O. Coussy Mécanique des milieux poreux, Éditions Technip, Paris, 1991

[9] C. David, P. Robion, B. Menendez, Anisotropy of elastic, magnetic and microstructural properties of the Callovo-Oxfordian shales (Meuse), in: 2nd International Meeting Clays in Natural & Engineered Barriers for Radioactive Waste Confinement, 2005

[10] J. Delay; A. Trouiller; J.-M. Lavanchy Propriétés hydrodynamiques du Callovo-Oxfordien dans l'Est du bassin de Paris : comparaison des résultats obtenus selon différentes approches, C. R. Geoscience, Volume 338 (2006)

[11] S. Escoffier, Caractérisation expérimentale du comportement hydromécanique des argilites de Meuse/Haute-Marne, doctorat de l'INPL, 2002

[12] L. Esteban, Y. Géraud, J.-L. Bouchez, Pore network connectivity in low-permeability clayed sediments from magnetic fabric data and oriented mercury injections, Phys. Chem. Earth, in press

[13] A. Giraud, V. Quoc, D. Hoxha, F. Homand, Coefficient de Biot dans les argilites de l'Est ; résultats expérimentaux et analyse micromécanique, Colloque ENPC « Microstructure et propriétés des Matériaux », 2005

[14] F. Homand, Mesures thermiques sur le site Est, rapport Andra DRP0.ENG98-009/A, 1998

[15] F. Homand, F. Villieras, Mesures des propriétés physiques d'échantillons de Meuse/Haute-Marne, Rapport Andra BRP0.ENSG95.007, 1995

[16] F. Homand; P. Duffaut Manuel de mécanique des roches, Presses des Mines, 2001

[17] F. Homand; A. Giraud; S. Escoffier; A. Koriche; D. Hoxha Permeability determination of a deep argillite in saturated and partially saturated conditions, Int. J. Heat Mass Transfer, Volume 47 (2004), pp. 3517-3531

[18] P.A. Hsieh; J.V. Tracy; C.E. Neuzil A transient laboratory method for determining the hydraulic properties of tight rocks. I. Theory, Int. J. Rock Mech. Min. Sci. & Geomech., Volume 18 (1981), pp. 245-252

[19] A. Koriche, Caractérisation du comportement couplé des argilites de Meuse/Haute-Marne aux états saturé et partiellement saturé, doctorat de l'INPL, 2004

[20] F.J. Pearson What is the porosity of a mudrock?, Geol. Soc. Spec. Publ., Volume 158 (1999), pp. 9-21

[21] P. Pellenard; J.-F. Deconinck Mineralogical variability of Callovo-Oxfordian clays from the Paris Basin and the Subalpine Basin, C. R. Geoscience, Volume 338 (2006)

[22] S. Sammartino, D. Bouchet, J.-C. Parneix, Construction d'un modèle conceptuel d'organisation de la porosité et de la minéralogie dans les argilites du site de Bure, rapport Andra DRP0ERM 01-018, 2001

[23] S. Sammartino; M. Siitari-Kauppi; A. Meunier; P. Sardini; A. Bouchet; E. Tevissen An imaging method for the porosity of sedimentary rocks: Adjustment of the PMMA method. Example of a characterization of a calcareous shale, J. Sediment. Res., Volume 72 (2001), pp. 937-943

[24] S. Sammartino; A. Bouchet; D. Prêt; J.C. Parneix; E. Tevissen Spatial distribution of porosity and minerals in clay rocks from the Callovo-Oxfordian formation (Meuse/Haute-Marne, eastern France), Implications on ionic species diffusion and rock sorption capability, Appl. Clay Sci., Volume 23 (2003), pp. 157-166

[25] J.F. Shao; Y. Jia; D. Kondo; A.S. Chiarelli A coupled elastoplastic damage model for semi-brittle materials and extension to unsaturated conditions, Mech. Mater., Volume 38 (2006), pp. 218-232

[26] O. Vincké, M. Boutéca, P. Longuemarre, Investigation of the poromechanical behavior of shales in elastic domain, SPE/ISMR 475 (1998) 515–520

Commentaires - Politique