Abridged English version
The aim of this study is to describe both the structure and water distribution of landslides using the geophysical parameters acoustic velocity and electrical resistivity ρ. The study is focused on the Super-Sauze site (Alpes-de-Haute-Provence, France), an earthflow-type landslide. Such landslides are featured by either movements occurring along discrete shearing surfaces [2,4] or by continuous deformations depending on local constraints and covered topography [1,7]. Composed by heterogeneous materials, more or less water saturated, their morphology reveals three spatial units identified from the top to the bottom: the main escarpment, the transit zone and the accumulation lobe. Such landslides are featured by velocities comprised between 0.005 and 0.3 m a day. The deformations may occur as a consequence of the slow and continuous erosion of a surface by run off that, as it penetrates the sediments' fissures, reduces their stiffness and forms a gravitational flow. The intensity of these phenomena is controlled by the density of fissures and the interstitial water pressure [9]. Non-intrusive geophysical methods, such as seismic refraction and electrical resistivity imaging, are well-adapted to studying the mechanical behaviour of landslides. The inversion of seismic travel times and electrical apparent resistivities reveals the mechanical properties of a terrain by the means of two physical models: the velocity field, based on recorded travel times, that provides information concerning the state of compaction of the layers; and the resistivity field mainly related to the variations in water content. These physical models are used to analyse the degree of correlation between the two parameters and ρ, with the intention of determining whether a specific geological behaviour can be characterized by a relationship between acoustic velocity and electrical resistivity.
The Super-Sauze earthflow (Fig. 1) was selected due to its particularly well-preserved natural environment, and because it has been monitored over several years [10]. It is representative of several slow earthflows observed in the French Alps: La Valette, Poche, Boulc or Les Dourbes. Situated in the Barcelonnette Basin, on the left bank of the River Ubaye, the earthflow extends 820 m from its highest point at an elevation of 2105 m, to its base at an elevation of 1740 m, with an average slope gradient of 25 degrees. It covers an area of some 17 hectares (Fig. 1A and B). It is composed of Callovian-Oxfordian black marls, known as ‘Terres noires’, with shades varying from black, to grey, to slightly blue. The surface is highly irregular, affected by plane fractures and surficial cracks [8], with several ravines in which crushed heterogeneous rocks and debris have accumulated (Fig. 2). A multidisciplinary study, started in 1996, allowed significative advances in conceptual and mechanical modelling of the earthflow [7]. A preliminary geophysical interpretation [13] also helps designing its main structures. We present here new results from complementary geophysical measurements consisting of two seismic refraction profiles, two electrical resistivity profiles, and a topographic survey using a DGPS.
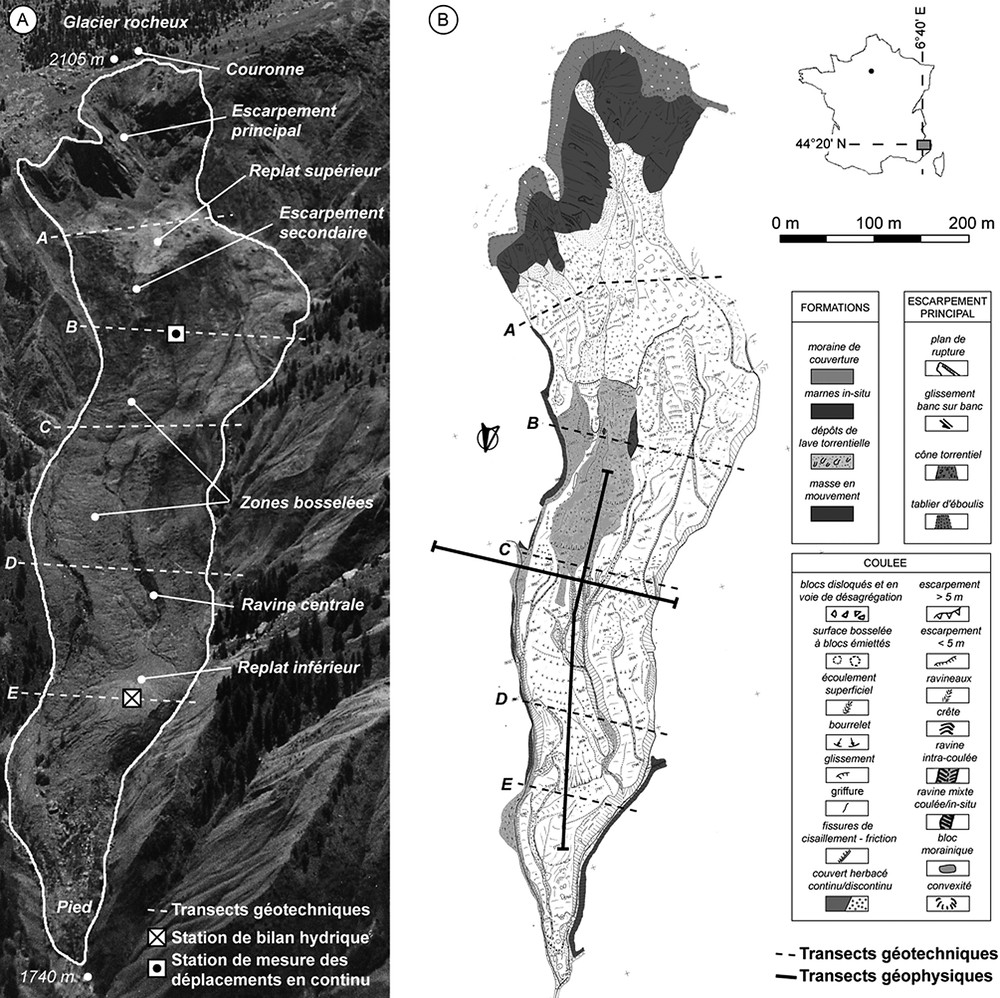
Photographie aérienne oblique du glissement-coulée de Super-Sauze et localisation des transects d'investigation géotechnique et géophysique.
Oblique aerial photograph of the Super-Sauze earthflow and location of the geotechnical and geophysical cross-sections.

(a) Accumulation de débris hétérogènes dans une ravine ; (b) fractures superficielles.
(a) Accumulation of heterogeneous debris in a gully; (b): surficial cracks.
The seismic profiles were performed along two orthogonal directions: a 325 m transverse (F) profile perpendicular to the axis of the earthflow (along line C on Fig. 1B), and a 235 m longitudinal (G) profile (Fig. 1B). A total of 66 geophones placed at a 5 m interval were used for the transverse profile. Shots were fired using a detonating cord, at a 15 m interval. Data processing and inversion of the first arrival traveltimes were undertaken using the JaTS seismic tomography software [3]. This code uses Fresnel volumes to compute wavepaths and a Simultaneous Iterative Reconstruction Technique (SIRT), reformulated according to a probabilistic approach, to estimate the P-wave velocity field. A L2 norm likelihood function is computed for each iteration for estimating the convergence of the process. Velocities in the earthflow were inverted along both the transverse (Fig. 3) and longitudinal profiles, and vary from 300 to 2400 m s−1 according to three layers, as already established from previous seismic refraction studies [12] and geotechnical sounding [10]: a surficial layer with low velocities ranging from 300 to 600 m s−1 (C1), a second layer with velocities ranging from 900 m s−1 to 1200 m s−1 (C2), and finally the marly bedrock, well defined by a transition zone, with high velocities ranging from 2100 to 2400 m s−1. On the transverse profile, the velocities on the mountain flanks remain high (1500 to 2500 m s−1).
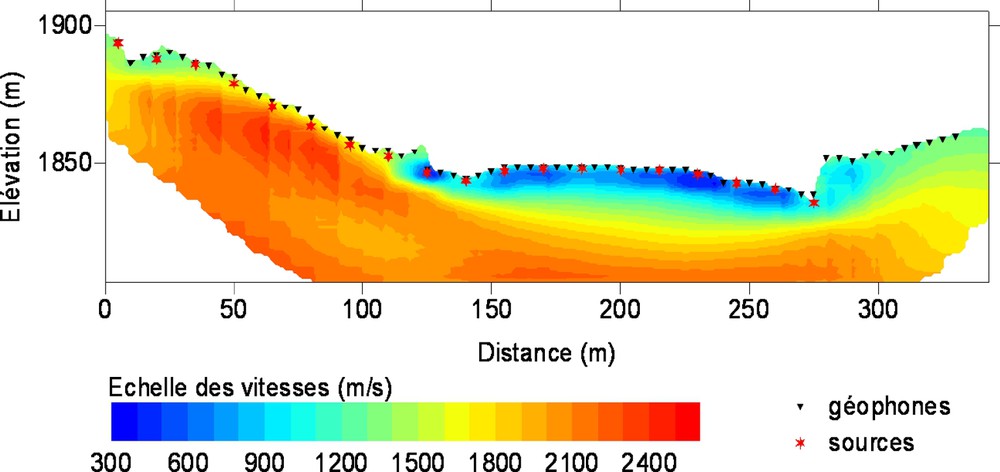
Modèle de champ de vitesse obtenu à partir de l'inversion des temps de trajet des premières arrivées au bout de cinq itérations.
Velocity field model obtained from first-arrival traveltimes inversion after five iterations.
Two electrical resistivity profiles were also performed in conjunction with the seismic profiles: a 316 m transverse profile with 80 electrodes at a 4-m interval, and a 315 m longitudinal profile with 64 electrodes at a 5-m interval. A total of 1026 and 650 data points were collected for the transverse and longitudinal profiles, respectively. Data processing and inversion were undertaken according to Loke [5] implementing a damped least-squared Gauss–Newton algorithm. The transverse profile (Fig. 4) exhibits a strong contrast in the resistivity pattern before and after the 150 m mark, corresponding to the transition between the mountain flank and the earthflow. Within the earthflow itself, the model distinguishes two layers, a highly conductive surficial layer with contrasted resistivity values ranging from 3 to 20 Ω m [13], and an underlying layer with average resistivity values.
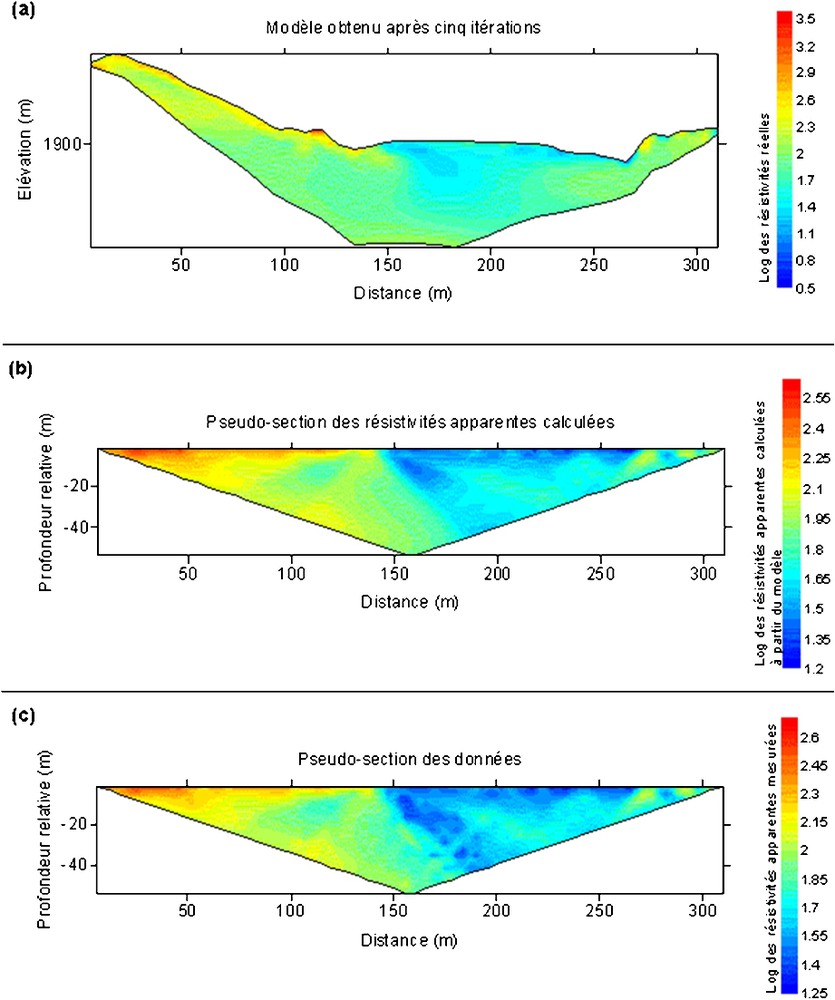
(a) Modèle des résistivités réelles, obtenu au bout de cinq itérations ; (b) pseudo-section des résistivités apparentes calculées ; (c) pseudo-section des résistivités apparentes mesurées.
(a) True resistivity model obtained after five iterations; (b) calculated apparent resistivity pseudosection; (c) measured apparent resistivity pseudosection.
We will base our discussion on the transverse profile only, as it clearly reveals the complex behaviour of the earthflow. From the seismic model (Fig. 3), three distinct layers can be distinguished, with velocities increasing with depth, reflecting the increasingly compact nature of the strata down to the easily distinguishable marly bedrock. The electrical resistivity imaging results (Fig. 4a) show two layers with resistivity values increasing with depth (C1–C2): a bowl-shaped surficial layer, which can be identified on the seismic profile, with low resistivity values ranging from 12.6 to 25.1 Ω m, and the bedrock, with resistivity values ranging from 4.5 and 12.2 Ω m. In order to go beyond a qualitative comparison between both data sets, a number of vertical sections were produced along the inverted horizontal profiles. For each vertical section, both the vertical gradient of the velocity and the logarithm of the resistivity were calculated. The results were then plotted on a graph (Fig. 5). On this graph the results of the vertical sections located on the mountain flanks are represented by black symbols, corresponding to the first 115 m of the profile, and green symbols, corresponding to the last 25 m of the profile (275–300 m). The black symbols plot relatively close together, apart from a few dispersed points that may reflect a change in the lithology or state of the rock (weathered rocks, for example). The green symbols also appear to be well grouped. This clustering probably reflects a homogeneous lithology little affected by weathering and stable in situ blocks, concurring with previous observations of the flanks of the earthflow. Between these points (from 125 to 265 m along the profile), three behavioural classes can be distinguished, indicated by blue, yellow, and red symbols on the graph, that result in two types of variation within the strata. One is related to the degree of mechanical porosity induced by fracturing, and the other to the degree of water saturation of this porous environment. Indeed, the increase in the values from 500 to 2300 m s−1 appears to be related to a decrease in fracture density with depth. The fracturing is linked to the deformation undergone by soil and rock material during the landslide, with this being more pronounced near the surface. The second noticeable variation is the high dispersion in the resistivity log data (1.2 to 2.4 Ω m) for the low velocity values, corresponding to the surficial stratum. For the higher velocity values, corresponding to deeper strata, the resistivity values tend towards an average value of 1.8 Ω m, which is in accordance with a decrease in the fracture density with depth. The various trends observed in the distribution of the data points for a specific elevation demonstrate that this behaviour varies laterally, as does the surface water content. This is due to the topography inducing a drainage pattern towards the ravines and away from the consequently dryer crests. It would seem, therefore, that the effect of surface fracturing differs, depending on whether the soil is saturated or not, or, in other words, whether the fractures are located along the ravines or the crests (Fig. 6). The immediate prospects of this study would be to identify a theoretical law linking acoustic velocity and electrical resistivity, enabling an explanation for the mechanical behaviour of the earthflow as presented in this article. The inversion of two geophysical parameters would consequently become an inversion of lithological behaviour, depending on the petrophysical properties.
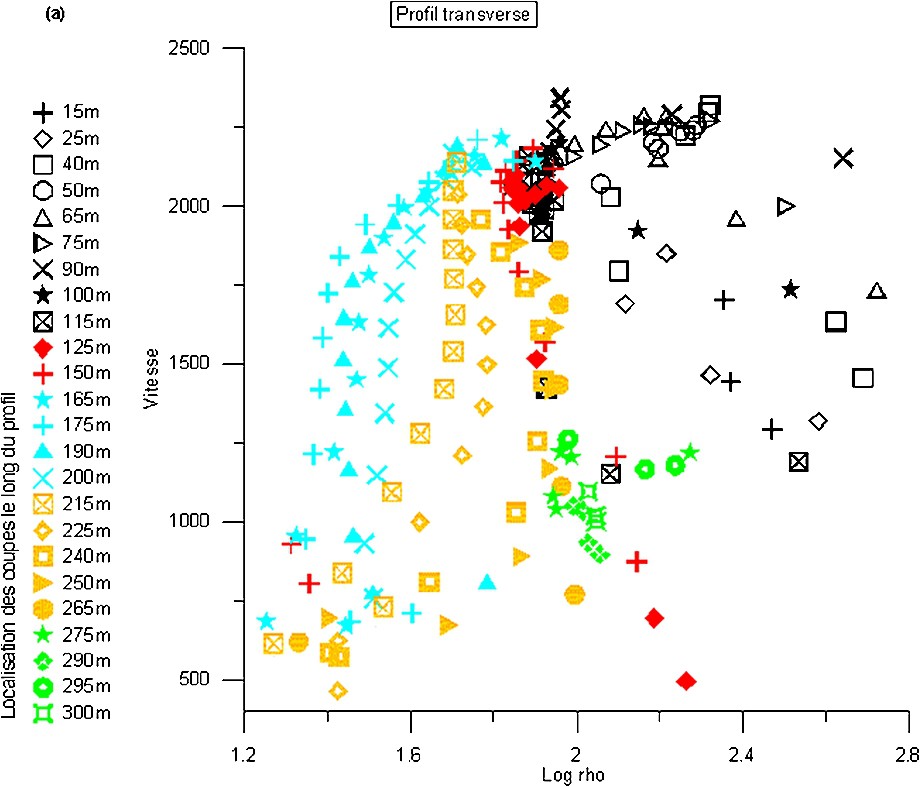
Vitesse en fonction de la résistivité électrique ρ pour différentes coupes verticales effectuées le long du profil transverse.
Velocity versus electrical resistivity ρ for several vertical sections selected along the horizontal transverse profile.
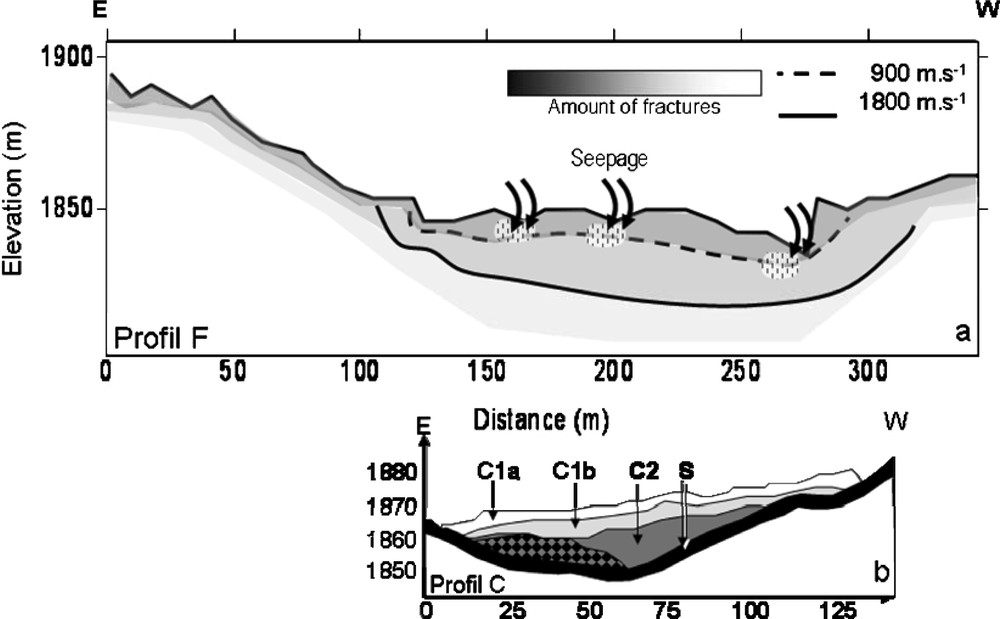
(a) Coupe schématique du profil transversal montrant la distribution des fissures sur les flancs et le glissement-coulée, ainsi que les zones d'infiltration situées dans le fond des ravines ; (b) coupe géotechnique identifiant les couches de la coulée (C1a et C1b), les anciennes coulées (C2) et le matériau en place (S) d'après Malet [7].
(a) Schematic vertical section of the transverse profile showing the distribution of fissures throughout the flanks and the earthflow, and the water saturated zones linking gullies and upper groundwater; (b) geotechnical cross-section identifying the two active layers of the earthflow (C1a and C1b), the old one (C2) and the basement (S) from Malet [7].
1 Introduction
Cette étude a pour but de caractériser la structure interne et l'état hydrique de matériaux argilo-marneux affectés par des glissements de terrain, à partir de paramètres géophysiques tels que la vitesse de propagation et la résistivité électrique ρ. Notre étude s'applique sur le site complexe du glissement-coulée de Super-Sauze (Alpes-de-Haute-Provence, France) représentatif des mouvements gravitaires à comportement visqueux.
Les glissements-coulées lents sont des phénomènes complexes, dans lesquels des masses de matériaux cohésifs (texture granulométrique fine) progressent lentement : (i) par un mécanisme de glissement le long de surfaces de cisaillement discrètes [2,4] ; (ii) par une déformation continue et différenciée [1,7] dont l'amplitude dépend des conditions locales de contraintes et de la forme de la topographie recouverte.
Ils présentent une morphologie caractéristique de langue boueuse, hétérogène et plus ou moins saturée d'eau. Ces phénomènes peuvent être classiquement divisés en trois unités spatiales distinctes : (i) une zone d'ablation à l'amont, qui présente une morphologie de détail caractéristique, associant un escarpement principal et à son pied des chaos de blocs ; (ii) une zone de transit, dans la partie intermédiaire, qui prend l'allure d'une coulée étirée, qui fossilise un (ou plusieurs) chena(ux) d'écoulement long(s), étroit(s) et pentu(s) (>20°) ; (iii) une zone d'accumulation à la base du versant, qui prend la forme d'un ou plusieurs lobe(s) étagé(s) et raide(s).
Ces glissements-coulées présentent des vitesses très variables, comprises en moyenne entre 0,005 et 0,3 m j−1. Ce mouvement continu (aucune phase d'arrêt) peut être maintenu sur de longues distances (hectométriques à kilométriques) et périodes de temps (>100 ans), par la combinaison de déformations de fluage (continues dans le temps) et de déformations plastiques (épisodiques), en fonction des variations des pressions interstitielles. La combinaison d'une faible résistance mécanique (résiduelle) des matériaux et de conditions d'alimentation en eau variable explique la cinématique saisonnière. Les glissements-coulées présentent en surface un système complexe de fissures qui sont des zones de faiblesses hydrologique et mécanique, qu'il convient de caractériser pour comprendre le comportement physique de ces phénomènes. En effet, l'amplitude des accélérations va dépendre de l'augmentation des pressions interstitielles et de leur dissipation, elles-mêmes contrôlées par les caractéristiques géomécaniques du matériau et par la densité de fissuration [9].
Les méthodes non intrusives de la géophysique, telles que la tomographie sismique ou l'imagerie électrique, sont adaptées à l'étude de ces paramètres. En effet, elles permettent d'obtenir les caractéristiques pétrophysiques d'un matériau par inversion des données mesurées. Dans notre cas, ce sont les temps de trajet en sismique et les résistivités apparentes en électrique qui constituent nos observations. L'inversion permet d'obtenir deux modèles distincts : le champ de vitesse acoustique, qui rend compte de l'état de porosité des matériaux et la distribution des résistivités électriques, qui renseigne sur les variations de teneurs en eau ou en argile. À partir de ces modèles, la corrélation des deux paramètres et ρ est étudiée, afin de vérifier s'il est possible de dégager des comportements caractérisés par une relation entre vitesses acoustiques et résistivités électriques.
2 Le site d'étude : le glissement-coulée de Super-Sauze
Le site de Super-Sauze a été choisi pour cette étude, car il représente un observatoire naturel (aucun ouvrage de mitigation) suivi et instrumenté depuis 1996 [10]. Il est représentatif de plusieurs glissements-coulées lents similaires observés dans les Alpes françaises, comme les glissements-coulées de La Valette, de Poche, de Boulc ou des Dourbes. Le glissement-coulée se situe dans le bassin de Barcelonnette, sur la rive gauche de l'Ubaye [11]. Il s'étend sur une longueur de 820 m, entre les altitudes 2105 m à la couronne et 1740 m au pied de la coulée pour une pente moyenne de 25° et une superficie de 17 ha (Fig. 1).
Le glissement-coulée s'est déclenché dans les marnes noires callovo-oxfordiennes, connues sous le nom de « Terres noires », présentant un faciès de schistes argileux noirs, gris ou légèrement bleutés. Les blocs et les panneaux qui se détachent de la couronne, de manière rétrogressive, par des ruptures planes [8], s'accumulent en se disloquant dans une ou plusieurs ravine(s), et forment, après leur déstructuration progressive, une coulée de débris à granulométrie hétérogène (Fig. 2). Le bassin torrentiel emprunté par la coulée présente une allure dissymétrique : le versant oriental, aux pentes moyennes (20°), est constitué d'une couverture morainique épaisse (jusqu'à 10 m), identifiée par sondages géotechniques et recouvrant le substrat marneux principalement dans la partie amont [7]. Le versant occidental est plus pentu (>30°) et constitué uniquement par le substrat marneux.
Depuis 1996, une étude multidisciplinaire de ce site a permis de proposer un modèle conceptuel de fonctionnement et de valider plusieurs modèles numériques de comportement [7]. Les investigations ont associé une analyse géomorphologique couplée à un traitement photogrammétrique, une prospection géotechnique (sondages et essais in situ et en laboratoire) et une investigation géophysique préliminaire [12,13]. Ces mesures ont permis de définir la position et la forme de la topographie recouverte, ainsi que la structuration verticale et latérale de la coulée [10]. Dans le cadre de cette étude, plusieurs types de mesures géophysiques complémentaires ont été réalisées sur le site : deux profils de sismique réfraction et d'électrique, ainsi que des relevés topographiques à l'aide d'un DGPS. Le protocole d'acquisition et les traitements effectués sont détaillés dans la section suivante.
3 Tomographies géophysiques : protocole d'acqusition et traitement des données
Deux profils sismiques ont été réalisés dans la zone de transit, l'un (F) transverse à la coulée, proche du transect géotechnique C (Fig. 1b), d'une longueur totale de 325 m, et l'autre (G) dans la direction de la plus grande pente du glissement-coulée, sur une longueur de 235 m. Pour le profil transverse : 66 géophones 10 Hz ont été placés tous les 5 m. Dix-neuf tirs au cordon détonant (100 g), espacés de 15 m, ont été effectués. Un système dit de « roll-along » a permis de déplacer virtuellement la flûte, pour n'enregistrer que les 48 traces disponibles sur un sismographe de type Géometrics StrataVizor. Le traitement des données sismiques par inversion des premiers temps d'arrivée a été réalisé grâce au logiciel de tomographie sismique JaTS [3]. Ce dernier permet d'estimer le champ de vitesse acoustique grâce à un algorithme de reconstruction algébrique de type SIRT (Simultaneous Iterative Reconstruction Technique). La spécificité de JaTS réside en premier lieu dans l'approche probabiliste qui a permis de reformuler le SIRT, de façon à la rendre plus stable. Le poids donné à chaque mise à jour du champ de vitesse est ainsi justifié par la probabilité qu'une observation en soit responsable. La fonction « objectif », calculée à chaque itération pour estimer la convergence utilise la norme L2. Le deuxième point concerne l'utilisation des volumes de Fresnel dans le calcul des temps de trajet : à l'inverse des rayons, cette modélisation des trajets sismiques a l'avantage de prendre en compte la résolution de l'onde, dépendant elle-même de la fréquence.
Deux profils de panneau électrique ont été réalisés conjointement aux profils sismiques. Le profil transverse (316 m) était composé de 80 électrodes espacées de 4 m. Un total de 1026 et de 650 mesures a été collecté respectivement pour le profil transverse (F) et le profil longitudinal (G). Les données ont été traitées puis inversées par la méthode de Loke [5]. Classiquement utilisée par le biais du logiciel RES2DINV, cette technique est basée sur une inversion par moindres-carrés amortis de type Gauss–Newton. Le problème direct est résolu en intégrant l'équation de Poisson par différences finies.
Sur la coulée, les deux tomographies sismiques indiquent des vitesses sismiques qui varient de 300 à 2400 m s−1. Un modèle vertical de vitesses en trois couches est identifié (Fig. 3) : une première couche superficielle, aux vitesses faibles, comprises entre 300 et 600 m s−1 ; une deuxième couche avec des vitesses comprises entre 900 et 1200 m s−1 et enfin, le socle marneux, bien délimité par une couche intermédiaire peu épaisse, avec les vitesses les plus élevées, de 2100 à 2400 m s−1. Cette structuration verticale des vitesses sismiques, identifiée par sismique réfraction dans Schmutz [12], correspond à la structure géotechnique proposée par Maquaire et al. [10], qui associe, de la surface vers la profondeur, (i) une couche géotechnique C1a–b de matériaux argilo-marneux remaniés, lâches, relativement peu consolidés et semi-perméable d'un point de vue hydrologique [7] ; (ii) une couche géotechnique C2 de matériaux remaniés, consolidés et imperméables ; (iii) le substrat marneux. Sur les versants, les vitesses sismiques sont importantes (1500 à 2500 m s−1), et bien différenciées de celles observées pour les matériaux de la coulée.
La tomographie électrique réalisée sur le profil transverse (Fig. 4) indique un fort contraste de résistivité entre le versant stable, taillé dans des moraines quaternaires, et les matériaux de la coulée. Sur ce dernier, un modèle vertical de résistivités en deux couches peut être identifié : un matériau très conducteur en surface (3 à 20 Ω m) est superposé à un matériau moyennement résistif. Ces résultats confirment la grande variabilité des résistivités électriques de la coulée, qui s'explique principalement par le contexte structural [12]. L'extension des profils sur les flancs, au-delà des limites de la coulée, met en évidence un comportement électrique beaucoup plus résistif. Ceci démontre l'efficacité des méthodes électriques pour délimiter les zones en mouvement dans ce contexte.
4 Discussion : corrélation sismique–électrique
Dans cette section, la discussion porte uniquement sur le profil transverse qui illustre le comportement complexe du glissement-coulée. Le modèle sismique (Fig. 3) présente trois couches distinctes, caractérisées par des vitesses croissantes avec la profondeur, qui correspondent aux deux couches géotechniques C1–C2, constituées de matériaux compactés avec la profondeur, et au substrat marneux parfaitement délimité. L'imagerie électrique (Fig. 4a) indique deux couches de résistivités croissantes. La couche superficielle présente une forme de cuvette que l'on identifie également sur l'image sismique.
Afin de comparer plus que qualitativement ces deux sources de données, plusieurs coupes verticales, le long des profils inversés, ont été réalisées. Pour chaque coupe, les gradients verticaux de la vitesse et du logarithme de la résistivité électrique ont été extraits, et représentés sur le graphe de la Fig. 5. Celle-ci indique que, sur les 115 premiers mètres du profil, qui correspondent au versant stable recouvert sur des épaisseurs de quelques mètres par des matériaux morainiques, les points (noirs) sont relativement regroupés. Les quelques points dispersés peuvent traduire un changement de lithologie (substrat marneux sous la couverture morainique) ou l'hétérogénéité de la couverture morainique (formation composée de blocs hétérométriques noyés dans une matrice limono-sableuse).
Sur les 25 derniers mètres du profil (à partir de l'abscisse 275 m), les points (en vert) sont également bien regroupés. Ceci traduit la présence d'une lithologie homogène (substrat marneux) avec peu de niveaux d'altération, et correspond aux observations géomorphologiques réalisées sur le versant ouest du bassin torrentiel. Entre ces versants (des abscisses 115 m à 275 m), trois comportements matérialisés par les points bleus, jaunes et rouges, sont observés. Ces comportements traduisent deux types de changement d'état, au sein du matériau remanié. Ils peuvent être mis en relation avec la densité de fissuration créant une porosité mécanique d'une part, et avec le degré de saturation en eau du milieu poreux d'autre part. Ainsi l'évolution croissante de la vitesse de propagation de 500 m s−1 à 2300 m s−1 semble liée à la diminution de la densité de fissuration avec la profondeur. En effet, l'existence de tensions distribuées verticalement au sein de la masse se traduit par une densité de fissuration plus importante en surface [6].
Le deuxième changement remarquable est le degré de dispersion du log de la résistivité (1,2 à 2,4 Ω m) pour les faibles vitesses sismiques (matériau de la couche superficielle C1). Pour les vitesses sismiques plus élevées (matériau de la couche profonde C2), les résistivités tendent vers une valeur moyenne de 1,8 Ω m, ce qui est en accord avec une diminution de la densité de fissuration en fonction de la profondeur. Les différentes tendances de la distribution des valeurs, pour une cote donnée, montrent que le comportement varie latéralement. Or, une variation latérale de l'état hydrique est observée à l'échelle de la coulée. Celle-ci provient de la topographie du site, qui draine les eaux météoriques vers les ravines, et a tendance à assécher les crêtes [9]. Il semblerait donc que l'influence des fissures présentes en surface soit différente, suivant qu'elles sont saturées ou pas (Fig. 6).
Les perspectives immédiates de cette étude sont de trouver une loi théorique d'évolution de la vitesse sismique et de la résistivité en fonction de l'état géomécanique des matériaux, qui permettrait de retrouver les comportements observés. Des lois empiriques existent – comme par exemple la loi d'Archie ou la loi de Wyllie – qui relient respectivement la résistivité électrique et la vitesse sismique à la porosité. Dans ce cadre, une étude de laboratoire sur échantillons pourrait être envisagée pour obtenir des informations plus précises sur les variations de la vitesse en fonction de la porosité et de l'argilosité par exemple. Ainsi, il serait possible de relier la vitesse et la résistivité par une loi applicable à ce type de matériau et d'objet et donc d'effectuer, non plus une inversion séquentielle de ces deux paramètres, mais une inversion de comportement géomécanique à partir des caractéristiques géophysiques. Dans cette perspective, d'autres investigations géophysiques conjointes sismique–électrique, sur différents sites et pour différents matériaux, devront aussi être réalisées pour constituer une base de données statistique permettant de définir cette loi.
5 Conclusion
Cette étude avait pour but de caractériser la structure interne et l'état hydrique du glissement-coulée de Super-Sauze (Alpes-de-Haute-Provence, France) à partir de la vitesse de propagation et de la résistivité électrique ρ. La coulée se situe dans les « Terres noires » du Callovo-Oxfordien et se compose de matériaux argilo-marneux remaniés, hétérogènes, très fissurés et plus ou moins saturés en eau. Ce contexte rend ce site représentatif des mouvements gravitaires à comportement visqueux. Des mesures de tomographie sismique et électrique ont été réalisées et étudiées le long d'un profil transverse à la coulée. Le traitement a consisté à inverser les temps de trajet des premières arrivées sismiques et les valeurs de la résistivité apparente, afin de produire des images de la vitesse acoustique et de la résistivité électrique le long de ces profils. Elles révèlent une structure composée de deux couches de matériaux déplacés superposées au substratum marneux au droit de la coulée ; les versants du bassin torrentiel s'individualisent nettement de part et d'autre de la coulée. La corrélation des valeurs de la vitesse acoustique en fonction de la résistivité électrique, relevées à différentes abscisses le long des profils, met en évidence plusieurs comportements rhéologiques, chacun relié à l'état de fissuration et à la saturation en eau du milieu. On caractérise ainsi les versants et le substratum comme des niveaux homogènes et stables, alors que la coulée révèle des zones plus ou moins fissurées en fonction de la profondeur et plus ou moins saturées en eau, en fonction des écoulements de surface guidés par la présence de ravines.
Remerciements
Ce travail a été réalisé dans le cadre du projet ACI CatNat SAMOA « Surveillance et Auscultation de MOuvements gravitaires Alpins » (coordinateurs : C. Delacourt, O. Maquaire, D. Amitrano) et financé partiellement par la direction de la recherche du BRGM. Les auteurs remercient A. Remaître et D. Moreno, qui ont participé à la mission d'acquisition sur le site.


