1 Introduction
The geothermal reservoir of Soultz-sous-Forêts, like most geological systems, contains structures of various sizes along which flow occurs; three main types of structures were identified: individual fractures, fracture clusters and major faults (Genter et al., 1997). In order to understand these flow systems and help with managerial decisions, large scale numerical models incorporating such heterogeneities have been developed. Yet, when the transport of solutes is involved, the choice of a dispersion law (possibly scale dependent) valid at the scale of an individual fracture remains an open issue (NAS Committee, 1996).
At this scale, tracer dispersion results from the combined action of the complex velocity field (varying both in the gap of the fracture and in its plane) and of mixing by molecular diffusion. The latter allows the tracers to move from one streamline to another and homogenizes the spatial distribution of the tracers. In the classical approach, tracer particles are assumed to perform a random walk superimposed over a drift velocity. The latter is the average of the fluid velocity over an appropriate volume (the representative elementary volume or REV) while smaller scale variations induce tracer spreading. At the REV scale, the average
| (1) |
Several experimental studies of breakthrough curves of solutes in natural fractures reported in the literature (Keller et al., 1999; Lee et al., 2003; Neretnieks et al., 1982; Park et al., 1997) measured dispersion coefficients increasing linearly with the mean flow U (or with Pe). Moreover, the value of the dispersivity ld = D/U observed agreed with the predictions of a perturbation analysis (Gelhar, 1986). These results suggested that dispersion is controlled (as in 3D porous media (Bear, 1972)) by spreading due to velocity variations associated to the geometry of the void structure. This determines the correlation length of the velocity field, leading to the so-called geometrical dispersion regime. However, flow in fractures is known to be frequently concentrated in long channels of high hydraulic conductance (Brown et al., 1998; NAS Committee, 1996; Tsang and Tsang, 1989). The velocity remains then correlated over distances which may be too large for establishing a Fickian dispersion regime. These previous experiments were all performed for a fixed path length: however, in order to test the validity of the Fickian description, one must measure the variation of the width of the mixing front with time t and check whether it increases, as expected, as t1/2.
Another key factor is dispersion resulting from the flow profile in the gap of the fracture: the variation of the velocity between the walls (where it cancels out) and the middle of the gap (where it has a maximal value) stretches the solute front. This creates a concentration gradient across the gap which is balanced by transverse molecular diffusion. The decorrelation of the velocity of the solute is then determined by the characteristic time for the diffusion of solute particles across the gap. This differs from the geometrical regime in which the decorrelation is determined by the geometrical structure of the fracture. Then, the longitudinal dispersivity scales like ld ∝ Pe in this so-called Taylor dispersion (instead of ld ∼ cst for geometrical dispersion).
In fractures, both dispersion regimes are expected to coexist (Detwiler et al., 2000; Ippolito et al., 1993; Roux et al., 1998): at low Péclet numbers (but large enough to neglect pure molecular diffusion), dispersion is controlled by the disordered geometry, while, at higher ones, Taylor dispersion becomes the leading dispersion mechanism. However, the critical Péclet number characterizing the transition still has to be determined. Also, the robustness of this model, when contact points between the fracture walls are present, must be tested.
We discuss in this article dispersion experiments dealing with these issues and carried out in transparent fractures with various degrees of heterogeneities. The geometries of the void space and the roughness of the walls of these models are described in Section 2.1. They range from a random wall roughness with a correlation length of the order of the aperture to a multiscale rough wall geometry similar to that observed in the field (Sausse, 2002); this latter case often leads to a strong flow channelization (Tsang and Tsang, 1989). In the present models, a relative shear displacement
In order to address these various issues, dispersion has been studied as a function of:
- • the distance traveled by the tracer;
- • the lateral scale of observation in the fracture plane over which the concentration is averaged. This scale ranges from a (meso)microscopic scale (i.e. the typical fracture aperture) up to the fracture width;
- • the fluid rheology in order to determine, without ambiguity, the main mechanisms controlling the dispersion: i.e. velocity profile in the fracture gap or velocity fluctuations in the fracture plane.
This contrasts with previous measurements realized at the outlet of the samples and in which the development of the mixing region and its spatial structure cannot be investigated.
2 Experimental setup and procedure
2.1 Experimental models and injection set-up
- •
Model 1: this model (Boschan et al., 2008) has two transparent surfaces of size 350 × 120 mm without contact points. The upper one is a flat glass plate and the lower one is a rough photopolymer plate. The wall roughness corresponds to randomly distributed cylindrical obstacles of diameter do = 1.4 mm and height 0.35 mm protruding out of the plane surface. The minimum aperture am of the model is the distance between the top of the obstacles and the flat glass plate with am = 0.37 ± 0.02 mm; the maximum and mean values are respectively aM = 0.72 ± 0.02 mm and
- •
Model 2: this model uses a periodic square array of obstacles of similar size as in model 1 but of rectangular and variable cross section and with their top in contact with the top plate. Flow takes then place in a two dimensional network of channels of random aperture (D’Angelo et al., 2007). The model contains 140 × 140 channels (real size 150 × 140 mm) with an individual length equal to l = 0.67 mm and a depth aM = 0.5 mm; their average width and standard deviation are
- •
Model 3: models 3 and 4 have complementary self-affine walls of size 350 × 90 mm, reproducing the roughness of natural fractures (Boschan et al., 2007). In model 3, a relative shear displacement δ = 0.75 mm parallel to the direction of the flow is applied between the walls. The mean of the fracture aperture is
- •
Model 4: in order to analyze the influence of the direction of the shear displacement, the direction of the shear for model 4 is now perpendicular to the direction of the flow (the corresponding standard deviation of the aperture is σa = 0.15 mm). This configuration (and that of model 5) is referred to as
- • Model 5: the shear displacement is also perpendicular to the mean flow but has a smaller amplitude δ = 0.33 mm: this results in a lower standard deviation of the mean aperture σa = 0.15 mm and in a weaker channelization.
All models are transparent and placed vertically with their open sides horizontal. The upper side is fitted with a leak-tight adapter allowing one to suck the fluid at a constant flow rate. The lower open side can be dipped into a bath containing the liquid. When the pump is switched off, the bath can be lowered before changing the fluid inside it. This allows one to obtain a flat initial front between the fluids (See Figure 1 in ref (Boschan et al., 2007)).
The models are illuminated from the back by a light panel and images are acquired using a high resolution camera. The pixel size is around 0.2 mm, i.e. lower than the typical fracture aperture. About 100 images of the distribution of the light intensity I(x,y,t) transmitted through the fracture are recorded at constant intervals during the fluid displacement using a digital camera with a high dynamic range. Reference images with the fracture saturated with the clear and dyed fluids (dye concentration c0) are also recorded before the experiments and after the full saturation by the displacing fluid. A calibration curve obtained independently through separate measurements is then used to map the local relative dye concentration 0 ≤ c(x,y,t)/c0 ≤ 1 (in the following, c0 is omitted and c(x,y,t) refers directly to the normalized dye concentration). The two fluids are of equal density: this is verified by performing twice the experiments at each flow rate value with the dyed fluid either displacing or displaced by the clear fluid. Comparing the results allows one to detect possible instabilities induced by residual density differences (the corresponding experiments are discarded). The two fluids are, of course, miscible and have the same viscosity.
2.2 Fluids preparation and characterization
The solutions used in the present work are either a Newtonian water-glycerol mixture or shear-thinning water-polymer (scleroglucan) solutions with a 500 or 1000 ppm polymer concentration. In all cases, the injected and displaced fluids have identical rheological properties. The Newtonian solution contains 10% in weight of glycerol and has a viscosity equal to 1.3 × 10−3 Pa s at 20 °C. The preparation and characteristics of the shear-thinning solutions are the same as those reported in (Boschan et al., 2007). The variation of the viscosity μ with the shear rate
| (2) |
Paramètres rhéologiques et nombres de Péclet pour les solutions de 500 et 1000 ppm de scléroglucane, utilisées dans la présente étude.
| Fluids | n |
|
μ0 mPa.s |
| W-Glycerol | 1 | – | 10 |
| 500 ppm | 0.38 ± 0.04 | 0.077 ± 0.018 | 410 ± 33 |
| 1000 ppm | 0.26 ± 0.02 | 0.026 ± 0.004 | 4500 ± 340 |
The two main dispersion mechanisms, i.e., Taylor dispersion (ld ∝ Pe) and geometrical dispersion (ld ∼ cst) are affected in opposite directions when a Newtonian fluid is replaced by a shear thinning solution. More precisely, the velocity contrasts between different flow paths are enhanced for a shear thinning fluid, resulting in an increase of the geometrical dispersion (without modifying the relation ld ∼ cst). By contrast, the velocity profiles in the gap become flatter: this reduces therefore Taylor dispersion, but still with ld ∝ Pe. Varying the fluid rheology modifies the relative influence of the two main dispersion mechanisms in opposite ways: the dominant one can therefore be identified unambiguously for each fracture geometry and flow rate.
3 Experimental results
3.1 Fracture model 1
In this model, flow takes place in the free space between a flat plate and a second one with protuberant obstacles. The latter perturb the flow velocity field: the local mean fluid velocity (averaged over the gap) is greater between the obstacles, where the aperture is largest than at their top, where it is minimal. These mean velocity variations in the fracture plane result in geometrical tracer spreading. As for the velocity profile in the fracture gap, it induces Taylor-like dispersion. The variation of the dispersivity ld = D/U as a function of Pe confirms that it is the sum of the two contributions discussed above with:
| (3) |
Experimental dispersivity variations as a function of Pe are plotted in Fig. 1 for the three fluids. These data sets are well adjusted (see lines in Fig. 1) by functions of the type shown in Eq. (3): the dispersivity increases at first slowly with Pe above
Variation of the experimental dispersivity ld as a function of the Péclet number in model 1. (, ): water-glycerol solution; (, ): 1000 ppm, (, ): 500 ppm polymer solutions. ld is determined from variations of the local concentration (filled symbols) or of its average over the model width (open symbols). Solid, dotted and dashed lines: fits of the data for each solution (in the above order) with Eq. (3).
Variation de la valeur expérimentale de la dispersivité ld en fonction du nombre de Péclet Pe dans le modèle 1. (, ) : solution eau-glycérol; solutions de polymère de concentrations: (, ) 1000 ppm et (, ) 500 ppm. ld est déterminée à partir des variations de la concentration locale (symboles pleins) ou de sa moyenne sur la largeur du modèle (symboles vides). Lignes continues, pointillées, tirets: ajustement des données par l’Éq. (3) pour chaque solution (dans l’ordre précédent). Masquer
Variation de la valeur expérimentale de la dispersivité ld en fonction du nombre de Péclet Pe dans le modèle 1. (, ) : solution eau-glycérol; solutions de polymère de concentrations: (, ) 1000 ppm et (, ) 500 ppm. lLire la suite
The values represented in Fig. 1 by filled symbols were obtained by fitting variations with time of the local concentration on each individual pixel by solutions of Eq. (1); this provides local values of both the dispersion coefficient D(x,y) and the transit time. The values of D(x,y) at points far enough from the inlet so that dispersion has reached a stationary regime are then averaged over x and y. A similar analysis was performed on the average of the local concentrations over the fracture width and its results are displayed by empty symbols in Fig. 1: they almost fall on the filled symbols demonstrating the lack of large scale concentration heterogeneities in the mixing front.
3.2 Fracture model 2
In this model, the obstacles extend over the full gap height and mimic gouge particles created by the failure of the rock and evenly distributed in the fracture (Section 2.1). The model is then a plane array of channels of random width: it can be considered as a 2D porous medium in which the pores correspond to the junctions between the channels. We show now that mixing at these junctions has a crucial influence on dispersion.
Fig. 2 displays variations of the dispersivity with the Péclet number deduced from time variations of the local concentration at the pore scale (filled symbols) and of its average over the fracture width (open symbols); it is seen that the values of ld obtained in both cases are similar so that, in the following, only global measurements will be discussed.

Variation of the dispersivity ld (mm) with the Péclet number for experiments with water-polymer solutions: (),(): 500 ppm concentration - (), () 1000 ppm. Open (resp. filled) symbols: averaging interval: 35 (resp. 0.4) mesh sizes. Dashed lines: Mean dispersivity values for the geometrical dispersion regime. Dotted line: power law fit of the variation for Pe > 10 (exponent 0.35 ± 0.03).
Variation de la dispersivité ld (mm) avec le nombre de Péclet Pe pour des expériences avec des solutions eau-polymère de concentrations: (),() 500 ppm et (), () 1000 ppm. Symboles ouverts (resp. pleins) : intervalle de moyennage : 35 (resp. 0,4) tailles de maille. Tirets : valeurs de dispersivité moyennes pour le régime de dispersion géométrique. Pointillés: ajustement par une loi de puissance de la variation pour Pe > 10 (exposant 0,35 ± 0,03).
For Pe < 10, ld = D/U, is nearly constant (i.e. D ∝ Pe), suggesting dominantly geometrical dispersion. As discussed in Sec. 3.1, the value of ld in this regime should depend strongly on the rheology of the solution: more precisely, it should increase with the polymer concentration as indeed observed here (like for model 1).
For Pe > 10, a second dispersion regime is observed, in which ld increases with Pe. Furthermore, the linear trend observed in a log-log coordinate shows that ld follows a power law of Pe (more precisely, ld ∝ Pe0.35 for Pe > 10). This result is in agreement with numerical simulations by Bruderer and Bernabe (Auradou et al., 2008) and differs from the Taylor dispersion regime ld ∝ Pe observed in model 1 at high Pe values. This difference is explained by the influence of the pore junctions. At low flow velocities (typically Pe < 10), tracer particles can explore effectively the local flow field by molecular diffusion during their transit time through a given junction: this distributes evenly the tracer concentration inside it which represents a perfect mixing condition. Then, the tracer concentration is equal in all outgoing paths and the probability to follow one of them is proportional to the corresponding flow rate (Adler and Thovert, 1999; Park et al., 2001). Therefore, in this regime, dispersion is controlled by the disordered geometry of the array of channels.
At higher Pe values (typ. Pe > 10), mixing at the junctions is no more perfect and the tracer concentration in slower channels (like those transverse to the mean flow) is lower compared to the perfect mixing situation. The dispersion characteristic becomes more similar to the case of capillary tubes (representing the fast flow channels) oriented along the flow direction. In this case, one would observe Taylor dispersion with ld ∝ Pe but the influence of flow redistribution at the junctions is quite large: this leads to a variation of ld as Pe0.35 intermediate between those observed in the geometrical and Taylor regimes. The origin of power law variations of ld with Pe is also discussed in detail in (Bijeljic and Blunt, 2006).
3.3 Fracture model 3
Like in model 1, the walls of this fracture do not have any contact point but, in contrast with it, the rugosities of the wall have been selected to reproduce the multi-scale roughness of most natural fractures (Section 2.1).
Such fractures are known to display high aperture channels perpendicular to the relative shear displacement
In model 3, flow is parallel to

Compared time variations of the average
Compared time variations of the average
Comparaison des variations temporelles de la moyenne
Comparaison des variations temporelles de la moyenne

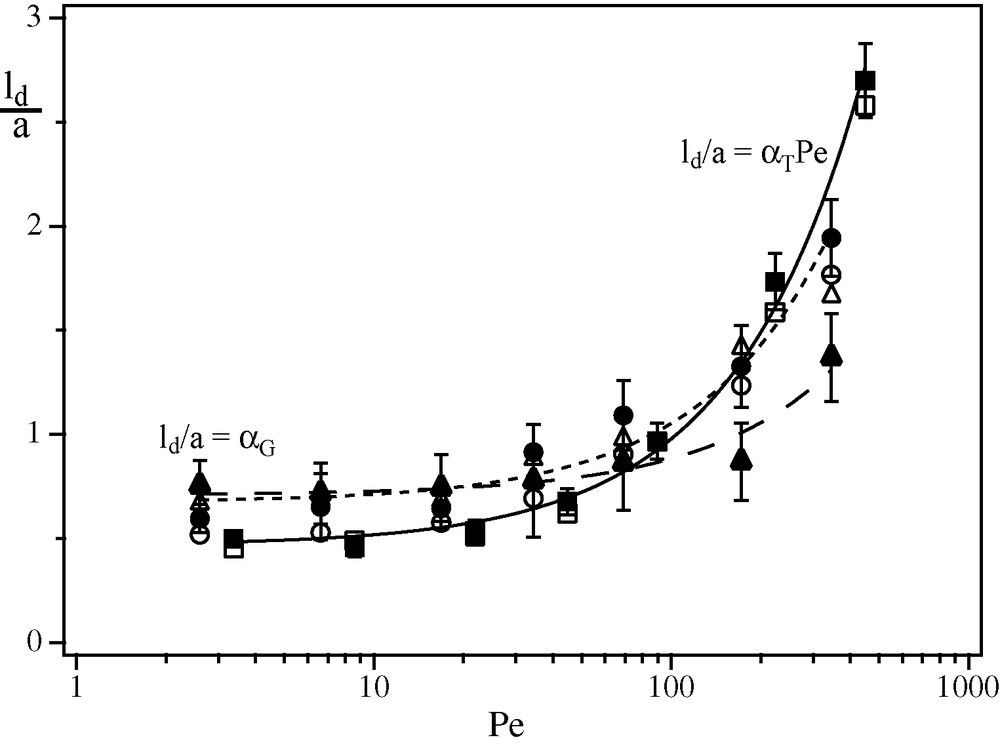
Variation of the normalized dispersivity ld/a as a function of Pe for model 3 and two different polymer concentrations. (, ): global dispersivities determined from concentrations averaged over the fracture width. (, ): local dispersivities determined from concentration variations on individual pixels. Lines: Taylor dispersion for plane parallel walls with the same mean gap as for model 3. (, ), dotted line: 1000 ppm polymer solution; (, ), dashed line: 500 ppm polymer solution; continuous line: Newtonian solution. Insert: variation of the ratio of the local and global dispersivities as a function of the Péclet number. (): 500 ppm solution. (): 1000 ppm solution. Masquer
Variation of the normalized dispersivity ld/a as a function of Pe for model 3 and two different polymer concentrations. (, ): global dispersivities determined from concentrations averaged over the fracture width. (, ): local dispersivities determined ... Lire la suite
Variation de la dispersivité normalisée ld/a en fonction de Pe pour deux concentrations en polymère différentes dans le modèle 3. (, ): dispersivités globales déterminées à partir de la moyenne de la concentration sur la largeur de la fracture. (, ) : dispersivités locales déterminées à partir des variations de concentration sur des pixels isolés. Lignes : dispersion de Taylor entre des parois planes et parallèles avec le même intervalle que pour le modèle 3. (, ), ligne pointillée: solution de polymère de concentration 1000 ppm ; (, ), tirets : solution de concentration 500 ppm; ligne continue : solution newtonienne. Insert : variation du rapport des dispersivités locale et globale en fonction du nombre de Péclet. () : solution de concentration 500 ppm. () : solution de concentration 1000 ppm. Masquer
Variation de la dispersivité normalisée ld/a en fonction de Pe pour deux concentrations en polymère différentes dans le modèle 3. (, ): dispersivités globales déterminées à partir de la moyenne de la concentration sur la largeur ... Lire la suite
For Pe > 12, the local dispersivity increases with Pe in qualitative agreement with theoretical expectations (ld ∝ Pe) and is also lower for the strongly shear-thinning 1000 ppm solution (open symbols). For both solutions ld is larger than predicted, particularly for the 500 ppm solution for which it is close to the Newtonian value. This may be due to the vicinity of the “plateau” domain of the rheological curve in which the solution behaves like a Newtonian fluid at low shear rates. For Pe ∼ 12, in which both solutions should be in this “plateau” regime, the dispersivities are, as expected, the same for the two solutions but still slightly higher than the theoretical value. At Pe < 10, ld rises again due to the influence of longitudinal molecular diffusion and its value is also the same for the two solutions (the [○] and [□] symbols coincide).
These values of the local dispersivity are compared in Fig. 4 to the global dispersivities determined from time variations of the concentration averaged over the fracture width (filled symbols): as seen in Fig. 4 and its insert, the local dispersivities are significantly smaller (at a same Péclet number and for a same solution). The front contours (c = 0.5) displayed in Fig. 5a and b for model 3 reveal fine structures of the mixing front: they reflect fluctuations of the velocity induced by the fracture wall roughness. Their magnitude is large enough to account for the additional increase of the global dispersivity with respect to pure Taylor dispersion (compared to local dispersion) but not enough to allow for the observation of a geometrical dispersion regime.
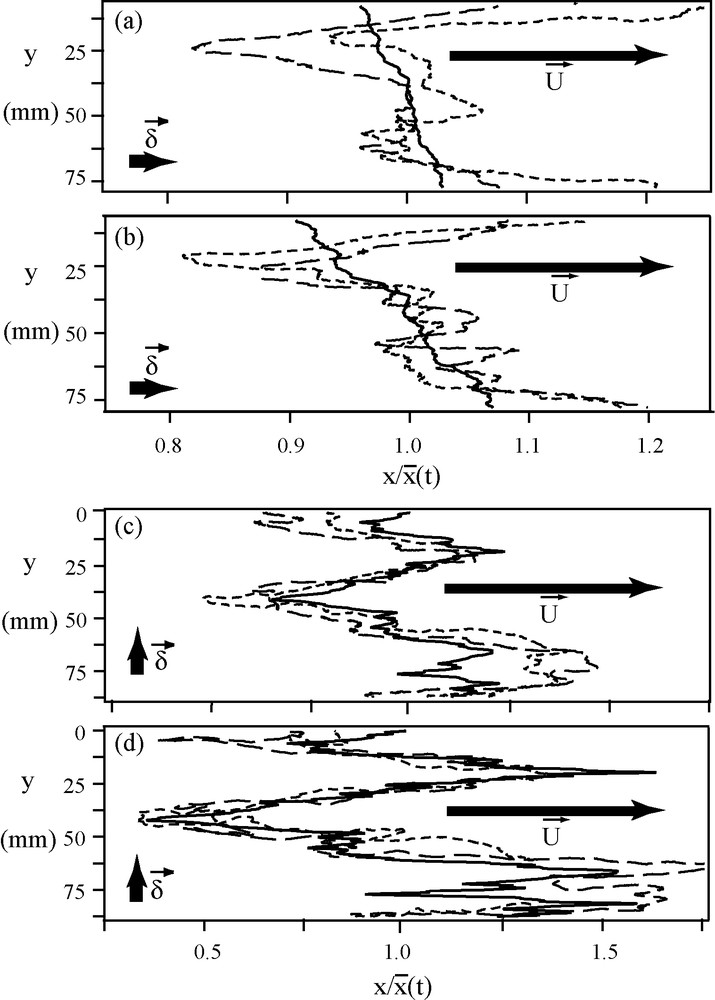
Experimental isoconcentration fronts (c = 0.5) in model 3 (graphs (a) and (b)) and in model 4 (graphs (c) and (d)) as a function of the normalized distance
Experimental isoconcentration fronts (c = 0.5) in model 3 (graphs (a) and (b)) and in model 4 (graphs (c) and (d)) as a function of the normalized distance
Fronts isoconcentrations expérimentaux (c = 0.5) dans le modèle 3 (graphiques (a) et (b)) et dans le 4 (graphiques (c) and (d)) en fonction de la distance normalisée
Fronts isoconcentrations expérimentaux (c = 0.5) dans le modèle 3 (graphiques (a) et (b)) et dans le 4 (graphiques (c) and (d)) en fonction de la distance normalisée
To conclude, in model 3 with
3.4 Fracture model 4
In model 3, the mean flow was perpendicular to the channels or to the ridges induced by the shear displacement: the correlation length of the velocity is then determined by the typical width of these structures. Model 4 has the same size as model 3, a same mean aperture and complementary rough walls with a self-affine geometry exactly identical to that used for model 3. However, the shear
The dispersion characteristics are then very different as can be seen by comparing isoconcentration fronts obtained for model 4 (Figs. 5c, d) and model 3 (Figs. 5a, b) at different times and in identical experimental conditions. More precisely, large fingers and troughs are observed for model 4 while none appears for model 3 (note that the horizontal scales is 3 times more expanded for model 3 than for model 4 in Fig. 5). Also, the amplitude of these features parallel to
These results show that front spreading is purely convective and that the total width Δx of the front parallel to
In order to predict these contrasts, we modelled the fracture aperture field as a set of independent parallel channels of aperture a(y) = <a(x,y)>x ((Auradou et al., 2006; Auradou et al., 2008)). A particle starting at a transverse distance y at the inlet is assumed to move at a velocity proportional to a(y)(n+1)/n; The theoretical profile xf (y,t) of the front at a time t is then:
| (4) |
Eq. (4) clearly predicts well the location and shape of the large “fingers” and “troughs” at both velocities for
This confirms that, for
For model 3, the hypothesis of the model are not satisfied and it does not reproduce the front geometry: however, the features of the front are generally visible at similar transverse distances y in Fig. 5a and b (at a given time). They likely reflect also, in this case, a convective spreading of the front due to velocity contrasts between the flow paths: however, there is no simple relation of the front geometry to the aperture field, in contrast with model 4.
One finds the same contrast with model 3 for the variations with time of the concentration displayed in Fig. 3. The time variation of the average
The same measurements have been performed (Boschan et al., 2007) on model 5 which has a similar wall geometry but corresponds to a smaller amplitude δ = 0.33 mm of the shear (still with
4 Conclusion
To conclude, the present experiments in 5 different models of rough fractures demonstrate that tracer dispersion depends crucially on the geometrical characteristics of the roughness. Investigating the dependence on the Péclet number and the influence of the fluid rheology allows one to identify the different mechanisms and their relative magnitude. The characteristics obtained with the different models can be grouped into two sets.
Models 1 and 2: both models correspond to obstacles with a single characteristic size. The height of the obstacles is smaller than the aperture for model 1 and equal to it in model 2: this models the case of gouge (or proppant) particles bridging the gap. In both cases, the size of the wall rugosities and the correlation length of the velocity field are small compared to the global size of the fracture. As a result, the variation with distance and time of the tracer concentration satisfies the convection dispersion equation (1); moreover, the corresponding values of D are independent of the fraction of the width of the model over which the concentration is averaged and of the distance from the inlet. Dispersion in these models may therefore be characterized by a single macroscopic dispersion coefficient.
At low Péclet numbers, one has, for both models, D ∝ U corresponding to geometrical dispersion due to the disorder of the velocity; in this regime, ld = D/U increases with the polymer concentration (i.e. with the shear-thinning character of the fluids) due to an enhancement of the velocity contrasts. Moreover, for model 1, the value of ld is close to that predicted from a small perturbation theory.
At higher Pe's, other characteristics of the structure of the void space such as the flow profile in the aperture (model 1) and the distribution of the tracer in the pore junctions (model 2) influence dispersion. For model 1, there is a transition towards Taylor dispersion with D ∝ Pe2. In model 2, D increases at high Pe values as Pe1.35: this exponent agrees with previous numerical simulations (Bruderer and Bernabé, 2001) and should depend on the distribution of the size of the obstacles. In this latter model, the transition between the different regimes is controlled by mixing at the scale of individual junctions.
Models 3, 4 and 5: The roughness of the walls of these models has a multiscale self-affine geometry similar to that of many fractured rocks; the walls of these fractures are complementary with a relative shear displacement either parallel
For
The variation of the local thickness of the front remains instead dispersive: for the smaller relative shear δ = 0.33 mm (model 5), the value of D corresponds to Taylor dispersion while, for model 4, it is larger.
For model 3
An important issue in the channelized fractures is whether the transverse exchange of tracer may be large enough so that a diffusive spreading regime is reached at very large distances. Recent work by other authors (Bauget and Fourar, 2008) report adjustments of dispersion curves in rough sandstone samples by a similar parallel channels model: however, the adjusted parameters vary in this case with the distance from the inlet. This may indeed result from some amount of transverse exchange reducing the channelization effect.
These results have a strong relevance to the efficiency of the recovery of heat through water circulation in geothermal reservoirs. There are also other possible applications to the prediction of seismic events from water circulation in the rock layers under stress.
Acknowledgments
We are indebted to R. Pidoux for his assistance. HA and JPH are supported by CNRS through GdR No. 2990) and by the European Community (STREP EGS PILOT PLANT - EC Contract SES-CT-2003-502706). This work was greatly facilitated by a CNRS-Conicet Collaborative Research Grant and by the Ecos Sud A03E02 program.


