1 Introduction
Ground penetrating radar (GPR) is a non-destructive method which, over the past 10 years, has been successfully used in vadose zone studies. It is used not only to estimate the moisture content of the soil (e.g. [15,16,18,21,23]), but also to detect and monitor the pollution infiltration at sites contaminated by light non-aqueous phase liquids (LNAPL). Examples of GPR reflection techniques used for the detection of liquid contaminants are given by Brewster and Annan [5], Daniels et al. [10], Sneddon et al. [27], and Hagrey [17]. Despite these successes, there is still some debate on the interpretation of the observed GPR results and on how the data can be used to determine the volume of the contaminated materials and its physical characteristics. Studies by Carcione and Seriani [6], Carcione et al. [7] and Cassidy [9] have shown, however, that it is possible to obtain important information on the nature and properties of the contaminants through the accurate use of advanced data modelling methods such as finite-difference time-domain (FDTD) combined with attenuation scattering analysis.
We simulated a water table aquifer (72 cm depth) by injecting water into a sandbox that also contains several buried objects. The GPR measurements were carried out with the PulseEkko1000 system (Sensors & Software, Canada) by using the 900 and 1200 MHz antenna, respectively for common mid point (CMP) and constant offset (CO) profiles. We extended the work reported by Loeffler and Bano [21] by injecting 100 L of diesel fuel (LNAPL) from the top of the sandbox above the water table. We used the same acquisition procedure and the same profile configuration as before fuel injection. The processed GPR data did not show any clear reflections from the plume pollution; nevertheless, travel times are extremely affected by the presence of the fuel and the main changes are on the velocity anomalies. In addition, the LNAPL in the vadose zone above the water table does not necessarily stay in one place, but it migrates laterally. We noticed that the reflection from the bottom of the sandbox, which is recorded at a nearly constant travel time when no fuel is present, is deformed by the presence of the pollution. The lateral extension of the plume pollution in the vadose zone is shown by plotting the travel time of the reflection from the bottom of the sandbox. Despite our efforts made to fill the tank with homogenized sand (without layering), we observed that the spreading of fuel plume is not uniform.
Furthermore, we repeated the same GPR measurements 45 days later (after fuel injection) and observed an unexpected and very clear GPR reflection above the water table (far from the fuel injection point). Therefore, a second aim of this work was to use finite-differences time-domain (FDTD) GPR modelling in combination with mixing dielectric models to determine the physical characteristics (such as a reliable estimate of the LNAPL saturation index) and the volume of the contaminated sand and to explain the origin of the observed reflections. Examples of real and synthetic GPR data will be shown.
2 Experiment set-up and GPR measurements before fuel injection
We have used the same experiment system with a sand resin box as presented by Loeffler and Bano [21]. The resin box has a diameter of 2 and is 0.98 m high (Fig. 1) and was filled with a fine calibrated sand having a diameter between 0.3 and 0.5 mm and containing three buried pipes at a depth of 48 cm (a water-filled PVC pipe, a steel pipe and an air-filled PVC pipe). The GPR measurements were carried out with the PulseEkko1000 system (Sensors & Software, Canada). CMP and CO profiles were obtained with a 900 and 1200 MHz shielded antenna, respectively. We performed 71 parallel monostatic profiles (Pxx on Fig. 1) separated by 2 cm, while the distance between measurements was also 2 cm.
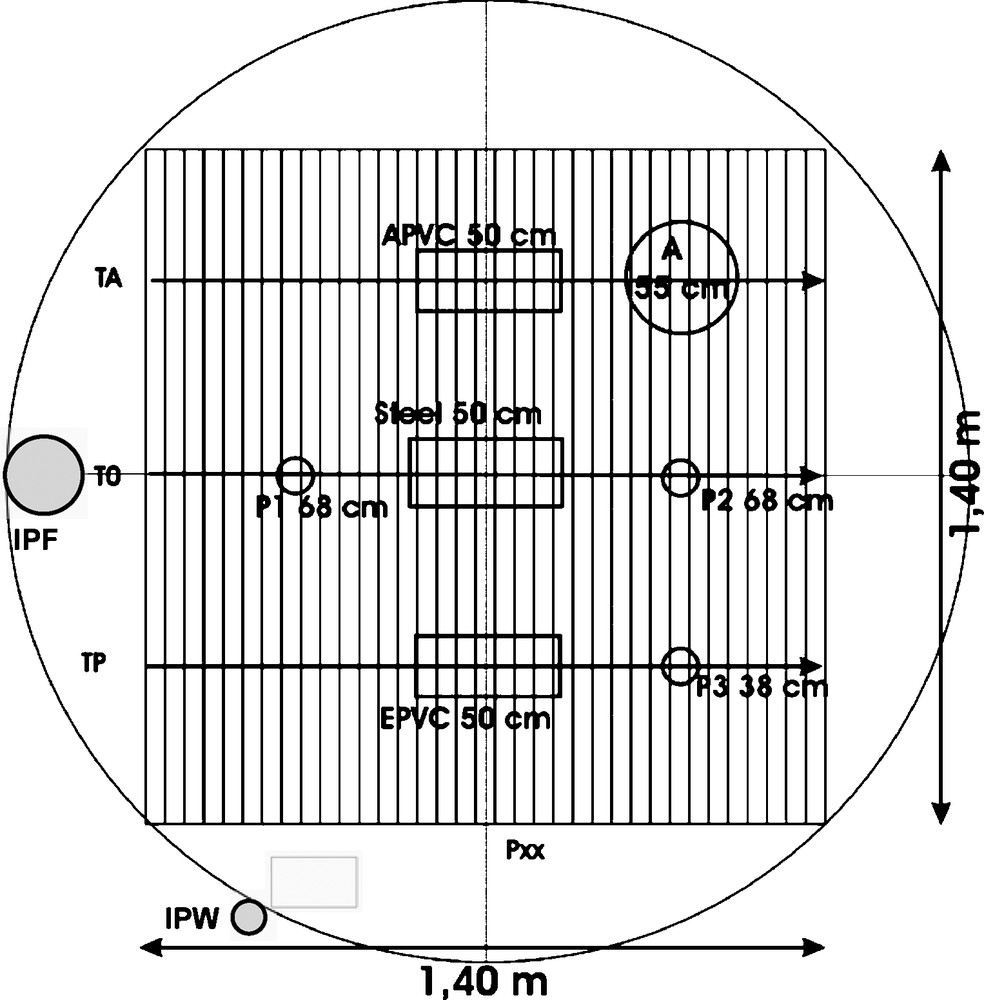
Plan view of the sandbox with the selected measurement grid (only alternate lines are shown, for clarity of the figure) and different objects. The depth of each object is also shown. IPF is the injection point (from the top) of the fuel and IPW is the injection point (from the bottom) of the water.
Grille de mesures, avec la position et la profondeur des objets. IPF est le point d’injection du gasoil et IPW est le point d’injection de l’eau.
The data were processed with in-house interactive GPR software written in Matlab on a PC-station. The quality of the data was improved by removing the low-frequency component (known as the DC component) with a running average filter in time. It is important to note that during the processing we used a linear gain control, and not automatic gain control (AGC). A linear gain control allows for the detection of small changes in signal amplitude which may be obliterated with the use of an AGC filter. The same parameters were used for all data in order to keep the relative amplitudes of the signals from one data set to the other.
After the water of the first experiment shown by Loeffler and Bano [21] was drained and the sandbox had rested for several months (from February 2003 to April 2004), we acquired (in April 2004) a 3D data set for this condition of the sand, considered at this moment as “dry” (see below for more details). In Fig. 2, we present the CO data of the “dry” sandbox acquired in November 2002 and in April 2004. The three diffraction hyperbolae noticeable in Fig. 2 represent reflections from three buried pipes (from left to right: WPVC, steel and APVC pipes; see also Fig. 1). The bottom of the sandbox is well imaged (dashed line in Fig. 2); however, the travel time of the bottom reflections presented in Fig. 2b is slightly larger than the travel time of the bottom reflections in Fig. 2a. This is due to the average velocity of the radar waves, which decreases in the case of Fig. 2b because of the retention of water into the pores after drainage (February 2003).

Profile P36 acquired on the dry sandbox: (a): in November 2002 and; (b): in April 2004. The diffraction events visible in this figure are due to different objects buried in the sand. The dashed line indicates the reflections from the bottom of the sandbox arriving a bit later for the data acquired in April 2004 (see discussion in the text).
Profils P36 acquis sur le sable sec : (a) : en novembre 2002 et ; (b) : en avril 2004. La ligne pointillée marque la réflexion du fond du bac qui arrive plus tard pour les données du mois d’avril 2004 (voir la discussion dans le texte).
Fig. 3 shows two CMP (CMP16 and CMP56) acquired on the dry sand (in April 2004). The CMP, located in the middle of the profiles P16 and P56 (see positions P1 and P2 in Fig. 1), do not show any noticeable difference and the average propagation velocity v (estimated from the bottom hyperbolic reflection) is the same on both CMP and its value is 0.105 m/ns. The sand is considered as homogeneous in this condition.
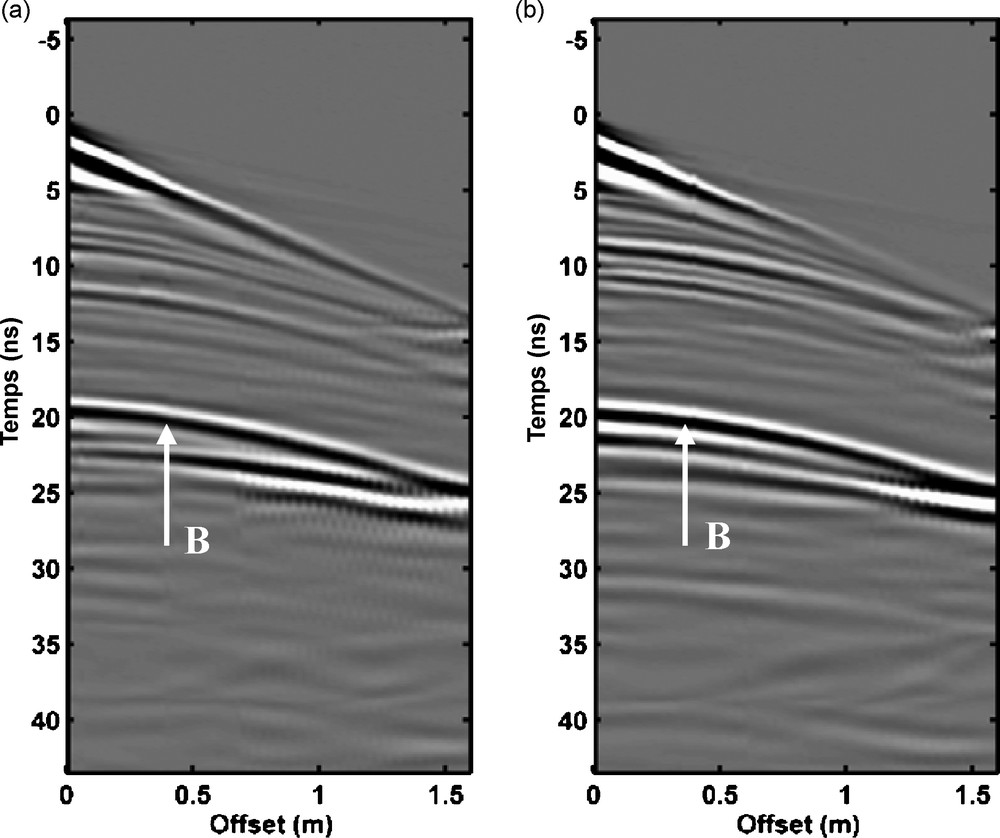
Two common mid points (CMP) obtained with a 900 MHz antenna on the dry sand in 2004: (a): CMP16 positioned in the middle of the profile P16; (b): CMP56 positioned in the middle of the profile P56. The strong reflection marked by B is the signal coming from the bottom of the sandbox.
Deux points milieux communs (CMP) acquis avec l’antenne de 900 MHz en 2004, dans le cas du sable sec : (a) : CMP16 ; (b) : CMP56.
We next injected water (240 L) up to a level of 26 cm from the bottom of the box (i.e., the water table was at a depth of 72 cm), and acquired (1 month later) another 3D data set. The quantity of injected water allowed us to estimate a porosity (φ) of 27%. This value is, however, smaller than that (39%) obtained in the first experiment [21]; nevertheless, this is an effective value and the discrepancy is probably due to the settling of the sand (about 2 cm) and the retention of water in the pores after drainage in February 2003. This value of porosity is consistent with the ones given by Banton and Bangoy [3] or Todd [28] for fine and calibrated sand.
3 GPR measurements after fuel injection
Afterwards, we injected 100 L of diesel fuel from the top of the sandbox above the water table. The injection point of the fuel (IPF) is shown in Fig. 1b. This fuel corresponds to the diesel found at a gas station and has a density of 0.84 g/cm3 [4], and therefore it is a light non-aqueous phase liquid (LNAPL). No settling of the sand has been observed after LNAPL injection. We repeated the same GPR acquisition scheme two more times:
- i) 12 days (in May 2004) after fuel injection;
- ii) 6 weeks (in June 2004) after fuel injection.
The relative dielectric permittivity or dielectric constant of LNAPL (κLNAPL) is considered constant and we, as many authors, (e.g. [7,8,26]) used a value of κLNAPL = 2. Note that the dielectric constant (κ) is dimensionless.
Fig. 4 shows the same profile T0 obtained with a 1200 MHz antenna before (with a water table at 72 cm depth) and after fuel injection. This profile is perpendicular to the Pxx profiles (crossing them in the middle; see Fig. 1) and goes over the steel pipe (at 50 cm depth) and the steel balls P1 and P2 (situated at 68 cm depth). The steel pipe is well imaged, while no diffractions coming from the steel balls P1 and P2 are observed, in both cases. The GPR data of Fig. 4, for the water table at 72 cm depth, do not show any clear reflections from the top of the saturated zone, which is the top of the capillary rise (of nearly 100% saturation) situated above the water table (e.g. [12]). This is a consequence of the existence of a transition zone above the saturated zone (e.g. [2]). Recall that in the transition zone the saturation decreases gradually, upward, from the saturated zone to the surface. Since the pipe is horizontal, we recorded it at a constant travel time of 9 ns (except for the semi-hyperbolic diffractions from the corners of the pipe) for the profile without fuel (Fig. 4a). By contrast, after fuel injection, the recorded travel time from the pipe is not constant. The travel time of the left corner of the pipe (at 9 ns in Fig. 4b) is shorter than the travel time of the right corner. Consequently, the area near the injection point (on the left of the pipe) has a higher propagation velocity than the area far from the injection point (on the right of the pipe). The dashed line indicates the reflections coming from the bottom of the sandbox, which is flat (nearly at 23 ns) in the case of Fig. 4a and considerably disturbed after fuel injection in Fig. 4b. The consequences of the pollution will be discussed in more detail in the following section.
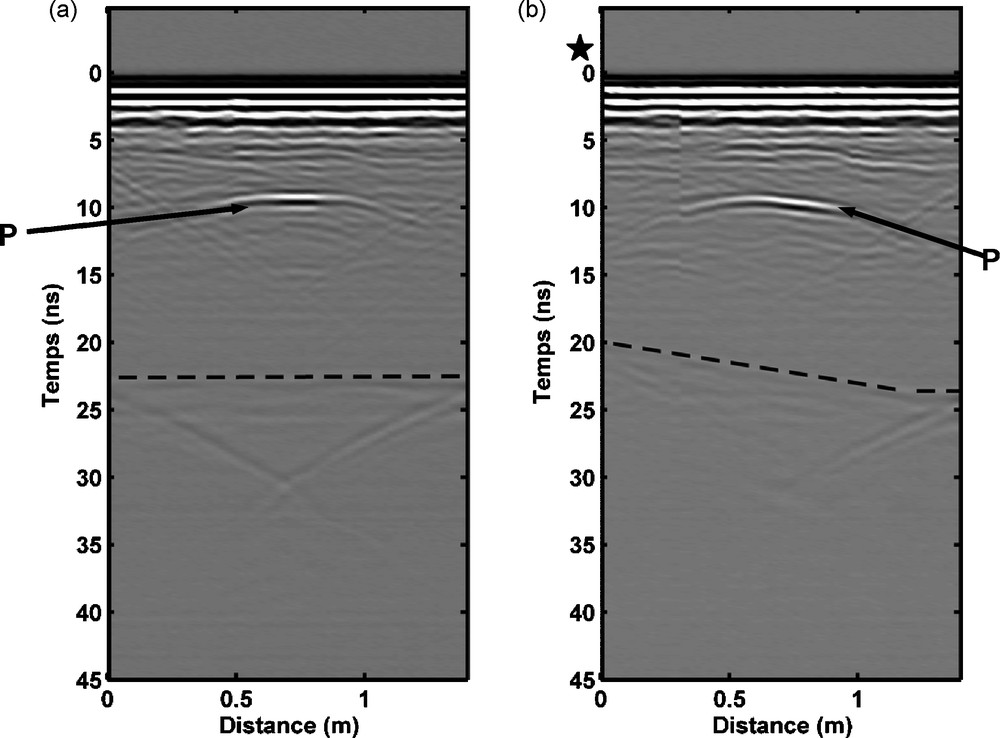
Data acquired on the sandbox (profile T0) with different saturation scenarios. (a): With a water table at a 72 cm depth; (b): After light nonaqueous-phase liquids (LNAPL) injection. P indicates the reflection from the steel pipe, the dashed line shows the reflection from the bottom of the sandbox and the star in (b) indicates the location of the fuel injection point.
Profils T0 : (a) : acquis avec un niveau d’eau à 72 cm de profondeur ; (b) : idem après l’injection du gasoil. P montre la réflexion du tube en acier, la ligne pointillée marque la réflexion du fond du bac. L’étoile en (b) indique l’emplacement approximatif du point d’injection du gasoil.
In Fig. 5, we compare two CMP acquired on both sides of the steel pipe (as in Fig. 3) after fuel injection. The CMP acquired in this situation are very different and the reflections from the bottom of the box on the CMP above P1 (cf. Fig. 5a) arrive earlier than the corresponding reflections on CMP above P2 (cf. Fig. 5b). There is a large variation of the average velocities of the GPR waves. The sandbox cannot be considered as homogeneous anymore in this condition.

The same common mid points (CMP) as in Fig. 3 acquired after fuel injection. (a): CMP16 situated above the steel ball P1; (b): CMP56 situated above the steel ball P2. The strong reflection marked by B is the signal coming from the bottom of the sandbox. For case (b), it arrives later than for case (a).
Les mêmes points milieux communs (CMP) que ceux montrés sur la Fig. 3 obtenus après l’injection du gasoil. (a) : CMP16 situé au-dessus la boule de pétanque P1. (b) : CMP56 situé au-dessus de la boule de pétanque. P2 La réflexion indiquée par B est le signal réfléchi du fond du bac. Dans le cas (b), cette réflexion arrive plus tard que dans le cas (a).
4 The consequences of the pollution on the GPR data
All the CO GPR profiles acquired 12 days (in May 2004) after fuel injection with a 1200 MHz antenna at the top of the sandbox do not show any clear reflections from the plume pollution. Therefore, in order to follow the lateral extension of the plume, we picked, in all profiles, the travel time of the reflections from the bottom of the box. Fig. 6 compares the results of the travel time (or the slowness) plots before and after fuel injection. Notice that the recorded time before injection (with a water level at a 72 cm depth) is not constant (Fig. 6a); a small difference (less than 2 ns) is observed between the zone situated near the water injection tap (with a recording time around 24 ns) and the zone situated far away from the tap (with a recording time around 22 ns). This is due to the non-homogeneous repartition of the water in the sandbox; the saturated zone is thicker near the tap than the zone far from the tap (see the left corner on the top of Fig. 6a). Hydrostatic equilibrium might not be completely reached at this state. We also observe three anomalies (in the middle in Fig. 6a) which are a consequence of the perturbation of the sandbox bottom reflection by the three pipes.
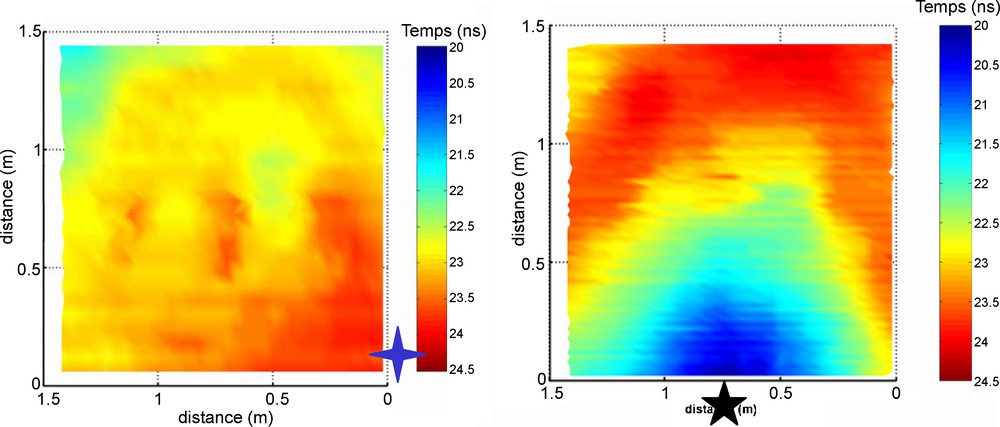
Recording time of the reflection from the bottom of the sandbox: (a): plan view with a water level at a 72 cm depth before fuel injection; (b): plan view after fuel injection. The colour scale is the same in all cases. The blue star in (a) is the location of the water tap (situated at the bottom of the box) and the black star in (b) is the location of the fuel injection point (situated on the top of the box).
Vues en plan du temps d’enregistrement du fond du bac, avec un niveau d’eau à 72 cm de profondeur dans le cas (a) avant l’injection du gasoil et (b) après injection du gasoil. L’étoile bleue en (a) montre l’emplacement du point d’injection de l’eau et l’étoile noire en (b) montre l’emplacement du point d’injection du gasoil.
Fig. 6b shows the result after fuel injection. The influence of fuel on the travel time is important and obvious. The area near the fuel injection point (in blue) is characterized by a higher velocity than the area situated far away from the injection point (in red). The travel times vary between 20 and 24.2 ns. We also note that the influence of the fuel is not the same over the entire sandbox; this might be due to an inhomogeneous repartition of the water before fuel injection. Such high velocities (near the fuel injection point) can be explained by the replacement (at least partially) of pore water by the fuel. It seems that the pore water has been pushed away and replaced by the fuel by a lateral flow. The water, replaced by fuel, moves and concentrates in the surrounding areas less (or not at all) polluted (see the top of Fig. 6b). Despite the efforts made to fill the tank with homogenized sand (without layering), we observe that the lateral migration of the fuel plume is non-uniform. This non-uniform spreading of fuel and/or trapping of zones of water along the free-product level is a likely explanation for the numerous GPR hyperbolae observed by Sauck [24], and Sauck et al. [25] in the plume during their field observations in Carson City Park, Michigan (Sauck, personal communication).
5 Discussion of the average relative dielectric permittivity
Relative dielectric permittivities were calculated from average velocities derived from direct ground wave and reflection hyperbolae on CMP profiles on the one hand, and from the diffraction hyperbolae (due to different objects buried inside the sand) observed on CO profiles on the other hand. The velocities estimated by using the direct ground waves represent, in fact, velocities from the surface of the sand. The mean precision of the velocities was between ±0.01 and ±0.02 m/ns. The average velocities were subsequently converted into dielectric permittivities. Details of this approach are presented by Loeffler and Bano [21].
The results for each data set (dry sand, with water at 72 cm depth, before and after fuel injection) are summarized in Table 1. The values of the permittivities calculated from the measurements performed in 2002 are also shown in brackets. From this Table 1, we note that the values of the permittivities estimated in 2002 and 2004 (see the two first columns) are very close for the sand down to a depth of 50 cm. By contrast, the values of κbottom (the average over the entire height of the box) are different. For instance, in the first column, κbottom has the values 6.7 (estimated in 2002) and 7.3 (estimated in 2004), respectively. This has been discussed previously and confirmed by Fig. 2. While the values of the permittivities after fuel injection are estimated on two different points P1 and P2, the value of κbottom estimated at P1 is very different from the one estimated at P2. Remember here that the distance between the points P1 and P2 is 80 cm.
Constantes diélectriques moyennes du sable pour différentes profondeurs avant et après injection du diesel. Les valeurs entre parenthèse ont été obtenues en 2002.
| Average dielectric permittivity | Dry sand | Water at 72 cm depth | With fuel (at P1) | With fuel (at P2) |
| κ surf | 4.2 (4.6) | 4.6 (4.6) | 4.6 | 4.6 |
| κ 38 | 4.3 (4.6) | 4,6 (4.6) | 4.6 | 4.6 |
| κ 50 | 4.3 (4.6) | 5.3 (5.5) | 5.3 | 5.8 |
| κ bottom | 7.9 (6.7) | 11.1–13.4 (11.4) | 9.4–10.2 | 12.5–13.4 |
6 Evolution of the pollution in time
We repeated the same GPR measurements 45 days (in June 2004) after fuel injection and observed an unexpected and very clear GPR reflection situated in the vadose zone above the water table (far away from the fuel injection point). Fig. 7 shows the results comparing the GPR data acquired at different periods. We compare the same profile T0 obtained with a 1200 MHz antenna; the first one is acquired in May 2004 (Fig. 7a) and the second in June 2004 (Fig. 7b). In Fig. 7b, we remark that a clear reflection appears (indicated by R) at the end of the profile. It is situated between 1 and 1.4 m laterally, and at 8 ns depth (in time).

Constant offset (CO) profiles acquired at different periods. (a): profile T0 acquired in May 2004; (b): profile T0 acquired in June 2004; (c): profile P56 acquired in May 2004; (d): profile P56 acquired in June 2004. The diffraction from the ball P3 is marked by the white arrow and the reflection observed in June 2004 is marked by R. The black arrows on the top of each section indicate the intersection between profiles.
Profils en offset constant (CO) acquis pendant différentes périodes. (a) : profil T0 acquis en mai 2004 ; (b) : profil T0 acquis en juin 2004 ; (c) : profil P56 en mai 2004 ; (d) : profil P56 en juin 2004. La diffraction de la boule de pétanque P3 est marquée par la flèche blanche et la réflexion observée en juin 2004 est marquée par R. Les flèches noires en haut indiquent l’intersection des profils.
To confirm the presence of this reflection we also show in Fig. 7 the profile P56 which is perpendicular to T0 and goes over P3 (the steel ball at 38 cm depth), P2 (the steel ball at 68 cm depth) and the clay cake A (see also Fig. 1). In Fig. 7d (acquired in June 2004), we observe the same reflection (marked by R) which is flat and continuous over the entire profile. This reflection is certainly due to a dielectric permittivity contrast between two layers within the vadose zone. Loeffler [20] compared the reflection coefficients of the steel ball P3 and the horizon R for the signals marked by a vertical dashed line in Fig. 7d and found that they have, approximately, the same negative value. Therefore, the origin of this reflection might be from the contact between two zones: a high-saturation zone underlying a low-saturation zone, which gives a negative reflection coefficient. A possible mechanism for this to happen is that the fuel coating the sand grains may have effectively displaced the water from the pores such that a dielectric permittivity contrast exists (e.g. [1]), far away from the fuel injection point, within the vadose zone. A new hydrostatic equilibrium is achieved for this condition of the sand. Other laboratory and field GPR studies (e.g. [10,11,17]) have also shown the displacement of the water by the fuel through a lateral flow. In the next Section, we try to model by FDTD the contact between these zones. We notice here that no such reflection is observed in the profile of Fig. 7c acquired in May 2004. The black arrows on the top of each figure indicate the intersection between the profiles T0 and P56.
7 Modelling of GPR data
The synthetic profiles were computed using the two-dimensional (2D) forward-modelling code developed by Girard [14]. The modelling is based on a finite difference time domain (FDTD) numerical scheme as proposed by Yee [29]. The code works on dispersive and inhomogeneous media with conductive losses. The soil dispersion is modelled by exponential functions in time of the Debye or Davidson-Cole types, which are incorporated into the FDTD scheme. The code uses the piecewise-linear recursive convolution (PLRC) technique, presented by Kelley and Luebbers [19], and is extended to the power-law functions or non-exponential functions in the time domain for the dielectric response. The perfectly matched layer is used as an absorbing boundary condition to simulate an open space.
To model the profile T0, we assumed a non-dispersive medium, which is justified by the fact that the fuel is a non-conductive material and has a low value of permittivity (κfuel = 2) and a high quality factor (e.g. [30]). The model used is shown in Fig. 8 and consists of sand (in orange) which is divided into three layers based on their fluid content; dry sand (κsand = 4.6 and h = 32 cm), transition zone (32 cm thick, in which the saturation decreases gradually upward) and saturated sand (35 cm thick, water table and capillary rise). The saturated sand with fuel (κsf = 3.8) is represented in yellow, the mixture of sand/air/fuel (κsaf = 4) in black, the mixture of sand/water/fuel (κswf = 15) in blue. The steel pipe (κsteel = 81) and the soil (κsoil = 4), are presented in red and brown, respectively. This conceptual model corresponds to a schematic distribution of the fuel concentration (below a point-pollution source) over a water table as described by Fetter [13] and Sauck [24].
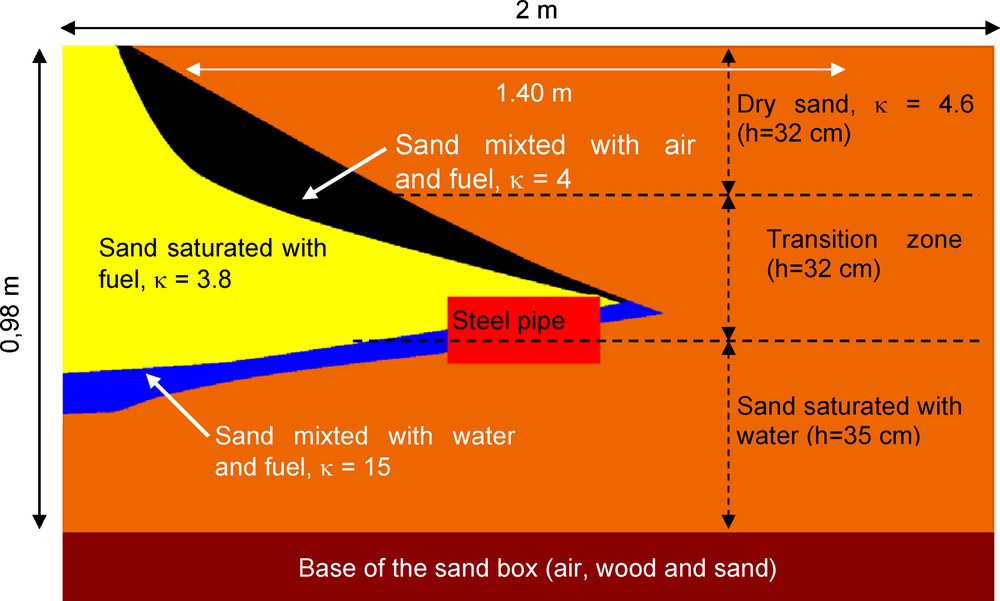
Conceptual model used for the simulation of profile T0 12 days (in May 2004) after fuel injection. The different coloured layers are explained in the text.
Modèle conceptuel utilisé pour la simulation du profil T0 12 jours (en mai 2004), après l’injection du gasoil. Les couches de différentes couleurs sont expliquées dans le texte.
To calculate the permittivity of the mixtures, we incorporated into the FDTD code the complex refractive index method (CRIM) for three- or two-phase medium (e.g. [22]) as follows:
| (1) |
| (2) |
Fig. 9 shows the modelled profile and the real profile T0 12 days after fuel injection. We observe that the modelling reflections from the pipe (P) and bottom (B) fit well with the real data. Nevertheless, some other signals, which are not visible in the real data, are observed in the synthetic profile. This is due to the discontinuities (interfaces) between different “layers” (zones) in our model of Fig. 8. See, for example, the passage from the layer of permittivity κ1 = 3.8 to the layer of permittivity κ2 = 15. However, the passage between “layers”, during the lateral fuel infiltration, is progressive and not as abrupt as represented in our model.
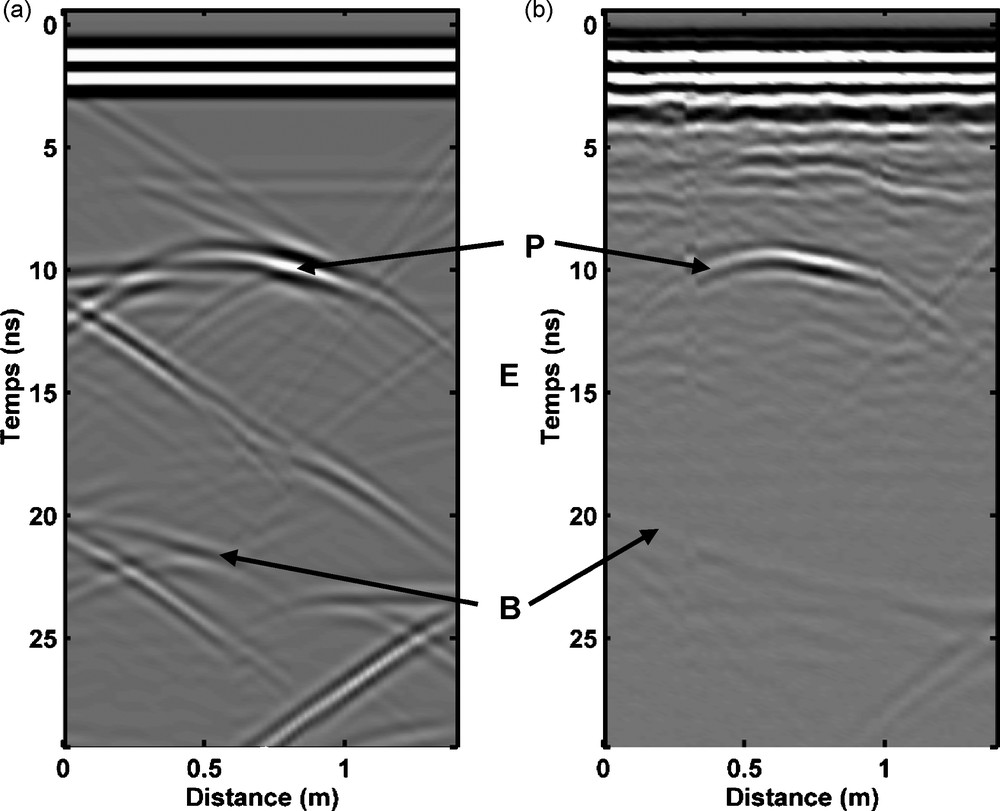
Profile T0 acquired 12 days (in May 2004) after fuel injection. (a): modelled profile and; (b): real profile. P and B indicate the reflection from the pipe and bottom, respectively.
Profil acquis 12 jours (en mai 2004) après l’injection du gasoil. (a) : profil modélisé et ; (b) : profil réel. P et B sont la réflexion du tube en acier et du fond du bac, respectivement.
In order to verify our hypothesis about the origin of the reflection Horizon R, observed 45 days after fuel injection, we ran one more time the modelling of profile T0. We used the same model as in Fig. 8, but with an interface (marked by a green line situated 14–16 cm above the initial saturated zone) separating two zones: a highly saturated sand (κ = 45) underlying a less saturated sand (see Fig. 10). The result of this modelling is shown in Fig. 11a from where we notice that the modelled reflection R fits well (in time and amplitude) with the same reflection observed in the real data of Fig. 11b. The same remarks discussed in the case of Fig. 9 stand for the case of Fig. 11.
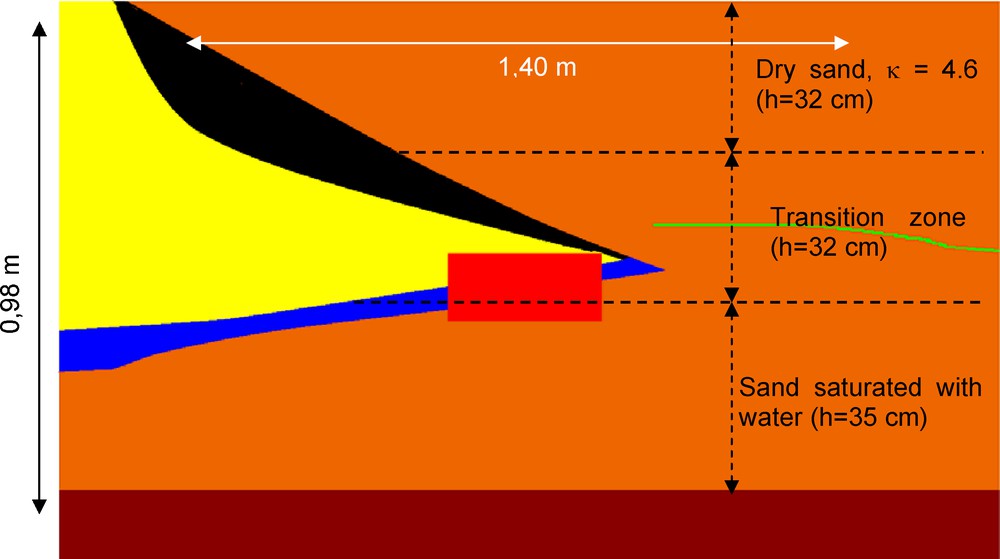
Model used for the simulation of profile T0 45 days (in June 2004) after fuel injection. The interface in green indicates the top of a layer of highly saturated sand.
Modèle utilisé pour la simulation du profil T0 45 jours (en juin 2004) après l’injection du gasoil. Le niveau de sable plus saturé en eau est en vert.
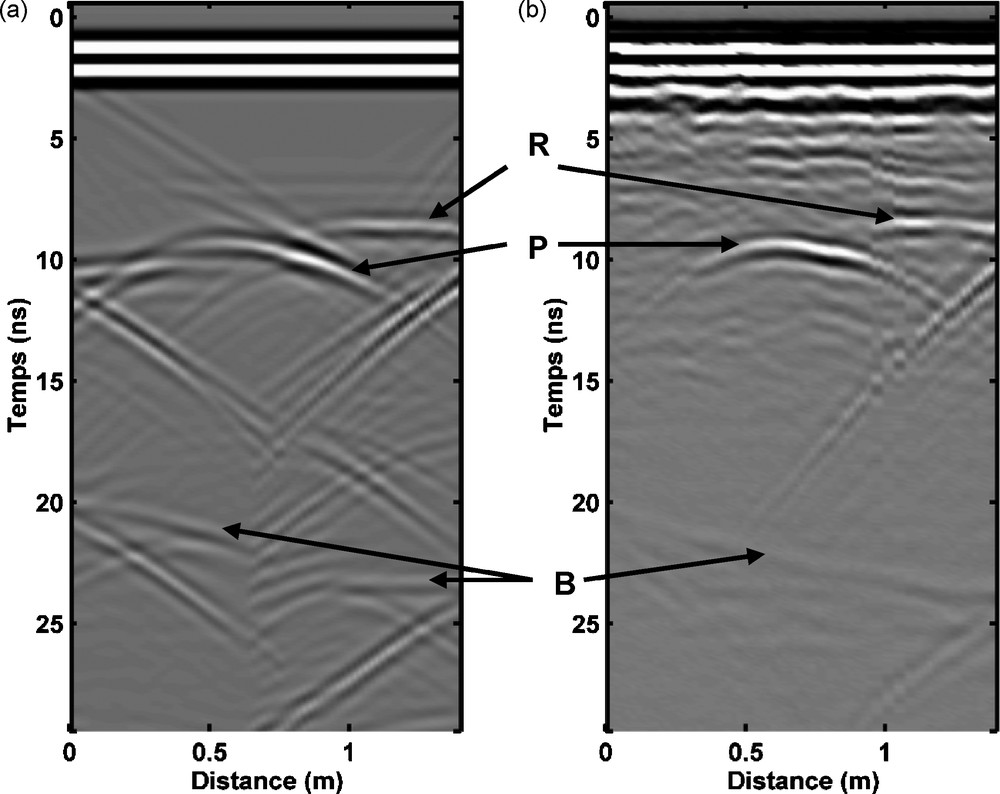
Profile T0 acquired 45 days (in June 2004) after fuel injection. (a): modelled profile and; (b): real profile. P and B indicate the reflections from the pipe and bottom, respectively. R indicates the “unexpected reflection” observed in June 2004.
Profil T0 45 jours (en juin 2004) après l’injection de gasoil : (a) : profil modélisé et ; (b) : profil réel. P et B sont la réflexion du tube en acier et du fond du bac, respectivement. R est l’interface apparue entre mai et juin 2004, liée au rééquilibrage hydrostatique.
8 Conclusion
A 4D GPR survey was carried out on a sandbox contaminated with diesel fuel in order to follow the extension and the evolution of the fuel plume in the sand. The GPR data do not show any clear reflections from the plume pollution; however, GPR velocities are extremely affected by the presence of the fuel and the main changes are on the travel time anomalies. The lateral extension of the plume pollution in the vadose zone is shown by comparing the plots of travel times (or slowness) of the reflection from the bottom of the sandbox, before and after fuel injection. The differences between the two plots are obvious and the influence of the fuel is not the same over the entire sandbox. The zone situated away from the injection point shows an increase in travel time, which implies a low velocity anomaly. The pore water has been replaced by the fuel through lateral flow by creating a highly saturated zone far from the fuel injection point. Some weeks later, we repeated the same GPR measurements and observed a nice reflection situated on the opposite side of the fuel injection point. Finally, the forward FDTD modelling method in combination with dielectric mixing models gave theoretical support to understand and determine the physical characteristics and the volume of the contaminated sand and explain the origin of the observed reflections from the contaminated vadose zone. A next logical step is to combine the GPR with suitable laboratory measurements of fluid content in the sandbox experiment. The quantitative parameters given by GPR measurements can be used to constrain a lateral flow model, which requires many unknown parameters. In order to follow the lateral flow of the plume, a joint GPR and lateral flow modelling is necessary.
Acknowledgments
One author (O.L.), during his thesis (2002–2005), has been financed by the European Commission under the HYbrid Geophysical technology for the Evaluation of Insidious contaminated Areas (HYGEIA) project. The GPR equipment was funded by université Louis-Pasteur and the INSU/CNRS program. We thank the Guest Editor Ghislain de Marsily as well as reviewer William A. Sauck and a second anonymous reviewer for their constructive comments and helpful suggestions that were much appreciated.


