1 Introduction
Associated plutonic intrusions or volcanic emissions within the same province frequently show composition discontinuities (all compositions are not seen equally), on a local or a larger scale (see, for example, Halmlyn and Keays, 1979; Leblanc and Ceuleneer, 1992). One also very often observes bimodal distributions; for instance for the volcanic rocks, on one side the basaltic terms, and the other side the felsic terms (trachytes, phonolites) whereas the intermediate compositions (andesites) are very little represented (for the equivalent plutonic rocks: gabbroic rocks on one side, granitic rocks on the other, with the relative scarcity of intermediate rocks such as quartz bearing diorites or syenites) (Baker, 1968; Bonnefoi et al., 1995; Chayes, 1963; Clague, 1978; Daly, 1925; Gagnevin et al., 2003; Marsh, 2002)). One speaks of the Daly gap for the absence of intermediate terms in the volcanic series of oceanic islands, but the situation is similar in the continental series. In the present article, we wish to explain these features, and particularly the bimodality of the rock compositions, by way of simple models.
Many models have already been proposed for the first understanding of the variety of the plutonic and/or volcanic rock compositions of the same province. The fractional crystallization model is the best example. It suffers important limitations: in the models that are derived from it, nonlinear (composition dependent) chemical partition coefficients between the solid and the liquid are not taken into account (the models are adapted to trace rather than major elements); the relative displacement between the solid and the liquid, and the possible chemical exchanges along this displacement are not taken into account: there is no space variable. This model can be developed within larger models. For convenience, we will distinguish three classes of processes: processes of chemical exchanges between liquids and solids; processes of thermal transfer and solidification; processes of relative movement between the solid and the liquid (in relation to tectonics, or to the density differences between the solid and the liquid). Each one of these classes deserves more thorough development (see (Baker and Mcbirney, 1985; Bons et al., 2004; Godard et al., 1995; Jaupart and Tait, 1995; Jellinek and Kerr, 2001; Kuritani, 2004), for example).
However, the models remain generally specialized in each of the three classes of processes. Coupled models exist, but they only relate to partial aspects of the phenomena, their variety being so large. Also, in the end, the models do not allow a satisfactory answer to the above questions (appearance of bimodality and of composition discontinuities). Many explanations were proposed (see previous papers for example) and we will not discuss them in detail. They generally take us away from the elementary phenomena of fusion/solidification, relative displacement and chemical exchange between the solid and the liquid, and utilize some various additional phenomena (multiple injections, contamination in an open system etc.). In this work, we would like to go back to the elementary phenomena, deciding to consider them together. This can only be done at the price of a great simplification of each of them, but the result is a fertile overall picture. In particular, these three phenomena will reduce to two independent dimensionless parameters. These will enable us to discuss the important types of behaviour of the systems. We will take as an example that of the evolution of a closed magmatic chamber. This will be a vertical column containing the magma (with or without some solids) at time zero, along one space dimension, the vertical axis (Fig. 1). The other case of an open system is simpler, in that it corresponds to the subsystem of a larger system, and will also be discussed briefly. The three classes of phenomena are simplified as follows:
- • Solidification is imposed by the thermal situation of the chamber, in particular the temperature gradient at the top. Without modelling all the heat transfers, we will consider that we are able to define a solidification rate q: this is the solid/solid + liquid proportion production per unit of time. This rate can be variable from one point to another of the chamber (one can restrict the solidification zone to the top of the chamber, or give any other conceivable evolution in space and time).
- • Relative movement between the solid and the liquid is described by its velocity: once the solid is formed, we will consider that it can go down and settle at the bottom because of the density differences. The velocity is a function of temperature (viscosity) and of the solid abundance. Other modes of relative displacement can be generated by the action of internal or external tectonics (filter press phenomenon for example), and/or when the solid crystallizes on the walls of the chamber. On the whole, we will consider that we are able to write a law for the relative movement velocity between the solid and the melt.
- • Chemical equilibrium between the solid and the melt may finally more or less achieve; we will consider that the kinetics law is governed by departure from equilibrium. The equilibrium partition law between the solid and liquid will be supposedly known in an analytical form. Importantly, this law can be nonlinear. By simplification, we will consider first the case of one independent chemical component.
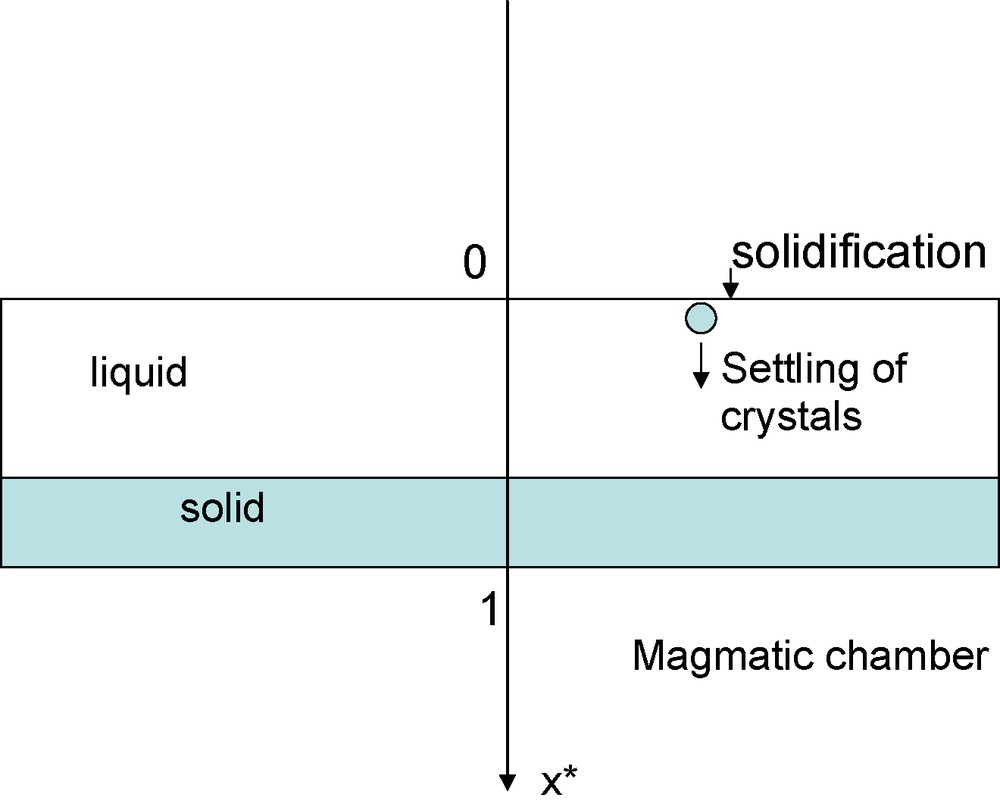
Schematic view of a magmatic chamber: the vertical axis is the dimensionless x-axis used in the text (variation between 0 and 1; it corresponds to thicknesses of several hundreds of meters for natural chambers). The solidification may take place in the upper part of the chamber; the crystals formed subsequently settle and fill the bottom of the chamber (solid).
Schéma d’une chambre magmatique. L’axe vertical représente la profondeur sans dimension figurée par la variable x, variant entre 0 et 1 (correspondant à des épaisseurs de quelques centaines de mètres pour des chambres naturelles). La solidification peut se faire dans la partie supérieure de la chambre ; les cristaux formés peuvent ensuite se sédimenter et remplir le bas de la colonne (partie solide).
In this approach, we took as a starting point the chromatographic model, as it is used for the understanding of metasomatic rocks; it calls upon similar simplifications for what relates to relative movement and chemical exchange phenomena. A major characteristic of this model is to account for the appearance of composition discontinuities, i.e. of plurimodal distributions of the crystallized rock compositions. We already proposed in a preliminary way its application to magmatic rocks, in particular in open systems, as also did other authors (for example Baker and Mcbirney, 1985; Boudreau, 2003; Godard et al., 1995; Guy, 1993; Guy, 2005; Hauri, 1997; Navon and Stolper, 1987; Sedqui and Guy, 2001). We want to give a more general approach (use of dimensionless parameters etc.) and extend it to the study of a closed magmatic chamber. We will show that, under relatively simple physical assumptions, the crystallization products can present a non-homogeneous distribution, in particular bimodal, starting from a homogeneous liquid. We present an abstract model and give the indications for applying it to some particular systems.
2 Modelling and defining dimensionless parameters
2.1 Variation of the solid/liquid proportion by solidification and sedimentation
The chamber, considered as a vertical column, is modelled along one space dimension. The axis is directed to the downward direction. The abscissa is noted x, the origin is taken at the higher point of the chamber. The total height is noted h; ps(x, t) or p(x, t) represents the solid volumic proportion (also called compactness) at position x and time t. The liquid or melt volumic proportion is thus pm = 1–p. Solids and liquids are incompressible. The hydrodynamic aspect of sedimentation is taken into account through the Richardson-Zaki law (Richardson and Zaki, 1954): U = U0(1–p)α, where U0 is the Stokes velocity, and α = 5. For p values higher than 0.7, the sedimentation velocity is almost zero. This accounts for what is observed in experimental work and nature. The Um liquid velocity is obtained by writing the total volume conservation. At any point, solid phase and liquid phase fluxes are equal and have opposite signs:
The solidification rate is represented by a function qs(x) or q(x) for the creation of solid volume per unit of total volume and unit of time. The x-dependency accounts for the fact that the solidification speed depends on temperature, and so on depth. In order to separate the intensity of the solidification process and its space variation, we will write q in the form of the product of a constant and a space function. So q (x) = q0.s(x); s(x) will be a simple function of x. In certain cases, s might also depend on p and t. The unknown function is p(x, t) and the conservation equation of the solid phase is written as:
The equation can be transformed by considering dimensionless time and space coordinates t* and x*.
It is then written in the form:
| (1) |
Initial and boundary conditions: the initial condition will be p (x, 0) = 0: at t = 0, the chamber is filled with magma, which then solidifies gradually, giving place to sedimentation. The conditions at top and bottom of the chamber are zero matter flux. It is considered that the bed of the settled solid has a null porosity, p = 1 (and thus U = 0). Other choices would be possible and lead to change space and time scales.
2.2 Chemical exchanges
One independent chemical component is taken into account, its concentration is noted C in the solid phase and Cm in the melt (kg/m3 of solid or liquid). The rate of variation of the chemical component is supposed to be proportional to the surface of the solid-liquid contact (reaction surface), and to a function G (Cm, C) describing the departure from equilibrium, the dimension of which is the same as for C. For a solid volume V with reaction surface Sr:
Solidification by itself also generates a chemical transfer from the liquid phase to the solid phase, without any chemical reaction, the rate of corresponding change is equal to qCm. The conservation equations of the chemical component are finally written as:
Time, space, the sedimentation velocity are transformed to dimensionless parameters in the same way as previously. The dimensionless concentrations are defined by ratios to the densities
The conservation equations are then written as:
| (2) |
This makes a second dimensionless coefficient appear: B = ahK/U0, the ratio of the reaction velocity to the settling velocity (Damköhler number). The system is finally governed by two dimensionless parameters, A and B, which reflect the ratios of preponderance between the three phenomena that come into play: sedimentation, solidification and chemical reaction. There remain however “form factors” or adjustable functions which are the space function s*(x*) and the isotherm g*(C*). One will note that, in order the preceding equations are consistent, the equality of ρm and ρs is implicit: in a first step we have assumed that there is no volume effect associated to solidification. Dimensionless velocities U* and are obtained by dividing corresponding velocities by U0.
3 Ranges of values for the useful physical parameters, form of the laws used
We need to define ranges and typical values for the principal physical parameters in the equations. Those are summarised in Table 1. We used various works (see already quoted works and (Jellinek and Kerr, 2001; Kirkpatrick et al., 1976; Schwindinger, 1999; White, 1997)) together with some semi-quantitative reasoning. The variety of natural situations is great (the preferred parameters chosen match the expertise of the authors) and other values of the parameters could be considered. For instance, the densities chosen refer mostly to mafic systems while felsic melts can be lighter than 2.6; the bubble effect could also be taken into account. The law chosen for the spatial distribution of solidification is given in Fig. 2 a and the isotherm chosen for the numerical experiments is given in Fig. 2b. On the whole, the two dimensionless parameters A and B can vary between 0.1 and 10 for the most current geological situations, but the extreme values are in the bracket 10−4, 104 or even 10−7, 107.
Liste des principaux symboles utilisés et valeurs typiques des paramètres correspondants.
| Symbol | Unit | Meaning | Range of values | Typical value |
| a | m−1 | 3/r | 102–106 | 103 |
| A | – | q0h/U0 solidification/sedimentation rates ratio | 10−4–104 | 10−1–100 |
| B | – | ahK/U0 chemical kinetics/sedimentation rates ratio | 10−4–104 | 100–101 |
| C or Cs | kg/m3 of solid | Concentration of chemical component in solid | 0–3 × 103 | |
| C m | kg/m3 of melt | Concentration of chemical component in melt | 0–3 × 103 | |
| C * | – | C/ρS dimensionless concentration in solid | 0–1 | |
| – | C/ρm dimensionless concentration in melt | 0–1 | ||
| D m | m2.s−1 | Liquid molecular diffusion coefficient | 10−8–10−12 | 10−10 |
| D s | m2.s−1 | Solid molecular diffusion coefficient | 10−12–10−16 | 10−14 |
| g | kg/m3 of melt | g(C) isotherm function | 0 to 3 × 103 | |
| g * | – | Dimensionless isotherm function | 0–1 | |
| G | kg/m3 of melt | G(Cm,C) = Cm – g(C) departure from chemical equilibrium | 0–3 × 103 | |
| h | m | Height of magmatic column | 30–300 | 102 |
| K | m.s−1 | Kinetics constant for the chemical exchange between solid and liquid | 10−7–10−14 | 10−13 |
| p or ps | – | Volumic proportion of solid (compactness) | 0–1 | |
| p m | – | Volumic proportion of melt = 1–p | 0–1 | |
| q or qs | s−1 | Rate of solid proportion production q = q0s(x) | 10−7–10−14 | 10−12 |
| q 0 | s−1 | Average rate of solid proportion production | 10−7–10−14 | 10−12 |
| r | m | Radius of the mineral grains | 10−6–10−2 | 10−3 |
| s | – | s(x) space function for solidification rate | 0–1 | |
| s * | – | Solidification rate space function for dimensionless abscissa | 0–1 | |
| S g S r | m−1 | Geometric/reaction surface per solid volume | 0–106 | 102 |
| t | s | time | 1010–1013 | 1011 |
| t * | – | U0t/h dimensionless time | 0–1 | |
| U or Us | m.s−1 | velocity of crystals | 10−4–10−9 | 10−7 |
| U 0 | m.s−1 | Stokes velocity (isolated crystals) | 10−4–10−9 | 10−7 |
| U m | m.s−1 | Melt velocity | 10−4–10−9 | 10−7 |
| V | m3 | Volume of solid | ||
| V1, V2 | – | Intra-class variance (bimodality criterion) | ||
| x | m | Depth abscissa in magmatic chamber | 0–300 | |
| x * | – | x/h dimensionless depth in magmatic chamber | 0–1 | |
| α | – | Exponential factor for the velocity law | 5 | |
| β | – | Coefficient for reactive surface Sr/Sg = (1–p)β | 0.3 | |
| ρ m | Kg.m−3 | Liquid density | 2.6–3 × 103 | 2.9 × 103 |
| ρ S | Kg.m−3 | Solid density | 2.9–3.2 × 103 | 3 × 103 |
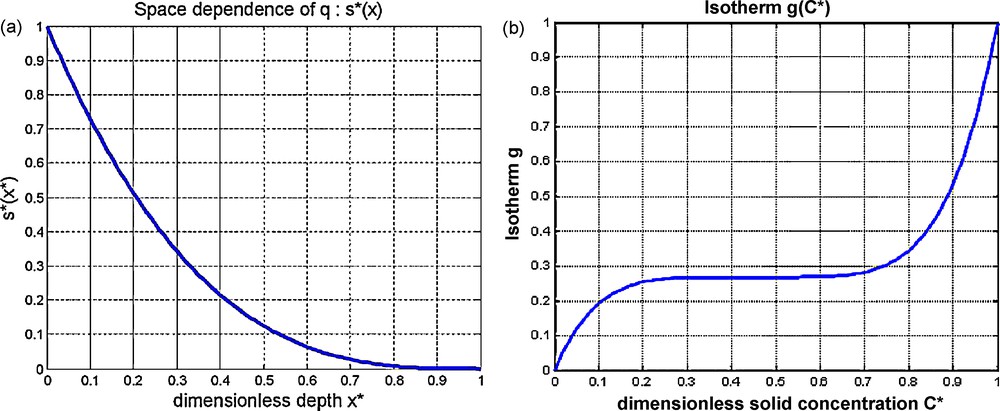
a: space function for dimensionless solidification s*(x*); this function intervenes as a factor to the speed of solidification q0 expressed in production of proportion of solid p. Solidification is maximum here at the top of the chamber (s* = 1 for x* = 0) and null at bottom (s* = 0 for x* = 1); b: dimensionless isotherm . The isotherm has two parts, representing each a solid phase, separated by a horizontal plateau corresponding to equilibrium between the two solids.
a : fonction d’espace s*(x*) pour la solidification, en fonction de la variable sans dimension x*. Cette fonction intervient en facteur de la vitesse de solidification q0 exprimée en termes de production de proportion de solide p. La solidification est ici maximale au sommet de la chambre (s* = 1 pour x* = 0) et nulle en bas (s* = 0 pour x* = 1) ; b : isotherme sans dimension . L’isotherme a deux parties, représentant chacune une phase solide, séparées par un plateau horizontal représentant l’équilibre entre les deux solides.
4 Numerical simulation and results
The sedimentation Eq. (1) and the system of chemical exchanges (2) are both solved numerically by a “finite volume” type method. A dissipative numerical scheme of Lax-Friedrich type was adopted in order to avoid as much as possible the numerical oscillations in the vicinity of the shocks. Non-linearities are treated implicitly for the sedimentation equation, explicitly for the reaction equations. The complete solidification of any zone located above the sedimentation front was prohibited, so that the front is never blocked. The two adjustable functions s* et g* were chosen as shown in Fig. 2a and b. The two dimensionless numbers A and B are chosen within the interval [0.1–10]. The initial condition , was fixed at 0.8 (an extreme value of 0 or 1 would not generate any chemical differentiation effect). A typical evolution of the compactness and composition profiles at three times are given in Fig. 3a–c, for A = 1 and B = 10. The distribution functions of the concentration in the solid at the end of the process are then drawn (obtained by kernel smoothing of the histograms) and we observe, in this case, a conspicuous bimodality in the distribution of the concentrations in the solid, whereas the initial condition in the magma was perfectly uniform. The profiles obtained, for various values of A and B (for the same s* and g* functions), give an idea of the various distributions of concentration: uni- or bimodality according to the values of A and B, for the selected functions s* and g* (Fig. 4a). The corresponding bimodality is shown in Fig. 4b. In Fig. 4c, an example of rather uniform distribution of concentration for A = 0.1, B = 1 is shown. Going from dimensionless time to physical time, one sees that the end of evolution (for values of t* of several tens of units) corresponds to times of thousands to hundreds of thousands years for typical values of the chambers.
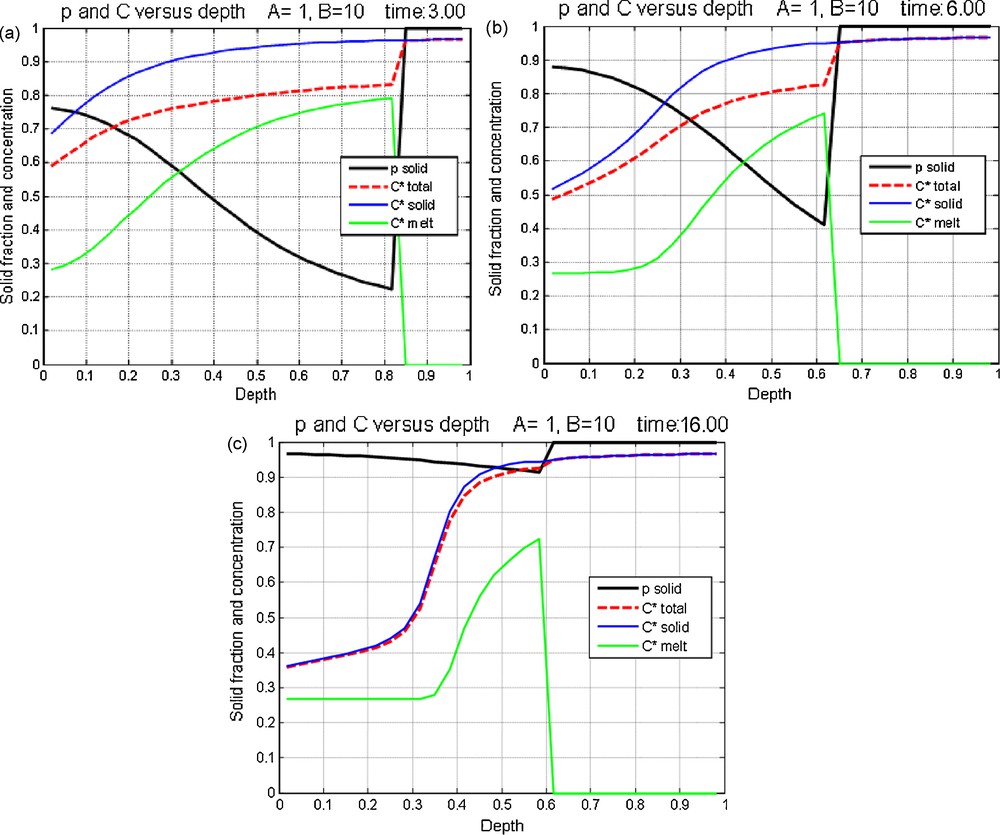
a, b, c: concentration profiles as a function of depth for various variables at different times. The solidification rate and the isotherm are given in Figs. 2a and 2b. The dimensionless parameters are A = 1 and B = 10 respectively. The black line depicts the solid proportion: sedimentation is observed at the bottom of the chamber, solid front raises with time. The initial condition is homogeneous with Cm = 0.8. The overall shape of the isotherm is concave, the solid is enriched with respect to the liquid. One observes an impoverishment of the solid (blue curve) when going up, with an inflection representing a discontinuity of composition between two plateaus. The green curve represents the composition of the liquid and the red curve that of the liquid + solid total. If the system is quenched, this last curve will give the final solid composition.
a, b, c : profils de différentes variables en fonction de la profondeur à différents temps. La loi de vitesse de solidification et l’isotherme sont donnés sur les Fig. 2a et b. Les paramètres sans dimension ont pour valeurs A = 1 et B = 10 respectivement. Le trait noir représente la proportion de solide p ; la sédimentation s’effectue au bas de la chambre, le front du solide remonte en fonction du temps. La condition initiale représente une concentration homogène avec Cm = 0,8. La forme d’ensemble de l’isotherme est concave, le solide est enrichi par rapport au liquide. En remontant, on observe un appauvrissement du solide (courbe bleue), avec une inflexion représentant une discontinuité de composition entre deux plateaux. La courbe verte représente la composition du liquide et la courbe rouge celle du total liquide + solide. Si le système est figé, cette dernière courbe donnera la composition du solide final.
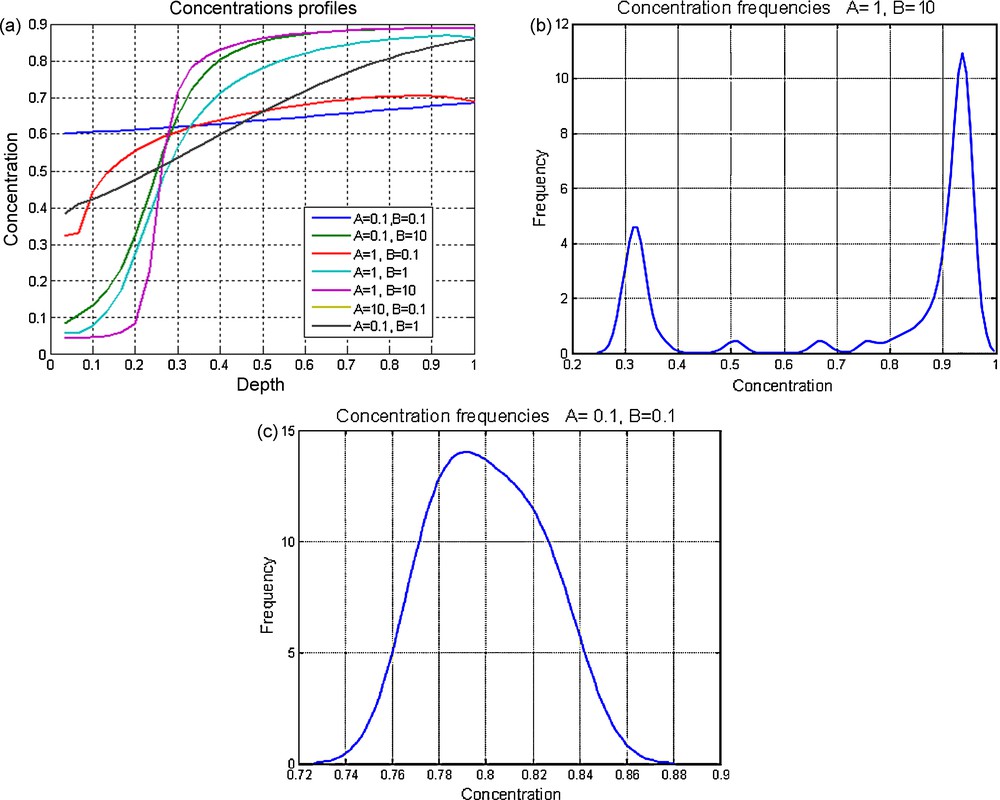
a: various types of spatial trends for the composition of the solid within the chamber at the end of the evolution, for various values of dimensionless parameters A and B: for the flat profile, one composition is selected; for the profile with constant slope, a range of compositions with same probability is selected; for the two-plateau profiles, the compositions are separated into two modes; b: frequency spectrum giving the proportions of the various compositions of the solid within the chamber (preceding experiment, A = 1, B = 10). There is a strong bimodality marked by two peaks, one close to C = 0.9 and the other close to C = 0.3; c: example of uni-modal spectrum (one rock composition, corresponding to that of the initial magma, is selected) for the values A = 0.1 and B = 0.1 of the dimensionless parameters.
a : différents types d’évolution spatiale pour la composition du solide dans la chambre à la fin de l’évolution, pour différentes valeurs des paramètres sans dimension A et B ; pour le profil plat, une composition est sélectionnée ; pour le profil avec une pente constante, une gamme de compositions équiprobables est sélectionnée. Pour le profil à deux plateaux, les compositions sont séparées en deux modes ; b : spectre de fréquences donnant les proportions des différentes compositions du solide dans la chambre (pour l’expérience précédente avec A = 1, B = 10). Il y a ici une forte bimodalité marquée par deux pics, l’un de composition proche de C = 0,9 et l’autre de composition proche de C = 0,3 ; c : exemple de spectre unimodal (une seule composition de la roche, correspondant à celle du magma initial, est sélectionnée) pour les valeurs A = 0,1 et B = 0,1 des paramètres sans dimension.
4.1 Visualization of the bimodality zones
In order to visualize the appearance of bimodality according to parameters A and B, we defined a “bimodality criterion”. A classification is done between two classes by a traditional method minimizing the intraclass variance. One can then propose as a criterion a real number involving the intraclass variances V1 and V2 and the distance between the centres of each class, C1 and C2. One does not take into account the ratio of the populations. Thus for example: criterion = |C1–C2|*(exp(–V1) + exp(–V2)). This gives the map in Fig. 5 (Log to the base 10), where the bimodality is very marked when the criterion goes close to or exceeds 1, in agreement with the first look at the preceding graphs. We see that the bimodality is obtained for A = solidification/sedimentation < 1 (the log is negative) and B = reaction/sedimentation > 1, or in other words, solidification < sedimentation < reaction.
Map of the values of dimensionless parameters A (solidification/sedimentation) and B (reaction/sedimentation) allowing the chemical composition bimodality of crystallized rocks. The zones of marked bimodality are in red. Bimodality is acquired in the condition: chemical reaction rates > sedimentation rates > solidification rates.
Carte des valeurs des paramètres sans dimension A (solidification/sédimentation) et B (réaction/sédimentation) permettant une bimodalité de composition des roches cristallisées. Les zones de forte bimodalité sont en rouge. La bimodalité est obtenue dans les conditions suivantes : vitesse de réaction chimique > vitesse de sédimentation > vitesse de solidification.
5 Discussion
Our main result is as follows: starting from very uniform initial conditions, the solidified rocks within the magmatic chambers may present a bimodal distribution of their chemical composition. This is understood within a modelling which takes into account the simultaneous action of the sedimentation, solidification and chemical reaction phenomena. The hyperbolic character of the equations plays an important part: the dynamic process of reaction is modelled in the same time as the relative movement of the solid with respect to the liquid. Even if the model remains elementary for the three phenomena, the mere coupling made it possible to clarify the appearance of bimodality. In order to illustrate the results, a particular choice of isotherms and of the space variation of the solidification rate was taken, but bimodality is generally obtained for nonlinear isotherms, due to the role of major elements in crystallization. The appearance of composition spatial discontinuities or shocks (that give rise to bimodality) can be qualitatively understood in the simplest cases of non-linear convex or concave isotherms. A convex isotherm depicts an enrichment of the chemical component in the solid as compared to the liquid. The rapid solidification (quenching) of such a liquid will give an “initial” composition of the solid that will be impoverished as compared to the “final” composition, i.e. that in equilibrium with the liquid. The respective positions of the initial point and of the final point on the isotherm can thus make a shock appear, according to the standard chromatography rules. A concave isotherm would equally lead to the appearance of shocks.
What are the geological factors that can account for the bimodality? The systems must have sufficient size, the evolutions must be long enough at elevated temperatures as to permit the chemical exchanges. These must be efficient (high parameter B value). There is an optimum range of values for parameter A: a too rapid solidification as compared to transport does not allow the bimodality: the system solidifies without chemical transfer. When solidification is too slow, there is not enough disequilibrium for shock appearance. Our model relates to any situation where a magma crystallizes (or equivalently where a rock melts) and where a subsequent reworking of chemical element distribution is made thanks to a differential movement or a separation between the solid and the liquid whatever the mechanism. If there is a tendency to local equilibrium, the process may give rise to products with differing proportions, even for homogeneous starting conditions. If, at a given time, the liquid escapes from such systems, its composition will be “quantified” in space. As a consequence, the emitted compositions within a volcanic system will vary in time along more or less discrete steps. We must then stress that our model thus explains possible bimodality both for the liquids and the solids: from the knowledge of the solid and liquid profiles in the chamber in Fig. 3, one could draw histograms for the solids as well as for the liquid: both would show possible (correlated) bimodalities. Generally, the standard interpretation for the above geological systems, with varied products separated by discontinuities, calls upon several distinct events. We stress that one phenomenon may be enough. If the initial compositions are not homogeneous, the gradients can degenerate into discontinuities. In open system, one already knows that the arrival of a magma in a rock system in disequilibrium can give rise to the propagation of discontinuity waves (Guy, 1993). Natural systems undoubtedly show intermediates between purely closed behaviours and purely open behaviours.
The simple model with one independent chemical component can be applied for systems with one solid solution phase, or a set of solid solution phases described by a single chemical parameter (e.g. the Fe/Fe + Mg ratio of olivines, the Al ratio of chromites, the non-linear fractioning of trace elements etc.), all other factors being equal. This may apply to small mono-mineralic magmatic chambers.
As a whole, the proposed model provides an intellectual framework to discuss the natural cases and the basis for future more complicated models. The development of our approach is related to our simplifications of the phenomena:
- • Texture, crystal size: absence of size variation, absence of chemical zoning etc. Absence of size variation may not be a problem insofar as the increase of size during crystallization is compensated by faster descent. Generally speaking, one can say that the various effects related to the size of the crystals are hidden in the kinetics and the movement laws.
- • Choice of chemical equilibration models: natural evidence of solid diffusion re-equilibration of crystals is generally poor. The more likely is that chemical disequilibrium induces solid melting (because of solidus variation with composition) and recrystallization makes the stable composition appear. This is similar to what occurs during reactive transfer of aqueous solution in porous media (dissolution recrystallization operates rather than true exchange of components by solid diffusion). Whatever the physical phenomenon taking place however, the modelling of chemical exchange by macroscopic laws involving surface transfer and thermodynamic disequilibrium gives a good agreement with reality. The heating effects are not taken into account insofar as the total balance of the transformation is practically null. Modelling by diffusion well accounts for the mass transfers necessary for equilibration (diffusion coefficient may be chosen intermediary between that of the liquid and the solid). The magnitude obtained for K parameter is similar to that for the water/rock interactions and can vary on several orders depending on the systems. This homogenizes the aspects of texture, size and mode of matter displacement.
- • Isotherm concept: taking into account more complicated systems of equations does not present an obstacle. The isotherm concept as a whole gathers all the mineralogical effects within a single formalism; the nature of the mineral which precipitates is simply a consequence of the value of the solution parameter for a more or less complex isotherm (with a plateau for example).
- • Taking into account of only one chemical component: we consider here that the phenomena involving that particular chemical component may be discussed independently from the other components of the magma. In reality, other chemical elements, like SiO2, play the role of solvent, which, at a given time in the chemical evolution, will give place to new mineral crystallizations and interfere with the other phenomena. The presence of several simultaneous minerals may also involve several simultaneous movements with possibly different speeds and complex interferences.
- • Simplification of the overall heating/cooling effects: the heating effects interfere with the other effects, in particular chemical. Part of the temperature pattern is controlled from the interior of the system and not from outside. The isotherm is independent of temperature (one could easily add a dependence). Similarly the movement law will depend on temperature. These dependencies may be hidden within a dependency on p, the evolution of which globally corresponds to a decrease in temperature.
Acknowledgements
The authors thank Daniel Garcia, Jacques Moutte, Pierre Boivin, Marie-Christine Gerbe, Ariel Provost, the geologists of the UMR 6524 “magmas and volcanos” for the stimulating discussions, and two anonymous reviewers for helpful comments.