1 Introduction
Air temperature is an important forcing variable for many environmental models, with a large range of applications concerning agronomy, hydrology or ecology. In snow hydrology, air temperature is obviously the main factor to partition liquid from solid precipitation (snowfall). It can be also used as the main driving variable to estimate snowmelt (Bloschl, 1991; Brubaker et al., 1996; Martinec, 1975; Richard and Gratton, 2001). Therefore, it is fundamental to obtain accurate spatially-distributed temperature values for the purpose of hydrological modelling in snowy areas.
Spatial interpolation is widely used to obtain air temperature estimates at any point of interest. Methods can be of deterministic or stochastic nature and differ according to data availability and scale of application. The most common methods are Kriging and Cokriging techniques (Matheron, 1963), Inverse-Distance Weighting (Legates and Willmott, 1990), Splining (Eckstein, 1989; Hutchinson and Gessler, 1994), and Polynomial regression (Myers, 1990). Many studies were carried out to distribute air temperature based on interpolation methods. Over a large study area in Japan, Ishida and Kawashima (1993) report errors between 1 and 3 K for the interpolation of hourly temperature data cokriged with elevation as an external drift factor. Hudson and Wackernagel (1994) also used cokriging with elevation for predicting air temperatures in Scotland, and showed that this technique performed better than simpler interpolation algorithms. Over smaller areas in Sweden, Soederstrom and Magnusson (1995) reported interpolation errors between 0.4 K and 1.6 K. All these studies have pointed out that the results of kriging are highly dependent on the spatial density and distribution of meteorological stations.
In mountainous areas, air temperature is controlled by different factors related to location and topography (Hudson and Wackernagel, 1994). Therefore, the use of interpolation methods cited above may generate substantial errors and biases (Robeson and Willmott, 1993; Willmott et al., 1991). Conventionally, the method of altitudinal lapse rate is used to estimate temperatures at different elevations (Dunn and Colohan, 1999; Singh and Singh, 2001). More sophisticated geostatistical method such as AURELHY (Bénichou and Le Breton, 1987) aims at accounting for the effects of additional topographic factors (slope, aspect). However, such methods require a dense network to be calibrated. This condition is not met in the majority of mountainous areas, especially in developing countries. Meteorological prediction may offer an alternative, but the grid of meteorological models is too coarse (1 to 10 km) for retrieving the spatial pattern of air temperature at a fine resolution over areas with a complex relief.
Satellite thermal infrared data allows retrieving the spatial distribution of the surface skin temperature over extended regions. Several studies, most of them based on coarse resolution data, aimed at using this information to map air temperature at a regional scale. For instance, the daily maximum air temperature field can be retrieved with an accuracy of about 2.5 K using land surface temperatures derived from NOAA-AVHRR (Vogt, 1996; Vogt et al., 1997). Due to the low spatial resolution of these data (1 km), these methods appear difficult to operate in mountainous regions.
In this context, the objective of this article is to investigate thermal infrared satellite data acquired to improve the description of the spatial distribution of air temperature at a fine resolution over mountainous areas. The study area is the Rheraya watershed, High-Atlas mountain range, Morocco. The joint analysis of ETM+ images, meteorological data set and digital elevation model allowed to set up a model (MSPAT) that simulates continuous (daily time step) and spatially distributed (90 m resolution) air temperatures. MSPAT simulations are compared to the altitudinal lapse rate method (LRM). The comparative evaluation of these two models is performed using air temperature recorded from meteorological stations and using snow cover maps derived from MODIS data at a 500m spatial resolution.
2 Datasets
The experiment took place within High-Atlas, a large mountain range in central Morocco (800 km long and 70 km wide). The highest peak is Jbel Toubkal, which culminates at 4174m above sea level. Precipitations in the mountains allow supplying several large irrigated areas in the surrounding plains (Boudhar et al., 2007; Chaponnière et al., 2005; Chehbouni et al., 2008). They are very irregular in time and space, which is typical of semi-arid areas. Snowfalls occur mainly during the winter season (November to April) in the upper parts of watersheds. The contribution of snowmelt to river flows is significant (between 20 and 45% of the total flows according to the characteristics of watershed, Boudhar et al., 2009).
The experimental data set was collected over the Rehraya atlasic sub-catchment (Fig. 1). This head watershed covers a surface area of about 225 km2 and is characterized by a semi-arid and mountainous climate (precipitation of 360 mm/year at the outlet). The elevation ranges from 1084 to 4167 m, and slopes are very steep, with an average grade of 19%.

The Rheraya watershed and its meteorological station network.
Le bassin versant de Rheraya et le réseau des stations météorologiques.
The experimental data set consist in climatic data, Landat ETM+ and MODIS images, and the SRTM Digital Elevation Model (DEM).
2.1 Climatic data
Air temperatures were recorded by the six meteorological stations located in Fig. 1. Their main topographic characteristics are summarised in Table 1, Supplementary data, online, Appendix A. These characteristics were retrieved from the DEM in the surroundings each meteorological stations. The stations are all located within or in the close vicinity of the Rheraya catchment, with a large range of altitudes (1400 m to 3200 m) and aspects (from 20° northern to 184° southern exposures). The Solar Position Algorithm (Reda and Andreas, 2003) was used to calculate sun position angle.
All these stations were equipped with HMP45C probes (Vaisala, Finland) that measure air temperature and vapour pressure on a half-hourly time step, except at the Caf station where only minimal and maximal temperatures are available. In order to have a maximal sampling, data analysis is performed for daily maximum air temperatures. As illustrated in the Fig. 2, the altitude is a principal factor controlling air temperature variation: an average lapse rate of –0.56 °C per 100 meters was observed during winter 2007/2008.
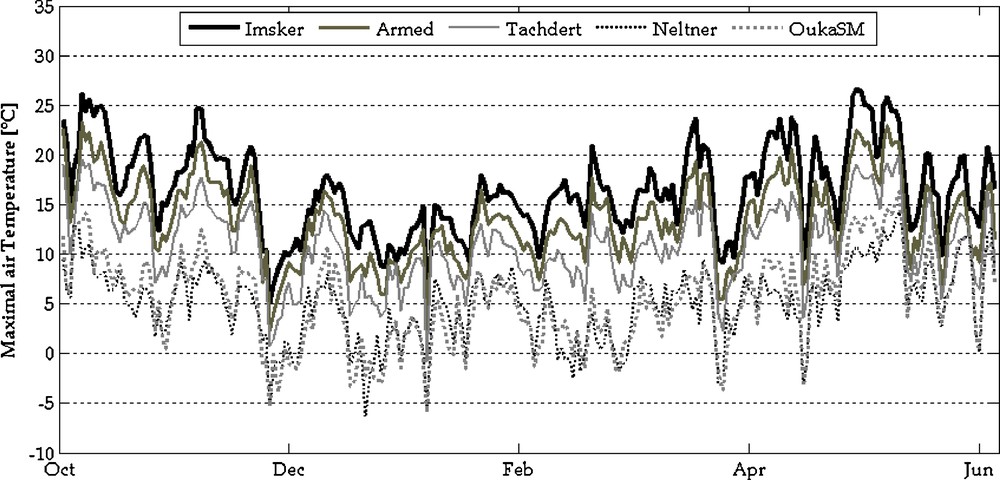
Maximal air temperature recorded at the available weather stations in 2007/2008.
Température de l’air maximale, enregistrée dans les stations météorologiques disponibles en 2007/2008.
2.2 Landsat ETM+
The Enhanced Thematic Mapper (ETM + ) sensor is operational onboard the Landsat 7 satellite. ETM+ observes the Earth in seven spectral bands, amongst which one in the thermal infrared region (ETM + 6: 10.40–12.50 μm). ETM+ images are acquired with a regular revisit time of 16 days at a spatial resolution of 30 m in the solar domain and 60 m for the thermal band (Table 2, Supplementary data, online, Appendix A). The scene size is 170 × 183 km when orbiting at an altitude of 705 km. For this study, six images were available over the Rheraya sub-catchment (Table 3, Supplementary data, online, Appendix A).
2.3 MODIS data
The Moderated Resolution Imaging Spectroradiometer (MODIS) is an Earth Observing System (EOS) instrument on board the Terra and Aqua platforms, launched in December 1999 and May 2002, respectively. The sensor observes the Earth from a sun-synchronous position near the polar orbit at an altitude of 705 km. The sensor scans ±55° from nadir in 36 spectral bands in the visible, near- and short-wave and thermal infrared parts of the electromagnetic spectrum. During each scan, 10 along-track detectors per spectral band simultaneously sample the Earth. From its polar orbit, MODIS views the Earth's entire surface ranging from every day at high latitudes to every other day at low latitudes (Justice et al., 1998).
In this article, we used the datasets of the daily surface reflectance product “MOD09GHK”, which is a product computed from the MODIS Level 1B land bands 1-7. Images were ordered from September 2003 to June 2006 through the Earth Observing System (EOS) data gateway (https://wist.echo.nasa.gov). The main characteristics of MODIS images are provided in Table 4, Supplementary data, online, Appendix A. In this study, we used surface reflectances acquired at 500m spatial resolution of 500m in the blue (band 3), the green (band 4) and the short-wave infrared (band 6) part of the electromagnetic spectrum.
2.4 Digital Elevation Model (DEM)
The digital elevation model (DEM) used in this study was derived from the Shuttle Radar Topography Mission (SRTM) data, which consists of a specially modified radar system that flew onboard the Space Shuttle Endeavour during an 11-day mission in February of 2000. It is an international project led by the U.S. National Geospatial-Intelligence Agency (NGA), U.S. National Aeronautics and Space Administration (NASA), the Italian Space Agency (ASI) and the German Aerospace Center (DLR). SRTM obtained elevation data on a near-global scale to generate the most complete high resolution digital topographic database of Earth, including three resolution products, of 1 km and 90 m resolutions for the world, and a 30 m resolution for the US (USGS, 2004). All SRTM data are freely available at: http://srtm.csi.cgiar.org/SELECTION/inputCoord.asp.
In this study, we used the STRM-DEM version 4 acquired at the full 90m spatial resolution over the area covered by landsat scenes (latitudes 30°28′ - 32°24′ North, longitudes 9°14’ and 9°9’ West). Altitude and derivatives (aspect and slope) were calculated through the ENVI DEM extraction module (© 2008 ITT Visual Information Solutions).
3 Methodology
ETM+ brightness temperature was first calculated (Section 3.1), then converted as a proxy of the maximal air temperature images (Section 3.2). The resulting images were analysed together with derivatives of the SRTM digital elevation model for understanding the topographical factors controlling the air temperature variability (Section 3.3). This analysis allowed to set up the MSPAT models that simulates continuous (daily time step) and spatially distributed (90 m resolution) air temperatures (Section 3.4). MSPAT simulations were compared to the altitudinal lapse rate method (LRM, described in Section 3.5). The comparative evaluation of these two models was performed using air temperature recorded from additional meteorological stations and using snow cover maps derived from MODIS data at a 500m spatial resolution. The snow mapping method is described in Section 3.6.
3.1 Brightness temperature calculation
The computation of brightness temperature from ETM + 6 data first requires the conversion of digital numbers to radiances. For this purpose we used the following formula developed by the National Aeronautics and Space Administration (Eq. (1), after Markham and Barker, 1986).
| (1) |
| (2) |
Once the spectral radiance L(λ) is computed, the brightness temperature at the satellite level can be directly calculated either by inverting Planck's radiance function for temperature (Sospedra et al., 1998) or by using approximation formula (Eq. (3)), after Goetz et al., 1995; Schott and Volchok, 1985, Wukelic et al., 1989:
| (3) |
3.2 Derivation of Maximal Air Temperature from ETM+
Maps of maximal air temperatures were established on the Rheraya watershed by combining ETM+ images and local measurements, with the assumption that air and brightness temperatures (Tb) are linearly related. In principle, there is a tight coupling between the surface and the air temperature under bare soil conditions. Coupling can also be strong when snowpack is below zero degree. Under melting conditions, snow surface is close to zero degree and there is little coupling with the air above. However, Tb distributions according to slope and elevation can be used as additional information to distribute spatially the variations in available melting energy (radiative or sensible heat) in all conditions for use within empirical degree days models1. It is therefore a proxy for these variations rather than a fully deterministic variable. For each image, the brightness temperatures (Tb) of the pixels that include weather stations were extracted and compared with maximal air temperatures (Tam) obtained from the meteorological stations. It appeared that Tb was well correlated with Tam, with a correlation coefficient R2 of 0.82 (Fig. 3). Tam were thus calculated for Tb using a unique regression equation (Tam = 0.7 × Tb–3.2) that was successively applied on each image.
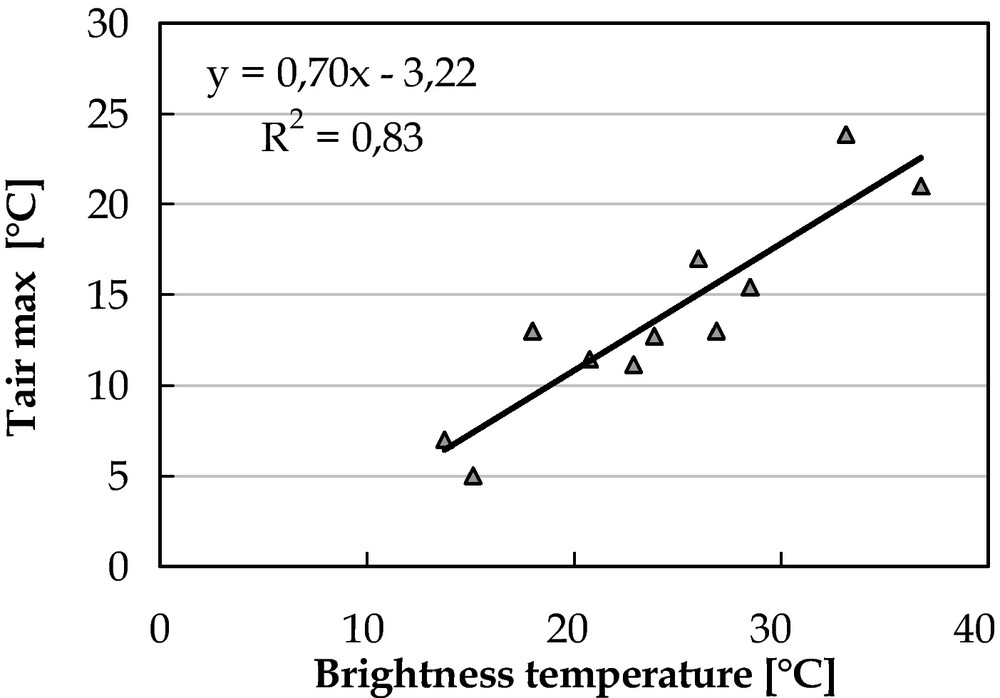
ETM+6 brightness temperatures versus maximal air temperature measurements.
Température de l’air mesurée en fonction de la température de brillance ETM+6.
3.3 Analysis of Maximal Air Temperature Variation
Fig. 4 represents an example of the co-variation of maximal air temperature and altitude over the Rheraya watershed in 27/02/2003. Not surprisingly, the two variables were found highly correlated, with a decrease by 18 °C of air temperature associated to a 3000 m difference in elevation. This corresponds to an equivalent lapse rate value of 0.60°/100 m. Not shown here, the Tam versus elevation curves extracted for the remaining images display the same pattern, with lapse rates varying between 0.43°/100 m to 0.75°/100 m. These values appear consistent with that of an international standard atmosphere (0.65 °C/100 m according to the International Civil Aviation Organization).
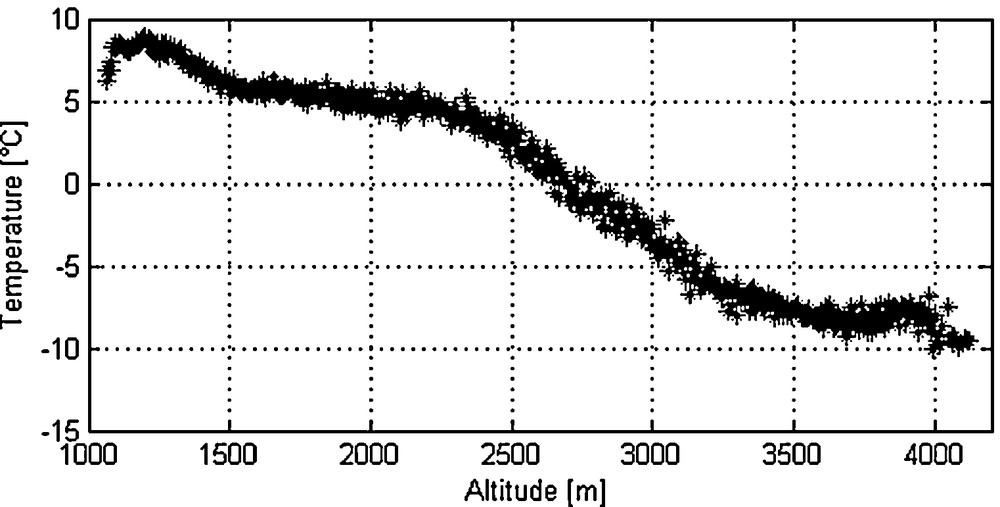
Air temperature as a function of altitude. The air temperature is calculated from ETM+6 (image of February 27, 2003) and averaged by 5 meters altitudinal zone.
Variation de la température de l’air en fonction de l’altitude. La température de l’air est calculée à partir d’images ETM+6 (image du 27 février 2003) et moyennée par tranche d’altitude de 5 m.
Fig. 5 provides an example of air temperature variations with aspect in February 27, 2003. The aspect values are expressed in degrees, with the values 0° (or 360°), 90°, 180° and 270° corresponding to the facing North, East, South and West, respectively. A difference of 10 °C in air temperature between northern and southern exposures was observed this day. The variations of air temperature with aspect followed a sinusoidal curve centred on about 140°, in coherence with the sun diurnal course (the sun azimuthal angle is 165° at the time of acquisition).

Aspect effect in air temperature variation. The air temperature is calculated from ETM+6 (image of February 27, 2003) and averaged by 2̊ zone.
Effet de l’exposition des versants sur la variation de la température de l’air. La température de l’air est calculée à partir d’images ETM+6 (image du 27 février 2003) et moyennée par bande de 2.
A deeper investigation shows that the dependence of Tam with aspect is function of altitude, slope and sun elevation. Fig. 6 presents the amplitude of Tam variations with aspects for seven altitudinal zones from 1000 to 4200 m (with steps of 400 m), together with slopes. Variations of Tam with exposures match the altitudinal distribution of slopes, especially during the winter period when the sun elevation is low. For the ETM+ image acquired in May with a maximal sun elevation of 77°, this effect appears very limited.
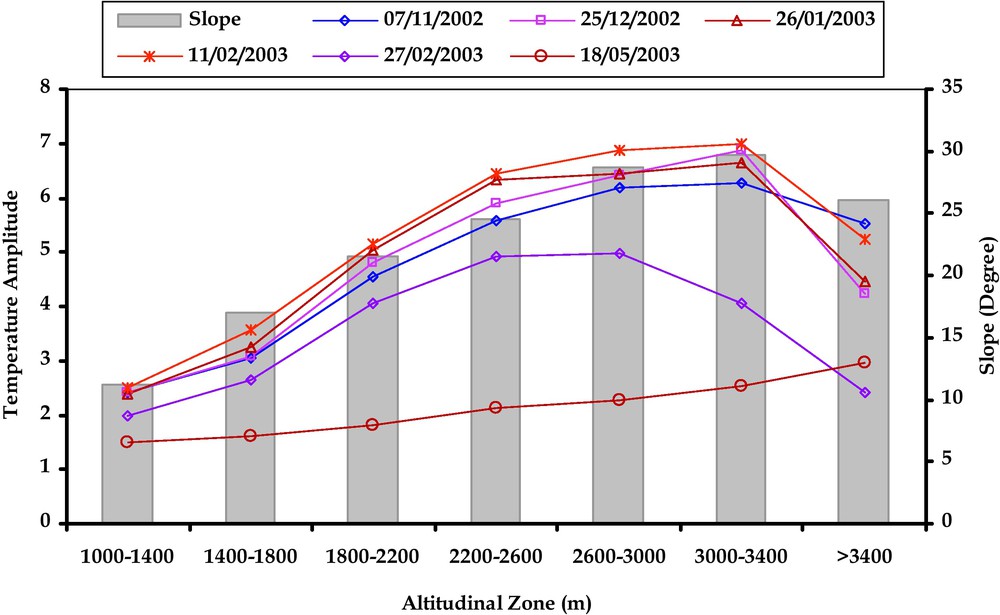
Comparison between slope and amplitude of temperature variation for each altitudinal band.
Comparaison entre la pente et l’amplitude de variation de la température de l’air pour chaque bande altitudinale.
3.4 Spatial distribution of Air Temperature (MSPAT model)
The air temperature in any point Tam(i,j) of the Rheraya sub catchment's was calculated from the air temperature recorded at one reference meteorological station (Tam(Iref,Jref), OukaSM and Armed stations, and topographical differences between this point and the reference station. These differences were accounted for using the MSPAT model with the altitude, exposition and slope extracted at the pixel (i,j) and at the location of the reference station (Eq. (4)). The MSPAT was set up to obtain daily images of maximal air temperature at a 90m spatial resolution.
| (4) |
where:G is the air temperature lapse rate calculated from the two reference meteorological stations (Armed and OukaSM) at a daily time step; is the difference in elevation between the reference station and the pixel where air temperature is calculated.
AS(I,j) and ASref are the aspect in degree of the pixel (i, j) and of the reference station, respectively.
For a given altitude, the model accounts for aspect, slope and sun elevation according to equations (Eqs. (5) and (6)). In details, the air temperature was calculated from the temperature averaged for a given altitudinal band with a correction of the effect of exposure based on a cosine function (Eq. (5)). The maximal air temperature was logically supposed to be the highest when the surface is fully oriented at South (aspect of 180°). The amplitude of the cosine was adjusted as a function of the ratio of the local slope to the sun elevation (A coefficient in Eq. (6) and Fig. 7).
| (5) |
| (6) |
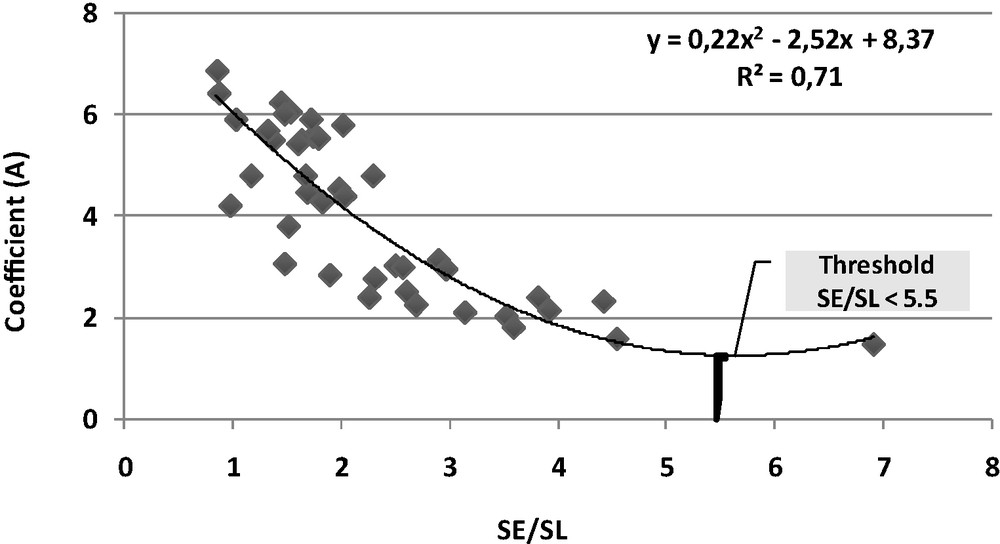
Relationship between the coefficient “A” and the ratio of the sun elevation angle to the average slope of each altitudinal zone for ETM+ date.
Relation entre le coefficient « A » et le rapport angle d’élévation solaire et pente moyenne de chaque tranche altitudinale pour les dates ETM+.
3.5 Lapse rate method (LRM)
In the lowest 10–15 km of the atmosphere, temperature declines with an increase in altitude. This decline, known as temperature lapse rate, is controlled by the balance between heat convection from the surface and radiative cooling. However, lapse rates vary with: (1) altitude, (2) season, (3) latitude, and (4) interactions between topography and weather (e.g. dry versus moist air and inversions).
The lapse rate method (LRM) takes the maximum air temperature observed at a reference station and extrapolates that value over the entire basin via a functional relationship between air temperature and elevation data. This method assumes 1) a linear relationship between air temperature and elevation, and 2) horizontal gradients due to topographic and orographic effects are negligible. In this study, the temperature lapse rates (G) on a daily basis using the stations where the longest dataset is available as:
| (7) |
Air temperature lapse rates were calculated for each study year and then applied to elevation data for Rheraya basin to determine air temperature for each pixel using air temperature measured at a reference station (Tam(Iref,Jref)) (Eq. (8)).
| (8) |
3.6 Estimates of snow-covered areas (SCA)
Snow-covered areas were estimated using two methods: (1) Simulation of snowfall and snowmelt, (2) Mapping using MODIS images.
3.6.1 Simulation
The snow cover fraction (SCA) was parameterized as an asymptotically function of the snow water equivalent (SWE) according to equation (Eq. (9)) (Anderson, 1976).
| (9) |
SWE was calculated as the balance between the accumulations processes (snowfall) and the ablation processes (snowmelt). During precipitation events, SWE increased by the daily snowfall if the mean air temperature is below 0 °C, otherwise precipitation is rain. Snowmelt was calculated with a classical temperature index described in Eq. (10).
| (10) |
Two sets of simulations were performed for years 2003/2004, 2004/2005 and 2005/2006 over the entire Rheraya watershed using a 90 m spatial grid, with the air temperature spatially distributed either with the MSPAT model or with the simple lapse rate method. In both case, the precipitations are distributed using the precipitations recorded at the ARMED station and an average observed elevation gradient of 0.03 mm/100m (Boudhar et al., 2009).
4 Mapping
To select the cloud-free data, we initially eliminated the images showing high reflectances in the blue band (on average higher than 20%) over the lower-lying areas close to the High-Atlas (approximately 5000 snow-free pixels, where the altitude is lower than 1000 meters). Indeed, these high reflectances are due to the presence of clouds on the Atlas foothills, and therefore probably on nearby Atlas summits. In a second phase, we identified clouds on the remaining images by visual examination. After this filtering phase, the number of useful images is respectively 44, 52 and 82 for the seasons 2003/2004, 2004/2005 and 2005/2006 (equivalent of 1 image per week).
The snow-mapping algorithm makes use of the contrast of reflectances between a visible band (MODIS band 4, 0.545–0.565 μm) and shortwave infrared band (MODIS band 6, 1.628–1.652 μm). These two bands were combined to calculate the normalized difference snow index (NDSI, Eq. (11)), which is a proxy of SCA (Hall et al., 2002).
| (11) |
In order to reduce errors due to variations of the background reflectance, we used the Modified Normalized Difference Snow Sndex (MNDSI, Eq. (12)). This approach was successfully tested by Chaponniere et al., 2005 using a snow index specifically designed for the SPOT-VEGETATION sensor. This methodology was applied for all cloud-free MODIS images acquired during three years from 2003 to 2005.
| (12) |
Here NDSI0 is the snow index of totally snow-free surfaces (computed, for each pixel, from images acquired in summer), and NDSI100 are the snow indices of pixels totally covered with snow (one single value was fixed as the maximum of NDSI on images acquired during winter).
5 Results and discussion
5.1 Model evaluation at Local scale
Daily maximum air temperatures modelled using MSPAT at the location of meteorological stations were evaluated against all measurements available over the Rheraya watershed, together with estimates of air temperature based on the lapse rate method (referred to as “LRM”). The evaluation was carried out using classical statistical variables (RMSE, BIAS, and R2).
Fig. 8 present the scatter plots between observed and simulated air temperatures during the 2007/2008 season, year with the largest number of available climatic data. Table 5 (Supplementary data, online, see Appendix A) shows the statistical variables obtained by comparing the predictions and the measurements of daily maximum daily air temperature on an annual basis. Biases and RMSE were null for the Armed station which provides with the reference air temperature. Bias was also null for the OukaSM station since it was used for calculating the altitudinal lapse rate. From the statistics calculated on the remaining stations, we noted that the performance of LRM and MSPAT models were similar, with moderate to excellent correlation (R2 from 0.35 to 0.94), low biases (from –0.5° to 1.2°) and error varying from 1 to 3.2°. The MSPAT model performed slightly better than the LRM method for 2 stations (Caf and Neltner), whereas it is the opposite for 2 others (Imsker and Tachdert). These results showed that, at local scale, the MSPAT model did not improve the estimate of air temperature.
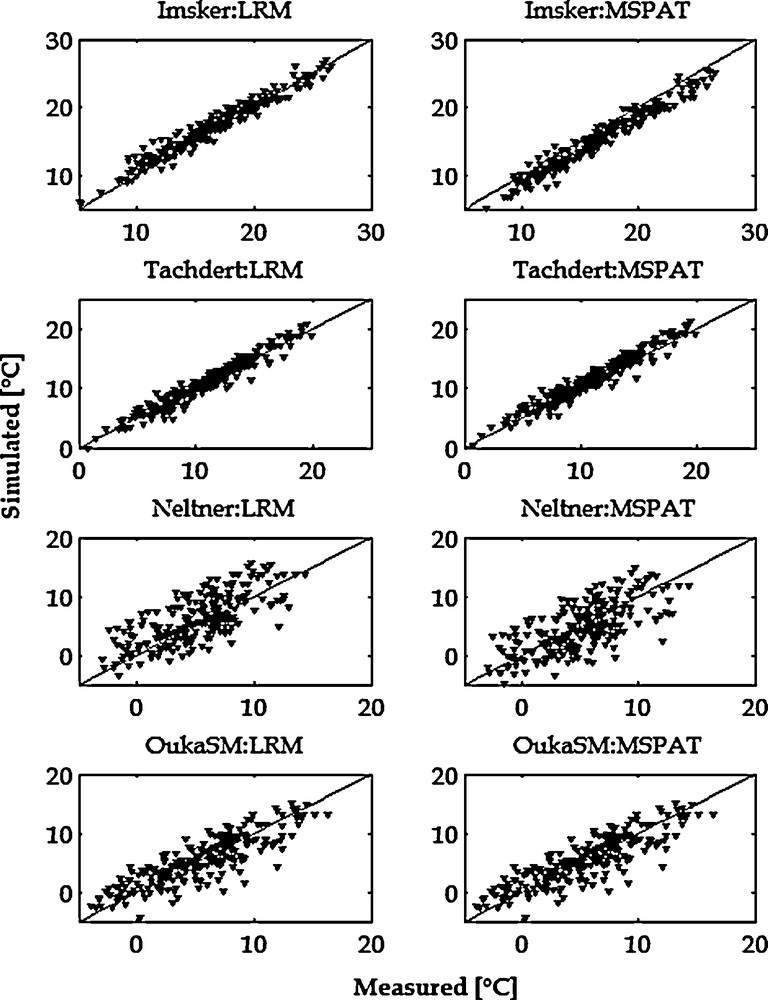
Comparison between observed and simulated air temperature using lapse rate method (LRM) and MSPAT model at different meteorological stations in 2007/2008.
Comparaison entre les températures de l’air observées et simulées, en appliquant la méthode du gradient altitudinal (LRM) et le modèle MSPAT dans les différentes stations météorologiques en 2007/2008.
5.2 Catchment scale
The snow-covered areas derived from MODIS data and simulated with climatic data (LRM and MSPAT models) were compared for the three seasons of study (2003–2004 to 2005–2006). The time series of SCAs averaged on the whole Rheraya watershed were plotted in Fig. 9. The two simulated snow covered area compared favourably to that derived from MODIS images. However, there was a slight underestimation of SCA simulated using the LRM method during the two previous years (2003 to 2005) and a slight overestimation of SCA simulated using the MSPAT model at the beginning of the last year (December 2005). The peaks of SCA were well modelled with the two methods, even though those occurring after generalized snowfall events were clearly underestimated. This smoothing effect was due to the use of an asymptotic function between SCA and snow water equivalent.
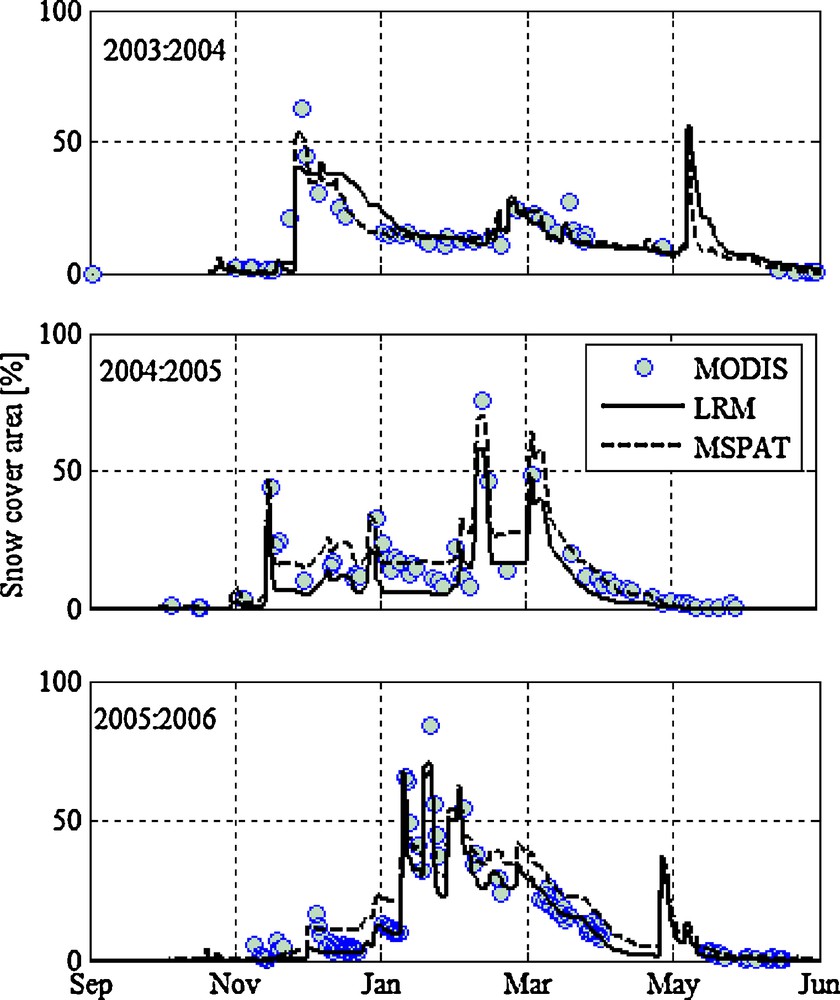
Snow depletion curve estimated with MSPAT model and LRM method in the Rheraya watershed.
Courbe de variation de l’enneigement dans le bassin versant de Rheraya, estimée avec le modèle MSPAT et la méthode LRM.
The Fig. 10 show three examples of SCA maps simulated by the two climatic models and derived from MODIS data during a snowmelt period between 03/12/2003 and 30/12/2003. Simulated SCA appeared much more realistic when the MSPAT model was used to distribute air temperature. This was obvious on the two first dates when looking at the north-eastern and at the western part of the catchment, as well as for the last date for which the spatial extent of snowy areas simulated using the LRM data pattern appeared too limited. This qualitative comparison allowed to show that patterns of SCA were not only matching altitude variations but also exposures. This was consistent with previous studies carried out at the scale of the whole High-Atlas mountains range showing that southern facing slopes have lower SCA than northern ones (Boudhar et al., 2007).
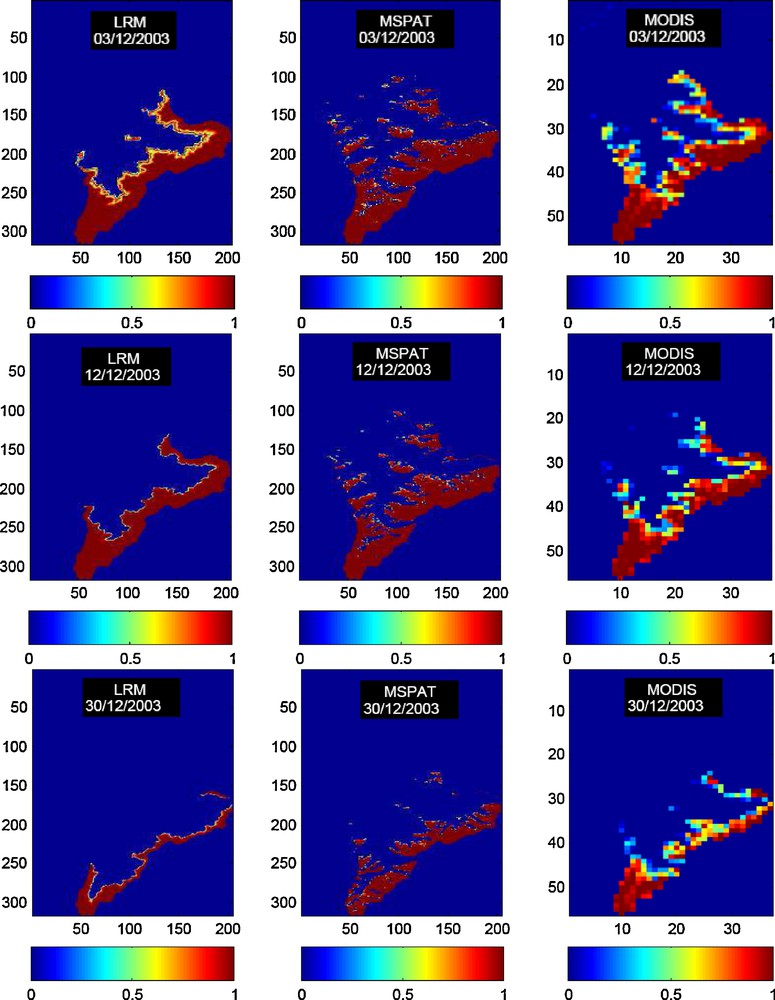
Snow-covered areas in the Rheraya watershed simulated with the lapse rate method (left, 90 m spatial resolution), MSPAT model (middle, 90 m resolution), and derived from MODIS (right, 500 m resolution).
Surfaces des neiges dans le basin versant de Rheraya, simulées par la méthode du gradient altitudinal (gauche, résolution spatiale de 90 m), le modèle MSPAT (centre, résolution spatiale de 90 m), et dérivées à partir des données MODIS (droite, résolution spatiale de 500m).
The scatter plot between SCA simulated by the two climatic models and derived from MODIS allowed to quantify the previous findings (Fig. 11). This comparison was carried out at a degraded resolution of 2 km2 in order to limit the impact of miss-registration between MODIS and simulated SCA images. SCA modelled with LRM model were found very under-estimated, especially during seasons 2004/2005 and 2005/2006. In contrast, SCA modelled using the MSPAT were less scattered. The statistics results for each season are summarized in Table 6, Supplementary data, online, see Appendix A. We noted a remarkable improvement of the SCA modelled with MSPAT model. This improvement was significant in the two seasons 2004/2005 and 2005/2006 with decreasing in bias by 2.9 and 1.8%, respectively. Theses differences in SCA estimating between LRM and MSPAT models are due principally to the aspect effect not taken account by LRM formulation. In the later, air temperature varies only with altitude and horizontal gradients due to topographic and orographic effects are negligible.
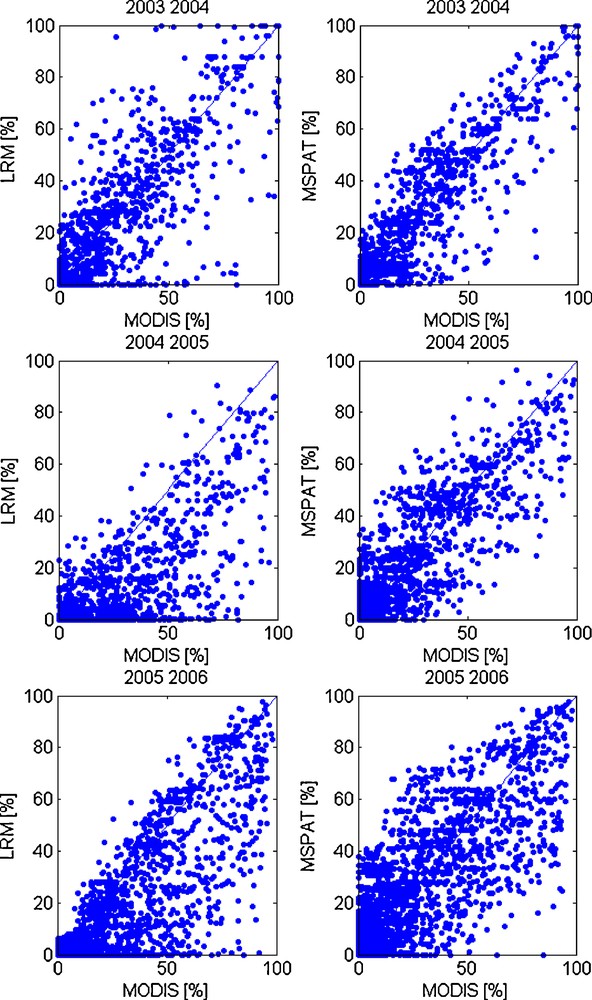
SCA modelled using lapse rate method and MSPAT method and computed with MODIS data, Comparison pixel by pixel of 2 km2.
Surfaces d’enneigement modélisées en utilisant la méthode du gradient altitudinal et le modèle MSPAT et extraites à partir des données MODIS, comparaison pixel par pixel de 2 km2.
6 Conclusion
This study focused on testing a method of air temperatures spatial variation, principally developed for high-relief mountain environments with scare meteorological data. The thermal infrared band of Enhanced Thematic Mapper (ETM + ) images was used to calculate the brightness temperature. Brightness temperatures were compared with maximal air temperature measured in meteorological stations available, and the correlation equation obtained allowed to compute maps of a proxy of the maximal air temperature. This information was used to characterize its spatial variation according to topographic factors (elevation, aspect and slope) and solar elevation angle. From this, we set up a model to spatialise air temperature.
The results of air temperature simulation with MSPAT model was compared with lapse rate model (LRM). The simulated air temperatures with the two models were similar at the location of available meteorological stations. Over all the study area, the models were evaluated using snow cover area (SCA) estimates. The last are then compared with SCA product mapped from MODIS data. Results showed that MSPAT model had a considerable improvement on the modelling SCA. It is thus believed that the pseudo air temperature approximated using ETM+ brightness temperature may be useful to monitor the dynamics of snowpacks. The approach developed here may be beneficial for hydrological applications, especially snowmelt modelling at watershed scale with scare data.
Acknowledgements
This study was supported by the research projects SUDMED (IRD-UCAM), PAI (Programme d’Action Intégrée du Comité Mixte Interuniversitaire Franco–Marocain, Jeune Equipe IRD, CREMAS), Volubilis (MA/06/148) and the PLEADeS Project (http://www.pleiades.es/) funded by the European Commission (Sixth PCRD).
1 Boudhar, A., Boulet, G., Hanich, L., Sicart, J.E. and Chehbouni, A., submitted. Measurement and modeling of the energy fluxes and melt rate of a seasonal snow cover at the Oukaimden site in the Moroccan High Atlas. Hydrology and Earth System Sciences.


