1 Introduction
It has been shown that correlating long time series of seismic ambient noise recorded at two stations makes it possible to retrieve the Earth response (i.e. the Green's function) between these two stations (e.g., Campillo, 2006; Gouédard et al., 2008; Larose et al., 2006; Sabra et al., 2005a; Shapiro and Campillo, 2004). This technique has provided useful results for studies of tomographic imaging (e.g., Sabra et al., 2005b; Shapiro et al., 2005; Yang et al., 2007; Yao et al., 2006, 2008) and monitoring (Brenguier et al., 2008a, 2008b; Sens-Schönfelder and Wegler, 2006; Wegler and Sens-Schönfelder, 2007).
In practice, since the ambient seismic noise is dominated by the surface-wave contributions, only the direct arrivals of surface waves are clearly visible in the noise-correlation signals. However, theory says that in the case of a perfectly isotropic noise field, the noise correlation provides the complete Green's function , including all types of waves that propagate between the two stations in xA and xB (e.g., Gouédard et al., 2008; Lobkis and Weaver, 2001; Roux et al., 2005; Sánchez-Sesma et al., 2006; Snieder, 2007; Wapenaar, 2004). If we let u(xA,t) and u(xB,t) denote time-dependent random wavefields recorded at two sensors, A and B, we can write:
| (1) |
| (2) |
| (3) |
In the ideal case, the later part of the noise correlation should contain the coda part of the Green's function, and it might be possible to correlate these waves as we correlate standard earthquake codas, to reconstruct the Green's function (Campillo and Paul, 2003). This is the concept of the so-called C3 method, i.e. re-correlating the coda of the noise-correlation functions to reconstruct the Green's function (Stehly et al., 2008).
For microseism records dominated by surface noise, the required spatial isotropy of the recorded wavefield is mainly produced by the distribution of sources and by the scattering of seismic waves in the medium. However, usually the distribution of the noise sources does not provide a perfect random noise field. In this case, the theoretical requirements are not completely fulfilled, and the noise correlation does not perfectly reconstruct the surface-wave Green's function, as some fluctuations remain in the correlation results. This, in practice, prevents the identification of other amplitude arrivals that are smaller than the predominant fundamental mode of the surface waves. This is the main limitation in the implementation of the C3 method, i.e. does the later part of the noise correlation contain the coda part of the surface-wave Green's function? Note that this is also a central issue for noise-based temporal monitoring of seismic velocity, for which measurements are performed on noise correlation codas.
In their recent study, Stehly et al. (2008) demonstrated successful results for the C3 function, clearly showing the direct surface-wave part of the Green's function. The success of this technique is an indication that the later part of the ambient noise correlations is meaningful and contains multiply scattered waves with properties of regular earthquake codas. Stehly et al. (2008) showed that the C3 method helps to improve the time symmetry of correlation functions, thereby increasing the quality of the data used in noise-based tomographic studies. Indeed, since the noise correlation functions should converge to the causal and anticausal Green's function (Eq. (2)), time symmetry in noise correlations may constitute a way of controlling the quality of the Green's function reconstruction from the correlation process. In particular, travel-time estimations must be the same in both causal and anticausal parts. That is why some tomographic studies use only time-symmetric noise correlations with good signal-to-noise ratios. Since Stehly et al. (2008), some studies have proposed a formalization of the C3 method (de Ridder et al., 2009; Garnier and Papanicolaou, 2009). In particular, Garnier and Papanicolaou (2009) proved the validity of this method based upon the stationary-phase analysis of the C3 function leading terms, and they confirmed that this method can enhance the quality of travel-time estimates in the case of anisotropic source distributions.
As indicated above, the noise-correlation technique has provided useful information for seismological applications, and this in spite of the imperfect reconstruction of the Green's function in correlation functions. In particular, an anisotropic source distribution leads to biased travel-times extracted from correlation functions (Froment et al., 2010; Weaver et al., 2009). One of the main issues in the improvement of noise-based measurements is thus to understand and eliminate these source effects in correlation results. In this study, we show the improvement of noise-based results in seismological applications through the use of the C3 method.
In Section 2, we present the data and the processing used in this study to compute the C3 function. In Section 3, we examine the time symmetry of the C3 function and its relationship with the station distribution in the network. Then, we discuss the interest of combining the information from the different correlation functions. Finally, we show the correlation function that is obtained by iterating the correlation process on the C3 coda. In particular, we investigate the evolution of the reconstruction of the Green's function throughout the iteration process.
2 Data and C3 computation
Throughout this study, we have used pairs of stations that are located in the Alps as part of a regional network of 150 broad-band stations. We consider the vertical motions of seismic ambient noise recorded continuously over one year. The noise processing is the same as in Stehly et al. (2008).
For each station pair, we correlate the noise records, which are pre-filtered in the 0.1–0.2-Hz frequency band, and the noise correlation (C1) is obtained by stacking all of the day-by-day correlations. We then apply the C3 method between two stations A and B, according to the following successive steps.
1. We take a third station, S, in the network located at xS, and we consider the result of the A-S and B-S noise correlations (C1) as the signal recorded at A and B, respectively, if a source was present at xS. The receiver in S thus has the role of a virtual source.
2. We then select a 1200-s-long time window (Tcoda) in the later part of the noise correlation (C1), beginning at twice the Rayleigh wave travel-time (i.e., in the same way as Stehly et al. (2008)). Note that the coda in both the positive and negative parts of the noise correlation (C1+ and C1−) are selected.
3. We cross-correlate the codas in the A-S and B-S noise correlations. Note that we whiten the codas between 0.1 and 0.2 Hz before correlation; the motivation for this processing is discussed later. We compute the correlation functions between the positive-time and negative-time codas to finally obtain two correlations that we denote as C3++S and C3−−S, respectively.
4. We average over the N stations of the seismic network to obtain C3++ and C3−−:
| (4) |
| (5) |
5. We stack C3++ and C3−− to obtain the actual C3 correlation function between A and B:
| (6) |
The steps described above highlight the difference in the correlation technique between noise correlations (C1) and the C3 method, that points out advantages of this iterative method. For instance, since the C3 method correlates signal that has been extracted from the C1 computation, it is expected to be more coherent than seismic ambient noise. Furthermore, we can distinguish coda and ballistic contributions in C1 functions (which is not possible in seismic noise); this provides scattering averaging in the correlation process when only coda waves are selected. Finally, we point out that, by construction, the virtual sources S are uncorrelated in the C3 method, which may not be the case for noise sources in C1 computation.
Fig. 1 illustrates the C1 and C3 correlation functions for one station pair. The good agreement between the pulse shapes in the C3 and C1 correlation functions shows that the C3 correlation process has extracted from the coda of the C1 correlation the necessary phase information to reconstruct the direct surface wave part of the Green's function.
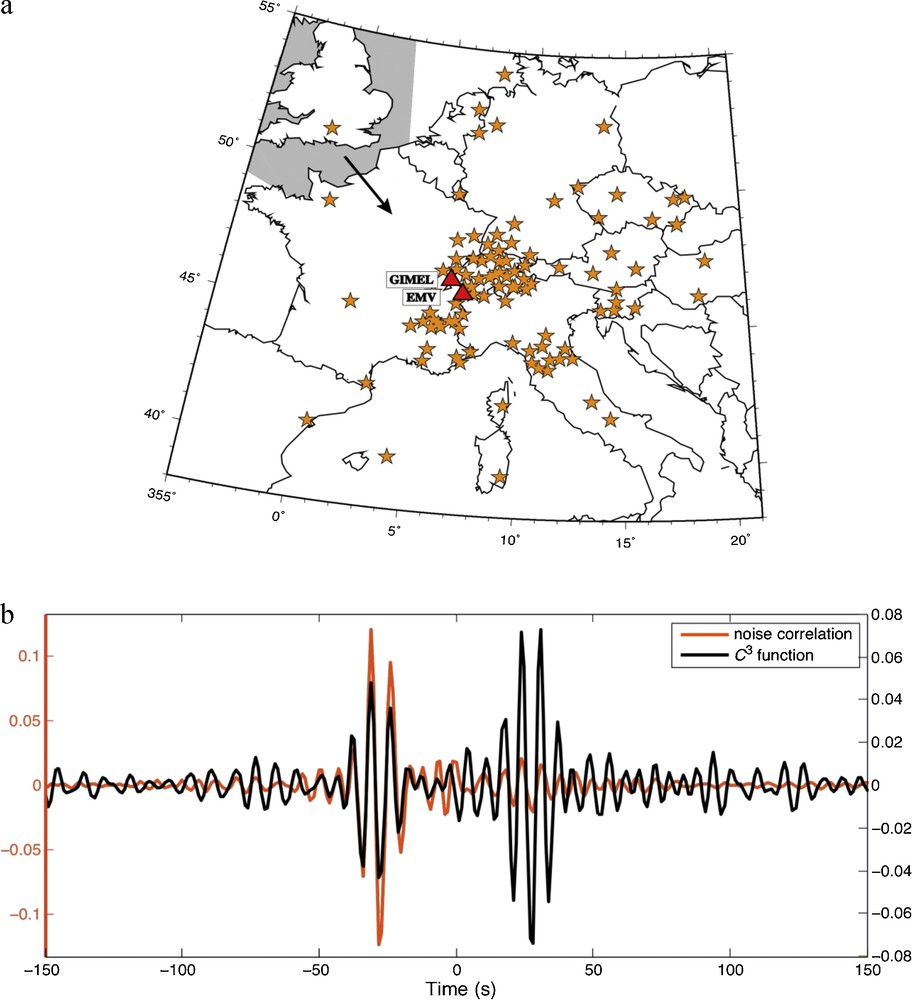
(a) Map of Europe with orange stars corresponding to about 100 stations of the network used as virtual sources to construct the C3 function between stations EMV and GIMEL (red triangles). The main direction of the ambient seismic noise in the vicinity of the station pair EMV-GIMEL is indicated by the black arrow, and corresponds to noise coming from the North Atlantic Ocean or the northern European coast (gray zone). (b) Noise correlation C1 (orange curve) and C3 function (black curve) between stations EMV and GIMEL. Note the different vertical scales (left and right, respectively) for the two normalized correlation functions.
(a) Carte de l’Europe avec les étoiles orange représentant les stations du réseau (environ 100), utilisées comme sources virtuelles pour construire la fonction C3 entre les stations EMV et GIMEL (triangles rouges). La direction principale du bruit sismique à proximité du couple EMV-GIMEL est indiquée par la flèche noire et correspond à un champ provenant de l’Atlantique Nord ou de la côte nord-européenne (zone grisée). (b) Corrélation de bruit C1 (courbe orange) et fonction C3 (courbe noire) entre les stations EMV et GIMEL. Noter les différentes échelles verticales (gauche et droite, respectivement) des deux fonctions de corrélation normalisées.
3 Network stations as virtual sources
3.1 Source signature in correlation functions
In the case of noise sources that are homogeneously distributed, the positive and negative parts of the noise-correlation functions are expected to be symmetric, as they represent the causal and anticausal parts of the Green's function, respectively. In practice, these two parts may not have the same amplitude, which reflects a difference in the energy flux that propagates between the two stations in both directions (Paul et al., 2005; van Tiggelen, 2003). Thus, if the source density (or virtual source power) is larger for one direction than for the other, a time asymmetry will be seen for the correlation function (Fig. 2). This means that the level of symmetry in the correlations, up to first order, is an indication of the source distribution.
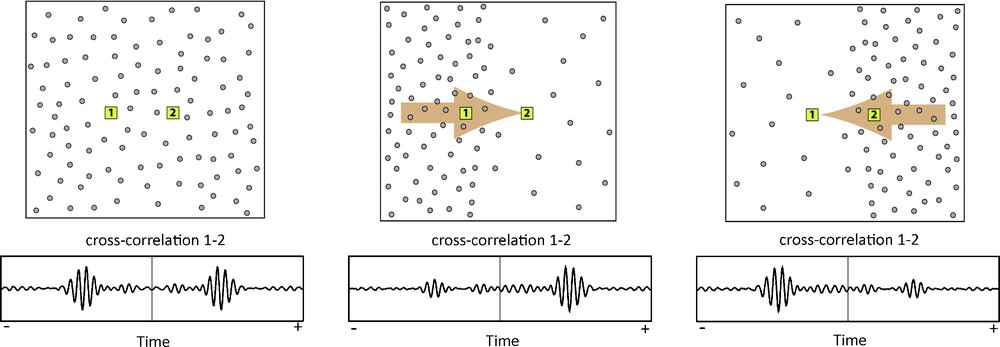
Schematic illustration of the relationship between the distribution of sources and the time symmetry of the correlation functions. (a) The sources (open circles) are homogeneously distributed around receivers 1 and 2. The resulting incoming wavefield in the vicinity of the receivers will thus be isotropic and the correlation between the fields recorded in 1 and 2 is time symmetric. In contrast, in (b) and (c) the density of sources is larger on one side, causing the energy flux to propagate in one preferential direction (arrows). The resulting correlation function is time asymmetric as a reflection of this preferential direction. Modified from Stehly et al., 2006.
Représentation schématique de la relation entre la distribution des sources et la symétrie temporelle des fonctions de corrélation. (a) Les sources (cercles vides) sont réparties de façon homogène autour des récepteurs 1 et 2. À proximité des récepteurs, le champ d’onde résultant sera donc isotrope et la corrélation des enregistrements en 1 et 2 sera symétrique en temps. Au contraire, en (b) et (c), la densité de sources est plus grande d’un côté, imposant un flux d’énergie se propageant dans une direction préférentielle (flèches). Le résultat de la fonction de corrélation est asymétrique en temps, reflétant cette direction particulière. D’après Stehly et al., 2006.
What makes C3 appealing is that, in theory, the “noise” sources that contribute to C1 and C3 are different. Considering the two stations A and B, the noise correlation (C1) is directly affected by the noise-source distribution. In contrast, the C3 method is based on the use of the network stations as virtual sources (Stehly et al., 2008). In this case, the symmetry in the C3 function should no longer reflect the noise-source distribution, but the distribution of the network stations around the path A-B.
3.2 Time symmetry of C3 and C1
To verify these theoretical expectations, we compare the time symmetry of both correlation functions (C1 and C3) for the particular case of the station pair HAU-BOURR (Fig. 3). In the C3 correlation process, we chose to select only the 55 network stations south of HAU-BOURR (see map in Fig. 3a). This means that the theoretical C3 virtual sources are localized south of the station pair of interest and opposite to the incident-noise direction, as the main source of noise is located in the North Atlantic ocean or on the northern European coast (e.g., Friedrich et al., 1998; Kedar et al., 2008; Landès et al., 2010; Stehly et al., 2006). Fig. 3b shows the results of both the C1 and C3 correlation functions for this geometry. The time symmetry of both signals shows two opposite peaks of maximum amplitude, which reflect a main energy flux propagating in opposite directions: from north to south for C1, and from south to north for C3. Note that the same convention is used for all of the correlation functions, i.e. the signal in negative (resp. positive) correlation times corresponds to waves propagating from north to south (resp. south to north). This observation indicates that the time symmetry of the two correlation functions is consistent with the location of their expected contributing source distributions.
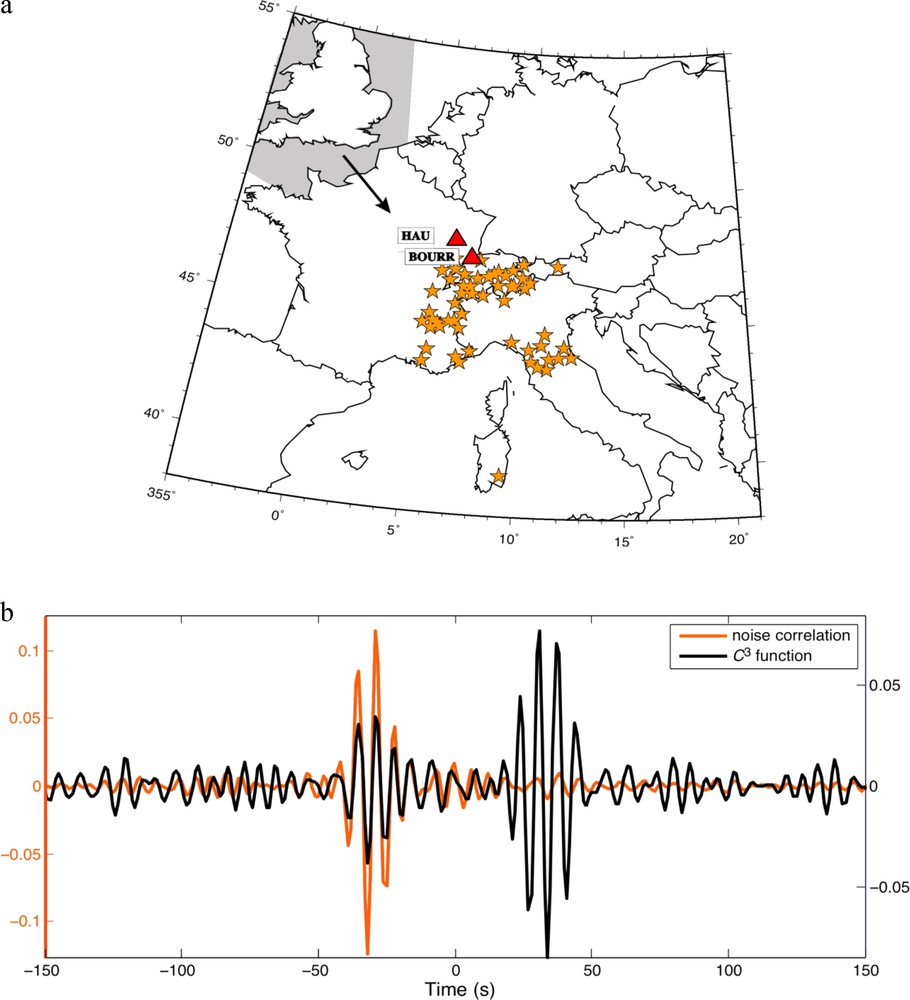
(a) Map of Europe with orange stars corresponding to the 55 stations of the network used as virtual sources to construct the C3 function between stations HAU and BOURR (red triangles). Note that all of the stations considered are located south of the HAU-BOURR path and opposite to the main source of noise located in the North Atlantic ocean or on the northern European coast (gray zone). The black arrow indicates the main direction of ambient seismic noise in the vicinity of the station pair HAU-BOURR. (b) Noise correlation C1 (orange curve) and C3 function (black curve) between stations HAU and BOURR for the geometry displayed in (a). Note the different vertical scales (left and right, respectively) for the two normalized correlation functions.
(a) Carte de l’Europe avec les étoiles orange représentant les 55 stations du réseau, utilisées comme sources virtuelles pour construire la fonction C3 entre les stations HAU et BOURR (triangles rouges). Noter que l’ensemble des stations considérées sont situées au sud du trajet HAU-BOURR et opposées à la source principale de bruit située dans l’Atlantique Nord ou sur la côte nord-européenne (zone grisée). La flèche noire représente la direction principale du bruit sismique, à proximité de la paire de stations HAU-BOURR. (b) Corrélation de bruit C1 (courbe orange) et fonction C3 (courbe noire) entre les stations HAU et BOURR pour la géométrie représentée en (a). Noter les différentes échelles verticales (gauche et droite, respectivement) des deux fonctions de corrélation normalisées.
However, the C3 function has a better time symmetry than C1. This indicates that the coda waves used to compute the C3 function constitute a more isotropic field than the ambient seismic noise. This can be explained by the nature of the coda waves, which correspond to waves scattered from the heterogeneities in the Earth subsurface (e.g., Aki and Chouet, 1975). This scattering process is expected to make the coda wavefield more isotropic, depending on the distribution of the scatterers in the medium and the lapse-time considered in the coda (Paul et al., 2005). To confirm the influence of the scattering in our observations, we compare the C3 results for the same station pair (HAU-BOURR) computed for two different time windows T, in the C1 correlation (Fig. 4). In the first case, we consider a 1200-s time window in C1, including the direct surface waves (Fig. 4a). This time window begins 15 s before the Rayleigh wave travel-time (i.e., twice the dominant period of the signals). We denote it as Tall, as it takes into account both the ballistic and the scattered waves. Due to the strong amplitude of the direct waves in the time window, we expect that their contribution will dominate in the C3 process. The resulting C3all function is shown in Fig. 4b. In the second case, we use C3coda for the C3 function calculated (as in Section 2) from a 1200-s time window Tcoda of the correlation located entirely after the direct arrivals (Fig. 4c).
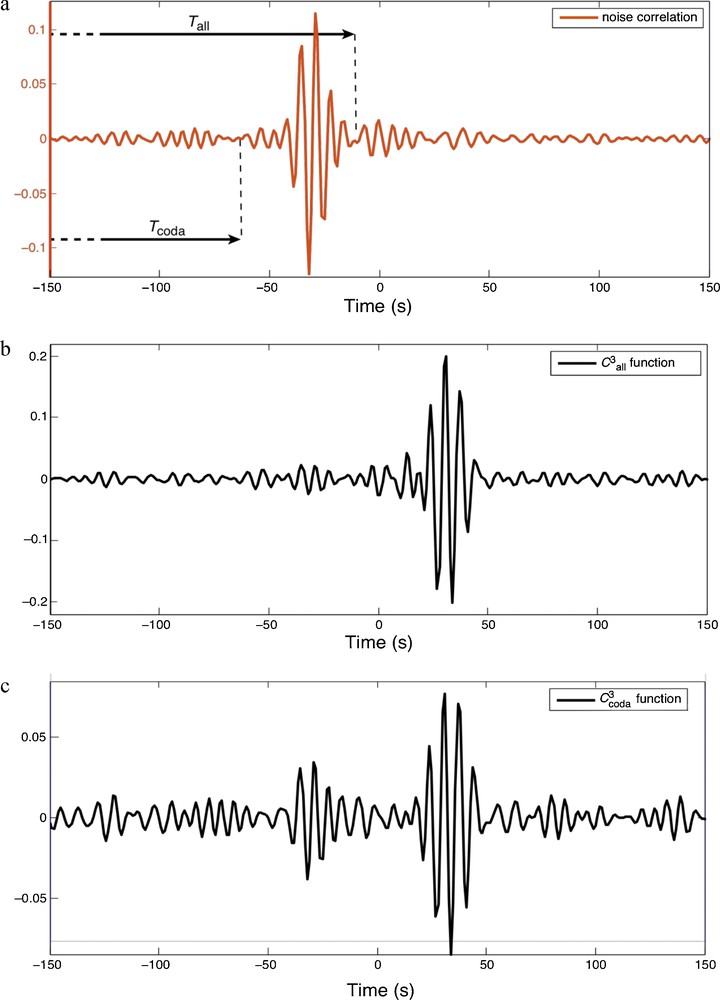
(a) Noise correlation C1 between stations HAU and BOURR. The start of the two 1200-s time windows used in the C3 processing is indicated: Tall and Tcoda. For the sake of simplicity, the windows are displayed in the negative correlation time for which the ballistic part is clear. (b, c) C3 functions between HAU and BOURR for the geometry displayed in Fig. 3a and obtained from the C1 correlation over Tall (b) and Tcoda (c). The maxima of these normalized correlation functions correspond to the level of coherence between the correlated signals. Note the different vertical scales for these three correlation functions.
(a) Corrélation de bruit C1 entre les stations HAU et BOURR. Le début des deux fenêtres temporelles de 1200 s utilisées dans le calcul de C3 (Tall et Tcoda) est indiqué. Par souci de clarté, les fenêtres sont indiquées dans les temps de corrélation négatifs où la partie balistique apparaît clairement. (b, c) fonctions C3 entre HAU et BOURR pour la géométrie représentée sur la Fig. 3a et obtenues par corrélation de C1 sur l’intervalle Tall (b) et Tcoda (c). Le maximum de ces fonctions de corrélation normalisées correspond au niveau de cohérence entre les signaux corrélés. Noter les différentes échelles verticales des trois fonctions de corrélation.
In view of the nature of the dominant waves involved in both of these computations, we can infer the origin of the energy flux observed in C3all and C3coda. The energy flux is expected to be totally controlled by the distribution of the virtual sources in the first case, whereas it must also be influenced by scattering (and the distribution of the scatterers) in the second case. The station distribution considered in this case helps in the separation of the different contributions to the time symmetry in the correlation process.
On the one hand, Fig. 4b confirms the role of network stations as virtual sources in the C3 method, as C3all shows complete time asymmetry, which reflects a directive energy flux in the opposite direction to the seismic noise direction that is consistent with the distribution of the network stations. On the other hand, the time symmetry is preserved in C3coda (Fig. 4c), which indicates the link between the scattering events and the wavefield isotropy in the correlation process. Finally, we notice the lower coherence observed in C3coda compared to C3all. This likely reflects the higher level of fluctuations in the coda of C1 than in its ballistic part. Note that the coherence in C3all is about twice as high as that in C1 in this geometry particularly favorable to C3all (i.e., a dense distribution of virtual sources in the alignment of receivers).
This analysis shows that the time symmetry of the C3 function does not depend any more on the distribution of the noise sources, but is instead essentially controlled by the distribution of the stations in the network when direct waves are selected, and is also influenced by the contribution of the scatterers when the C3 process is performed from the coda. This means that the sources in the C3 method are controllable to a certain extent, which is a noticeable advantage compared to the C1 process, which usually suffers from uneven noise-source distribution.
4 Combining information from the different correlation functions
The C3 method is an alternative method for the reconstruction from seismic noise of the Green's function between two points, and we have shown that it can improve noise-based measurements, especially by making correlation functions independent of the noise source. However, this iterative method can also be viewed as a way to obtain several estimates of the Green's function between two points that can be used to complement each other for tomography purposes. Indeed, noise-based tomography requires unbiased travel-time measurements between station pairs. In the case of a directive noise, it has been shown that the noise-correlation functions carry the footprint of the noise-source direction, which can lead to biased travel-time estimations. In general, when both the causal and anticausal parts of the noise-based correlation functions are reconstructed, the travel-time estimation is said to be unbiased. Further bias might come from a poor signal-to-noise ratio in the correlation functions, which also prevents satisfactory measurements of the travel-time.
We show in Fig. 4 for a given station pair, that the combination of the C1 and C3 results may alleviate these bias. In this case, we have seen that both the C3coda and C3all functions provide information with respect to C1 since they exhibit also the time-reversed counterpart of the ballistic signal reconstructed in C1. Note that in the general case, this information is provided by C3coda, since the time symmetry of the C3all function is strongly controlled by the station distribution. There are therefore configurations for which the information in C1 and C3all is redundant. On the other hand, in terms of coherence, C1 and C3all can provide an advantage with respect to C3coda for better-quality measurements to be obtained. Besides, Fig. 4 shows a higher level of coherence in C3all than in C1.
Several aspects have roles in the improvement of the correlation results. In the present study, we have mentioned in particular the noise-source effects, time symmetry and coherence. The C3 functions complement C1 by contributing to one or several of these aspects. The different correlation functions can thus be viewed as complementary information that can be considered together to improve noise-based tomography analysis.
5 Iterating the correlation process
The results presented in the previous sections have shown that it is possible to reconstruct (at least partially) the Green's function by iterating the correlation process from C1 to C3. These results emphasize that the late arrivals in the C1 function still carry information about the propagation medium since the correlation of the C1 coda averaged over the station networks allows the reconstruction of the direct arrivals.
We can then ask about the next iterative step, i.e. is it possible to use the coda of the C3 function to reconstruct part of the Green's function?
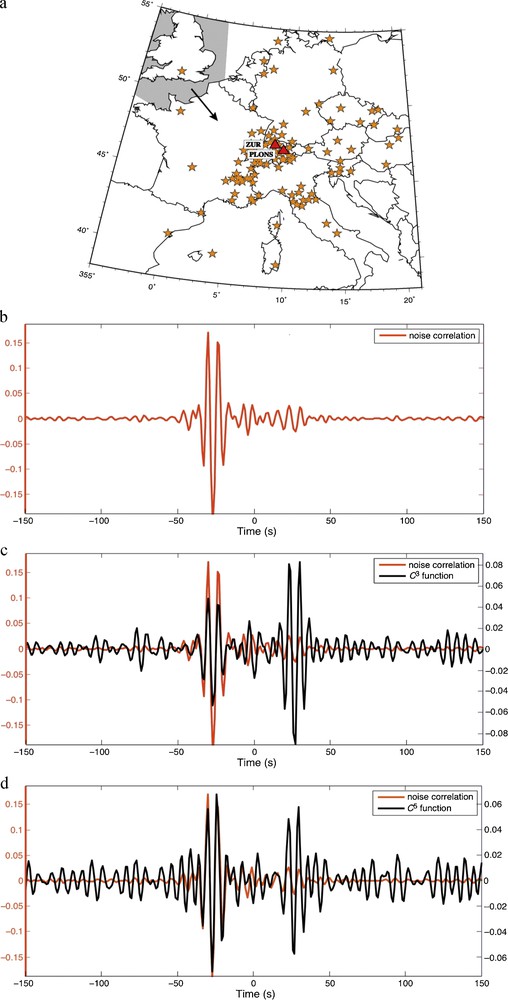
For Fig. 5, we computed the C5 function1 for a particular station pair from the coda of the C3 functions averaged over the network station pairs. Note that in Fig. 5 we compare correlation functions instead of Green's function. The relation between the Green's function and the correlation function (Eq. (2)) refers implicitly to a time derivative that is written as in the frequency domain. When dealing with correlation of correlations, an extra ω2 − term is introduced into the counterpart of Eq. (2), which becomes . This implies a difference in the spectral content of the Green's function and the correlation function that becomes more pronounced during the iteration process. However, the spectral whitening used in our processing maintains the spectrum as almost constant in a narrow band during the iteration. This allows us to consider that the spectrum variations remain negligible throughout the iteration process.
The good agreement between the direct arrivals of the C5 and the C1 functions shows that some coherent signal is still present in the coda of the C3 function. This result supports the idea that the C5 function could also be used in noise-based tomography or for monitoring techniques. However, we observe in Fig. 5 that the signal-to-noise ratio in the C5 function is smaller than that in the C3 function, which was also smaller than that in the C1 function (note the decrease in the coherence level in Fig. 5b, c and d). This might limit the practical interest of this iterative correlation process in geophysical inversion techniques.
Sabra et al. (2005c) proposed a theoretical expression for the level of fluctuations in the C1 function that helps in the understanding of the Green's function reconstruction during the iterative correlation process. They considered a white-noise model and a finite bandwidth B. In the case of normalized correlations (Eq. (3)), the expected level of fluctuations, n, is given by:
| (7) |
The stack over N virtual sources, as performed in the C3 method, leads to an expected fluctuation level in the C3 function of (e.g., Larose et al., 2008; Stehly et al., 2008):
| (8) |
Measurements of the level of fluctuations carried out for the iterative correlation functions have shown good agreement with Sabra et al. (2005c). This means that the fluctuation levels observed (Fig. 5) are indeed controlled by the evolution of B, T and N during the iterative correlation process. In the following, we examine the evolution of these different parameters in this iteration process:
1. The frequency bandwidth B: in the frequency domain, the correlation consists of multiplying the spectra. If the frequency content is peaked, the correlation process heightens the contrast between the frequencies, which, in practice, amounts to having a narrower spectral content (B is decreasing). This corresponds to a loss of information, which in Eq. (7) leads to higher fluctuation levels in the correlations. In our case, the noise spectrum between 0.1 Hz and 0.2 Hz is peaked near 0.14 Hz, and this peak will be accentuated throughout the successive iterative steps. To prevent this loss of spectral information, we whiten the selected coda between 0.1 Hz and 0.2 Hz, so as to correlate a flat spectrum signal in the same frequency band at each iteration step.
2. The duration T: it is well established that correlation results are highly dependent on the duration of the ambient noise time series. In the present study, C1 has been calculated from one year of seismic ambient noise, and C3 results from the average of about 200 correlations (C3++ and C3−− averaged over a hundred stations) performed on a time window of T = 1200 s extracted from the C1 coda. Considering Eq. (8), this results in larger fluctuations in the C3 function than in C1. As the fluctuation level is higher in C3 than in C1, the C5 function was computed from the selection of a shorter time window in the C3 coda, which results in a stronger fluctuation level in the C5 function. This explains why the level of fluctuations will always increase through the correlation iterations after the C3 processing.
3. The number of virtual sources N: Eq. (8) gives a level of fluctuations that is decreasing as . This means that the stacking over many virtual sources improves the C3 processing. However, N remains the same after the C3 function, and therefore this parameter does not influence the fluctuation level in the higher-order correlation functions.
This analysis shows that the level of fluctuations can be improved in the C3 correlation (with respect to the C1 correlation) by considering large networks (and thus more virtual sources), although it is limited by the decrease in the time interval T after the C3 iteration.
6 Conclusions
The present study shows that the later part of the noise correlation contains coherent signals that can allow the reconstruction of the Green's function by the so-called C3 method. Indeed, the C3 correlation function clearly shows the direct surface-wave part of the Green's function, and the success of the next iterative step, which is C5, shows that coherent signals are also present in the coda of the C3 function.
This method can be useful to improve noise-based measurements, especially by suppressing source effects that are caused by non-isotropic source distributions. Two points should be emphasized. First, the C3 method is computed from scattered waves that have already been extracted in the C1 function. Secondly, we have shown that the C3 correlation function loses its dependency on the noise-source spatial distribution, and instead highly depends on the network stations that have the role of virtual sources. Thus, both scattering and an even spatial distribution of stations help in converging toward a two-sided Green's function with this technique. The C3 method can therefore help in the resolution of problems that arise from uneven source distributions in the primary noise correlations (C1).
However, fluctuations in C3coda are higher than in C1, and this might mitigate the practical interest in this higher-order correlation function for tomography purposes. We can adopt a somewhat different approach by combining information from the different correlation functions. Indeed, the C1 and C3 correlation functions provide several travel-time estimations that can be viewed as complementary information for noise-based tomography inversions.
Acknowledgements
All the seismic data used in this study have been obtained from the IRIS DMC (http://www.iris.edu/), the ORFEUS database (http://www.orfeus-eu.org/), the ETH Zürich, the CEA (Commissariat à l’Énergie Atomique, France), and the LGIT (Laboratoire de Géophysique Interne et Tectonophysique de Grenoble, France). We thank N. Shapiro, U. Wegler and D. Draganov for their helpful comments and suggestions. One of the authors (B.F.) acknowledges the support of Shell Research. This research was supported by European Research Council (Advanced grant Whisper).
1 As for C3, the exponent indicates the number of C in the correlation function description. The C5 function corresponds to the Correlation of Coda of the C3 function. (a) As for Fig. 1a, here for the station pair PLONS-ZUR. (b) Noise correlation C1 between stations PLONS and ZUR. (c, d) Iterated correlation functions C3 (c) and C5 (d) superposed on the noise correlation for the geometry displayed in (a). In view of the level of fluctuations in (d), the C5 function displayed can be considered as symmetric. Note the different vertical scales (left and right, respectively) for the different normalized correlation functions. (a) Même que Fig. 1a pour la paire de stations PLONS-ZUR. (b) Corrélation de bruit C1 entre les stations PLONS et ZUR. (c, d) Fonctions de corrélation itérées C3 (c) et C5 (d) superposées à la corrélation de bruit, pour la géométrie représentée en (a). Compte tenu du niveau de fluctuations en (d), la fonction C5 peut être considérée comme symétrique. Noter les différentes échelles verticales (gauche et droite, respectivement) des différentes fonctions de corrélation normalisées.