Determination of the interstitial velocity field in the swash zone by Ultrasonic Doppler Velocimetry (UDV)

Mustapha Kamel Mihoubi; Michel Bélorgey; Ahmed Kettab

doi:10.1016/j.crte.2012.05.001

Stratigraphy, sedimentology

Determination of the interstitial velocity field in the swash zone by Ultrasonic Doppler Velocimetry (UDV)
[Détermination du champ des vitesses interstitielles en zone de swash par vélocimétrie Doppler ultrasonique (VDU)]

Présenté par : Ghislain de Marsily

Mustapha Kamel Mihoubi ^1,² ; Michel Bélorgey ³ ; Ahmed Kettab ²

¹ Laboratoire de mobilisation et valorisation des ressources en eau (MVRE), École nationale supérieure d’hydraulique (ENSH), BP 31, 09000 Blida, Algeria
² Laboratoire de recherches des sciences de l’eau (LRS-EAU), École nationale polytechnique (ENP), avenue Hacène Badi, BP 182, El Harrach, Algeria
³ UMR-CNRS 6143, laboratoire de morphodynamique continentale et côtière (M2C), université de Caen, 2–4, rue des Tilleuls, 14000 Caen cedex, France

Comptes Rendus. Géoscience, Volume 344 (2012) no. 5, pp. 312-318.

Résumés

Anglais
Français

The experimental study of the hydrodynamics of the sediments and the physical analysis of the process of exchange at the water-sediment interface in a zone of swash are essential for the understanding of the sedimentary transport processes in coastal environments, in particular to control and forecast the evolution of the coastline. The objective of this study was to exploit the technique of Ultrasonic Doppler Velocimetry (UDV) to examine the evolution of the velocity field at the water-sediment interface in a zone of swash in various conditions of incidental regular waves in a wave flume. The velocities were measured in different conditions of the swash within the sediment bed, and in the fluid vein at the swash edge. These measurements show: an exponential distribution of velocities inside the sediment bed; a difference in the velocity gradient at the water-sediment interface, between the velocity in the water vein at the swash edge and the interstitial flow in the swash. The measurements obtained in the wave flume made it possible to observe an evolution of the velocity profiles according to the phases of the swash, which are characterized by a phase shift between the free flow at the swash edge and the interstitial flow during the two phases of the swash: uprush and backwash.

L’étude expérimentale de l’hydrodynamique des sédiments et l’analyse physique du processus d’échange à l’interface eau-sédiment en zone de swash revêtent un intérêt capital pour la compréhension du processus de transport sédimentaire en milieu côtier, notamment par le contrôle et la prévision du trait de côte. L’objectif de cette étude a été d’exploiter la technique de vélocimétrie Doppler ultrasonore (VDU) pour l’étude de l’évolution du champ des vitesses à l’interface eau-sédiment en zone de swash pour différentes conditions de houles régulières incidentes en canal à houle. Les vitesses sont mesurées pour différentes situations du swash au sein du lit sédimentaire, dans la veine fluide de la langue de swash, mettent en évidence : une répartition exponentielle des vitesses à l’intérieur du lit de sédiment ; une différence de gradient de vitesse à l’interface eau-sédiment, entre la vitesse dans la lame d’eau de la langue de swash et l’écoulement interstitiel dans la nappe du swash. Les mesures obtenues en canal à houle ont permis de constater une évolution du profil des vitesses suivant les phases du swash, qui sont caractérisées par un déphasage entre l’écoulement libre de la langue de swash et l’écoulement interstitiel durant les deux phases du swash : jet de rive et retrait.

Métadonnées

Reçu le : 2010-12-01
Accepté le : 2012-05-08
Publié le : 2012-05-01

DOI : 10.1016/j.crte.2012.05.001

Keywords: Interstitial velocity, Swash, Uprush, Backwash, Wave, Ultrasonic, Velocimetry, Interface
Mot clés : Vitesse interstitielle, Jet de rive, Retrait, Houle, Vélocimétrie, Ultrasonique, Interface

Affiliations des auteurs :

Mustapha Kamel Mihoubi ^{1, 2} ; Michel Bélorgey ³ ; Ahmed Kettab ²

@article{CRGEOS_2012__344_5_312_0,
     author = {Mustapha Kamel Mihoubi and Michel B\'elorgey and Ahmed Kettab},
     title = {Determination of the interstitial velocity field in the swash zone by {Ultrasonic} {Doppler} {Velocimetry} {(UDV)}},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {312--318},
     publisher = {Elsevier},
     volume = {344},
     number = {5},
     year = {2012},
     doi = {10.1016/j.crte.2012.05.001},
     language = {en},
}

TY  - JOUR
AU  - Mustapha Kamel Mihoubi
AU  - Michel Bélorgey
AU  - Ahmed Kettab
TI  - Determination of the interstitial velocity field in the swash zone by Ultrasonic Doppler Velocimetry (UDV)
JO  - Comptes Rendus. Géoscience
PY  - 2012
SP  - 312
EP  - 318
VL  - 344
IS  - 5
PB  - Elsevier
DO  - 10.1016/j.crte.2012.05.001
LA  - en
ID  - CRGEOS_2012__344_5_312_0
ER  -

%0 Journal Article
%A Mustapha Kamel Mihoubi
%A Michel Bélorgey
%A Ahmed Kettab
%T Determination of the interstitial velocity field in the swash zone by Ultrasonic Doppler Velocimetry (UDV)
%J Comptes Rendus. Géoscience
%D 2012
%P 312-318
%V 344
%N 5
%I Elsevier
%R 10.1016/j.crte.2012.05.001
%G en
%F CRGEOS_2012__344_5_312_0

Mustapha Kamel Mihoubi; Michel Bélorgey; Ahmed Kettab. Determination of the interstitial velocity field in the swash zone by Ultrasonic Doppler Velocimetry (UDV). Comptes Rendus. Géoscience, Volume 344 (2012) no. 5, pp. 312-318. doi : 10.1016/j.crte.2012.05.001. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2012.05.001/

Version originale du texte intégral

Notations

C _A	Average velocity of wave propagation of the emission	m/s
C _R	Average velocity of wave propagation of the return	m/s
C	Sound velocity in water. This value is also valid for porous media (C ≅ 1500 m/s)	m/s
H	Height of the incidental wave	m
L	Wave length of the incidental wave	m
T	Period of the incidental wave	s
T _up	Duration of the uprush	s
T _b	Duration of the backwash	s
f _D	Frequency shifted by the Doppler Effect	MHz
f _O	Frequency of emission	MHz
f _R	Frequency of return	MHz
l ₁	Travel distance of the wave in the emission phase	m
l ₂	Travel distance of the wave during the return phase	m
u	Flow velocity at the edge of the swash	m/s
u _moy	Average flow velocity flow in an uprush phase	m/s
u _max	Maximum flow velocity at the edge of the swash	m/s
h _W	Height of the swash wave	m
h _b	Depth of the sediment bed in a swash zone	m
z	Elevation above the level of the water-sediment interface	m
α _w	Characteristic parameter of the incident wave	----
θ	Angle of the ultrasonic beam with the flow axis	(°)
τ	Transit time of the wave between the emission and reception	s

1 Introduction

The phenomenon of sediment transport is associated with physical processes which are still poorly known. For lack of adequate instrumentation, the modelling of this phenomenon is still based on two types of independent studies exploited simultaneously: (i) analysis of the velocity field in the free flow; and (ii) measurement of interstitial velocities in the flow in homogeneous porous media with a constant hydraulic gradient.

Most of the studies on which was based the modelling of the velocity field in steady-state free flow were made with an impermeable bottom where the flow velocity becomes zero. The studies of the interface between a porous environment and a fluid vein in the case of a free-surface flow are very few. In 1967, Beavers and Joseph noticed that in the case of a confined flow in a pipe partly blocked by a porous material, there can be a non-zero tangential flow at the wall. It is thus necessary to determine a new condition which takes into account the characteristics of the flow in the porous medium and at the water-sediment interface. In order to better understand the physical processes associated with this phenomenon, we adapted the technique of Ultrasonic Doppler Velocimetry (UDV) to the instantaneous measurement of the local interstitial velocities in a swash zone within a sediment bed of a reflective-shore type for the various conditions of incidental waves (swell). The swash zone is very sensitive to coastal morphodynamic processes, particularly unpredictable at the coastline. It constitutes a true border between the marine and the coastal domains, characterized by a water depth of a few millimetres, and a slope of about 10% (Brocchini and Peregrine, 1996). This zone is also called the run-up area because of its situation between the set-up and the set-down (Butt and Russell, 2000).

Recent work has indicated the presence of a fluidized flow in the top layer of the sediment bed during the two phases of the swash, keeping in mind that during the uprush and backrush, water infiltration and exfiltration occur, and vortices and swirls are formed causing sediment transport (Butt et al., 2001, 2004).

2 Material and method

2.1 Principle of velocity measurements

The measurement device is the UDV, functioning in pulsated mode: DOP 1000 (model 1032), which uses the Doppler Effect on pulsated ultrasonic waves, to determine directly the interstitial velocity inside the pores of the considered porous medium. See the reference work on velocity measurements by UDV (Lhermitte, 1983; Takeda, 1986) and the theory of ultrasonic wave propagation at the fluid-solid interface (Macocco et al., 2005).

If we consider a wave emitted at position x₁ and time t₁ by the transducer on the particle at time ${t^{'}}_{1}$ having travelled a distance l₁ with a velocity C_A in the medium (Fig. 1), then:

l_{1} = C_{A} (t_{1} - {t^{'}}_{1})

(1)

Fig. 1
Diagram of propagation of an ultrasonic wave.
Schéma de propagation d’une onde ultrasonore.

Returning, it travels the same distance with a return velocity C_R and thus arrives on the transducer at time ${t^{″}}_{2}$ such that:

{t^{″}}_{1} - t_{1} = l_{1} (\frac{1}{C_{A}} + \frac{1}{C_{R}})

(2)

The wave emitted by the transducer at time t₂ = t₁ + τ, where τ is the period of the wave, returns to the transducer at time ${t^{″}}_{2}$ , having travelled the distance l₂ at a position x₂ such that:

{t^{″}}_{2} - t_{2} = l_{2} (\frac{1}{C_{A}} + \frac{1}{C_{R}})

(3)

The corresponding arrival period is thus:

τ^{″} = {t^{″}}_{2} - {t^{″}}_{1} = t_{2} - t_{1} + (l_{2} - l_{1}) (\frac{1}{C_{A}} + \frac{1}{C_{R}})

(4)

If u and C are the mean fluid velocity and the sound velocity in the medium, respectively, the wave velocities in the medium C_A from the transducer to the target and C_R from the target to the transducer become, considering the angle alpha between the direction of the fluid particle and the ultrasonic beam, also known as the Doppler angle:

C_{A} = C - u \cos θ

(5)

C_{R} = C + u \cos θ

(6)

assuming that u << C:

\frac{1}{C_{A}} + \frac{1}{C_{R}} \approx \frac{2}{C}

(7)

Additionally:

l_{2} - l_{1} = (x_{2} - x_{1}) \cos θ = - u τ \cos θ

(8)

we can write:

τ^{″} = τ (1 - \frac{2 u \cos θ}{C})

(9)

Switching to the frequency domain, we can express the frequency shift between the emission f_o and the reception f_r by the Doppler frequency f_D:

\frac{f_{r} - f_{o}}{f_{o}} = \frac{f_{D}}{f_{o}} = \frac{2 u \cos θ}{C}

(10)

in other words:

u = \frac{C \cdot f_{D}}{2 \cdot f_{o} \cdot \cos θ}

(11)

If we add to this frequency measurement that of the travelling time (back and forth) of the wave sequence, we can reach the position of the particle. Thus, in a pulsated mode, we can obtain the desired space-time resolution, i.e. establish the velocity profile at suitable exploration depths along the ultrasonic beam.

2.2 Wave flume

The experiments to study the effects of the incidental wave on the velocity field in a swash zone were made in a flume with regular waves, 18.0 m long with a rectangular section, 0.50 m wide and with 0.6 m high walls. We simulated many wave conditions for incidental periods ranging between 1.0 to 6.5 seconds and a water depth in the wave flume of 0.35 m (Fig. 2).

Fig. 2
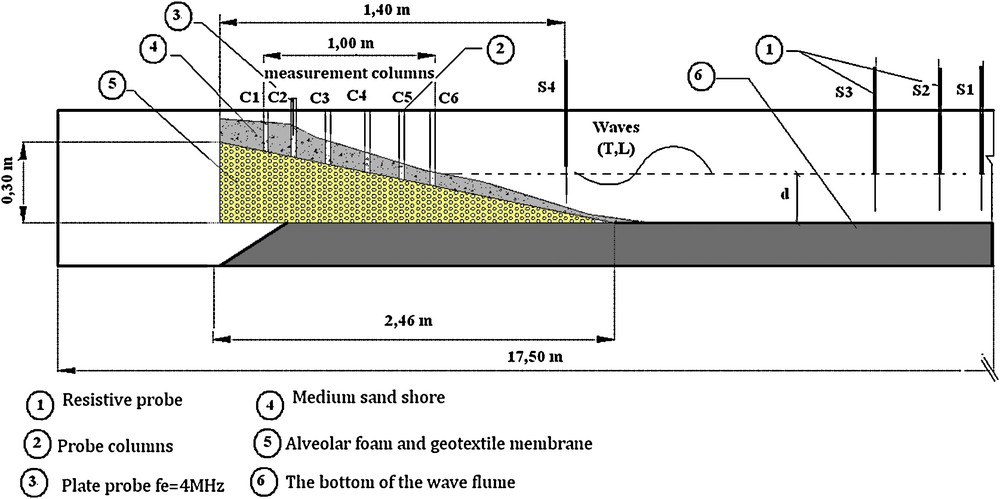
Longitudinal section of the swash flume with the zone of velocity measurements.
Coupe longitudinale du canal à houle avec la zone de mesures des vitesses.

According to the conditions of the incidental waves and the position of the swash formation, we used six columns to measure the velocities and establish the vertical velocity profiles. The columns were filled with water in order to have acoustic coupling for the ultrasonic field. The shoreline bordering the beach, where the swash zone is situated, consists of a sediment bed with medium sand of mean grain-size D₅₀ = 500 μm and 32.2% porosity, which extends over 2.5 m and is 0.45 m high.It is necessary to specify that a calibration device was set to validate the interstitial velocity measurements in the sediment bed by the UDV technique for the study of a free-surface flow on a permeable bed, made of various materials such as: alveolar foam, glass beads and medium sand (Mihoubi et al., 2008). The vertical velocity profile is defined with respect to a coordinate system (Fig. 3) which takes into account the depth of the flume and the average profile of the beach, measured before the beginning of the experiments.

Fig. 3
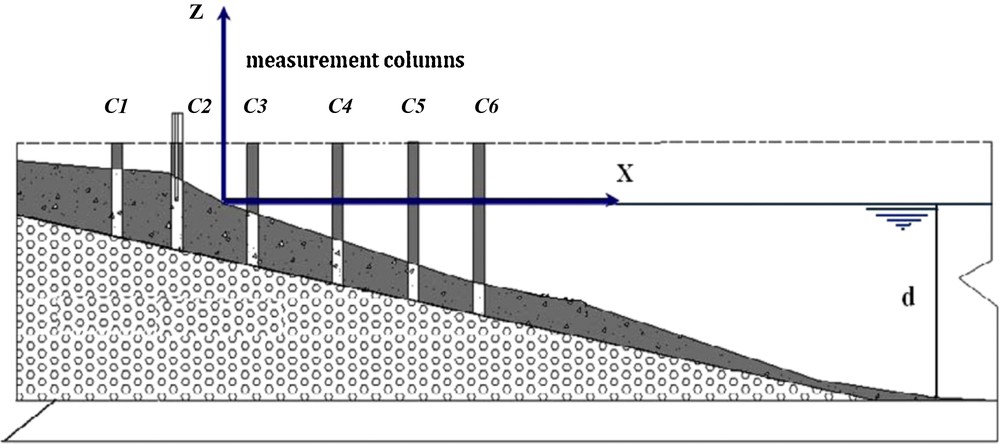
Probe with columns and coordinate system for the vertical velocity profile in a swash zone.
Colonnes à sonde et référentiel de mesures du profil vertical des vitesses en zone de jet de rive.

All of the measurements of velocities and of the water surface levels in the flume are synchronized by a data logger. We used a triggering system driven by a SA32 Type AOIP measuring station, which makes it possible to define the swing threshold for the peak level of the incidental waves, i.e. at the arrival of the crest of the wave.

The probe is a piezoelectric transducer with an emission frequency of 4 MHz and a diameter of 12 mm. It is placed on a supporting structure 24.0 mm wide, 400 mm long and 2.7 mm thick, forming an incidence angle of 25° with the flume axis. The vertical displacement of the UDV probe is governed by a differential micrometric incrementor, by which it is possible to obtain a maximum number of micro-displacements and of measurement points in the sediment bed and at the interface fluid–sediment. The minimal displacement of the UDV device is 0.5 mm. In Table 1, we present the various conditions of incidental waves in our different tests.

Incidental waves	Swash
Water depth d (m)	Period T (s)	Height H (m)	Wave length L (m)	Ratio T_up/T_b (−)	Uprush velocity u_moy (m.s⁻¹)	Water depth h_w (cm)
	6.40	0.0050	10.63	0.24	0.35	0.75
0.285	3.20	0.0340	5.20	0.38	0.46	1.60
	1.90	0.0387	2.96	0.82	0.71	1.60

	5.30	0.0082	7.65	0.33	0.46	2.10
0.270	3.20	0.036	5.14	0.35	0.36	2.10
	2.80	0.0147	4.41	0.26	0.92	2.50

	3.40	0.0277	5.28	0.40	0.34	2.15
0.260	2.90	0.0126	4.55	0.36	0.75	1.80
	2.10	0.0171	3.32	0.30	0.91	2.10

	3.40	0.0214	5.19	0.37	0.64	2.00
0.250	2.80	0.0302	4.26	0.33	0.81	2.20
	2.10	0.0498	3.21	0.48	0.75	2.10

	2.80	0.0230	4.22	0.36	0.77	2.50
0.240	2.10	0.0376	3.04	0.32	0.91	2.60
	1.90	0.0387	2.75	0.30	0.53	3.10

	5.30	0.0268	7.56	0.44	0.84	2.60
0.230	4.60	0.0134	5.43	0.38	0.61	2.10
	2.80	0.0603	4.09	0.32	0.51	2.10

3 Data processing

The ultrasonic beam delivered by the probe is cylindrical (slightly conical beyond a certain distance). In our case, it was placed on a horizontal plane perpendicular to the median plane of the flow. The particles subjected to this beam emit an answering echo collected by the probe. This echo, which depends on the angle between the ultrasonic beam and the direction of the flow, has two major characteristics:

• its frequency, which provides the velocity of the particles (Doppler Effect);
• its intensity, which depends on the size of the particles.

The signal emitted by the particles is then treated in two different and quite distinct ways:

• one related to the size of the particles;
• the other related to the dimension of the ultrasonic beam.

In the interstitial velocity within the sediment, there are particles of two quite different sizes:

• very large sediment particles;
• very small particles in suspension in the fluid which circulates between the pores.

By eliminating the echoes of great intensity in the received signal, we eliminate the echoes resulting from the large sediment particles whose velocity furthermore is zero (except at the water–sediment interface where sediment transport can exist, but this will be the subject of a forthcoming specific study). We keep only the echoes resulting from the particles suspended in the fluid (with the classical assumption that they have the same velocity as the fluid).

Keeping in mind that in a porous medium, the calibration tests showed that the velocities were estimated with an uncertainty interval varying from 75 to 80% and have a Gaussian distribution. Compared to the value of the average velocity and its standard deviation in the measurement volume, we estimated that the absolute measurement error on the velocity was ±0.2 mm/s.

4 Results

Fig. 4 represents the spectra of the various incidental and reflected waves in the flume, calculated with the method of the three fixed resistive probes (Mansard and Funke, 1980). The spectral decomposition of the signal of the free surface is obtained by a “Fast Fourier Transform” algorithm (FFT). In our case, this method is the most suitable because of the presence of a regular swash which interacts with itself, i.e. a swash at a variable phase velocity (Molin, 2002).

Fig. 4
Spectra of incidental and reflected waves generated in the wave flume.
Spectres des houles incidentes et réfléchies générées dans le canal à houle.

The analysis of the vertical velocity profiles under various conditions of incidental waves made it possible to distinguish a phase-lag between the free flow in the swash wave and the interstitial flow in the sediment bed.

Fig. 5 shows the delay of the interstitial flow following the vertical position of the swash. The maximum velocities recorded during the uprush phase provide an exponential vertical velocity profile in the sediment bed and at the interface of the swash zone, under the various studied conditions of incidental waves (Fig. 6):

\frac{u}{u_{\max}} = A_{w} \exp [α_{w} (\frac{z}{h_{b}})]

(12)

Fig. 5
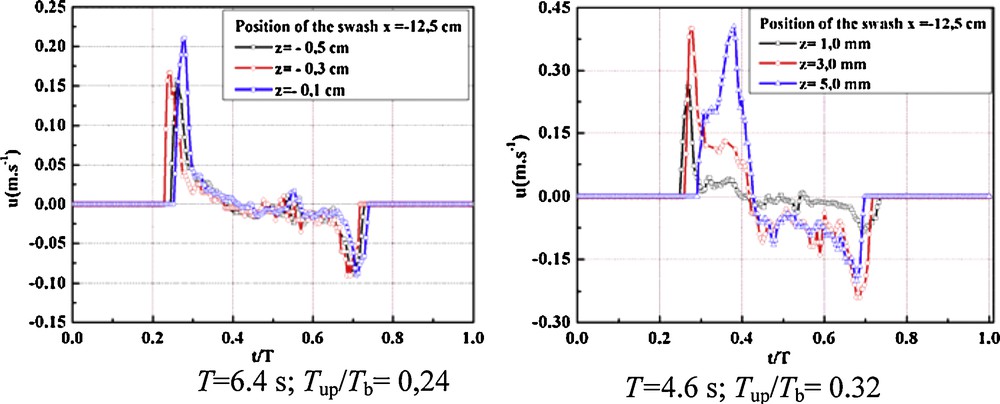
Evolution of the instantaneous velocity profiles in the swash zone at different elevations z.
Évolution du profil des vitesses instantanées en zone de jet de rive à différentes hauteurs z.

Fig. 6
a: Profile of maximum velocities in an uprush phase; b: maximum interstitial velocities and linear regression characterizing the parameter α_w value.
a : Profil des vitesses maximales en phase de jet de rive ; b : vitesses interstitielles maximales et régression linéaire caractérisant la valeur du paramètre α_w.

A_w: parameter characteristic of the hydrodynamics of the flow in the porous medium and of the velocity at the interface of the free-flow and porous flow;

α_w: parameter characterizing the nature of the velocity field in the sediment bed. It depends only on the porosity of the medium and on the conditions of the incidental waves.

Let:

U = \frac{u}{u_{\max}} and Z = \frac{z}{h_{b}}, with, Z < 0

(13)

From the shape of the function ln (U) = f (Z), we obtain directly the value of the α_w parameter characterizing the interstitial flow in the sediment bed. The experiments showed that the value of α_w depends on the characteristics of the flow generated by the swash in the swash zone. In this context, the study of the evolution of parameter α_w as a function of the incident wave characteristic $1 / \sqrt{T}$ shows an exponentially decreasing relation (Fig. 7).

Fig. 7
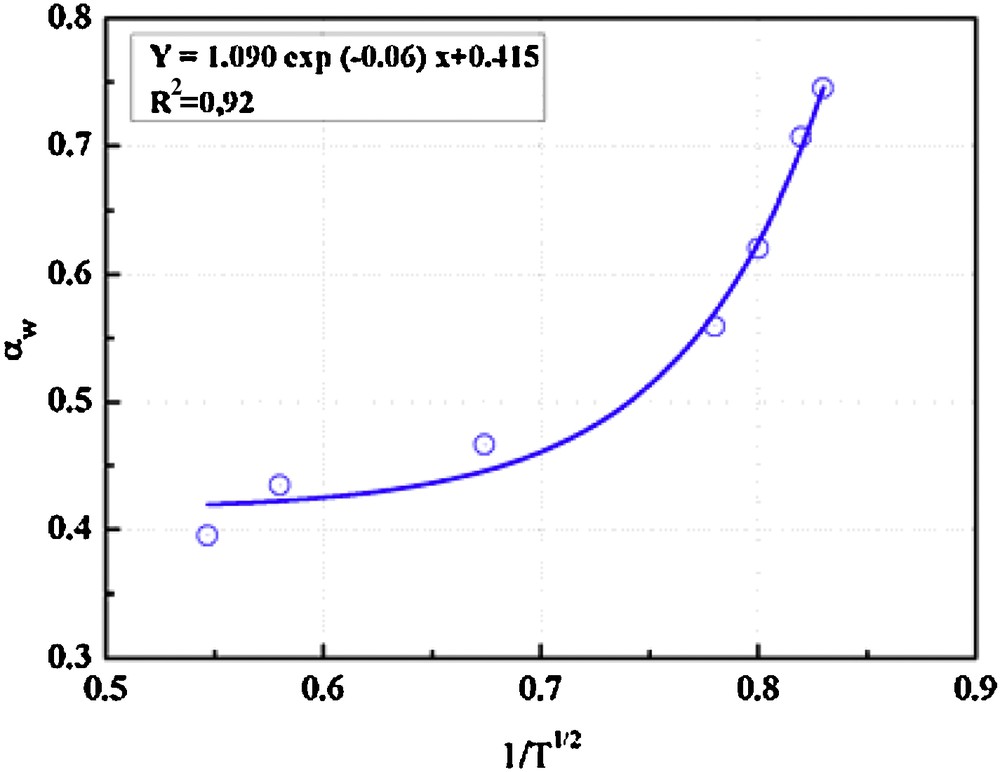
Evolution of the α_w parameter as a function of the period of the incidental wave.
Évolution du paramètre α_w en fonction de la période de la houle incidente.

This parameter also depends on the properties of the porous medium such as its porosity, its hydraulic conductivity and the diameter of the pores or interstices.

5 Conclusion

The analysis of the maximum velocity field in the phase of uprush in a swash zone over a porous sediment shows an exponential vertical velocity profile which depends not only on the characteristics of the sediment bed (porosity, hydraulic conductivity, mode of flow in the pores and interstices of the sediments), but also on the conditions of the incidental waves, in particular of their periods. In this context, our tests demonstrated non-linear relations between parameter α_w, which characterizes the velocity field and the local mode of flow in the sediment bed, and the period of the incidental swash.

The results show that the traditional models to determine the constraint on friction at the wall are not adequate, since they are based mainly on the characteristics of free flow without taking into account the nature of the sediment bed and the interaction processes occurring at the interface.

These first results suggest the need for a new approach to the analysis of the sediment transport criterion which must take into account the reality of the governing physical processes during the phases of the swash at the water-sediment interface.

Acknowledgements

This study was carried out with the financial help from the intergovernmental cooperation programme for higher education between Algeria and France (PROFAS). Our gratitude also goes to Professor Olivier Thual and an anonymous reviewer for their positive comments on an earlier draft of this article.

Bibliographie

[Beavers and Joseph, 1967] G.S. Beavers; D. Joseph Boundary conditions at a naturally permeable wall, J. Fluid Mech., Volume 30 (1967), pp. 197-207

[Brocchini and Peregrine, 1996] M. Brocchini; D.H. Peregrine Integral flow properties of the swash zone and averaging, J. Fluid Mech., Volume 317 (1996), pp. 241-273

[Butt and Russell, 2000] T. Butt; P.E. Russell Hydrodynamics and cross-shore sediment transport in the swash zone of natural beaches, J. Coastal Res., Volume 16 (2000) no. 2, pp. 255-268

[Butt et al., 2001] T. Butt; P.E. Russell; I. Turner The influence of swash infiltration-exfiltration on beach face sediment transport: onshore or offshore?, Coastal Engineering, Volume 42 (2001) no. 1, pp. 35-52

[Butt et al., 2004] T. Butt; P.E. Russell; J. Puleo; J. Milles; G. Masselink The influence of bore turbulence on sediment transport in the swash and inner surf zones, Continental Shelf Research, Volume 24 (2004), pp. 757-771

[Lhermitte, 1983] R. Lhermitte Doppler sonar observation of tidal flow, J. Geophys. Res., Volume 88 (1983), pp. 725-742

[Macocco et al., 2005] K. Macocco; Q. Grimal; S. Naïli; C. Soize Modélisation probabiliste d’une expérience ultrasonore : calcul de la dispersion sur les mesures de célérité, C. R. Mecanique, Volume 333 (2005), pp. 565-573

[Mansard and Funke, 1980] E.P.D. Mansard; E.R. Funke The measurement of incident and reflected spectra using a least squares method, Proc. 17th Costal Eng. Conf., ASCE (1980), pp. 154-172

[Mihoubi et al., 2008] M.K. Mihoubi; M. Bélorgey; A. Kettab Analysis, in a free surface steady flow, of the interstitial velocity field inside a sedimentary bed, C. R. Geoscience, Volume 340 (2008), pp. 858-864

[Molin, 2002] B. Molin Hydrodynamic structures offshore, Technip (2002), p. 440

[Takeda, 1986] Y. Takeda Velocity measurement by ultrasound Doppler shift method, Int. J. Fluid Flow, Volume 7 (1986), pp. 313-318

Commentaires - Politique

Ces articles pourraient vous intéresser

Analysis, in a free surface steady flow, of the interstitial velocity field inside a sedimentary bed

Mustapha Kamel Mihoubi; Michel Bélorgey; Ahmed Kettab

C. R. Géos (2008)

Storm extreme levels and coastal flood hazards: A parametric approach on the French coast of Languedoc (district of Leucate)

Brice Anselme; Paul Durand; Yves-François Thomas; ...

C. R. Géos (2011)