Plan
Comptes Rendus
no. 9

Hydrology, environment
Measuring runoff by plots at different scales: Understanding and analysing the sources of variation
[Mesure du ruissellement au moyen de parcelles à différentes échelles : compréhension et analyse des sources de variation]

Présenté par : Ghislain de Marsily

Lawani Adjadi Mounirou1  ; Hamma Yacouba1 ; Harouna Karambiri1 ; Jean-Emmanuel Paturel1, 2 ; Gil Mahé2
1 Institut international d’ingénierie de l’eau et de l’environnement, laboratoire hydrologie et ressources en eau, rue de la Science, 01-BP-594, Ouagadougou 01, Burkina Faso
2 Laboratoire hydrosciences Montpellier, maison des sciences de l’eau, université Montpellier II, place Eugène-Bataillon, CC MSE, 34095 Montpellier cedex 05, France
Comptes Rendus. Géoscience, Volume 344 (2012) no. 9, pp. 441-448.

Résumés

The decrease of runoff with the increase in area is not a new fact. The scale effect depends on the spatial and temporal variability of different factors, including the surface characteristics and hydrodynamic properties of the soil and the vegetation development. The purpose of our work is to study the relative influence of the sources of variation of runoff from a small Sahelian catchment on several types of soil surfaces features. Plots of different sizes (1, 50 and 150 m2) on cultivated soils and degraded soils (non-cultivated with three different types of crusts) were monitored for two consecutive years. The results show that the runoff coefficients of rainfall events range from 4 to 65% on cultivated soils and 16 to 96% on uncultivated bare and degraded soils. A statistical and dimensionless analysis shows that in degraded environments, the processes generating runoff on plots of 50 and 150 m2 are identical and significantly different from the unit plot (1 m2). The decrease in runoff with increasing scale becomes more pronounced when rainfall duration decreases. In cultivated areas, this result is not observed. Additional measurements are needed to better understand the differences in functioning at various scales of observations.

La diminution de la lame d’eau ruisselée avec l’accroissement de la superficie n’est pas un fait nouveau. L’effet d’échelle dépend de la variabilité spatiotemporelle de différents facteurs, y compris les états de surface, les propriétés hydrodynamiques des sols et la croissance de la végétation. L’objectif de notre travail est d’étudier le rôle relatif des sources de variation du ruissellement d’un petit bassin sahélien, sur plusieurs types d’états de surface. Des parcelles de différentes tailles (1, 50 et 150 m2) sur sols cultivés et sur sols dégradés (non cultivés avec trois différents types de croûtes) ont été suivies pendant deux années consécutives. Les résultats montrent que les coefficients de ruissellement par événements varient entre 4 et 65 % sur les sols cultivés et 16 et 96 % sur les sols non cultivés dégradés. Des analyses statistiques et dimensionnelles montrent qu’en milieu dégradé, les processus de génération de ruissellement sur les parcelles de 50 et 150 m2 sont identiques et significativement différents de la parcelle unitaire (1 m2). La diminution du ruissellement avec l’augmentation de l’échelle devient plus prononcée avec la décroissance de la durée de pluie. En milieu cultivé, ce résultat n’est pas observé. Des mesures complémentaires sont nécessaires pour mieux appréhender les différences de fonctionnement aux différentes échelles d’observations.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crte.2012.08.004
Keywords: Plot, Runoff, Soil surface feature, Hydrologic process, Scale effect, Sahel
Mot clés : Parcelles, Ruissellement, État de surface des sols, Processus hydrologiques, Effet d’échelle, Sahel
Lawani Adjadi Mounirou 1 ; Hamma Yacouba 1 ; Harouna Karambiri 1 ; Jean-Emmanuel Paturel 1, 2 ; Gil Mahé 2

1 Institut international d’ingénierie de l’eau et de l’environnement, laboratoire hydrologie et ressources en eau, rue de la Science, 01-BP-594, Ouagadougou 01, Burkina Faso
2 Laboratoire hydrosciences Montpellier, maison des sciences de l’eau, université Montpellier II, place Eugène-Bataillon, CC MSE, 34095 Montpellier cedex 05, France 
@article{CRGEOS_2012__344_9_441_0,
     author = {Lawani Adjadi Mounirou and Hamma Yacouba and Harouna Karambiri and Jean-Emmanuel Paturel and Gil Mah\'e},
     title = {Measuring runoff by plots at different scales: {Understanding} and analysing the sources of variation},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {441--448},
     publisher = {Elsevier},
     volume = {344},
     number = {9},
     year = {2012},
     doi = {10.1016/j.crte.2012.08.004},
     language = {en},
}
TY  - JOUR
AU  - Lawani Adjadi Mounirou
AU  - Hamma Yacouba
AU  - Harouna Karambiri
AU  - Jean-Emmanuel Paturel
AU  - Gil Mahé
TI  - Measuring runoff by plots at different scales: Understanding and analysing the sources of variation
JO  - Comptes Rendus. Géoscience
PY  - 2012
SP  - 441
EP  - 448
VL  - 344
IS  - 9
PB  - Elsevier
DO  - 10.1016/j.crte.2012.08.004
LA  - en
ID  - CRGEOS_2012__344_9_441_0
ER  - 
%0 Journal Article
%A Lawani Adjadi Mounirou
%A Hamma Yacouba
%A Harouna Karambiri
%A Jean-Emmanuel Paturel
%A Gil Mahé
%T Measuring runoff by plots at different scales: Understanding and analysing the sources of variation
%J Comptes Rendus. Géoscience
%D 2012
%P 441-448
%V 344
%N 9
%I Elsevier
%R 10.1016/j.crte.2012.08.004
%G en
%F CRGEOS_2012__344_9_441_0
Lawani Adjadi Mounirou; Hamma Yacouba; Harouna Karambiri; Jean-Emmanuel Paturel; Gil Mahé. Measuring runoff by plots at different scales: Understanding and analysing the sources of variation. Comptes Rendus. Géoscience, Volume 344 (2012) no. 9, pp. 441-448. doi : 10.1016/j.crte.2012.08.004. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2012.08.004/

Version originale du texte intégral

1 Introduction

In the Sahel, surface runoff constitutes the main source of water resources available for human, agricultural and pastoral activities. The mobilization and management of this resource in this region are very sensitive to the variability of climate (Mahé and Paturel, 2009) and require tools to quantify the runoff aptitude of the different types of soils of a catchment. However, the complexity of hydrological processes, their large variability in space and time, raise a number of basic questions on watershed hydrology (Beven, 1995; Blöschl and Sivapalan, 1995): at which scales do the major runoff physical processes occur? Which scales have to be selected for measurements and observations?

In recent decades, the evaluation of runoff has referred to experimental plots from 1 m2 to several tens of m2. These studies have shown and justified that runoff decreases with increasing plot surfaces. However, the causes of the identified scale effect are related to the characteristics of the plots, their localization on the hillslope and the objectives of each study. Thus, Cerdan et al., 2004, Gomi et al., 2008, and Mayor et al., 2011 justify the scale effect on plots by the spatial variability of soil infiltration capacity. Others indicate the dynamics of the intensity of precipitation (Stomph et al., 2002; Van de Giesen et al., 2005, 2011) and threshold effects for some processes (Le Bissonnais et al., 2006) or the development of emergent properties of soils at certain scales (Reaney et al., 2007).

In the Sahel regions, several “soil surface features units” have been identified (Casenave and Valentin, 1992) and their hydrodynamic and morphological characteristics play a significant role in the formation of runoff and the subsequent transfer within the hydrographic network. Consequently, variability in surface conditions, soil surface crusting, vegetation, and roughness can all produce different hydrologic regimes at different spatial scales.

In this study, we propose to analyze the scale effect on two types of surfaces:

  • • cultivated soils;
  • • degraded uncultivated soils, and we make an attempt to identify the factors explaining this observed scale effect.

2 Materials and methods

2.1 Study site, experimental design and measurements protocol

Runoff measurements were performed for 2 years (2010–2011) on the Tougou watershed (37 km2) located in the Sahel zone of Burkina Faso (Fig. 1). The geographical coordinates of its outlet are: 13° 40′ 56′′ N and 2° 13′ 39′′ E. It is characterized by a unimodal annual rainfall regime, and the average annual rainfall varies between 400 and 650 mm. Rainfall shows an irregular distribution over the year: large storms occurring from early or mid-May to mid- or late October provide 95% of the annual rainfall, while the other 7 months are dry. Rainfall from July to September is about 80% of annual rainfall. There has been, on average over 2 years, respectively nine, 13 and eight rainfall events (rainfall ≥ 1 mm) during these 3 months. In the high rainy season, rainstorms are recorded mainly in August and September, with maximum intensities that can reach 130 mm/h during 5 min and 70 mm/h during 30 min. The watershed, like other Sahelian watersheds, is characterized by Hortonian runoff because soils have little vegetation cover and encrusted surfaces, and a relatively deep aquifer with as main recharge points the bottom of the beds of the river network (Favreau et al., 2002).

Fig. 1

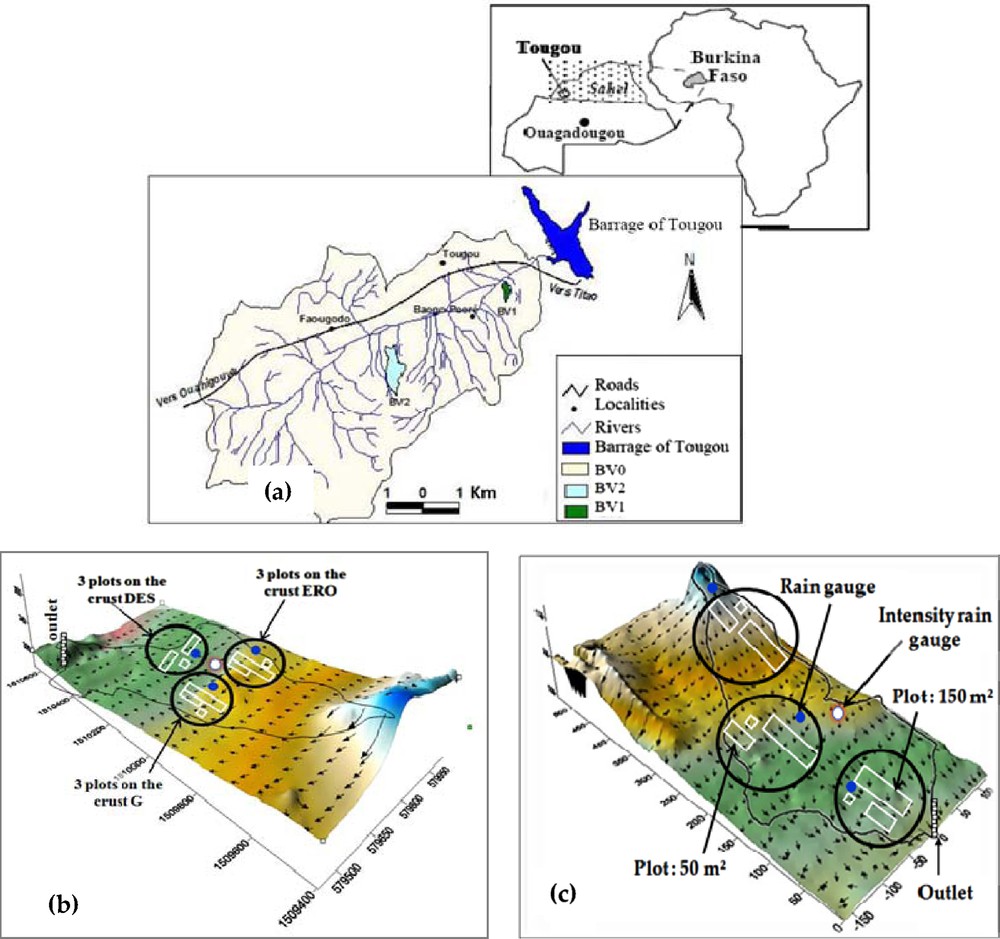
(a) The Tougou watershed and location of sub-basins; (b) sub-basin in degraded soils and experimental plots; (c) sub-basin in cultivated soils and experimental plots.

(a) Bassin versant de Tougou et localisation des sous-bassins ; (b) sous-bassin en sols dégradés et parcelles expérimentales ; (c) sous-bassin en sols cultivés et parcelles expérimentales.

In the catchment, two homogeneous hydrological units in terms of land use were identified on the basis of a thematic mapping of soils and cropping systems: the first hydrologic unit is a cultivated sub-basin (6.1 ha) and the second is a degraded uncultivated sub-basin (33.8 ha). These two units represent the main soil surface feature of the catchment area according to Casenave and Valentin (1992).

Inside each of these hydrological units, three sites were identified. On each site, a block of three plots (1 m2 (1 × 1), 50 m2 (10 × 5) and 150 m2 (25 × 6)) was installed. A network of 12 rain gauges (one per site) and five tipping bucket rain gauges (one per hydrological unit) were placed across the watershed to monitor the spatial variability of the rainfall. Each year, except for a few rainy episodes which were localised only on portions of the watershed, the entire rainfall network has always recorded some rain but with amounts varying between stations.

An overview of the experimental setup is shown in Fig. 1. The experimental design by soil surface types is presented in Table 1. Tillage, crop type and soil physical properties are described in Table 2. The hydrodynamic properties of the soil are strongly heterogeneous in cultivated areas, as evidenced by the magnitude of the parameter changes in this sub-basin. However, within the same site, the variations are much weaker. Thus, on each site, the hydrodynamic properties of the soil are assumed to be homogeneous. Only the micro-relief (slope and storage capacity) is different from one plot to another. Although the crop types are almost identical on the three sites, we observe a difference in the tillage type although we cannot tell if it is significant.

Table 1

Dispositif expérimental de l’étude.

Name of site Name of the units Type of hydrological surface Size Average slope (%) Type of surface feature Type of land use
Site S1 S1-1 Plot 1 m2 1.60
S1-50 Plot 50 m2 1.80
S1-150 Plot 150 m2 1.35
Site S2 S2-l Plot 1 m2 1.70 Cultural (C) Cultivated soils
S2-50 Plot 50 m2 1.40
S2-150 Plot 150 m2 1.60
Site S3 S3-1 Plot 1 m2 4.00
S3-50 Plot 50 m2 4.20
S3-150 Plot 150 m2 2.85
Site S4 S4-1 Plot 1 m2 0.75 Erosion (ERO)
S4-50 Plot 50 m2 1.25
S4-150 Plot 150 m2 0.93
Site S5 S5-1 Plot 1 m2 0.90 Gravelly (G) Degraded and uncultivated soils
S5-50 Plot 50 m2 0.96
S5-150 Plot 150 m2 0.80
Site S6 S6-1 Plot 1 m2 2.30 Desiccation (DES)
S6-501 Plot 50 m2 2.10
S6-502 Plot 50 m2 3.55
BV1 Sub-catchment 6.1 ha 1.91 Cultural (C) Cultivated soils
BV2 Sub-catchment 33.8 ha 1.18 ERO, G, DES Degraded and uncultivated soils
Table 2

Labour, type de culture et propriétés physiques des sols des six sites.

Site Soil type Tillage type Crop type Ksat
(mm/h)		 Ksat
(Casenave and Valentin, 1992)		 Bulk density Da
(g/cm3)		 Porosity
(%)
S1 Loam Light tillage + weeding + mounding Millet, sorghum and cowpea 21–25 1.40–1.46 45–47
S2 Sandy Means tillage + weeding + mounding Millet, sorghum and cowpea 27–33 15–35 1.36–1.44 46–49
S3 Sandy gravelly Light tillage Millet, sorghum and groundnut 16–19 1.46–1.48 44–45
S4 Dry clay No tillage No crop 2–2.5 2–4 1.58–1.61 39–40
S5 Gravelly 3–3.5 3–5 1.88–1.94 27–29
S6 Sand 12–15 10–20 1.66–1.70 36–37

2.2 Methodology of analysis

Statistical analysis was conducted on runoff coefficients to detect the scale effect for each type of soil surface. The aim was to investigate whether on each soil surface type, the mean of the runoff coefficient (arithmetic mean of the event values) was equal or significantly different on the three observation scales. The statistical analysis was made to determine, for each soil surface characteristics, the minimum representative area of the elementary processes causing the runoff.

To that end, we applied a nonparametric test, the Kruskall-Wallis test, at the threshold of 5% using the TANAGRA software (H0 = equality of the mean values of the runoff coefficient of the three plots of the same site). The Kruskall-Wallis test is the generalization of the Mann-Whitney test, which compares two samples. The power of each test has been calculated to allow confidence in the obtained result, especially when it signals “not significant”.

Then, the sources of variation were analysed on the same surface characteristics, then between them.

Since the measured hydrodynamic properties are homogeneous, the assumption that the source of variation was the slope, which differs from one plot to another, was tested. To better understand the scale effect, it is necessary to remove the influence of the slope on the runoff. For this, we defined a dimensionless number Pr, which is the ratio of the runoff coefficient of the plot by the square root of its slope. This dimensionless number Pr can be considered as the potential runoff of the plot thus overcoming the effect of the slope on runoff production. This formulation is similar to Manning's equation, which also uses the square root of the slope. Indeed, the storage surface on each plot is dependent on the runoff intensity, in steady-state regime, and on a parameter (Lafforgue, 2009) relying on the characteristics of the plot (roughness and slope). An increase of the slope causes a decrease of the storage surface, and this effect is all the more significant since the slope is weak.

To approach the scale effect between two samples, we used a scale factor defined as the ratio between the dimensionless number Pr of the largest scale (Prl) and of the smallest scale (Prs). Van de Giesen et al. (2000) defined a similar ratio by directly using the runoff coefficients of the plots.

The heterogeneity of soil hydraulic properties was tested as a source of variation in runoff on soils with different surface characteristics. For this, we compared the runoff potential of plots of equal size.

In both cases, the observed scale effect was analysed by taking into account the rainfall characteristics.

3 Results and discussion

3.1 Spatial variability of runoff

Table 3 shows at various scales the mean runoff coefficient of the main soil surface characteristics of the watershed. A comparison of results obtained on units of different land use clearly shows that the runoff is significantly higher on bare and degraded soils than on cultivated ones. These results confirm those of Rey et al. (2004) and illustrate the role of vegetation in the protection against surface hydric erosion.

Table 3

Pluviométrie et ruissellement observés pour les années 2010 et 2011 et pour différentes échelles.

Location Name of the plot Year 2010 Year 2011
Total rainfall
(mm)		 Runoff coefficient Total rainfall
(mm)		 Runoff coefficient
Average Standard deviation Coefficient of variation Average Standard deviation Coefficient of variation
Site S1: cultivated S1-1 645 0.320 0.213 0.665 460 0.279 0.123 0.441
S1-50 0.285 0.190 0.666 0.209 0.120 0.575
S1-150 0.272 0.158 0.580 0.181 0.134 0.744
Site S2: cultivated S2-1 651 0.191 0.142 0.741 461 0.208 0.111 0.533
S2-50 0.186 0.109 0.588 0.177 0.115 0.650
S2-150 0.132 0.114 0.864 0.121 0.080 0.657
Site S3: cultivated S3-1 652 0.276 0.171 0.621 459 0.256 0.133 0.520
S3-50 0.246 0.143 0.580 0.183 0.099 0.539
S3-150 0.218 0.140 0.644 0.142 0.103 0.724
Site S4: erosion S4-1 654 0.654 0.206 0.315 468 0.696 0.151 0.217
S4-50 0.711 0.217 0.305 0.760 0.132 0.174
S4-150 0.613 0.209 0.341 0.657 0.145 0.222
Site S5: gravelly S5-1 663 0.726 0.213 0.293 466 0.770 0.154 0.200
S5-50 0.658 0.229 0.348 0.700 0.146 0.209
S5-150 0.599 0.221 0.369 0.640 0.152 0.238
Site S6: desiccation S6-l 659 0.473 0.233 0.492 466 0.499 0.156 0.313
S6-501 0.264 0.126 0.480 0.296 0.087 0.293
S6-502 0.342 0.172 0.504 0.382 0.101 0.265
BV1 649 0.159 0.076 0.478 460 0.142 0.073 0.518
BV2 664 0.484 0.153 0.316 473 0.497 0.093 0.188

In cultivated areas, the event values of the runoff coefficient of plots of 50 m2 vary from 4 to 58%. The average value of the runoff depth for each scale of observation varies from one site to another. The low values of runoff were measured on site S2 because of the hydrodynamic properties of the soil surface and the tillage type (Table 2). Low runoff occurs when rain falls after a dry period or after tillage of the plots. Tillage generally decreases the bulk density, increases the porosity and changes the granulometric distribution of the soil, which causes an increase in surface storage (decrease in the connectivity rate of furrows) and an increase in the soil seepage potential (Ahuja et al., 1998; Allmaras et al., 1966; Xu and Mermoud, 2001). On the other hand, the highest runoff takes place when the soil is already wet, and in the case of exceptional rainfall events and thunderstorms.

In bare and degraded environments, runoff varies according to the nature of the crust. It is much higher on erosion (ERO) and gravelly (G) crusts than on the desiccation (DES) crust. On the 50 m2 plots, the event values of the runoff coefficient vary between 16 and 95% for the ERO and G crusts, and between 10 and 70% for the DES crust. The lowest runoffs are generally caused by small amounts of rain, which correspond to low-intensity rainfall events. On the other hand, the high runoff coefficients are recorded during high-intensity rainfall events even if the total amount of rainfall is not very large.

3.2 Statistical analysis of the runoff at various scales

The results of statistical tests applied to the obtained runoff coefficient series are shown in Table 4. The size of each series is 41 for the plots in cultivated areas and 52 in bare and degraded environments. According to the Kruskal-Wallis test, the H0 hypothesis (equality of the mean values of the runoff coefficient of the three plots at the same site) is accepted for the two cultivated sites S1 and S3, and rejected for the four other sites. However, the power of the tests for these two sites is not satisfactory when we consider the low obtained values. For the last cultivated site S2, the hypothesis H0 is rejected and the values of the power of the tests are acceptable: there is a consensus to consider a power of 80% suitable for a first kind risk. Note that the larger the sample size, the higher the power. Additional measurements must be carried out on these three sites to conclude on the equality or not of the means of the runoff coefficients.

Table 4

Résultats des tests statistiques.

Name of the site Type of plot Name of the test
Kruskal-Wallis Mann-Whitney
Results Hypothesis H0 Results Power of the test
(%)
Hypothesis H0 Power of the test
(%)
Site S1: cultivated 1 m2 Acc 31 μ 1 m 2 = μ 50 m 2 Acc 20
50 m2 μ 1 m 2 = μ 150 m 2 Acc 38
150 m2 μ 50 m 2 = μ 150 m 2 Acc < 10
Site S2: cultivated 1 m2 Rej 67 μ 1 m 2 = μ 50 m 2 Acc < 10
50 m2 μ 1 m 2 = μ 150 m 2 Rej 64
150 m2 μ 50 m 2 = μ 150 m 2 Rej 64
Site S3: cultivated 1 m2 Acc 54 μ 1 m 2 = μ 50 m 2 Acc 22
50 m2 μ 1 m 2 = μ 150 m 2 Acc 54
150 m2 μ 50 m 2 = μ 150 m 2 Acc 19
Site S4: erosion 1 m2 Rej 90 μ 1 m 2 = μ 50 m 2 Rej 85
50 m2 μ 1 m 2 = μ 150 m 2 Rej 86
150 m2 μ 50 m 2 = μ 150 m 2 Acc 54
Site S5: gravelly 1 m2 Rej 84 μ 1 m 2 = μ 50 m 2 Rej 82
50 m2 μ 1 m 2 = μ 150 m 2 Rej 85
150 m2 μ 50 m 2 = μ 150 m 2 Acc 62
Site S6: desiccation 1 m2 Rej 96 μ 1 m 2 = μ 50 m 2 Rej 94
50 m2 μ 1 m 2 = μ 50 m 2 Rej 95
50 m2 μ 50 m 2 = μ 50 m 2 Acc 75

On the other hand, on bare and degraded sites, the high values of the power of the test confirm the alternative hypothesis: the average runoff coefficients at the tested scales are significantly different. According to the Mann-Whitney test, the mean values of the plots of 50 and 150 m2 are equal but significantly different from the 1 m2 plots at the threshold of 5%. From these results, we can say that on degraded sites, a plot of 50 m2 is sufficient to study the elementary processes of runoff generation.

3.3 Measure of the scale effect

Fig. 2 shows the average values of the scale factor of the plots. A trend is observed on degraded soils. The ratio of runoff potential between plots of 50 and 1 m2 is about 0.86 for the erosion and gravelly crusts and 0.60 for the desiccation crust. This means that for a slope length ratio equal to 1/10, an isolated plot of 1 m2 generates about 1.16 times more runoff per unit surface than an area of 50 m2 for the erosion and gravelly crusts, and about 1.66 times more for the desiccation crust. Moreover, the ratio of potential runoff between the plots of 150 and 50 m2 is equal to 1 for the three crusts. This also confirms the results of the statistical analysis of the functioning of the plots in degraded areas. We can confirm that it is the same dominant processes that occur at both scales. It can be assumed that beyond a length of 10 m (= length of the plot of 50 m2), there is sufficient runoff energy for the entire flow from upstream to reach the downstream of the plot.

Fig. 2

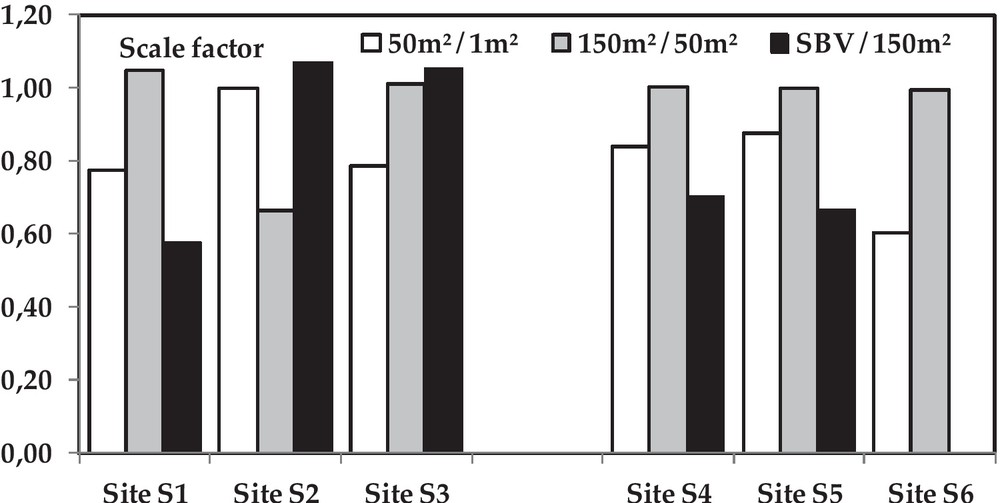
Scaling factors for runoff at different scales of observation on six sites (S1 to S3: cultivated sites; S4 to S6: degraded sites).

Facteurs d’échelle pour le ruissellement à différentes échelles d’observation pour les six sites (S1 à S3 : sites cultivés ; S4 à S6 : sites dégradés).

On cultivated soils, the values of the scale factor vary much more, depending on the site: this is due to the heterogeneity of the soil surface characteristics of the sub-basin. Sites S1 and S3 have a similar hydrological behaviour; the ratio between 50 and 1 m2 plots is about 0.77. However, the same ratio between the plots of 150 and 50 m2 is about 1.03. This means that the runoff-generating surfaces on the plots of 50 m2 are fragmented whereas they are connected on the plots of 150 m2. This phenomenon can be explained by the depressions caused by the tillage. This dimensionless analysis confirms that both in cultivated soils and bare and degraded soils, runoff decreases as the plot size increases.

3.4 Factors explaining the scale effect

In order to understand the causes of this scale effect, we compared the mean runoff coefficients per plot of the same size, and the runoff coefficients by events of three plots on each of the soil surface types.

The comparison of plots of the same size showed that the mean runoff coefficient varies significantly from one site to another. These results concur with those of Cammeraat (2004) and show that the measurement site strongly influences the results. They are related to the variation of the hydrodynamic properties of soil surface characteristics: slope and in cultivated areas, tillage techniques (Table 2).

At the same scale of observation, the production of runoff depends more on the hydrodynamic properties of soils surface characteristics than on the rainfall parameters. Some results of the comparison between the runoff coefficients per rainfall event on the three plots within the same site are illustrated in Fig. 3. The coordinates of each point correspond: on the x-axis, to the event runoff coefficient of the smaller plot and on the y-axis, to the event runoff of the largest plot. The black dots in Figs. 3a,b correspond to rainfall events of short duration or low intensity.

Fig. 3

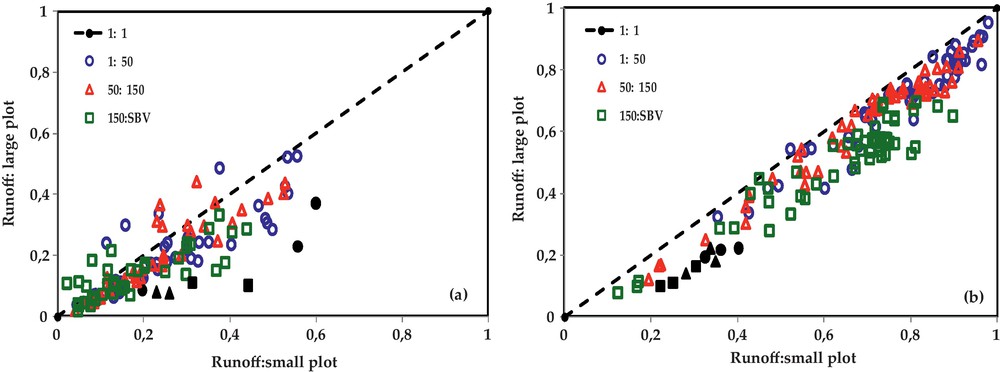
Comparison by event of the runoff coefficients of three plots set up on each of the surface textures: (a) cultivated site S3; (b) degraded site S5.

Comparaison, par évènement, des coefficients de ruissellement de trois parcelles installées sur chacune des textures de surface : (a) site cultivé S3 ; (b) site dégradé S5.

On degraded and bare soils (Fig. 3b), we see that almost all dots in the cloud are below the diagonal. The surface characteristics have not changed, the slope of the plots and the dynamics of precipitation are the only sources of variation.

On the cultivated soils (Fig. 3a), the results are a little mixed due to the edaphic soil conditions (tilled or not) of the plots which are not the same before each rain event. Some dots on the three graphs are above the diagonal. They correspond to the points where the conditions of surface characteristics are different. For example, some (150: SBV) dots are above the diagonal because the plot of 150 m2 is tilled while much of the sub-basin is not. If the soil moisture and surface characteristics are comparable, the runoff decreases with the increase in the plot size.

The analysis by class of rainfall events corroborates those of Stomph et al. (2002) who showed that the decrease in runoff with increasing slope length becomes more pronounced with shorter rain duration.

4 Conclusions

The results presented in this article illustrate the complexity of the hydrological processes and the number of parameters involved in the genesis of runoff. Through this study, we identified and analysed at different plot scales the causes of the well-known phenomenon of “decreasing runoff when the area of the plots increases”. Our results show that the scale effect observed in the runoff is mainly due to the spatial heterogeneity of soil-surface characteristics. It becomes more pronounced when the duration of the rain decreases.

For both cultivated and bare and degraded soil surfaces, the scale effects are not the same and the position on the hill slopes of measurement plots strongly influences the results.

On the basis of statistical and dimensionless analyses, the results show that in degraded environments, the runoff generation processes on plots of 150 and 50 m2 are identical and significantly different from those on the 1 m2 plot. In cultivated areas, additional measures are needed to better understand the differences in functioning at various scales. In cultivated areas, the tillage increases soil infiltration, and reduces the connectivity of runoff areas.

Indeed, the scale effect issue is critical when attempting to transpose to larger spatial scales, the knowledge of the processes discovered at the scale of a plot. Our results are consistent with other studies that indicate the existence of a large-scale effect between the plot and the watershed.

Acknowledgments

The study received financial support from the European Union within the framework of the AMMA program (African Monsoon Multidisciplinary Analyses), the Swiss Cooperation (SDC) and IRD/HSM (HydoSciences Montpellier). The authors thank all field observers, technicians and trainees who contributed to data collection. They also thank the two reviewers Pierre Dubreuil and Bénédicte Augeard, and an anonymous referee for constructive suggestions to improve this article.

Bibliographie

[Ahuja et al., 1998] L. Ahuja; F. Fieldler; G. Dunn; J. Benjamin; A. Garrison Changes in soil water retention curves due to tillage and natural reconsolidation, Soil Sci. Soc. Am. J., Volume 62 (1998), pp. 1228-1233

[Allmaras et al., 1966] P. Allmaras; R. Burwell; W. Larson; R. Holt Total porosity and random roughness of the interrow zone as influenced by tillage, USDA, Washington, 1966 (Report 7)

[Beven, 1995] K. Beven Linking parameters across scales: subgrid parametrizations and scale dependent hydrological models, Hydrol. Process, Volume 9 (1995), pp. 507-527

[Blöschl and Sivapalan, 1995] G. Blöschl; M. Sivapalan Scale issues in hydrological modelling. A review, Hydrol. Process, Volume 9 (1995), pp. 251-290

[Cammeraat, 2004] L.H. Cammeraat Scale dependent thresholds in hydrological and erosion response of a semi-arid catchment in Southeast Spain, Agr. Ecosyst. Environ., Volume 104 (2004), pp. 317-332

[Casenave and Valentin, 1992] A. Casenave; C. Valentin A runoff capability classification system based on surface features criteria in semi-arid areas of West Africa, J. Hydrol., Volume 130 (1992), pp. 231-249

[Cerdan et al., 2004] O. Cerdan; Y. Le Bissonnais; G. Govers; V. Lecomte; K. Oost; A. Couturier; C. King; N. Dubreuil Scale effect on runoff from experimental plots to catchments in agricultural areas in Normandy, J. Hydrol., Volume 299 (2004), pp. 4-14

[Favreau et al., 2002] G. Favreau; C. Leduc; C. Marlin; A. Guéro Une dépression piézométrique naturelle en hausse au Sahel (Sud-Ouest du Niger), C. R. Geoscience, Volume 334 (2002), pp. 395-401

[Gomi et al., 2008] T. Gomi; R.C. Sidle; S. Miyata; K. Kosugi; Y. Onda Dynamic runoff connectivity of overland flow on steep forested hillslopes: scale effects and runoff transfer, Water Resour. Res., Volume 44 (2008), p. W08411 (doi:10.1016/2007WR005894)

[Lafforgue, 2009] A. Lafforgue Détermination des variations de la capacité d’absorption d’un sol en place sous averses simulées/Obtaining variations of field infiltration capacity from simulated rainstorm experiments, Hydrol. Sci. J., Volume 23 (2009) no. 3, pp. 355-372

[Le Bissonnais et al., 2006] Le Bissonnais, Y., Raclot, D., Andrieux, P., Moussa, R., Louchart, X., Voltz, M., 2006. Effets d’échelle et variabilité de l’érosion entre parcelle et bassin versant en région de vignoble méditerranéen (France). In: Actes de la session VII organisée par le Réseau E-GCES de l’AUF au sein de la conférence ISCO de Marrakech (Maroc), pp. 325–330.

[Mahé and Paturel, 2009] G. Mahé; J.E. Paturel 1896–2006 Sahelian annual rainfall variability and runoff increase of Sahelian Rivers, C. R. Geoscience, Volume 34 (2009) no. 7, pp. 538-546

[Mayor et al., 2011] A.G. Mayor; S. Bautista; J. Bello Scale-dependent variation in runoff and sediment yield in a semiarid Mediterranean catchment, J. Hydrol., Volume 397 (2011), pp. 128-135

[Reaney et al., 2007] S.M. Reaney; L.J. Bracken; M.J. Kirkby Use of the connectivity of runoff model (CRUM) to investigate the influence of storm characteristics on runoff generation and connectivity in semi-arid areas, Hydrol. Process, Volume 21 (2007), pp. 894-906

[Rey et al., 2004] F. Rey; J.-L. Ballais; A. Marre; G. Rovéra Rôle de la végétation dans la protection contre l’érosion hydrique de surface, C. R. Geoscience, Volume 336 (2004), pp. 991-998

[Stomph et al., 2002] T.J. Stomph; N. De Ridder; T.S. Steenhuis; N.C. Van de Giesen Scale effects of hortonian overland flow and rainfall-runoff dynamics: laboratory validation of a process-based model, Earth Surf. Proc. Land., Volume 27 (2002), pp. 847-855

[Van de Giesen et al., 2000] N.C. Van de Giesen; T.J. Stomph; N. de Ridder Scale effects of Hortonian overland flow and rainfall runoff dynamics in a West African catena landscape, Hydrol. Process, Volume 14 (2000), pp. 165-175

[Van de Giesen et al., 2005] N.C. Van de Giesen; T.J. Stomph; N. de Ridder Surface runoff scale effects in West African watersheds: modelling and management options, Agr. Water Manage., Volume 72 (2005), pp. 109-130 (doi:10.1016/j.agwat.2004.09.007)

[Van de Giesen et al., 2011] N.C. Van de Giesen; T.J. Stomph; A.E. Ayaji; F. Bagayoko Scale effects in Hortonian surface runoff on agricultural slopes in West Africa: field data and models, Agr. Ecosyst. Environ., Volume 142 (2011) no. 1–2, pp. 95-101

[Xu and Mermoud, 2001] D. Xu; A. Mermoud Topsoil properties affected by tillage practices in North China, Soil Till. Res., Volume 60 (2001), pp. 11-19

Commentaires - Politique

Ces articles pourraient vous intéresser

Future climate or land use? Attribution of changes in surface runoff in a typical Sahelian landscape

Roland Yonaba; Lawani Adjadi Mounirou; Fowé Tazen; ...

C. R. Géos (2023)

1896–2006 Sahelian annual rainfall variability and runoff increase of Sahelian Rivers

Gil Mahé; Jean-Emmanuel Paturel

C. R. Géos (2009)

Efficiency of contour benches, filling-in and silting-up of a hillside reservoir in a semi-arid climate in Tunisia

Noamen Baccari; Mohamed Rached Boussema; Jean-Marie Lamachère; ...

C. R. Géos (2008)