Abridged English version
A tidal bore is a positive surge propagating upstream that may form when a significant amplitude rising tide enters shallow, gently sloping and narrowing rivers. If qualitative observations of high-intensity tidal bores (i.e. mascaret in French) have been made in many places worldwide, only a few field experiments (e.g. Simpson et al., 2004; Wolanski et al., 2004) have been devoted to a quantitative study of the tidal bore dynamics. In this paper, we present a study on tidal bore occurrence and dynamics in the two main macrotidal French estuaries: the Seine and Gironde/Garonne estuaries. The field campaigns were conducted simultaneously in the Seine and Garonne Rivers in 2011 around autumn equinox (low flow discharges). In the Seine River, we chose two field sites: the first one in Caudebec-en-Caux (55 km upstream from the estuary mouth), located where tidal bore intensity reached its maximum amplitude until the mid-1960s, and the second one in Val-des-Leux, 100 km upstream from the estuary mouth. The Garonne field site was situated at Podensac, 126 km upstream from the estuary mouth. This site was selected owing to the presence, during spring tide, of well-developed undular tidal bores (Fig. 1). Pressure sensors (Ocean Sensor System) were moored in the three sites. High-frequency (10 Hz) pressure measurements were converted to water depth, taking into account non-hydrostatic effects. Our method has been validated by comparing its results with direct acoustic surface tracking measurements (AWAC, Nortek).

Illustration de la forme caractéristique des ressauts de marée ondulés de forte intensité (i.e. mascarets) dans la Garonne. Photo aérienne réalisée le 10 septembre 2010 à 500 m en aval de notre site de mesure de Podensac. La largeur du plan d’eau, à basse mer, est de 145 m. TR = 6,3 m (marnage sur site), F = 1,26.
Illustration of the characteristic shape of high-intensity undular tidal bore propagating in the Garonne River. Aerial photograph taken 10 September 2010, 500 m downstream our field site in Podensac. The low tide wetted width is 145 m. TR = 6.3 m (local tidal range), F = 1.26.
Fig. 2 presents time series of water elevation when the tide flow turns to rising at Podensac (Garonne). We observe at spring tide (Fig. 2a) a well-developed undular tidal bore, characterized by a Froude number equal to 1.24 and a first wave-front height of 1.57 m. During the 2011-campaign, tidal bores occurred for all tides even at neap tide (Fig. 2b), where a low intensity tidal bore (F = 1.04) formed. These observations are consistent with previous long-term experiments in 2010 (Bonneton et al., 2011c, d), which showed that tidal bores occur in Podensac for a large majority of tides: around 90% during autumn equinox (low flow discharges) and 60% during spring equinox (high flow discharges). In the Seine River, tidal bores have nearly disappeared due to river training and dredging. For instance, we did not observe tidal bore at Caudebec-en-Caux even for the highest spring tide. However, further upstream at Val-des-Leux, we have identified well-developed tidal bores (Fig. 3). For the highest tide, we observe (Fig. 3a) an undular bore characterized by a Froude number of 1.07 and a first wave-front height of 1.02 m. Fig. 4 presents the evolution of the dimensionless wavelength (λ/D1) of the secondary wave field as a function of the Froude number, for both Seine and Garonne data. When the Froude number is larger than a critical value Fc (Fc ∼ 1.1 at Podensac), λ/D1 is in agreement with Lemoine's theory and laboratory experiments conducted in rectangular channels (Favre, 1935; Treske, 1994). This undular tidal bore regime corresponds to high-frequency and high-steepness secondary waves (Figs. 1 and 2a) and is named mascaret in French. For F < Fc, the high-frequency mode strongly decreases in amplitude and the wave field is then dominated by low-frequency waves (large λ/D1), which are not easily observable without quantitative water-depth measurements. Tidal bores, observed for the first time at Val-des-Leux (Seine), correspond to this low-frequency and low-steepness regime.
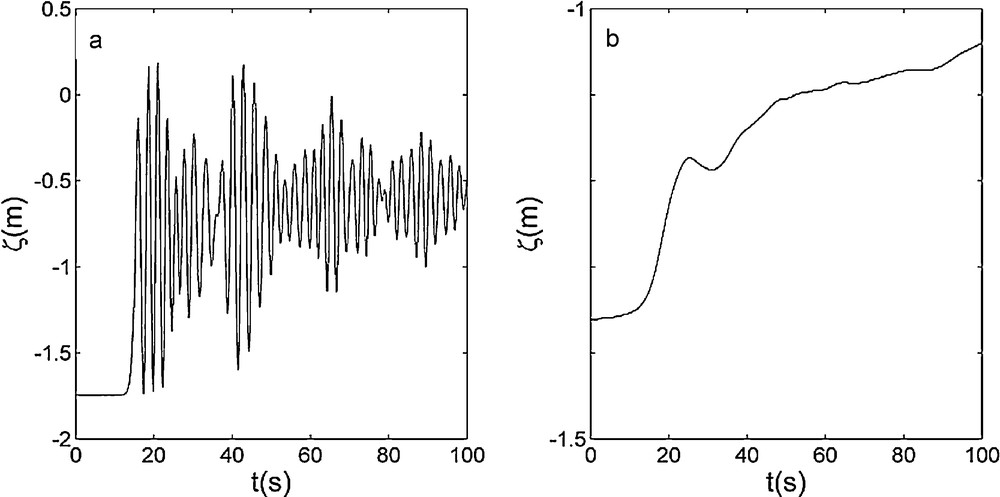
Évolution temporelle de l’élévation du plan d’eau (cote NGF-IGN69) à Podensac (Garonne) au début de la marée montante. Marées d’équinoxe 2011 : a : marée de vive-eau le 31 août (5 h38’ TU), coef = 111, TR = 6,17 m, F = 1,24 ; b : marée de morte-eau le 6 septembre (22h49’ TU), coef = 42, TR = 4,27 m, F = 1,04.
Time evolution of water elevation (NGF-IGN69) at Podensac (Garonne) when the tidal flow turns to rising. Equinox tides 2011: a: spring tide of 31st August (5 h38’ UT), coef = 111, TR = 6.17 m, F = 1.24; b: neap tide of 6th September (22h49’ UT), coef = 42, TR = 4.27 m, F = 1.04.
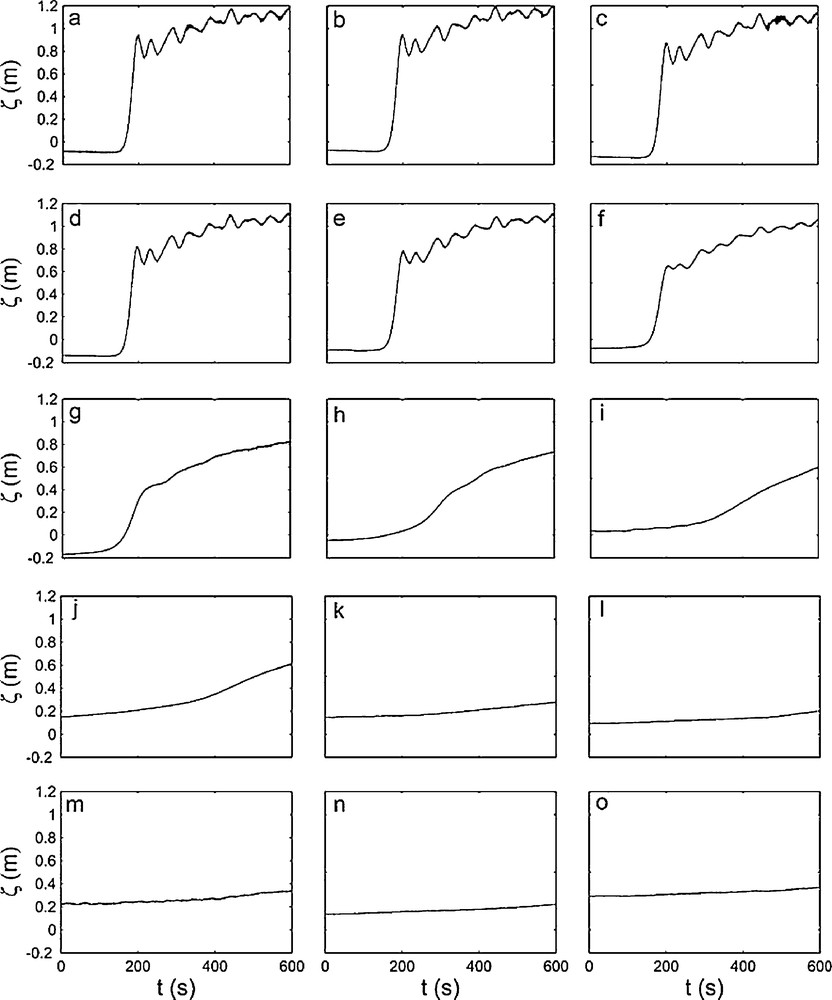
Évolution temporelle de l’élévation du plan d’eau (cote NGF-IGN69) à Val-des-Leux (Seine) au début de la marée montante. Marées d’équinoxe en 2011 du 31 août (10 h42’ TU) au 7 septembre (16h42’ TU). TR est le marnage local et non pas celui à l’entrée de l’estuaire : a : coef = 111, TR = 3,68 m, F = 1,07 ; b : coef = 108, TR = 3,65 m, F = 1,07 ; c : coef = 105, TR = 3,72 m, F = 1,07 ; d : coef = 99, TR = 3,72 m, F = 1,06 ; e : coef = 92, TR = 3,61 m, F = 1,06 ; f : coef = 85, TR = 3,44 m, F = 1,05 ; g : coef = 76, TR = 3,40 m, 1,04 ; h : coef = 67, TR = 3,14 m ; i : coef = 59, TR = 3,13 m ; j : coef = 51, TR = 2,75 m ; k : coef = 45, TR = 2,60 m ; l : coef = 42, TR = 2,41 m ; m : coef = 42, TR = 2,24 m ; n : coef = 45, TR = 2,45 m ; o : coef = 49, TR = 2,35 m.
Time evolution of water surface elevation (altimetry NGF-IGN69 system) at Val-des-Leux (Seine) when the tide flow turns to rising. Equinox tides in 2011 from the 31 August (10 h42’ UT) to the 7 September (16h42’ UT). TR is the field site tidal range: a: coef = 111, TR = 3.68 m: F = 1.07; b: coef = 108, TR = 3.65 m, F = 1.07; c: coef = 105, TR = 3.72 m, F = 1.07; d: coef = 99, TR = 3.72 m, F = 1.06; e: coef = 92, TR = 3.61 m, F = 1.06; f: coef = 85, TR = 3.44 m, F = 1.05; g: coef = 76, TR = 3.40 m, 1.04; h: coef = 67, TR = 3.14 m; i: coef = 59, TR = 3.13 m; j: coef = 51, TR = 2.75 m; k: coef = 45, TR = 2.60 m; l: coef = 42, TR = 2.41 m; m: coef = 42, TR = 2.24 m; n: coef = 45, TR = 2.45 m; o: coef = 49, TR = 2.35 m.
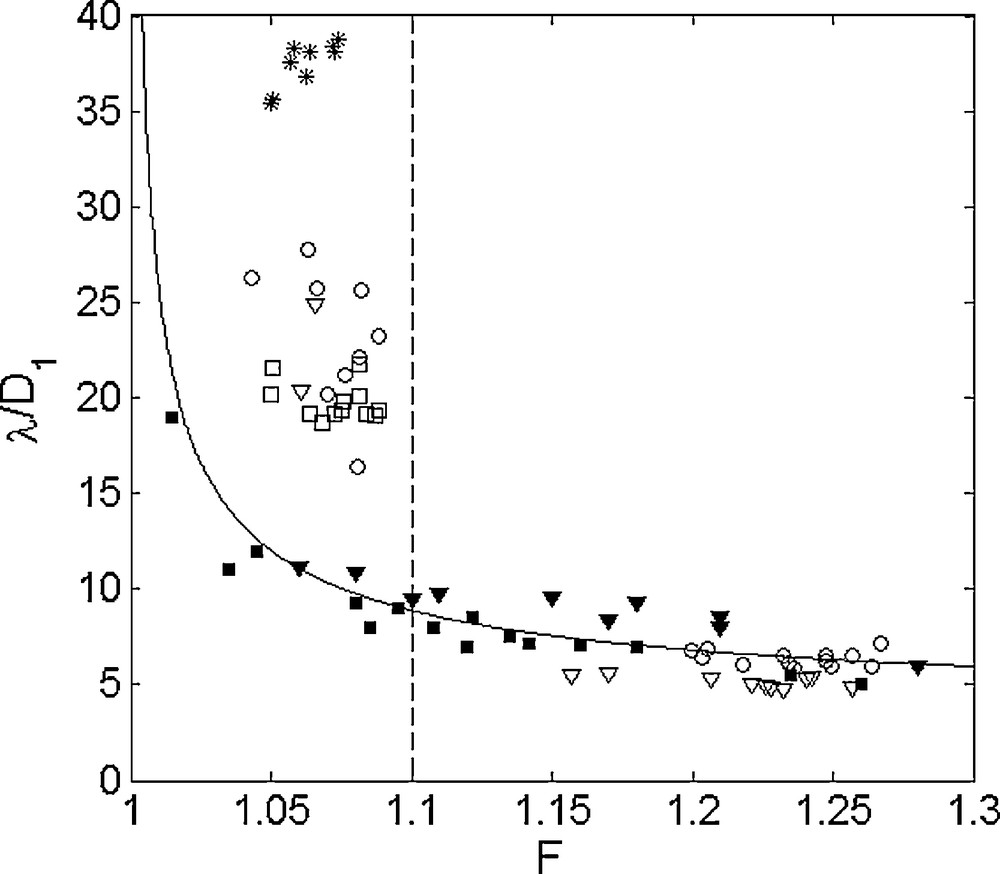
Longueur d’onde adimensionnée en fonction du nombre de Froude F. : TBG1 ; : TBG2 ; ▿ : Garonne 2011 ; : Seine 2011 ; : canal rectangulaire, Treske (1994) ; : canal rectangulaire, Favre (1935) ; ––– : théorie de Lemoine (1948).
Dimensionless wavelength in function of the Froude number F. : TBG1; : TBG2; ▿: Garonne 2011; : Seine 2011; : rectangular channel, Treske (1994); : rectangular channel, Favre (1935); –––: Lemoine's theory (1948).
1 Introduction
Lorsqu’une marée de forte amplitude se propage dans un estuaire convergent de faible pente, on peut observer, au début du flot, la formation et la propagation d’un ressaut en translation. Nous dénommerons, par la suite, ce phénomène ressaut de marée (noté RM), terminologie inspirée de « tidal bore » en anglais. Nous réserverons le terme mascaret, conformément à son usage commun et aux définitions des dictionnaires, aux RM suffisamment intenses (déferlants ou non déferlants) pour être facilement perceptibles à l’œil nu (Fig. 1). S’il existe de nombreuses observations qualitatives des RM de fortes intensités (i.e. mascarets) dans différents estuaires du monde, peu d’études ont analysé quantitativement leur dynamique en milieu naturel (exemple : Simpson et al., 2004 ; Wolanski et al., 2004) et, en particulier, sur une large gamme de nombres de Froude incluant des RM de faibles intensités (Bonneton et al., 2011a, c, d). Pourtant, les RM peuvent jouer un rôle important sur les écosystèmes estuariens, en particulier en termes de mise en suspension des sédiments et d’érosion des berges (Chanson, 2011). Il est donc essentiel d’avoir une meilleure connaissance de l’occurrence et de l’intensité des RM dans les principaux systèmes fluvio-estuariens macrotidaux.
Parmi les grands estuaires français, la Seine et le système Gironde/Garonne/Dordogne ont été les deux environnements macrotidaux où l’on observait les mascarets les plus fréquents et intenses (Comoy, 1881). Les aménagements très importants entrepris à partir du milieu du xixe siècle, en termes d’endiguement, de dragage ainsi que d’exploitation des granulats, ont eu un fort impact sur la propagation de la marée et donc sur l’occurrence, l’intensité et la localisation des mascarets (Foussard et al., 2010 ; Malandain, 1988 ; Parisot et al., 2010). Afin de contribuer à une meilleure caractérisation de l’état actuel des RM dans les grands estuaires français, nous avons réalisé en 2011 deux campagnes de mesures simultanées sur la Seine et la Garonne, lors des marées d’équinoxe d’automne. En nous appuyant sur ces deux campagnes, ainsi que sur les mesures réalisées sur la Garonne en 2010 (Bonneton et al., 2011a, c, d), nous présentons dans cet article une analyse de l’occurrence et de la dynamique des RM dans la Seine et la Garonne.
La structure des ressauts en translation est principalement contrôlée par le nombre de Froude F, défini par , où cb est la célérité du front et D1 et u1 les profondeur et vitesse (intégrée suivant la verticale) à l’avant du ressaut. Lorsque F est faiblement supérieur à 1, les ressauts sont de forme ondulée et non déferlants. Dans des canaux rectangulaires, pour le régime non déferlant, il est bien connu (Favre, 1935) que la structure des ondulations secondaires évolue progressivement lorsque F augmente, avec, en particulier, une augmentation de l’amplitude et une diminution de la longueur d’onde. L’augmentation de la cambrure avec F conduit au déferlement de la première onde, lorsque F devient supérieur à F1 (F1 de l’ordre de 1,2–1,3). Les ondes secondaires voient leur amplitude diminuer avec F et elles disparaissent pour F > F2 (F2 de l’ordre de 1,45–1,5), laissant place à un ressaut pleinement déferlant. Les ressauts de marée observés de par le monde sont le plus souvent de type ondulé (non déferlant ou partiellement déferlant) et très rarement de type pleinement déferlant (Chanson, 2011). Dans cet article, nous analysons la structure du champ d’ondes secondaires associé aux RM ondulés. Nous montrons que, dans un milieu fluvial naturel, avec des berges en pente douce, il existe un changement de régime pour les RM autour d’un nombre de Froude critique Fc. Pour F > Fc, on observe des ondes secondaires de fortes cambrures, aux caractéristiques voisines de celles observées en canal rectangulaire. Ce type de RM ondulé, énergétique et visuellement observable, correspond au phénomène dénommé en français mascaret ou la barre (les RM pleinement déferlants et non ondulés sont aussi qualifiés de mascaret). En revanche, pour F < Fc les RM ondulés sont caractérisés par une cambrure beaucoup plus faible que celle observée en canal rectangulaire pour un même nombre de Froude.
2 Sites d’étude
Des mascarets très puissants pouvaient autrefois se former dans la Seine. Ils atteignaient leur intensité maximale à Caudebec-en-Caux, avec une hauteur du premier front de vague dépassant 2,0 m (Foussard et al., 2010). Le front d’onde pouvait alors déferler sur toute la largeur du fleuve (Malandain, 1988). Des travaux continus d’endiguement et de dragage de la Seine, depuis le milieu du xixe siècle, ont conduit à la formation d’un chenal uniforme et profond (profondeur supérieure à 10 m) qui n’est plus favorable à la formation de mascaret. Sa dernière apparition sous sa forme spectaculaire a eu lieu en 1963, et sa quasi-disparition s’est produite suite à l’aménagement de l’embouchure en 1979 (Foussard et al., 2010). Cependant, par forts coefficients de marée, une onde de faible intensité peut être encore visible en amont de Caudebec-en-Caux entre Duclair et Sahurs (Loïc Le Louargant, communication personnelle). Afin d’étudier les RM sur la Seine, nous avons identifié deux sites d’étude. Le premier, à Caudebec-en-Caux, situé à 55 km en amont de l’embouchure (le point 0 étant l’extrémité ouest de la digue du Ratier), a été choisi pour des raisons historiques, car il était le lieu où les mascarets étaient autrefois les plus intenses. Le second site instrumenté a été Val-des-Leux situé à 100 km en amont de l’embouchure, dans une zone semblant actuellement plus propice à la formation de RM. Les mesures ont été réalisées du 25 août au 13 septembre 2011. Nous nous sommes focalisés plus particulièrement sur les marées comprises entre les vives-eaux du 31 août (coef. 111) et les mortes-eaux du 6 septembre (coef. 42). Dans la Seine, le marnage (TR), par vives-eaux, décroît fortement lors de la propagation de la marée dans le fleuve. Pour la marée de vive-eau du 31 août, TR a évolué de 7,50 m à l’embouchure de l’estuaire à 4,85 m à Caudebec-en-Caux, puis 3,70 m à Val-des-Leux. En morte-eau, le 6 septembre, TR est passé de 3,45 m à l’embouchure à 2,70 m à Caudebec-en-Caux, puis 2,25 m à Val-des-Leux. Sur ces deux sites, l’onde de marée est très asymétrique, avec une durée du montant de 4 h 5 min en vive-eau. Le débit moyen sur la période de mesures a été de 216 m3/s, valeur très légèrement supérieure au débit moyen à cette saison, mais bien inférieur au débit moyen annuel de 365 m3/s. Pour les marées de vive-eau, la profondeur hydraulique à basse mer était de 7,7 m à Val-des-Leux.
Dans le système fluvio-estuarien Gironde/Garonne/Dordogne, par forts coefficients, des mascarets intenses sont actuellement observables aussi bien dans la Garonne que dans la Dordogne, avec des hauteurs de vagues (Hb) pouvant dépasser 1,5 m. Dans le cadre de cette étude, nous nous sommes concentrés sur la dynamique des RM dans la Garonne. Comoy (1881) observait à son époque que le mascaret pouvait se former légèrement en amont de la confluence des deux rivières et atteignait son amplitude maximale légèrement en amont de Bordeaux, à environ 94 km en amont de l’embouchure (le point 0 étant situé au Verdon), pour ensuite diminuer d’intensité et disparaître vers Portets (115 km en amont de l’embouchure). La localisation des mascarets dans la Garonne est à présent fortement décalée en amont du fleuve. Ils se forment dorénavant en amont de Bordeaux, atteignent une amplitude maximale proche de Podensac (126 km en amont de l’embouchure), puis décroissent et disparaissent vers Langon (141 km en amont de l’embouchure) (Bonneton et al., 2011d). Ce décalage vers l’amont des RM est à relier aux fortes augmentations de marnage dans la Garonne, observées depuis le milieu du xixe siècle en amont de Bordeaux (jusqu’à 3 m d’augmentation à Cadillac entre 1847 et 1961). De plus, Castaing et al. (2006) ont montré que ce phénomène s’était poursuivi à la suite des dragages ainsi que des extractions de granulat qui ont fortement modifié le lit du fleuve à partir des années 1960. Afin de caractériser la dynamique actuelle des RM dans la Garonne, deux campagnes de mesures de grande ampleur ont été réalisées en 2010 (Bonneton et al., 2011a, c, d) autour des marées d’équinoxe de printemps, du 24 février au 15 avril (campagne TBG1), et des marées d’équinoxe d’automne, du 1er septembre au 22 octobre (campagne TBG2). Des mesures complémentaires ont été mises en œuvre pendant les marées d’équinoxe d’automne 2011, au même moment que celles réalisées sur la Seine. Nous avons choisi le site de Podensac (126 km en amont de l’embouchure), qui est une zone où le marnage est proche de sa valeur maximale dans la Garonne et où les mascarets sont de fortes intensités. Pour la marée de vive-eau (31 août 2011, coef. 111) TR a évolué de 5,04 m à l’embouchure de l’estuaire (le Verdon) à 6,17 m à Podensac. En morte-eau (6 septembre 2011, coef. 42) TR est passé de 2,35 m à l’embouchure à 4,27 m à Podensac. Sur ce site, l’onde de marée est très asymétrique avec une durée du montant de 3 h 12 min en vive-eau. Le débit moyen sur la période de mesures a été de 135 m3/s, valeur inférieure à la moyenne pour cette période qui est de l’ordre de 180 m3/s. La profondeur hydraulique à basse mer a peu varié autour d’une valeur moyenne de 2,7 m.
3 Méthodes
Dans cet article, nous analysons principalement des mesures d’élévation de la surface libre. En 2011, nous avons mouillé, sur chacun des deux sites de la Seine, un capteur de pression (Ocean Sensor System) programmé en continu à une fréquence d’acquisition de 10 Hz. Les capteurs étaient placés à côté des marégraphes de Caudebec-en-Caux et de Val-des-Leux, dans des profondeurs d’eau à marée basse (pour les plus basses mers) respectivement de 1,0 m et 1,5 m. Pour le site de Podensac sur la Garonne en 2011, outre des mesures de profils de courant et de turbidité qui ne seront pas décrites dans cet article, nous avons réalisé des mesures de pression à 10 Hz (Ocean Sensor System) à la fois dans l’axe du fleuve et sur les berges. Les dispositifs expérimentaux de 2010 pour les campagnes TBG1 et TBG2 sur la Garonne ont été décrits dans Bonneton et al. (2011a, c).
Pour les RM les plus intenses que nous ayons observés, le champ d’ondes secondaires est caractérisé par une forte cambrure et un rapport λ/D ∼ 5, où D est la profondeur hydraulique et λ la longueur d’onde. Ce rapport caractérise un champ d’onde modérément non hydrostatique. Il est donc nécessaire d’appliquer une correction non hydrostatique à la pression mesurée pour estimer la hauteur d’eau. Pour cela, nous avons utilisé une approche classique basée sur une transformée de Fourier du signal et l’application, sur chaque mode, d’une correction non hydrostatique reposant sur la théorie linéaire des vagues. Pour valider notre approche, nous avons confronté les hauteurs d’eau issues de mesures de pression avec celles obtenues simultanément par mesure acoustique directe de la surface libre lors de la campagne TBG2. Ces mesures ont été réalisées à partir d’un AWAC (Nortek) à une fréquence d’acquisition de 2 Hz. Dans la situation la plus défavorable en termes de non-linéarité et de non-hydrostaticité (RM intenses), l’erreur maximale induite par notre correction non hydrostatique sur l’amplitude des ondes secondaires est inférieure à 10 %.
Des profils bathymétriques précis des sections instrumentées sur la Seine et la Garonne nous ont permis de calculer les profondeurs hydrauliques D et le nombre de Froude F. Le nombre de Froude est déterminé à partir des mesures de hauteurs d’eau de part et d’autre du front d’onde moyen et en appliquant la conservation de la masse et de la quantité de mouvement à travers la section du fleuve. Pour estimer la longueur d’onde λ de la première ondulation, nous avons utilisé λ = cbT, où T est la période et cb est la célérité du ressaut. La période s’obtient facilement à partir des signaux de pression. La célérité a été calculée à partir de la relation , où g est la gravité et D1 et u1 sont respectivement la profondeur hydraulique et la vitesse horizontale intégrée sur la verticale, à l’avant du ressaut (i.e. en aval par rapport à la direction de propagation du RM). Pour les campagnes de mesure sur la Garonne, u1 a été calculée à partir de mesures ADCP RDI acquises à 2 Hz. Des mesures directes de Cb, obtenues à partir du calcul du déphasage entre deux capteurs de pression synchronisés, nous ont montré que la relation utilisée pour Cb conduisait à des erreurs inférieures à 5 %. Dans le cas de la Seine, n’ayant pas de mesures directes de u1 pendant notre campagne, nous nous sommes appuyés sur les hypothèses suivantes :
- • dans cette portion de fleuve, où l’onde de marée est très asymétrique, on observe, lors de la marée descendante, l’établissement d’un courant de jusant qui reste pratiquement constant jusqu’à la renverse de marée basse ;
- • la valeur maximale de ce courant évolue peu en fonction du coefficient de marée.
À partir des données de la littérature, nous avons estimé cette valeur u1, à Val-des-Leux par faible débit fluvial, à –0,7 m/s. Il est à noter que cette correction est faible par rapport à Cb, dont l’ordre de grandeur pendant la campagne de mesures à Val-des-Leux était de 8,4 m/s.
4 Formation des ressauts de marée
Les observations sur la Garonne à Podensac en 2010, sur près de 200 marées, ont permis de quantifier pour la première fois l’occurrence des RM dans cet environnement (Bonneton et al., 2011c). Pour la campagne TBG1, réalisée à la fin de l’hiver autour des marées d’équinoxe de printemps, des RM sont observés pour 60 à 64 % des marées. Pour les marées d’équinoxe d’automne de la campagne TBG2, on observe, pour le même type de forçage tidal à l’entrée de l’estuaire, des RM plus intenses avec une occurrence de l’ordre de 85 à 90 %. L’incertitude sur la quantification de l’occurrence vient du fait que pour des nombres de Froude faiblement supérieurs à 1, l’identification des ressauts et de leur champ d’ondes secondaires devient difficile (discussion de la Fig. 3). La différence marquée entre les deux campagnes de mesures est liée à des débits fluviaux très différents. À la fin de l’été, par faible débit fluvial, on observe une forte amplification de l’onde de marée, lors de sa propagation entre l’entrée de l’estuaire et Podensac (Bonneton et al., 2011d). Les forts débits à la fin de l’hiver vont atténuer très fortement ce phénomène et donc être moins favorables à la formation de RM.
Les mesures complémentaires à Podensac en 2011 lors des marées d’équinoxe d’automne (de vive-eau à morte-eau) ont été réalisées pour des débits fluviaux similaires à ceux de TBG2. Cependant, des RM ont été identifiés pour l’ensemble des 16 marées analysées. La différence d’occurrence des RM entre cette campagne 2011 et TBG2 est due au fait qu’en 2010, le coefficient de marée minimal était de 32, alors qu’en 2011, la marée de morte-eau était de plus forte amplitude avec un coefficient de 42. La Fig. 2 présente les ressauts observés en 2011 pour les deux situations extrêmes que sont les marées de vive-eau et morte-eau. Pour la marée de vive-eau (Fig. 2a), on observe un RM intense, caractérisé par un nombre de Froude de 1,24 et des ondes secondaires de fortes amplitudes. La hauteur du premier front d’onde, Hb, atteint 1,57 m et la période de la première vague est de 2,6 s. La structure du RM, présentée sur la Fig. 2a, est représentative des mascarets de la Garonne, avec un champ d’ondes secondaires fortement cambrées et organisé sous la forme de groupes d’ondes (modulation à une période de l’ordre de 25 s). Le déferlement se produit sur les berges et localement au milieu du fleuve pour les vagues les plus intenses au sein des groupes d’ondes (Bonneton et al., 2011c). Pour la marée de morte-eau (Fig. 2b), on observe un RM de très faible intensité (F = 1,04) et un champ d’ondes secondaires peu développé (Hb = 0,19 m), avec des oscillations à des périodes beaucoup plus longues que celles des mascarets, de l’ordre de 15 s. Bien que de très faible intensité, ce RM est néanmoins caractérisé par une vitesse d’élévation maximale, dζ/dt|max = 2, 2 × 10−2m/s, d’au moins un ordre de grandeur supérieur à celle observée pour les rares cas sans RM, lors des marées d’équinoxe d’automne en 2010. Nos résultats montrent que les RM se forment dans la Garonne pour une large majorité de marées et qu’ils peuvent même se produire pour des marées de morte-eau comme nous l’avons observé en 2011.
Les mesures réalisées à Caudebec-en-Caux sur la Seine n’ont pas permis d’identifier de RM. L’absence de RM dans la zone où ils étaient historiquement les plus intenses s’explique à la fois par les aménagements et dragages de toute la partie aval du fleuve, qui ont modifié les caractéristiques globales de l’onde de marée, mais aussi par des raisons plus locales. La zone de Caudebec-en-Caux au début du xixe siècle était particulièrement dangereuse pour la navigation du fait de hauts fonds. Les dragages dans cette zone ont été très importants, en particulier dans la seconde moitié du xxe siècle (Documentation GIP Seine-Aval), avec un approfondissement des chenaux de plus de 4 m.
En revanche, à Val-des-Leux, 45 km en amont de Caudebec-en-Caux, des RM peuvent être clairement identifiés. La Fig. 3 présente l’évolution temporelle de l’élévation du plan d’eau à Val-des-Leux, au début de la marée montante, pour les marées d’équinoxe allant du 31 août au 7 septembre 2011. Ces observations, réalisées en même temps que celles sur la Garonne (Fig. 2), représentent les premières mesures de RM ondulés dans la Seine. Pour les six marées les plus intenses (Fig. 3a–f), on observe la présence de RM ondulés bien développés, caractérisés cependant par des nombres de Froude modérés compris entre 1,05 et 1,07. Pour la marée la plus intense (Fig. 3a), la hauteur du premier front d’onde est de 1,02 m et la période T est égale à 34 s. Ce ressaut est tout à fait significatif, puisque le plan d’eau va s’élever d’un quart du marnage en moins de 50 s. Malgré des conditions de marnage et de profondeur d’eau beaucoup moins favorables que sur la Garonne (TR = 3,70 m, D1 = 7,7 m à Val-des-Leux ; TR = 6,17 m, D1 = 2,7 m à Podensac), la distorsion de l’onde de marée sur 100 km depuis l’embouchure permet néanmoins la formation d’un RM d’intensité significative. Pour les marées de faibles amplitudes (Fig. 3j–o), on observe une évolution progressive de la marée montante, sans présence de RM. Les Fig. 3g–i illustrent la transition progressive entre les RM bien développés et l’absence de RM. Sur la Fig. 3g, on observe un RM très faible (F = 1,04) qui devient pratiquement imperceptible lors de la marée suivante (Fig. 3h). Le même type de transition a été obtenu en 2010 pour la Garonne (Bonneton et al., 2011c).
5 Structure du champ d’onde secondaire
Notre connaissance des ressauts ondulés repose en grande partie sur des études théoriques et expérimentales pour des canaux de forme simple et le plus souvent rectangulaire. Dans de tels canaux, les caractéristiques des ressauts ondulés non déferlants évoluent de façon continue en fonction de l’intensité du ressaut. Lorsque le nombre de Froude augmente, l’amplitude des ondes secondaires croît et la longueur d’onde, λ, décroît (Favre, 1935 ; Treske, 1994 ou Chanson, 2011). Cette évolution est assez bien reproduite par la théorie de Lemoine (1948), comme le montrent les résultats de Favre (1935) et Treske (1994) sur la Fig. 4. En milieu naturel, les fleuves ont généralement des berges en pente douce. Sur les sites que nous avons étudiés, les pentes étaient comprises entre 10 et 35 %. Ces pentes douces ont un très fort impact sur la structure des ondes secondaires par rapport à ce qu’on peut observer dans des canaux rectangulaires (Bonneton et al., 2011c, d ; Treske, 1994). Si la structure du ressaut moyen est pratiquement homogène dans la direction transverse au fleuve (Bonneton et al., 2011c, d), en revanche, le champ d’onde secondaire va présenter une très forte variabilité spatiale (Fig. 1). De plus, la structure du champ d’onde ne va pas évoluer de façon continue en fonction du nombre de Froude, comme l’illustre la Fig. 4. Cette figure présente l’évolution de la longueur d’onde de la première vague, λ, adimensionnée par la profondeur hydraulique à l’avant du ressaut, D1, en fonction de F. L’ensemble des mesures présentées a été réalisé au voisinage de l’axe du fleuve, excepté pour celles de Val-des-Leux. La Fig. 4 met en évidence un changement de comportement, ou transition, autour d’un nombre de Froude Fc (Fc ∼1,1 à Podensac). Pour F > Fc, on observe des oscillations à haute fréquence (Fig. 2a) avec des longueurs d’onde adimensionnées, en accord avec celles mesurées pour des ressauts ondulés se propageant dans un canal rectangulaire. En revanche, lorsque F devient inférieur à Fc, le mode haute fréquence voit son amplitude fortement décroître et il laisse place à des ondes de longueurs d’onde beaucoup plus grandes. Un tel phénomène avait déjà été identifié par Treske (1994), pour des ressauts en translation se propageant dans un canal trapézoïdal. Nous avons aussi observé, comme cet auteur, qu’au voisinage des berges, le mode basse fréquence était dominant même lorsque F > Fc.
Lorsque F > Fc, la cambrure des ondes secondaires est suffisamment intense pour que le RM soit observable visuellement en milieu naturel (Fig. 1) et il est alors dénommé dans le langage courant mascaret. En revanche, pour F < Fc, les ondes secondaires sont de faibles cambrures et difficilement observables in situ, sans mesure précise et haute fréquence de l’évolution de la hauteur d’eau. Cependant, ce type de phénomène est associé à une hydrodynamique intense avec par exemple, pour un Froude de 1,08 à Podensac, une variation de l’intensité de la vitesse horizontale de 1 m/s en 21 s (Bonneton et al., 2011a). Les RM observés dans la Garonne lors des forts débits fluviaux (TBG1), même pour un coefficient de marée de 116, sont tous de type « faible cambrure » et ne peuvent pas être qualifiés de mascarets. Il est intéressant de noter que, pour ce régime (F < Fc), les valeurs λ/D1 sont cohérentes pour les trois campagnes de mesures sur la Garonne, alors que deux d’entre elles ont été réalisées pour des débits fluviaux et donc des D1 très différents.
Les RM ondulés que nous avons identifiés sur la Seine appartiennent aussi à ce régime « faible cambrure ». Cela explique pourquoi, malgré des hauteurs de vagues très significatives (Hb∼1 m), ces RM n’avaient pas été identifiés jusqu’à présent sur la Seine. Les valeurs λ/D1 sont supérieures, pour un même F, à celles mesurées sur la Garonne. Le fait que les mesures sur la Seine aient été réalisées proches des berges peut expliquer partiellement ces différences. Cependant, pour ces faibles nombres de Froude, Treske (1994) a montré en laboratoire et Bonneton et al. (2011c) in situ, que le champ d’onde secondaire était beaucoup plus homogène, perpendiculairement au sens de propagation, que celui observé pour F > Fc (Fig. 1). Cet écart entre les deux sites semble davantage relié aux différences de pente des berges. Des berges de faible pente, telles que celles de Val-des-Leux, conduisent pour un même nombre de Froude à des longueurs d’onde adimensionnées plus grandes.
6 Conclusions
Nous avons montré que, dans un milieu fluvial naturel, avec des berges en pente douce, il existe un changement de régime pour les RM ondulés autour d’un nombre de Froude critique Fc. Lorsque F < Fc, le champ d’onde secondaire est dominé par des ondes basses fréquences de faibles cambrures, alors que des ondes de plus hautes fréquences et de fortes cambrures deviennent dominantes lorsque le nombre de Froude dépasse Fc. Dans le second cas, les RM sont généralement visuellement observables et correspondent au phénomène dénommé dans le langage courant mascaret. Nous avons montré que l’occurrence des RM en milieu fluvio-estuarien était jusqu’à présent sous-estimée (Chanson, 2011), car le régime « faible cambrure » (F < Fc) n’est pas facilement appréhendable sans mesure haute fréquence de la hauteur d’eau. Grâce à ce type de mesure, nous avons pu identifier des RM ondulés de « faible cambrure » dans la Seine et présenter les premières mesures quantitatives de ce phénomène. Nous avons montré que sur la Seine la localisation des RM, par rapport à celle du milieu du xxe siècle, s’est fortement décalée vers l’amont. Le même phénomène de décalage vers l’amont a aussi été observé dans la Garonne. Nous avons aussi montré que, dans la Garonne, les RM étaient présents pour une large majorité de marées et que, par faible débit fluvial, il pouvait même se développer par marée de morte-eau. Cette réévaluation de l’occurrence des ressauts de marée, en particulier dans des environnements comme la Seine où ils semblaient, suite à des aménagements, avoir en partie disparu, ouvre de nouvelles perspectives sur le rôle qu’ils jouent dans les écosystèmes fluvio-estuariens et, en particulier, sur les échanges sédimentaires. Les modèles de propagation de marée dans ces environnements ne décrivent pas actuellement les processus dispersifs associés au RM. Leur modélisation en milieu naturel va donc nécessiter le développement de nouveaux modèles non hydrostatiques (Bonneton et al., 2011b).
Remerciements
Ce travail a été réalisé dans le cadre du projet MASCARET (Région Aquitaine), avec des financements complémentaires de l’université de Bordeaux-1. Nous remercions l’ensemble des personnes qui ont été impliquées dans ces campagnes de mesures et tout particulièrement G. Oggian, S. Capo, N. Pochon (EPOC) et F. Pradalier (CKBN). Les Voies Navigables de France (VNF) de Cadillac nous ont été d’un très grand soutien pour le mouillage des instruments dans la Garonne, ainsi que Y. Lavigne pour les photos aériennes. Merci à Loic Michel de la société RDI pour nous avoir prêter un ADCP. Nous remercions P. Tournier et C. Guillon (Grand Port Maritime de Rouen) et J.-P. Lemoine (GIP Seine-Aval) pour leur aide lors de la campagne de mesures sur la Seine. Nous remercions P.-Y. Lagrée, D. Mouazé et H. Michallet pour leurs commentaires constructifs en tant que rapporteurs, qui ont contribué à améliorer cet article.


