Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India

Priya Narayanan; Ashoke Basistha; Sumana Sarkar; Sachdeva Kamna

doi:10.1016/j.crte.2012.12.001

External geophysics, climate

Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India
[Analyse de tendance et modélisation ARIMA des données de pluviosité de pré-mousson pour l’Ouest de l’Inde]

Présenté par : Michel Petit

Priya Narayanan ¹ ; Ashoke Basistha ² ; Sumana Sarkar ¹ ; Sachdeva Kamna ¹

¹ Department of Natural Resources, TERI University, 10, institutional Area, Vasant Kunj, New Delhi 110070, India
² DGM (Hydro Civil), Lahmeyer International India Pvt. Ltd, New Delhi, India

Comptes Rendus. Géoscience, Volume 345 (2013) no. 1, pp. 22-27.

Résumés

Anglais
Français

Spatial and temporal variability of rainfall over different seasons influence physical, social and economic parameters. Pre-monsoon (March, April and May – MAM) rainfall over the country is highly variable. Since heat lows and convective rainfall in MAM have an impact on the intensity of the ensuing monsoons, hence the pre-monsoon period was chosen for the study. The pre-whitened Mann Kendall test was used to explore presence of rainfall trend during MAM. The results indicate presence of significant (at 10% level) increasing trend in two stations (Ajmer, Bikaner). The practical significance of the change in rainfall was also explored as percentage changes over long term mean, using Theil and Sen's median slope estimator. Forecast using univariate ARIMA model for pre-monsoon months indicates that there is a significant rise in the pre-monsoon rainfall over the northwest part of the country.

La variabilité spatiotemporelle de la pluviosité sur différentes saisons influence les paramètres physiques, sociaux et économiques. La pluviosité pré-mousson (mars, avril et mai – MAM) sur la région est extrêmement variable. La période pré-mousson a été choisie pour cette étude, étant donné que l’abaissement de chaleur et la pluviosité convective pour la période MAM ont un impact sur l’intensité des moussons qui suivent. Le test Mann Kendall de pré-blanchiment a été utilisé pour explorer la possibilité d’une évolution de la pluviosité pendant la période MAM. Les résultats indiquent une tendance significative à l’accroissement (à un niveau de 10 %) dans deux stations (Ajmer et Bikaner). La signification pratique du changement dans la pluviosité a aussi été explorée dans le sens de changements sur une moyenne à long terme utilisant l’estimateur de pente moyenne de Theil et Sen. La prévision utilisant le modèle ARIMA à une variable pour les mois de pré-mousson indique une augmentation significative de la pluviosité de pré-mousson dans la partie nord-occidentale de la région.

Métadonnées

Reçu le : 2012-05-03
Accepté le : 2012-12-11
Publié le : 2013-01-01

DOI : 10.1016/j.crte.2012.12.001

Keywords: Pre-monsoon, Rainfall trend, India, Pre-whitened Mann Kendall Test, Theil and Sen's Median Slope, Forecast, Auto Regressive Integrated Moving Average (ARIMA)
Mot clés : Pré-mousson, Tendance de la pluviosité, Test Mann Kendall de pré-blanchiment, Pente médiane de Theil et Sen, Prévision, Moyenne mobile intégrée régressive automatique (ARIMA)

Affiliations des auteurs :

Priya Narayanan ¹ ; Ashoke Basistha ² ; Sumana Sarkar ¹ ; Sachdeva Kamna ¹

¹ Department of Natural Resources, TERI University, 10, institutional Area, Vasant Kunj, New Delhi 110070, India
² DGM (Hydro Civil), Lahmeyer International India Pvt. Ltd, New Delhi, India

@article{CRGEOS_2013__345_1_22_0,
     author = {Priya Narayanan and Ashoke Basistha and Sumana Sarkar and Sachdeva Kamna},
     title = {Trend analysis and {ARIMA} modelling of pre-monsoon rainfall data for western {India}},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {22--27},
     publisher = {Elsevier},
     volume = {345},
     number = {1},
     year = {2013},
     doi = {10.1016/j.crte.2012.12.001},
     language = {en},
}

TY  - JOUR
AU  - Priya Narayanan
AU  - Ashoke Basistha
AU  - Sumana Sarkar
AU  - Sachdeva Kamna
TI  - Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India
JO  - Comptes Rendus. Géoscience
PY  - 2013
SP  - 22
EP  - 27
VL  - 345
IS  - 1
PB  - Elsevier
DO  - 10.1016/j.crte.2012.12.001
LA  - en
ID  - CRGEOS_2013__345_1_22_0
ER  -

%0 Journal Article
%A Priya Narayanan
%A Ashoke Basistha
%A Sumana Sarkar
%A Sachdeva Kamna
%T Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India
%J Comptes Rendus. Géoscience
%D 2013
%P 22-27
%V 345
%N 1
%I Elsevier
%R 10.1016/j.crte.2012.12.001
%G en
%F CRGEOS_2013__345_1_22_0

Priya Narayanan; Ashoke Basistha; Sumana Sarkar; Sachdeva Kamna. Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India. Comptes Rendus. Géoscience, Volume 345 (2013) no. 1, pp. 22-27. doi : 10.1016/j.crte.2012.12.001. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2012.12.001/

Version originale du texte intégral

1 Introduction

Climate variability in the dry and arid parts of India poses a great risk to the people and resources of these regions (INCCA, 2010) as the smallest fluctuations of weather parameters like precipitation not only damage the agriculture and economy of the region but disturb the overall water cycle (Krishna Kumar et al., 2004; Zhang et al., 2011). Study of the space-time variability of rainfall assumes great importance for India, as its economy is largely dependent on agriculture (Davey and Peilke, 2005). Undeniable regional and global impacts have been observed due to the slightest variability in the precipitation patterns (Dash et al., 2004; New et al., 2001; Pal and Al-Tabbaa, 2009). Time series analysis is used to understand this random mechanism and to predict future series based on past data.

The study explores the rainfall behavior in the pre-monsoon season over a period 1949–2009 for the western part of India; the importance of this study is that it uses long series station-wise data for western part of India, which is semi-arid and has extremely low pressure conditions and intense dust storms during this season. Differential heating of land and sea is the precursor for monsoons, so understanding the trend of rainfall during these months in the north-western part of India is important to understand the overall pattern of monsoon (Bhutiyani et al., 2009; Chatterjee et al., 2009; Das et al., 2002).

The statistical and practical significance of trend was analyzed using a pre-whitened Mann Kendall test, percentage changes over the long term mean were calculated using Theil Sen's median slope estimator. Forecast was done using ARIMA model for a period 2010 to 2030. We have tried to understand the changes in pre-monsoon rainfall which is distinctly convective in nature and has direct influence on different monsoon branches. Computation of trends during the pre-monsoon season gives a clear indication of performance of subsequent monsoons if correlated with meteorological attributes. The study indirectly focuses on the changes and connection in the western branch (which is special because this region is influenced by dust storms) of the monsoon, and the overall trend of pre-monsoon rainfall in the country.

2 Methodology and data

Data used for this study were obtained from Indian Meterological Department (IMD). Monthly Rainfall data for March, April, May (MAM) for six stations (Abu (Ab), Ahemdabad (Ah), Ajmer (Aj), Amritsar (Am), Bikaner (Bk), Jodhpur (Jd)) for a period of 60 years were analyzed. Consistency checks and data gaps were filled according to standard procedures. Trend analysis was performed on rainfall data using a pre-whitened Mann Kendall Test, autocorrelation removal was done in the required datasets at the chosen level of significance (α = 10%). The magnitude and practical significance of trend has been estimated using the Theil and Sen's median slope estimator, and by assessing the percentage change over the mean for the period concerned (Yue and Hashino, 2003; Yue et al., 2002).

In this study, a rank-based non-parametric Mann Kendall (MK) test is used. The MK test is the most common test used for trend analysis of hydro meteorological data (Yue et al., 2002). The limitation of the MK test is that in the case of positive autocorrelation present in series, it shows a positive trend even when trend is not present (Bayazit and Önöz, 2007). The pre-whitened Mann Kendall (PWMK) test was developed by Von Storch to remove the effect of autocorrelation from the series (Bayazit and Önöz, 2007). The pre-whitened Mann Kendall test removes the autocorrelation at lag 1 assuming an AR (1) model and then applies Mann Kendall test to the independent series (Bayazit and Önöz, 2007; Yue et al., 2002), in case autocorrelation is detected at the same significance level.

2.1 Mann Kendall test

The null hypothesis H₀ states that the data series is independent and identically distributed and the alternate hypothesis H₁ states existence of a trend.

The general MK test has test statistics S defined as:

S = \sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} (x_{j} - x_{i})

(1)

where x_j is the sequential data series, n is the length of the data set and

S g n (y) = \{\begin{cases} 1 if (y > 0) \\ 0 if (y = 0) \\ - 1 if (y < 0) \end{cases}

(2)

Results of Mann Kendall test are supposed to be normally distributed for n ≥ 8 with mean and variance described as:

E (S) = 0

(3)

V (S) = \frac{n (n - 1) (2 n + 5) + \sum t_{i} (t_{i} - 1) (2 t_{i} + 5)}{18}

(4)

where t_i is the number of ties present with i as extent. The standardized Z statistics is computed by

Z = \{\begin{cases} S - 1 / \sqrt{V (S)} S > 0 \\ 0 S = 0 \\ S + 1 \sqrt{V (S)} S < 0 \end{cases}

(5)

The standard MK statistic Z follows the standard normal distribution with zero mean and unit variance.

2.2 Pre-whitened Mann Kendall test

A modification of the MK test, PWMK test is generally applied in presence of autocorrelation. The removal of autocorrelation is accomplished by:

{x^{'}}_{t} = x_{t + 1} - r_{1} x_{t}

(6)

where r₁ is the autocorrelation coefficient at lag 1 and is represented as:

r_{1} = \frac{\sum_{t = 1}^{n - 1} ((x_{t} - {\bar{x}}_{t}) (x_{t + 1} - {\bar{x}}_{t + 1}))}{{[\sum_{t = 1}^{n - 1} ({(x_{t} - {\bar{x}}_{t})}^{2} {(x_{t + 1} - {\bar{x}}_{t + 1})}^{2})]}^{\frac{1}{2}}}

(7)

Here ${\bar{x}}_{t}$ and Var (x_t) are the sample mean and sample variance of the first (n–1) terms and ${\bar{x}}_{t + 1}$ and Var (x_t+1) is the sample mean and sample variance of the next (n–1) terms. The presence of significant autocorrelation in the series is checked by Student's t test (Cunderlik and Burn, 2004), where the null hypothesis of no autocorrelation is rejected if $|t| \geq t_{α / 2}$

t = r_{1} \sqrt{\frac{n - 2}{1 - r^{2}}}

(8)

The MK test was applied after the removal of the autocorrelation wherever it was present at the chosen level of significance (α = 10%).

2.3 Theil and Sen's median slope estimator

The magnitude of trend has been estimated using the Theil and Sen's median slope estimator. This method gives a robust estimate of trend (Yue et al., 2002) as it is not influenced by outliers. The slope estimates of N pairs of data are first computed by

Q_{i} = (x_{j} - x_{k}) / (j - k) f o r i = 1, n

(9)

Here x_j and x_k are data values at time j and k, respectively, where (j > k).

The median of the N values of Q_i is the Sen's estimator of slope where:

N = n (n - 1) / 2

(10)

The trends which have statistical significance might not have practical significance and vice versa (Yue and Hashino, 2003), hence the practical significance of trend was assessed by estimating the Theil and Sen's median slope and assessing the percentage change over the mean for the period concerned.

3 Forecasting

Climate modelling using GCMs has been used extensively to predict pattern of climatic variables globally (IPCC, 2007). However, GCM forecasts have certain limitations (Sun et al., 2009; INCCA, 2010). In recent years, time series modelling approach for climatic variables is gaining popularity amongst researchers (Boochabun et al., 2004; Chattopadhyay and Chattopadhyay, 2010), and has been followed here.

3.1 Choice of model and parsimony

In the current study, ARIMA model has been used for forecasting rainfall for the period 2010–2030. ARIMA modeling predicts future values as a product of several past observations and random errors (Yurekli et al., 2007). As a modeling technique, ARIMA has been beneficial for predicting hydro meteorological parameters (Boochabun et al., 2004; Chattopadhyay and Chattopadhyay, 2010; Chattopadhyay et al., 2011; Hipel et al., 1977).

The ARIMA (p, d, q) can be expressed as (Box et al., 2007):

{\bar{z}}_{t} = ϕ_{1} {\bar{z}}_{t - 1} + ϕ_{2} {\bar{z}}_{t - 2} + \dots + ϕ_{3} {\bar{z}}_{t - p} + a_{t} - θ_{1} {\bar{z}}_{t - 1} - θ_{2} {\bar{z}}_{t - 2} - \dots θ_{3} {\bar{z}}_{t - q}

(11)

where

{\bar{z}}_{t} = z_{t} - μ

, and a_t is the shock. By introducing the Backward shift operator (B), Eq. (11) can be written as:

ϕ (B) {(1 - B)}^{d} z_{t} = θ (B) a_{t}

(12)

The modeling process includes model identification and diagnostic checking. The identification test is done to obtain the value of order of differencing ‘d’ in ARIMA (p, d, q) and also the values of AR and MA operators. The need for differencing to make the series stationary has been thoroughly explained by Dickey and Fuller (1979).

3.2 ADF test for unit roots

Δ y_{t} = α_{0} + β t + α_{1} Y_{t - 1} + \sum_{i = 1}^{p} d_{i} Δ y_{t - 1} + u_{t}

(13)

where ΔY_t = Y_t – Y_t−1, with the null hypothesis H₀: α₁ ≠ 0 versus H1: α₁ = 0, tested on the basis of the t-statistic. H₀ is rejected if the t-statistic is smaller than the critical value at 10% significance level (–1.62).

Climatic data has no fixed mean, and for ARIMA modeling, stationarity is a prerequisite. So when the observed data exhibits trend and heteroscedasticity, application of differencing, a log or a square root transformation is required to reduce it to a stationary series (Yurekli et al., 2007). Parsimonious model selection was done by using Akaike Information Criterion (AIC), a model with minimum AIC being considered.

The AIC is expressed in the form:

AIC (p, q) = N In (σ_{ε}^{2}) + 2 (p + q)

(14)

where p and q are the lags of the ARIMA (p, d, q).

After fitting the parsimonious model, the residuals were subjected to a diagnostic test to check the randomness of the residuals. An ARIMA model with random residuals at particular significance level (α = 10%) is considered as the best fit model. The randomness was checked using the Ljung–Box test statistics for checking the presence of autocorrelation in the residual series.

The Rank test was used as another test of randomness. It is particularly suitable for detecting presence of linear trend in the time series. Here P is defined as the number of pairs (i, j) such that y_j > y_i (Brockwell and Davis, 2009). The assumption of randomness of the series y_j is rejected at level α if $|P - μ_{P}| / σ_{P} > ϕ_{1 - α / 2}$ .

The whiteness of the residual was checked by examining the Residual ACFs (RACF) of the models. The RACF can be calculated by Hipel et al. (1977):

r_{k} (\hat{a}) = \sum_{t = K + 1}^{n} ({\hat{a}}_{t} {\hat{a}}_{t - k}) / \sum_{t = 1}^{n} {\hat{a}}_{t}^{2}

(2)

where

\hat{a}

is the residual series.

The ARIMA model for each station was then used to forecast the rainfall values until 2030.

4 Results and discussions

Sixty years of data have been analysed for six stations on the western side of India. Table 1 represents the location of stations and the mean rainfall. The stations located on the western side of India fall in the semi-arid zone which is characterized by both scant and random convective rainfall. Statistical significance at (α = 10%) level is analysed for all six stations, From Fig. 1 it is evident in terms of Z statistics that an overall positive trend is observed in April, May for almost all the stations and negative trend in March for four stations; however, at the α = 10% level of significance, two stations (Ah), (Ab) do not show any trend in rainfall during MAM. Significant trend in rainfall is observed in (Bk), (Jd) in April and (Bk), (Am) in May. Two stations (Aj), (Bk) show significant trend for the entire pre-monsoon season. Monthly level analysis of the percentage change in rainfall showed an overall rise for two stations Bk, Am during MAM.

Station	Latitude	Longitude	Altitude (msl)	Mean MAM rainfall (mm)	Standard deviation (mm)
Abu (Ab)	24.48	72.78	1722	21.2	43.5
Ahmdabad (Ah)	23.1	72.6	55	10.5	21
Ajmer (Aj)	26.45	74.63	486	21.3	25.9
Amritsar (Am)	31.6	74.9	234	74.3	57.2
Bikaner (Bk)	28	73.3	227	47.1	81.2
Jodhpur (Jd)	26.28	73.03	230	32.9	58.2

Fig. 1
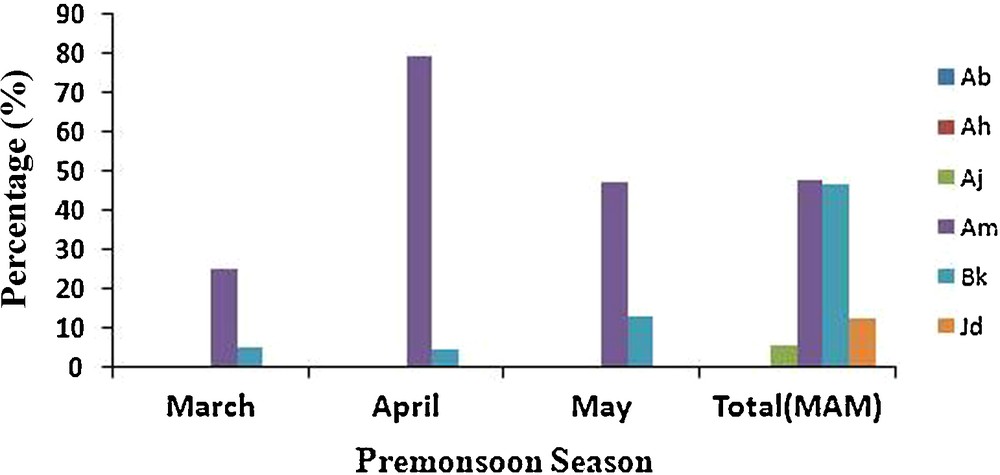
Percentage change (α = 10%) rainfall for different stations during pre-monsoon season.
Pourcentage de changement de pluviosité (α = 10 % pour différentes stations pendant la saison de pré-mousson.

Rainfall in the pre-monsoon period is due to formation of semi permanent heat lows over the northwest parts of India and central parts of Pakistan during the summer months (Chandrashekhar, 2010). The rise in the surface air temperature since 1971 (Krishna Kumar et al., 2004) during the months of March, April and May probably suggests intensification of the convective heating over the region extending from 24°N to 37°N and 68°E to 89°E (Indo Gangetic Plain, Northwest Rajasthan, western India, Indian peninsular region); the trends obtained in the study are consistent with these observations. Similar findings have been reported by Kothawale et al., 2010, indicating the presence of an increasing trend in the number of hot days and hot nights over entire India. The increasing trend in rainfall in the northwest parts of Rajasthan especially in (Bk) and (Aj) might be due to intense heat lows and resultant rainfall. Further, the month of May is characterized by major reversal of surface winds that brings warm, moist and unstable air from Indian Ocean into the Indian Peninsular region under the influence of land sea thermal contrast, which plays a major role in the establishment of planetary scale monsoon circulation over the entire subcontinent for coming months (Chandrashekhar, 2010). Recent studies on the impacts of aerosols on the Indian Summer Monsoon rainfall (Gautam et al., 2009; Lau et al., 2006; Nigam and Bollasina, 2010) have found increasing aerosol loading in the pre-monsoon months (MAM). Lau et al. (2006) reports build up of aerosol loading in the MAM, peaking up in May over the entire North, Northwest India and Indo Gangetic Plains. The source of aerosol in these regions are from the dust transported from deserts of Saudi Arabia, Afghanistan and Pakistan along with black carbon from local emissions (Gautam et al., 2009; Lau et al., 2006). Studies by Beegum et al. (2009), Bollasina and Nigam (2009) and Kumar et al. (2009) have found increased black carbon loading in the recent period. These changes in atmospheric aerosol loading can be correlated with the changes in the rainfall trends.

4.1 ARIMA forecasting

ARIMA modeling was done for forecasting the pre-monsoon rainfall for all the six stations. Root Mean Square Error (RMSE) was computed to check the accuracy of model fitting in Table 2, and Fig. 2 by comparing the forecast results for 2000 to 2009 using input data from 1949 to 1999. The most parsimonious model with minimum AIC, which passed the test of randomness were selected for forecasting rainfall until 2030. The model parameters, along with diagnostic statistics and predicted rainfall as percentage, change over long term mean, see Table 2. From forecast results stations (Ab), (Ah) show negative change in pre-monsoon rainfall: this could be attributed to rapid local change in land use land cover. The stations like Bk show positive change in rainfall; this could be due to the high fine aerosols load in that region (Sarkar et al., 2005).

Station	ARIMA Model	AIC	RMSE	Test of Randomness	% change for 2030
				LBQ/P	Rank test Statistics
Ab	(2,2,3)	334.26	11.82	0.31	0.39	–0.86
Ah	(2,2,1)	303.81	26.58	0.15	0.2	–0.4
Aj	(2,2,2)	308.52	24.08	0.61	0.23	20.9
Am	(1,0,4)	126.02	33.33	0.12	0.54	13.21
Bk	(1,2,1)	358.46	57.83	0.22	0.25	31.13
Jd	(2,2,1)	348.93	95.27	0.45	0.68	25.66

Fig. 2
Percentage change of rainfall for observed (1949–2009) and predicted (2010–2030) years for all stations.
Pourcentage de changement de pluviosité pour les années observées (1949–2009) et prévisionnelles (2010–2030) pour toutes les stations.

This part of India has extremely high temperatures, and the further convective nature of rainfall in MAM makes it more sensitive to local land use land cover changes. Hence detecting the long term change in mean values, as done in this study, gives a possible idea of changes in rainfall pattern in the study area.

5 Conclusion

Analysis of long-term time series (1949–2009) for western region stations using the non-parametric pre-whitened Mann Kendall test showed evident changes in rainfall pattern during the pre-monsoon season. Four stations (Amritsar, Bikaner, Jodhpur and New Delhi) in the north-western and western part of the country show increase in pre-monsoon rainfall of 10% or more; while at two stations (Ajmer and Bikaner) it was statistically significant. Analysis at a monthly level shows statistically significant increasing trend in May rainfall at six stations distributed over a wide expanse. Forecast results from ARIMA modelling show that (Ab), (Ah) have negative change due to rapid local change in land use. Further studies are needed to understand factors affecting pre-monsoon rainfall.

Acknowledgements

Authors extend sincere thanks to following people and agencies for the support: IMD, Helmut Lutkepohl and Markus Kratzig (for software JMulTi), Brockwell and Davis (for ITSM 2000 ARIMA model) and University Grants Commission (UGC) for the financial support.

Bibliographie

[Bayazit and Önöz, 2007] M. Bayazit; B. Önöz To prewhiten or not to prewhiten in trend analysis, Hydrol. Sci. J., Volume 52 (2007) no. 4, pp. 611-624

[Beegum et al., 2009] N.S. Beegum; K. Krishna Moorthy; S. Suresh Babu; S.K. Satheesh; V. Vinoj; K.V.S. Badarinath; P.D. Safai; P.V.S. Devara; S. Singh; D.U.C. Vinod; P. Pant Spatial distribution of aerosol black carbon over India during Pre-monsoon Season, Atmos. Environ., Volume 43 (2009), pp. 1071-1078

[Bhutiyani et al., 2009] R.M. Bhutiyani; S.V. Kale; J.N. Pawar Climate change and the precipitation variations in the northwestern Himalaya: 1866–2006, Int. J. Climatol., Volume 30 (2009) no. 4, pp. 535-548

[Bollasina and Nigam, 2009] M. Bollasina; S. Nigam Absorbing aerosols and pre-summer monsoon hydro climate variability over the Indian subcontinent: the challenge in investigating links, Atmos. Environ., Volume 94 (2009), pp. 338-344

[Boochabun et al., 2004] K. Boochabun; W. Tych; N.A. Chappell; P.A. Carling; K. Lorsirirat; S. Pa-Obsaeng Statistical modelling of rainfall and river flow in Thailand, J. Geol. Soc. India, Volume 64 (2004), pp. 503-515

[Box et al., 2007] G.E.P. Box; G.M. Jenkins; G.C. Reinsel Time Series Analysis: forecasting and control, Pearson Education, 2007 (pp. 8–12)

[Brockwell and Davis, 2009] P. Brockwell; R. Davis Time Series: theory and Methods, Springer International Edition, 2009 (pp. 310–313)

[Chandrashekhar, 2010] A. Chandrashekhar Basics of Atmospheric Sciences, PHI Learning Private Limited, 2010 (pp. 280–306)

[Chatterjee et al., 2009] S. Chatterjee; S. Ghosh; K.U. De Reduction of number of parameters and forecasting convective developments at Kolkata (22.53°N, 88.33°E), India during pre-monsoon season: an application of multivariate techniques, Indian J. Radio Space Phys., Volume 38 (2009), pp. 275-282

[Chattopadhyay and Chattopadhyay, 2010] S. Chattopadhyay; G. Chattopadhyay Univariate modelling of summer-monsoon rainfall time series: comparison between ARIMA and ARNN, CR Geoscience, Volume 342 (2010), pp. 100-107

[Chattopadhyay et al., 2011] S. Chattopadhyay; D. Jhajharia; G. Chattopadhyay Univariate modelling of monthly maximum temperature time series over northeast India: neural network versus Yule–Walker equation based approach, Meteorol. Appl., Volume 18 (2011), pp. 70-82

[Cunderlik and Burn, 2004] J.M. Cunderlik; D.H. Burn Linkages between regional trends in monthly maximum flows and selected climatic variables, J. Hydrol. Eng., Volume 9 (2004) no. 4, pp. 247-255

[Das et al., 2002] M.R. Das; K.R. Mukhopadhyay; M.M. Dandekar; R.S. Kshirsagar Pre-monsoon western disturbances in relation to monsoon rainfall, its advancement over NW India and their trends, Curr. Sci., Volume 11 (2002), pp. 1320-1321

[Dash et al., 2004] S.K. Dash; R.J. Kumar; K.M. Shekhar On the decreasing frequency of monsoon depressions over the Indian region, Curr. Sci., Volume 86 (2004) no. 25, pp. 1404-1411

[Davey and Peilke, 2005] C.A. Davey; R.A. Peilke Microclimate exposures of surface based weather stations: implications for the assessment of long-term temperature trends, Bull. Am. Meteorol. Soc., Volume 86 (2005) no. 4, pp. 497-504

[Dickey and Fuller, 1979] D.A. Dickey; W.A. Fuller Estimators for autoregressive time series with a unit root, J. Am. Stat. Assoc., Volume 74 (1979), pp. 427-431

[Gautam et al., 2009] R. Gautam; N.C. Hsu; K.M. Lau; M. Kafatos Enhanced pre-monsoon warming over the Himalayan-Gangetic region from 1979 to 2007, Ann. Geophys., Volume 27 (2009), pp. 3691-3703

[Hipel et al., 1977] K.W. Hipel; A.I. McLoed; W.C. Lennox Advances in Box Jenkins Modeling. 1. Model Construction, Water Resour. Res., Volume 13 (1977) no. 3, pp. 567-575

[INCCA, 2010] INCCA: Indian Network for Climate Change Assessment, 2010. Climate change and India: a 4X4 assessment a sectoral and regional analysis for 2030s. 15, 36–38.

[IPCC, 2007] IPCC The Physical Science Basis. Contribution of working group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, New York, 2007 (pp. 589–663)

[Kothawale et al., 2010] D.R. Kothawale; J.V. Revadekar; K. Rupa Kumar Recent trends in pre-monsoon daily temperature extremes over India, J. Earth Syst. Sci., Volume 119 (2010) no. 1, pp. 51-65

[Krishna Kumar et al., 2004] K. Krishna Kumar; K. Rupa Kumar; G.R. Ashrit; R.N. Deshpande; W.J. Hansen Climate impacts on Indian agriculture, Int. J. Climatol., Volume 24 (2004), pp. 1375-1393

[Kumar et al., 2009] R. Kumar; K. Narasimhulua; R.R. Reddy; K. Rama Gopal; L. Reddy; Siva Sankara; G. Balakrishnaiaha; K. Krishna Moorthy; S. Suresh Babu Temporal and spectral characteristics of aerosol optical depths in a semi-arid region of southern India, Sci. Total Environ., Volume 407 (2009), pp. 2673-2688

[Lau et al., 2006] K.M. Lau; M.K. Kim; K.M. Kim Asian Summer monsoon anomalies induced by aerosol direct forcing; the role of Tibetian Plateau, Climate Dyn., Volume 26 (2006), pp. 864-885

[Nigam and Bollasina, 2010] S. Nigam; M. Bollasina “Elevated heat pump” hypothesis for the aerosol–monsoon hydro climate link: “Grounded” in observations, J. Geophys. Res., Volume 115 (2010), p. D16201

[New et al., 2001] M. New; M. Todd; M. Hulme; P. Jones Precipitation measurement and trend in the twentieth century, Int. J. Climatol., Volume 21 (2001), pp. 1899-1922

[Pal and Al-Tabbaa, 2009] I. Pal; A. Al-Tabbaa Trends in seasonal precipitation extremes – an indicator of “climate change” in Kerala, India, J. Hydrol., Volume 367 (2009), pp. 62-69

[Sarkar et al., 2005] S. Sarkar; R. Chokngamwong; G. Cervone; R.P. Singh; M. Kafatos Variability of aerosol optical depth and aerosol forcing over India, Adv. Space Res. (2005), pp. 1-7

[Sun et al., 2009] D.Z. Sun; Y. Yu; T. Zhang Tropical water vapour and cloud feedbacks in climate models: a further assessment using coupled simulations, J. Climate, Volume 22 (2009) no. 5, pp. 1287-1304

[Yue et al., 2002] S. Yue; P. Pilon; G. Cavadias Power of the Mann Kendall and Spearman's rho test for detecting monotonic trends in hydrological series, J. Hydrol., Volume 259 (2002), pp. 254-271

[Yue and Hashino, 2003] S. Yue; M. Hashino Long term trends of annual and monthly precipitation in Japan, J. Am. Water Resour. Assoc., Volume 39 (2003) no. 3, pp. 587-596

[Yurekli et al., 2007] K. Yurekli; H. Simsek; B. Cemek; S. Karaman Simulating climatic variables by using stochastic approach, Build. Environ., Volume 42 (2007), pp. 3493-3499

[Zhang et al., 2011] Q. Zhang; C. Xu Yu; X. Chen; Z. Zhang Statistical behaviours of precipitation regimes in China and their links with atmospheric circulation 1960–2005, Int. J. Climatol., Volume 31 (2011) no. 11, pp. 1665-1678

Commentaires - Politique