1 Introduction
Broadly, isotope geochemistry and cosmochemistry use isotopic analyses in natural materials to explore the history of anything from asteroids to oceans. For decades, these fields primarily investigated isotopic differences caused by either mass-dependent fractionation of light isotopes (e.g., H, C, O) or radioactive decay of one isotope to another. As instrumentation, methods, and theory evolved, additional causes for isotopic variation in natural systems were discovered, such as non-mass-dependent fractionation, spallation reactions, and nucleosynthetic anomalies. This work is an attempt to review the evidence of the recently recognized type of non-mass-dependent fractionation found in nature — the nuclear field shift effect.
The conventional equilibrium mass-dependent theory, as developed by Urey (1947) and Bigeleisen and Mayer (1947), is based on the difference of zero-point vibrational energy between different isotopologues (two chemically similar molecules with different isotopic composition). Following this theory, the mass-dependent isotopic fractionation between two isotopes of mass m1 and m2 of an element X is predicted to be proportional to the mass difference divided by the product of the mass: (m2 − m1)/(m1 × m2) and to the inverse of the temperature square (1/T2). A majority of kinetic isotopic effects are also mass-dependent and are proportional to ln(m1/m2) (Young and Galy, 2004). Together these equations represent the foundation of modern isotope geochemistry; they have been confirmed in laboratory experiments and employed in a multitude of applications related to earth, environmental, and planetary sciences (Johnson et al., 2004; Valley and Cole, 2001). However, one of the major assumptions of equilibrium isotope fractionation theory is that the size of the nucleus has no volume and is considered a point charge. Therefore, according to the standard theory, the effect of the nucleus on the electrostatic potential is similar for all isotopologists, which implies that the minimum of the vibrational energy is also similar for all isotopologists.
Laboratory experiments in 1989 by Fujii et al. (1989) recognized the first non-mass-dependent fractionation of the odd atomic mass 235U in a redox reaction [U(IV)/U(VI)] (see Fig. 1). Although these results were attributed to the nonzero nuclear spin of 235U, a conclusion that was later shown to be incorrect, this groundbreaking study did provide proof that the volume of the nucleus cannot be wholly ignored when calculating isotopic fractionation. The odd/even isotopic effect created during chemical exchange reactions was further discovered for the elements Gd, Zn, Sr, and Ba (Chen et al., 1992; Nishizawa et al., 1993, 1994).
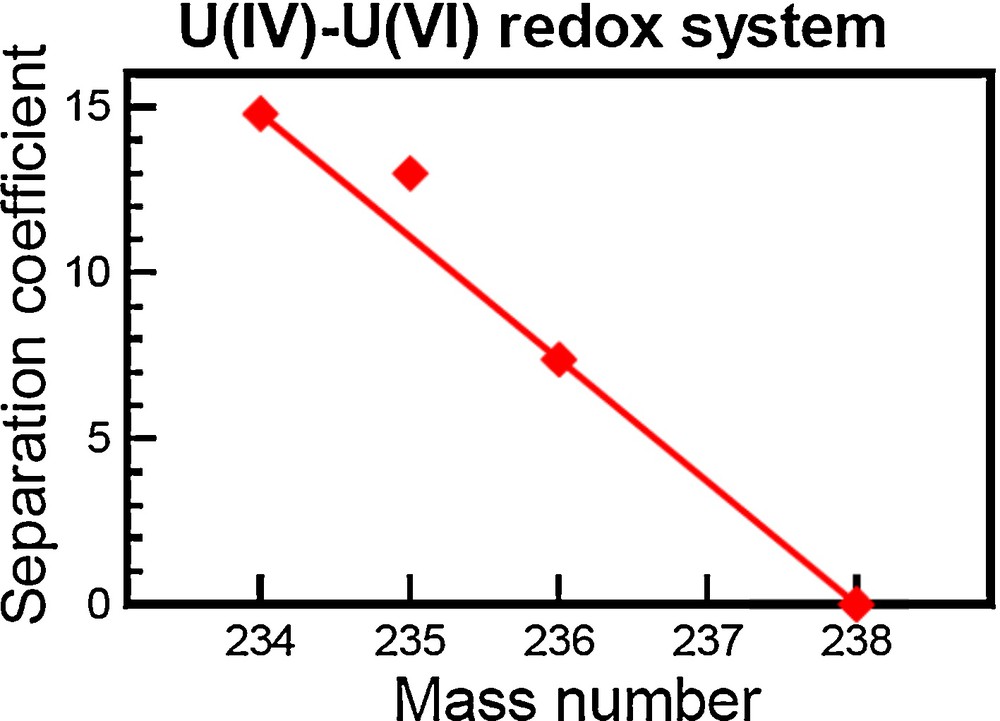
Logarithms of U isotope-separation factor during U(IV)–U(VI) liquid-liquid extraction. The separation coefficient corresponds to an isotopic fractionation in parts per ten thousand compared to an initial solution.
Reproduced from Bigeleisen (1996).
The origin of odd/even isotopic fractionation was theoretically explained in 1996 by Bigeleisen (1996). Bigeleisen (1996) conducted calculations of U isotope fractionation for the complete equation originally outlined by Bigeleisen and Mayer (1947). Bigeleisen (1996) found that effects from nuclear spin were almost two orders of magnitude smaller than the observed U isotope fractionation, whereas effects from the size and shape of the nucleus on the electrostatic potential were similar in magnitude to the observed U isotope fractionation. The nuclear size and shape affects the minimum point of the vibrational frequency, which varies between isotopologues and can therefore create an isotopic effect. In the literature, this effect is sometimes called nuclear size and shape effect, nuclear volume effect, or nuclear field shift effect; we will use the later notation, nuclear field shift (NFS). The NFS effect is proportional to the difference (δ) in the mean-square charge radius between isotopes as well as to the total electron density at the nucleus ǀΨ(0)ǀ2 (Bigeleisen, 1996; Schauble, 2007). The electron density at the nucleus largely correlates positively with the mass of the isotope and the number of s-electrons and, as such, larger NFS effects are predicted for heavier elements that can possess variable numbers of s-electrons.
The nucleus is particularly compact when considering isotopes with a magic number of nucleons (20, 28, 50, 82, and 126). At the first order, isotopes with magic number nucleons show a smooth change in with increasing neutron number, which sometimes appears proportionate to the mass number (see Fig. 2). At the second order, most elements show an odd/even effect, whereby the odd atomic mass isotopes have a smaller than the even atomic mass isotopes. This is illustrated on Fig. 2, which plots the relative difference in the between the different isotopes of molybdenum (Mo) as a function of the mass number. The even atomic mass isotopes (92Mo, 94Mo, 96Mo, 98Mo, and 100Mo) are aligned on a straight line, while the odd atomic mass isotopes (95Mo and 97Mo) plot slightly under this line. This difference in between odd/even atomic mass isotopes forms the basis of the NFS effect.
Change of mean-square charge radii of Mo.
Data are from Fricke and Heilig (2004).
The basic equation describing total equilibrium isotope fractionation (i.e., conventional mass-dependent and NFS) was provided by Bigeleisen (1996) and can be simplified and recast by using the standard epsilon notation (Equation (1)):
| (1) |
The NFS theory introduced by Bigeleisen (1996) motivated the search for non-mass-dependent isotopic fractionation in laboratory-scale chemical exchange experiments and in ab initio calculations for a multitude of elements (e.g., Abe et al., 2008, 2010; Fujii et al., 2009a,b,c, 2011; Ismail et al., 2000). The development of higher precision isotopic measurements by multiple collection-inductively coupled plasma-mass-spectrometry (MC–ICP–MS) occurring simultaneously with the publication of Bigeleisen's NFS theory have directly influenced the observation of non-mass-dependent isotopic fractionation in laboratory experiments. In addition to observations in laboratory experiments, NFS-driven isotopic fractionation of lighter elements has also been suggested to occur under natural conditions (e.g., Fujii et al., 2006a,b; Schauble, 2007), and it is likely that more natural NFS isotopic fractionation will be discovered in the future.
For heavy elements (Z > 80), the NFS effect becomes a major source of equilibrium isotopic fractionation in nature, and in some cases can be much more prevalent than conventional mass-dependent isotopic fractionation (Schauble, 2007; Stirling et al., 2007b). The most striking examples are U (Z = 92) and Tl (Z = 81), for which isotopic fractionation up to a few per mil per atomic mass unit that can be attributed to the NFS effect have been measured in natural systems (Nielsen and Rehkämper, 2011; Stirling et al., 2007a; Weyer et al., 2008). Mercury (Hg; Z = 80) also shows isotopic fractionation in natural environments. Kinetic effects unrelated to the NFS have been proposed to account for the majority of Hg fractionation (Bergquist and Blum, 2009), but a contribution from NFS has also been suggested (Zheng and Hintelmann, 2010). While it is known that the NFS effect plays a more minor role in the fractionation of lighter isotopes, it has nevertheless been hypothesized that NFS could be the cause of certain isotopic anomalies observed for lower-mass elements in some meteoritic samples (Fujii et al., 2006a,b).
The NFS effect is defined as an equilibrium fractionation (Bigeleisen, 1996). However, NFS has been shown to occur for Hg isotopes in a kinetic reaction (Zheng and Hintelmann, 2010), which most likely is explained by transition states within the kinetic reaction that can obtain full or partial isotopic equilibrium (Fujii et al., 2009a). The nuclear charge distribution creates an electric field, and the resulting isotopic difference causes the atomic energy levels to shift. This shift displaces the electronic molecular states of the equilibrium and transition states (Fujii et al., 2009a). Besides the NFS effect, a nuclear spin effect in kinetic systems is known as “magnetic isotope effect” (Buchachenko, 2009). It reflects a magnetic field effect on the spin of excited molecules or radical pairs. The rates of reaction between radical pairs are changed, not by the difference in isotopic mass, but by the hyperfine interaction between electronic and nuclear spins.
In the present paper, we review the natural isotopic variation that has been attributed to the NFS effect. In the first section, we present the results concerning U and Tl isotopes in low-temperature environments. In the second section, we review the different isotopic variations measured in meteorites that have been hypothesized to be caused by NFS. We go on to show that NFS alone cannot exclusively be the source of these isotopic anomalies. Finally, we propose a new model to explain isotopic anomalies measured in certain meteoritic samples by combining nucleosynthetic heterogeneities with the NFS effect.
2 Application of nuclear field shift to low-temperature environments: examples from uranium and thallium
2.1 Uranium
Of the naturally occurring heavy elements that are significantly affected by the NFS effect, U is unique in the resulting direction of isotope fractionation. The oxidation of heavy elements, like Hg and Tl, generally involves the loss of 6s electrons, which reduces the electron density at each nucleus. However, because the redox transition of the predominant oxidation states of U in the natural environment, U(IV) and U(VI), involves 5f electrons, this transition actually increases the charge density at the nucleus, consequently reversing the isotopic effect of the NFS effect as compared to Hg and Tl (see below for the example of Tl). This means that conventional mass-dependent isotopic fractionation and the NFS effect work in opposition. However, since the mass-dependent isotopic fractionation is very small at such heavy masses, only the stronger NFS effect can create observable 238U/235U fractionation (Schauble, 2007). This effect was first observed in the natural environment by studies demonstrating variability in the terrestrial 238U/235U ratio (Stirling et al., 2007a; Weyer et al., 2008). The samples measured in these studies strongly suggested that low-temperature redox transitions were the major cause of 238U/235U fractionation and clearly showed that the reduced species of U was isotopically heavier than the oxidized species (Fig. 3). Again, this pattern contrasts with what would be predicted by the conventional mass-dependent fractionation theory, in which heavy isotopes should be enriched in the oxidized species. The observed pattern provides evidence that the predicted NFS effect, rather than difference in mass, is the driving force behind the observed 238U/235U fractionation.
The ranges of various modern terrestrial reservoirs are shown in solid boxes with the corresponding U isotope ratio on the x-axis. The expected direction of U isotope fractionation during U reduction is shown, along with the predominant redox state of U over the range of environments. Data has been recalculated using the revised value of the SRM950a standard (Richter et al., 2010).
Figure reproduced from Weyer et al. (2008).
The confirmation of natural variability in the 238U/235U ratio caused by the NFS effect and the improved precision at which the ratio can now be measured have created many opportunities for new work using the U isotope system. Here we address some of the areas in which the 238U/235U ratio has become a new tool to investigate a variety of scientific questions.
2.2 History of O2 in the ocean
While the timing and history of oxygen in Earth's atmosphere is fairly well constrained, the history of oxygen in Earth's oceans remains a matter of intense debate. This is especially true for relatively short-lived anoxic events, some of which may have been responsible for catastrophic mass extinctions. Certain geochemical properties of U make it an ideal candidate to study the amount of dissolved oxygen in the ocean over geologic time. First, U is a redox-sensitive element that predominantly exists in nature in one of two oxidation states, U(VI) or U(IV). The oxidized form of U is soluble in the natural environment, whereas the reduced form is essentially insoluble. Second, U has a long residence time in the oceans (∼ 500 kyr), which leads to not only a homogeneous U concentration of seawater (Klinkhammer and Palmer, 1991; Ku et al., 1977) but also a homogeneous U isotope composition (Stirling et al., 2007a; Weyer et al., 2008). These properties of U, coupled with confirmation that the low-temperature redox transition of U is the primary cause of 238U/235U fractionation on Earth (Bopp et al., 2009, 2010; Brennecka et al., 2010b; Stirling et al., 2007a; Weyer et al., 2008), have made the 238U/235U ratio a useful tool for investigating the history of ocean oxygenation at a global scale.
Specifically, periods of decreased levels of dissolved oxygen in the ocean increase the flux of reduced U to anoxic facies, preferentially removing 238U from seawater and driving seawater isotopically light (Montoya-Pino et al., 2010). Sediments deposited during a time of decreased dissolved oxygen record — either directly as in carbonates (Brennecka et al., 2011b) or indirectly as in black shales (Montoya-Pino et al., 2010) — the 238U/235U composition of the ocean at that time. These sediments also provide a means to quantify ocean anoxia at different times in Earth's history. Due to the great extent of the carbonate rock record over space and time, an emerging 238U/235U paleoredox proxy utilizing both carbonates and black shales has the potential to help produce a much more complete record of the history of oxygen in the global oceans, while complimenting existing paleoredox proxies.
2.3 Quantifying bioreduction and bioremediation
Uranium contamination in surface and groundwaters can be a significant public health hazard. Consequently, abundant U mining and processing activities can create the need for monitoring and occasional remediation. Because the reduced form of U is essentially insoluble, and therefore immobile, reduction of U is a common goal in these remediation efforts. However, monitoring such U reduction efforts is not always straightforward and can be complicated by dilution and sorption effects in the area of interest.
The finding that measurable 238U/235U fractionation occurs during reduction (Stirling et al., 2007a; Weyer et al., 2008) provided the basis for a potential new method of monitoring U remediation at contaminated sites (Bopp et al., 2009). Subsequent observation has shown that in situ biostimulation of U-reducing bacteria can cause increased U reduction and, in turn, U isotope fractionation. This fractionation is attributed to the NFS effect arising during enzymatic reduction of U(VI) to U(IV) (Bopp et al., 2010). While the reduction and immobilization of U is generally the ultimate goal of U remediation efforts, monitoring the 238U/235U ratio has the potential to provide a direct measurement of the extent of reduction in the system and provide insight into the progress of the remediation effort.
2.4 Effect of nuclear field shift on geochronology
High-precision U–Pb and Pb–Pb dating are based on the decay of isotopes of U (238U and 235U) to isotopes of Pb (206Pb and 207Pb). In order to determine an age, precise knowledge of the ratio of the parent U isotopes is required. Prior to 2007, no natural sample had been measured that departed from the accepted 238U/235U value of 137.88. Accordingly, that ratio was taken to be invariant in all Solar System materials. Evidence of variable 238U/235U ratios on Earth (Stirling et al., 2007a; Weyer et al., 2008) sparked multiple studies on a variety of sample sets evaluating the fidelity of past assumptions in U–Pb and Pb–Pb geochronology in both terrestrial and extraterrestrial materials. For example, work on refractory inclusions in meteorites has suggested that large variations in the 238U/235U in the earliest solids are largely caused by the existence and subsequent decay of 247Cm (247Cm→235U, t1/2 ≈ 15.6 Ma) (Brennecka et al., 2010b). Other work on bulk meteorites has shown that little to no variation exists in the 238U/235U ratio outside of refractory inclusions (Brennecka and Wadhwa, 2012; Brennecka et al., 2010a; Connelly and Bizzarro, 2011; Kaltenbach et al., 2011). Recently, Hiess et al. (2012) investigated a range of terrestrial U-bearing minerals commonly analyzed in U–Pb geochronology and found significant natural variation in 238U/235U ratios. While the cause of the 238U/235U variation in these minerals, and a variety of meteoritic samples is not yet fully understood, the recognition of values outside uncertainty of the previously assumed value has forced a substantive change in the previously established procedures of U geochronology.
2.5 Isotopic fingerprinting of ore deposits
Uranium has received a great deal of attention from government officials and scientists worldwide, largely due to the fissile properties of the 235U nucleus. By far, the largest portion of uranium research has been dedicated to energy production, either in the form of nuclear reactors or nuclear weapons, with the acquisition of U from ore deposits being a primary step. Uranium ore represents not only a valuable commodity but also an internationally regulated nuclear material. Uranium deposits occur worldwide in a variety of geologic settings and can be divided into three major depositional settings based on the redox environment and temperature of deposition. Broadly, U deposits are categorized into the following types: U deposited by redox processes at low-temperature, U deposited by redox processes at high-temperature, and non-redox deposits in which U was deposited prior to the rise of O2 in the atmosphere (Brennecka et al., 2010b).
Because U is a regulated nuclear material, the ability to trace the origin of U ore is of great interest to the international nuclear forensic community. Because the 238U/235U ratio of a U ore body is largely controlled by the geologic setting in which it is deposited, the 238U/235U ratio is a way to track the geologic and geochemical history of a sample. Measuring the U isotopes may provide isotopic “fingerprints” of individual U mines (Brennecka et al., 2010b; Richter, 1999).
As with any isotope fractionation, including NFS fractionation, the magnitude of the effect is dependent upon the temperature at which the event occurs. Conventional mass-dependent fractionation is a function of 1/T2 (Bigeleisen and Mayer, 1947). The magnitude of NFS fractionation is also a function of T, but instead scales as 1/T (Schauble, 2007). At high-temperatures, extra energy in the system essentially mutes the amount of isotope fractionation, making the small differences even smaller and, in the case of U, imperceptible. At the lower temperatures of water-rock interaction on the Earth's surface, this fractionation is measurable. As an example, U ore deposits that are formed under reducing conditions at low-temperatures have markedly higher 238U/235U ratios than those deposited under reducing conditions at high-temperatures (Bopp et al., 2009; Brennecka et al., 2010a,b) or those deposited in a non-redox-related setting (Brennecka et al., 2010a). Consequently, by precisely measuring the 238U/235U ratio of U from an ore deposit, it is possible to determine the most likely type of deposit (low-temperature redox deposit vs. high-temperature redox deposit/non-redox) from which the sample was mined, thus narrowing the possible source regions and geologic settings of a sample from an unknown origin.
3 Thallium
Thallium has two isotopes with masses of 203 and 205 atomic mass units. Due to its high atomic mass, conventional stable isotope fractionation theory (Bigeleisen and Mayer, 1947) predicts only a very small amount of equilibrium isotope fractionation for Tl (Fujii et al., in press). Therefore, it was at first considered surprising that Tl was found to be one of the elements for which the largest stable isotope variation per relative mass difference has been detected (i.e., 3.5 per mil for every percent mass difference). At present, the process(es) responsible for the large isotopic variation in Tl is (are) still being debated, but it is proposed that NFS plays a substantial role (Nielsen and Rehkämper, 2011).
Based on theoretical considerations, the NFS effect likely accounts for the majority of equilibrium isotope fractionation of Tl, while the conventional mass-dependent effect accounts for about 25% of total isotope fractionation (Fujii et al., in press; Schauble, 2007). However, because Tl only has two stable isotopes (203Tl and 205Tl), the effects cannot be distinguished. Both fractionation mechanisms produce enrichment of the heavy (205Tl) isotope in oxidized (III) Tl when in equilibrium with reduced (I) Tl. Thus, theoretical calculations have been able to approximate the magnitude of Tl isotope variation observed on Earth (Schauble, 2007).
Only a few processes have been found to produce definitive fractionation of Tl isotopes. Most materials on Earth appear to be isotopically very similar: the upper mantle, the lower oceanic crust, the continental crust, rivers, and detrital sedimentary particles are all indistinguishable (Nielsen et al., 2004, 2005, 2006a,b) (Fig. 4). This uniformity may be related to the extremely oxidizing conditions required to form significant amounts of Tl(III) such that natural processes rarely involve this oxidation state of Tl, preventing equilibrium isotope fractionation in excess of a few tenths of per mil. To date, the two main reservoirs that display significant Tl isotope variation are ferromanganese (Fe–Mn) marine sediments and low-temperature altered upper oceanic crust (Nielsen et al., 2006b; Rehkämper and Nielsen, 2004; Rehkämper et al., 2002), which are characterized by heavy and light isotope compositions, respectively.
Tl isotopic composition of the different terrestrial reservoirs analyzed to date. Also shown are fluxes of Tl to the oceans in Mmol per year, as well as the residence time of Tl in seawater.
Figure modified from Coggon et al. (2009).
Upper altered oceanic crust is enriched in Tl via percolation of cold (< 50 °C) seawater on the ridge flanks. Interaction between seawater and extrusive basalts causes precipitation of minerals with high Tl abundances that are depleted in 205Tl (Nielsen et al., 2006a). It is unknown exactly which phases contain the most Tl, but sulfides have been suggested as the major Tl sink (Coggon et al., 2009). Given these uncertainties, the primary mechanism of Tl isotope fractionation in altered oceanic crust remains unclear, but kinetic isotope fractionation during diffusion from seawater into alteration phases appears to be more likely than equilibrium isotope fractionation (Nielsen and Rehkämper, 2011).
Pure hydrogenetic Fe–Mn crusts form through direct precipitation of Fe and Mn-oxyhydroxides from seawater in places of little or no other sedimentation. Thallium is about seven orders of magnitude more concentrated in these deposits compared to seawater (Rehkämper et al., 2002, 2004) due to adsorption primarily onto the Mn-oxide phase vernadite (Koschinsky and Hein, 2003; Peacock and Moon, 2012). Thallium incorporation and isotope fractionation in ferromanganese deposits have been studied in some detail and it is almost certain that an equilibrium process (NFS) is responsible for the approximately two per mil difference between seawater and hydrogenetic ferromanganese crusts (Peacock and Moon, 2012; Rehkämper et al., 2002). Seawater, like most terrestrial materials, is completely dominated by Tl(I) (Byrne, 2002; Nielsen et al., 2009), but analyses of the oxidation state of Tl in Fe-Mn crusts reveal predominantly Tl(III). Furthermore, vernadite has been found to oxidize and adsorb Tl into the mineral structure (Peacock and Moon, 2012). Ongoing laboratory experiments have confirmed that this adsorption-oxidation reaction is most likely responsible for the large Tl isotope fractionation observed between seawater and Fe-Mn crusts. Since mass-dependent Tl isotope fractionation produces only sub-per mil isotope effects, NFS fractionation is very likely the primary cause of the large Tl isotope fractionation factor in Fe-Mn sediments.
4 Application of nuclear field shift to high-temperature environments and meteorites
Non-mass-dependent isotopic variations were first discovered in a rare type of calcium–aluminum-rich inclusions (CAIs) of the undifferentiated meteorite Allende (Clayton et al., 1977; Wasserburg et al., 1977). Based on the anomalous isotopic compositions of oxygen and magnesium, these unusual CAIs were named “Fractionated and Unknown Nuclear effects” (FUN) CAIs. It was proposed that these isotopic anomalies represented pre-solar nucleosynthetic products that escaped homogenization in the early Solar System. Subsequent work showed more non-mass-dependent isotopic effects in these FUN inclusions for many other elements beyond oxygen and magnesium: Ca, Ti, Cr, Fe, Zn, Sr, Ba, Nd, and Sm (Birck and Allègre, 1984; Lee et al., 1978; McCulloch and Wasserburg, 1978a,b; Niederer et al., 1980; Niemeyer and Lugmair, 1981; Völkening and Papanastassiou, 1990a,b). Anomalies in these elements were attributed to the non-homogenization of nucleosynthetic products. Recent improvement in analytical methods and mass-spectrometry has permitted the resolution of smaller isotopic anomalies in some meteorite whole rocks for a variety of elements (e.g., Mo, Ru, Ca, Sr) (Burkhardt et al., 2011; Chen et al., 2010; Dauphas et al., 2002, 2004; Moynier et al., 2010, 2012; Simon et al., 2009; Yin et al., 2002). As with FUN CAIs, these anomalies are usually interpreted as representing pre-solar isotopic compositions, even if it is difficult to account for all of the anomalies by nucleosynthetic processes (Birck, 2004; Consolmagno and Cameron, 1980; Dauphas et al., 2004). The discovery of non-mass-dependent isotopic fractionation of oxygen during kinetic processes (Thiemens and Heindrich, 1983) suggested that oxygen isotopic anomalies could have chemical origins instead of nucleosynthetic. Correspondingly, it has been proposed that at least part of the anomalies observed for heavy elements might have chemical origins through the NFS effect (Brennecka et al., 2011a; Fujii et al., 2006a,b; Moynier et al., 2009).
For elements with at least three isotopes, isotopic data are usually normalized to a reference ratio. Fujii et al. (2006a) showed that the equation (1) can be recast to:
| (2) |
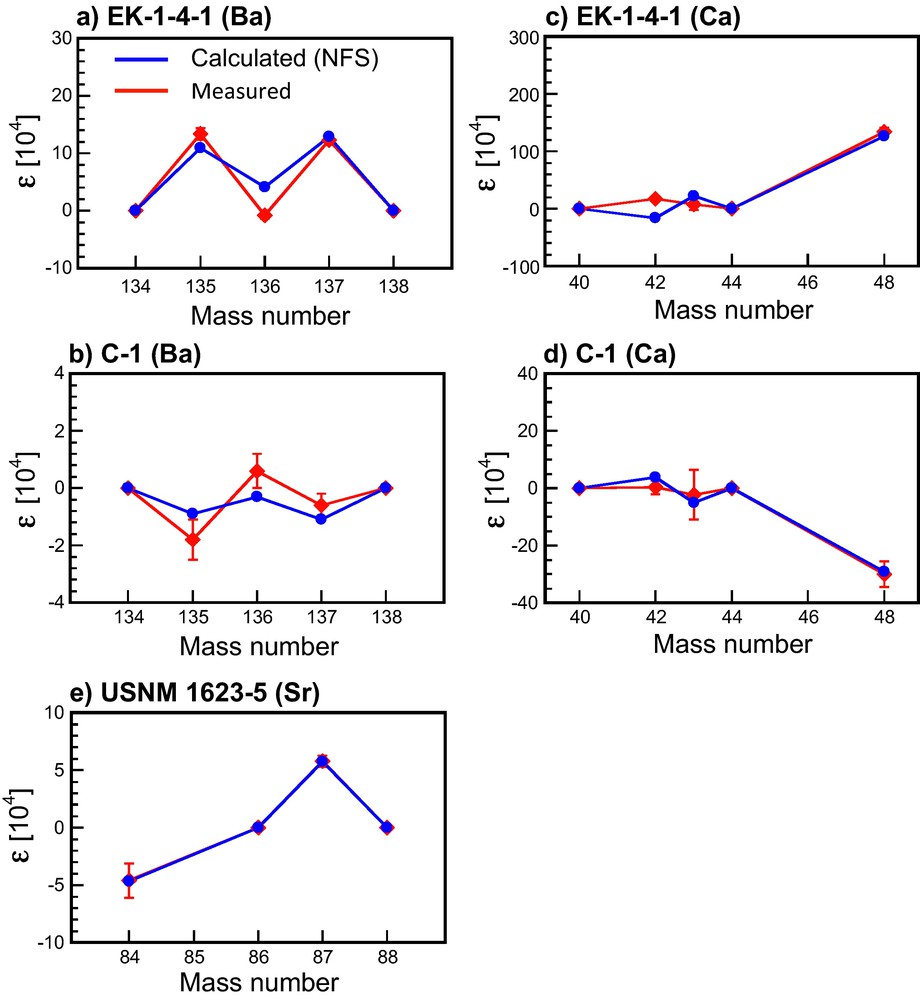
The NFS theory (blue dots, calculated using equation (2)) reproduces a fair amount of the isotopic anomalies measured in the FUN inclusions (red dots, data from the literature) for Ba, Sr, and Ca. The data are reported using the ɛ notation (see equation (2)). The errors are smaller than the size of the marker.
Reproduced from ref. (Fujii et al., 2006a).
Much smaller isotopic anomalies (∼ 1 part in 10 000) have recently been observed in regular (non-FUN) CAIs for many elements [e.g., Sr, Ba, Nd, Eu, Mo, Te, and Sm; (Brennecka et al., 2011a,b; Moynier et al., 2006, 2009, 2012)]. Like FUN CAIs, some of the anomalies in regular CAIs can be explained by NFS theory, while some isotopic patterns are mismatched. This again suggests that only some of the anomalies are due to NFS, and the majority of the anomalies would have a nucleosynthetic origin. Interestingly, it is also not possible to perfectly predict these anomalies by nucleosynthetic mixing (See Fig. 6 for Mo). Consequently, these anomalies require a more complicated scenario beyond single component nucleosynthetic mixing. On Fig. 6, we show the individual effects (left and middle panels) and the combined effect (right panel) for the Mo isotopic anomalies observed in CAIs from Allende. Combining NFS and nucleosynthetic effects produces the best fit (R2 = 0.950 vs. 0.880) to the data. The same kind of data fitting can be applied to any isotopic anomalies of heavy elements measured in meteorites.
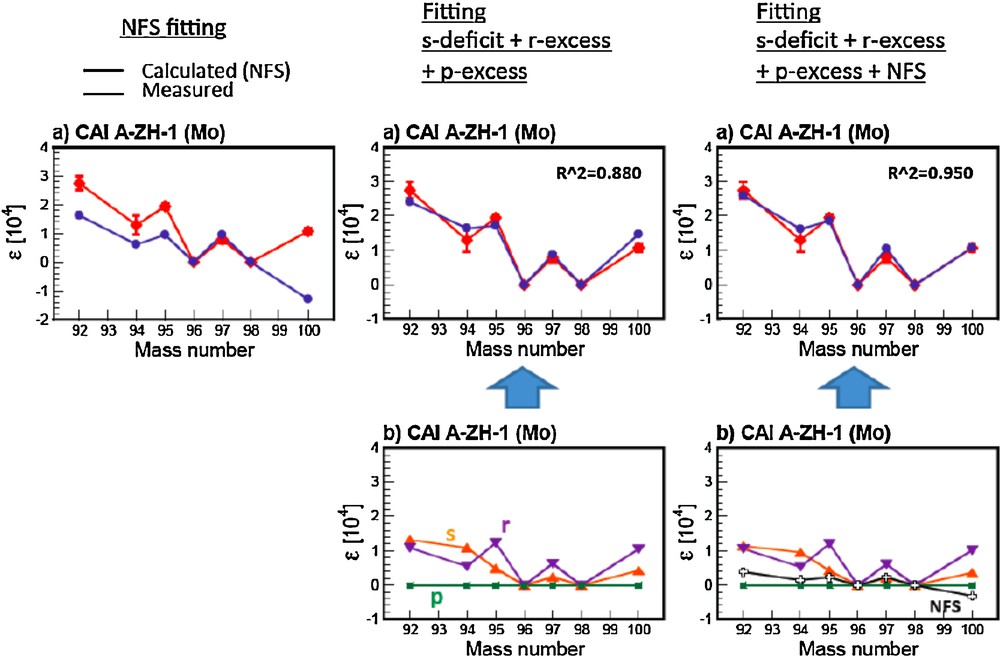
Comparison between the Mo isotopic anomalies measured in CAIs by Burkhardt et al. (2011) and the prediction of the NFS effect (left panel); nucleosynthetic mixings (middle panel) and a combination of NFS effect and nucleosynthetic effect (right panel). The NFS effect is calculated using the equation (1).
While the isotopic anomalies in refractory inclusions can be explained by a combination of NFS and nucleosynthetic effects, that is not the case for all meteoritic samples. Large Mo and Ru isotopic anomalies have been recently measured in whole rock samples of iron meteorites (Burkhardt et al., 2011; Dauphas et al., 2002, 2004; Yin et al., 2002), which can be explained by NFS theory. Additionally, coupled Mo and Ru isotopic data from the CM2 meteorite Murchison also fit nicely by NFS theory (Fujii et al., 2006b), suggesting that NFS is the primary cause of isotopic variation in this sample (Fujii et al., 2006b).
The NFS effect is predicted to be small for elements lighter than 100 amu, (Knyazev and Myasoedov, 2001; Schauble, 2007) because of its proportionality with the total electron density at the nucleus ǀΨ(0)ǀ2 (see above). Fujii et al. (in press) discussed theoretical calculations that show ∼ 10 ɛ/amu NFS isotope fractionation is possible for elements such as Hg, Tl, Pb, or U, while for elements like Mo, Ru, or Pd, the effect is between 0.5 to 3 ɛ/amu. For even lighter elements, such as Ni or Zn, the NFS effect is estimated to be only 0.2 to 0.3 ɛ/amu. The magnitudes stated above apply only to fractionation at room temperature and would be smaller at higher temperatures, as the NFS effect decreases as a function of 1/T. For example, the effect for Hg, Tl, Pb, and U decreases to 2 ɛ/amu at 1000 °C, while the effect for Mo, Ru, and Pd decreases to 0.1–0.6 ɛ/amu. Thus, the magnitude of the anomalies (especially for the FUN CAIs) does not appear to be consistent with the NFS theory based on a single-stage isotopic fractionation. Multi-stage isotopic fractionation or Rayleigh-type distillation would enhance the NFS effects, as it does for conventional stable isotopic fractionation. However, given that regular mass-dependent Rayleigh-type distillation is likely significantly larger than NFS effects for masses < 100 amu, it is difficult to reconcile this scenario with the large anomalies measured for Ca, Ti, Cr, and Sr in FUN inclusions. Such an explanation would call for special conditions in which different mechanisms of mass-dependent isotopic fractionation canceled out. One possibility is that kinetic and equilibrium isotope fractionations worked in opposition to each other and were therefore canceled out. However, the remarkable similarity between the FUN inclusion isotope patterns and the nuclear root-mean-square radii (Figs. 5–6) gives tentative evidence that at least some of the variation was caused by NFS.
Together these considerations suggest that non-mass-dependent isotopic anomalies observed in meteorites may primarily originate from incomplete mixing of nucleosynthetic components. However, it is necessary to consider potential effects from NFS fractionation, especially for small isotope anomalies of a few epsilon or less.
Acknowledgements
FM acknowledged the support of NASA COSMO #NNX12AH70G, and EXO #NNX12AD88G. The authors thank Anat Shahar as well as two anonymous reviewers for their thorough reviews, which greatly improved the quality of this manuscript. Celeste is particularly thanked for a very careful editing of the manuscript.