1 Introduction
Compressional seismic body waves differential travel time residuals and free oscillations reveal a large-scale cylindrical anisotropy in the Earth's inner core: seismic waves travel faster along the north–south (NS) axis than within the equatorial plane (Morelli et al., 1986; Poupinet et al., 1983; Woodhouse et al., 1986). Over the following years, this observation was refined with evidence of both hemispherical and radial variations of the anisotropy level and geometry. Recent studies indicate up to 4.4% and 1% anisotropy in the western and eastern hemispheres, respectively (Deuss et al., 2010; Garcia and Souriau, 2000; Irving and Deuss, 2011; Niu and Chen, 2008; Tanaka and Hamaguchi, 1997), with an almost isotropic layer – 60 km deep in the most recent studies – at the top of the inner core surrounding a more anisotropic region (Creager, 1999; Garcia and Souriau, 2000; Shearer, 1994; Song and Helmberger, 1995; Waszek and Deuss, 2011), and, possibly, an innermost inner core with yet different properties (Beghein and Trampert, 2003; Calvet et al., 2006; Ishii and Dziewoński, 2002; Niu and Chen, 2008; Sun and Song, 2008a,b), although the presence of an innermost inner core is not required in the analysis of more recent datasets (Lythgoe et al., 2013). In this paper, we present models aiming at reproducing global NS anisotropy and its depth variation.
Seismic anisotropy observed at the global scale is the signature of single-crystal anisotropy of the solid material in the inner core. For simplicity, we consider an inner core made of pure iron as other “light” elements are not clearly identified (e.g. Alfè et al., 2002; Antonangeli et al., 2010; Badro et al., 2007; Tsuno et al., 2013). Although other phases have been proposed (Belonoshko et al., 2008; Dubrovinsky et al., 2007; Kuwayama et al., 2008; Vočadlo et al., 2003), we consider a pure hcp- or ɛ-Fe inner core, in agreement with recent experimental studies (Tateno et al., 2010), and assume dominant basal slip, with contributions of prismatic and pyramidal slip (Merkel et al., 2012).
Global anisotropy requires the alignment of anisotropic single-crystals. Processes for generating such textures include solidification texturing acquired at the inner core boundary (ICB) during the growth of the inner core (Bergman, 1997; Brito et al., 2002) and/or plastic deformation due to internal dynamics after the solidification (Deguen and Cardin, 2009; Jeanloz and Wenk, 1988; Karato, 1999; Takehiro, 2010; Yoshida et al., 1996). These models often result in complex textures that can be difficult to interpret at the global scale. As such, the interpretation of seismic data is often simplified by introducing “structural” inner core models, with different layers of distinct anisotropy (e.g., Bergman, 1997; Calvet et al., 2006; Lythgoe et al., 2013; Stixrude and Cohen, 1995; Sun and Song, 2008a).
In this paper, we address the issue of scaling microscopic properties, such as single-crystal elasticity of ɛ-Fe to the macroscopic observations of seismic travel times. We first study the seismic response and estimate the anisotropy of structural model inner cores, based on procedures used in seismological studies. We later extend the results by coupling a dynamical model of inner core formation with a numerical model of texture development in ɛ-Fe, computing the time evolution of textures in the inner core, and simulating the measurement of seismic anisotropy. At last, we discuss the synthetic global anisotropy in comparison to the observed results in order to deduce conclusions for the inner core.
2 Structural models
2.1 Inner core structural models
Following procedures used in previous studies (Bergman, 1997; Calvet et al., 2006; Lythgoe et al., 2013; Stixrude and Cohen, 1995; Sun and Song, 2008a), we first build simple structural inner core models. In each model, the inner core is built with different layers with distinct anisotropies (Figs. 1 and 2).
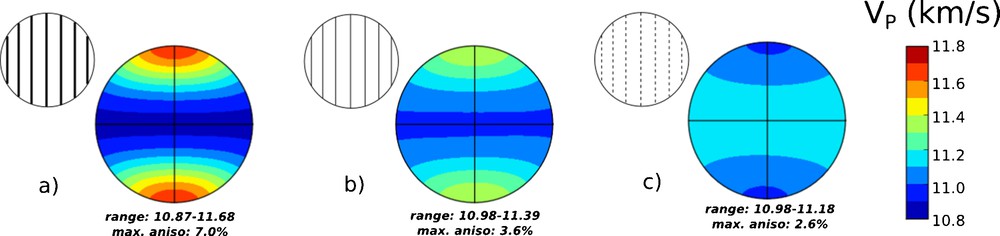
(Color online.) Elastic models used for structural models. a: elastic moduli of Laio et al. (2000) with a 100% alignment of the c-axes of the polycrystal in the NS directions, later labeled as “strongly” anisotropic; b: elastic moduli of Laio et al. (2000), with a 50% alignment of the c-axes of the polycrystal in the NS directions, later labeled as “mildly” anisotropic; c:elastic moduli of Laio et al. (2000), with an alignment of the c-axes of the polycrystal in the equatorial plane, later labeled as “dendritic”. Insets indicate the corresponding simplified representation used in later figures.
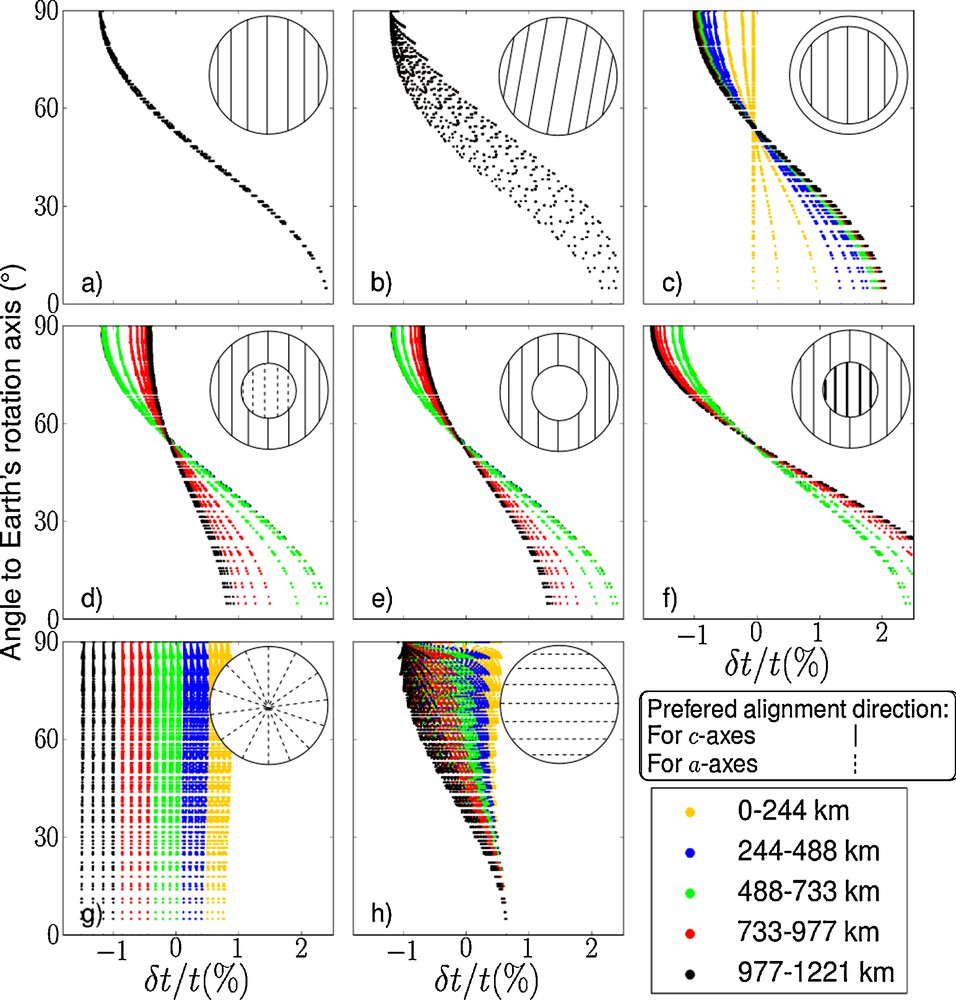
(Color online.) Travel time residuals (in %) plotted against the angle of the seismic ray to the Earth's rotation axis. Results are plotted for different structural inner core models (insets, with lines according to the conventions defined in Fig. 1). Colors indicate the depth of turning point for the ray.
Elastic properties of ɛ-Fe at inner core conditions from first principles models and experiments are still debated (e.g., Antonangeli et al., 2006; Laio et al., 2000; Mao et al., 1998; Martorell et al., 2013; Sha and Cohen, 2010; Steinle-Neumann et al., 2001; Stixrude and Cohen, 1995; Vočadlo et al., 2009) and do not especially match those of the inner core. Here, we intend to understand the seismic response of simple models, extracting the signature of the inner core substructure on the depth and orientation dependence of travel time residuals. As such, and although they will affect the numerical values of global seismic anisotropy, the actual values of elastic moduli we use are not the main focus in our analysis.
Seismic waves are faster along the NS direction than in the equatorial plane. Considering anisotropy at the scale of a single-crystal, this matches the symmetry of wave propagation in an hcp single-crystal with the c-axis faster than the a-axis. We therefore choose a set of elastic constants for ɛ-Fe with the c-axis faster than the a-axis. Among published sets of elastic moduli for ɛ-Fe, we select the results of Laio et al. (2000) that agree with this constraint with single-crystal elastic moduli (in GPa) C11 = 1554; C12 = 742; C13 = 820; C33 = 1796; C44 = 414. We then build two polycrystals with various levels of alignment of the c-axes of the crystallites (100%, 50%, Fig. 1a, b), producing two materials with distinct anisotropic signatures, later labeled as “strongly” and “mildly” anisotropic. Solidification textures have also been proposed as a source for anisotropy in the inner core (Bergman, 1997; Brito et al., 2002). For hcp materials, solidification textures align the c-axes of the polycrystal perpendicular to the direction of solidification (Bergman, 1997; Bergman et al., 2003; Brito et al., 2002). Fig. 1c presents the anisotropy of such a polycrystal. This model will be labeled as “dendritic”.
Considering the diversity of inner core anisotropy models published in the literature, we investigate the response of eight different structural models (Fig. 2):
- • an homogeneous inner core with mildly anisotropic elastic properties aligned with the Earth's rotation axis;
- • an homogeneous inner core with mildly anisotropic elastic properties tilted 10° away from the axis of rotation;
- • a mildly anisotropic inner core surrounded by a 150-km deep isotropic region;
- • an inner core with a mildly anisotropic outer inner core and a dendritic inner inner core of radius 550 km;
- • an inner core with a mildly anisotropic outer inner core and an isotropic inner inner core of radius 550 km;
- • an inner core with mildly anisotropic outer inner core and a strongly anisotropic inner inner core of radius 550 km;
- • an inner core with a spherical crystallization and dendritic elastic properties;
- • an inner core with a cylindrical crystallization and dendritic elastic properties.
More than 100,000 synthetic seismic rays are randomly generated to probe the whole inner core and simulate seismic measurements (Fig. 3). For each ray, we then estimate the normalized seismic travel time residual:
| (1) |
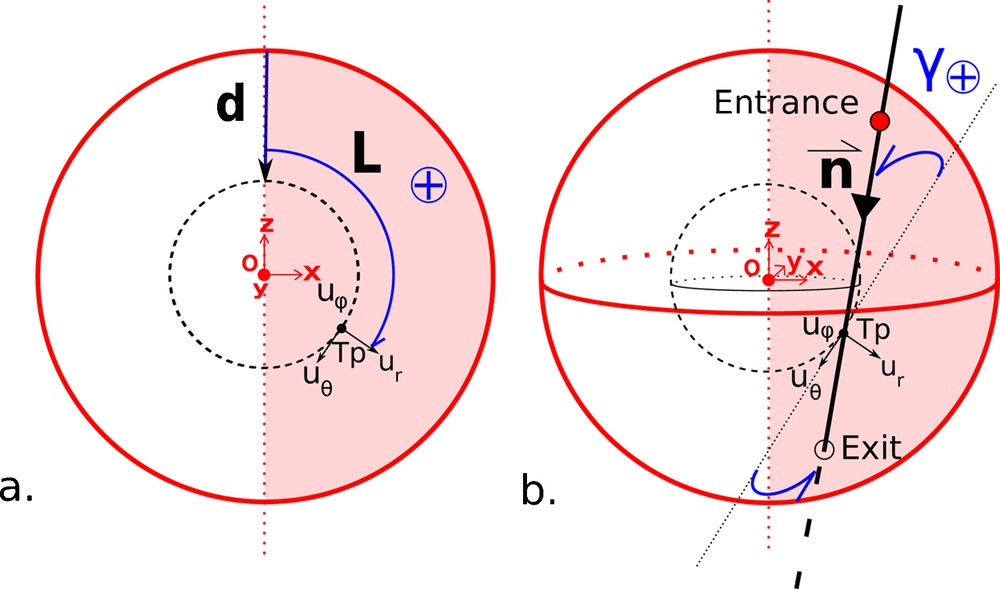
(Color online.) Geometrical construction of inner core seismic rays. They are classified using three scalars: the depth of its turning point, d, (the deepest point of the ray) [0–1220 km], the latitude of its turning point, L [0–180°], and the angle between the ray at its turning point and the meridional plane containing the turning point, γ [0–360°]. The length of the ray is then divided into straight segments between the entrance and exit points on a 20 × 72 × 72 regular grid in d, L, and γ. For each segment, we evaluate the slowness of the material by solving the Christoffel equation with the local elastic tensor.
2.2 Results for single-layer inner cores
In our first structural model, with a mildly anisotropic inner core aligned with the rotation axis (Fig. 2a), the inner core behaves as a giant single-crystal with its c-axis aligned with the NS axis and a minimum velocity in the equatorial plane. The global anisotropy is equal to the anisotropy at the microscopic scale and travel time residuals are independent of the depth of the ray turning point. Provided enough anisotropy at the single-crystal scale, it can match the observed data in terms of global anisotropy.
The second structural model (Fig. 2b) consists of a mildly anisotropic inner core, with the fast axis tilted by 10° from the Earth's rotation axis, as suggested by some seismic models (Romanowicz et al., 1996; Song and Richards, 1996; Su and Dziewonski, 1995). The 10° tilt produces a spread of travel time residuals that, in average, look similar to those of the model in Fig. 2a. As in the previous case, there is no depth dependence of the travel time residuals.
2.3 Effect of an isotropic superficial layer
Other seismological models (Creager, 1999; Garcia and Souriau, 2000; Shearer, 1994; Song and Helmberger, 1995; Waszek and Deuss, 2011) lead to an isotropic layer at the top of the inner core. Such models, with a 150-km thick isotropic region (Fig. 2c), produce no anisotropy for superficial rays, while the deeper rays, below follow a similar trend as observed for an inner core with homogeneous properties, with a reduced amplitude of the anisotropy relative to that of the polycrystal model, and with mean anisotropy increasing with the depth of the turning point. With an isotropic layer reduced to 60 km, the transition to anisotropy will be more superficial, while deeper rays will show little difference to those obtained for a fully homogeneous inner core. Also note that, for a given depth of turning point, there is no spread of travel time residuals.
2.4 Effect of an innermost inner core
Ishii and Dziewoński (2002) proposed an innermost inner core of 300-km radius that exhibits distinct elastic properties relative to the bulk inner core. This is supported by more recent studies (e.g., Beghein and Trampert, 2003; Calvet et al., 2006; Niu and Chen, 2008; Sun and Song, 2008a, 2008b), at perhaps a larger radius of 400–550 km. This hypothesis is tested in Fig. 2d, e, and f, assuming an inner inner core radius of 550 km. Five hundred and fifty kilometers lies in the upper limit of innermost inner core radius estimates (Calvet et al., 2006; Sun and Song, 2008a). However, we intend here to investigate whether such an innermost inner core can be detected using differential travel times and its effect of global anisotropy. As such, our conclusion are not heavily dependent on the exact radius of this innermost inner core.
Our first model (Fig. 2d) consists of a mildly anisotropic outer inner core with an inner inner core with opposite elastic properties, i.e., with the slow axes of the polycrystal aligned with the Earth's rotation axis. Travel time anomalies are similar to those of Fig. 2a for superficial rays. Anisotropy decreases with depth with, therefore, a strong depth dependence of the residuals.
Results are similar if the inner inner core is fully isotropic (Fig. 2e), with travel time residuals similar to those of Fig. 2a for superficial rays and a decrease of anisotropy with depth.
An inner inner core with strongly anisotropic properties (Fig. 2f) with similar properties than the outer inner core, hence, twice stronger, produces measurements similar to that in Fig. 2a for superficial rays, with an increase of anisotropy with depth. Do note, however, that the increase of anisotropy with depth is small and could be difficult to detect in actual seismic measurements.
2.5 Dendritic models
Finally, solidification texturing during the formation of the inner core was also suggested as a possible source of inner core anisotropy (Bergman, 1997; Brito et al., 2002). In this hypothesis, inner core anisotropy is a record of the formation of the inner core.
Our first model (Fig. 2g) considers a radial dendritic growth of the inner core (Fearn et al., 1981). In this model, the slow directions of the polycrystal align in a radial direction, resulting in an inner core with spherical elastic symmetry. Travel time residuals depend on the depth of turning point of the ray. They are insensitive to the angle to the NS axis. This model is, hence, seismically isotropic.
An alternative dendritic model is based on a cylindrical growth (Fig. 2h) of the inner core (Bergman, 1997). In this model, the direction of solidification is perpendicular to the Earth's rotation axis. c-axes of the polycrystal are perpendicular to the solidification direction and, hence, align on a cylindrical surface parallel to the Earth's rotation axis. For such model, anisotropy is weak for superficial rays and increases with the depth of turning point. The trend for deeper rays is similar to that observed for a simple polycrystalline model as in Fig. 2a, with a reduced anisotropy and, for each depth of turning point, more spread of the travel time residuals.
2.6 Conclusion for structural models
We observe a strong variability in terms of depth dependence of the travel time residuals that depends on the model. Spread of data points is also a key for differentiating the different structural models. As such, we find that most models apart from that of Fig. 2h are in line with seismic observations relative to a NS fast direction of propagation of rays. Models, such as models c to e and h also show a gradual increase of anisotropy with depth, in agreement with observations (Souriau, 2003). Our simulations also show that the observation of a gradual evolution of the anisotropy with depth is not inconsistent with structural models having a discontinuity in elastic properties. However, we note that the resolution of seismic observations does not allow such a precise differentiation between structural models. Thus models of Fig. 2c to f and h may all be considered adequate candidates for reproducing seismic observations (Irving and Deuss, 2011).
As a conclusion, we find that structural models produce a complex, depth and orientation dependent pattern of anisotropy, which may be consistent with seismic observations of a global NS anisotropy. However, these observation-driven structural models, with homogeneous elastic properties in each layer, are difficult to reconcile with a spherical inner core growth involving polycrystalline processes.
More realistic geodynamical models producing a cylindrical component of anisotropy involve solidification (Bergman, 1997), possibly coupled with stress-induced recrystallization or plastic deformation resulting from either convection (Jeanloz and Wenk, 1988), heterogeneous growth of the inner core (Yoshida et al., 1996), or magnetic forcings (Buffett and Wenk, 2001; Karato, 1999; Takehiro, 2010). Some are tested below.
3 Geodynamical models
3.1 Overview of inner core geodynamical models
The core crystallizes from the center outward because the melting temperature of the core mixture increases with depth faster than the (adiabatic) core geotherm. Inner core crystallization induces potential deformation and, hence, development of anisotropy inside the inner core. Such processes, coupled with radiogenic heating, have been proposed to induce a thermal forcing as a drive for convection (Buffett, 2009; Jeanloz and Wenk, 1988), with a potential chemical stratification (Deguen and Cardin, 2011). Other models for generating deformation inside the core include magnetic forcing (Buffett and Wenk, 2001; Karato, 1999; Takehiro, 2010) or heterogeneous growth of the inner core controlled by thermal motions in the outer core (Deguen et al., 2011; Yoshida et al., 1996).
Most of those models are axisymmetric and, hence, cannot account for the hemispheric dependence of seismological data. To address this issue, geodynamical models considering a thermal translation of the core were recently considered in the literature (Alboussière et al., 2010; Deguen et al., 2013; Mizzon and Monnereau, 2013; Monnereau et al., 2010).
Our study focuses on differential growth mechanisms (Fig. 4), assuming that geostrophic convection in the outer core results in faster crystallization in the equatorial belt of the inner core. The resulting topography is continuously relaxed by a quadrupolar viscous flow within the inner core (Yoshida et al., 1996), named hereafter Yos–Ran. The reason for this choice is that, among the published models, this model generates a large amount of large-scale deformation in the inner core and that, thanks to its simplicity, it is a good test case for investigating the development of anisotropy with deformation. Anisotropy in such a model can be enhanced by the addition of solidification induced pre-texturation at the ICB, named Yos–Ptex, and deformation due to the bulk effect of a stable density stratification that localizes the motions by minimizing any radial motion, named Yos–Strat. Non-axisymmetric models, such as those involving thermal translation of the inner core, are out of the scope of this study, which focuses on models preserving a symmetry around the axis of rotation of the Earth.
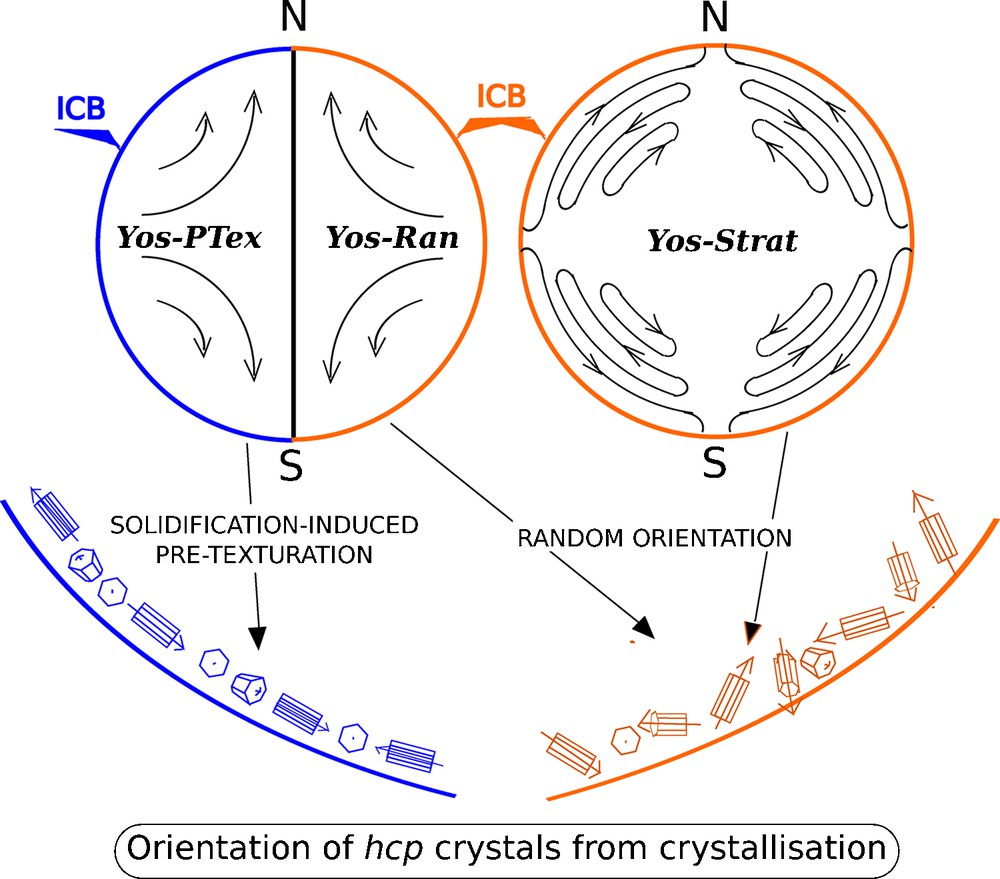
(Color online.) Schematic view of the geodynamical models used in this paper. Yos–Ptex and Yos–Ran are deduced from the quadrupolar model of Yoshida et al. (1996). In Yos–PTex, hcp crystals solidify at the ICB with their c-axes lying preferentially in the plane of the ICB (blue), while in Yos–Ran, we assume a random solidification texture (red). Yos–Strat is an extension of the model of Yoshida et al. (1996) assuming a stable density stratification (Deguen and Cardin, 2009). In this case, deformations are significant and solidification textures are quickly erased. The results presented here are therefore limited to random solidification textures.
3.2 ɛ-Fe texture induced by the geodynamical model
Our model is based on the code described in Deguen and Cardin (2011), with neutral chemical stratification (B = 0) and an equatorial growth rate twice faster than at the poles (S2 = 2/5). Continuous relaxation of the dynamic topography results in a flow from the equator to the poles with a quadrupolar pattern inside the whole inner core. Using methods developed in a previous study (Deguen et al., 2011), we compute the position and deformation for 100 markers introduced at the ICB during inner core growth. Texture along markers are then calculated for a 3000 grains aggregate of ɛ-Fe using the Los Alamos viscoplastic self-consistent (VPSC) code of Lebensohn and Tomé (1993).
In the Yos–Ran model, the aggregate is created at the ICB with a random texture, i.e. with an equal probability for any crystal orientations. We assume dominant basal slip, with contributions of prismatic and pyramidal slip (Merkel et al., 2012). In this model, texture is weak in the outer portions of the inner core and only significant closer to the center of the inner core. It corresponds to a pure shear deformation texture with a distribution of the a-axes of the polycrystal along the polar axis of the inner core (Fig. 5a).
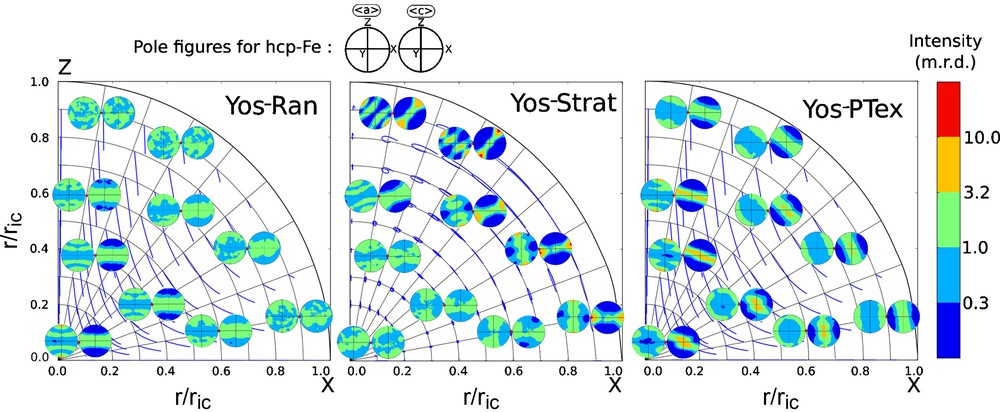
(Color online.) Pole figures of the a and c directions representing present-day textures in ɛ-Fe aggregates at various locations of the inner core. Blue lines are the trajectories of the polycrystalline aggregates after crystallization at the ICB. Contours are in multiple of a random distribution (logarithmic scale). Left: Yos–Ran; middle: Yos–Strat; right: Yos–PTex geodynamical models. ric is the radius, normalized to that of the inner core.
Model Yos–Strat includes the effect of a chemical or thermal stratification within the inner core [B* = –106 in the model of Deguen et al., 2011]. Stratification suppresses radial motion in the bulk of the inner core. The equatorial bulge is relaxed by plastic flow within a superficial horizontal layer where deformation is concentrated. Stratification concentrates textures in the top of the inner core, while, near the center, textures are weak due to the small deformation applied to the polycrystal (Fig. 5b).
Textures are weak in the outer regions of model Yos–Ran. In parallel, multiple studies suggested solidification textures as a potential source of inner core anisotropy (Bergman, 1997; Bergman et al., 2003; Brito et al., 2002). Model Yos–Ran is hence completed by introducing solidification textures with the c-axes within the plane of the ICB (Model Yos–PTex, Fig. 5c). The crystallization texture at the ICB evolves as the aggregates flow deep into the inner core. On the other hand, aggregates that remain in the outer regions of the core tend to preserve the original solidification textures.
3.3 Calculation of travel time residuals
In order to obtain seismic residuals with a fast NS axis, compression wave velocities of ɛ-Fe in such a model should be maximum along the a-axis. This requirement is the opposite of that of structural models described in the previous section. As such, the set of elastic moduli selected previously (Laio et al., 2000) will not allow a successful model inner core anisotropy.
Recent published models (Sha and Cohen, 2010; Steinle-Neumann et al., 2001; Vočadlo et al., 2009) exhibit such velocity profiles for ɛ-Fe at core conditions. In the results of Sha and Cohen (2010), the anisotropy of ɛ-Fe single-crystals at core condition lies in the order of 1%. This quasi-elastic isotropy is problematic for explaining inner core anisotropy. The results of Steinle-Neumann et al. (2001) do provide large anisotropy at core conditions, but the approximation used in those calculations has been controversial (Gannarelli et al., 2003). Consequently, we selected the published results of Vočadlo et al. (2009) at 5500 K with single-crystal elastic moduli (in GPa) C11 = 1646; C12 = 1253; C13 = 995; C33 = 1559; C44 = 153. These numbers imply a sound velocity along the c-axis 5% slower than that along the a-axis.
At each point of the grid of each geodynamical model (Fig. 5), the local elastic tensor is calculated by weighting the single-crystal elastic tensor with the aggregate texture, in the Hill approximation. Solving the Christoffel equations, we are then able to calculate P-wave velocities for any direction of propagation (Fig. 6). Travel time residuals are then calculated using the procedure described in Fig. 3.
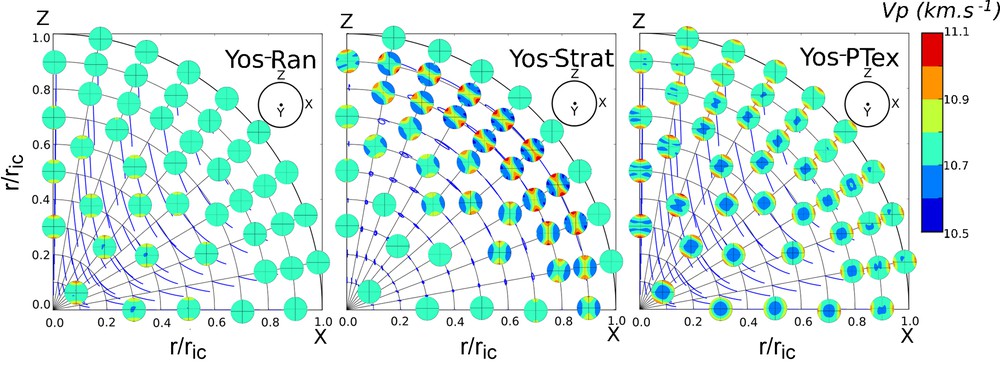
(Color online.) P-wave velocity (in km/s) in a meridional plane for geodynamical models Yos–Ran (left), Yos--Strat (middle), and Yos–PTex (right). Calculations are based on the textures of Fig. 5 and the single-crystal elastic moduli of Vočadlo et al. (2009) at 5500 K. ric is the radius, normalized to that of the inner core.
Our model allows a detailed analysis of anisotropy, including the depth and orientation dependence of the travel time residuals (Fig. 7). However, seismological studies usually do not have the resolution necessary to investigate the full details of inner core anisotropy. Different strategy were put forward to overcome the small amount of data. A global view could be obtained by using spherical harmonics (Poupinet et al., 1983). Alternatively, it was proposed to fit travel times residuals using (Creager, 1992)
| (2) |

Travel time residuals (dots) plotted against the angle of the seismic ray to the Earth's rotation axis for the three geodynamical models of Fig. 4. Colors indicate the depth of turning point of the ray. The thick purple line is the fit of Eq. (2) to the data. Numbers in the insets indicate the average anisotropy for each model. (For interpretation of references to color in this figure, the reader is referred to the web version of this article).
where a, b and c are adjustable parameters and ζ is the angle between the ray and the Earth's rotation axis. The quantity b + c is the difference between polar (ζ = 0°) and equatorial (ζ = 90°) residuals, and is a measure of the global inner core anisotropy often reported in the literature. Recent results by Irving and Deuss (2011) on their entire catalog of PKPdf-bc differential travel time residuals reveal a 3.3 to 3.8% global NS anisotropy. This observation is regionally dependent: a subset of data in the western hemisphere leads to an anisotropy ranging from 4.5 to 4.8%, while the eastern hemisphere is only 0.5 to 1.4% anisotropic.
3.4 Results for model Yos–Ran
For this model, we find positive time residuals for rays parallel to the axis of rotation (at 0°, Fig. 7a). Equatorial path travel time residuals are small, sometimes negative: seismic waves travel faster along polar paths. The global shape of the time residuals is similar to seismic observations, even if actual polar observations are scarce.
Travel time residuals do not exceed 1%. As such, this model cannot account for global seismological observations. Reasons from this disagreement are as follow:
- (i) aggregates with the strongest textures, in the inner portions of the inner core, do not display such simple anisotropy features as a pure single-crystal of ɛ-Fe and, hence, are averaged out over the path of the ray;
- (ii) in this model, most of the inner core is isotropic, and hence contributes to an isotropic signal at the global scale.
This model, on the other hand, clearly displays a depth dependence of the time residuals: rays with deeper turning points would lead to a larger anisotropy. This is in broad agreement with seismic observations. In this case, deformation in the superficial layers of the model is small. Consequently, the outer portion of the core is nearly isotropic and would lead to negligible travel time residuals, whatever the direction of propagation of the ray.
The fit of Eq. (2) to the data leads to a global anisotropy of 0.7% (Fig. 7a). This global anisotropy is clearly below most seismological estimates. Nevertheless, the shape of the anisotropy as a function of the angle to the axis of rotation of the Earth is appropriate. With such a quadrupolar flow, the single-crystal anisotropy should increase by a factor of ∼ 5 in order to match the reported global anisotropy. In other words, with such model, a single-crystal anisotropy on the order of 15% would be required for a 3% global seismic anisotropy.
3.5 Results for model Yos–Strat
Chemical stratification concentrates textures in upper portions of the inner core (Fig. 5b). In this model, the anisotropy is dominated by fast P-wave velocities in the horizontal direction (Fig. 6b). At intermediate depths, we can observe some component of NS anisotropy, reminiscent of the features of the non-stratified model.
The travel time residuals are complex and spread over almost 3% (Fig. 7b). As expected, the large deformation in this model allows for a larger anisotropy than for models such as Yos–Ran. On the other hand, the fit of Eq. (2) to the data leads to a global anisotropy of 0.8% (Fig. 7b). In average, this model does lead to faster waves along the north axis than in the equatorial plane, as observed in seismology. Data points, on the other hand, are spread and complex, with residuals found far away from the fit of Eq. (2).
The depth dependence of the anisotropy is opposite to seismic observations: anisotropy is low for the deepest rays while travel times for shallower rays do set a trend for a global NS anisotropy.
This model does not broadly agree with seismic observations. On the other hand, and as already shown with the structural models, these results emphasize how the spread and depth dependence of travel time residuals hold important information. Both are strongly affected by structural features of the Earth inner core.
3.6 Results for model Yos–Ptex
Relative to model Yos–Ran, ICB crystallization textures in model Yos–Ptex enhances anisotropy in the outer regions of the inner core (Fig. 6c). In the deeper portions of the inner core, crystallization textures are largely erased by plastic deformation and the resulting velocities resemble that of model Yos–Ran. Due to the spherical symmetry of the crystallization process, P-wave velocity profiles in the shallower portions of the inner core do display a strong spherical symmetry.
Travel time residuals lie between –0.05% and 2% (Fig. 7c). Also, note the very strong depth dependence of the residual. On the other hand, the average global anisotropy of such model is low, of the order of 0.3%, due to the spherical symmetry of the crystallization textures. Whatever the depth of the turning point, observations are similar, with a maximum global anisotropy of 0.3%, with faster arrivals for deeper rays. As such, this model is not in line with seismic observations.
4 Discussion and conclusion
We developed a new method for scaling microscopic properties, such as single-crystal elasticity of ɛ-Fe to the macroscopic observations of seismic travel times. Using elastic models for ɛ-Fe published in the literature, it appears difficult to obtain a 3.3–3.8% global anisotropy, as proposed in recent works (Irving and Deuss, 2011). Calculations were repeated for other published models for ɛ-Fe (Laio et al., 2000; Sha and Cohen, 2010; Soderlind et al., 1996; Steinle-Neumann et al., 2001; Stixrude and Cohen, 1995) and, within the scope of our geodynamical models, the single-crystal anisotropy was not sufficient to match that observed in inner core seismic studies.
Elastic moduli of Steinle-Neumann et al. (2001) do allow for a 2% global anisotropy whereas, in recent years, calculations have converged towards more isotropic models (e.g., Sha and Cohen, 2010; Vočadlo et al., 2009). It should be noted, however, that dynamics simulations suggest a strong non-linear behavior of ɛ-Fe at 360 GPa, just before melting (Martorell et al., 2013). This strongly non-linear effect in Fe could occur in the inner core, and hence provide enough anisotropy to match seismic observations. Anisotropy at the single-crystal scale may also be increased by including the effect of elements other than Fe.
Using simple structural models and a proper set of elastic moduli, it is possible to match seismic observations. We find no measurable anisotropy for rays propagating at small depth when a superficial isotropic layer is considered. The existence of an innermost inner core may be unraveled by a depth dependence of the residuals, but it is difficult to strictly identify the elasticity of the material in the central region. We also note that it is not straightforward to conclude on the sharpness of internal interfaces between regions of different elasticity with travel time data because of the integration of the residuals over the whole inner core portion of the ray.
Structural models provide an easy interpretation of the seismic data. On the other hand, those models offer little clues regarding the dynamics and the physical processes at play during the formation of the inner core. In more realistic models, such as random and fast crystallization at the equator (Yoshida et al., 1996, i.e. Yos–Ran), averaging along seismic rays reduces the global anisotropy by a factor of seven relative to that of the single-crystal. A strong local anisotropy is reduced at the global scale by other regions where the anisotropy displays a different orientation. Stratification produces a complex and localized deformation and anisotropy, stronger than in Yos–Ran. Despite averaging effects, the global anisotropy increases by about 15%, with an apparent symmetry around the Earth's rotation axis. Solidification textures, on the other hand, introduce a spherical symmetry in the local anisotropy. Global anisotropy is then reduced by a factor of 2.
We observe a strong depth dependence of the PKP-wave travel time residuals that depends on the model. Spreading of data points is also a key for differentiating the different geodynamical models. As such, we find that simple models, such as Yos–Ran are more in line with seismic observations relative to models including stratification or solidification textures for which the depth dependence and spread of travel time residuals is wrong. This emphasizes that a simple fit as in Eq. (2) through the dataset oversimplifies the data. Such fit smooths out the depth dependence and the spread of the travel time residuals, which are deeply related to the tectonics of the inner core.
Finally, it is likely that the scarce geographical coverage of seismic data does not correctly probe the full inner core. As such, it would be of interest to characterize the under-sampling of actual observations. Numerical models, such as those presented here, could be used to investigate the reliability of the observational constraints using actual entry and exit points of ray paths used in seismic studies.
We therefore suggest that the analysis and parameterization of seismic data progress towards constraining the depth and geographical dependence of travel time residuals, with additional information on the spread, to allow a better characterization of processes of inner core formation.
Acknowledgments
The authors wish to thank D. Antonangeli and A. Deuss for their reviews and the Geodynamo group for useful discussions. This work has been financed by the program PNP of CNRS/INSU, OSUG@2020, and the doctorate program of Université Joseph-Fourier, Grenoble (France). Calculations have been made at the Centre de Calcul Commun of OSUG. RD was supported by grant EAR-0909622 from the National Science Foundation.


