1 Introduction
In the paper that motivated this commemorative issue of Comptes rendus Geoscience, Poupinet et al. (1983) discovered anomalous wave propagation in the inner core, which was soon interpreted in terms of inner core elastic anisotropy (Morelli et al., 1986; Woodhouse et al., 1986), where the direction parallel to the spin axis is 3–4% fast. Since then there has been considerable research on the inner core, investigating its structure seismically (see Souriau, 2007 for a review), and trying to understand the origin of the structure using mineral physics and geodynamics (see Deguen, 2012; Sumita and Bergman, 2014 for reviews).
Explanations for inner core elastic anisotropy include a shape preferred anisotropy (Singh et al., 2000), or a lattice preferred orientation (also known as texturing). The latter could be caused by solidification (Bergman, 1997, 1998; Karato, 1993) or by deformation. Deformation could be driven by convection (Buffett, 2009; Cottaar and Buffett, 2012; Deguen and Cardin, 2009; Gubbins et al., 2013; Jeanloz and Wenk, 1988), the liquidus not aligned with the gravitational equipotential (Yoshida et al., 1996), Maxwell stresses (Buffett and Wenk, 2001; Karato, 1999), or Ohmic heating (Takehiro, 2011). Neither deformation nor solidification have by themselves, however, been able to explain the varied seismic inferences that include depth (Shearer, 1994; Song and Helmberger, 1995) and longitudinal (Deuss et al., 2010; Tanaka and Hamaguchi, 1997) dependence of the elastic anisotropy, longitudinal variations in the isotropic velocity (Niu and Wen, 2001), and an attenuation anisotropy that itself may vary longitudinally and with depth (Cormier, 2007; Creager, 1992; Souriau and Romanowicz, 1996; Yu and Wen, 2006). Longitudinal variations could be due to long-term mantle control (Aubert et al., 2008) or inner core translation (Alboussière et al., 2010; Al-Khatatbeh et al., 2013; Bergman et al., 2010; Monnereau et al., 2010). Also puzzling is a decrease in the P wave velocity gradient at the base of the outer core (Souriau and Poupinet, 1991), which has been interpreted as a dense fluid layer (Alboussière et al., 2010; Cormier, 2009; Gubbins et al., 2008, 2011).
Making an explanation of these seismic inferences more difficult to pin down is the uncertainty of the elastic properties of hexagonal close packed (hcp) iron under inner core conditions (Antonangeli et al., 2006; Gannarelli et al., 2005; Steinle-Neumann et al., 2001; Stixrude and Cohen, 1995) and even the stable phase of iron under inner core conditions (Belonoshko et al., 2003; Vocadlo et al., 2003a, 2003b), though hcp still seems to be arguably the most viable candidate (Tateno et al., 2010). Also unknown is the deformation mechanism and, if by dislocation creep, the available slip systems. Hence the viscosity is also unknown. There have been attempts (Wenk et al., 1988) to model the texture that results from a geodynamically suggested inner core deformation, assuming a deformation mechanism and slip systems for hcp iron, including an initial solidification texture (Deguen et al., 2011). Studies that incorporate mineral physics into geodynamic modeling are promising, but the inputs remain uncertain.
We therefore began these experiments in an effort to understand the deformation, and annealing, of directionally solidified metallic alloys. In particular, parameters such as the grain size, microstructure, secondary phases, and impurities can affect the deformation mechanism. Directionally solidified metallic alloys typically have a columnar structure elongated in the growth direction. These columnar crystals (grains) are composed of parallel primary dendrites, in which the secondary phase is distributed both along grain boundaries and as intragranular pockets between dendrites. In hcp alloys the dendrites take the form of platelets, with the growth direction parallel to basal planes, in the <101′0> direction, and c-axes of different grains oriented randomly in the plane transverse to growth (Fig. 1), though fluid flow in the melt can also align the c-axes (Bergman et al., 2002, 2003).
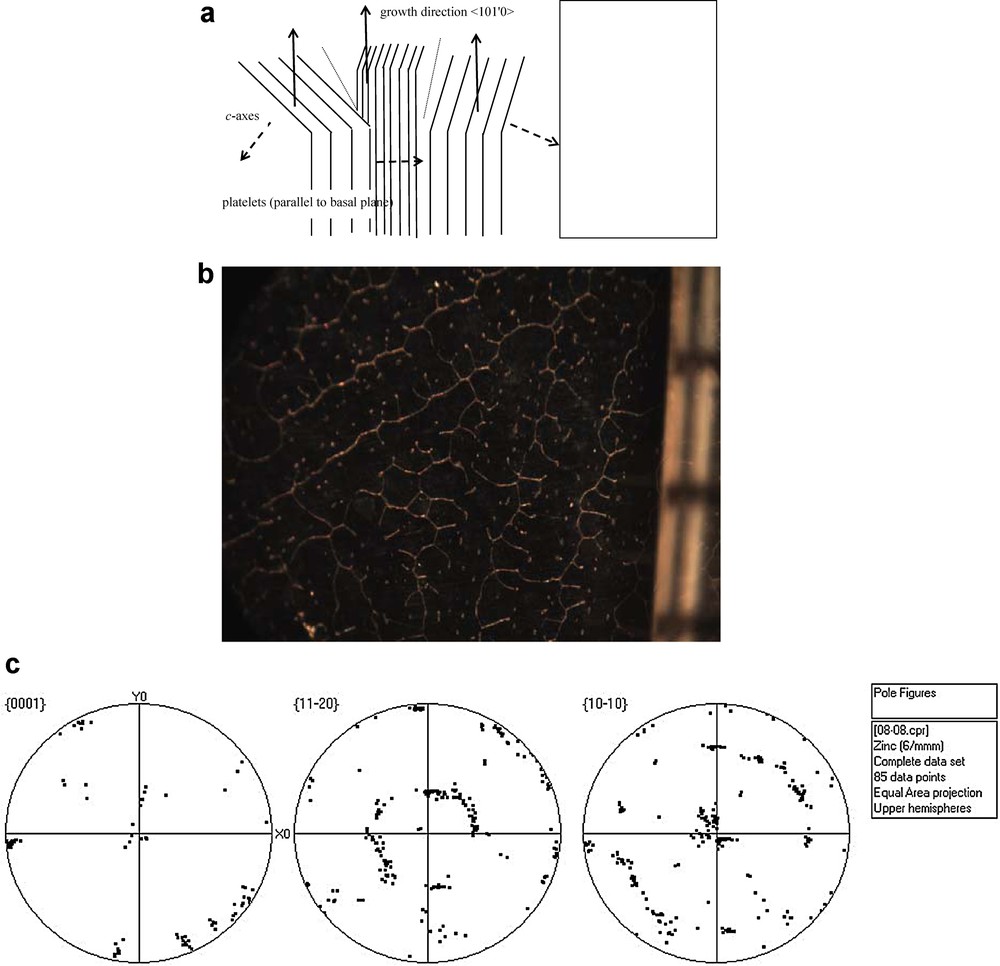
a. Cartoon showing side view of directionally solidifying hcp alloy. Parallel platelets form a single crystal, with dotted lines showing grain boundaries. Dashed c-axes are perpendicular to platelets. b. Micrograph of directionally solidified Zn–3 weight % Sn, transverse to growth. The darker phase is the Zn-rich phase, the lighter, Sn-rich. Platelets, side-branches, and a grain boundary from bottom left to top right are visible. Tick marks represent 1 mm in all micrographs (Color online.). c. A set of pole figures for the sample shown in Fig. 1b, relative to the growth direction. The growth direction is <101’0>, with the c-axes primarily transverse to growth. The symmetry of the hcp crystal is such that 101’0 poles near the center also plot on a circle 60° away, and 112’0 poles along a circle at 30° also plot along a circle at 90°.
Under laboratory conditions the columnar grains in directionally solidified metallic alloys are typically several cm long in the growth direction, and about 0.5 cm transverse. The Earth's inner core has been predicted to be growing dendritically (Deguen et al., 2007; Fearn et al., 1981; Shimizu et al., 2005), and scaling (Kurz and Fisher, 1992) laboratory growth to the inner core (admittedly many orders of magnitude!) we predicted a transverse grain size on the order of hundreds of meters (Bergman, 1998), which is in agreement with estimates from seismic scattering (Cormier et al., 1998) and attenuation (Karato, 2008). However, most studies of deformation mechanisms (Frost and Ashby, 1982) understandably begin with a fine grained, equiaxed, randomly oriented, homogeneous sample, though there has been work on high temperature creep of directionally solidified cubic alloys of industrial importance (Flemings, 1974). Such alloys have been found to be stronger due to their resistance to diffusion creep. The high pressures needed to study deep earth materials can be obtained only on the small length scales of diamond and multi-anvil cells, which generally precludes large grains or microstructure such as grains with shape anisotropy. The subject of this study is thus to understand how microstructure, e.g., large, textured, columnar dendritic grains such as one might expect in the inner core (Bergman, 1997; Fearn et al., 1981), affects the deformation mechanism and viscosity, especially for hcp alloys, which have relatively few slip systems.
2 Experimental procedure
The basic concept of the experiment involves high temperature (0.97 the melting temperature of pure Zn, Tm = 419 °C) torsion of directionally solidified Zn-rich Sn. Because of the necessarily large sample size we perform the experiments at atmospheric pressure, transmitting the torque from the motor/gearbox shaft using the method of keying (Fig. 2) described by Paterson and Olgaard (2000). Zn is hcp at atmospheric pressure, and the Zn–Sn system forms a eutectic.

(Color online.) Torsion sample before deformation, showing gripping teeth and vertical foil marker.
We first directionally solidify Zn–Sn ingots (1875 grams, 4.45 cm in diameter, and approximately 17 cm high), and then take cylindrical sections (1.5 cm tall) from various heights in the ingots to characterize the solidification microstructure and texture. The directionally solidified ingots have grain sizes that range between 3 and 5 mm in cross-section, and as long as 3 cm in length. The primary platelet spacing varies between about 0.2 and 0.5 mm (Fig. 1b). Although not by an ideal margin, the outer minus inner radii (0.90 cm), and perhaps more importantly the mean circumference (10.7 cm) of the bored-out samples is large compared with the platelet spacing and the cross-sectional grain size, i.e., the samples are polycrystalline in the direction of strain. The grain size in the original solidification direction, parallel to the axis of the cylindrical section, is currently taller than the height h = 1.5 cm of the section. We may eventually carry out experiments on samples with a larger h. The need for large sections to insure polycrystallinity is opposed by better uniformity of strain in sections with a small difference between outer and inner radii.
From the directionally solidified ingots, we then machine keyed samples for the torsion apparatus. For each experiment we bring the sample to high homologous temperature, typically 0.97 Tm, which takes about 1.5 hours, and then begin the torsion. We use a servo motor with a 700:1 low backlash gearbox, with a maximum continuous output torque of 120 N·m. The servo allows a one hundred fold range of angular rotation rates, with a resolution of 1 part in 1000. We measure the applied torque via a strain gage on the gearbox output shaft. Because the alloy is a good thermal conductor, uniformity of temperature should not be a problem, but we check this by means of multiple thermocouples inserted into holes machined into the crucible. At the end of the experiment we quench the sample, and again examine the microstructure and texture after standard metallographic preparation.
We rotate the shaft at a constant angular rate θ’, giving a strain rate ɛ’ = rθ’/h at a given radius r in the ring-shaped sample of height h. By making the difference (0.90 cm) between the outer (2.15 cm) and inner (1.25 cm) radii of the sample smaller than its mean radius (1.7 cm), we minimize differences in strain rate across the sample. A foil marker in the sample allows us to check the actual strain post-mortem. The maximum shear stress σ (at the outer radius) is related to the measured torque τ by:
| (1) |
To determine the stress exponent n, we intended to measure the steady state torque in a series of experiments at different strain rates. At high homologous temperature and low to moderate stress, the conditions applicable in both the inner core and the experiments, the relationship between strain rate ɛ’ and shear stress σ in the steady state is given by a power law,
| (2) |
After quenching, we examine the microstructure optically, and carry out electron back scattered diffraction (EBSD) to determine the texture. We created pole figures using a uniform density of points in the region of interest. We estimate an uncertainty of no more than 5° in the measured orientation of the sample surface relative to the specimen growth direction. These uncertainties arise due to the metallographic preparation, sample mounting in the SEM, and mechanical stage alignments. In all of the pole figures, the original growth direction lies at the center.
3 Results
We first carried out a set of experiments at the same strain rate in order to check the reliability and repeatability of our apparatus. In the meantime, even this set of experiments has started yielding interesting results on hardening, which may bear on inner core viscosity. Fig. 3 shows the torque–strain curves for directionally solidified Zn-rich Sn alloys with columnar, dendritic microstructure deformed at a strain rate ɛ’ = 3.3 × 10−6 s−1 at the sample's outer edge. This is a small strain rate by lab standards, though strain rate estimates in the inner core range from 3 × 10−18 s−1–10−15 s−1 (Cottaar and Buffett, 2012; Yoshida et al., 1996).
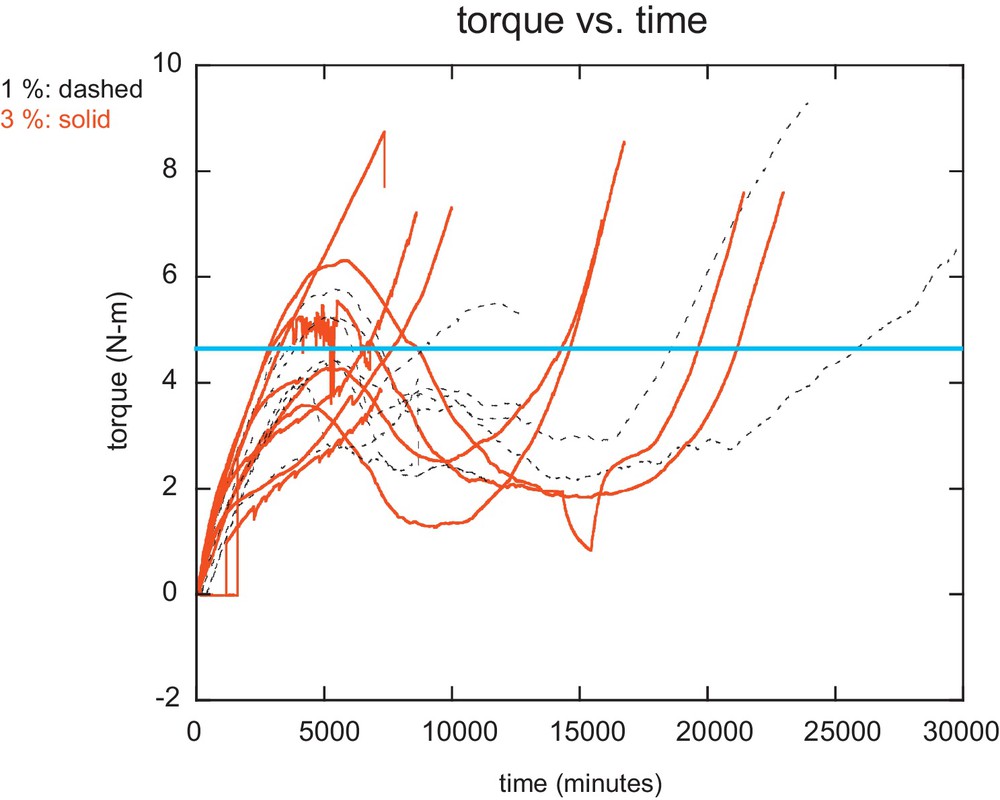
(Color online.) Torque–strain curves for Zn–Sn alloys under torsion. Early experiments on Zn–3% Sn did not show the local maxima and minima; all subsequent experiments do, for unknown reasons. The decrease in the magnitude of the torque around 15,000 minutes in one curve is due to the motor temporarily shutting off. The heavy blue line at 4.4 N·m is the expected steady state torque for deformation of pure zinc with a grain size of 0.1 mm and our sample geometry (Frost and Ashby, 1982).
Surprisingly, the torque (and hence the stress, from (1)) does not level off as one might expect for steady state deformation (see the calculations in the Discussion section), but rather continues to increase, suggesting hardening by some means. Because of this, (2) is no longer applicable, and we have not yet run experiments at a range of strain rates. Interestingly, the rate of hardening appears to be % Sn dependent, with the slope steeper for 3% Sn alloys than for 1% Sn alloys. We investigated whether this hardening might be due to dislocation or grain boundary pinning by oxides (Ramar and Schaublin, 2012), but we carried out experiments in a reducing atmosphere, which made no difference, and we used a microprobe to look for oxides, which we did not find. We also looked for a fine distribution of secondary phase using a microprobe, as a fine distribution of even liquid drops has been suggested to cause dislocation pinning and hence hardening (Ingrin et al., 1991), but the evidence for this in our samples was doubtful, and we will need transmission electron microscopy (TEM) to study dislocations, which we intend to do in future work.
One can see in Fig. 4a and b evidence of the original columnar grains, now tilted, and perhaps some evidence for the original platelets. The strains rθ/h are order one. One can also see small voids that look like microcracks. There is no evidence for recrystallization in Fig. 4, in agreement with the calculations in the Discussion section. Lastly, results from EBSD (Fig. 4c) are inconclusive concerning the texture. While there is certainly loss of solidification texture (Fig. 1c), there is still some texture that we do not yet understand, and we need data from more experiments.

a. Outside view of Zn–1% Sn sample twisted to a shaft angle of 52.5°, showing tilted metal alloy and foil. The maximum strain roθ/h = 1.3 at the outer radius r. b. Tangential view of Zn–3% Sn twisted to a shaft angle of 30°, for a maximum strain of 0.75. One can see tilted grains, and perhaps original platelets. Microcracks (and bubbles from the mounting resin) are also present. There is a 1000 μm marker towards the bottom right. c. A set of pole figures for Zn–1% Sn twisted to a shaft angle of 102° (color online).
4 Discussion
Fig. 3 shows the torque–strain curves for a set of our experiments at one strain rate, ɛ’ = 3.3 × 10−6 s−1. For the directionally solidified alloys deformed at constant strain rate, the measured torque τ, and hence the stress σ, have not reached a steady state, so that we could not determine σ and the stress exponent n by simultaneously solving (1) and (2), even had we data for a range of strain rates. To get a sense of the magnitude of the torques shown in Fig. 3, we can use data for steady state deformation of pure Zn (Frost and Ashby, 1982) with a grain size of 0.1 mm deformed (via diffusion creep) at 0.97 Tm at ɛ’ = 3.3 × 10−6 s−1. This yields σ = 2.9 × 105 Pa, and using (1) (with n = 1) a torque τ for our sample geometry equal to about 4.4 N·m for steady state deformation, which we are exceeding without any evidence that the torque is approaching the steady state.
On the other hand, the grain size in our experiments is much larger, and although the platelet spacing is likely more relevant because the platelet boundaries can serve as a source of atoms, even the platelet spacing is between 0.2 and 0.5 mm (Fig. 1b). Using this as the effective grain size, and b = 2 for Nabarro–Herring (diffusion) creep, (2) suggests that if diffusion creep is still the primary deformation mechanism, the steady state stress and hence the torque could be 4 to 25 times larger than 4.4 N·m. However, as the effective grain size increases it seems likely that the primary deformation mechanism might switch from diffusion creep to power law creep or that dynamic recrystallization might occur. Nevertheless it is possible that we have simply not yet reached a steady state regime, so that yet longer experiments at this strain rate might be necessary.
We had hoped, of course, that the micrographs and EBSD data would give insight into the deformation mechanism. For instance, diffusion creep usually results in no texture, whereas dislocation creep does (Karato, 2008). Unfortunately, the path from the solidification texture (Fig. 1c) to the deformed texture (Fig. 4c) is still unclear, hopefully more data will help.
Moreover, there is no evidence for recrystallization in Fig. 4a or b, and using d/b = K (σ/G)−s, where d is the recrystallization grain size, K and s are empirical constants of orders 100 and 1.2, respectively (Derby, 1991), we estimate a recrystallized grain size of 7 mm, suggesting that in this set of experiments there is not enough driving stress for recrystallization.
This has led us to our current hypothesis, that the hardening is microstructural, as a result of the large, textured columnar grains and the relative lack of slip systems in hcp metals. The micrograph Fig. 4b is suggestive of semi-brittle behavior, perhaps due to the limited number of slip systems associated with hcp metals. Because the directionally solidified crystals are large and textured, there are a limited number of slip systems in the direction of local strain (Fig. 5), rendering dislocation creep difficult (the von Mises condition requires five independent slip systems to achieve homogeneous deformation). Moreover, because the grains are large the conditions are also not favorable for diffusion creep in spite of the high temperature. Twinning can accommodate some strain, but not likely all (Dieter, 1986). The unfavorable conditions for creep may therefore lead to heterogeneous deformation (Karato, 2008). There is one report in the literature (Edwards et al., 1974) of texturing in Zn leading to high temperature hardening (by a factor of 100!), and also in hcp sea ice (Cole et al., 1998).
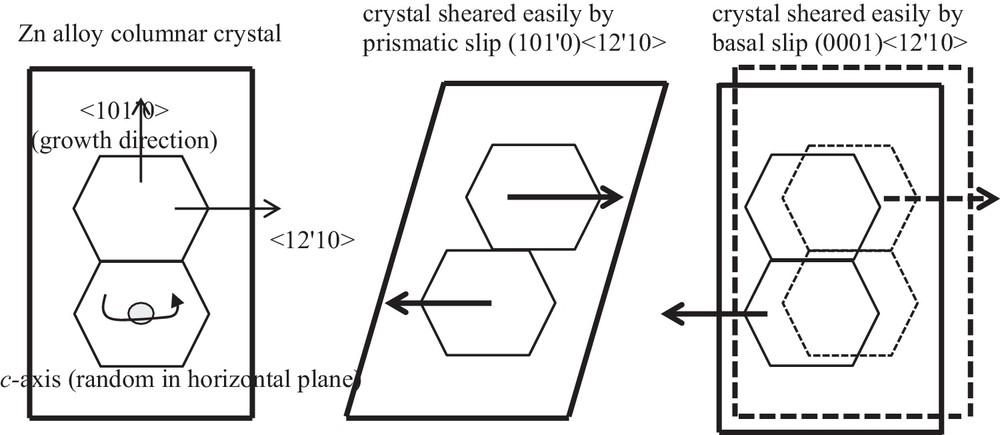
Diagram showing easily sheared direction of columnar crystals via two slip systems. Not all strains are easily accommodated by available slip systems.
In our samples the cracks seem to be present primarily along grain boundaries, and may have been melt-filled during deformation. Obviously under high pressure cracking is unlikely due to the volumetric changes, but one might expect lower ductility and more heterogeneous deformation. We did run one torsion experiment on a fine grained, equiaxed, randomly oriented Zn–3% Sn alloy, and it exhibits less brittleness and cracking after quenching, which supports our hypothesis. Unfortunately the strain gage failed and we do not yet have torque data for such samples.
The slip planes of iron under inner core conditions are of interest for dislocation creep because the associated rotation would likely be the source of texturing if deformation is responsible for the elastic anisotropy. Based on the c/a ratio, Wenk et al. (1988) used titanium as an analog and so assumed that slip occurs along prism planes, (101’0), and in the close packed <12’10> direction. Such slip would cause c-axes (which they assumed slow) to lie in the equatorial plane for shear parallel to the inner core surface, as one might expect for low order convection. Poirier and Price (1999) pointed out, however, that stacking fault energies are better predictors of active slip planes than is the c/a ratio, and predicted that primary slip in iron under inner core conditions is likely to be basal (0001) <12’10>. At least at temperatures below 1000 K this was supported by Wenk et al. (2000), and also by Merkel et al. (2004), who also found some prismatic slip (101’0) <12’10> associated with twinning. Not incidentally, Zn at atmospheric pressure also exhibits basal slip (0001) <12’10>.
Microstructural hardening would impact the deformation mechanism and viscosity of the inner core. Estimates of inner core viscosity η come from geodynamics and mineral physics, and to some extent from seismology, and range from 1011 Pa·s to 1021 Pa·s. On the low end, van Orman (2004) determined from a deformation mechanism map that for the large grain size (> 10−2 m) and small stress (< 104 Pa) likely in the inner core, the inner core is in the regime of Harper–Dorn creep. Harper–Dorn creep is due to dislocation glide, but the dislocation density is independent of the applied stress, so that n = 1. It is thus a Newtonian viscosity, which van Orman found to be 1011 Pa·s. This is very low considering the observations of shear waves in the inner core (Wookey and Helffrich, 2008), and the existence of Harper–Dorn creep has been questioned (Blum et al., 2002; Karato, 2008), especially in materials that are not ultra-pure (Cheng et al., 2009).
At the high end, Yoshida et al. (1996) estimated the viscosity at 1021 Pa·s by finding the deformation mechanism—diffusion or power law (they did not consider Harper–Dorn) creep—that gives the minimum stress associated with their estimated strain rate associated with non-equipotential growth of the inner core and anisotropy development. Since diffusion creep is grain size sensitive they found the grain size by assuming a balance between grain growth and recrystallization for the stress associated with diffusion creep. They obtained a grain size of meters, which yielded diffusion creep as the operative mechanism, and hence a Newtonian viscosity. Reaman et al. (2011) argued that due to grain growth with increasing depth into the inner core, the deformation mechanism switches at a shallow depth from diffusion to dislocation creep, perhaps explaining the isotropic layer at the top of the inner core (Shearer, 1994). They further stated that the viscosity within the region of the inner core deformed via dislocation creep would be in the range 1020–1022 Pa·s.
Recently, Gleason and Mao (2013) measured the shear strength of hcp iron at core pressures and room temperature, and extrapolated to core temperatures. They found the bulk shear strength is about 60% less than previous estimates (Hemley et al., 1997), suggesting that lower stresses can result in dislocation creep. However, these experiments do not take into account microstructure. Vocadlo (2007) reviews viscosity of the inner core and summarizes that from a microphysical view the viscosity due to diffusion creep is of the order 1021 d2 Pa·s, where the grain size d could be between 10−3 and 103 m (so that η = 1015–1027 Pa·s), and that due to dislocation creep is 1023/ρ Pa·s, where the dislocation density ρ could be between 106 and 1013 m−2 (so that η = 1010–1017 Pa·s). The overall viscosity adds inversely, since the mechanisms operate in parallel. Clearly, inner core deformation and viscosity remain highly uncertain (as do other parameters such as thermal conductivity (Pozzo et al., 2012) and partition coefficients of the light elements (Alfe et al., 2002), so that the convective state of the inner core, including translation, is also uncertain (Deguen et al., 2013).
5 Conclusions and future work
In this preliminary study of the torsional deformation of directionally solidified Zn-rich Sn alloys, we find that the alloys exhibit hardening, with a constant increase in the measured torque required to twist the sample at constant applied strain rate. Our hypothesis is that the hardening is a result of the microstructure, with relatively few slip systems available in hcp metals to accommodate the strain. The samples show microcracks suggestive of semi-brittle behavior. Our results suggest microstructure can harden a directionally solidified hcp alloy at high temperatures, which has not been previously considered, and may increase estimates of inner core viscosity. Such hardening might not occur for a finer grained, equiaxed, randomly oriented alloy because of the likelihood that many of the small, randomly oriented grains in such a sample can accommodate the required shear either through diffusion creep or through dislocation creep with the available slip systems. It is thus likely to be more ductile. Although we are using an analog material, an hcp Zn-rich alloy at atmospheric pressure, we believe the results will apply in a general way to an hcp iron alloy under inner core conditions.
Clearly the results we present here represent an initial study. In addition to testing our microstructural hardening hypothesis through the torsional deformation of a fine grained Zn-rich Sn alloy, we intend to carry out torsional deformation at different strain rates and potentially longer times, of different hcp metals (the numbers of which are limited, perhaps a Mg alloy), and of cubic alloys such as Pb-rich Sn that have more slip systems. We might also carry out tensile tests (that have a simpler geometry) on directionally Zn–Sn alloys. To test the hypothesis that samples might be hardened by dislocations being pinned by drops of the secondary phase, we are learning to prepare samples for TEM using the focused ion beam technique. We also hope we might learn about the dislocation structure and density using TEM. Finally, we also need to spend more time studying the microstructure and producing more pole figures using EBSD. We hope these efforts will help us to understand the deformation of directionally solidified alloys, and hence the dynamics of the inner core, such as convection and compaction (Sumita et al., 1996), and to interpret seismic inferences of inner core anisotropy.
Acknowledgements
The authors would like to thank Philippe Cardin and Sébastien Merkel for inviting Michael Bergman to present at the Symposium on the 30th Anniversary of the Discovery of Inner Core Anisotropy in Grenoble, France, October 2013, Shun-ichiro Karato and Sébastien Merkel for comments that significantly improved the science and presentation of the manuscript, and the US NSF for support.


