1 Introduction
Understanding the transport of water, ions, gas or oil through clay barriers is essential in the contexts of hydrology, petroleum and gas reservoir engineering, as well as the geological disposal of radioactive waste (ANDRA, 2005; Bradbury and Baeyens, 2003) or CO2 sequestration (DePaolo and Cole, 2013; Gaus, 2010). Clay rocks display a complex multiscale structure, from the regular stacking of aluminosilicate lamellae on the microscopic scale to their disordered assembly into particles on mesoscopic scales (10−9 to 10−6 nm) with corresponding interlayer and interparticle porosities, up to the macroscopic assembly of clays with other minerals (e.g., carbonates or quartz). To this hierarchy of length scales correspond a variety of physicochemical phenomena occurring over times spanning several orders of magnitude, many of them being associated with the structural charge of the mineral surface: chemical reactivity of surface sites, electrostatic interactions between the surface and ions in the interstitial solution, specific ion effects, wetting, swelling, electrokinetic couplings, etc. The electromagnetic signature of materials, in response to applied electromagnetic or acoustic waves, is at the basis of many logging tools and of seismo-electric exploration (see, e.g., Pride, 1994).
From the modelling point of view, this challenge set by multiple length and time scales can only be addressed within the framework of a multiscale strategy. On the one hand, this means adopting various complementary descriptions of the same system to capture different types of complexities. The reorganization of electrons around nuclei during chemical reactions requires using quantum descriptions, but their computational cost limits their use to a few hundred atoms (Boek and Sprik, 2003; Liu et al., 2013; Suter et al., 2008). Molecular simulations allow us to accurately describe clay layers and interlayers as well as the interface between clay particles and solutions over a few nanometres (Boek et al., 1995; Ferrage et al., 2011; Greathouse and Cygan, 2006; Hensen and Smit, 2002; Marry et al., 2002; Michot et al., 2012; Rotenberg et al., 2010a; Sposito et al., 1999). Mesoscopic simulations are then needed to model phenomena in pores with sizes in the range 10–100 nm (Boek and Venturoli, 2010; Rotenberg et al., 2010b; Stukan et al., 2010). On the other hand, one should make the link explicit between the various levels of description, exploiting more accurate models to calibrate coarser ones retaining the relevant information on larger scales. This “bottom-up” strategy includes, for example, using ab initio calculations to parameterize force fields (Cygan et al., 2004), or molecular simulation to derive simple kinetic models (Carof et al., 2014; Dufrêche et al., 2010; Rotenberg et al., 2007a,b). Even though all the references cited above are applications to clay minerals, this strategy is of course very general and has been successful in many other contexts.
In the present work, we review some recent theoretical and numerical developments in our group, using molecular and mesoscale simulations to address a number of issues related to the transport of ions, water and other fluids in clays. In Section 2, we first illustrate the interest of various simulation techniques to gain insight into geochemistry problems: ab initio molecular dynamics (MD) to predict the acidity of clay edge sites, classical MD to understand the thermodynamics of ion exchange, and Grand-Canonical Monte Carlo (GCMC) to investigate the interaction of clay interlayers with CO2 reservoirs. In Section 3, we then show the interest of a multiscale simulation strategy to describe the transport of water and ions in clays, including electrokinetic couplings, from the molecular to the macroscopic sample scale, using a combination of molecular simulation, lattice-based mesoscopic simulation (Lattice Boltzmann Electrokinetics) and Pore Network Models.
2 Geochemistry: insights from simulation on the molecular scale
In order to predict the transport and retention of mobile species in complex, interfacial materials such as clays, one first needs to understand the underlying microscopic mechanisms. Here we examine three examples of such processes for which molecular simulation proved very useful in complementing experimental approaches.
2.1 Acidity of clay edges
Lateral surfaces of clay particles may provide sorption sites contributing significantly to the retention of heavy metal cations. This sorption depends largely on the protonation state of the various edge sites, which is controlled by their pKa and the pH of the solution (Tournassat et al., 2013). Fig. 1 illustrates silanol SiOH and aluminol AlOH and AlOH2 sites on the (0 1 0) surface of a dioctahedral TOT clay. Titration experiments only provide a global measure of the surface state and do not allow one to assess the state of individual sites (which however matters for cation sorption) (Bourg et al., 2007). In practice, an efficient strategy consists in introducing a priori or experimental structural information in semi-empirical models such as MUSIC (Hiemstra et al., 1996; Machesky et al., 2008) in order to reproduce the titration curve (Tournassat et al., 2004).
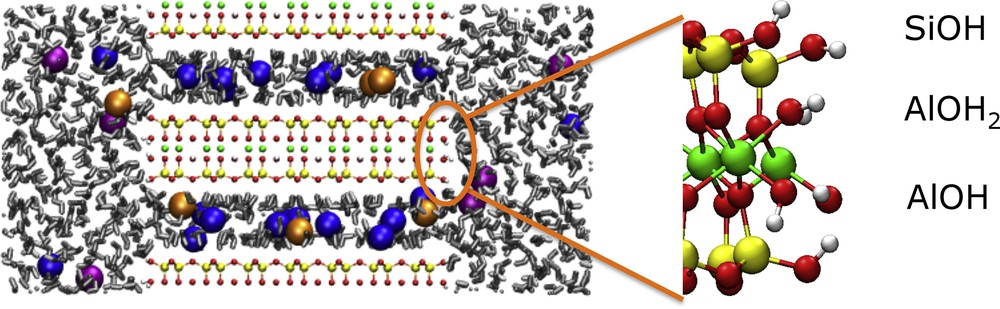
Lateral surfaces of clay particles display edge sites arising from the reaction of broken SiO and AlO bonds with water molecules. The resulting groups, here silanol and aluminol on the (0 1 0) surface of a dioctahedral TOT clay such as montmorillonite, may protonate or deprotonate depending on the pH of the interstitial solution. The pKa of each site can be determined separately from ab initio simulations, whereas experimental titration data can only provide global information. Colour code: yellow = Si, green = Al, red = O, white = H. In the left part water molecules are in grey and the spheres represent Na+ (blue), Cs+ (orange) and Cl− (pink) ions. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of the article.) Masquer
Lateral surfaces of clay particles display edge sites arising from the reaction of broken SiO and AlO bonds with water molecules. The resulting groups, here silanol and aluminol on the (0 1 0) surface of a dioctahedral TOT clay such as montmorillonite, ... Lire la suite
In this context, molecular simulation is an attractive alternative for evaluating the acidity of individual sites. The pKa is related to the reaction free energy for the transfer of the surface proton to a water molecule, e.g., for a silanol group:
| (1) |
By combining AIMD with thermodynamic integration (Sulpizi and Sprik, 2010), we computed the free energy for the deprotonation reaction (1) of SiOH, AlOH and AlOH2 sites on the (0 1 0) surface of pyrophyllite (Tazi et al., 2012). SiOH is slightly more acidic than AlOH2, with pKa values close to 7 for both sites, whereas AlOH does not deprotonate in water (pKa ∼ 22). In addition, the reorganization free energy, arising from bond length relaxation and solvent reorganization after deprotonation, is an important contribution to the overall free energy and cannot be neglected. For example, the strong stabilization of SiO− after deprotonation is explained by the arrival of two water molecules donating H-bonds. Following the same strategy, Liu et al. recently extended this study to assess the role of AlIII→MgII substitutions near edges in montmorillonite (Liu et al., 2013). It was found that Mg substitutions increase the pKa of the neighbouring SiOH group by 2–3 pKa units. Overall, these studies suggest that the sites mainly responsible for heavy cation sorption should be the deprotonated SiOH and AlOH2 sites.
2.2 Ion exchange
One of the most important processes governing cation retention by clays is cation exchange, between ions in solution and interlayer counterions, as illustrated in Fig. 2. The exchange of interlayer Na+ counterions by Cs+ in solution is thermodynamically favourable (ΔrG < 0) and exothermic (ΔrH < 0). It was generally admitted that this was the result of favourable interactions (of various origins) between the Cs+ cation and the clay surface. This point of view was challenged by Teppen and Miller (2006), who computed by molecular simulation the free energy associated with the replacement of Na+ by larger alkaline cations, and found that this contribution was in fact unfavourable for the exchange.
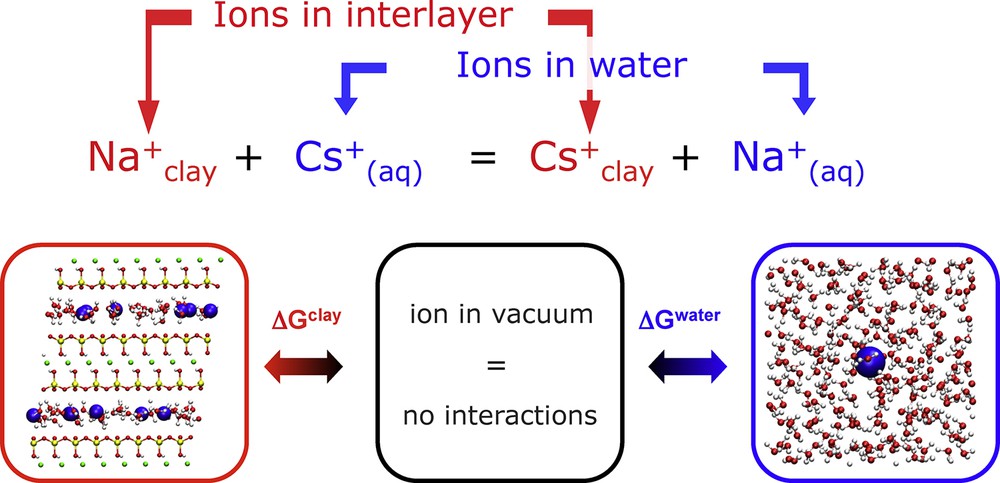
(Color online.) Cation exchange reaction between the clay interlayer and an aqueous solution. The contributions of both phases to the overall enthalpy and Gibbs free energy can be analyzed separately in molecular simulations.
The following thermodynamic cycle separates the contribution of ion replacement in both the clay interlayer (with a fixed number of water molecules per cation) and the aqueous phase (“aq” subscript):
| (2) |
This cycle involves the exchange reaction with ions in the gas phase (“g” subscript), where there are no interactions, used as a reference state. The associated thermodynamic quantities are the hydration enthalpy of both cations ΔhHNa and ΔhHCs, the standard ionic exchange reaction with the gas phase
While the thermodynamics of ion exchange can be studied by considering only the initial and final bulk states, understanding the exchange process requires taking into account explicitly the interface between the interlayer and the aqueous solution via the lateral surface. Using the setup illustrated in the left part of Fig. 1, we found that for Na-montmorillonite in the bilayer state water and cations can exchange via the edges with no or small activation barriers, whereas anions are excluded from the interlayer (we estimated the associated free energy cost to ∼23 kJ mol−1 in that case) (Rotenberg et al., 2007c). For larger distances between the surfaces and larger salt concentrations, this anion exclusion becomes less dramatic and some salt may enter the nanopores. In order to assess systematically the effect of salt concentration and interlayer distance on the ratio between the “internal” and “external” salt concentrations (Donnan effect), we introduced a continuous solvent model, parameterized on molecular simulation (Jardat et al., 2009). The correlations between ions modulate the salt exclusion, and two regimes were found: at low reservoir concentrations, the Coulomb attraction between ions increases the amount of salt in the interlayer space compared to the Poisson–Boltzmann predictions, while at high concentrations excluded volume (due to the finite size of the ions) dominates.
2.3 Contact with a CO2 reservoir
Several options are currently considered for the geological sequestration of CO2. One of them is to inject supercritical CO2 in saline aquifers: This fluid would partly be dissolved and trapped physically (microbubbles) or chemically (carbonate precipitation) in such porous formations, but some would eventually rise by buoyancy as a separate phase until it encounters an impermeable caprock. It is then important to predict the evolution of the often clay-rich caprock due to the contact with the reservoir (Gaus, 2010). In this context too, molecular simulation gives access to the microscopic mechanisms at play (Hamm et al., 2013). Among the many possible scenarios, we have considered the possibility of clay interlayer swelling or dehydration. In the latter case, this would lead to the shrinkage of clay particles, resulting in fractures increasing the permeability of the caprock.
To that end, we performed Grand-Canonical Monte Carlo simulations of sodium montmorillonite clays in contact with H2O and CO2 reservoirs. The number of molecules in the interlayer fluctuate as a result of matter exchange with the reservoirs which set the chemical potentials of the fluid (see Fig. 3). For given thermodynamic conditions in the reservoirs we monitor the interlayer composition and pressure for each interlayer distance, from which we determine the swelling free energy. The thermodynamically stable states then correspond to the minima of this free energy. For the considered thermodynamic conditions (T = 348 K and P = 125 bar) we found that from the initial state with H2O only, the contact with the CO2 reservoir does not change the location of these minima (in other words, we should not expect swelling or shrinkage) (Botan et al., 2010). We further investigated the structure and dynamics of CO2 intercalated in montmorillonite interlayers, demonstrating in particular the slowing down of all interlayer species in the presence of CO2. Experiments have confirmed the presence of intercalated CO2 in hydrated montmorillonite interlayers (Giesting et al., 2012a,b) and recent molecular dynamics studies provided further insights into the interlayer properties (Cygan et al., 2012; Myshakin et al., 2013).
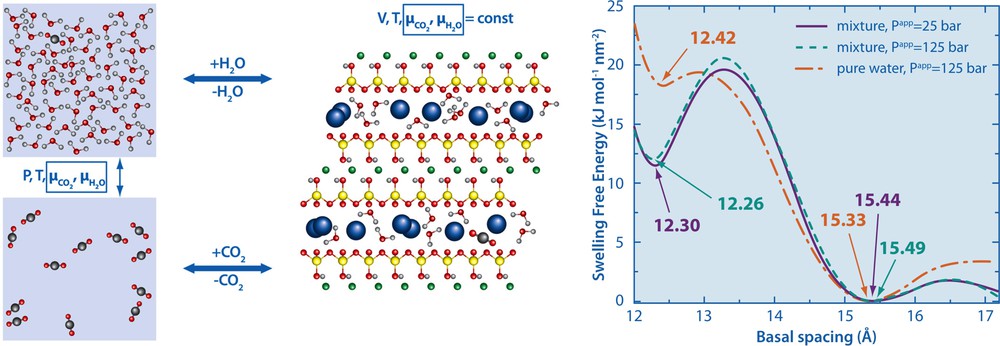
(Color online.) Grand-Canonical Monte Carlo simulations. H2O and CO2 molecules are exchanged between the interlayer of a sodium montmorillonite clay and the reservoirs, which set the chemical potentials of both species. While in the reservoirs, under the considered pressure and temperature, a H2O-rich phase and a CO2-rich phase coexist, one finds only the intercalation of CO2 molecules inside the hydrated interlayers, which corresponds to the minima of the swelling free energy as a function of the basal spacing (right). See Botan et al. (2010) for more information. Masquer
(Color online.) Grand-Canonical Monte Carlo simulations. H2O and CO2 molecules are exchanged between the interlayer of a sodium montmorillonite clay and the reservoirs, which set the chemical potentials of both species. While in the reservoirs, under the considered pressure and ... Lire la suite
3 Transport, from the molecular to the sample scale
Modelling the transport of fluids in charged multiscale materials such as clay is a challenge because it is limited by the smallest pores, with sizes in the 1–100-nm range, where interfacial effects such as wetting or electrokinetic couplings play a dominant role. Under confinement down to the nanometre scale, one should also expect the departure from continuous hydrodynamics (Bocquet and Charlaix, 2010). Once continuous transport equations on the pore scale are known (e.g., Stokes), they can be upscaled to the corresponding ones (e.g., Darcy's law) on the macroscopic sample scale, using numerical or analytical homogenization approaches. Here we illustrate how simulations on three different scales allow one to assess the relevance of continuous models, to solve the electrokinetic equations on the pore scale, and to upscale the electrokinetic couplings in complex heterogeneous materials.
3.1 Hydrodynamics in clay nanopores
Using MD simulations, we investigated the applicability of continuous hydrodynamics (Navier–Stokes equation) in clay nanopores, with pore widths ranging from 2 to 9 nm (Botan et al., 2011). Fig. 4 illustrates the simulated setup for sodium montmorillonite clay surfaces separated by 3.5 nm. The solvent density displays strong oscillations near the surface, reflecting the layering of water over 2–3 molecular diameters. Depending on their size and valency, cations may form either inner-sphere or outer-sphere complexes at the surface (Greathouse and Cygan, 2006; Marry et al., 2008). In the absence of substitutions in the mineral layers (hence of counterions), the basal surfaces are hydrophobic, even though the presence of hydroxyl groups may render the competition between water–water and water–surface interactions more delicate, as in the case of talc (Rotenberg et al., 2011).
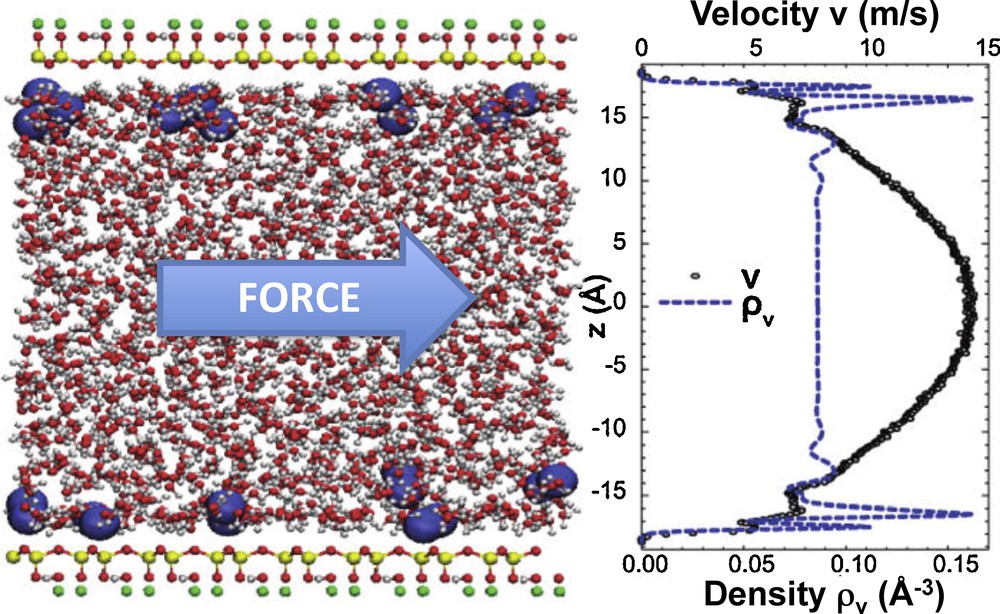
Non-equilibrium molecular dynamics. Under the effect of an applied force, mimicking a pressure gradient, the steady-state flow profile (black symbols) may deviate from the prediction of continuous hydrodynamics, in particular due to the layering of the solvent density (blue dashed line) at the surfaces. When the distance between sodium montmorillonite clay surfaces exceeds 3 nm, the velocity profile far from the surface is reasonably well described by a Poiseuille flow; however only if a slip boundary condition is introduced, with a slip length derived from molecular simulations. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of the article.) Masquer
Non-equilibrium molecular dynamics. Under the effect of an applied force, mimicking a pressure gradient, the steady-state flow profile (black symbols) may deviate from the prediction of continuous hydrodynamics, in particular due to the layering of the solvent density (blue dashed ... Lire la suite
Reprinted with permission from Botan et al. (2010). Copyright 2011 American Chemical Society.
Once the pore composition is known for given thermodynamic conditions (e.g., from prior Grand-Canonical Monte Carlo simulations, see Section 2.3), it is possible to simulate the effect of a pressure gradient by applying a force along the surface on the fluid. The steady-state velocity profile is then measured and compared to the prediction of continuous hydrodynamics (parabolic Poiseuille flow profile in this case). For sufficiently large pores, this profile is parabolic near the centre of the pore, and the effective viscosity corresponding to the measured curvature is comparable to the bulk viscosity. However, deviations are observed near the surface, as an expected result of layering. More importantly, the profile far from the surface is reproduced by the Navier–Stokes equation only if a slip boundary condition is used. This in turn allows the determination of the corresponding slip length from molecular simulation. The latter is very small (∼2.1Å), but its effects on the overall flow through the pore can be large for pore widths of a few nanometres.
More recently, we followed the same strategy to investigate the electro-osmotic flow induced by an electric field along the clay surfaces (Botan et al., 2013; Rotenberg and Pagonabarraga, 2013). Here again, in order to reproduce the molecular simulation results with continuous equations, it is essential to introduce appropriate slip boundary conditions at the clay/solution interface, as had been previously observed in equilibrium MD (Dufrêche et al., 2005). This study also confirmed the limitations of the Poisson–Boltzmann equation for the description of the ionic profiles and of the resulting electric force profile in the presence of the applied electric field.
3.2 Electrokinetic couplings on the pore scale
While molecular simulation provides the most accurate description of the clay/solution interface, its computational cost prevents its use for large systems that are necessary to capture the effect of the complex pore structure over 10–100s of nanometres. To that end, one relies on simpler descriptions. The standard model for electrokinetic couplings on the pore scale is thus the so-called Poisson–Nernst–Planck (PNP) model, which couples (i) the Nernst–Planck equation for the transport of ions under the combined effects of advection, diffusion and migration due to the local electric field, (ii) Poisson's equation to determine the electrostatic potential from the electric charge distribution and (iii) Navier–Stokes (NS) equations for the evolution of the fluid under local pressure and electric potential gradients, taking into account viscous dissipation.
These equations can be solved numerically using finite element or volume methods. For example, Adler and co-workers used this direct numerical resolution in various complex systems (random packings, reconstructed and fractured porous media) (Coelho et al., 1996; Marino et al., 2001), demonstrating in particular a universal electrokinetic behaviour if appropriate rescaled quantities are introduced (Gupta et al., 2006, 2008). Recently, alternative methods have been proposed to simulate electrokinetic effects starting from a more fundamental description of the fluid than the PNP and NS equation (Pagonabarraga et al., 2010). For example, Capuani et al. proposed a hybrid lattice based approach (Lattice Boltzmann Electrokinetics, LBE) to capture the coupling of hydrodynamic flow with ion transport and the simulation of electrokinetic effects in colloidal suspensions (Capuani et al., 2004; Pagonabarraga et al., 2005). We applied this method to porous media and extended it to charged liquid–liquid interfaces (Rotenberg et al., 2008, 2010b) as well as to capture the effect of salt concentration gradients (osmosis) (Obliger et al., 2013).
As an example of the application of LBE in the perspective of a numerical homogenization strategy, Fig. 5a reports the coefficients of the transfer matrix describing cation and anion fluxes under an applied potential gradient, in a cylindrical channel of fixed radius and surface charge density, as a function of salt concentration. These fluxes include both the direct effect of the electric field on the ions (Nernst–Einstein contribution, proportional to the ion concentrations and their mobility) and the electro-osmotic contribution (advection by the fluid flow). The former drives cations and anions in opposite directions, while the latter, in the present case of a negative surface charge, increases the cation flux and mitigates that of anions. Such numerical simulations also allow one to assess the validity of approximate analytical theories obtained by linearizing the Poisson–Boltzmann equation, which can be used in models on larger scales (see Section 3.3). Fig. 5b reports the relative error of this approximate solution compared to the non-linear one for a fixed channel radius, as a function of the surface charge density and of the salt concentration.
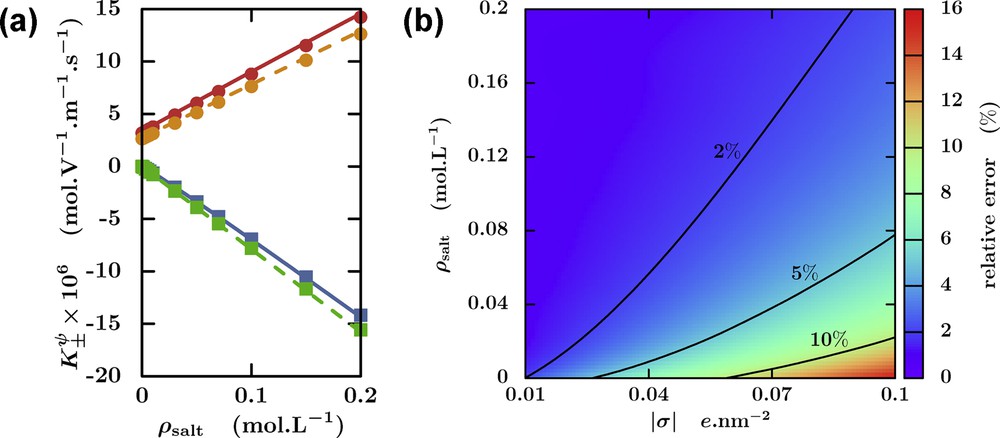
Lattice Boltzmann Electrokinetics (LBE). (a) Coefficients of the transfer matrix describing the cation (•) and anion (▪) fluxes under an applied potential (ψ) gradient, in a cylindrical channel of radius 5 nm and surface charge density σ = −0.08 e nm−2, as a function of salt concentration ρsalt. The total electrical permeability
Lattice Boltzmann Electrokinetics (LBE). (a) Coefficients of the transfer matrix describing the cation (•) and anion (▪) fluxes under an applied potential (ψ) gradient, in a cylindrical channel of radius 5 nm and surface charge density σ = −0.08 e nm−2, as ... Lire la suite
Reprinted with permission from Obliger et al. (2013). Copyright 2013 by the American Physical Society.
3.3 Electrokinetics: from the pore scale to the sample scale
Once transport properties are known on the pore scale, it is sometimes possible to upscale rigorously from a mathematical point of view the PNP equations using the homogenization approach (Allaire et al., 2010), even introducing mechanical couplings (Moyne and Murad, 2006a,b) or extensions to capture non-ideality of the electrolyte (Allaire et al., 2014). While very general in principle, most studies of electrokinetic couplings consider simple geometries (slits or cylinders) with dimensions and surface charge densities estimated from the macroscopic properties of the real system. Direct numerical simulation on complex porous networks is typically limited, due to the high computational cost, to system sizes in the range of tens to hundreds of nanometres. In order to investigate electrokinetic couplings on larger scales, including the effect of the heterogeneity of the material, we have recently proposed a simplified description based on the Pore Network Model (PNM). Such a model, originally developed by Fatt (1956) to predict multiphase flow properties in porous media, describes the porosity as a network of pores connected by channels, as illustrated in Fig. 6a. It has been extensively used and extended by petrophysicists in various situations, such as capillarity and multiphase flow through porous media (Békri et al., 2005; Blunt, 2001; van Dijke and Sorbie, 2002), or mineral dissolution and precipitation in the context of CO2 sequestration (Algive et al., 2010).
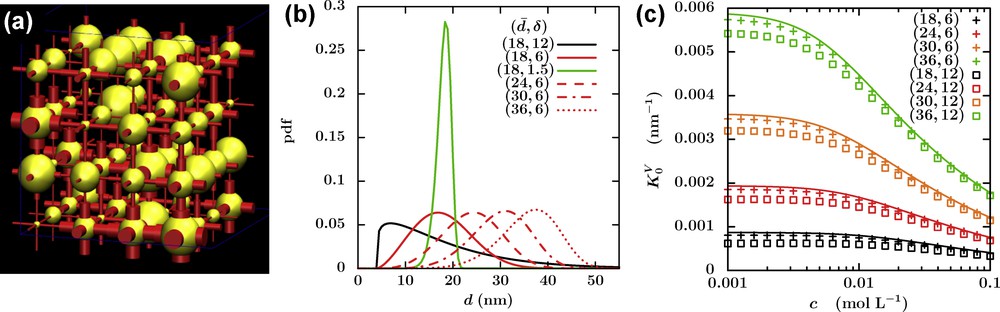
Pore Network Model. (a) Transport properties on the network scale are determined by the transport matrix of each channel (red) connecting pores (yellow). (b) Channel diameter distribution, here of the Weibull form, for several average (
Pore Network Model. (a) Transport properties on the network scale are determined by the transport matrix of each channel (red) connecting pores (yellow). (b) Channel diameter distribution, here of the Weibull form, for several average (
Panels (b) and (c) reprinted with permission from Obliger et al. (2014). Copyright 2014 by the American Physical Society.
In a nutshell, the PNM approach amounts to solving a set of conservation equations on the nodes of the network (in analogy with Kirchhoff's law for a network of resistors), on the basis of local fluxes through the channels connecting the nodes, under the effect of external macroscopic gradients. In the case of electrokinetic couplings, this requires introducing a transport matrix for each channel relating the solvent, cation and anion fluxes to the pressure, concentration and potential gradients across the channel. In addition, the matrix for each channel depends not only on its diameter and surface charge density, but also on the salt concentration in the pores at both ends, via the Donnan equilibrium (see Section 2.2), so that the problem to be solved numerically is a non-linear one (Obliger et al., 2014).
From the knowledge of the transfer matrix on the channel scale, either analytically using approximations or numerically, e.g., from LBE simulations as described in Section 3.2, and of the channel diameter distribution, one can finally determine the macroscopic transfer matrix on the network scale. Examples of such distributions are shown on Fig. 6b, together with the effect of the sample heterogeneity on the macroscopic electro-osmotic coupling coefficient. In general, the coefficients of this matrix qualitatively behave as their microscopic counterpart for a channel with the average diameter. However, the combined effects of electrokinetic couplings on the local scale and of heterogeneity result in a decrease of the overall transport coefficients. This decrease is more pronounced for large surface charge densities and low salt concentrations. In addition, for a given average diameter, more heterogeneous samples result in stronger effects, due to the presence of smaller pores. With this new numerical tool at hand, we are currently examining the case of the Callovo-Oxfordian argilite in the context of the geological disposal of radioactive waste in France.
4 Conclusion
We have illustrated here some recent applications of multiscale modelling to the transport of ions, water and CO2 in clays. On the one hand, simulations on different scales allow us to address the physicochemical processes underlying the geochemical and transport behaviour of these fluids in the interparticle pores and at the surface of clay minerals. On the other hand, upscaling the descriptions from the molecular level to the macroscopic scale without forgetting the fundamental role of interfaces on the mesoscopic scale provides a means to capture complex phenomena such as electrokinetic couplings. This multiscale approach, followed in our group mainly in the case of transport, is also very fruitful for the description of other properties of clays, such as mechanical ones (Brisard and Dormieux, 2010; Carrier et al., 2014). Extensions to more complex fluids would also provide an efficient route for the modelling of hydrocarbons in oil and gas shales.
In the future, one should also benefit from recent numerical (Tyagi et al., 2013) and experimental (Brisard et al., 2012; Levitz, 2007) developments for the generation of realistic numerical samples for the description of real materials. As a recent example, Robinet et al. recently simulated the diffusion of solutes in 3D-images of a Callovo-Oxfordian clay-rich rock obtained by SEM and micro-CT experiments to investigate the effect of mineral distribution (Robinet et al., 2012). Multiscale experiments using NMR also provide an ideal tool to investigate the multiscale dynamics of mobile species in such complex materials (Porion et al., 2013).
Acknowledgements
The authors are grateful to many colleagues and students who have contributed to this work over the last ten years, in particular Alexandru Boţan, Sami Tazi, Amaël Obliger, Magali Duvail, Antoine Carof, Natalie Malikova, Jean-François Dufrêche, Rodolphe Vuilleumier, Jean-Pierre Hansen, Daniel Coelho, Benoît Noetinger, and Samir Bekri.



Vous devez vous connecter pour continuer.
S'authentifier