The major ion, 87Sr/86Sr, and δ11B geochemistry of groundwater in the Wyodak-Anderson coal bed aquifer (Powder River Basin, Wyoming, USA)

Damien Lemarchand; Andrew D. Jacobson; Damien Cividini; François Chabaux

doi:10.1016/j.crte.2015.05.007

Hydrology, Environment (Surface Geochemistry)

The major ion, ⁸⁷Sr/⁸⁶Sr, and δ¹¹B geochemistry of groundwater in the Wyodak-Anderson coal bed aquifer (Powder River Basin, Wyoming, USA)

Damien Lemarchand ¹ ; Andrew D. Jacobson ²; Damien Cividini ¹; François Chabaux ¹

¹ Laboratoire d’hydrologie et de géochimie de Strasbourg; université de Strasbourg/EOST, CNRS, 1, rue Blessig, 67000 Strasbourg, France
² Department of earth and planetary sciences, Northwestern university, Technological Institute, 2145 N. Sheridan road, IL 60208, Evanston, USA

Comptes Rendus. Géoscience, Volume 347 (2015) no. 7-8, pp. 348-357.

Abstract

We developed a multicomponent, 1D advective transport model that describes the downgradient evolution of solute concentrations, ⁸⁷Sr/⁸⁶Sr ratios, and δ¹¹B values in the Wyodak-Anderson Coal Bed (WACB) aquifer located in the Powder River Basin, Wyoming, USA. The purpose of the study was to evaluate the chemical vulnerability of groundwater to potential environmental change stemming from the extraction of coal bed methane and shale gas. Model calculations demonstrate that coupling between microbial activity and the dissolved carbonate system controls major ion transport in the WACB aquifer. The analysis of ⁸⁷Sr/⁸⁶Sr ratios further reveals the importance of ion-exchange reactions. Similarly, δ¹¹B data emphasize the significance of pH-dependent surface reactions and demonstrate the vulnerability of the aquifer to the long-term acidification of recharge water.

Supplementary Materials:
Supplementary materials for this article are supplied as separate files:

Metadata

Received: 2015-02-02
Accepted: 2015-05-21
Published online: 2015-07-07

DOI: 10.1016/j.crte.2015.05.007

Keywords: Powder River, Boron isotopes, Strontium isotopes, 1D reactive transport, Modeling

Author's affiliations:

Damien Lemarchand ¹; Andrew D. Jacobson ²; Damien Cividini ¹; François Chabaux ¹

¹ Laboratoire d’hydrologie et de géochimie de Strasbourg; université de Strasbourg/EOST, CNRS, 1, rue Blessig, 67000 Strasbourg, France
² Department of earth and planetary sciences, Northwestern university, Technological Institute, 2145 N. Sheridan road, IL 60208, Evanston, USA

@article{CRGEOS_2015__347_7-8_348_0,
     author = {Damien Lemarchand and Andrew D. Jacobson and Damien Cividini and Fran\c{c}ois Chabaux},
     title = {The major ion, {\protect\textsuperscript{87}Sr/\protect\textsuperscript{86}Sr,} and {\protect\emph{\ensuremath{\delta}}\protect\textsuperscript{11}B} geochemistry of groundwater in the {Wyodak-Anderson} coal bed aquifer {(Powder} {River} {Basin,} {Wyoming,} {USA)}},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {348--357},
     publisher = {Elsevier},
     volume = {347},
     number = {7-8},
     year = {2015},
     doi = {10.1016/j.crte.2015.05.007},
     language = {en},
}

TY  - JOUR
AU  - Damien Lemarchand
AU  - Andrew D. Jacobson
AU  - Damien Cividini
AU  - François Chabaux
TI  - The major ion, 87Sr/86Sr, and δ11B geochemistry of groundwater in the Wyodak-Anderson coal bed aquifer (Powder River Basin, Wyoming, USA)
JO  - Comptes Rendus. Géoscience
PY  - 2015
SP  - 348
EP  - 357
VL  - 347
IS  - 7-8
PB  - Elsevier
DO  - 10.1016/j.crte.2015.05.007
LA  - en
ID  - CRGEOS_2015__347_7-8_348_0
ER  -

%0 Journal Article
%A Damien Lemarchand
%A Andrew D. Jacobson
%A Damien Cividini
%A François Chabaux
%T The major ion, 87Sr/86Sr, and δ11B geochemistry of groundwater in the Wyodak-Anderson coal bed aquifer (Powder River Basin, Wyoming, USA)
%J Comptes Rendus. Géoscience
%D 2015
%P 348-357
%V 347
%N 7-8
%I Elsevier
%R 10.1016/j.crte.2015.05.007
%G en
%F CRGEOS_2015__347_7-8_348_0

Damien Lemarchand; Andrew D. Jacobson; Damien Cividini; François Chabaux. The major ion, ⁸⁷Sr/⁸⁶Sr, and δ¹¹B geochemistry of groundwater in the Wyodak-Anderson coal bed aquifer (Powder River Basin, Wyoming, USA). Comptes Rendus. Géoscience, Volume 347 (2015) no. 7-8, pp. 348-357. doi : 10.1016/j.crte.2015.05.007. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2015.05.007/

Version originale du texte intégral

1 Introduction

The Powder River Basin (Wyoming, USA) is one of the most active areas for coal bed methane production (EIA, 2007). Major ion mass balances and radiogenic isotope measurements (e.g., Sr, Nd, U, Th) are powerful tools for analyzing the rates and mechanisms of water–rock interaction during groundwater transport. Numerous studies have utilized these techniques to develop comprehensive models that describe the origin and compositional evolution of groundwater in silicate and carbonate aquifers (e.g., Banner and Hanson, 1990; Bullen et al., 1996; Jacobson and Wasserburg, 2005; Johnson and DePaolo, 1997; Lucas et al., 2010; Maher et al., 2006; Négrel and Petelet-Giraud, 2010). By comparison, only a few studies have examined water/rock interactions in coal bed aquifers (Bartos and Ogle, 2002; Bates et al., 2011; Brinck et al., 2008; Frost et al., 2002; Rice et al., 2000) and at present, models describing the geochemistry of these unique aquifer systems are relatively scarce (Bartos and Ogle, 2002).

To address this problem, we analyzed the downgradient evolution of dissolved major ions, ⁸⁷Sr/⁸⁶Sr ratios and ¹¹B/¹⁰B ratios (expressed below as δ¹¹B in ‰) along a 102 km flow path in the Wyodak-Anderson coal bed (WACB) aquifer in the Powder River Basin (PRB). The opportunity to sample groundwater in the WACB aquifer has increased, owing to the expansion of wells for extracting microbially-produced methane (e.g., Frost et al., 2002; Rice et al., 2000). Importantly, microbial methanogenesis is known to concurrently modify carbonate equilibria conditions and major ion concentrations in organic-rich aquifers (e.g., McIntosh et al., 2004). By analogy to the methanogenic Antrim Shale in the Michigan Basin, microbial methanogenesis is expected to greatly influence the compositional evolution of WACB groundwater (McIntosh et al., 2004), but the lack of major ion characterizations has hindered consensus on the overall reaction pathway occurring within the aquifer (Bartos and Ogle, 2002). Other factors affecting the transport of major ions may include sulfate reduction, ion-exchange, and cross-formational mixing (Bartos and Ogle, 2002; Frost et al., 2002; Rice et al., 2000). However, the interrelationships between these various processes, as well as their rates and relative controls on solute geochemistry, are presently unknown.

In this paper, we use a 1D multicomponent advective transport model to determine reaction pathways and rates required to produce the observed water chemistry in the WACB aquifer. The model incorporates new geochemical data for both groundwater and coal samples. To evaluate the downgradient evolution of Sr²⁺, we treat dissolved ⁸⁷Sr/⁸⁶Sr ratios as dynamic tracers of progressive water–rock interaction (Johnson and DePaolo, 1997; Maher et al., 2006). That is, dissolved ⁸⁷Sr/⁸⁶Sr ratios measured at a given distance downgradient reflect the physical properties of fluid transport (e.g., velocity, cross-formational mixing, etc.) as well as the chemical properties of the dissolving, precipitating, or exchanging solid phases (e.g., Sr concentration, ⁸⁷Sr/⁸⁶Sr ratio, rate of reaction, etc.). Importantly, because the Sr isotope model is linked to the major element data through mass-balance relationships, we are able to present an integrative and self-consistent interpretation of the factors controlling groundwater geochemistry in the WACB aquifer. We further couple this information with the behavior of B isotopes, which can elucidate the nature of water–rock interactions, in particular pH-dependent processes, as well as those resulting from water-mass mixing (e.g., Cividini et al., 2010; Gonfiantini and Pennisi, 2006; Lemarchand and Gaillardet, 2006; Vengosh et al., 1994; Zhao et al., 2011).

2 Sampling site

2.1 Geological characteristics

The study region is located in north-eastern Wyoming near the eastern margin of the ∼35,000-km² Powder River Basin (Fig. 1). The Paleocene Fort Union Formation, which is subdivided into the Tullock, Lebo, and Tongue River Members, contains sandstone, siltstone, mudstone, claystone, carbonaceous shale, limestone, and coal (Ellis, 2002; Warwick and Stanton, 1988). The thickest and most laterally continuous coal beds in the PRB belong to the Wyodak-Anderson Coal Zone (WACZ) in the Tongue River Member (Bartos and Ogle, 2002; Ellis et al., 1999; Flores and Bader, 1999; Flores et al., 1999). At least eleven individual coal beds compose the WACZ (Flores et al., 1999). The beds developed from raised peat mires that were dissected or overrun by meandering fluvial systems fed by ancestral alluvial fans at the margin of the PRB (Ellis, 2002; Flores and Bader, 1999; Warwick and Stanton, 1988). Between the top of the uppermost bed and the bottom of the lowermost one, the entire WACZ is ∼180 m thick (Ellis, 1999). Individual beds ranging in thickness from a few centimeters to > 60 m (Frost et al., 2002) are separated by clastic sedimentary rocks ranging in thickness from a few centimeters to ∼45 m (Ellis, 1999).

Fig. 1
Map showing sample locations (S1, W1–W9) and the generalized geology of the study area. Groundwater flow is to the northwest. Inset shows the location of the Powder River Basin (PRB) within the geographic context of the USA. Small box within the inset shows the approximate location of the study site within the PRB.

The coal is non-marine, low-sulfur, and subbituminous in rank (Ellis, 2002; Ellis et al., 1999; Flores and Bader, 1999; Van Voast, 2003). Small amounts of silicate, carbonate, phosphate, sulfate, sulfide, and metal oxide minerals are present in WACZ coal (Brownfield et al., 2005; Crowley et al., 1993; Palmer et al., 2000). Mineral sources include volcanic ash fall, Eolian deposition, and fluvial delivery during peat formation; in situ alteration of primary minerals during diagenesis, coalification, and groundwater flow; and direct precipitation from solution (Brownfield et al., 2005; Crowley et al., 1993; Palmer et al., 2000). Of these minerals, quartz and kaolinite are the most prevalent (Brownfield et al., 2005). Trace carbonates include calcite and dolomite (Brownfield et al., 2005). No studies have reported halite. The WACZ outcrops along the eastern margin of the PRB. In this region, natural burning of coal has baked overlying sediments to form clinker, which has a distinct orange to red color (Heffern and Coates, 1999; Warwick and Stanton, 1988). The Tongue River Member is overlain by the Eocene Formation, which has a similar depositional history and lithology as the Fort Union Formation (Flores and Bader, 1999). The Wasatch Formation is aerially exposed in much of the PRB (Bartos and Ogle, 2002).

2.2 Hydrological characteristics

The aquifer recharges through infiltration of precipitation and stream-flow loss in the clinker zone. The clinker is highly permeable, but a low-permeability zone at the base can delay water infiltration and cause accumulation above the coal (Bartos and Ogle, 2002). Following recharge, groundwater flows through west-to-northwest trending fractures in the coal. The fracture porosity in the aquifer is ∼1% (DOE, 2003). The matrix porosity of the coal itself is also ∼1% (DOE, 2003). The hydraulic conductivity ranges between 56 and 100 m/yr (Bartos and Ogle, 2002), and the hydraulic gradient is ∼1.5·10⁻³ (Daddow, 1986). The gross water velocity is ∼10 m/yr. Shales and fine-grained units belonging to the Wasatch Formation confine the top of the aquifer, while thick, low-permeability units belonging to the Lebo Member confine the bottom. At present, the extent of vertical connectivity between the WACB aquifer and the overlying Wasatch aquifer is unclear. Vertical hydraulic conductivities in the WACB aquifer are ∼1 to 2 orders of magnitude less than horizontal hydraulic conductivities, but downward leakage may occur in regions where the hydraulic head in the WACB aquifer is less than that in the Wasatch aquifer (Bartos and Ogle, 2002; Frost et al., 2002).

3 Samples and analytical methods

Ten water samples were collected, one from a spring discharging from clinker at the eastern margin of the PRB (S1), and nine from continuously pumping coal bed methane (CBM) production wells completed in the WACB aquifer (W1–W9; Fig. 1). We assume that S1 represents input to the aquifer and that wells W1–W9 lie along a nominal hydrologic flow path, with W1 intersecting the youngest water and W9 intersecting the oldest water. Before sampling, a closed flow-through cell was attached to the wellhead in order to purge the wells with at least one well volume of water. Samples were collected after pH, temperature, and conductivity stabilized.

Water was passed through 0.45-μm filter capsules and collected in acid-cleaned HDPE bottles. Cation samples were acidified to pH = 2 with concentrated, ultrapure HCl immediately after collection. Cation and Sr concentrations were measured by Inter-Mountain Laboratories, Inc. in Sheridan, WY, using a Varian VistaPro ICP-OES, and anion concentrations were measured using a Dionex DX-100. The uncertainties are better than 10% (± 2 SD).

Strontium isotope ratios were determined on a VG Sector mass spectrometer following the procedure traditionally used at the LHyGeS (e.g., Riotte and Chabaux, 1999). Boron concentrations were measured at LHyGeS using a Thermo X-Series II Q-ICP-MS, following the method presented in Cividini et al. (2010). ¹¹B/¹⁰B ratios were measured at LHyGeS by negative thermo-ionization mass-spectrometry using a Thermo-Finnigan Triton and the total evaporation method (TE-NTIMS) following the procedure developed by Foster et al. (2006). Results are expressed with the classical δ¹¹B notation (the permil deviation from the standard NIST SRM 951, certified value = 4.0436). Each sample was analyzed for B isotope ratios at least three times, with repeated analyses giving an analytical uncertainty of 0.8‰ (± 2 SD).

4 Results

Field parameters, ⁸⁷Sr/⁸⁶Sr ratios and δ¹¹B values measured in the water samples are given in Table 1. (Solute concentrations are given in Table S1, Supplementary Information.) The data are reported in increasing order downgradient. Major ion concentrations are plotted as a function of distance in Fig. 2. In general, the major ion abundances observed for S1 and W1–W9 are consistent with results reported in prior studies of the clinker recharge zone and the greater WACB aquifer (e.g., Bartos and Ogle, 2002; Rice et al., 2000). Following recharge, Ca²⁺, Mg²⁺, Na⁺, Cl⁻, and HCO₃⁻concentrations display four trends with increasing distance downgradient: S1-W1, W1–W3, W3–W6, and W6–W9 (Table S1 and Fig. 2).

	Distance	T	pH	[Sr²⁺]	⁸⁷Sr/⁸⁶Sr	[B]	δ¹¹B
	(km)	(°C)		μmol/L		μg/L	(‰)
S1	0	18.3	8.42	31.84	0.7121	372	4.6
W1	10	15.4	7.18	2.72	0.713	159	24.1
W2	22	13.7	7.18	5.82	0.7125	196	20.4
W3	30	19.2	7.1	6.07	0.7135	155	23
W4	48	21.7	7.87	5.63	0.7138	98	15.1
W5	53	20.1	7.64	5.46	0.7143	100	14
W6	76	26	7.46	4.50	0.7162	99	19
W7	98	21.9	7.6	4.53	0.7125	94	20.3
W8	101	20.5	7.62	3.29	0.7124	110	19.8
W9	102	19.6	7.98	2.12	0.7124	68	26.9

Fig. 2
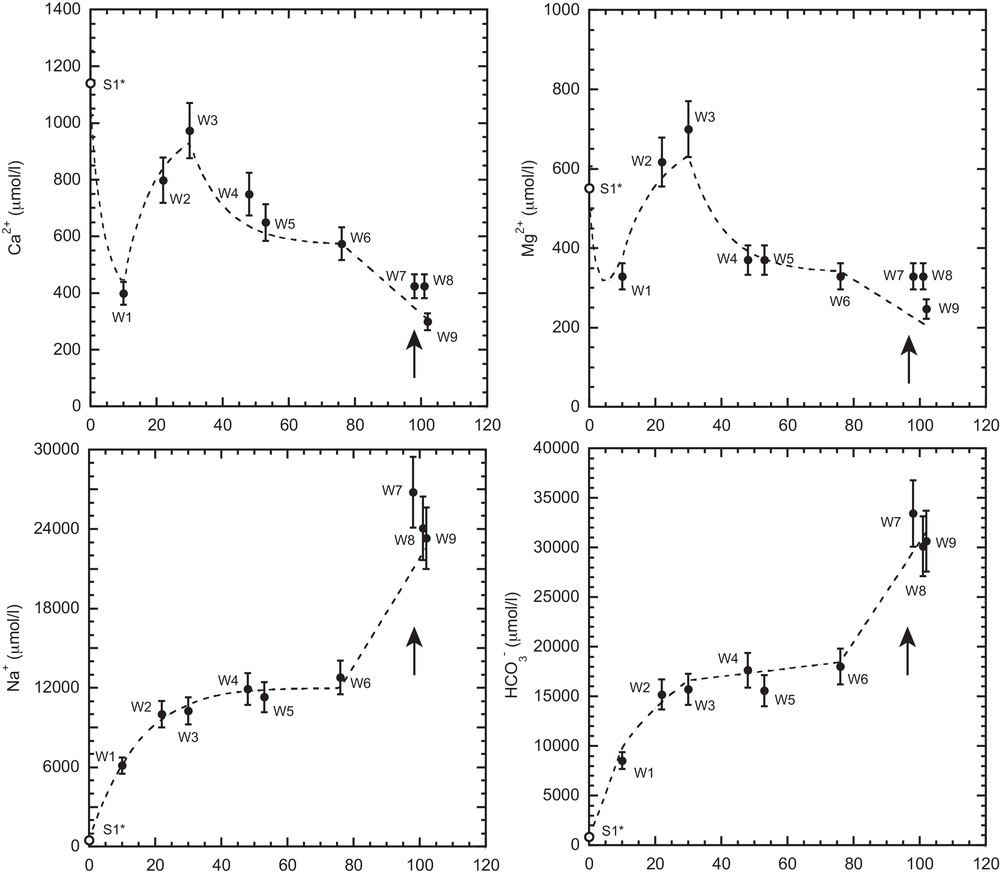
Major ion concentration versus distance for water samples. S1* (open symbol) corresponds to the S1 sample corrected for evaporation (see text). Arrows indicate the addition of water from the overlying Wasatch aquifer. Error bars display the 10% uncertainty of the concentration measurements. Dashed line shows theoretical model output.

Like major elements, Sr²⁺ and B concentrations in S1 are high relative to the range observed in W1–W9. The downgradient evolution of Sr²⁺ shown in Fig. 3a closely follows the trend observed for Ca²⁺. Between S1 and W6, dissolved ⁸⁷Sr/⁸⁶Sr ratios increase from 0.712384 to 0.716245 (Fig. 3b). One exception to this trend is W2, which has an ⁸⁷Sr/⁸⁶Sr ratio of 0.712534. Between W6 and W9, dissolved ⁸⁷Sr/⁸⁶Sr ratios decrease to 0.712372.

Fig. 3
Sr²⁺, ⁸⁷Sr/⁸⁶Sr, B and δ¹¹B versus distance for water samples. S1* (open symbol) corresponds to the S1 sample corrected for evaporation (see text). Arrows indicate the addition of water from the overlying Wasatch aquifer. Dashed line shows theoretical model output.

Concentration and isotope ratio data for B are presented in Fig. 3c,d. The B concentrations are similar to those observed in other aquifers (e.g., Pennisi et al., 2006a). B isotopic compositions (δ¹¹B) span a relatively large range (from 4.6‰ to 26.9‰) and inversely correlate with pH, except for W9.

5 Discussion

5.1 Chemical composition of the recharge water

Sample S1 was collected during the summer months, whereas most of the recharge occurs during the spring snowmelt (Martin et al., 1988). Therefore, the high solute concentrations observed in S1 relative to W1–W9 likely reflect evaporative concentration during groundwater infiltration. Because Cl⁻is not involved in the chemical reactions that affect the transport of major ions (see discussion below and Bartos and Ogle, 2002), we assume that Cl⁻undergoes conservative transport and that the background Cl⁻concentration in the aquifer is 200 μmol/L (inferred from W1–W6). This value is consistent with average concentrations observed in the clinker recharge zone (Rice et al., 2002). We thus deduce that S1 is evaporatively concentrated by a factor ∼5, which is applied to all other solute concentrations (Fig. 2). Because B isotopes behave conservatively during water evaporation (Gaillardet et al., 2001), no isotopic shifts are expected.

5.2 1-D mass transport model

The groundwater evolution from a Ca–SO₄-type to a Na-HCO₃-type composition reflects several reactions commonly observed in organic-rich aquifers. These reactions include the coupling of sulfate reduction (sfr), methanogenesis (met), and ion-exchange (ixc), with dolomite dissolution (dol) and calcite dissolution and precipitation (cal) (e.g., Chapelle and McMahon, 1991; McIntosh et al., 2004):

2 {CH}_{2} O + S {O_{4}}^{2 -} \underset{sfr}{⟶} H_{2} S + 2 HC {O_{3}}^{-}

2 {CH}_{2} O + H_{2} O \underset{met}{⟶} {CH}_{4} + H^{+} + HC {O_{3}}^{-}

{Na}_{2} (coal) + X_{Ca} {Ca}^{2 +} + X_{Mg} {Mg}^{2 +} \underset{ixc}{⟶} [{Ca}_{X_{Ca}} {Mg}_{X_{Mg}}] (coal) + 2 {Na}^{+}

2 H^{+} + CaMg {({CO}_{3})}_{2} \underset{dol}{⟶} {Ca}^{2 +} + {Mg}^{2 +} + 2 HC {O_{3}}^{-}

H^{+} + {CaCO}_{3} \underset{cal}{⟷} {Ca}^{2 +} + HC {O_{3}}^{-}

where CH₂O is the idealized formula for organic matter, X_Ca is the fraction of dissolved Ca²⁺ exchanged for Na⁺

(0 \leq X_{Ca} \leq 1)

, and X_Mg is the fraction of dissolved Mg²⁺ exchanged for Na⁺

(X_{Mg} = 1 - X_{ca})

.

We use a simple multicomponent numerical optimization model to calculate effective reaction rates occurring between initial and final waters along the flow path. The model uses the method of least-squares minimization to estimate the optimal rates for the above reactions that best reproduce the measured concentrations for a given transport velocity. The model is based on the following steady state 1D advective transport equation, in which diffusion is neglected:

ν \frac{\partial {[i]}_{w}}{\partial_{x}} = \sum_{k} n_{k}^{i} J_{k}

(1)

where v is the groundwater flow velocity (m/yr), [i]_w is the dissolved concentration of ion i in water w (μmol/L), x is the downgradient distance (m),

n_{k}^{i}

is the stoichiometric coefficient of ion i in reaction k, and J_k is the effective rate of reaction k (μmol/L/yr). In the model, we use a combination of two rate laws, a linear rate law (l) and an equilibrium rate law (eq). The linear rate law (zero order kinetics) assumes that reaction rates are constant and do not change as the composition of the fluid changes. The equilibrium rate law (first order kinetics) describes the dependence of the reaction rate on the departure from equilibrium. We use the linear rate low to model sulfate reduction, methanogenesis, and Wasatch water inflow. Sulfate reduction and methanogenesis are usually considered to follow first order or Monod kinetics (e.g., Furukawa et al., 2004). However, we lack sufficient information to develop such rate expressions for these reactions. Therefore, we view the linear rate law as the most straightforward approximation. For most of the flow path (S1–W6), we use the equilibrium rate law to model ion-exchange. Because Na⁺ increases linearly between W6 and W9, we use the linear rate law to model ion-exchange in this section of the aquifer. In all cases, to model ion-exchange, it is necessary to know the fractions of Ca²⁺ and Mg²⁺ that exchange for Na⁺ on coal surfaces (X_Ca and X_Mg, respectively). Because these data are not readily available, we assume for simplicity that X_Ca and X_Mg equal 0.55 and 0.45, respectively, which is consistent with observations that Ca²⁺ preferentially exchanges for Na⁺ relative to Mg²⁺ (Fletcher and Sposito, 1984). We treat dolomite dissolution as an irreversible reaction, whereas we allow calcite to both dissolve and precipitate. To account for solute addition by vertical leakage from the overlying Wasatch aquifer, we use the Cl⁻mass balance to calculate the effective rate of Cl⁻inflow

(J_{was}^{l})

, and we use molar ion/Cl⁻ratios reported for the Wasatch aquifer (Bartos and Ogle, 2002) to estimate the rate at which other solutes originating in the Wasatch aquifer are added to the WACB aquifer. Given the above, the following equations describe solute transport along the four segments of the flow path:

ν \frac{d {[S {O_{4}}^{2 -}]}_{w}}{dx} = J_{sfr}^{l}

(2)

ν \frac{d {[{Cl}^{-}]}_{w}}{dx} = J_{was}^{l}

(3)

ν \frac{d {[{Na}^{+}]}_{w}}{dx} = k_{ixc} ({[{Na}^{+}]}_{w}^{eq} - {[{Na}^{+}]}_{w}) + {(\frac{Na}{Cl})}_{was} J_{was}^{l}

(4)

ν \frac{d {[{Mg}^{2 +}]}_{w}}{dx} = k_{dol} ({[{Mg}^{2 +}]}_{w}^{eq} - {[{Mg}^{2 +}]}_{w}) - 0.50 X_{Mg} K_{ixc} ({[{Na}^{+}]}_{w}^{eq} - {[{Na}^{+}]}_{w}) + {(\frac{Mg}{Cl})}_{was} J_{was}^{l}

(5)

ν \frac{d {[{Ca}^{2 +}]}_{w}}{dx} = k_{cal} ({[{Ca}^{2 +}]}_{w}^{eq} - {[{Ca}^{2 +}]}_{w}) + k_{dol} ({[{Mg}^{2 +}]}_{w}^{eq} - {[{Mg}^{2 +}]}_{w}) - 0.50 X_{Ca} k_{ixc} ({[{Na}^{+}]}_{w}^{eq} - {[{Na}^{+}]}_{w}) + {(\frac{Ca}{Cl})}_{was} J_{was}^{l}

(6)

ν \frac{d {[HC {O_{3}}^{-}]}_{w}}{dx} = J_{met}^{l} + 2 J_{sfr}^{l} + 2 k_{dol} ({[{Mg}^{2 +}]}_{w}^{eq} - {[{Mg}^{2 +}]}_{w}) + k_{cal} ({[{Ca}^{2 +}]}_{w}^{eq} - {[{Ca}^{2 +}]}_{w}) + {(\frac{HC {O_{3}}^{-}}{Cl})}_{was} J_{was}^{l}

(7)

Modeled reaction rates are reported in Table S2, and comparisons between the measured and modeled solute concentrations are shown in Fig. 2. Overall, there is reasonable agreement between the measured and modeled concentrations, suggesting that the reactions considered adequately describe major ion transport in the WACB aquifer. However, we acknowledge that the modeled rates rely on numerous assumptions and that the solutions may not be unique, but they are the best ones to fit the data with the numerical method employed. The main conclusion is that the coupling between organic matter oxidation by bacteria to produce methane and the dissolved carbonate system is a key mechanism for solute evolution in the WACB aquifer. Without the microbial modification of carbonate equilibrium conditions, the aquifer waters would most likely display much lower Na⁺ and HCO₃⁻concentrations prior to the onset of vertical leakage. While most of the methane in the PRB may have been thermogenically produced ∼10–35 Ma (Rice, 1993), it appears that microbial methanogenesis has modified the chemistry of WACB fluids for at least the past 10 kyr, which is roughly the age of the oldest water in the aquifer estimated by dividing the flow path distance (102 km) by the water velocity (10 m/yr).

5.3 Geochemical evolution of Sr²⁺ in the WACB aquifer

Given the major ion model results, we evaluate the transport of Sr²⁺ to characterize more precisely the sources and reactions controlling groundwater geochemistry. By analogy to Ca, decreasing Sr concentrations between S1 and W1 could represent either uptake during calcite precipitation or adsorption onto coal surfaces. Increasing concentrations between W1 and W3 likely result from carbonate dissolution, whereas decreasing concentrations between W3 and W9 are consistent with adsorption onto coal surfaces. However, increasing ⁸⁷Sr/⁸⁶Sr ratios between S1 and W6 are not predicted by this model and indicate that a source of radiogenic Sr²⁺ is required. Assuming that Si behaves conservatively during transport, the modest Si increase between S1 and W6 does not support the hypothesis of silicate mineral dissolution. Alternatively, the increase of dissolved ⁸⁷Sr/⁸⁶Sr ratios with increasing distance downgradient can be attributed to the release of radiogenic, labile Sr²⁺ adsorbed to coal surfaces. This is consistent with a radiogenic ⁸⁷Sr/⁸⁶Sr ratio (0.71569) observed by Frost et al. (2002) in a previous study of the WACB aquifer. To test this hypothesis, we assume that the aquifer waters are in steady state, and we treat Sr²⁺ ion-exchange reactions in a manner identical to normal dissolution and precipitation reactions (Johnson and DePaolo, 1997; Maher et al., 2006). The transport equation describing the evolution of dissolved Sr²⁺ concentrations is:

ν \frac{d {[{Sr}^{2 +}]}_{w}}{dx} = {(\frac{Sr}{Ca})}_{Cal} k_{cal} ({[{Ca}^{2 +}]}_{w}^{eq} - {[{Ca}^{2 +}]}_{w}) + {(\frac{Sr}{Mg})}_{dol} k_{dol} ({[{Mg}^{2 +}]}_{w}^{eq} - {[{Mg}^{2 +}]}_{w}) + {(\frac{Sr}{cl})}_{was} J_{was}^{l} + {}^{Sr}J_{in}^{l} - K_{out} {[{Sr}^{2 +}]}_{w}

(8)

where [Sr²⁺]_w is the concentration of dissolved Sr²⁺; (Sr/Ca)_cal is the molar Sr/Ca ratio of calcite; (Sr/Mg)_dol is the molar Sr/Mg ratio of dolomite; and (Sr/Mg)_was is the molar Sr/Cl ratio of Wasatch water.

The transport equation describing the evolution of dissolved ⁸⁷Sr/⁸⁶Sr ratios is:

ν \frac{d R_{w}}{dx} = \frac{1}{{[{Sr}^{2 +}]}_{w}} [{(\frac{Sr}{Ca})}_{Cal} K_{Cal} ({[{Ca}^{2 +}]}_{w}^{eq} - {[{Ca}^{2 +}]}_{w}) (R_{Cal} - R_{w}) + {(\frac{Sr}{Mg})}_{dol} K_{dol} ({[{Mg}^{2 +}]}_{w}^{eq} - {[{Mg}^{2 +}]}_{w}) (R_{cal} - R_{w}) + {(\frac{Sr}{Cl})}_{was} J_{was}^{l} (R_{was} - R_{w}) + J_{in}^{Sr} (R_{coal} - R_{w})]

(9)

where R_w, R_dol, R_cal, R_was, and R_coal are the ⁸⁷Sr/⁸⁶Sr ratios of Wyodak water, dolomite, calcite, Wasatch water, and labile Sr²⁺ on coal surfaces, respectively. We model the input of Sr²⁺ from coal surfaces (desorption) using a linear rate law, whereas we model the output of Sr²⁺ from water (adsorption) as being proportional to the amount of Sr²⁺ present in solution.

Comparisons between the measured and modeled data are shown in Fig. 3a,b. Between S1 and W1, dolomite dissolution and desorption add Sr²⁺ at rates of 5.0 and 1.2 nmol/L/yr, respectively, whereas adsorption removes Sr²⁺ at a rate of 9.8 nmol/L/yr. Here, dissolved ⁸⁷Sr/⁸⁶Sr ratios increase because the desorbed Sr²⁺ is radiogenic (Frost et al., 2002). Between W1 and W3, the total average input rate from carbonate dissolution and desorption slightly exceeds the average adsorption rate (4.8 vs. 5.3 nmol/L/yr, respectively). As shown in Fig. 3b, dissolved ⁸⁷Sr/⁸⁶Sr ratios in this region of the aquifer first undergo an initial decrease when the rates of dolomite dissolution and calcite precipitation are highest. As the rates decrease during the approach to carbonate mineral saturation, the desorption contribution becomes more significant, and dissolved ⁸⁷Sr/⁸⁶Sr ratios increase. This behavior is tentatively confirmed by the agreement between W2 and the theoretical output (Fig. 3b). Between W3 and W6, Sr²⁺ concentrations decrease because the sorption rate exceeds the desorption rate (0.54 vs. 0.20 nmol/L/yr). However, dissolved ⁸⁷Sr/⁸⁶Sr ratios undergo a steady increase because desorbing Sr²⁺ continues to mix with Sr²⁺ in the fluid phase. Lastly, between W6 and W9, Wasatch water inflow delivers unradiogenic Sr²⁺ (0.71266) at a rate of 1.7 nmol/L/yr, but Sr²⁺ concentrations decrease because the average removal rate is more rapid (2.5 nmol/L/yr). These results demonstrate that exchange reactions exert an important control on the downgradient evolution of Sr²⁺.

5.4 B geochemistry in the WACB aquifer

Because B is highly soluble, its concentration in formation waters strongly correlates with salinity, a chemical property that has prompted numerous groundwater studies to use B as a tracer of water salinization (e.g., Vengosh et al., 2002), anthropogenic contamination (e.g., Pennisi et al., 2006b), thermal maturation of organic matter (e.g., Williams et al., 2013), and hydraulic fracturing (e.g., Warner et al., 2014). Moreover, B has been recognized as a potential contaminant worthy of regulation. Interest in coupling B isotopes with major elements and Sr isotopes is based on 1) the need to understand the reactions that control B distributions in groundwater, particularly in aquifers considered for water or mineral resources exploitation (e.g., Millot and Négrel, 2007; Pennisi et al., 2006), and 2) the chemical properties of B isotopes that help elucidate water/rock interactions, in particular those that are pH-dependent (e.g., Hemming et al., 1995; Lemarchand et al., 2007; Schmitt et al., 2012; Spivack et al., 1987). Fig. 4 provides a review of published relationships between pH and the B partition coefficient (K_d) and the B isotopic fractionation factor (α). In the pH range of the WACB samples, both B species are present in solution. Therefore, dissolved B isotope ratios are strongly linked to solution pH through the cumulative effects of adsorption/desorption reactions and carbonate precipitation/dissolution (e.g., Lemarchand et al., 2007; Ruiz-Agudo et al., 2012).

Fig. 4
Review of K_d–pH and α–pH relationships. “Resin” data are from Lemarchand (2001); “humic acids” data are from Lemarchand et al., 2005; “birnessite” and “goethite” data are from Lemarchand et al., 2007; “carbonate” data are from Hemming et al. (1995) and Goldberg and Forster (1991); “sediments” data are from Spivack et al. (1987).

It is difficult to model the reactive transport of B using the equations above because neither B concentrations nor the isotope composition of expected sources and sinks are known. Similarly, data are lacking for the isotopic fractionation factor (α) and the partition coefficient (K_d) corresponding to the various reactions. Nonetheless, the B mass balance in WACB waters and the inverse correlation between δ¹¹B values and pH (Fig. 5) provide evidence that pH-dependent reactions control the B distribution. This reduces the B transport modeling to equilibrium reactions involving B exchange between groundwater and host minerals.

Fig. 5
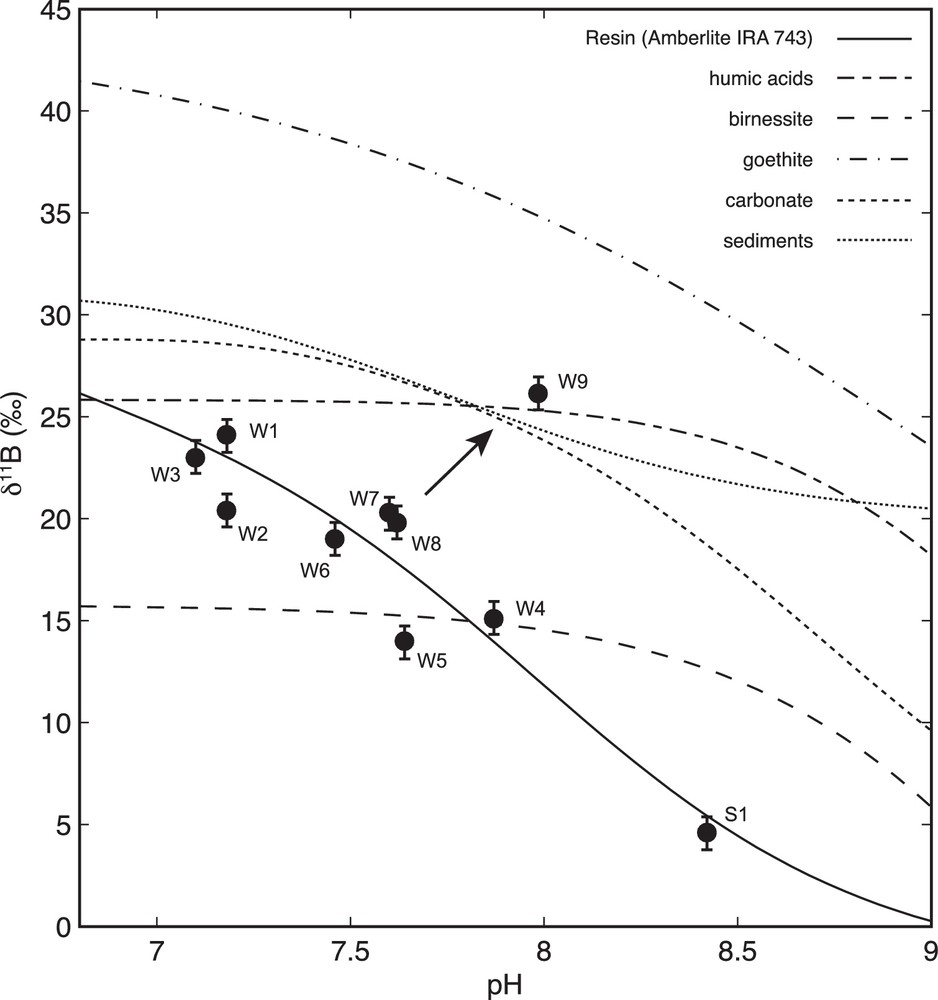
Comparison of dissolved and theoretical δ¹¹B versus pH assuming different natures of the reactive surface. Arrow indicates the addition of water from the overlying Wasatch aquifer Theoretical curves derive from the same studies as those in Fig. 4.

The pH-dependency of dissolved B interactions with mineral or organic surfaces is related to the distribution and structure of the surface complexes formed (Goldberg et al., 2000; Lemarchand et al., 2005, 2007). These studies demonstrate that all B-surface interactions can be rationalized by the combined formation of trigonal/tetrahedral, monodendate/bidendate, and inner-sphere/outer-sphere complexes. Depending on the reaction, differences between the formation constants of B-surface complexes induce different K_d–pH and α–pH relationships (Fig. 4), which can be implemented in an inverse model to identify the chemical reactions controlling dissolved B concentrations. Because B concentrations are dilute, the partitioning between solution and surfaces can be modeled using the following simplified expression:

C_{w} = \frac{w r}{w r + K_{d}} \cdot C_{T}

(10)

where wr is the dimensionless water/rock ratio, C_w and C_T are the B concentrations in groundwater and the total quantity of B (adsorbed + dissolved) per mass of water, respectively.

Similarly, the B isotopic ratio of the groundwater (R_w) can be conveniently expressed using only the total isotopic ratio (R_T), the water/rock ratio (wr), the partition coefficient (K_d), and the fractionation factor (α):

R_{w} = \frac{w r + K_{d}}{w r + α K_{d}} \cdot R_{T}

(11)

In aquifers, where the water/rock ratio is small (wr << 1), and for elements like B with high chemical affinities for most of mineral surfaces (K_d >> 1), Eq. (11) reduces to:

R_{w} \approx \frac{R_{T}}{α}

(12)

Using Eq. (12) and the α–pH relationships published for different surface minerals (carbonates, river sediments, metal-oxides, organic compounds, Fig. 4b and references therein), we modeled groundwater δ¹¹B values using R_T = 4.042 (δ¹¹B = –0.4‰) and determined that the Amberlite IRA 743 resin (a resin with organic-like reactive groups comprising mannitol and tertiary amine groups grafted on a polystyrene backbone) is the best chemical analog for the reactive surfaces in the WACB aquifer. The modeled R_T value is very close to the one observed in S1, and it is noteworthy that the entire dataset along the 100-km flow path can be explained with a unique R_T value, except for the last wells (W9), for which major elements and Sr reveal water inflow from the overlying aquifer. This suggests a single or strongly buffered source of B to the aquifer. Coal samples from the Wyodak-Anderson Basin have high but variable B contents (from 39 to 282 μg/g) and low δ¹¹B values (from –11 to –25‰, Williams and Hervig, 2004). The presence of B-rich coal beds, together with the B model results revealing the organic-like behavior of the host material, indicates that coal is the most important source and sink of B. This conclusion is consistent with the Sr isotope modeling discussed above. Accordingly, we used Eq. (10) with the K_d–pH relationship of the Amberlite IRA743 resin to model the downgradient evolution of B concentrations in WACB groundwater. A very good agreement between modeled and observed B data occurs when C_T is set to 23,580 μg/g. This high C_T value does not have particular meaning because it is derived from the exceptionally high B affinity (K_d) for the Amberlite IRA 743 resin and assumes that coal is the only surface in contact with water. More likely, B has a reduced affinity for coal than for mannitol, and other minerals with even lower B affinities dilute the coal. Therefore the assumed C_T value probably represents an upper limit, but one interesting implication is that most of the WACB groundwater samples can be modeled with a unique C_T value, which suggests that B evolves in the steady state in most of the WACB aquifer.

Environment implications – While B has a high chemical affinity for organic surfaces, such as coal, which magnifies exchange between groundwater and host surfaces in the WACB aquifer, other host minerals, like clays, may show elevated B partition coefficients, possibly leading to similar pH-dependent behavior. For instance, in the Cornia Plain aquifer, Italy (Pennisi et al., 2006), the Strengbach watershed, France (Cividini et al., 2010), and the French Guiana coastal aquifer (Négrel et al., 2002), similar inverse correlations between δ¹¹B and pH have been described (Fig. 6), indicating that pH-dependent controls on B transport are likely fundamental. However, the non-marine Hastings aquifer in southeastern England (Mather and Porteous, 2001, not shown) does not show a clear relationship with pH. Water mixing with adjacent aquifers, host minerals, like sandstone, having lower B partition coefficients, and more acidic solutions (in a pH range where the boric acid form dominates) might explain the apparent exception. Finally, significant B adsorption onto host surfaces can be expected in aquifers where pH-dependent ion-exchange reactions dominate. In the case of recharge water acidification by atmospheric CO₂ rise or anthropogenic contamination, adsorbed B will transfer to solution and potentially exceed safe drinking water limits.

Fig. 6
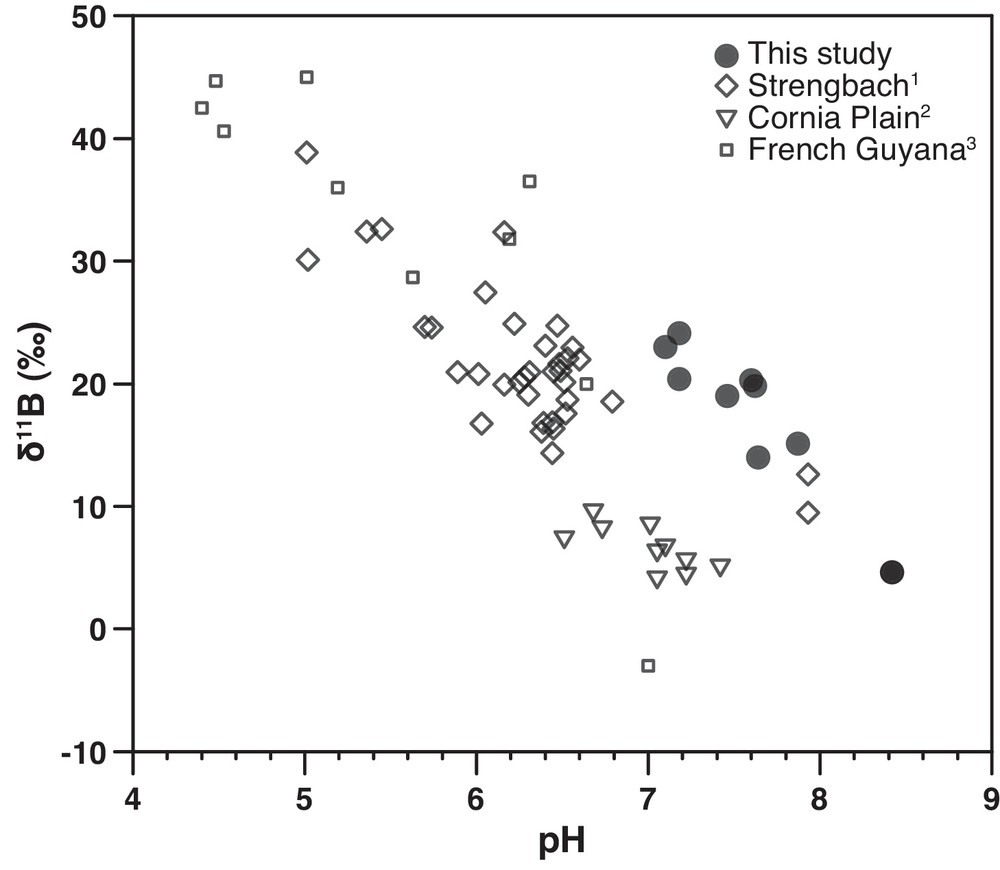
δ¹¹B versus pH in groundwaters and surface waters. ¹data from Cividini et al. (2010). ²data from Pennisi et al. (2006). ³data from Négrel et al. (2002).

6 Conclusions

This study identifies geochemical processes occurring in the WACB aquifer. Major ion concentrations, ⁸⁷Sr/⁸⁶Sr ratios, δ¹¹B values were used to determinate and quantify the main reactions controlling the downgradient chemical evolution of groundwater.

A 1D mass transport model provides evidence that the oxidation of organic matter by bacteria is a key mechanism controlling carbonate equilibria conditions.

Groundwater Sr concentrations reflect carbonate mineral dissolution and adsorption on coal surfaces. Isotopic analyses identify the release of labile radiogenic Sr²⁺ from coal surfaces, as well as water input from the overlying Wasatch formation.

Concentration and isotope ratio data for B further confirm the importance of pH-dependent ion-exchange reactions. Boron concentrations in groundwater could increase if acidification occurs.

References

[Banner and Hanson, 1990] J.L. Banner; G.N. Hanson Calculation of simultaneous isotopic and trace element variations during water–rock interaction with applications to carbonate diagenesis, Geochim. Cosmochim. Acta, Volume 54 (1990), pp. 3137-3213

[Bartos and Ogle, 2002] T.T. Bartos; K.M. Ogle Water quality and environmental isotopic analyses of ground-water samples collected from the Wasatch and Fort Union Formations in areas of coal bed methane development – implications to recharge and groundwater flow, eastern Powder River Basin, Wyoming, USGS Water Resources Investigations Report 02-4045 (2002), p. 89

[Bates et al., 2011] B.L. Bates; J.C. McIntosh; K.A. Lohse; P.D. Brooks Influence of groundwater flowpaths, residence times and nutrients on the extent of microbial methanogenesis in coal beds: Powder River Basin, USA, Chem. Geol., Volume 284 (2011), pp. 45-61

[Brinck et al., 2008] E.L. Brinck; J.I. Drever; C.D. Frost The geochemical evolution of water coproduced with coal bed natural gas in the Powder River Basin, Wyoming, Environ. Geosci., Volume 15 (2008), pp. 153-171

[Brownfield et al., 2005] M.E. Brownfield; J.D. Cathcart; R.H. Affolter; I.K. Brownfield; C.A. Rice; J.T. O’Conner; R.A. Zielinski; J.H. Bullock; J.C. Hower; G.P. Meeker Characterization and modes of occurrence of elements in feed coal and coal combustion products from a power plant utilizing low-sulfur coal from the Powder River Basin, Wyoming, U.S. Geological Survey Scientific Investigation Report 2004-5271 (2005), p. 36

[Bullen et al., 1996] T.D. Bullen; D.P. Krabbenhoft; C. Kendall Kinetic and mineralogic controls on the evolution of groundwater chemistry and ⁸⁷Sr/⁸⁶Sr in a sandy silicate aquifer, northern Wisconsin, Investigation Report 2004-5271USA, Geochim. Cosmochim. Acta, Volume 60 (1996), pp. 1807-1821

[Chapelle and McMahon, 1991] F.H. Chapelle; P.B. McMahon Geochemistry of dissolved inorganic carbon in a coastal plain aquifer1. Sulfate from confining beds as an oxidant in microbial CO₂ production, J. Hydrol., Volume 127 (1991), pp. 85-108

[Cividini et al., 2010] D. Cividini; D. Lemarchand; F. Chabaux; R. Boutin; M.C. Pierret From biological to lithological control of the B geochemical cycle in a forest watershed (Strengbach Vosges), Geochim. Cosmochim. Acta, Volume 74 (2010), pp. 3143-3163

[Crowley et al., 1993] S.S. Crowley; L.F. Ruppert; H.E. Belkin; R.W. Stanton; T.A. Moore Factors affecting the geochemistry of a thick, subbituminous coal bed in the Powder River Basin: volcanic, detrital, and peat-forming processes, Org. Geochem., Volume 20 (1993), pp. 843-853

[Daddow, 1986] P.B. Daddow Potentiometric surface map of the Wyodak-Anderson coal bed, Powder River structural basin, Wyoming, 1973–84, U.S. Geological Survey Water Resources Investigations Report 85-4305 (1986) (scale 1:250000)

[EIA, 2007] EIA (Energy Information Administration) 2007. Annual energy outlook 2007, with projections to 2030. DOE/EIA-0383.

[Ellis, 1999] M.S. Ellis Assessment of Wyodak-Anderson coal resources in the Powder River Basin, Wyoming and Montana (W.R. Miller, ed.), Coal bed methane and tertiary geology of the Powder River Basin: Wyoming Geological Society Association Guidebook, 1999, pp. 43-60 (50th Annual Field Conference)

[Ellis, 2002] M.S. Ellis Quality of economically extractable coal beds in the Gillette coal fields as compared with other tertiary coal beds in the Powder River Basin, Wyoming and Montana, U.S. Geological Survey Open File Report 02-174 (2002), pp. 1-20

[Ellis et al., 1999] M.S. Ellis; R.M. Flores; A.M. Ochs; G.D. Stricker; G.L. Gunther; G.S. Rossi; L.R. Bader; J.H. Schuenemeyer; H.C. Power Gillette coalfield, Powder River Basin: geology, coal quality, and coal resources, 1999 Resource assessment of selected tertiary coal beds and zones in the northern Rocky Mountains and Great Plains region, U.S. Geological Survey Professional Paper, 1999 (1625-A, chapter PQ)

[Fletcher et al., 1984] P. Fletcher; G. Sposito; C.S. LeVesque Sodium-calcium-magnesium exchange reactions on a montmorillonitic soil: I. Binary exchange reactions, Soil Sci. Soc. Am. J., Volume 48 (1984), pp. 1016-1021

[Flores and Bader, 1999] R.M. Flores; L.R. Bader, 1999 Resource assessment of selected tertiary coal beds and zones in the northern Rocky Mountains and Great Plains region, U.S. Geological Survey Professional Paper 1625-A (1999), p. PS1-PS49 (Chapter PS)

[Flores et al., 1999] R.M. Flores; A.M. Ochs; L.R. Bader; R.C. Johnson; D. Vogler Framework geology of the Fort Union coal in the Powder River Basin, 1999 Resource assessment of selected tertiary coal beds and zones in the northern Rocky Mountains and Great Plains Region, U.S. Geological Survey Professional Paper 1625-A, 1999 (Chapter PS)

[Foster et al., 2006] G.L. Foster; Y. Ni; B. Haley; T. Elliott Accurate and precise isotopic measurement of sub-nanogram sized samples of foraminiferal hosted boron by total evaporation NTIMS, Chem. Geol., Volume 230 (2006) no. 1–2, pp. 161-174

[Frost et al., 2002] C.D. Frost; B.N. Pearson; K.M. Ogle; E.L. Heffern; R.M. Lyman Sr isotope tracing of aquifer interactions in an area of accelerating coal bed methane production, Powder River Basin, Wyoming, Geology, Volume 30 (2002), pp. 923-926

[Furukawa et al., 2004] Y. Furukawa; A.C. Smith; J.E. Kostka; J. Watkins; C.R. Alexander Quantification of macrobenthic effects on diagenesis using a multicomponent inverse model in salt marsh sediments, Limnol. Oceanogr., Volume 49 (2004), pp. 2058-2072

[Gaillardet et al., 2001] J. Gaillardet; D. Lemarchand; C. Göpel; G. Manhès Evaporation and sublimation of boric acid: application for boron purification from organic-rich solutions, Geostandards Newsletter, Volume 25 (2001) no. 1, pp. 67-75

[Goldberg and Forster, 1991] S. Goldberg; H.S. Forster Boron sorption on calcareous soils and reference calcites, Soil Science, Volume 152 (1991) no. 4, pp. 304-310

[Goldberg et al., 2000] S. Goldberg; S.M. Lesch; D.L. Suarez Predicting boron adsorption by soils using soil chemical parameters in the constant capacitance model, Soil Sci. Soc. Am. J., Volume 64 (2000), pp. 1356-1363

[Gonfiantini and Pennisi, 2006] R. Gonfiantini; M. Pennisi The behaviour of boron isotopes in natural waters and in water–rock interactions, J. Geochem. Exploration, Volume 88 (2006), pp. 114-117

[Heffern and Coates, 1999] E.L. Heffern; D.A. Coates (1999), pp. 231-252

[Hemming et al., 1995] N.G. Hemming; R.J. Reeder; G.N. Hanson Mineral-fluid partitioning and isotopic fractionation of boron in synthetic calcium carbonate, Geochim Cosmochim Acta, Volume 59 (1995), pp. 371-379

[Jacobson and Wasserburg, 2005] A.D. Jacobson; G.J. Wasserburg Anhydrite and the Sr isotope evolution of groundwater in a carbonate aquifer, Chem. Geol., Volume 214 (2005), pp. 331-350

[Johnson and DePaolo, 1997] T.M. Johnson; D.J. DePaolo Rapid exchange effects on isotope ratios in groundwater systems 2. Flow investigation using Sr isotope ratios, Water Resour. Res., Volume 33 (1997), pp. 197-209

[Lemarchand, 2001] D. Lemarchand Géochimie isotopique du bore : érosion continentale, bilan océanique et paléo-pH, Université Denie Diderot, 2001 (PhD thesis, 350 p)

[Lemarchand and Gaillardet, 2006] D. Lemarchand; J. Gaillardet Transient features of the erosion of shales in the Mackenzie basin (Canada), evidences from boron isotopes, Earth Planet. Sci. Lett., Volume 245 (2006) no. 1–2, pp. 174-189

[Lemarchand et al., 2005] E. Lemarchand; J. Schott; J. Gaillardet Boron isotopic fractionation related to boron sorption on humic acid and structure of surface complexes formed, Geochim. Cosmochim. Acta, Volume 69 (2005), pp. 3519-3533

[Lemarchand et al., 2007] E. Lemarchand; J. Schott; J. Gaillardet How surface complexes impact boron isotope fractionation: evidence from Fe and Mn oxides sorption experiments, Earth Planet. Sci. Lett., Volume 260 (2007), pp. 277-296

[Lucas et al., 2010] Y. Lucas; A.D. Schmidt; F. Chabaux; A. Clément; B. Fritz; Ph. Elsass; S. Durand Geochemcial tracing and hydrogeochemical modelling of water–rock interactions during salinization of alluvial groundwater (Upper Rhine valley, France), Appl. Geochem., Volume 25 (2010), pp. 1644-1663

[Maher et al., 2006] K. Maher; D.J. DePaolo; J.N. Christensen U–Sr isotopic speedometer: fluid flow and chemical weathering rates in aquifers, Geochim. Cosmochim. Acta, Volume 70 (2006) no. 17, pp. 4417-4435

[Martin et al., 1988] L.J. Martin; D.L. Naftz; H.W. Lowham; J.G. Rankl Cumulative potential hydrologic impacts of surface coal mining in the eastern Powder River Structural Basin, northeastern Wyoming, U.S. Geological Survey Water Resources Investigations Report 88-4046 (1988) (201 p)

[Mather and Porteous, 2001] J.D. Mather; N.C. Porteous The geochemistry of boron and its isotopes in groundwaters from marine and non-marine sandstone aquifers, Appl. Geochem., Volume 16 (2001), pp. 821-834

[McIntosh et al., 2004] J.C. McIntosh; L.M. Walter; A.M. Martini Extensive microbial modification of formation water geochemistry: case study from a midcontinent sedimentary basin United States, Geol. Soc. Am. Bull., Volume 116 (2004), pp. 743-759

[Millot and Négrel, 2007] R. Millot; P. Négrel Multi-isotopic tracing (δ⁷Li δ¹¹B, ⁸⁷Sr/⁸⁶Sr) and chemical geothermometry: evidence from hydro-geothermal systems in France, Chem. Geol., Volume 244 (2007), pp. 664-678

[Négrel and Petelet-Giraud, 2010] P. Négrel; E. Petelet-Giraud Geochemistry, isotopic composition (δ¹⁸⁰ δ²H, ⁸⁷Sr/⁸⁶Sr, ¹⁴³Nd/¹⁴⁴Nd) in the groundwater of French Guiana as indicators of their origin, interrelations, C. R. Geoscience (2010), pp. 786-795 (342-10)

[Négrel et al., 2002] P. Négrel; E. Petelet-Giraud; W. Kloppmann; J. Casanova Boron isotope signatures in the coastal groundwaters of French Guiana, Water Resour. Res., Volume 38 (2002) no. 11 ([44–1–44–5])

[Palmer et al., 2000] C.A. Palmer; S.J. Mroczkowski; A. Kolker; R.B. Finkelman; J.H. Bullock Chemical analysis and modes of occurrence of selected trace elements in a Powder River Basin coal and its corresponding simulated cleaned coal: a technical report by the U.S Geological Survey, U.S. Geological Survey Open File Report 00-323 (2000) (53 p)

[Pennisi et al., 2006] M. Pennisi; G. Bianchini; A. Muti; W. Kloppmann; R. Gonfiantini Behaviour of boron and strontium isotopes in groundwater-aquifer interactions in the Cornia Plain (Tuscany Italy), Appl. Geochem., Volume 21 (2006), pp. 1169-1183

[Rice, 1993] D.D. Rice Composition and origin of coal bed gas (B.E. Law; D.D. Rice, eds.), Hydrocarbons from coal: American Association of Petroleum Geologists Studies in Geology, 38, 1993, pp. 159-184

[Rice et al., 2002] C.A. Rice; T.T. Bartos; M.S. Ellis Chemical and isotopic composition of water in the Fort Union and Wasatch formations of the Powder River Basin Wyoming and Montana: implications for coal bed methane development. Rocky Mountain Association of Geologists, USGS report (2002), pp. 00-372

[Rice et al., 2000] C.A. Rice; M.S. Ellis; J.H. Bullock Water co-produced with coal bed methane in the Powder River Basin Wyoming: preliminary compositional data, U.S. Geological Survey Open File Report 00-372 (2000), p. 18 p

[Riotte and Chabaux, 1999] J. Riotte; F. Chabaux (²³⁴U/²³⁸U) activity ratios in freshwaters as tracers of hydrological processes: the Strengbach watershed (Vosges France), Geochim. Cosmochim. Acta, Volume 63 (1999), pp. 1263-1275

[Ruiz-Agudo et al., 2012] E. Ruiz-Agudo; C.V. Putnis; M. Kowacz; M. Ortega-Huertas; A. Putnis Boron incorporation into calcite during growth: Implications for the use of boron in carbonates as a pH proxy, Earth Planet. Sci. Lett. (2012), pp. 345-348 (9-17)

[Schmitt et al., 2012] A.D. Schmitt; N. Vigier; D. Lemarchand; R. Millot Processes controlling the stable isotope compositions of Li, B Mg and Ca in plants, soils and waters: a review, C. R. Geoscience, Volume 344 (2012) no. 11–12, pp. 704-722

[Spivack et al., 1987] A.J. Spivack; M.R. Palmer; J.M. Edmond The sedimentary cycle of the boron isotopes, Geochim. Cosmochim. Acta, Volume 51 (1987), pp. 1939-1949

[Van Voast, 2003] W.A. Van Voast Geochemical signature of formation waters associated with coal bed methane, AAPG Bull., Volume 87 (2003), pp. 667-676

[Vengosh et al., 2002] A. Vengosh; J. Gill; M. Lee Davisson; G. Bryant Hudson A multi-isotope (B, Sr, O, H, and C) and age dating (³H⁻³He and ¹⁴C) study of groundwater from Salinas Valley, California: Hydrochemistry, dynamics, and contamination processes, Water Resour. Res., Volume 38 (2002) (9–1–9–17)

[Vengosh et al., 1994] A. Vengosh; K.G. Heumann; S. Juraske; R. Kasher Boron isotope application for tracing sources of contamination in groundwater, Environ. Sci. Technol., Volume 28 (1994), pp. 1968-1974

[Warner et al., 2014] N.R. Warner; T.H. Darrah; R.B. Jackson; R. Millot; W. Kloppmann; A. Vengosh New tracers identify hydraulic fracturing fluids and accidental releases from oil and gas operations, Sci. Technol., Volume 48 (2014) no. 21, pp. 12552-12560

[Warwick and Stanton, 1988] P.D. Warwick; R.W. Stanton Depositional models for two tertiary coal-bearing sequences in the Powder River Basin, Wyoming, USA, J. Geol. Soc. London, Volume 145 (1988), pp. 613-620

[Williams and Hervig, 2004] L.B. Williams; R.L. Hervig Boron isotope composition of coals: a potential tracer of organic contaminated fluids, Appl. Geochem. (2004)

[Williams et al., 2013] L.B. Williams; J. Środoń; W.D. Huff; N. Clauer; R.L. Hervig Light element distributions (N, B Li) in Baltic Basin bentonites record organic sources, Geochim. Cosmochim. Acta, Volume 120 (2013), pp. 582-599

[Zhao et al., 2011] K.-D. Zhao; S.-Y. Jiang; E. Nakamura; T. Moriguti; M.R. Palmer; S.-Y. Yang Fluid–rock interaction in the Qitianling granite and associated tin deposits South China: evidence from boron and oxygen isotopes, Ore Geol. Rev., Volume 43 (2011) no. 1, pp. 243-248

Comments - Policy