1. Introduction
X-ray micro-tomography (XMT) imaging has unraveled the complex structure of many geological materials for 30 years. The technique is based on the attenuation of X-rays crossing a sample, which depends on the X-ray energy and on the atomic composition and density of the material under investigation. The development of XMT relies on three-dimensional (3D) reconstruction of the internal and external structure of a sample from a series of two-dimensional (2D) radiographs taken at different rotation angles. Every voxel in the reconstructed volume represents the linear average X-ray attenuation coefficient of the different phases contained in this volume element. Additional information about the sample mineralogy, chemical composition or phase identification can be obtained by coupling XMT to X-ray diffraction imaging, X-ray fluorescence imaging, dual-energy or spectral imaging near the absorption edge, or by using specific XMT imaging setup like phase-contrast, holotomography or grating interferometry [e.g., Wolf et al. 2017; Suuronen and Sayab 2018; Sittner et al. 2021; McDonald et al. 2009].
Useful information about the XMT technique and fields of geosciences explored are reviewed in a fruitful and exhaustive list of articles [e.g., Carlson 2006; Carlson et al. 2003; Van Geet et al. 2001; Cnudde and Boone 2013; Maire and Withers 2014; Wildenschild et al. 2002]. Specific reviews are dedicated to pore-scale flow [Blunt et al. 2013; Wildenschild and Sheppard 2013], reactive transport [Noiriel 2015], structural geology and rock mechanics [Renard 2012; Fusseis et al. 2014b], high pressure science [Guignot et al. 2020] and dynamic processes in geologic systems [Marone et al. 2020].
Advances in 3rd generation synchrotron facilities in the 1990’s and in laboratory systems more recently have opened and increased the access of the technique to various research domains. In particular, improvements in optics and detectors, and increasing computational power and data storage have initiated the progressive transition from 3D geometry imaging to 4D time-lapse imaging and 4D real-time imaging, also called dynamic imaging or 4D XMT. The sample is imaged repetitively during dynamic processes at discrete time steps that vary according to: (i) the rate of the process, and (ii) the duration necessary to record a set of radiographs. Time-lapse imaging involves imaging at discrete time steps, e.g., hours, days or months, during the process, whereas real-time imaging involves fast and continuous imaging. In the latter case, the time step, ranging from a few seconds to minutes, corresponds to the acquisition duration of the whole set of radiographs. Depending on these constraints, imaging is performed either in situ or ex situ using specifically designed setups to control flow, temperature, and pressure (see Section 2). Fast tomography imaging provides direct visualization to rapidly evolving or unstable systems, such as flowing fluids (liquid, gas) or reacting components. In addition, it greatly reduces artifacts inherent to motion of fluids [Marone et al. 2017; Villanova et al. 2017] previously encountered. Dynamic acquisition, e.g., high-frequency time-lapse acquisition, involves continuous imaging of the sample, a technique also called X-ray tomoscopy [García-Moreno et al. 2019]. The time lapse between two image acquisitions is limited by the exposure time and the number of radiographs taken, in relation with the sample composition (highly absorbent materials require a longer exposure time) and the desired quality of the reconstructed volume (a lower number of radiographs increases artifacts). For instance, a number of radiographs reduced to a few hundreds can decrease acquisition down to 50 ms [Marone et al. 2017]. The recent upgrade to 4th generation synchrotron facilities with brighter photon beams, such as the Extreme Brilliant Source at the European Synchrotron Radiation Facility [Rack 2020], offers an unprecedented opportunity for high-frequency time-lapse acquisition in the domain of Digital Rock Physics.
This article focuses on recent developments and applications of time-lapse 4D X-ray micro-tomography imaging to study dynamic processes in the field of geosciences. We review different applications where visualization through time has unravelled the complex interplay between geochemical reactions, fluid flow, transport, and deformation processes in rocks.
2. Experimental apparatuses
2.1. Coupling 4D imaging with experiments
XMT imaging lies in the acquisition of a few hundreds to thousands of radiographs of a sample while rotating on a mechanical stage. The radiographs are used to generate the sinograms and ultimately the sample absorption 3D map by staking the set of reconstructed 2D slices [Marone et al. 2010; Maire et al. 2001]. The range of rotation angles depends on the X-ray beam characteristics. While the parallel beam generated by synchrotron sources produces a complete set of radiographs over 180°, X-ray tubes in laboratory systems produce divergent X-rays, thus making a 180° plus fan angle rotation compulsory for 3D volume reconstruction. Practically, the set of radiographs is generally produced over 360° on laboratory XMT scanners to get a better signal-to-noise ratio.
XMT imaging is performed either ex situ or in situ. Several devices, from flow-through cells to rock deformation rigs, have been developed to analyse the response of rock samples to thermo-hydro-bio-mechano-chemical solicitations, with applications ranging from CO2 sequestration, enhanced oil recovery, and reactive transport, to geomechanics, geological engineering, and geohazards. For ex situ imaging, the sample is removed from and replaced in the experimental apparatus and placed on the stage at every imaging step. In that case, the 3D data sets must be registered afterwards, i.e., put in the same coordinate system (see Section 3). A rigid transformation involving translation and rotation along the x–y- and z-directions allows for further image difference and visualization of geometry modifications through time. In contrast, in situ imaging requires the whole setup to be placed next to the X-ray beam, while the sample remains positioned on the rotation stage. A few major constraints are identified. First, rotation of the sample and sample holder must be allowed. In some setups, the whole setup is rotated, requiring a high weight-bearing rotation stage. In others, the mobile flow/deformation cell is installed on the sample stage and connected to immobile components set aside, e.g., thanks to slip rings and flexible tubing and connectors. In any case, the setup must not interfere with X-rays, for instance through obliteration of part or totality of the incident beam at certain angles of rotation. Indeed, the presence of absorbent components in the radiographs at discrete angular positions will alter volume reconstruction by producing artifacts. The core holder itself, which also absorbs X-rays, should not reduce much the flux of photons passing through the sample. To increase the photon flux, a white (i.e., polychromatic) beam may be preferred over a monochromatic X-ray source, even if it generates more noise in the images. In some cases, however, the high absorption and filtering properties of the core holder permit to work with a pink beam (i.e., filtered white beam) instead of a white beam in order to obtain a greater photon flux and potentially much faster acquisitions while maintaining a high signal-to-noise ratio.
The size of the sample is intimately related to the imaging resolution, with the sample diameter in most experiments equal to the voxel size times the number of pixels of the camera in the x- or y-direction (about 2500), such that the entire sample fits in the camera field of view. Samples are generally about 1 cm in diameter, thus allowing a good compromise between the voxel size, the spatial resolution of the structures (about 5 μm) and the quest for representative elementary volume (REV) [Bear 1972]. The voxel-resolution-to-sample-size constraint can be overcome through horizontal or vertical multi-scanning and stitching of the sub-volumes after reconstruction. Local micro-tomography is another option [Baruchel et al. 2000]. In the later case, the sample diameter is larger than the field of view of the camera and a subvolume inside the sample is imaged. The reconstructed image can be affected by artefacts caused by the external parts of the sample whose absorption is recorded in a limited number of radiographs. Multi-scale imaging at different resolutions [Hébert et al. 2015; Peng et al. 2014] can benefit from local tomography to resolve fine structures and derive properties at larger scales, e.g. micro-porosity, in rocks that exhibit heterogeneities spanning several length scales.
The highest spatial resolutions, up to 20 nm voxel size, can be achieved with nano-tomography or X-ray transmission microscopy. In that cases, the X-ray beam is focused ahead of the sample (of size below 1 mm) down to a focal spot that serves as a point source [Withers 2007].
2.2. Flow-through cells
Flow-though cells are designed to explore the response of samples to thermo-hydro-bio-chemical processes in the sub-surface at reservoir conditions, or to quantify the pore-scale distribution of two or more fluids within a sample during drainage and imbibition displacements. The system is generally divided in four parts: (i) a core holder, (ii) a fluid system, (iii) a set of sensors to measure the fluid and rock properties, and (iv) a data acquisition system to record parameters and control the whole system [Gouze et al. 2017].
Much effort has been done in the past years to design flow-through cells to conduct experiments relevant to in situ aquifer and reservoir conditions [Iglauer and Lebedev 2018] (Figure 1a). Such designs are suitable to reproduce the high pressure and elevated temperatures imposed by the hydrostatic, lithostatic, and geothermal gradients upon sub-surface conditions.
(a) Example of flow-through device to inject fluids at reservoir conditions and desired partial pressures of CO2 in rock samples; adapted from the setup ICARE [Luquot et al. 2013]. (b) The Hades triaxial rock deformation apparatus developed for in-situ imaging [Renard et al. 2016]. The sample is wrapped into a polymer jacket and located between two pistons that impose the axial loading (𝜎1). The confining pressure (𝜎3) is sustained by oil pressure. Two pumps connected to the fluid line inlet and outlet impose the pore fluid pressure (Pf). The entire body of the rig is heated to the desired temperature.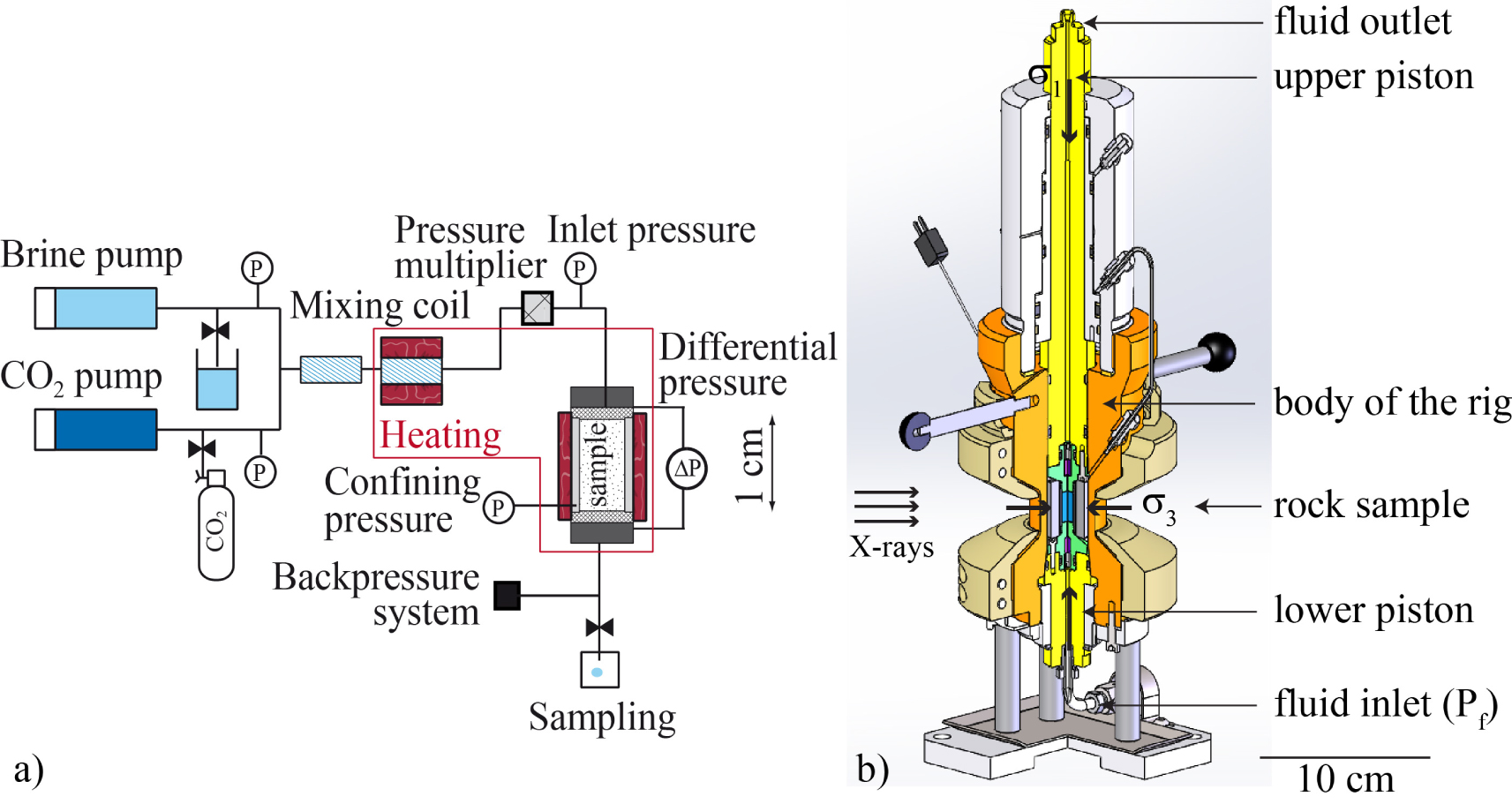
The fluids circulate along the fluid line. One or several pumps control the injection of fluids, and the confining and eventually the axial fluid pressures. The working temperature is reached thanks to a heating system. When no confinement is required, for instance in experiments under atmospheric conditions, mm- to cm-size packed columns are also suitable [Noiriel et al. 2012; Rad et al. 2013; Godinho et al. 2016]. Otherwise, the samples are placed in a core holder and confined to avoid fluid leakage. Reservoir conditions are achieved in high pressure flow-through cells made of materials capable to handle high radial and axial pressures, e.g., aluminum alloy (up to 69 MPa for aviation grade) [Silin et al. 2011; Oren et al. 2019; Herring et al. 2014; Andrew et al. 2014b; Li et al. 2015], carbon fiber [Iglauer et al. 2011], thermoplastic PEEK composite [Saenger et al. 2016], titanium, hastelloy [Luquot and Gouze 2009] or stainless steel. A set of sensors completes the fluid line or the core holder to record the changes in fluid chemistry and rock physical properties during the experiment. Fluid pressure is generally regulated by back-pressure controllers. Absolute or differential pressure transducers are used to measure the pressure difference between the sample inlet and outlet, which is related to the permeability through Darcy’s law [Darcy 1856]. Linear variable displacement transducers (LVDT) can be added to measure axial strain [Cil et al. 2019].
Fluid characteristics are monitored through online measurements of pH, electrical conductivity or other geophysical parameters [Noiriel et al. 2004; Vialle et al. 2014; Wu et al. 2011]. Recent improvements in online fluid composition determination include Raman spectroscopy probe [Randi et al. 2014]. When fluid composition cannot be assessed directly, fluid samplers allow for sampling under working fluid temperature and pressure, for further determination of pH or/and elemental composition.
Some setups can be mounted directly on the rotation stage for in situ imaging during multi-phase flow or tracer injection experiments. Flow may be stopped during scan acquisition to avoid artifacts inherent to the movement of fluids. A first imaging of the sample is generally performed prior to fluid injection, at the pressure conditions of the experiment. This data set is used as the initial reference state prior to experiment and is subtracted from the following 3D volumes.
2.3. Rock deformation apparatuses
Rock deformation apparatuses are designed to explore the physical and deformation properties of rocks, e.g., mechanical strength, microstructure evolution, elastic wave velocity and attenuation coefficient in response to earthquake or geomechanical solicitations. However, most rock physics laboratory experiments suffer from major limitations because: (i) direct information about deformation processes inside non-transparent rock samples cannot be obtained without potential unloading artefacts, including fatigue effects and loss of fluid pressure and heat, and (ii) acoustic emission monitoring, which plays the central role in several of these experiments, records only the seismic part of the deformation. Therefore, the time evolution of the 3D deformation field and microstructure geometry inside the samples before and during laboratory earthquakes remain inaccessible. XMT imaging overcomes some of these limitations by simultaneously measuring both the seismic and aseismic components of the rock deformation in well-controlled laboratory experiments. Much effort has been done to design rock deformation apparatuses to conduct experiments at pressure and temperature relevant of the sub-surface in situ conditions. The two main limitations of the first XMT experiments were: (i) the flux of photons, which was not high enough to penetrate the thick walls of existing pressure vessels and (ii) the sample environment, of the order of a few kilograms, was too heavy to be carried on the rotation stage. For these reasons, the first dynamic XMT in situ experiments on rock materials used portable core holders made of Plexiglas® or glass [Chen et al. 1996; Renard et al. 2004; Viggiani et al. 2004]. Later on, rock deformation apparatuses suitable to in situ XMT imaging and that can reproduce pressure and temperature conditions at several meters to few kilometers depth have been built [Hasan and Alshibli 2012; Fusseis et al. 2014a; Renard et al. 2016; Voltolini et al. 2019; Butler et al. 2020; Cil et al. 2019]. The high X-ray absorption of the core holder, made for instance of titanium [Renard et al. 2016], is overcome by the higher photon flux and sensitivity of the detectors, and by the use of an incident X-ray pink beam instead of a monochromatic beam. The core holders are designed to absorb X-ray wavelengths in a way the X-ray beam crossing the rock sample is about monochromatic. In several triaxial rock deformation apparatuses [Renard et al. 2016; Butler et al. 2020], the confining pressure, axial stress, and pore fluid pressure are controlled independently. These apparatuses use samples of several millimeters in diameter and up to one centimeter in length, such as the Hades apparatus (Figure 1b), which can deform rock samples at conditions of up to 100 MPa confining pressure, 100 MPa pore fluid pressure, 200 MPa axial stress, and temperature of 200 °C. A torsional deformation can also be applied by shearing two rock cylinders separated by a slip surface along which friction occurs [Zhao et al. 2017]. In all these apparatuses, the sample remains in the core holder and the entire setup rotates over at least 180°. For more extreme conditions, the large sample environment around the X-ray transparent gasket does allow for the rotation of the setup, and another technical solution was developed to overcome the possible presence of absorbent components in the field of view. In that case, the high-pressure setup remains fixed, while the sample chamber fully rotates with the top and bottom anvils that pressurize the sample [Wang et al. 2005; Yu et al. 2016]. The weight of the sample assembly neither limits the rotation, nor the small X-ray angular access to the sample. This technology has been applied in the Ultra-fast Tomography Paris–Edinburgh cell (UToPEc) to perform dynamic XMT acquisitions on samples of 8 mm3 in volume at pressures up to 15 GPa and temperatures of 1000 K [Philippe et al. 2016; Boulard et al. 2018].
3. Four-dimensional image processing
3.1. Data set registration and image subtraction
The observation and quantification of microstructure and rock properties evolution in experiments lies on 3D data set comparison through time. To do this, the successive XMT volumes must be registered in the same coordinate system. Registration is required when the sample has been removed from the rotation stage between two imaging experiments (ex situ imaging) or when misalignment is observed during in situ experiments. It constitutes a crucial step in image processing to compare data sets with each other [Wildenschild and Sheppard 2013].
Registration is not mandatory for in situ imaging, where the sample remains fixed on the rotation stage during the whole experiment and returns to its initial position after acquisition. In situ acquisition is preferred for experiments involving mechanical deformation, as sample deformation would make difficult non-rigid registration. When the sample is fixed, it becomes possible to calculate the displacement and deformation fields using for instance digital volume correlation (DVC) (see further in Section 3).
In absence of mechanical deformation, registration consists of a rigid body transformation involving three translations and three rotations along and around the -x, -y, and -z axes. The coefficients of the (4 × 4) transformation matrix are determined from identification of at least three landmarks in the different volumes. Alternatively, more optimized algorithms based on image intensity distribution, image structure or neuronal network [Maes et al. 1997; Zitová and Flusser 2003] have been developed to optimize a similarity measure in between two volumes, e.g., mutual information, invariant moments or cross-correlation. Depending on the sample geometry and its evolution through time, one technique is preferred over another to determine the transformation matrix.
Registration starts with a reference volume, generally the initial data set. Sometimes, a given volume at time ti serves as reference and the following one at ti+1 is registered thanks to this reference. The transformation matrix is applied to the volumes to be registered, followed by interpolation of the greyscale intensity of translated and rotated voxels. Resampling of the voxel intensity through a linear interpolation among the neighbour voxels in the new coordinate system is common, although more complex algorithms like cubic or Lanczos resampling exist [Duchon 1979].
Once registration is achieved, one-to-one comparison of 3D greyscale volumes may involve image normalization, i.e., rescaling of the histograms so that a given material in the sample, e.g., air or a rock element, will have the same distribution of intensities in every volume (Figure 2). Normalization also improves image visualization by adjusting the contrast through scaling of the range of intensity values. Additional denoising of the data sets with 3D median or non-local means filters is also common [Buades et al. 2005].
Example of a sandstone sample at two stages of a dissolution experiment at pH 5.5. Cross sections (a,b) before and (c,d) after image registration and normalization; the white circles correspond to a common pattern in the two images. (e) Corresponding histograms of the initial data sets are also shown, showing that the peaks for quartz and calcite are not superimposed. (f) Image difference (initial-final) after image registration and normalization showing the sample geometry evolution, including dissolution of the carbonate cement and disaggregation of some quartz grains.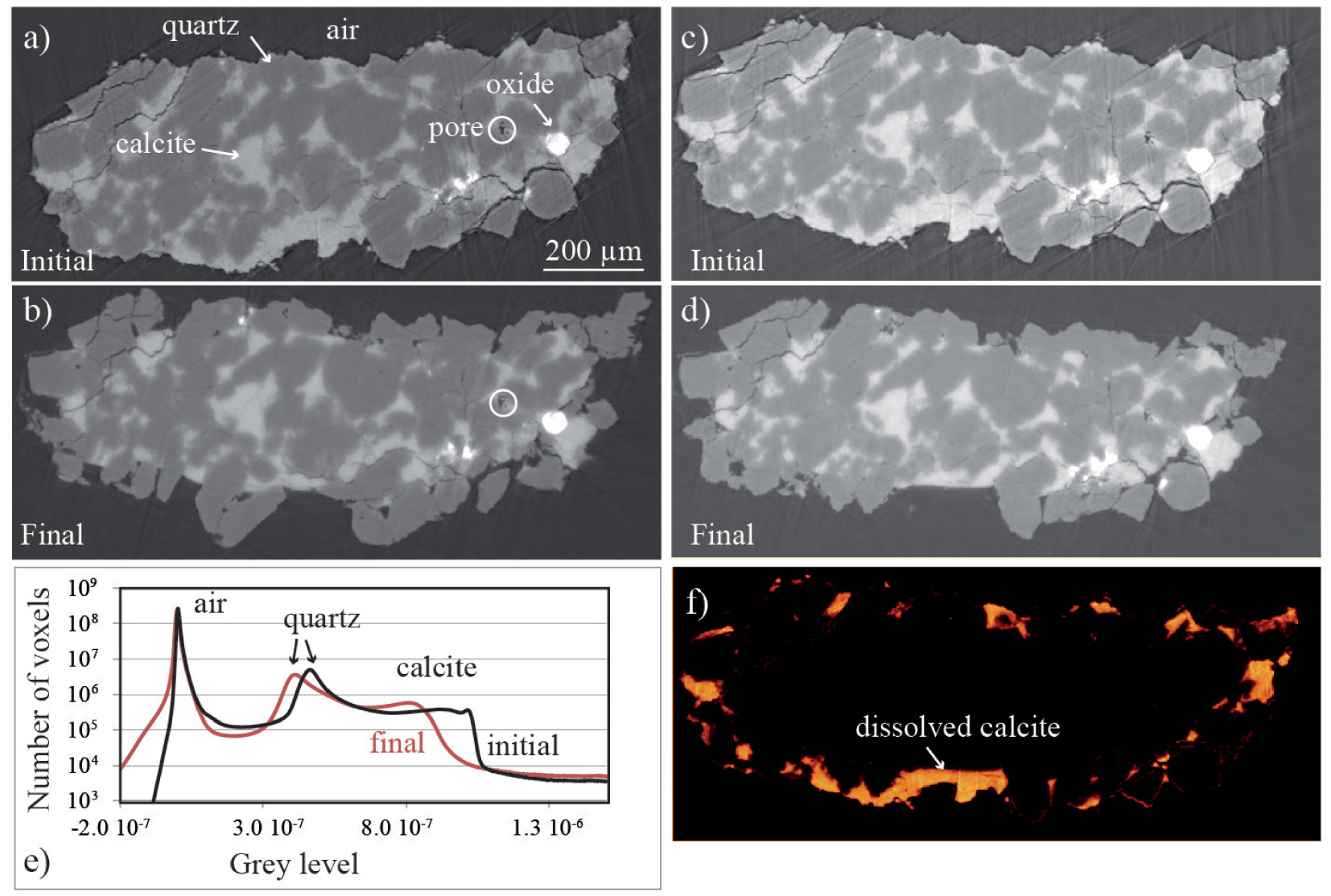
After these steps, one often proceeds to data set segmentation to assign the different solid and fluid phases in the sample a unique label, e.g., 0 for air, 1 for solid, 2 for liquid.
3.2. Data set segmentation and field representation
Segmentation is an essential step for locating the different materials and extracting parameters characterizing the samples, like the volume occupied by the different phases, the position of the interface between two phases, or the phase connectivity and network properties. In addition, digitization of the pore space and rock matrix is necessary to perform direct simulations of flow or mechanical deformation of the solid. Segmentation of XMT volumes is often based on the image intensity distribution, but can possibly be combined with morphological criterion [Meyer and Beucher 1990]. The simplest way to separate two phases is to select a threshold in the greyscale histogram. However, simple thresholding often fails to properly distinguish in between phases. Indeed, noise inherent to XMT does not imply a single greyscale intensity for a given phase, but rather a distribution of intensities that generally overlap with others and follow Poisson distributions [Cnudde and Boone 2013]. In this case, more complex algorithms like anisotropic diffusion filters are more suitable. Watershed segmentation based on region-growing is also efficient to ignore the overlaps in the modes characterizing the greyscale histogram. More recently, segmentation based on machine learning has emerged, e.g., convolutional neural networks. From supervised algorithms in which training features are combined to identified regions of interest in the original image [Arganda-Carreras et al. 2017], to unsupervised algorithms that do not require any training images or ground true labelling of voxels [Kim et al. 2020], several methods can be explored to produce voxel-based segmentation.
3.3. Interface tracking
XMT offers the opportunity to resolve fluid–fluid, fluid–mineral and mineral–mineral interfaces, which are key elements in multi-phase flow or geochemical processes occurring at the sub-surface. When the absorption contrast between two phases of close density is too small to be detected, phase contrast XMT can be used to enhance the boundary between the two phases in contact [Cloetens et al. 1996]. After segmentation and labelling of the different phases, identification and tracking of the interface motion becomes possible. The different methods to extract and represent the interface displacement from XMT volumes as their limitations are described in Noiriel and Soulaine [2021]. Under flow or reactive conditions, fluid–fluid or fluid–mineral interface shift can be directly linked to the rate of fluid displacement or the amount of solid removed or precipitated by reactive fluids. The velocity of the interface shift is defined as:
| (1) |
If evaluation of the motion of sharp, relatively flat interfaces from 3D data sets does not pose a serious problem, it is far more complicated to deal with curved or smeared (i.e. diffuse) interfaces [Noiriel and Soulaine 2021]. Evaluation of the displacement between two time steps lies in the calculation of the distance between two surfaces, i.e., the interface at times ti and ti+1 (Figure 3a). From the 3D interface discrete geometry derived from XMT, the vectors normal to the reference surface S(ti) are calculated, then normal rays are projected until they intercept the second surface S(ti+1). The choice of the reference surface is important as propagation distances and directions depend intimately on the curvature of the interface [Sethian 1999].
Example of interface tracking during dissolution of a calcite crystal. (a,b) Internal views of the crystal at two time steps (initial and after 3 h of experiment); the solid is transparent and the mineral–fluid interface is in blue color. (c) Mapping of displacement vectors normal to the surface at t0.
In addition, the recession of an interface up to its complete disappearance (e.g., full mineral dissolution), the formation of a new interface (e.g., gas bubble nucleation), the displacement of a closed surface (e.g., solid particle), or the splitting of a given phase volume (e.g., oil ganglia formation) are examples that illustrate the difficulty for tracking some types of interfaces through time. In multi-phase fluid flow, especially, tracking the interface may be difficult because of the large number of interfaces and the large amount of deformation they experience. In that case, tomographic X-ray particle tracking velocimetry [Dubsky et al. 2012; Mäkiharju et al. 2021] techniques may be preferred to measure the fluid velocity and characterize flow more efficiently than XMT.
3.4. Digital volume correlation
Time-lapse XMT imaging produces series of volumes whose geometry may evolve with time due to deformation. Techniques have been developed to analyze the incremental strain between successive imaging experiments. When the deformation is large enough, for example when fractures form or pores collapse, a simple visualization and segmentation of the porosity or fracture voids makes it possible the quantification of volumetric strain in crystalline and porous rocks [Renard et al. 2018; Huang et al. 2019; Cartwright-Taylor et al. 2020]. However, in many experiments strain may be locally very small, and the local displacements are smaller than the voxel size.
In this case, digital volume correlation allows for calculation of the local displacements in pairs of images (Figure 4), which comprise a reference image and a deformed image [Bay et al. 1999; Lenoir et al. 2007; Hall et al. 2010]. The deformation field is obtained by optimizing a cross-correlation or a least-squares function that maximizes the matching accuracy between the grey scale intensity values of sub-volumes taken in the two images. Sub-volumes are typically of the order of 10 × 10 × 10 voxels or larger, such that they contain enough information about the sample microstructure, and the contrast for volume correlation is maximized. By identifying similar patterns across pairs of volumes, digital volume correlation produces three-dimensional incremental displacement fields from which the six independent components of the second rank three-dimensional incremental strain tensor may be calculated. These incremental strain fields reveal strain localization that occurred during the time interval between two imaging acquisitions. The calculation of the incremental displacement field is performed at the sub-voxel scale, typically in the range 0.01–0.001 voxel size.
(a) Concept of digital volume correlation where a pair of XMT images is used to calculate the incremental strain. The reference image is divided into subvolumes which are identified in the deformed image. The translation vector u and the strain corresponding to the deformation of the subvolume are calculated. (b) Two images of a porous andesite rock before and after deformation, and (c) resulting identification of a shear fracture with sub-voxel displacement. Adapted from Heap et al. [2020].
To characterize the resolution of strain values obtained from digital volume correlation analysis, and thus the lower limit of robust strain values, digital correlation analyses can be performed on the same volume (i.e., auto-correlation), or using two data sets for which the user expects no significant geometry changes (i.e., no strain), for example by imaging the same sample twice without changing the experimental conditions. The incremental strain field can be resolved with a strain resolution in the range 10−4–10−1, depending on the quality of the images. Other quantities may also be calculated, such as the divergence and the curl of the displacement field, the invariants of the strain tensor and the evolution of strain populations within a sample [Renard et al. 2019b], including recent developments based on machine learning techniques to unravel statistical correlations in the data sets [McBeck et al. 2020]. Several digital volume correlation open source codes are available to the scientific community [Tudisco et al. 2017; Yang et al. 2020a].
4. Applications to thermo-hydro-mechano-chemical processes
In the following sections, a brief overview of applications of 4D XMT in geosciences is given, with a specific focus on thermo, hydrodynamical, mechanical and/or chemical coupled (THMC) processes in the sub-surface.
4.1. Fluid flow and multi-phase flow
Flow in consolidated and unconsolidated porous media is a field that benefited a lot from XMT imaging, since the pioneering works of Spanne et al. [1994] and Coles et al. [1998] to extract the topology of the porous network and fluid-filled pore space following the displacement of oil by water. Since, an increasing number of multi-phase flow and gas trapping experiments during imbibition or drainage have been performed after doping fluids with contrast agents. Multiphase flow is central to a wide range of geological, industrial and environmental processes, including enhanced oil recovery, CO2 storage in geological reservoirs, water infiltration in soils, and groundwater contamination by non-aqueous phase liquid (NAPL) [Wildenschild and Sheppard 2013]. The first time-lapse images of fluid distribution were acquired with CT scanners [Vinegar and Wellington 1987; Wang et al. 1984] with a spatial resolution, however, insufficient to describe fluid partitioning within the pore space. In contrast, XMT imaging provides information at the pore scale. While the first XMT studies have limited themselves to about two sets of observations since fluid flow generates motion artifacts during acquisition [Culligan et al. 2004; Seright et al. 2002; Wildenschild et al. 2002; Turner et al. 2004], fast X-ray micro-tomography now allows for direct visualization of moving fluids in course of imbibition or drainage [Berg et al. 2013; Bartels et al. 2019]. In the studies, the dry or fully saturated sample is generally imaged first and then compared with time-lapse data sets showing the fluid distribution in the pore space.
Extensive experimental efforts have been put forward to relate the saturation and relative permeability curves during imbibition or drainage to pore-scale visualization of the fluid distribution [Porter et al. 2010]. Visualization provides all the information to unravel the complex interplay between the effects of capillarity, wetting, and viscous instability within the heterogeneous pore network. Compared to transparent micro-models developed to study multi-phase flow, XMT offers the possibility to work with real rock samples, whose pore space is often heterogeneous at many scales, from peloid or intraclast micro-pores, grain boundaries or clay fraction, to cm-scale vugs or large-scale fractures. Distribution of fluids between the rock micro- and macro-porosity can be quantified [Boone et al. 2014]. In addition, micro-models are unable to reproduce the complex fluid–rock interface properties, the wettability of mineral surfaces being an important factor governing the flow and trapping of the different fluid phases, e.g., water, oil or CO2.
Time-lapse imaging gives new insights in the dynamics of the fluid phases, including thin films formation, capillary trapping, fluid–fluid interface motion, interfacial curvature, Haines jump, occurrence of snap-off at the pore throats with formation of isolated ganglia, and pinch off and merging of interfaces [Brusseau et al. 2008; Reynolds et al. 2017; Voltolini and Ajo-Franklin 2019; Scanziani et al. 2018; Lin et al. 2018; Scanziani et al. 2020; Alhosani et al. 2020; Spurin et al. 2020; Alhosani et al. 2021; Kim et al. 2022]. Contact angles, which are important indicators of the wetting characteristics of a fluid-solid interface, can also be determined [Andrew et al. 2014b; Scanziani et al. 2017]. Measurements show a certain variability, explained by contact angle hysteresis during wetting phase advance or recession, and by grain surfaces of variable roughness.
The physics of capillary trapping can also be assessed. In the context of CO2 sequestration, the entrapment of a non-wetting phase through ganglia formation helps to immobilize CO2 in the pore space [Iglauer et al. 2011; Zuo et al. 2017], whereas it is detrimental to hydrocarbon production in the context of enhanced oil recovery. Snap-off occurs when a non-wetting fluid displaces a wetting fluid in pore-throat constrictions (Figure 5), leading to the breakup of droplets and formation of ganglia [Berg et al. 2013; Andrew et al. 2014a; Rucker et al. 2021; Singh et al. 2017; Tanino and Blunt 2012; Scanziani et al. 2020].
Visualisation of multi-phase flow in porous media at three different time steps (1 to 3), where snap-off events at narrow pore throats (red arrows) promote oil trapping (blue arrow) during imbibition; the solid is transparent and the oil phase is in orange-brown color. Reprinted from [Berg et al. 2013]. (Used with permission of PNAS, from Berg et al. [2013], Figure 5.)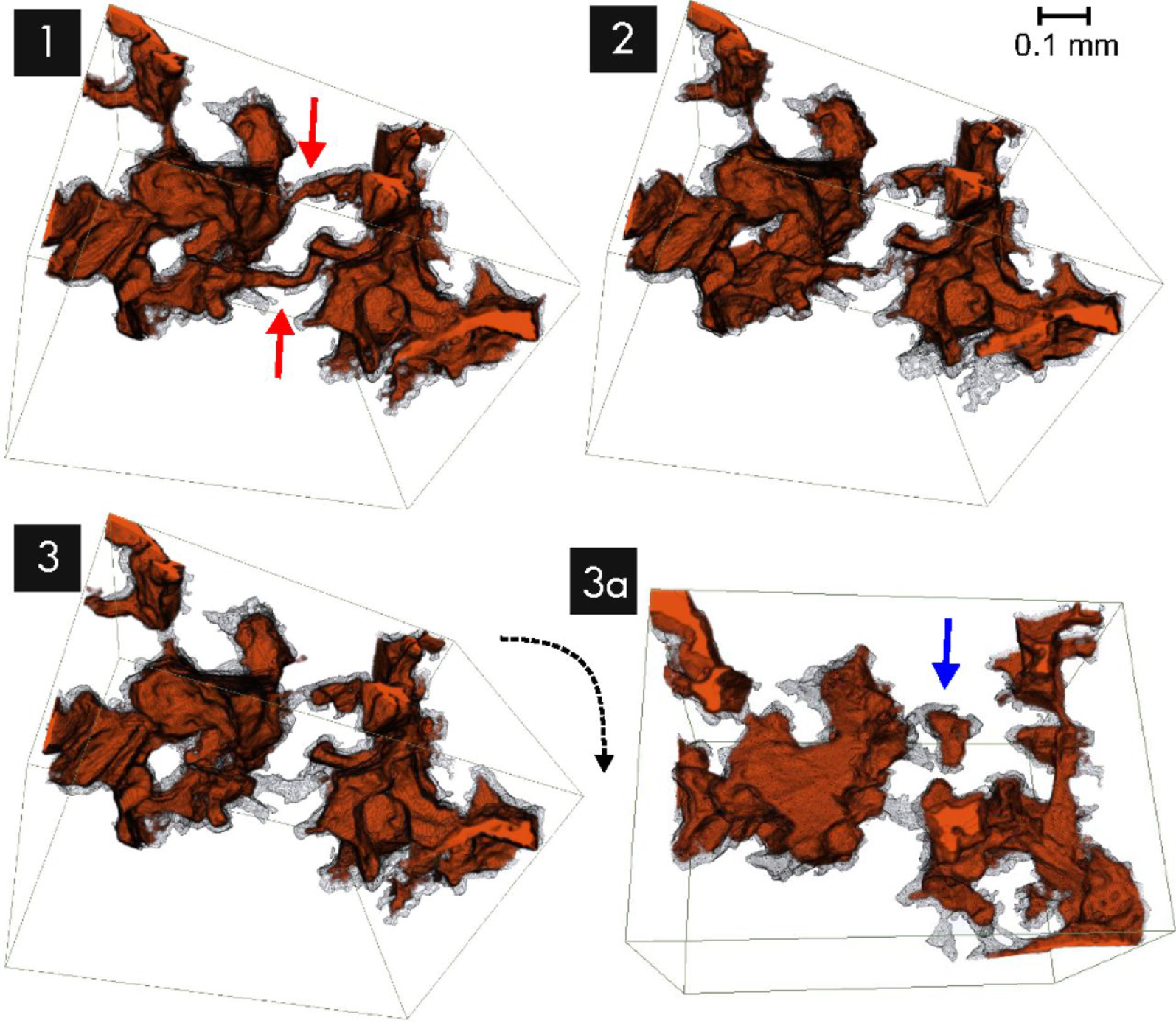
Minimization of the entrapment and enhancement of oil mobilization during enhanced oil recovery is possible thanks to a reduction of the capillary forces, through a decrease of the interfacial tension and alteration of the wettability. With this regards, the effect of low-salinity flooding or additives, e.g., polymers, surfactants or nanoparticles, to reverse the wettability of mineral surface from oil-wet to water-wet has been evaluated [Unsal et al. 2019; Singh et al. 2016; Rane et al. 2021; She et al. 2021; Javanbakht et al. 2017; Pak et al. 2018; Qin et al. 2020; Andrews et al. 2021]. The effect of gas injection, i.e., three-phase flow in either immiscible or near-miscible gas conditions has also been assessed [Alhosani et al. 2019]. The techniques can also apply to the in situ remediation of contaminated groundwater by NAPL [Pak et al. 2020]. Multi-phase flow has also been studied in fracture networks and the effects of fracture morphology on the distribution and transport of immiscible fluid phases has been investigated [Karpyn et al. 2007; Van Stappen et al. 2018]. More extreme conditions, with a case study relevant to magma migration in the Earth’s mantle deserves to be mentioned [Giovenco et al. 2021].
Fast X-ray micro-tomography has also benefited to tracer or colloid injection experiments in transient flow conditions [Bultreys et al. 2016; Van Offenwert et al. 2019; Molnar et al. 2015, 2016], complementary to larger scale studies of diffusive [Polak et al. 2003] or advective–dispersive transport that involved 3D imaging [Boon et al. 2016, 2017]. The experiments are based on the addition of a contrast agent in the tracer, e.g., iodine-rich brine or silver nanoparticles, compared to the fluid used initially to saturate the sample. First, calibration is performed by saturating and imaging the sample with the tracer at different concentrations, in order to correlate the tracer concentration to the grey level in the pore space. To alleviate random noise inherent to XMT, Van Offenwert et al. [2019] decomposed the pore space into individual pore bodies, then averaged the grey level over each pore body to retrieve the tracer arrival time and filling time through the porous network.
4.2. Mineral reactivity
XMT-based studies on mineral reactivity are emerging. They have focused on the reactivity of single crystals and minerals, or have explored coupled dissolution/precipitation processes or phase transformation in rocks and rock aggregates. XMT makes possible a detailed description of pore-scale fluid interface dynamics at the sub-micrometer scale (Figure 6), which is complementary to mass balance evaluation, atomic- or nanometer-scale evaluation of the interfacial properties, or numerical approaches using for instance a Kinetic Monte Carlo (KMC) model [Kurganskaya and Luttge 2016].
Visualisation of the fluid–mineral interface displacement during dissolution of a limestone aggregate at pH 4. The red square is 512×512 pixels in size, and the interface roughness is observed to decrease with time. Reprinted from Noiriel and Soulaine [2021]. (Used with permission of Springer, from Noiriel and Soulaine [2021], Figure 2).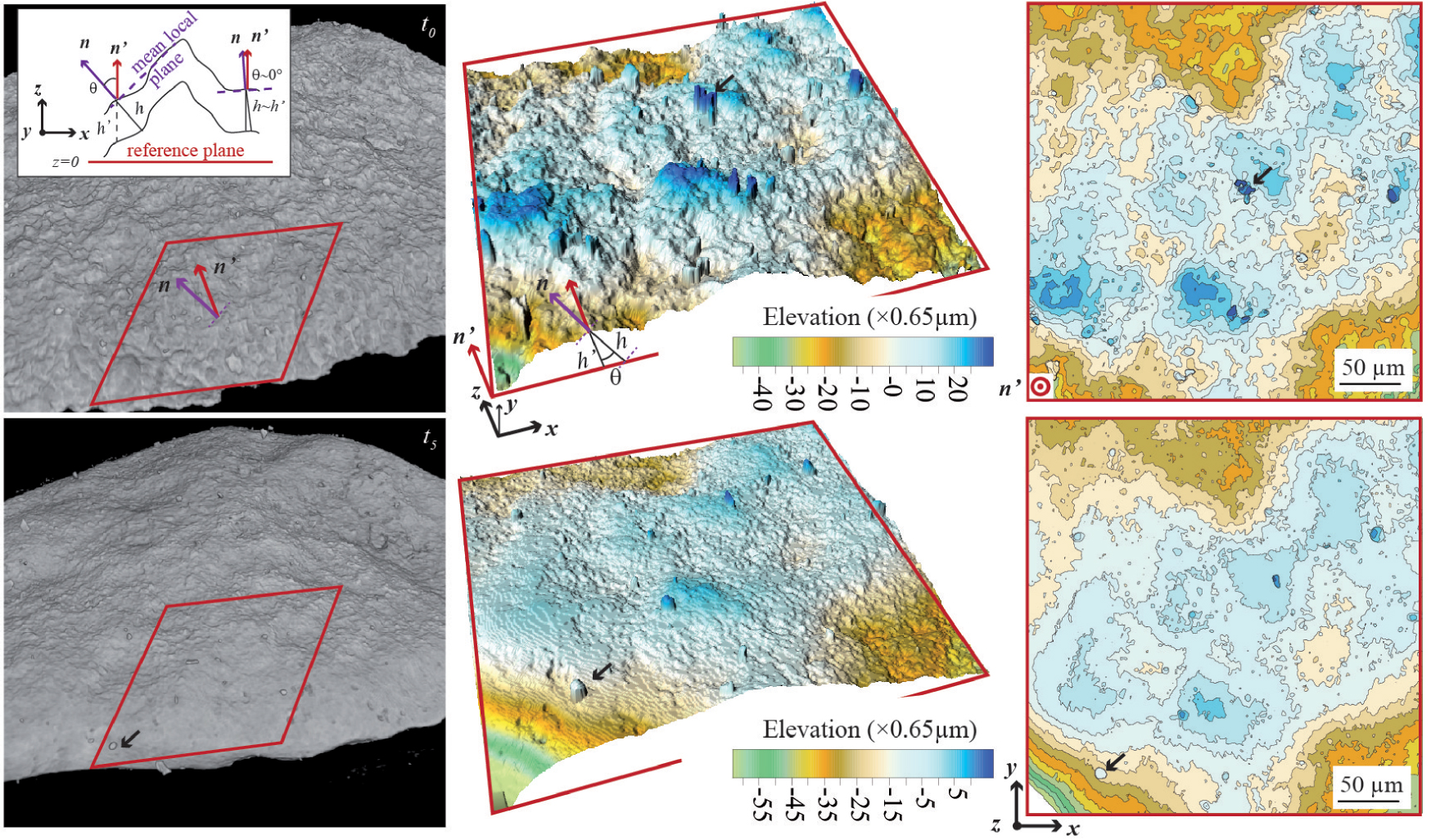
Pure diffusion or uniform flow field is assumed near the fluid–mineral interface, so that flow and transport effects can be decoupled from the intrinsic mineral reactivity. The density and the size of nuclei can be resolved in precipitation experiments [Yuan et al. 2021]. From image subtraction during crystal dissolution [Noiriel et al. 2019, 2020; Yuan et al. 2019], it becomes possible to calculate and map the retreat at the crystal surface, as well as the local reaction rate at any surface element, i.e., any pixel at the fluid–crystal interface (see for instance Noiriel et al. [2020] for more details about the procedure). The technique is complementary to classical methods measuring the surface retreat, e.g., atomic force microscopy (AFM) or vertical scanning interferometry (VSI) and extends the measurements in the third dimension. Therefore, it provides the dissolution rate distribution for a whole crystal, thanks to the unlimited depth of investigation of XMT. For instance, it is particularly suitable to investigate calcite dissolution under acidic conditions [Noiriel et al. 2019, 2020; Yuan et al. 2019], where dissolution is enhanced at the crystal corners and edges compared to the flat crystal faces, or to evaluate the poisoning effects of Pb2+ on the crystal morphology evolution and rate distribution [Yuan et al. 2019].
Leaching experiments of cementitious materials [Burlion et al. 2006; Rougelot et al. 2009; Bossa et al. 2015] or ore particles [Kodali et al. 2011; Gao et al. 2021; Eckley and Ketcham 2019; Ram et al. 2020; Lo et al. 2016] have also benefited of XMT imaging to explore the porous network structure evolution, derive rates at which these processes occurs, and in the latter case determine the extent of valuable mineral recovery.
XMT has also revealed the complex interplay during dissolution/precipitation coupled reactions or phase transformation, which are explored using either single crystals [Kim et al. 2021] or aggregates confined in pressure vessel. For example, Fusseis et al. [2012] and Bedford et al. [2017] have provided insights in the dehydration reactions during heating of gypsum (CaSO4, 2H2O) and subsequent transformation into bassanite (CaSO4, 0.5H2O), whereas Zheng et al. [2017] have investigated the hydration of periclase (MgO) into brucite (Mg(OH)2). Carbonation of olivine in the context of CO2 sequestration has also been explored [Zhu et al. 2016; Xing et al. 2018]. Especially, XMT is suitable to follow reaction fronts and evaluate the volumetric variations associated to these processes, e.g., creation or destruction of porosity.
4.3. Reactive flow
Mineral reactivity involves changes in the pore space architecture, thus affecting the flow and transport properties along the flow paths (Figure 7). The flow-through core holders described in Section 2 are useful setups for coupling visual examination of the rock geometry evolution to measurements of physico-chemical parameters like porosity, permeability, dispersivity or reaction rates. The first studies that benefited from 4D XMT focused on single-phase reactive flow experiments for modeling permeability evolution as a function of porosity, 3D pore geometry, and fluid–rock interface reactivity [Noiriel et al. 2005; Bernard et al. 2005]. Modelling of the flow and transport properties, as upscaling from the pore scale to the Darcy’s scale is another challenge linked to reactive flow experiments [Noiriel et al. 2012].
Visualisation of preferential precipitation of calcite in the main flowpaths of an artificial fracture grooved with two channels. The rock is a dolomitic limestone. (a) Initial aperture field derived from XMT; the sample was 50 mm in length and only the part close to the inlet is shown. (b) Aperture reduction after 16.7 days of reactive flow. Modelling of reactive flow in a model fracture geometry shows evolution of the fluid velocity (arrows) and local permeability (background color) between initial (t0) and final (tf) time. For more information about the experiment and modelling of reactive transport, see Noiriel et al. [2021].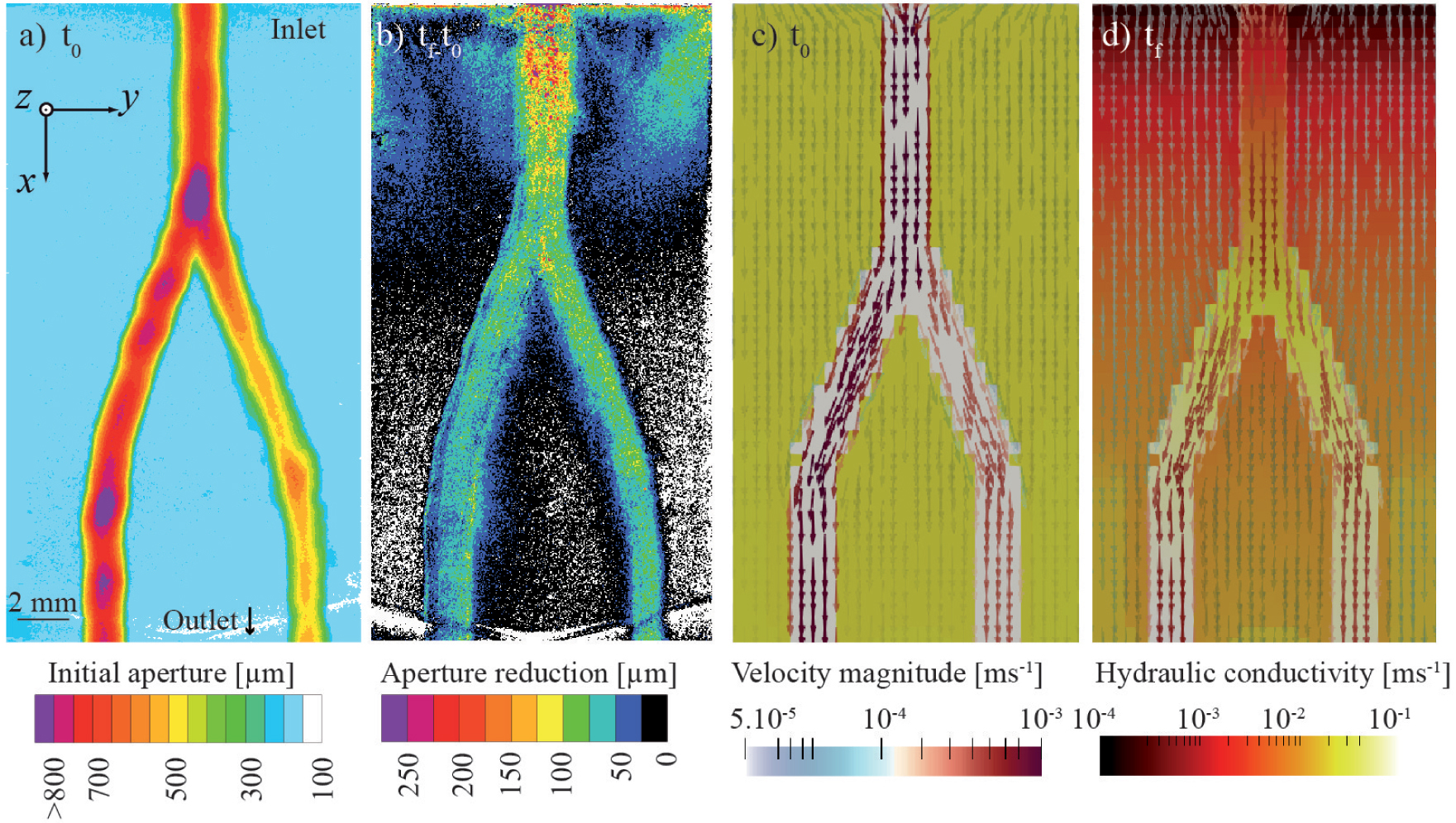
A specific attention has been paid over the last 20 years to the study of the fate of CO2 in porous and fractured rocks. Dissolution of CO2(g) into water, by acidifying aqueous fluids, should promote mineral dissolution near the injection wells, while precipitation of carbonated phases is expected further in the reservoir following the release of chemical elements and supersaturation with respect to carbonate minerals. Many experiments have been performed at different pressures, temperatures, partial pressures of CO2(g) and fluid compositions in various reservoir and cap rocks, including limestone, dolostone, sandstone, basalt, and shale. The impact of mineral reactivity to the porosity–permeability curves has been explored in relationship with microstructual modifications [Noiriel et al. 2004, 2005; Qajar and Arns 2022] or with the Péclet and Damkhöler numbers [Luquot and Gouze 2009; Noiriel et al. 2013; Menke et al. 2015, 2017a, 2018; Al-Khulaifi et al. 2017, 2018], two parameters that weight the relative contribution of advective to diffusive transport, and of the chemical reactions to transport, respectively.
The formation of preferential flow paths, from conical to highly ramified wormholes [Golfier et al. 2002] is not solely a function of the Péclet and Damkhöler numbers, and studies have also emphasized the geometry and the mineral or structural control of reservoir rock on the development of reaction fronts [Luquot and Gouze 2009; Smith et al. 2013; Luquot et al. 2014; Garcia-Rio et al. 2014; Qajar and Arns 2017a, b; Al-Khulaifi et al. 2019; Privalov et al. 2019; Menke et al. 2017b; Yang et al. 2020b; Leger et al. 2022]. Heterogeneities arise both from the pore space structure and from the chemical and mineralogical distribution of the solid phases. In particular, the rock textures combining highly reactive minerals (e.g., sulfates, carbonates) to low reactive minerals (e.g., silicates) promote unexpected behaviours during dissolution processes, like permeability reduction despite net dissolution [Gouze et al. 2003; Noiriel et al. 2007b, a; Ellis et al. 2013; Spokas et al. 2019].
Alteration of silicates, through of the release of cations (Ca2+, Mg2+, Fe2+) can promote precipitation when solution becomes supersaturated with respect to other mineral phases. Precipitation can be very local, homogeneous or highly heterogeneous at the pore scale depending of the fluid composition evolution within pores, and on the mineral surface energy for nucleation and growth [Noiriel et al. 2016]. Besides, the dynamics nature of crystal growth and mineral precipitation has been investigated in porous columns packed with glass beads and carbonates mimicking analogues of sandstone and limestone [Noiriel et al. 2012, 2016; Godinho et al. 2016; Godinho and Withers 2018], examining the role of bacteria-induced mineral precipitation [Wu et al. 2011]. Fractures have also been investigated to explore the role of precipitation on the reorganization of flow and transport [Menefee et al. 2020; Noiriel et al. 2021].
Soil physics and cultural heritage studies have also benefited from 4D XMT imaging. The effects of salinity on the evaporation rates in granular porous media [Rad et al. 2013], the pore structure change or the cracking dynamics and clay desiccation have been assessed [Keyes et al. 2016, 2017; DeCarlo and Shokri 2014; Dewanckele et al. 2012]. The studies have also pointed to the role of heterogeneities on transport and reactions processes. Thermal effects, studied through freeze–thaw cycling, permit to better link the crystallization-induced stress to the amount of pores filled by crystals [De Kock et al. 2015]. In most of the studies, mechano-coupling is also involved in the reactive flow processes.
4.4. Rock deformation and mechano-chemical coupling
Rock deformation experiments that use 4D imaging have opened a new era in rock physics and geomechanics to improve our knowledge of fluid-mediated and stress-controlled deformation mechanisms [Renard et al. 2004; Viggiani et al. 2004; Gratier et al. 2015; Macente et al. 2019]. With the development of triaxial deformation apparatuses installed on synchrotron beamlines, it is now possible to analyze several important geomechanical and geophysical processes. For example, the growth of microfractures prior to system-size failure in crystalline rocks are identified as an important process during the preparation phase of laboratory earthquakes (Figure 8). The evolution of the microfracture network when approaching failure was described as a critical phase transition [Renard et al. 2018; Cartwright-Taylor et al. 2020], characterized by a competition between dilation, compaction, and left-lateral and right-lateral shear [Renard et al. 2019a].
Evolution of a monzonite crystalline rock toward system-size failure under triaxial loading. The rock is represented in blue and grey shades and microfractures that developed during loading are in red. The sample, 5 mm diameter and 10 mm height, was under a constant confining pressure of 25 MPa and the axial loading, indicated above each image, was increased by steps until the sample failed, producing a laboratory earthquake. The final failure was preceded by the nucleation, growth, and coalescence of microfractures in the sample that represent precursors to the final catastrophic failure. See Renard et al. [2019a] for more information about the experiment.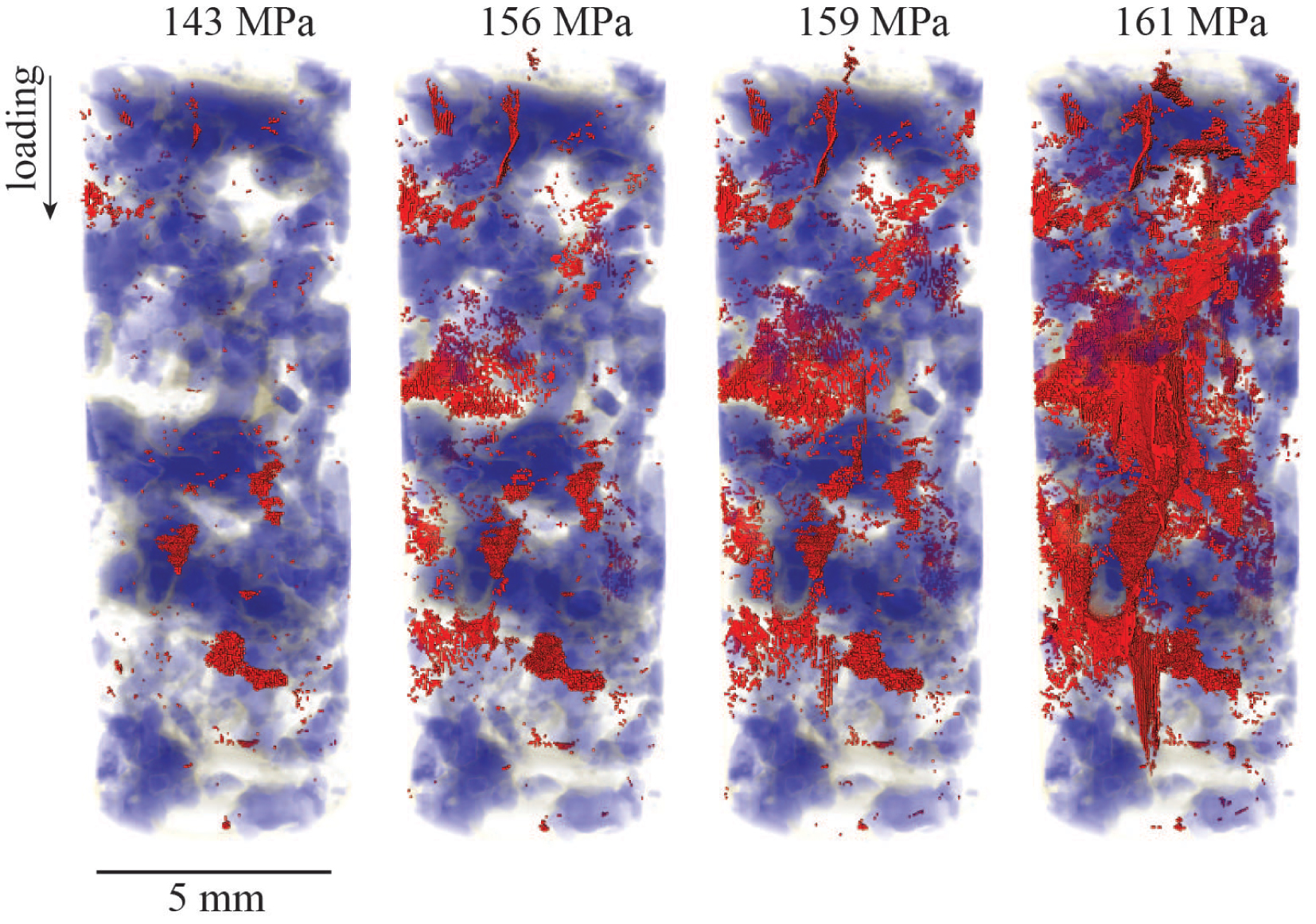
The impact of fluids on pore pressure buildup and rock damages, either fluids released from dehydration reactions [Marti et al. 2021] or fluids promoting hydration reactions [Voltolini and Ajo-Franklin 2020] have also been investigated.
In reservoir geology, how porosity evolves during reservoir compaction, shale maturation, and formation of faults controls permeability. These topics are highly relevant for hydrocarbon exploration, carbon dioxide or nuclear waste storage, and more generally transport of fluids in geological reservoirs and caprocks. XMT experiments have quantified the mechanisms of strain localization in porous sand and sandstones [Louis et al. 2007; Hall et al. 2010; Renard et al. 2019b], limestones [Huang et al. 2019], and shales [Lenoir et al. 2007; McBeck et al. 2018; Voltolini and Ajo-Franklin 2020; Voltolini et al. 2017]. Shale maturation was reproduced under in situ conditions to demonstrate that the heating of kerogen leads to the formation of microfractures and fluid expulsion. The mechanism that couples thermal, hydraulic, and brittle deformation processes controls the primary migration of hydrocarbon from the source rocks to the reservoir [Tissot et al. 1987] is now accessible using 4D XMT imaging [Kobchenko et al. 2011; Panahi et al. 2013; Saif et al. 2016].
5. Perspectives
Four dimensional XMT imaging has proved its relevance to unravel the complex evolution of minerals and porous and fractured rocks inherent to thermal, chemical, hydrodynamical or mechanical solicitations. The technique provides new insights in the THMC coupled processes occurring in the sub-surface.
The recent upgrade to fourth generation synchrotron facilities, such as the Extreme Brilliant Source at the European Synchrotron Radiation Facility (France) [Rack 2020], and the coming upgrades at the Advanced Light Source (USA), Spring-8 (Japan), and Swiss Light Source—to cite only the first ones—offers unprecedented opportunities to develop rock physics and flow dynamics experiments. X-ray sources ten to hundred times brighter and with a higher fraction of coherent photons than the third generation of synchrotrons open ways to real-time acquisition in the domain of Digital Rock Physics. Together with the construction of rotation stages that can carry loads of several hundreds kilograms [Cotte et al. 2019] and designed flow-through and triaxial cells for in situ imaging, these technology developments contribute to run experiments with unprecedented sample volumes (several cm3), pressures (up to 1 GPa) and temperature conditions (up to 500 °C), and to characterize processes that progress very quickly. Time limitation for multi-scan imaging or imaging of highly absorbent samples should be overcome, and it will be possible to perform 3D XMT scans at different sample distances or of dense materials within seconds. A remaining limitation may be how fast the sample can be rotated without interfering with the geological process studied, e.g. through the increase of centrifugal forces that could affect the fluid phase distribution.
Coupling 4D XMT imaging of geological processes with other imaging or monitoring techniques based on X-ray diffraction, X-ray fluorescence, X-ray grating interferometry, or acoustic emission tomography, becomes also possible, providing supplementary data about chemical composition, micro-porosity distribution, mineral phase distribution, characterization of phase transformation, and seismic processes. The increase in brightness and coherence also offers a major step towards multi-scale imaging of samples and processes.
Visualisation of the distribution of the fluid and solid phases in rocks, as evolution of the pore space, rock matrix and interfaces during thermal, flow, mechanical or geochemical reactions will offer in return unprecedented constraints for numerical modelling in multi-phase flow, geomechanics, geophysics or reactive transport domains, in order to unravel the processes at the core during thermo-hydro-mechanico-chemical solicitations of rocks.
For the first time, it is now possible, through both synchrotron technology developments and building of the next generation of core holders and rock deformation apparatuses, to image geological processes as they occur at depth. These developments will open a new era in several domains of geosciences where the study of rock evolution is necessary for progress on important societal challenges in the domains of georesources (geothermal energy, storage of energy and wastes), geohazards (earthquakes, landslides, volcanoes and glacier instabilities), and groundwater production.
Conflicts of interest
Authors have no conflict of interest to declare.
Acknowledgments
CN is very grateful to the Académie des Sciences for awarding of the Prize Michel Gouilloud-Schlumberger, and also thanks the Paul Scherrer Insitute for provision of synchrotron radiation beamtime at Swiss Light Source, TOMCAT beamline X02DA. FR acknowledges funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program (grant agreement No. 101019628 BREAK), the European Synchrotron Radiation Facility for provision of synchrotron radiation facilities, and Benoît Cordonnier for assistance in using beamline ID19.




 CC-BY 4.0
CC-BY 4.0