1. Introduction
In the last two decades, the advent of dense networks of seismic stations and the use of seismic noise to reconstruct Green’s functions between station pairs have opened up new possibilities for studying the internal structure of the Earth and its temporal evolution. Indeed, several theoretical studies have established that the correlations of random wavefields between two receivers yields the Green’s function of the medium between these two receivers, assuming that the wavefield is equipartitioned (see for instance Weaver and Lobkis [2001], Wapenaar [2004], Roux et al. [2005], Colin de Verdière [2006a, b], Sánchez-Sesma and Campillo [2006], Campillo [2006], Margerin and Sato [2011]).
This has led to a new interest in the study of seismic ambient noise. Indeed, the possibility to recover the Green’s function between (ideally) any pair of stations has been widely and successfully used to image the Earth’s structure [Shapiro and Campillo 2004; Shapiro et al. 2005; Sabra et al. 2005], and to monitor changes in seismic wave velocity resulting from the response of the Earth’s crust to seismicity and tectonic processes [Brenguier et al. 2008; Chen et al. 2010; Rivet et al. 2011; Zaccarelli et al. 2011; Froment et al. 2013; Soldati et al. 2015; Wang et al. 2019], as well as to environmental changes such as thermoelastic stress and precipitation [Sens-Schönfelder and Wegler 2006; Meier et al. 2010; Lecocq et al. 2017; Clements and Denolle 2018; Taira et al. 2018; Poli et al. 2020; Barajas et al. 2021; Vidal et al. 2021; Berbellini et al. 2021; Hillers et al. 2015; Wang et al. 2017; Mao et al. 2022].
The ideal case for retrieving Green’s functions would be to have a spatially homogeneous distribution of stationary noise sources and to average the noise correlations over a sufficiently long time interval. However, in practice, the long-period seismic noise comes from discrete locations and the noise field is neither isotropic nor fully equipartitioned. In other words, the ambient seismic noise does not fully satisfy the assumptions of the theory. Indeed, at periods greater than 1 s, the seismic noise is mainly generated by the interaction between the atmosphere, the ocean and the solid Earth by different mechanisms depending on the period considered, and it consists mainly of surface waves with a smaller amount of body waves [Toksoz and Lacoss 1968; Ekström 2001; Landès et al. 2010; Boué et al. 2013; Gualtieri et al. 2014].
In the 1–20 s period band, the seismic noise is dominated by two distinct energy peaks, the primary and secondary microseisms, which are observed globally. The primary microseism has periods similar to the main swell (10–20 s) with a maximum energy at about 14 s. It results from a direct interaction between the swell and the sea floor in shallow water [Hasselmann 1963]. The secondary microseism peak is more energetic and has -on average- a dominant period around 7 s. It is generated by the non-linear interaction of swell reflections near the coast or by swells propagating in opposite directions in the deep ocean that cause half-period (5–10 s) pressure variations [Longuet-Higgins and Jeffreys 1950; Hasselmann 1963; Ardhuin and Herbers 2013]. In this particular case, the pressure fluctuation in the water column does not present an exponential decay with depth, making it possible to generate seismic noise in deep water. For primary and secondary microseisms, the complexity of the noise field is increased by lateral variations in seafloor bathymetry and in the scattering properties of the crust that affect the ocean-solid earth coupling and tend to randomise the wavefield [Saito 2010; Ardhuin 2018; Lu et al. 2022].
In Europe, the use of seismic noise correlations for tomographic and monitoring studies has been supported by the development of permanent networks of stations across the continent complemented by the deployment of large and dense temporary networks such as IberArray and Pyrope in the Pyrenees, Cifalps I&II and AlpArray in the greater Alpine region [Díaz et al. 2010; Chevrot et al. 2014; Zhao et al. 2015; Hetényi et al. 2018; Paul et al. 2022].
Many authors have studied the origin of seismic noise in Europe in the 3–20 s period band. Several approaches have been used to investigate the sources of seismic noise on a continental scale using either distant arrays distributed across Europe [Essen et al. 2003; Chevrot et al. 2007; Juretzek and Hadziioannou 2016] or even seismic arrays on different continents [Friedrich et al. 1998; Stehly et al. 2006; Retailleau et al. 2017]. Other studies have instead focused on the origin of the noise at specific networks and locations [Pedersen and Krüger 2007; Beucler et al. 2015; Tanimoto et al. 2015; Craig et al. 2016; Lepore and Grad 2020; Guerin et al. 2022]. On the other hand, Lu et al. [2020] used a decade (2011–2019) of data collected at all European broadband stations to map lateral variations of the noise field properties. All these studies indicate that the north Atlantic ocean, in particular south of Greenland and off the coast of the British Isles and Norway, are the main sources of surface waves in the 3–20 s period band, with additional contributions from the Mediterranean coast (see for example Evangelidis and Melis [2012], Lu et al. [2022]).
Further development of imaging and monitoring methods based on noise correlations can be supported by a better understanding of the noise field and its variations in time and space. In particular, most studies to date have focused on the origin of microseisms at 3–20 s, and little is known about the generation of seismic noise at shorter periods (1–3 s). Gimbert and Tsai [2015] and Gal et al. [2015] have shown that seismic noise in the 0.5–2 s period band is mostly caused by local wind-waves occuring less than 2000 km of the seismic station rather than by the ocean swell like at periods greater that 3 s. Using three components array analysis at a dense array located in Pilbara, Autralia Gal et al. [2017] found that Rayleigh waves are more energetic than Love waves between 1.5–3 s, Rayleigh waves coming from convex coastlines, and Love waves from seafloor sedimentary basins. In addition to allowing the study of velocity changes associated with earthquakes [Maeda et al. 2010; Zaccarelli et al. 2011; Soldati et al. 2015], the 1–3 s period band is of particular interest for tracking changes in groundwater levels, providing a unique opportunity to monitor the response of the crust to the hydrological cycle [Poli et al. 2020; Barajas et al. 2021].
Unlike previous studies of the seismic noise in Europe, we do not aim at investigating the origin of the seismic noise per se. Instead, our aim is to study how lateral variations of the noise field affect the speed of convergence of the noise auto-correlations coda waves and thus the possibility of monitoring velocity changes in the Earth’s crust. Indeed, we may wonder how the temporal resolution of monitoring studies is affected by the dynamics of seismic noise sources? In particular, at the European scale, do autocorrelation coda waves converge everywhere at a similar rate, or are there lateral variations that are due either to different scattering properties of the crust or to the dynamics of the seismic noise sources?
To answer these questions, we first study the origin of the seismic noise and its seasonal variations around 2 and 7 s of periods. We then introduce a proxy to quantify whether the seismic noise is stationary (Section 3). This allows us to characterise the dynamics of the short-period seismic noise at the European scale. This makes it then possible to study the relationship between the dynamics of the seismic noise and the convergence speed of the auto-correlations coda waves (Section 4). We highlight the influence of seasonal variations of the contribution of the Atlantic Ocean and of the particular dynamics of the Adriatic and Aegean seas that influence the reconstruction of coda waves. Finally, this allows us to show that the temporal resolution and the accuracy with which it is possible to measure velocity changes at short periods exhibit lateral variations across Europe. Our results shows that there is a strong contrast between southern and northern Europe, depending on whether the influence of the Adriatic/Aegean Sea or the Atlantic Ocean dominates.
2. Average noise wavefield in Europe
2.1. Data used
We use all broadband stations with publicly available data in Europe in 2021 located between −5 and 31 degrees of longitude and between 34 and 53 degrees of latitude. To complete the stations coverage in the Pyrenees, we included the temporary networks Pyrope (X7, 2011–2013) and IberArray (IB, 2009–2011). We thus use data from 47 European networks and 1960 stations for which we have at least 300 days of data. The stations map is presented in Figure 1. We represent with red triangles the stations with data in 2021, with blue triangles the IberArray network and with yellow triangles the Pyrope network.
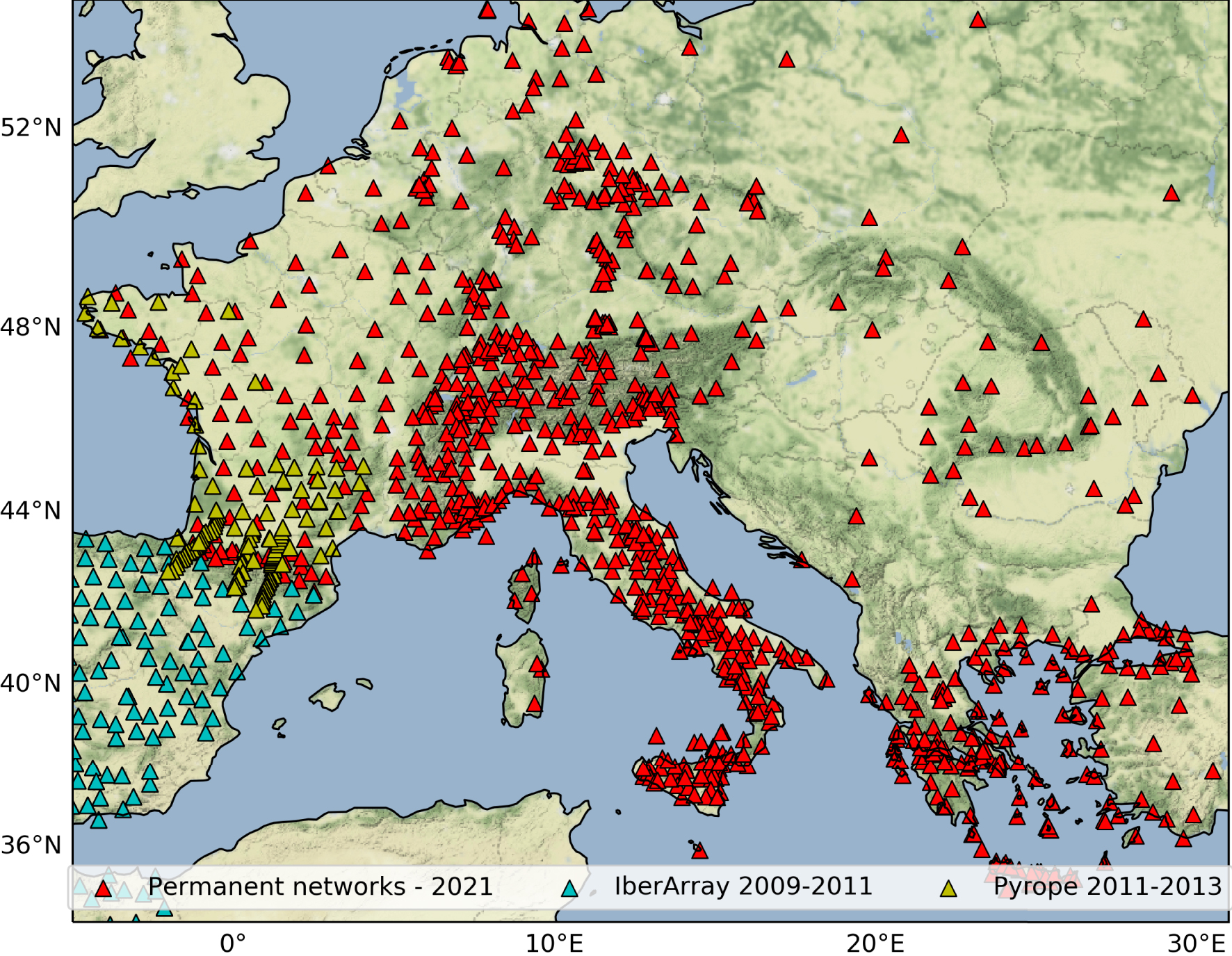
Map of the broadband seismic networks used in this study including permanent networks for which we use continuous noise records from 2021 (red triangles), the IberArray network (2009–2011, blue triangles) and the Pyrope network (2011–2013, yellow triangles).
2.2. Median level in Europe
To study the average noise level across Europe and its seasonal variations, we use an approach inspired by McNamara and Buland [2004] by analysing continuous waveform data without removing any signal such as earthquakes or instrumental glitches. We processed the vertical records of each station day by day. Each daily record was band pass filtered between 0.5 s and 300 s, corrected from the instrumental response, decimated to a sampling frequency of 5 Hz. For each station and for each day of data we compute Power Spectral Densities (PSD) with a sliding window of one hour with no overlap. A 10% cosine taper is applied to both ends of each 1 h segment to suppress the effect of side lobes in the Fast Fourier Transform. The PSD of each 1 h segment is obtained from the FFT of the seismic data. Finally the PSDs are converted into decibels with respect to velocities.
To obtain the median noise level at each station as a function of the season, we compute for each station the median noise level for January–February (winter) and July–August (summer). We remind the reader that we used data from 2009–2013 from the IBerArray and the Pyrope temporary network in the Pyrenees, and from 2021 elsewhere (see Figure 1). We use specifically the median rather than mean to reduce the contribution of large amplitude events such as earthquakes and glitches. The median noise level obtained during the winter and the summer at 2 s and 7 s of periods are presented in Figure 2. The noise level depends mainly on the distribution and energy of noise sources and on the attenuation of seismic wave during their propagation. It is also influenced by the scattering of waves by crustal heterogeneities and topography [Wu and Aki 1985; Snieder 1986; Levander 1990]. In addition, sedimentary basins affect the wave field in complex ways, amplifying certain frequency ranges [Sánchez-Sesma et al. 1988; Boué et al. 2016; Gisselbrecht et al. 2023].
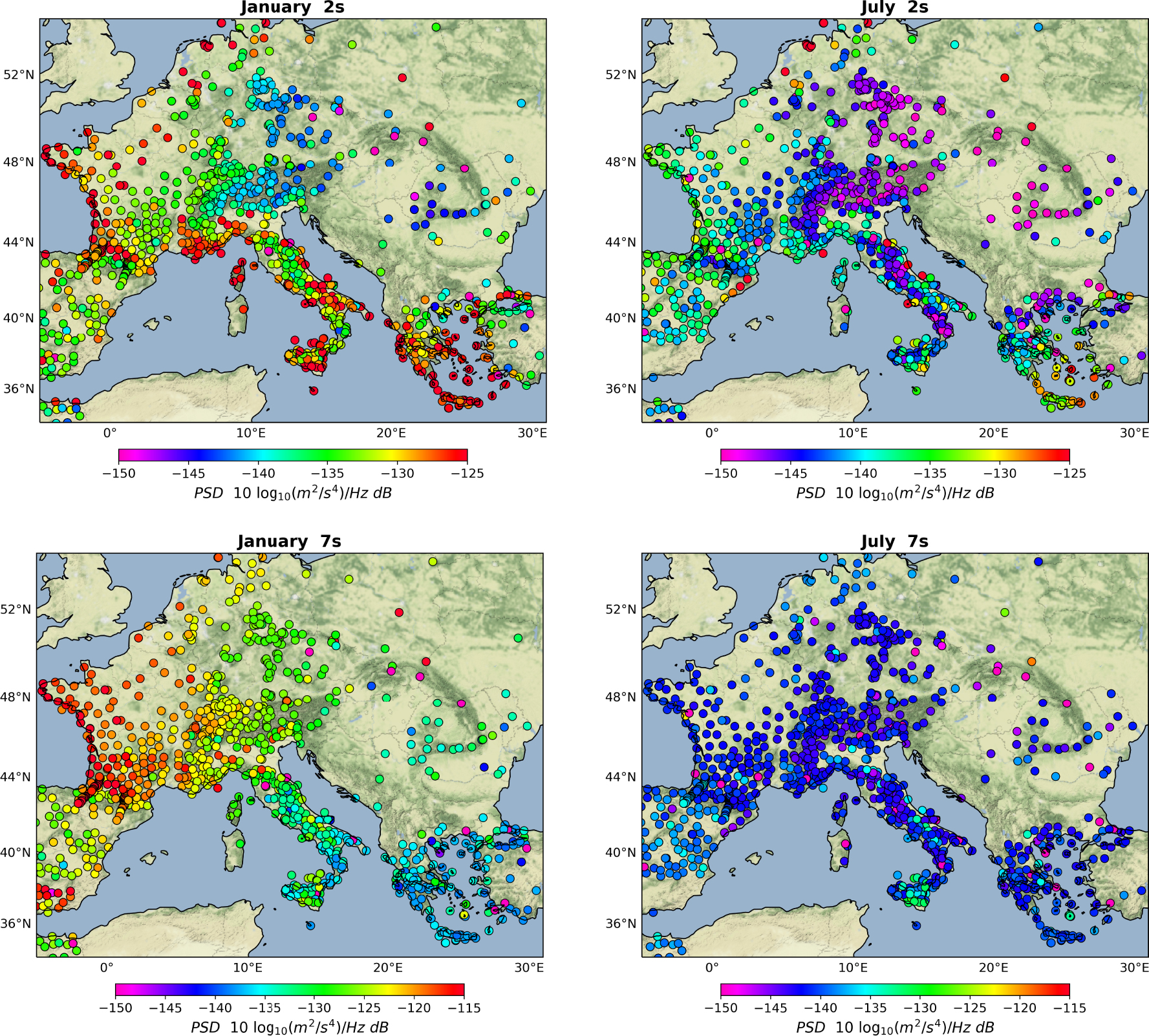
Spatial distribution of the median noise level at 2 s and 7 s of period in January (left) and July (right).
As shown on the lower panels in Figure 2, at 7 s in January we observe a large-scale variation of the median seismic noise level across Europe. The noise level is maximum on the west coast of France (−115 dB) and it decreases progressively towards the southeast, the minimum being reached in Greece (−140 dB). This noise level gradient is consistent with a dominant noise source located in the north Atlantic ocean as it was previously observed by various studies [Friedrich et al. 1998; Stehly et al. 2006; Chevrot et al. 2007; Kedar et al. 2008; Retailleau et al. 2017].
On the other hand, during the month of July we observe an almost homogeneous noise level in Europe, with a median level of −140 dB. This illustrates that at 7 s of period the noise level in Europe varies strongly depending on the season, the noise level being higher during the winter in the northern hemisphere when the wave height is larger in the north Atlantic ocean.
We observe that the seismic noise level differs strongly at 2 s period, indicating that the distribution of seismic noise source is not the same at 2 s and 7 s of period (Figure 2). In January at 2 s of period, the noise level is maximum on the coast reaching −125 dB on the west coast of France, southeast France, and in southern Greece. Conversely, the noise level decreases towards the East (and not towards the southeast as it was the case at 7 s of period) when moving away from the Mediterranean and Atlantic coasts. Thus, the minimum median noise level is reached in Romania (−145 dB). This indicates that the seismic noise is mainly generated locally near the Atlantic and Mediterranean coasts.
Just as at 7 s of period, the median noise level at 2 s exhibits clear seasonal variations, the noise level decreasing in the summer. However the lateral variation of the seismic noise level remains similar during the summer and the winter. Thus in July the median noise level range reaches −135 dB in the west part of France and Spain and decreases towards the East becoming less than −145 dB past Switzerland.
In addition to this West–East gradient, we note that in Italy the noise level is larger towards the Mediterranean and the Adriatic coast (about −140 dB) than in the Apennines (−147 dB). This observation is compatible with a generation of seismic noise along the coasts. Similarly, high noise levels are also observed in Greece (for example, the Cyclades).
To summarise, the noise level maps show that the origin and the seasonal variations of the micro-seismic noise differ at 2 s and 7 s of period. At 7 s, the median noise level is consistent with a dominant noise source located in the north Atlantic ocean, while in the summer the homogeneity of the noise level indicates a distant origin, probably with a significant contribution of the southern hemisphere. On the other hand, there is no clear local maximum near the coasts that would indicate a local coupling. This seasonal variation implies that the quality of the Green function retrieved from cross-correlation may differ during the summer and the winter. Hence for tomographic studies, simultaneously using data recorded during winter and summer is a common way to improve the quality of the traveltime measurements performed on noise correlations. For monitoring applications, it implies that the precision of the δv∕v measurements may depend on the season.
Conversely, at 2 s of period, the lateral variations of the seismic noise are similar in January and July suggesting that the sources are always located in the same areas. In January as well as in July the maximum noise levels are reached in specific regions along the coasts, hence indicating local coastal noise sources. This is consistent with theoretical expectations: at 2 s of period the primary and secondary mechanism can generate seismic noise in shallower water than at 7 s [Longuet-Higgins and Jeffreys 1950].
2.3. Dominant periods in the 2–10 s period band
Figure 3 shows a spatial map of the dominant period of the seismic noise measured in the 2–10 s period band corresponding to the secondary microseism. It represents the period at which the median PSD of the seismic noise record is maximum. The median PSD is defined as the median of the PSDs computed with a one-hour sliding window. If the noise originated from a single region, and assuming a constant quality factor across Europe, the dominant period of the noise should increase smoothly with distance from the source [Lu et al. 2022]. However, this is not what we observe in either January or July (Figure 3) between 2–10 s, the seismic noise is influenced by two distinct source regions located in the north Atlantic and in the south-east Mediterranean. Thus the spatial distribution of the dominant period results from the interaction between these two source areas. This interaction is itself dependent on the season.
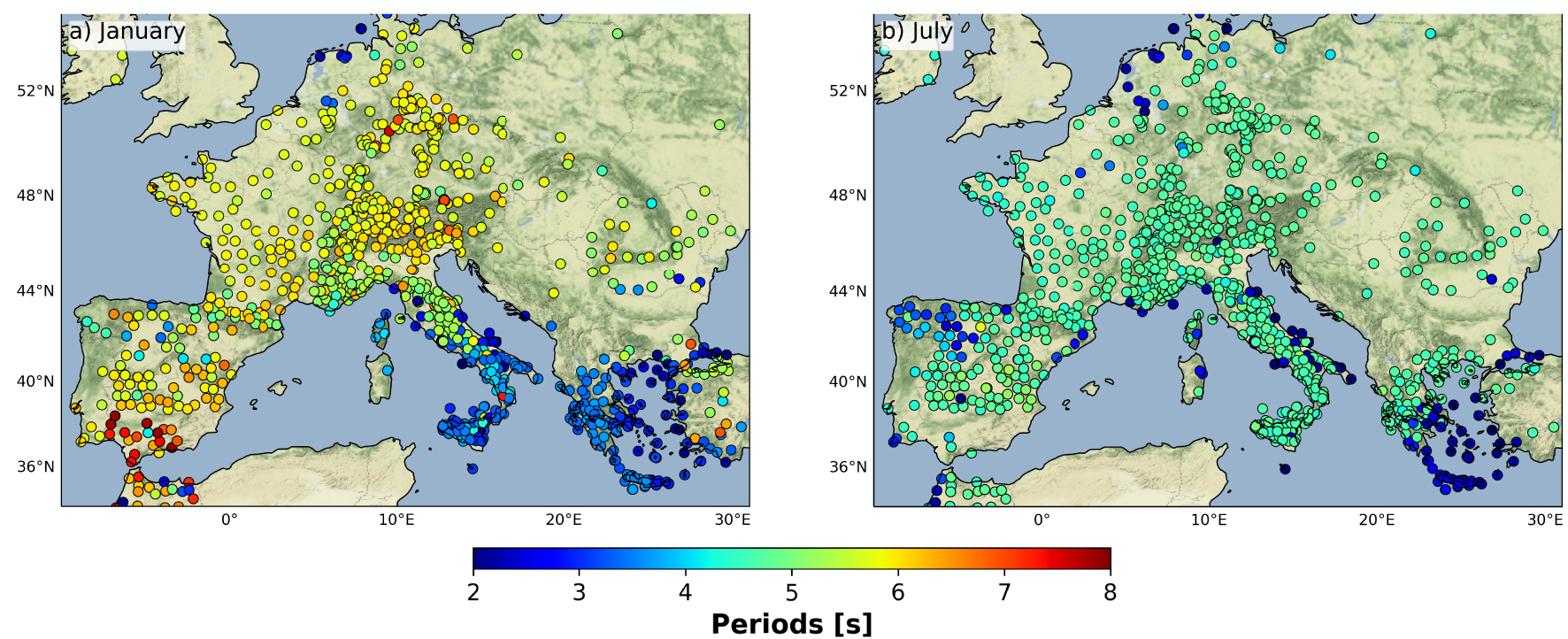
Spatial distribution of the dominant period of seismic noise: period at which the median PSD of the seismic noise is maximum in (a) January and (b) July. The median PSD is defined as the median of PSDs computed with a sliding window of one hour that is shifted by 5 min.
In January (Figure 3a), the dominant period is 6 s in northern Europe (France, Germany, Switzerland). It decreases progressively towards the south-east to about 5 s in northern Italy. This would be consistent with a dominant source located in southeastern Europe. However, we note an abrupt change between northern Italy and southern Italy where the dominant period is less than 3.5 s. In Greece values lower than 3 s are observed around the Aegean Sea. These observations are consistent with a dominant noise source in the south-east Mediterranean explaining the north-west/south-east gradient of the dominant period, with moreover a short-period noise source close to the southern Italy coastline explaining the abrupt change observed in Italy.
In July, the spatial distribution of the dominant period is completely different (Figure 3b). We observe a shift toward shorter periods, with a dominant period of 5 s throughout Europe with 3 exceptions: in southern Greece, near Galicia (Spain) and at several stations on the Italian, French and Spanish coasts, the dominant period is less than 3.5 s. This suggests that short period microseismic noise is generated locally close to in these areas.
These observations have two implications for monitoring studies: the seasonal behaviour of the seismic noise does not guarantee that noise correlations coda waves converge to a similar waveform in summer and winter and as we will see in the next sections the coda of correlations in coastal regions dominated by a 2 s period in summer converges more slowly.
3. Dynamic of the noise wavefield in Europe in the 0.5–0.7 Hz frequency band
In the previous section we presented the noise level in Europe at 2 s and 7 s and the dominant period of seismic noise records. In the present section we study the dynamics of the seismic noise and its temporal evolution specifically in the 0.5–0.7 Hz frequency band. We choose specifically to focus on this frequency band since it is often used to monitor the temporal evolution of the crust using seismic noise correlations in particular for tracking groundwater level change [Poli et al. 2020; Barajas et al. 2021]. Moreover, little is known about the generation of seismic noise in the period band, since previous studies on the secondary micro-seismic noise tend to focus on the 3–20 s period band. We use only European networks for which we have continuous record in 2021, and we thus discard the data of the IberArray and Pyrope experiments.
3.1. Quantifying the stationarity of the wavefield
Our goal is to quantify the impact of the dynamic of the seismic ambient noise on the convergence of coda waves obtained from noise correlations. To that end, in this section we define a proxy to quantify whether the seismic noise is stationary or not. We look for a proxy that does not depend on the amplitude of the seismic noise, since a change of noise level per se does not modify the waveform of the correlations. Instead, we design a proxy which depends only on the temporal evolution of the frequency content of the seismic noise.
To define this proxy, we first compute at each station PSDs with a 30 min sliding window which is shifted by 5 min. These 30-min PSDs are then used to quantify the temporal evolution of the frequency content of the seismic noise over several time scales ranging from 1 day to 30 days, independently of the amplitude of the seismic noise. We thus define a stationarity coefficient (SC) obtained in the following way:
- Each 30 min PSD is smoothed over frequency using a moving average gaussian filter having a width of 0.05 Hz. We thus study specifically the first order variations of the frequency content of the noise.
- Each 30 min PSD is then normalised by its energy in the target frequency band, i.e. 0.5–0.7 Hz.
- At each date, we define the current PSD as the PSD computed with a 30 min window that ends at the current date, and the N-days PSD as the PSDs averaged over the previous N-days, with N ranging from 1 day to 30 days. We then compute the normalised correlation coefficients of the current PSD and each N-days PSD. We note that this correlation coefficient is independent of the noise level and depends only on temporal evolution of the frequency content of the noise.
- Finally, we define the stationarity coefficient for each 30 min window as the lowest coefficient of correlation between the current and the N-days PSDs. A stationarity coefficient close to 1, indicates that the current 30 min PSD is similar to the PSDs averaged over the previous N days, i.e. that the noise is stationary over all time scales. A value close to 0 indicates that the current PSD differs strongly from at least one of the PSD averaged over the N previous days, i.e. that the frequency content of the noise is not stationary on at least one time scale.
3.2. Stationarity coefficient at a single station in Italy
Figure 4 shows as an example the stationarity coefficient measured in the 0.5–0.7 Hz frequency band at the station NRCA located close to Norcia in Italy from June 6th to June 30th. As shown on the upper panel, the stationarity coefficient typically varies between 0.96 and 1 which reflects the usual variability of the frequency content of the seismic noise. In addition to these variations, we observe several events on June 14, 15, 18 and 30 during which the stationarity coefficient drops to values below 0.94 for a few hours.
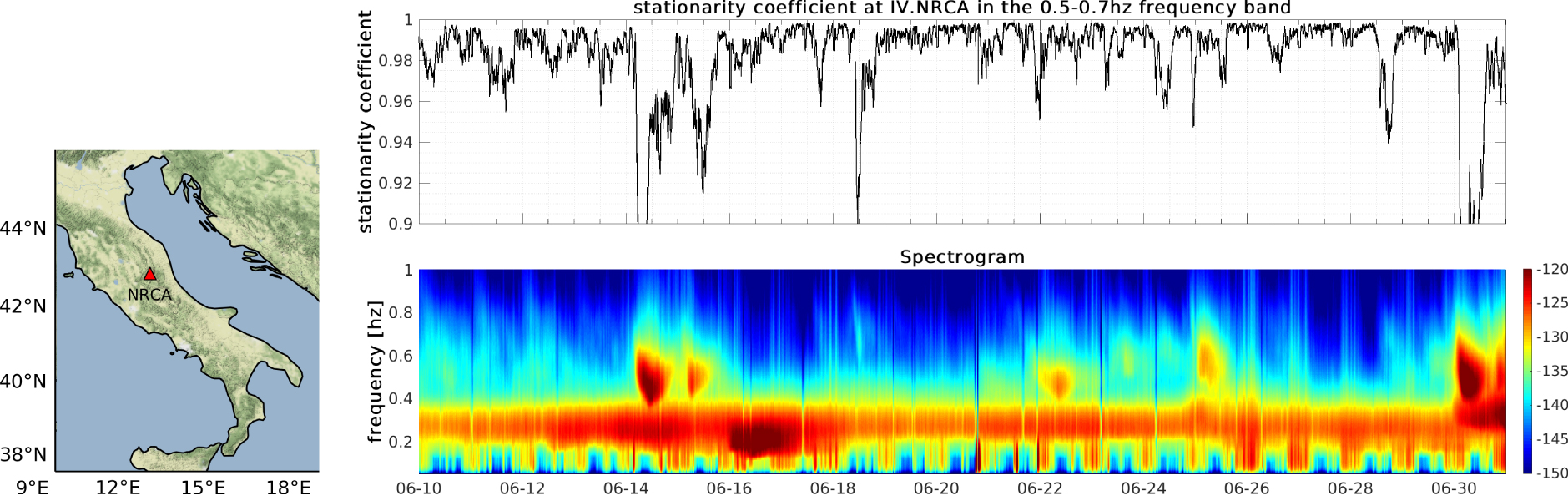
(Left) Map showing the location of the NRCA station located in Norcia, Italy. (Right, upper panel) Stationarity coefficient measured at the station NRCA in the 0.5–0.7 Hz from june 6th to June 30th. (Right, lower panel) Spectrogram in dB measured at the station NRCA in the 0.05–1 Hz frequency band on the same date. The 0.5–0.7 Hz frequency band where the stationarity coefficient is measured is shaded in gray. The dates of type I and type II events are indicated by red and white marks. Masquer
(Left) Map showing the location of the NRCA station located in Norcia, Italy. (Right, upper panel) Stationarity coefficient measured at the station NRCA in the 0.5–0.7 Hz from june 6th to June 30th. (Right, lower panel) Spectrogram in dB measured at ... Lire la suite
Looking at the spectrogram presented on the lower panel in Figure 4, we can correlate changes in the stationarity coefficient with changes of the frequency contents of the noise. We first observe that in central Italy, the seismic noise has a maximum of energy between 0.2 and 0.4 Hz which corresponds to the secondary microseismic peak. This peak of energy is continuous in time. Above 0.4 Hz,—apart from particular events—the energy of the noise decreases continuously with frequency. In addition to this average behavior, we observe two kinds of microseismic events:
- The first type of events are characterised by a clear increase ( ∼5–10 dB) of the noise level above 0.4 Hz. This occurs on June 14, 15, 22, and 30. These events modify the decay of the noise level with frequency measured between 0.5 and 0.7 Hz, and are thus associated with a drop of the stationarity coefficient which become less than 0.94 (Figure 4 upper panel).
- On June 18th we observe a second kind of event: a local maximum of energy appears between 0.5 and 0.8 Hz, the noise level remaining in the usual range. This type of event, characterized by a first order change in the shape of the spectrum but without a significant change in noise level, is associated with a sharp drop in stationarity coefficient which become less than 0.9.
This example illustrates that the stationarity coefficient computed in the 0.5–0.7 Hz allows us to distinguish the usual fluctuations of the frequency content of the seismic noise (SC > 0.96) from discrete events lasting a few hours (SC < 0.94) corresponding to either (1) microseismic events characterized by a sharp increase in the noise level between 0.4–0.6 Hz, or (2) to a first order change in the shape of the spectrum.
3.3. Stationarity coefficient maps for two particular events
In this section we quantify the spatial extent of the noise wavefield perturbations that were introduced in the previous section. We would like to know if they are detected at the scale of Europe, or if on the contrary they are located in a particular region. To that end, we look at the spatial distribution of the stationarity coefficient for the events of June 30th and June 18th that were discussed in the previous section.
3.3.1. Stationarity coefficient map for the June 30 event
The first event that occurred on June 30th was detected along the Adriatic coastline as shown in Figure 5. The lower panel in Figure 5 shows the seismic noise recorded at the station IV.NRCA located in central Italy (see Figure 4) filtered in the 0.5–0.7 Hz frequency band. The time series runs from June 29 to July 2. The amplitude of the seismic noise increases by a factor of 3 from June 30 to July 1 compared to the noise level of June 29th. This change in amplitude observed in the time domain is also visible in the spectrogram computed at the same station (Figure 5, third panel): in addition to the secondary microseismic peak visible at 0.2–0.4 Hz, an increase in energy is observed between 0.4 and 0.7 Hz from June 30 to July 2.
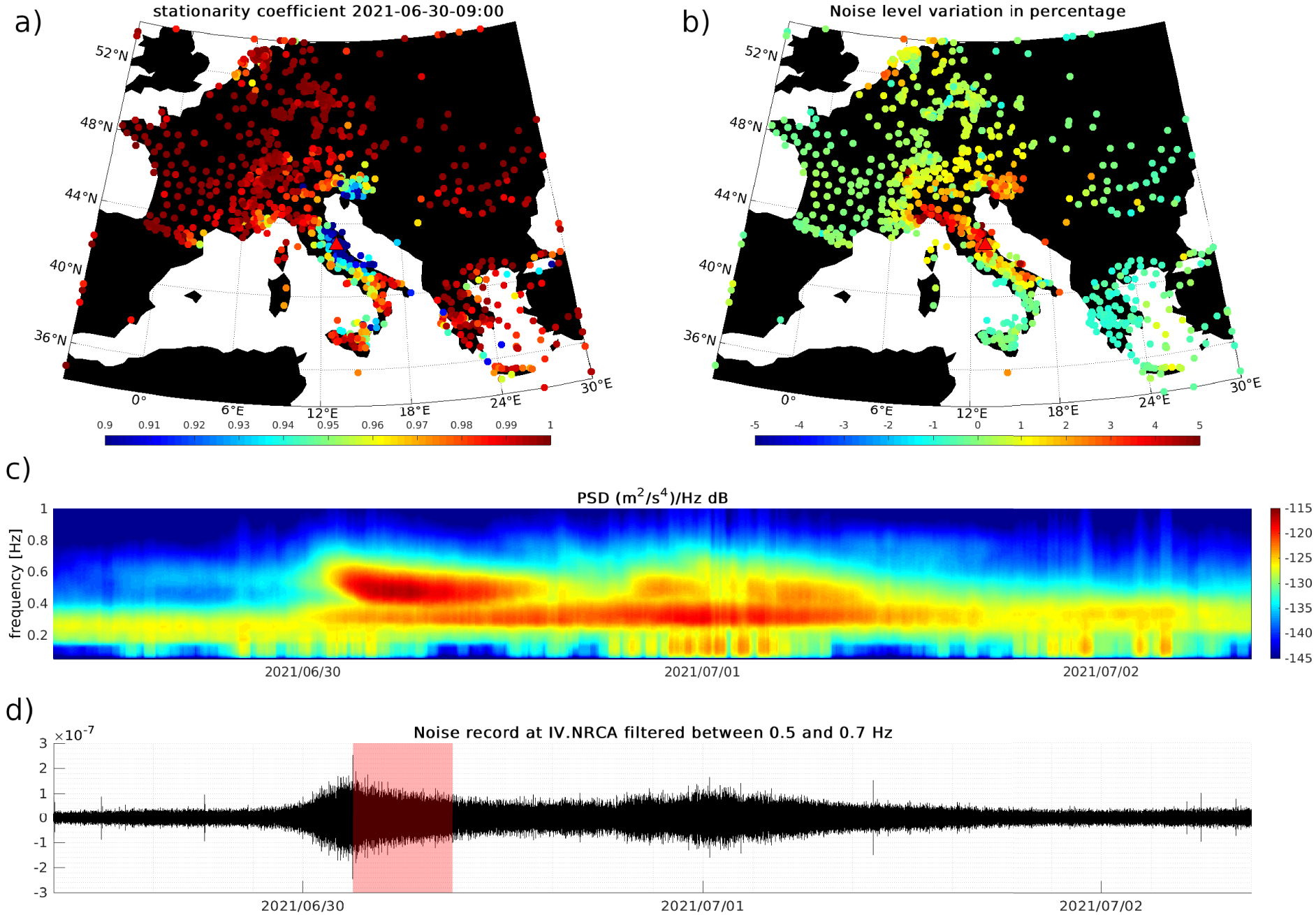
Detail of the June 30 microseismic event. (a) The spatial distribution of the stationarity coefficient measured between 0.5 and 0.7 Hz on June 30, averaged from 6:00 a.m. to 9:00 a.m. (b) Map of the relative change in the percentage of the average noise level on June 30 between 3:00 a.m. and 9:00 a.m. compared to the average noise level of the last 10 days. (c) Spectrogram in dB computed at the station NRCA located in central Italy from June 29 to July 2 with a sliding window of 30 min shifted by 5 min. (d) Vertical noise record at the station NRCA filtered between 0.5 and 0.7 Hz from June 29 to July 2. Masquer
Detail of the June 30 microseismic event. (a) The spatial distribution of the stationarity coefficient measured between 0.5 and 0.7 Hz on June 30, averaged from 6:00 a.m. to 9:00 a.m. (b) Map of the relative change in the percentage of the ... Lire la suite
In order to see which European stations are affected by this event, we present in Figure 5a, the value of the stationarity coefficient of June 30, 2021 averaged between 3 to 9 a.m. We note that over the whole of Europe the stationarity coefficient is greater than 0.97 except around the Adriatic Sea, in particular in Italy and Slovenia where we obtain values lower than 0.95. This indicates that this event originates from the Adriatic Sea.
This event is also associated with an increase in noise level between 0.4 and 0.7 Hz. Figure 5b shows the difference between the measured noise level measured on June 30, 2021 between 3:00–9:00 a.m. and the noise level averaged over the past 10 days. This difference is expressed as a percentage. Across Europe the noise level is similar on June 30 and the previous 10 days, with the exception of the stations located around the Adriatic Sea in Italy and Slovenia where the noise level increases by more than 3%.
To summarize, this microseismic event lasted almost 2 days and induced a change in noise level and in the frequency content of the noise detectable locally around the Adriatic Sea in Italy and Slovenia, but not elsewhere in Europe.
3.3.2. Stationarity coefficient map for the June 18 event
The second event occurred on June 18th around 4 p.m. In contrast to the previous example, it is not associated with a significant change in the amplitude of the noise level at station IV.NRCA (Figure 6, bottom panel). As shown in the spectrogram in Figure 6, usually between 0.6 and 0.8 Hz, the noise energy decreases with frequency, except on June 18 when a local maximum of energy is observed. However, the absolute noise level varies little, the noise level being about −135 dB on June 18 compared to −140 dB on the other days.
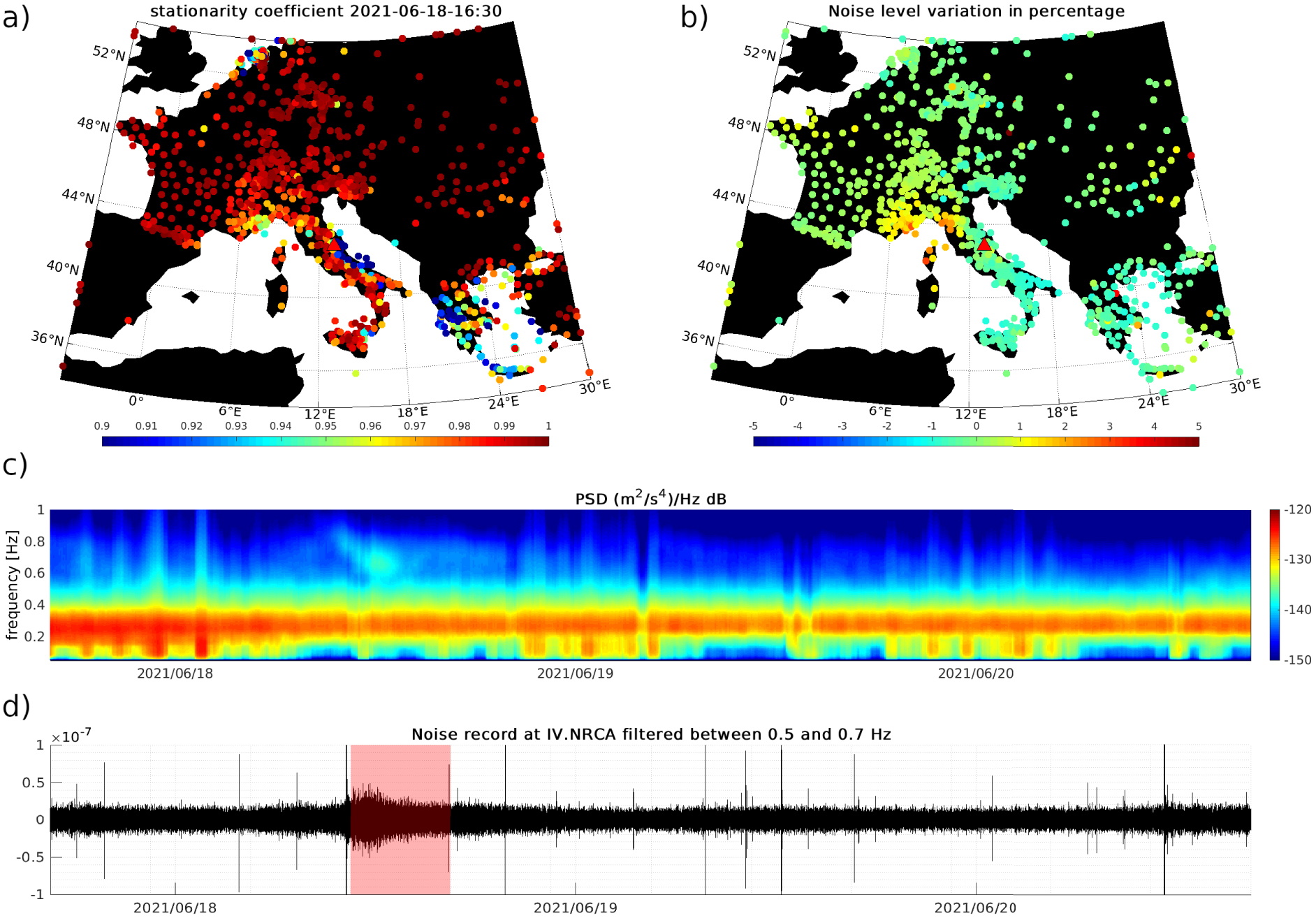
Detail of the June 18 microseismic event. (a) The spatial distribution of the stationarity coefficient measured between 0.5 and 0.7 Hz on June 18, averaged from 13:30 to 16:30 a.m. (b) Map of the relative change in the percentage of the average noise level on June 30 between 10:30 and 16:30 a.m. compared to the average noise level of the last 10 days. (c) Spectrogram in dB computed at the station NRCA located in central Italy from June 17 to June 20 with a sliding window of 30 min shifted by 5 min. (d) Vertical noise record at the station NRCA filtered between 0.5 and 0.7 Hz from June 17 to June 20. Masquer
Detail of the June 18 microseismic event. (a) The spatial distribution of the stationarity coefficient measured between 0.5 and 0.7 Hz on June 18, averaged from 13:30 to 16:30 a.m. (b) Map of the relative change in the percentage of the ... Lire la suite
This change in the shape of the noise spectrum, induces a decrease in the stationarity coefficient measured on the Adriatic coast of Italy as shown in Figure 6a. Elsewhere in Europe, the noise is stationary, the stationarity coefficient remaining above 0.96 except around the Aegean Sea. However, this event is not associated with a significant change in noise levels, so that at the European stations the noise level is similar on June 18 and during the previous 10 days (Figure 6b). This illustrates the stationary coefficient allows detecting events that are not clearly visible on the absolute noise level but that are nevertheless likely to affect the noise correlations waveform.
3.4. Stationarity of the noise field at the scale of Europe
In this section, we seek to quantify whether the noise wavefield is stationary at the scale of Europe. In particular, we wish to identify lateral variations in the dynamics of the seismic noise wavefield that could affect seismic waves velocity variations measurements (δv∕v) obtained from seismic noise correlations.
On Figure 7, we present the percentage of time when the stationarity coefficient is less than 0.98 in the 0.5–0.7 Hz frequency band during the months of January (left panel) and July (right panel). First of all, we observe larger values in July than in January indicating the seismic noise is more unstable in summer than in winter. In January the wavefield is extremely stable in the north of the Alps, especially in France, Germany, Holland and Romania. On the contrary, the stationarity coefficient is lower than 0.98 more than 20% of the time around the Aegean Sea and in Italy along the Mediterranean and Adriatic coasts. This means that there is a particular dynamic in the Aegean and Adriatic seas generating microseismic events that are detected between 0.5 and 0.7 Hz. The fact that these two seas are almost closed areas may explain this particular dynamic by favouring coastal reflections.
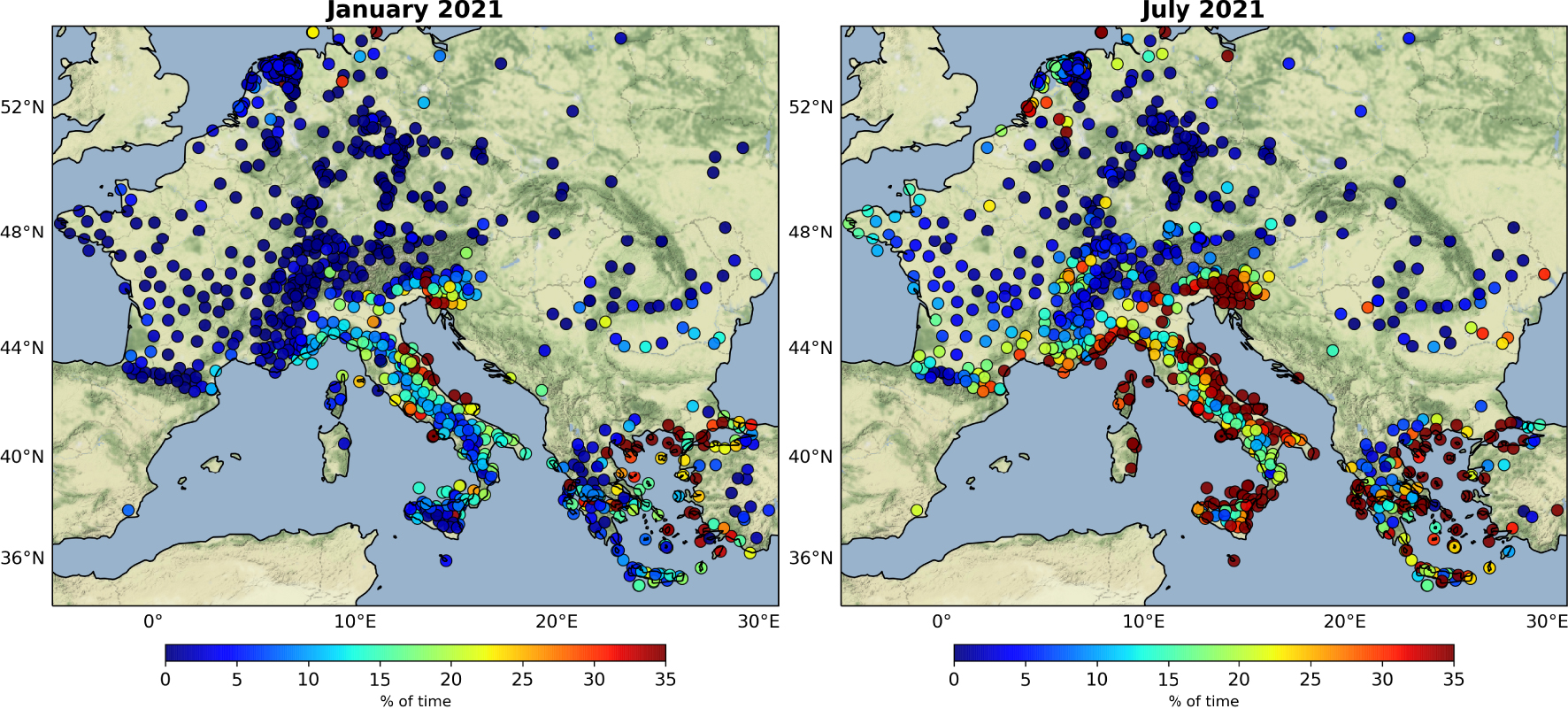
Percentage of time where the stationarity coefficient is less than 0.98 in January 2021 (left) and August 2021 (right) in the 0.5–0.7 Hz frequency band.
This contrast between Italy, Greece and the rest of Europe is more significant in July (Figure 7, right panel). The stationarity coefficient is below 0.98, more than 30% of the time around the Aegean Sea, the Adriatic Sea and in the south of France along the Mediterranean coast. Conversely, few events are detected elsewhere in Europe.
This indicates that there is a particular dynamic off the southern coast of Europe that generate high frequency (>0.4 Hz) microseismic noise, especially in the Adriatic and Agean seas that are enclosed spaces. These high-frequency events are visible mainly along the southern coastline of Europe, and attenuate rapidly so that they are not detected further away on the continent. The number of detected events is larger during the summer than during the winter (Figure 7). It is difficult to say whether this is because microseismic noise coming from the north Atlantic has less energy in summer than in winter (Figure 2) which reveals the dynamics of the Mediterranean, or whether the Mediterranean is indeed more active in summer than in winter.
4. Dynamic of seismic noise and convergence of auto-correlations coda waves
Central Italy and Greece are amongst the most seismically active areas in Europe so that there is a particular interest to follow the spatial-temporal evolution of the mechanical properties of the earth’s crust related to the seismic cycle in these regions. Seismic noise (auto)-correlations coda waves offers a unique opportunity to measure the evolution of seismic wave velocity (δv∕v) over time [Brenguier et al. 2008]. Measuring the δv∕v on several frequency bands allows in theory to measure the changes at different crustal depths. However, in southern Europe, above 4 s of period, seasonal variations in the distribution of noise sources create apparent velocity variations that are strong enough to mask the dynamics of the crust. Thus several studies such as Poli et al. [2020], Barajas et al. [2021] focus specifically on the 1–2 s period band. Measuring the δv∕v at different lapse-time makes it then possible to assess at least qualitatively the depth of the detected changes in the crust [Obermann et al. 2013, 2014; Poli et al. 2020].
To monitor the temporal evolution of the medium using seismic noise correlation coda waves, ideally we would like the noise sources to be stable over time so that changes in the coda would reflect only changes in the medium and would not be biased by changes in the distribution of the noise sources. However, we have seen that between 1–3 s the seismic noise field exhibits seasonal variations and that moreover microseismic events lasting several hours up to a few days are regularly detected around the Adriatic and the Aegean Sea. They can represent up to 30% of the records around the Adriatic coast.
We now quantify the impact of these microseismic events on the convergence speed of noise correlations coda waves. In other words, we investigate whether the dynamics of the noise affect the temporal resolution at which changes can be detected in the crust. To monitor the temporal evolution of the crust, the most common approach is to evaluate the relative change in velocity over time by comparing coda waves of a reference correlation with a set of correlations computed with a sliding window of N-days.
Noise correlations coda waves emerge from a constructive averaging process, so that the signal-to-noise ratio of the coda waves depends on the amount of data used to compute the correlations [Sabra et al. 2005; Weaver and Lobkis 2005]. Weaver et al. [2011], have shown that when the stretching method is used to infer velocity changes, the root mean square of the errors of the estimate of the relative velocity change between a reference correlation and an N-days(auto)correlations is given by:
| (1) |
To quantify the precision of the δv∕v measurements, we study how C varies spatially when considering 1-day, 3-days and 20-days auto-correlations. We study specifically the 2–3 s period band which is particularly interesting for monitoring studies of southern Europe, longer periods measurements being contaminated by seasonal changes of the source. We consider specifically auto-correlations to avoid any influence of varying inter-station distance. We study separately the convergence of autocorrelations computed at each European station in summer (July–August) and winter (January–February), and we consider two different time windows in the coda: 5–25 s which correspond to the beginning of the coda and to a single scattering regime and 20–40 s where coda waves are closer to a multiple scattering regime.
Specifically, for each station, we compute daily auto-correlations in summer and winter. We did not apply any temporal or spectral normalization to the noise records as our aim is not to discuss the effect of processing on the convergence of the auto-correlations. The daily auto-correlations are normalized to one and then stacked to obtain N-day correlations. This normalization reduces the contribution of the most energetic days. For each season, we define a reference auto-correlation that is the correlations averaged over the considered season (2 months). To evaluate the average correlation coefficient between N-days auto-correlations and the reference, we select randomly N daily auto-correlations that are then normalized to one and stacked to obtain an N-days auto-correlation. We then compute the correlation coefficient between this N-days auto-correlation and the reference auto-correlation for two different time windows: 5–25 s and 20–40 s that may typically be used for monitoring studies. This procedure is repeated 10 times and we average the result to obtain the average correlation coefficient between N-days auto-correlations and the reference. Here we show the result obtained for daily auto-correlations (N = 1), 3-days (N = 3) and 20-days auto-correlations (N = 20).
4.1. Results for the 5–25 s time window
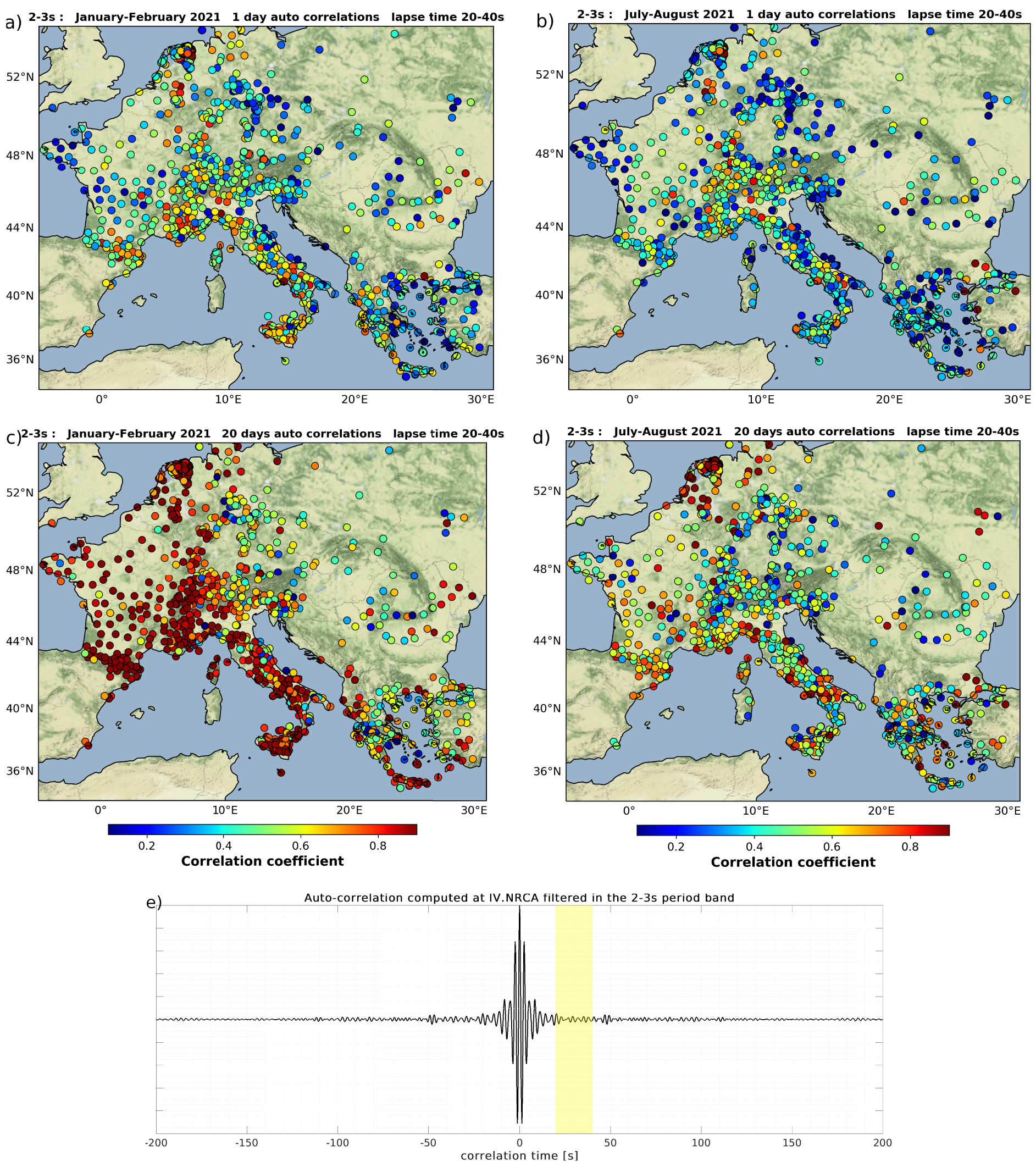
We present the results obtained for the 5–25 s (beginning of the coda) and the 20–40 s time windows in Figures 8 and 9, respectively. The bottom panel of Figure 8 shows an example of auto-correlation computed at station IV.NRCA and filtered between 2 s and 3 s period, with the 2–25 s coda window shaded in yellow. We note immediately a strong correlation between the results presented in Figures 7 and 8a,b: the average correlation coefficients calculated between daily auto-correlations and the reference are strongly correlated to the percentage of time where the stationarity coefficient is less than 0.98 (Figure 7). This is true for the winter (Figure 8a) and in summer (Figure 8b). In winter, the average correlation coefficient is close to 1 in France, Germany, the Netherlands and Romania, where the stationarity coefficient is greater than 0.98 more than 95% of the time. Conversely, around the Adriatic Sea, the coda of daily auto-correlations differs from the reference and the correlation coefficients are around 0.7 in Italy and 0.5 in Slovenia.
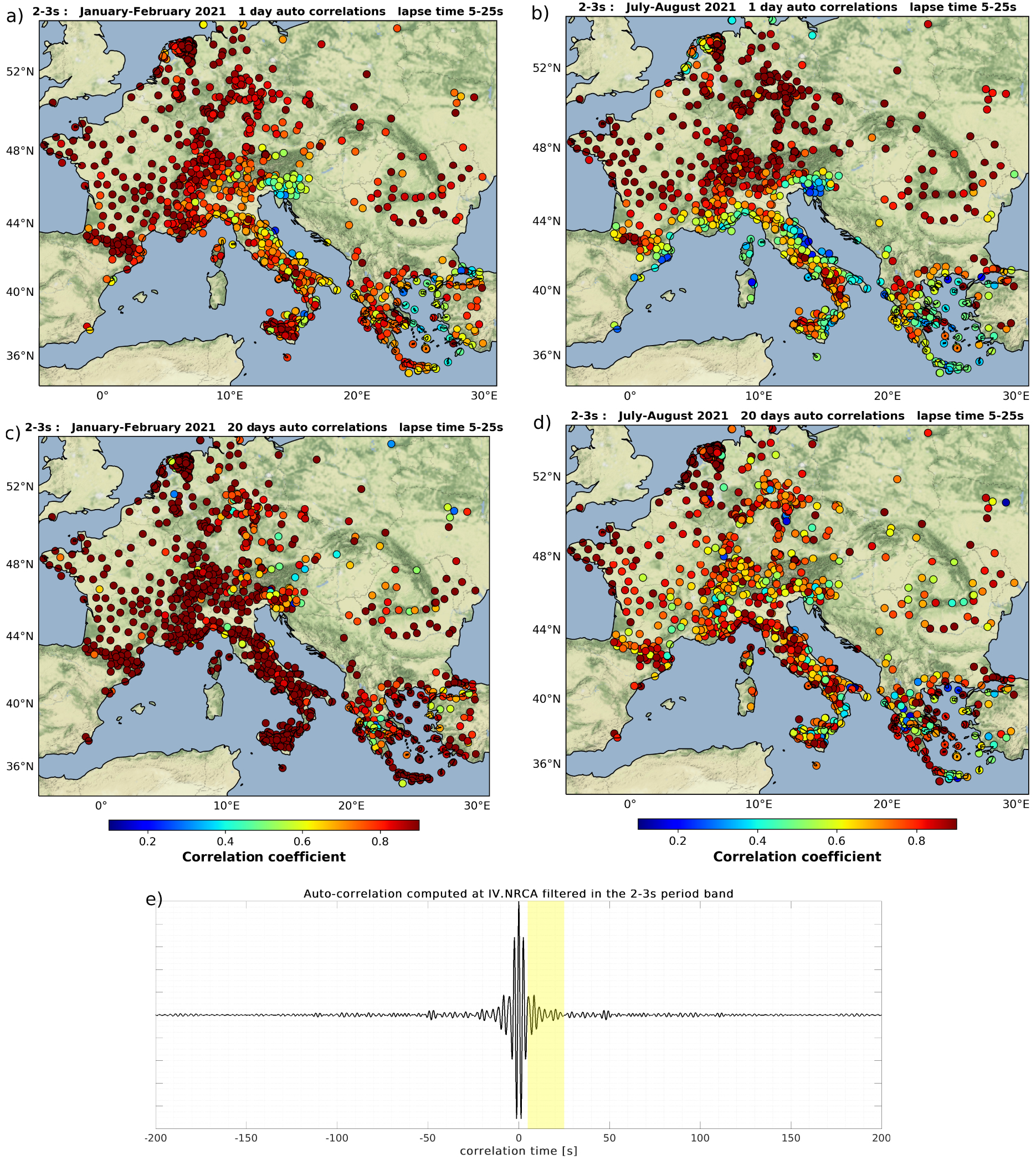
Average correlation coefficient between one day auto-correlations and a reference averaged over two months obtained in the 2–3 s period band and for the time window 5–25 s (a) in January–February and (b) in July–August. (c), (d), (e), (f) are similar to (a) and (b) but for 3 and 20-days auto-correlations. (g) Example of an auto-correlation at the Italian station NRCA filtered in the 2–3 s period band and averaged over one year (2021). The 5–25 s time window that is studied here is shaded in yellow. Masquer
Average correlation coefficient between one day auto-correlations and a reference averaged over two months obtained in the 2–3 s period band and for the time window 5–25 s (a) in January–February and (b) in July–August. (c), (d), (e), (f) are similar to ... Lire la suite
Average correlation coefficient between one day auto-correlations and a reference averaged over two months obtained in the 2–3 s period band and for the time window 20–40 s (a) in January–February and (b) in July–August. (c), (d), (e), (f) are similar to (a) and (b) but for 3 and 20-days auto-correlations. (g) Example of an auto-correlation at the Italian station NRCA filtered in the 2–3 s period band and averaged over one year (2021). The 20–40 s time window that is studied here is shaded in yellow. Masquer
Average correlation coefficient between one day auto-correlations and a reference averaged over two months obtained in the 2–3 s period band and for the time window 20–40 s (a) in January–February and (b) in July–August. (c), (d), (e), (f) are similar to ... Lire la suite
In summer, we observe a contrast between the Mediterranean coast and the rest of Europe: the average correlation coefficients are close to 1 everywhere in Europe except along the Mediterranean and Adriatic coast where we observe correlation coefficients between 0.2 and 0.7. This result is directly correlated with the stationarity coefficient analyses presented in Figure 7: the areas where high frequency microseismic events are detected are those where the daily auto-correlations coda waves differ the most from the reference.
Considering 3-day autocorrelations, the correlation coefficient becomes more spatially homogeneous in winter and summer (Figure 8c,d). However, we still observe the imprint of the dynamics of noise sources on the convergence speed of the auto-correlations coda waves: the mean correlation coefficient between the 3-days correlations and the reference are close to 0.8 in Italy and around the Aegean Sea and greater than 0.9 further north. In summer correlation coefficients are lower, especially near the Mediterranean and Adriatic coasts. In other words, the noise wavefield is less stationary during the summer than the winter (Figure 7) which slows down the convergence of the auto-correlations coda waves. On the other hand with 20-days autocorrelations, the correlation coefficient are close to one everywhere in Europe whatever the season (Figure 8e,f).
4.2. Results for the 20–40 s time window
As we go into larger lapse-time, coda waves are more scattered by the medium heterogeneities, so that we expect to lose gradually the imprint of the source. This could reveal the influence of the later variations of the crust on the convergence speed of the coda waves. Lu et al. [2020] have shown that the wavefield is more random in the Alps which constitute a highly heterogeneous medium. However, as shown in Figure 9, we do not observe a clear correlation between the convergence of the coda waves and the geology: despite the Earth’s crust in the Alps and the Apennines is thought to be highly heterogeneous, it does not improve significantly the convergence of the coda waves at least in the 20–40 s lapse time window.
On the other hand, the influence of the dynamic of the seismic noise wavefield is still clearly visible and is two-fold. Firstly, the convergence of the auto-correlation coda waves depends strongly on the season. Considering 3 days or 20-days auto-correlations (Figure 9c–f), the correlation coefficients are larger during winter when the frequency content of the noise is more stable than in summer. This is especially true in the westernmost part of Europe. Secondly, during winter and summer we observe lateral variations. With 3-days auto-correlation (Figure 9c,d) there is a clear contrast between Western and Eastern Europe. In winter the average correlations coefficient with the reference is greater than 0.7 in France and Switzerland, and less than 0.5 in Romania, Greece, Slovenia and Italy along the Adriatic coastline. This lateral variation remains clearly visible in winter and summer when considering 20-days auto-correlation (Figure 9e,f).
4.3. Temporal resolution for monitoring studies in the 2–3 s period band
We now look at the extent to which the dynamics of the seismic noise, and in particular the microseismic activity around the Adriatic and Aegean seas limits the temporal resolution with which it is possible to measure velocity changes between 2 and 3 s. To that end, we map the spatial variation of the smallest number of days N for which the average correlation coefficient C between an N-day auto-correlation and a 2-month reference auto-correlation is greater than or equal to a given threshold (Figure 10). The reference auto-correlation being averaged over 60 days, we explore a numbers of days N ranging from 1 to 59.
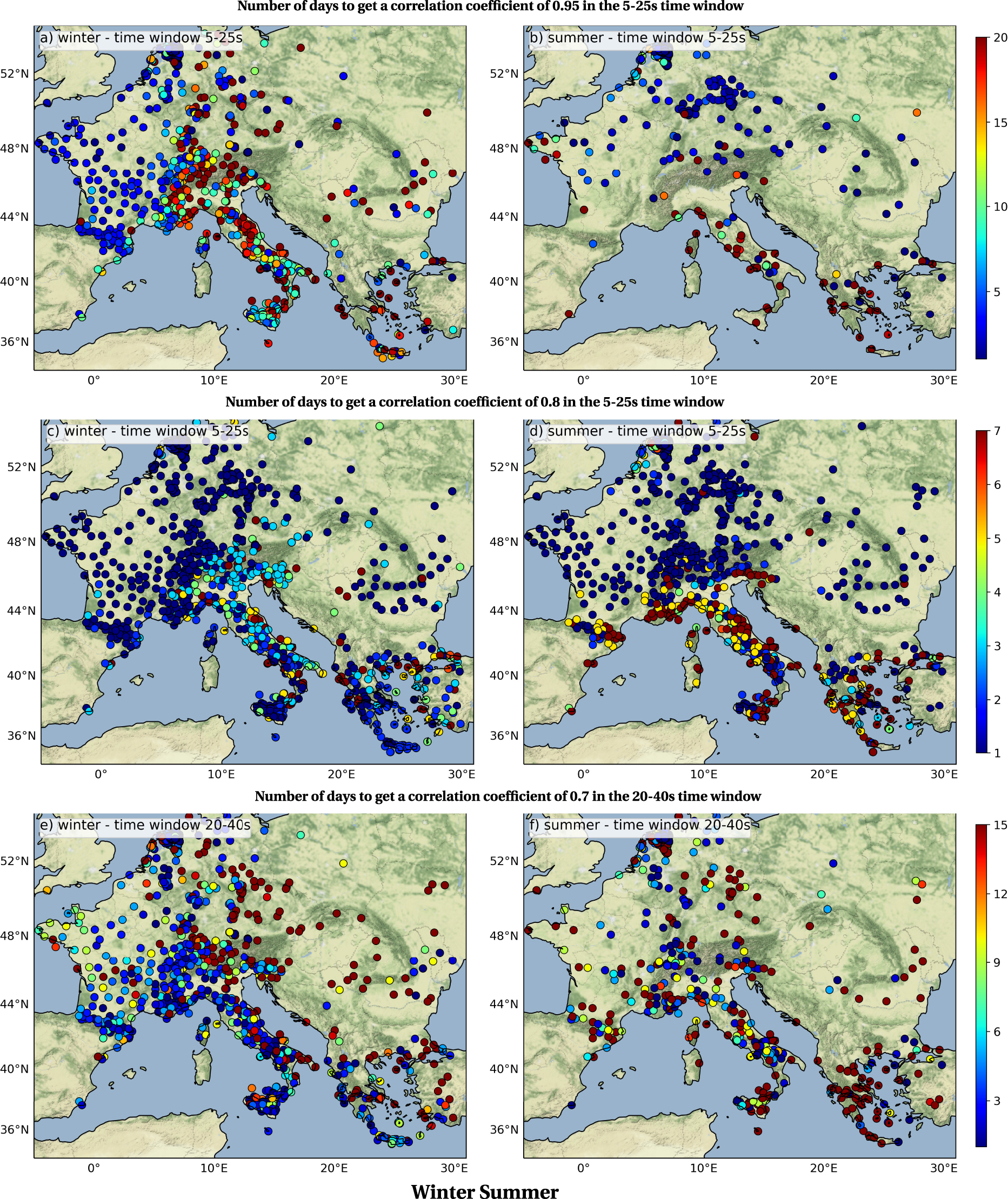
Number of days required to get a correlation coefficient greater than 0.95 between a reference auto-correlation averaged over the season (2 months) and a N-day auto-correlation, in the time window 5–25 s corresponding to the beginning of the coda, in (a) winter (January–February) and (b) summer (July–August). (c) and (d) are similar to (a) and (b) but for a correlation coefficient of 0.8. (e) and (f) are similar to (a) and (b) but for the 20–40 s time window and a correlation coefficient of 0.7. Masquer
Number of days required to get a correlation coefficient greater than 0.95 between a reference auto-correlation averaged over the season (2 months) and a N-day auto-correlation, in the time window 5–25 s corresponding to the beginning of the coda, in ... Lire la suite
In Figure 10a,b we represent the number of days N required to get a correlation coefficient C of 0.95 considering the coda time window 5–25 s. According to Equation (1), when measuring relative velocity changes δv∕v with the stretching method, a correlation coefficient of 0.95 over the time window 5–25 s between 2 and 3 s of period implies that the errors on the estimate of the relative velocity changes have a root mean square of 0.07% [Weaver et al. 2011]. This may seem large, as the velocity changes associated with large magnitude earthquakes and the hydrological cycle are of the order of 0.1% [Sens-Schönfelder and Wegler 2006; Brenguier et al. 2008; Chen et al. 2010; Zaccarelli et al. 2011; Barajas et al. 2021; Mao et al. 2022]. This is due to the fact that we consider measurements made at a single station over a relatively small time window (5–25 s). In winter, the convergence speed of the auto-correlation in the 5–25 s time window is faster in France (N < 10 days) than further east in Germany, Switzerland, and Italy (N > 15 days). In summer the speed of convergence decreases as the noise field is less stationary. More than 20 days are required to get a correlation coefficient greater than 0.95 along the Mediterranean Adriatic coast and around the Aegean sea.
Figure 10c,d represent the number of days N needed to obtain on the 5–25 s time window a correlation coefficient C of 0.8. This corresponds to an RMS of the δv∕v measurement errors of 1.6%. We see a sharp contrast between two regions: in winter it takes less than 3 days in the northwest (France, Germany, Switzerland) to obtain a correlation coefficient of 0.8. On the contrary, it takes more than 3 days in Italy, Austria and Slovenia. In summer, the spatial variation of N relates directly to the percentage of time for which the stationarity coefficient is lower than 0.98 (Figure 7): the coda of correlation converges more slowly in Greece, Italy, on the south coast of France (N > 10 days) where short period microseismic events are detected, and the convergence is faster on the rest of the continent (N < 3 days) where the noise is more stationnary.
Figure 10e,f presents the speed of convergence of the auto-correlations coda waves over the 20–40 s time window for C = 0.7. This corresponds to a RMS of the δv∕v measurement errors of 1.1%. For this time window the results are different: the effect of the dynamic of the noise sources is less visible. In particular in summer, the number of days required to achieve C = 0.7 varies randomly from site to site with no clear regional variations.
These results indicate that the evolution of noise sources over time, the interaction between the north Atlantic and the southeastern Mediterranean source region and its seasonal variations, the dynamics of sources on smaller time scales in the Adriatic and Aegean Seas, limits the convergence speed of the noise auto-correlations coda waves and thus the temporal resolution of monitoring studies. The impact of local noise sources along the coast limits the temporal resolution particularly on the 5–25 s coda window. Seasonal variations in seismic noise affect the two time windows 5–25 s and 20–40 s, the convergence being slower in summer than in winter. Thus, even when going further into the coda, the imprint of the source dynamics is still visible. In winter as in summer, there is a clear difference between Western and Eastern Europe, the temporal resolution of the δv∕v measurements decreasing towards the East.
5. Conclusion
The aim of this work was to study the relationship between the dynamics of the noise field across Europe and the convergence speed of noise auto-correlation coda waves. It shows that the accuracy and temporal resolution with which it is possible to detect changes in the medium at 2 s period presents strong seasonal and lateral variations that depends on the time window which is analysed.
The noise level maps computed using all available broadband seismic stations in Europe in 2021, complemented by temporary stations from the Pyrope and IberArray networks, show strong seasonal variations at 2 s periods and a clear increase in noise level near the Atlantic and Mediterranean coast. This suggests that the seismic noise originates simultaneously from the Mediterranean Sea and the Atlantic Ocean and attenuates as it propagates across the continent (Figure 2).
To study the dynamics of the noise field, we introduce a proxy that quantifies the non-stationarity of the frequency content of the noise independently of its amplitude. It shows that in the regions mainly influenced by the north Atlantic ocean, the frequency content is stable over time which is favourable for monitoring the Earth’s crust (Figure 7). Conversely, this proxy allows us to detect short periods microseismic events originating from the southeast of the Mediteranean sea. This highlights that unlike the north Atlantic ocean, the Mediterranean sources are intermittent and generate an unstable wavefield over time (Figures 5, 6).
Noise level maps and noise stationarity maps (Figures 2, 7) show that the dynamics of the seismic noise operates on two distinct time scales that modulate the speed of convergence of correlations coda waves. First, the noise field evolves seasonally: this results in seasonal changes in the noise level, but also in the relative influence zones of the Atlantic Ocean and the Mediterranean Sea. In addition, there are dynamics on a smaller time scale of the order of hours to days related to the intermittent generation of short period noise by the Adriatic and Aegean Seas, which are closed areas.
The contribution of these two main areas and the existence of these two time scales imply that the convergence speed of the correlation coda waves varies spatially, and that this spatial variation itself depends on the season and the lag-time considered. The beginning of the coda is the most sensitive to the dynamics of the noise sources over short times, and its convergence speed directly reflects the lateral variations of the noise non-stationarity (Figures 7, 8). At longer times, over the 20–40 s coda window, convergence is slower, the influence of Mediterranean dynamics is weaker, but there remains a strong contrast between Western Europe where convergence is faster while as one moves away from the Atlantic Ocean, convergence of correlations slows down (Figure 9).
To summarise, this study shows that the spatial and temporal variability of the noise sources determines to first order the accuracy and temporal resolution with which it is possible to detect changes in the crust at 2 s of period, while lateral variations of scattering properties have less influence. In particular, the influence of strong heterogeneities of the alpine crust on the convergence speed of the coda is not clearly seen.
6. Origin of data
Waveform data used in this paper belong to the networks with codes:
CL [Corinth Rift Laboratory Team And RESIF Datacenter 2013], CQ [Geological Survey Department Cyprus 2013], CR [University of Zagreb 2001], CZ [Charles University in Prague (Czech) et al. 1973], EI [Dublin Institute for Advanced Studies 1993], ES [Instituto Geografico Nacional, Spain 1999], FR [RESIF 1995], GE [GEOFON Data Centre 1993], GR [Federal Institute for Geosciences and Natural Resources (BGR) 1976], GU [University of Genoa 1967], HA [University of Athens 2008], HC [Technological Educational Institute of Crete 2006], HL [National Observatory of Athens, Institute of Geodynamics, Athens 1975], HP [University of Patras 2000], HS [Hessian Agency for Nature Conservation, Environment and Geology 2012], HT [Aristotle University of Thessaloniki 1981], HU [Kövesligethy Radó Seismological Observatory (Geodetic And Geophysical Research Institute, Research Centre For Astronomy And Earth Sciences, Hungarian Academy Of Sciences (MTA CSFKGGIKRSZO)) 1992], IV [Istituto Nazionale di Geofisica e Vulcanologia (INGV) 2005], KO [Kandilli Observatory And Earthquake Research Institute, Boğaziçi University 1971], LX [Instituto Dom Luiz (IDL) - Faculdade de Ciências da Universidade de Lisboa 2003], MD [Geological and Seismological Institute of Moldova 2007], MN [MedNet Project Partner Institutions 1990], NI [OGS (Istituto Nazionale di Oceanografia e di Geofisica Sperimentale) and University of Trieste 2002], NL [KNMI 1993], NS [University of Bergen 1982], OE [ZAMG - Zentralanstalt für Meterologie und Geodynamik 1987], OT [University of Bari “Aldo Moro” 2013], OX [Istituto Nazionale di Oceanografia e di Geofisica Sperimentale - OGS 2016], PM [Instituto Português do Mar e da Atmosfera, I.P. 2006], RD [RESIF 2018], RO [National Institute for Earth Physics (NIEP Romania) 1994], SJ [Seismological Survey of Serbia 1906], SK [ESI SAS (Earth Science Institute Of The Slovak Academy Of Sciences) 2004], SL [Slovenian Environment Agency 1990], SX [University of Leipzig 2001], UD [Main Center of Special Monitoring 2010], UP [SNSN 1904].
We also used data of temporary experiments, PYROPE (network code X7 (2010–2014), Chevrot et al. [2017] and IberArray [Institute Earth Sciences “Jaume Almera” CSIC (ICTJA Spain) 2007].
Declaration of interests
The authors do not work for, advise, own shares in, or receive funds from any organization that could benefit from this article, and have declared no affiliations other than their research organizations.
Dedication
The manuscript was written through the contributions of all authors. All authors have given approval to the final version of the manuscript.
Funding
Real-time Earthquake Risk Reduction for a Resilient Europe (RISE) project Grant agreement number 821115 (LS, ED, PR).





 CC-BY 4.0
CC-BY 4.0