1. Introduction
Sedimentary basins are subsiding domains filled with various deposits, where the dynamics are driven by material supply, deformation, climate and base level variations. Although the regional boundary conditions control the types of basins (e.g., strike-slip, flexural, rift, marginal and foreland basins—[Allen and Allen 2013]), the sediment supply controls the nature of the infilling. Low inputs allow the precipitation of autogenic carbonates, whereas larger terrigenous fluxes result in the accumulation of clays, sands or conglomerates. During diagenesis and burial, the deposits acquire various mechanical behaviours. For instance, sandstones and carbonates tend to have generally brittle behaviour, whereas clays and evaporites are more viscous depending on the stress conditions (strain rate and deviatoric stresses). Furthermore, differences in compaction may generate some layers with high fluid pressure, which favours viscous behaviour. This may increase the contrast with upper and lower brittle layers. The horizontal layering resulting from such variations in lithology constitutes a major mechanical heterogeneity, which has an impact on the propagation and shape of faults and thus the overall structure of the basin [McClay and Scott 1991, Nalpas et al. 1999, Withjack and Callaway 2000]. Improving the mechanical understanding of such a rheological-layered system is of major interest for the management of natural resources trapped or stored in reservoirs and sealed by clayey layers and for the intermediate-depth or deep geological disposal of nuclear waste in clayey rocks.
Previous works on extensional systems [McClay and Scott 1991, Withjack and Callaway 2000, Roche et al. 2012, 2013] and compressive systems [Nalpas et al. 1999, Barrier et al. 2002] have shown the impact of rheological layering on the deformation of sedimentary basins. The fault dip angle (higher or lower compared to a typical dip), the fault geometry (planar, flat and ramp, curve, three-dimensional shape), the number of faults and their connection are impacted by mechanical layering. Moreover, this deformation of multilayered systems can also generate associated structures such as extensional folds [Withjack and Callaway 2000, Homberg et al. 2017] or long wavelength flexures.
Rheological properties of the material
| Brittle layers | Cohesion (Pa) | Friction angle (°) | Density | Grain size (μm) |
|---|---|---|---|---|
| Sand | ≈10 | 30–35 | 1.4 | 250–300 |
| (Fontainebleau quartz—Sibelco, France) | ||||
| Glass microbeads | ≈300 | 20–22 | 1.5 | 180–200 |
| (CVP, France) | ||||
| Viscous layers | Viscosity (Pa/s) @ 20 °C | Density | ||
| Transparent silicone putty | 3 × 104 | 1 | ||
| (GS1 RG 70 009—Rhône-Poulenc) | ||||
| Pink silicone putty | 6 × 104 | 1.3 | ||
| (SGM 36—Rhône-Poulenc) | ||||
Many modelling studies (see the review of Dooley and Schreurs, 2012) were performed within a purely strike-slip context using different kinds of materials: clay [Riedel, 1929, Cloos, 1928, 1955, Tchalenko, 1970, Wilcox et al., 1973, Soula, 1984, Lazarte and Bray, 1996, Atmaoui et al., 2006], dry sand [Emmons, 1969, Naylor et al., 1986, Richard et al., 1989, Richard, 1990, 1995, Burbidge and Braun 1998, Schöpfer and Steyrer, 2001, [Viola et al. 2004, Le Guerroué and Cobbold 2006]], and rheologically stratified materials [Wilcox et al., 1973, Odonne and Vialon, 1983, Richard et al., 1989, [Dauteuil and Mart 1998, Casas et al. 2001]]. These works reveal a complex faulting pattern varying along the strike-slip boundary even in experiments with uniform mechanical layers. Several works investigated the parameters driving the fault patterns in pull-apart basins [McClay and Dooley 1995, Dooley and McClay 1997, Schreurs and Colletta 1998, Sims et al. 1999, Wu et al. 2009, Corti et al. 2020]. The addition of a viscous layer allows producing en échelon folds [Odonne and Vialon, 1983] or along-strike bulging [Dauteuil and Mart 1998], that is, the genesis of associated features that can be symptomatic of strike-slip context. Although these studies focused on the specific areas of strike-slip domains such as pull-apart basins or on oblique (transpressive or transtensive) boundaries, the role of rheological layering in the strike-slip setting remains largely unexplored.
In this study, we investigated the structures generated by strike-slip boundary conditions to provide a 3D view of the deformation pattern that could be present in a nonuniform mechanical system. We used analogue modelling because of the scale investigated (basin in the upper crust), the nonlinear mechanical properties of the rocks and the 3D nature of the structures associated with this context [Richard et al. 1991, Dauteuil and Mart 1998]. The results provide some guidelines to interpret features generated in a strike-slip context.
2. Experimental set-up
Earth materials exhibit two main mechanical behaviours (brittle and viscous) depending on the lithology, temperature, pressure, deformation rate and fluid pressure [Kirby 1983, Kohlstedt et al. 1995]. The variation in these parameters with depth generates a rheological layering that can be seen as the succession of brittle and ductile layers approximated in analogue modelling using adapted materials [Davy and Cobbold 1991, Graveleau et al. 2012, Schellart and Strak 2016]. The brittle behaviour was simulated with Fontainebleau sand and manufactured glass microbeads and the ductile behaviour with two types of silicone putty (pink and transparent). Table 1 summarizes the different mechanical properties. The rheological dimensioning of these materials was described in previous works [Davy and Cobbold 1988, Le Guerroué and Cobbold 2006, Panien et al. 2006, Vasquez et al. 2018]. For the scaling of physical parameters, we followed the methodology described by Davy and Cobbold [1991] and Vasquez et al. [2018]. The physical scaling used is as follows: 1 km in nature corresponds to 1 cm in the model and 1 cm/yr in nature to 1 cm/h in the model.
Oblique view and schematic block diagram of the experimental apparatus. The apparatus placed on a rigid board is composed of two grey plexiglass drawers freely sliding on the board. The right drawer is pulled by a step-by-step motor. The model comprises five layers, the description of which is given in Table 1. Physical properties and scaling are described in Tables 1 and 2.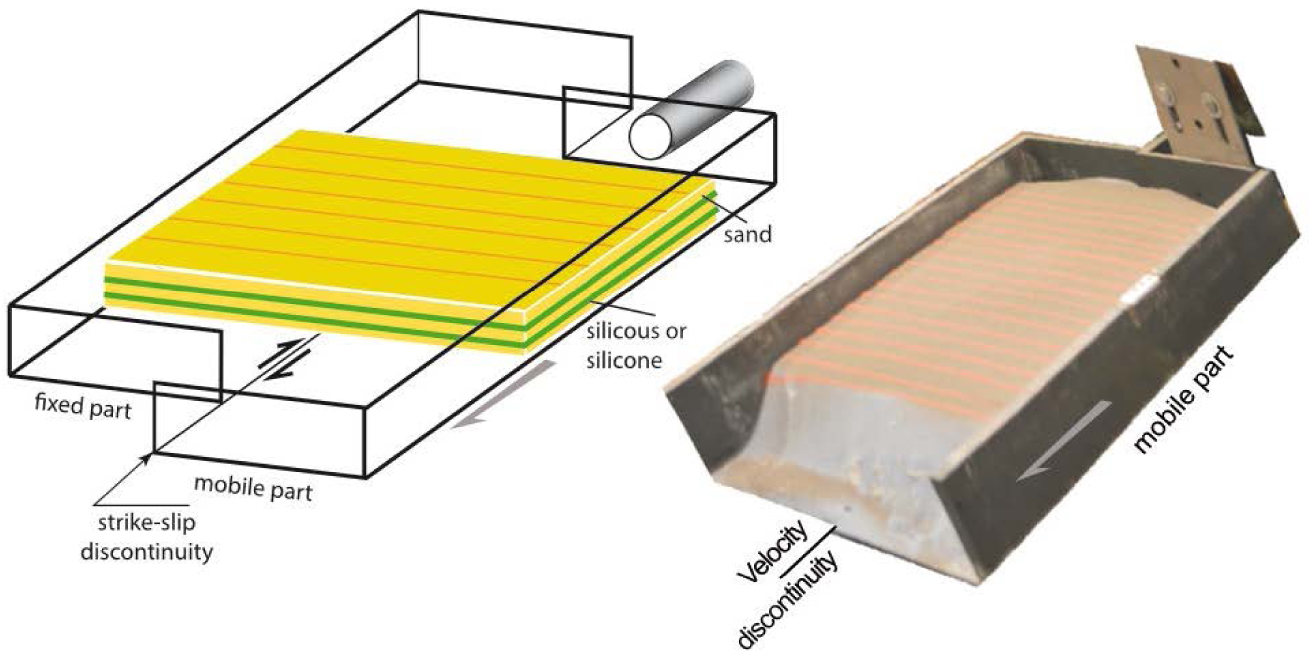
Experimental conditions
| Decro-1 | Decro-2 | Decro-4 | Decro-5 | Decro-3 | |
|---|---|---|---|---|---|
| (Figure 2a) | (Figure 2b) | (Figure 2c) | (Figure 2e) | (Figure 2d) | |
| Layering | Sand–silicone 1 | Sand–silicone 2 | Sand–silicone 2 | Sand–silicone 2 | Sand–silica |
| Thickness (cm) | 1/1/1/1/1 | 1/1/1/1/1 | 1/0.5/1/0.5/1 | 1/1/1/1/1 | 1/1/1/1/1 |
| Displacement (cm) | 7 | 7 | 7 | 7 | 7 |
| Velocity rate (cm/h) | 1 | 1 | 1 | 3 | 3 |
| Rheological layering |  |  |  | 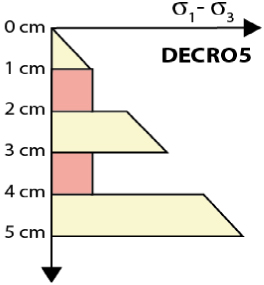 | 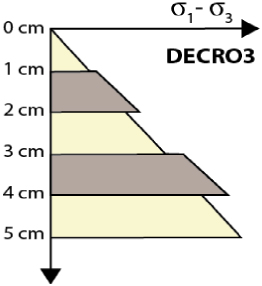 |
| Strength ranking | 2 | 3 | 1 | 4 | 5 |
| Mean deviatoric stresses | 4.8 | 3.15 | 2.2 | 2.3 | 0.9 |
Note: The thickness row displays the thickness of each layer from top to bottom; the number in bold corresponds to intermediate layers. In the rheological layering row, the section in dark grey is silicone 1, medium grey is silicone 2 and light grey is silica powder. The whole given strength is relative (without units) and corresponds to the area of the rheological profile from the weakest (1) to the strongest (5). The mean of deviatoric stresses is the average of the differences in deviatoric stresses from one layer to another. Thus, high values indicate high rheological contrasts.
The models are constructed in a 1 m long and 40 cm wide box designed with two drawers: one fixed and one mobile pushed by a step-by-step motor (Figure 1). The sliding border of the two drawers defines a strike-slip velocity discontinuity above which deformation occurs in the model. Five experiments are conducted. All of them comprise five layers. Models Decro-1, Decro-2, Decro-4, and Decro-5 have three layers of 1 cm thick Fontainebleau sand and two layers of either 1 cm thick or 0.5 cm thick silicone putty. Model Decro-3 consists of alternating silica powder and sand layers. All models are 5 cm in height except Decro-4, which is 4 cm in height. Two different pulling rates are tested: 1 cm/h and 3 cm/h. The change in rate modifies the strength of the silicone putty: the higher the rate, the stronger the silicone. The rate does not modify the mechanical properties of the sand [Kirby 1983, Ranalli 1987, Kohlstedt et al. 1995]. Surface and oblique pictures are taken during the experiment. Finally, the models are cut into several vertical cross-sections every 4 cm to provide 3D data sets. The properties of the five experiments are summarized in Table 2, snapshots of surface views and selected cross-sections are displayed in Figure 2 and larger views are presented in the Supplementary material.
3. Faults in brittle layers
Five analogue experiments at the end of the deformation (see Table 2 for the experimental set-up). For each experiment, the surface view (right column) and two or three line drawings of the sections are given (left column). The dotted zones inside the silicone layer trace the path of viscous deformation. The label of the section includes the distance from the border without the motor.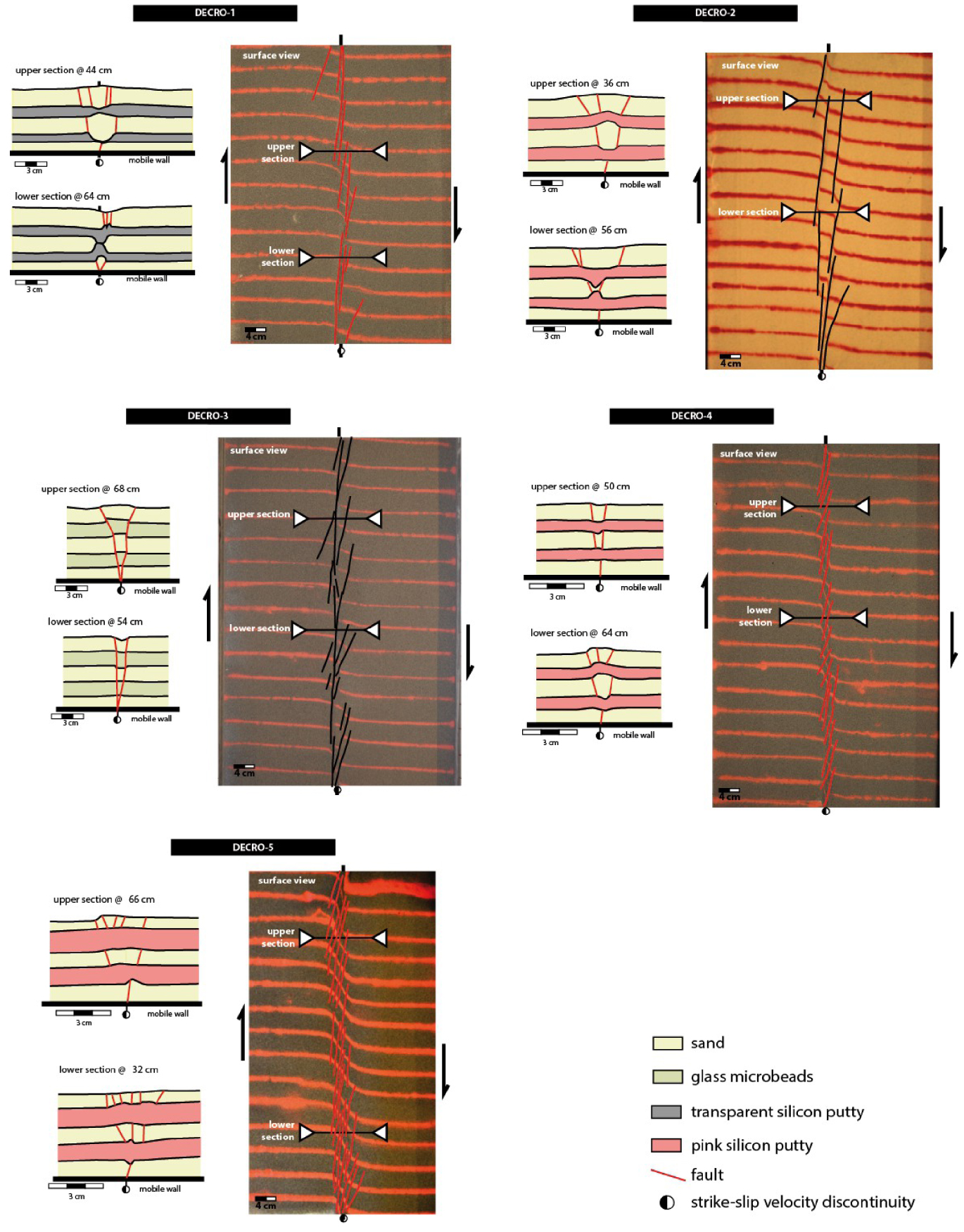
Regardless of rheological layering, the analogue experiments display deformations with some common characteristics, which we describe first. Surface views and cross-sections show that the deformation is focused into a narrow shear band affected by numerous faults (Figure 2). In horizontal view, the faults systematically display an en échelon pattern with a mean 9°–14° obliquity relative to the basal strike-slip discontinuity (Figure 3) corresponding to R-faults in the Riedel shear system. The highest angles are close to the experiment border, resulting from edge effects. The fault azimuths roughly decrease as their lengths increase (Figure 3). This means that the faults tend to become parallel to the velocity discontinuity as they grow. Likewise, a positive correlation between the width of the deformed band and the fault azimuth indicates that the fault orientation drives the width of the deformed band. In the vertical plane, the faults are difficult or impossible to detect because they laterally offset the layers and have very small or no vertical throw. However, they are often associated with a change in layer thickness or in layer dip (flexure and fold). We did not systematically observe the genesis of one type of associated feature depending on rheological layering. Folds and flexures change along the strike of the deformed zone and exist at different depths.
In all of the experiments, the faults grow upward from the basal strike-slip discontinuity. The number of faults decreases with depth as previously described in Le Guerroué and Cobbold [2006]. In the experiments with silicone layers (Decro-1, Decro-2, Decro-3, and Decro-5), the lowest sand layer is only affected by one fault, whereas the uppermost layer is affected by up to five faults. New faults appear at the top of each silicone layer, which react as a local velocity discontinuity. The fault dip does not change significantly at each layer interface. Secondary faults appear in the surface layer. In the experiment with silica powder (Decro-3; Figure 2), two main faults with opposite dip are nucleated at the strike-slip discontinuity located at the base of the experiment, and they propagate upward. The fault dip slightly changes at each interface separating the sand layers from the layers of glass microbeads. Therefore, a change in the friction angle of cohesive layers modifies the fault dip, which does not act as a velocity discontinuity. These results show that rheological layering controls the geometry and upward propagation of the faults: (i) the fault dip when the faults cut through layers with different friction angles (a decrease in the friction angle, flattening the fault dip) and (ii) the nucleation of new faults at each interface between brittle and viscous layers (the fault number increases at each interface).
Relations among the fault length, the fault azimuth and the width of the deformed band. The upper plot displays the negative relationships between the length and the azimuth and the lower plot shows the positive relation between the width of the deformed band and the fault azimuth.
The faults mainly accommodate the strike-slip motion as imposed by the boundary conditions. However, some of them show a small vertical throw generated with either normal or reverse throw. As expected in such a strike-slip context, the vertical displacements (up to 0.6 mm) along the faults are lower than the horizontal displacements (7 cm), that is, less than two orders of magnitude. This vertical component is worth mentioning because even if it is small, it is observed at the basin scale, on seismic profiles or in the field. In the same experiment, some sections display faults with reverse components and other sections show faults with normal components. Furthermore, some faults with reverse and normal components may coexist within the same section. Therefore, the type of fault (strike slip with a normal or a reverse component) varies along the strike of the deformed band and through the depth despite the boundary and kinetic conditions remaining similar during the experiment. The multilayered medium deformed by horizontal shearing applied at the boundaries generates intrinsic conditions, allowing upward and downward displacements.
4. Changes in layer shape
In addition to the brittle deformation described above, the five layers display other types of deformation within the shear band: thinning, thickening and folding. Thinning is accommodated by normal oblique-slip faults in the sand and silica layers and by boudins in the silicone and cohesive layers. Reverse oblique-slip faults in the sand layers as well as thick bulges in both types of layers accommodate thickening. No folding occurs when there are only cohesive layers such as those in the Decro-3 experiment.
Surprisingly, different deformation styles coexist within the same section except in the experiment without a viscous layer (Decro-3). One layer may be thinned, while another is thickened or folded. This means that there is strong decoupling of deformation between layers having different rheological behaviours. Therefore, strike-slip boundary conditions can simultaneously induce thinning and thickening, indicating that such a deformation pattern is not symptomatic of extensive and compressive contexts, respectively. This observation has important implications for the interpretation of geological cross-sections or seismic lines in geophysical surveys. Although opposite deformation styles are frequently interpreted as belonging to different tectonic conditions in a polyphase history, the present work reveals that they may have occurred during a single deformation stage. The experiment comprising only cohesive layers is deformed by positive or negative flower structures as previously described by Le Guerroué and Cobbold [2006].
Variations in thicknesses of the five layers along the velocity discontinuity in each experiment. Note the wavelength for the thickness that is in opposite shift.
In addition to the changes in deformation pattern with depth, the deformation also evolves along strike. The different sections of the same experiment display changes in deformation style. Thinned, stretched or folded domains succeed each other within the same layer (Figure 4). The variations in layer thickness display a roughly periodic pattern. The wavelength is approximately 16 cm, that is, ±3.2 times the whole thickness of the experimental structure. This ratio is consistent with that from the literature [Martinod and Davy 1994, Davy and Cobbold 1988, Dauteuil and Mart 1998], which predicts that the deformation wavelength ranges from 3 to 5 times the thickness of the layer involved in the deformation. In the experiments with viscous layers (Figure 4), the thickness for the basal silicone layer displays longer wavelengths than the thicknesses for the middle layers, and the thickness for the upper sand layer shows shorter wavelengths than the thicknesses for the middle layers. The deformation wavelength roughly displays an opposite phase shift between the viscous and cohesive layers. A thinning of the viscous layer fits with a thickening of the cohesive layer. The amplitudes of deformation wavelength in the sand are often higher than those in the silicone. The viscous layers are more often thinned than thickened, while the cohesive layers thicken more easily than the viscous layers.
In the experiment with five cohesive layers (Decro-3), the layer thickness also displays variations with wavelengths that have an opposite shift (Figure 4). The wavelength amplitude is smaller for the more cohesive layer (silica layer). The wavelength corresponds to a succession of positive and negative flower structures in which the vertical throw decreases downward to become null at the base of the system. Previous experiments with one mechanical layer only display positive flower structures [Richard et al. 1991, McClay and Bonora 2001, Le Guerroué and Cobbold 2006]. In our experiment, negative flower structures are associated with the thinning of the basal layer. Al-Zoubi et al. [2006], Hang et al. [2017] and Carlini et al. [2019] described natural cases with alternation positive and negative structures strike on deformed zones.
5. Physical parameters driving the deformation
This experimental modelling reveals a more complex deformation pattern in a multilayer system affected by simple strike-slip boundary conditions than in a single-layer system (e.g., [Richard et al. 1991, McClay and Bonora 2001, Le Guerroué and Cobbold 2006]). These previous analogue modelling experiments explored the structural pattern in simple-layer experiments: only positive flower structures were generated. In our experimental study using a small-scale model with different cohesive layers, we generated positive and negative flower structures associated with different deformation modes in intermediate layers. The thickness variations in the most cohesive layers (glass microbeads) display smaller amplitudes. In other words, the less cohesive layers (Fontainebleau sand) are the most deformed layers. Thus, we advance the hypothesis that the difference in cohesion strength between two layers controls the changes in layer thickness, whereas the friction angle does not largely influence the fault geometry as indicated in the experiment with the sand and silica powder. In consequence, a deformation pattern characterized in a vertical section is not symptomatic of the boundary conditions. Folding or bulging does not necessarily result from regional compression, for instance, or a transpressive component imposed on the fault zone. However, the association of different deformation patterns both through depth (observed in a section) and along strike can be attributed to strike-slip boundary conditions in a multilayer set-up. Nemser and Cowan [2009] described a vertical change in fault pattern, which occurs where the lithology changes abruptly. We suggest that the rheological contrast between cohesive layers may drive the capacity to generate one type or two types of flower structure (positive or negative). It is possible that the local heterogeneities induce stress changes, which promote local shortening or thinning in a global context of horizontal shearing.
Schematic 3D block diagram showing the various structures affecting the layers in a strike-slip context. This work reveals that all these features coexist in the same experiment. The association of extensive and compressive features is symptomatic of strike-slip boundary conditions.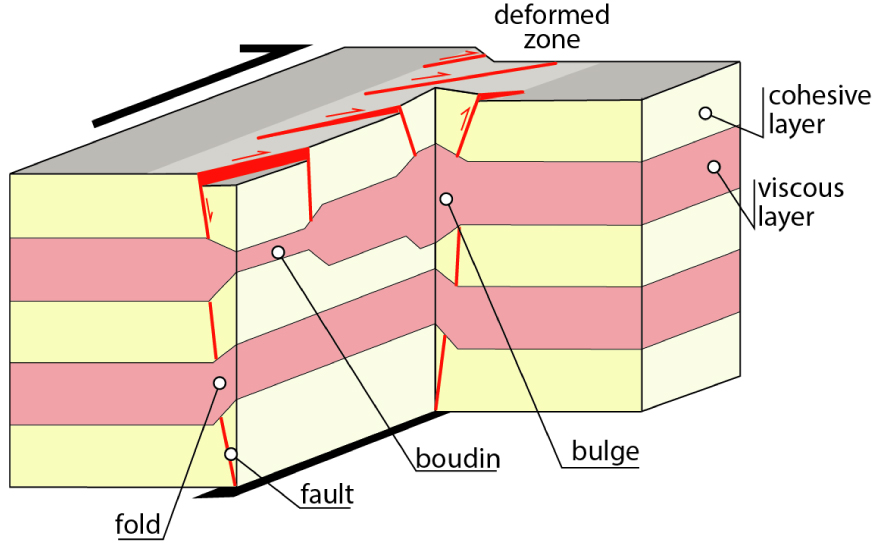
Strength ratio between layers (colour symbols) compared to the wavelength amplitude (grey vertical bars at bottom) for the five experiments. The strength ratio is estimated at each interface between two layers by dividing the deviatoric stresses of the sand layer by the deviatoric stresses of the silicone/microbead layer. The inset at top right shows the location where the strength ratios are estimated. Decro-1 displays the lowest ratio because of the low viscosity of the viscous layers and Decro-3 has the highest ratio because of the absence of viscous layers.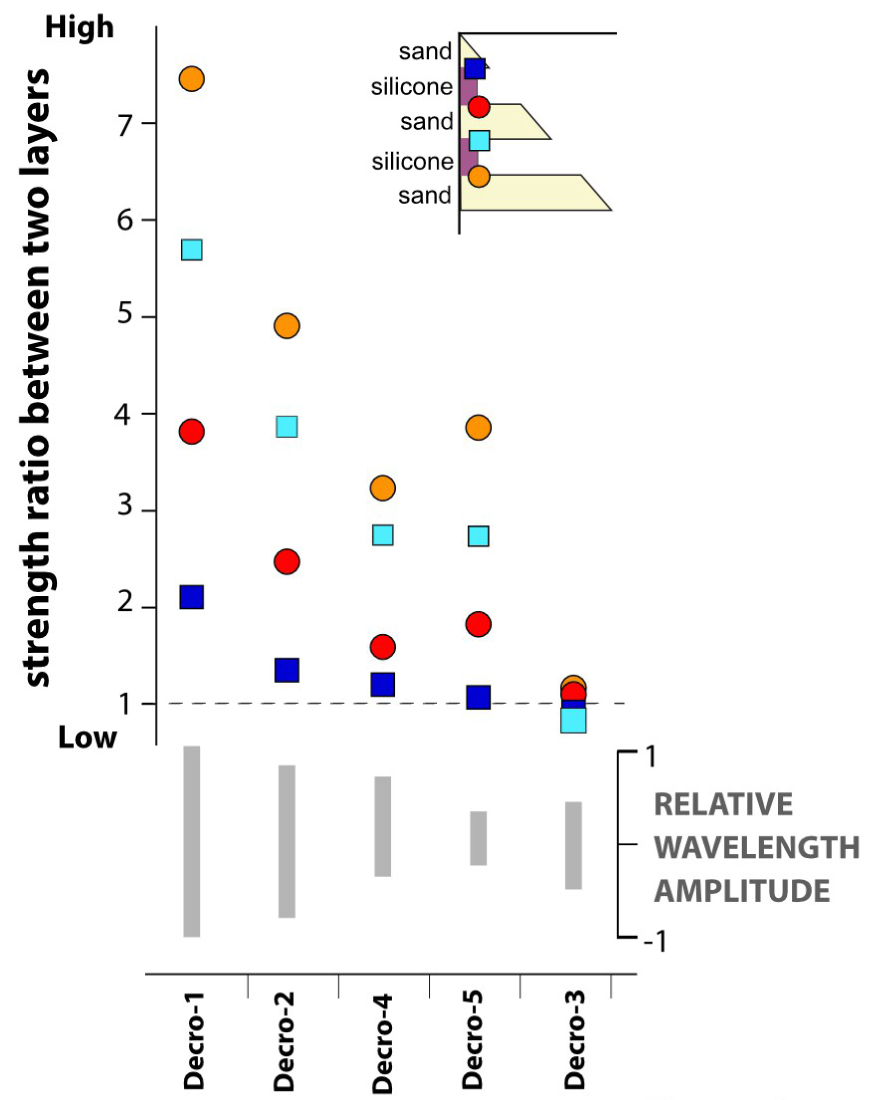
All the structures that affect the different layers are summarized in the 3D block diagram of Figure 5: strike-slip faults, normal oblique-slip faults and reverse oblique-slip faults for the cohesive layers and boudins, bulges and folds for the viscous layers. The spatial distribution of these features evolve along both strike and depth. The organization of the structures generates variations in layer thickness (thinning and thickening) out of phase between cohesive and viscous layers. The amplitude of the wavelength is different in each experiment and is directly linked to the strength ratio between cohesive and viscous layers (Figure 6). The higher the amplitude, the greater the strength ratio. The variations in the wavelength for the layer thickness clearly illustrate the importance of mechanical layering and of the coupling between different layers in the deformation distribution and pattern (Figure 6). The Decro-1 experiment, which has the highest mean strength ratio between the viscous and cohesive layers, displays the highest wavelength range, whereas the Decro-3 experiment, with the lowest mean strength ratio, displays a very small range of amplitudes for the wavelength deformation. Therefore, the main process that drives the deformation is the strength contrast between the different mechanical layers. The wavelength amplitude increases as the strength coupling decreases.
6. Conclusions
This experimental work highlights the fundamental role of rheological layering of a system in a strike-slip setting. The layering drives several characteristics of the deformed zone: the width of the shear zone, the fault pattern, the vertical displacements and the variations in thickness layers deformed in the shear zone. In the same experiment, thinning, thickening and folding domains alternate with a wavelength that is proportional to the whole thickness of the model. Rheological layering increases the number of faults generated relative to the experiment with only one layer. The amplitude of layer thinning/thickening is driven by the rheological coupling between different layers. Therefore, the interpretation of geological sections and seismic lines in a strike-slip setting is questioned. The proposed multiphase history must be reconsidered with caution if no 3D data set is available to constrain the 3D deformation pattern. A guideline for detecting unexpected strike-slip boundary conditions is the coexistence of thickening and thinning features in the same vertical section.



 CC-BY 4.0
CC-BY 4.0