1 Introduction
Exposure of clay soils to varying climatic conditions can induce settling that affects the structures built into these soils: shallow foundations, drainage channels, and the buffers of radioactive waste disposals. The complex hydromechanical behaviour of clay materials is basically connected to their fabric (Alonso et al., 1987, 1999; Gens and Alonso, 1992; Push, 1982), which has been the main subject of several studies on the micro- and macrostructure of soils (Al Mukhtar et al., 1996; Ben Rhaiem et al., 1986, 1998; Bruand and Tessier, 2000; Cui et al., 2002a; Cuisinier and Masrouri, 2005a; Hoffmann et al., 2007; Lloret et al., 2003; Nowamooz, 2007; Nowamooz and Masrouri, 2008; Nowamooz and Masrouri, 2009; Nowamooz and Masrouri, 2010; Pusch and Yong, 2003; Pusch et al., 1999; Wan et al., 1995). These studies have led to the development of an elastoplastic model for swelling soils (Alonso et al., 1999). This model takes into account the swelling and shrinkage accumulation of strain during the wetting and drying cycles and the equilibrium state reached at the end several wetting and drying cycles indicative of the elastic behaviour of samples (Al-Homoud et al., 1995; Alonso et al., 2005; Basma et al., 1996; Chen, 1965; Chu and Mou, 1973; Day, 1994; Dif and Bluemel, 1991). However, the influence of the initial state of the soil on the swelling and shrinkage accumulation and on the equilibrium state for the wetting and drying paths is necessary to be analysed.
The pore-size distribution (PSD) obtained by the mercury intrusion porosimetry (MIP) test has been used as an essential method in soil fabric studies. It has been observed that the double structural level is much more evident on the dry side of the optimum point of the compaction curve than on the wet side which shows a homogeneous structure (Barden and Sides, 1970; Collins and McGown, 1974; Sridharan et al., 1971). It has been observed that mechanical loading significantly influences the macropores without producing important modifications in the mesopores for compacted tills (Simms and Yanful, 2004) and for compacted bentonite (Hoffmann et al., 2007). Additionally, it will be helpful that the experimental MIP results be compared by the other soil fabric method such as nitrogen adsorption (BET) tests.
Further investigations are necessary regarding to the soil fabric of the swelling soils due to the hydric solicitations. Additionally, it can be examined that whether the soil's initial state (loose or dense) influences the soil fabric at the equilibrium state.
In this context, this article addresses the influence of the wetting and drying paths on soil fabric of compacted bentonite and silt mixtures at two different initial dry densities corresponding to loose and dense states.
2 Experimental techniques
The experimental techniques used in this study include osmotic and vapour equilibrium techniques for the suction imposition, MIP and nitrogen adsorption (BET) tests for the soil fabric.
2.1 Suction imposition and measurement techniques
The hydric behaviour of the samples was obtained using two different suction imposition techniques:
- • the first technique was the osmotic technique for suctions less than 8.5 MPa. The molecular weight of PEG chosen for these osmotic tests was 6000 Da (1 Dalton, Da = 1.6605 × 10−24 g), which makes it possible to impose a maximum suction of 8.5 MPa (Cuisinier and Masrouri, 2005b; Delage et al., 1998). A semi-permeable membrane (Spectra/PorR n84) was introduced in between the sample and the PEG solution to prevent PEG macromolecules from passing and moving toward the sample;
- • the second method used was the vapour equilibrium or the salt solution technique (Lide, 2002) with suctions between 8.5 and 287.9 MPa (Table 1).
Caractéristiques des sels sélectionnés.
| Saturated Salt solution | Solubilitya (g of salt per litre of water) | Relative humidity (%) | Imposed suction (MPa) |
| LiCl, x H2O | 827 | 12 | 287.9 |
| MgCl2, 6 H2O | 567 | 33 | 150.6 |
| K2CO3, 2 H2O | 1097 | 44 | 113.2 |
| Mg(NO3)2, 6 H2O | 689 | 54 | 83.6 |
| NaCl | 360 | 75 | 38.9 |
| KCl | 341 | 86 | 20.5 |
| KNO3 | 320 | 94 | 8.5 |
a Values from Lide (2002) given for 20 ± 0.1 °C.
To analyse the influence of several wetting and drying cycles on the soil fabric, fourteen samples of each studied soil were subjected to four successive suction cycles between 0 and 20 MPa. A suction of 20 MPa (close to the initial suction of both samples) was applied using the KCL salt solution (Table 1). To saturate several samples at the same time, the samples were put one over the other and placed in a PVC cylinder with a diameter slightly larger than the initial sample diameter, covered with porous stones on both sides and then immersed for 72 hours in demineralised water to reach a suction close to zero. At the end of each suction phase, two samples were taken one for the soil parameter measurements and the other for MIP tests. The following wetting and drying cycles were then applied to the remaining samples.
The total suction was measured using the filter paper technique (ASTM, 1995). The filter paper was introduced into the container without coming into contact with the soil so as to measure total suction. A period of 15 days is generally necessary to reach a state of equilibrium with the relative humidity in the measuring container.
2.2 Volume measurements
To obtain all the soil parameters, such as void ratio (e) and dry density (ρd) at the end of each suction phase, a petroleum product named Kerdane was employed to determine the volume of voids, and hence, the variation of volume during free wetting and drying processes (Tessier, 1975). The Kerdane contact angle is more than 90°, and therefore, it is a non-wetting fluid. Samples were weighed and then submerged in Kerdane. Total volume of the samples was then determined using Archimede's principle.
To obtain other soil parameters, such as water content (w) and saturation degree (Sr), the samples were dried in the oven at 60 °C. To check the complete dry state after 48 hours of drying in oven at 60 °C, some samples were also put in the oven at 105 °C for 24 hours: no additional mass change was observed.
2.3 Soil fabric tests
The MIP and BET tests were used to evaluate the PSD.
MIP tests were performed to evaluate the PSD of the studied materials. MIP tests were conducted using a porosimeter (Micromeritics Technology), where the mercury pressure was continuously raised from 0.007 to 450 MPa and the device was able to detect pore diameters ranging from 300 μm to 3 nm according to the Jurin-Laplace law , where the interfacial tension σ and the contact angle θ are 0.073 N.m−1 and 0° for water, r (μm) is the pore radius and s (MPa) is the suction. The MIP tests required dehydrated samples with volumes less than 3000 mm3 (limited by the sample holder and the cell stem volume). Starting with a prepared and compacted sample, the MIP specimens were carefully trimmed into cubes and subsequently freeze-dried to remove the pore water and placed in a desiccator until testing. Freeze-drying was selected for our MIP study as an alternative to oven drying to prevent the effects of shrinkage on drying. Soil pieces were quickly frozen with liquid nitrogen (temperature of −196 °C) and then placed in a freeze-drier at least 72 h for the sublimation of the water before the MIP tests. One assumption is that the larger pores can be intruded from the outside without the mercury having to penetrate through smaller pores. However, it is possible that large pores with a small access diameter are not intruded until high pressures are reached; as a result, their volume appears to be associated with much finer pores. Therefore, in this article we prefer to use the term “pore access diameter” rather than “pore diameter.”
The total pore volume, i.e., the volume of the pores in a predetermined pore-size range, can also be determined from the nitrogen adsorption (or desorption) test. Many parameters that describe the pore structure of a sample, for example the pore volume, specific surface area and PSD, can be determined. The specific surface area was estimated by Brunauer, Emmett and Teller (BET, Brunauer et al., 1938). It should be mentioned that we used the method by Barrett, Joyner and Hallenda (BJH, Barrett et al., 1951) to develop the PSD in nitrogen adsorption and desorption techniques. The pore-diameter range that can be determined is from 0.3 to 300 nm, and this range is not completely covered by mercury porosimetry (Delage et al., 2006; Lloret et al., 2003). With nitrogen adsorption, only the open pores are determined and the cylindrical pore model is assumed in PSD measurements using the BJH method. The desorption isotherm in the characterisation of the PSD is affected by the pore network; when the pressure is reduced, liquid will evaporate from large open pores, but pores of the same size that are connected to the surface with narrower channels remain filled (Allen, 1997). Consequently, the shape of the PSD of each method will be different.
The common parameter to these two MIP and BET methods is the PSD. The superposition of the results from these two methods generally agreed for cement-base materials (Diamond, 1971). This superposition was also made for soils (Bruand and Prost, 1987, Fiès, 1992; Fiès and Bruand, 1990, 1998; Reatto et al., 2009), but still further investigations are necessary.
3 Studied soils
The study was conducted with an artificially prepared mixture of 40% silt (natural soil coming from Xeuilly region close to Nancy city in France, Nowamooz, 2007) and 60% bentonite FVO (commercialized by Société Française de Bentonites et Dérivés [S.F.B.D.]). The mineralogical composition of the compacted materials was determined by X-Ray Diffraction (XRD). The silt contained 60% quartz, 20% montmorillonite, 11% feldspar, and the remaining part was made up of kaolinite and mica. The bentonite FVO was composed of more than 90% of calcium montmorillonite with the Cation Exchange Capacity (CEC) of 85 cmol + /kg (or meq/100 g). The main geotechnical properties of the materials and of the mixture are shown in Table 2. The particle size used to prepare the samples was less than 400 μm (obtained by sieving). The initial dry densities of the compacted soil were 1.27 and 1.55 Mg/m3, respectively, under two vertical pressures of 1000 and 3000 kPa and an initial water content of 15% in the dry side of optimum. In this paper, these samples are respectively called loose (L) and dense (D).
Caractéristiques des sols utilisés dans cette étude.
| Soil | Liquid limit (%) | Plasticity index (%) | Specific gravity (Gs) |
| Silt | 52 | 15 | 2.71 |
| Bentonite | 111 | 30 | 2.63 |
| Mixture | 87 | 22 | 2.68 |
The initial matrix and total suction of these samples, measured by the filter paper method (ASTM, 1995), was respectively about 20 ± 1 and 21 ± 2 MPa, and accordingly we can estimate the osmotic suction between 1 and 2 MPa. As the suction value can be considered independent of the mechanical loading for the samples compacted on the dry side of optimum (Nowamooz and Masrouri, 2008; Romero et al., 1999), the initial suction of all the compacted samples is considered to be 20 MPa at the initial water content of 15%.
As the osmotic suction term measured by the filter paper method was between 1 and 2 MPa for the studied soils, the matrix and total suctions imposed consequently by osmotic or vapour equilibrium techniques presented a good correspondence in the transitory suction value (8.5 MPa) between the two methods.
Fig. 1 presents the variation of incremental mercury intrusion volume versus the pore access diameter for both samples with different initial dry densities (L and D samples). Based on the classification of IUPAC (1997), the pores with widths exceeding about 0.05 μm are called macropores; those with widths not exceeding about 0.002 μm are called micropores and the pores of intermediate size are called the mesopores. The distributions show two distinct structural levels for the compacted bentonite-silt mixture: meso- and macropores. The dominant diameter of about 5 μm corresponds to the macropores of both samples. The mesopores present their peak at 0.011 μm. The peak of micropores cannot be detected by the mercury porosimetry results.
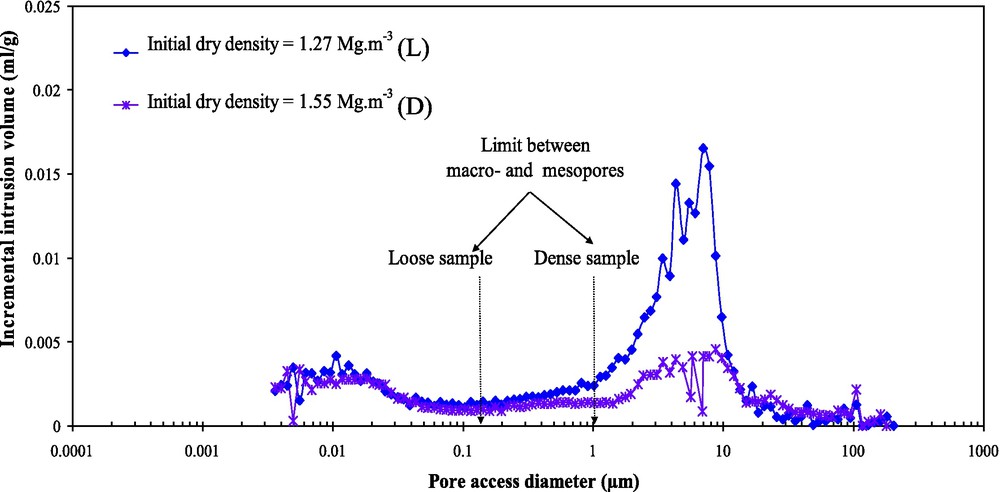
Results of mercury porosimetery test on densely and loosely compacted bentonite and silt mixtures.
Résultats des essais de porosimétrie au mercure sur le mélange de bentonite/limon compacté à l’état lâche et dense.
A wide range of pore size between 0.1 and 0.3 μm for the loose sample and between 0.1 and 2 μm for the dense sample can be taken as the boundary pore size between the macro- and mesopores. Further explanation on the pore-size limit between the macro- and mesopores will be given in the following section.
A nitrogen gas adsorption technique was then used to observe the smaller pores for both of the studied materials (adsorption path) in Fig. 2. The results show the existence of the micropores that could not be measured by the MIP tests when there was another dominant value. A pore diameter close to 0.002 μm can be considered as the pore-size limit between the meso- and micropores.
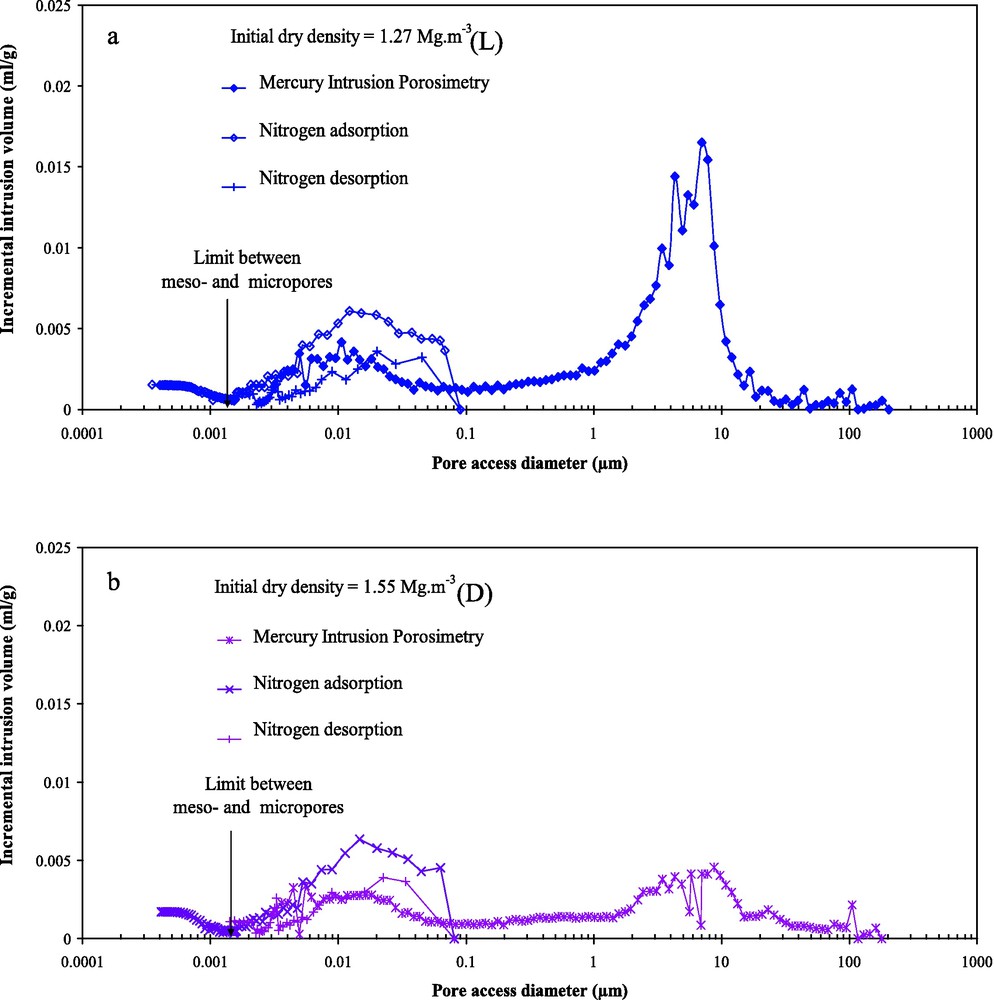
Results of mercury porosimetery and a nitrogen adsorption and desorption test on a compacted bentonite and silt mixture for a: a) loose sample and b) dense sample.
Résultats des essais de porosimétrie au mercure et de l’adsorption/désorption d’azote test sur le mélange de bentonite/limon compacté à l’état : a) lâche et b) dense.
Fig. 2 also compares the PSD between the nitrogen desorption and adsorption paths. It shows that there is a better correspondence between the experimental results of the mercury intrusion prosimetry (MIP) and nitrogen desorption technique. However, since the desorption path does not produce enough points to determine the micropores and consequently the diameter limit between the meso- and micropores, the adsorption path will be used to conclude on the influence of the suction cycles on the soil fabric (especially micropores) in the following section.
4 Cyclical controlled-suction tests and the soil fabric
In this section the influence of the wetting and drying paths on the soil fabric of the compacted bentonite and silt mixture is studied.
4.1 Hydric behaviour during a single cycle of wetting and drying
The variation in the void ratio relative to the suction (e-log s) is presented in Fig. 3 for the loose and dense compacted mixtures obtained using two suction imposition techniques for both samples (L and D samples): the osmotic and salt solution techniques. Points A and A′ indicate the initial state of the loose and dense samples, respectively, corresponding to an initial suction of 20 MPa and an initial water content of 15%. The initial diameter and height of the samples were 35 and 10 mm, respectively. Thereafter, a wide range of suctions between 0 and 287.9 MPa was applied to the samples with an initial suction of 20 MPa, producing a wetting path for the suctions between 0 and 20 MPa and a drying path for the suctions between 20 and 287.9 MPa. All of the saturated samples were finally dried again with a maximum suction of 287.9 MPa.
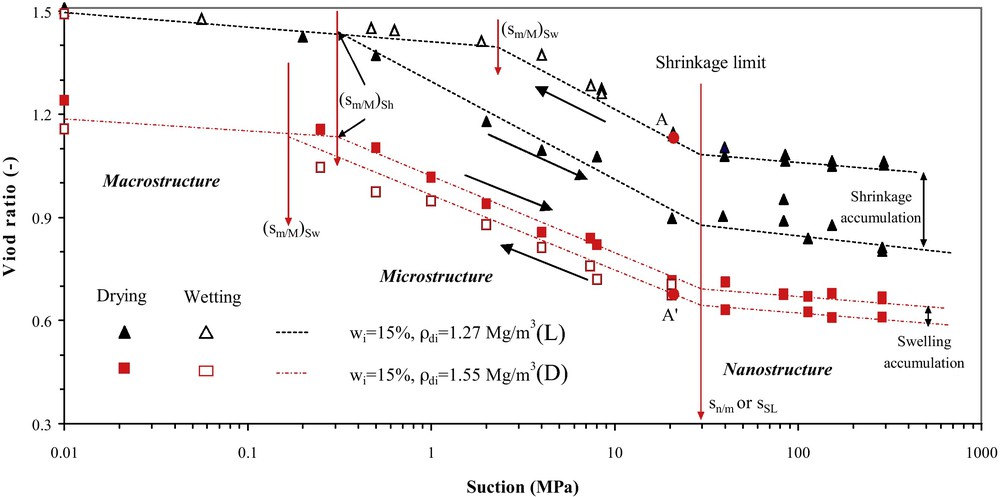
Void ratio variation of densely and loosely compacted bentonite and silt mixtures during a single wetting and drying cycle.
Variation de l’indice des vides du mélange de bentonite/limon compacté, aux états lâche et dense, lors d’un cycle de séchage et d’humidification.
The following conclusions can be drawn based on the results in the plane (e-log s) presented in Fig. 3:
- • the “shrinkage limit” suction (sSL) is estimated to be about 30 MPa for both samples with the curves presenting a slight slope variation for suctions higher than 30 MPa. This shrinkage limit suction is not influenced by either the wetting-drying cycles or by the soil's initial density;
- • another slope variation can be observed for the wetting and drying paths between 0 and 20 MPa. Since this suction limit is modified during the wetting and drying paths, we use the (sm/M)Sw term for the wetting path (swelling) and (sm/M)Sh for the drying path (shrinkage). The suction (sm/M)Sw is about 0.2 MPa for the dense sample and 2 MPa for the loose sample. Both samples present the same suction limit value (sm/M)Sh of 0.3 MPa during the drying path;
- • at the end of a single wetting/drying cycle between 0 and 20 MPa, the loose samples produced a shrinkage accumulation while the dense soil produced a swelling accumulation. The shrinkage or swelling accumulation of the samples can be inferred from the (sm/M)Sw and (sm/M)Sh values, depending on whether the initial (sm/M)Sw value is higher or lower than the initial (sm/M)Sh value for the loose and dense samples.
The suction limits estimated at 2 MPa for the loose samples and 0.20 MPa for the dense samples in Fig. 3 can be related to a diameter limit about 0.15 μm for the loosely compacted samples and 1.50 μm for the densely compacted samples according to Jurin-Laplace equation (while neglecting the adsorption phenomenon). We select these diameters as the pore size separating the macro- and mesopores in Fig. 1.
Since the adsorption phenomenon controls the suction value, the Jurin-Laplace law cannot be applied to the pore sizes to estimate the sn/m value. The shrinkage limit suction (sSL) of 30 MPa may be a good option for this suction limit value between the meso- and micropores (sn/m).
4.2 Hydric behaviour during several wetting and drying cycles
Fig. 4 shows the void ratio variations versus the suction for both loose and dense compacted samples (L and D samples) during several wetting and drying cycles between 0 and 20 MPa. The dense samples produced a cumulative swelling strain during the suction cycles, while a shrinkage accumulation was observed for the loose samples. This swelling or shrinkage accumulation is more intensive during the first suction cycle. The suction cycles reached a unique equilibrium state on account of the elastic behaviour of the samples.
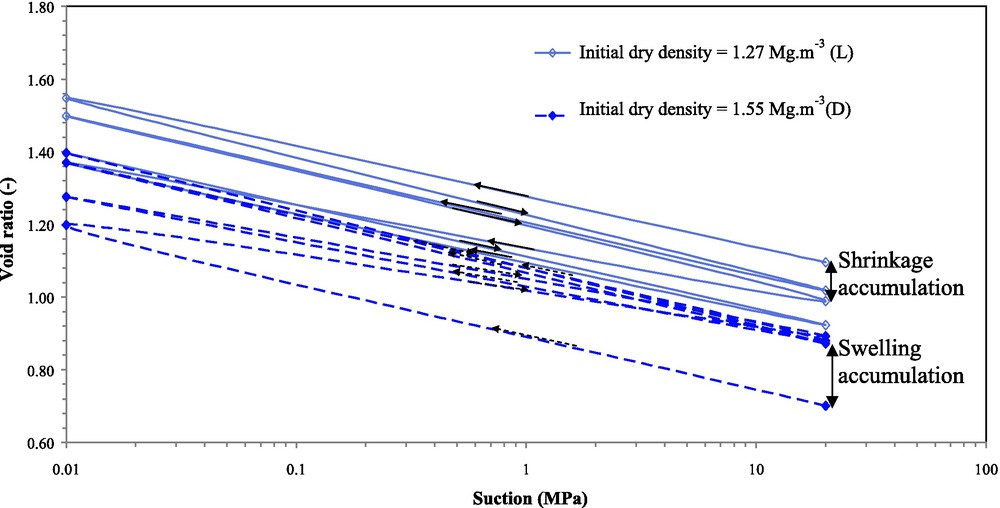
Variation of the void ratio in cyclic controlled-suction paths at a null vertical stress for densely and loosely compacted bentonite and silt mixtures.
Variation de l’indice des vides du mélange de bentonite/limon compacté, aux états lâche et dense, lors de plusieurs cycles de succion sous une contrainte verticale nulle.
The void ratio corresponding to a suction of 20 MPa is 0.92, corresponding to an initial dry density of 1.40 Mg/m3 that we defined as the elastic void ratio (e0el). If the soil was initially compacted at this initial dry density, the wetting and drying cycles would produce no shrinkage or swelling accumulation. In other words, the samples prepared at this void ratio have a completely elastic behaviour for all the imposed suctions.
MIP and nitrogen gas adsorption tests were also carried out during the last wetting and drying cycles at suctions of 0 and 20 MPa for both samples (L and D samples). At the equilibrium state, the samples with different initial macropores (Fig. 1) showed very similar structures (Figs. 5 and 6). At the suction of 0 MPa, the dominant diameter of the macropores attained a maximum value of 50 μm, while a minimal value of 20 μm was obtained at the dry state (s = 20 MPa). Both techniques showed that the suction cycles did not influence the small pores of neither the mesopore nor the micropore.
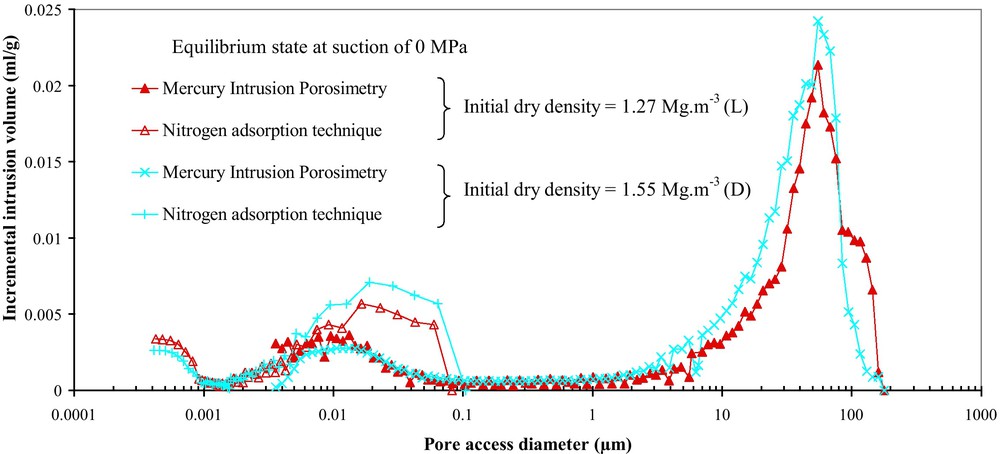
Soil fabric of densely and loosely compacted bentonite and silt mixtures after four wetting and drying cycles at a suction of 0 MPa.
Structure interne du mélange de bentonite/limon compacté, aux états lâche et dense, après l’application de quatre cycles de séchage et d’humidification à la succion de 0 MPa.
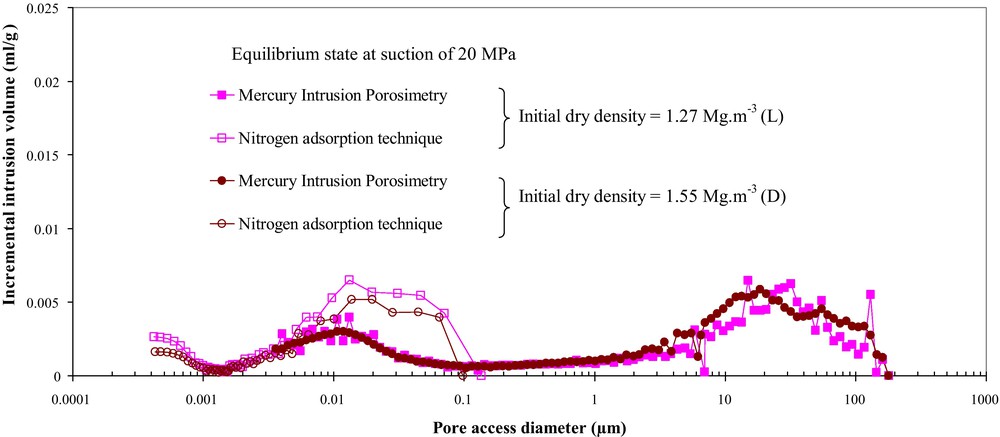
Soil fabric of densely and loosely compacted bentonite and silt mixtures at the end of four wetting and drying cycles at a suction of 20 MPa.
Structure interne du mélange de bentonite/limon compacté, aux états lâche et dense, après l’application de quatre cycles de séchage et d’humidification à la succion de 20 MPa.
At the equilibrium state, the evolution of the incremental mercury intrusion volume versus the pore access diameter was compared with the previous MIP and nitrogen gas adsorption results for the loosely and densely compacted samples (L and D samples in Figs. 7 and 8).
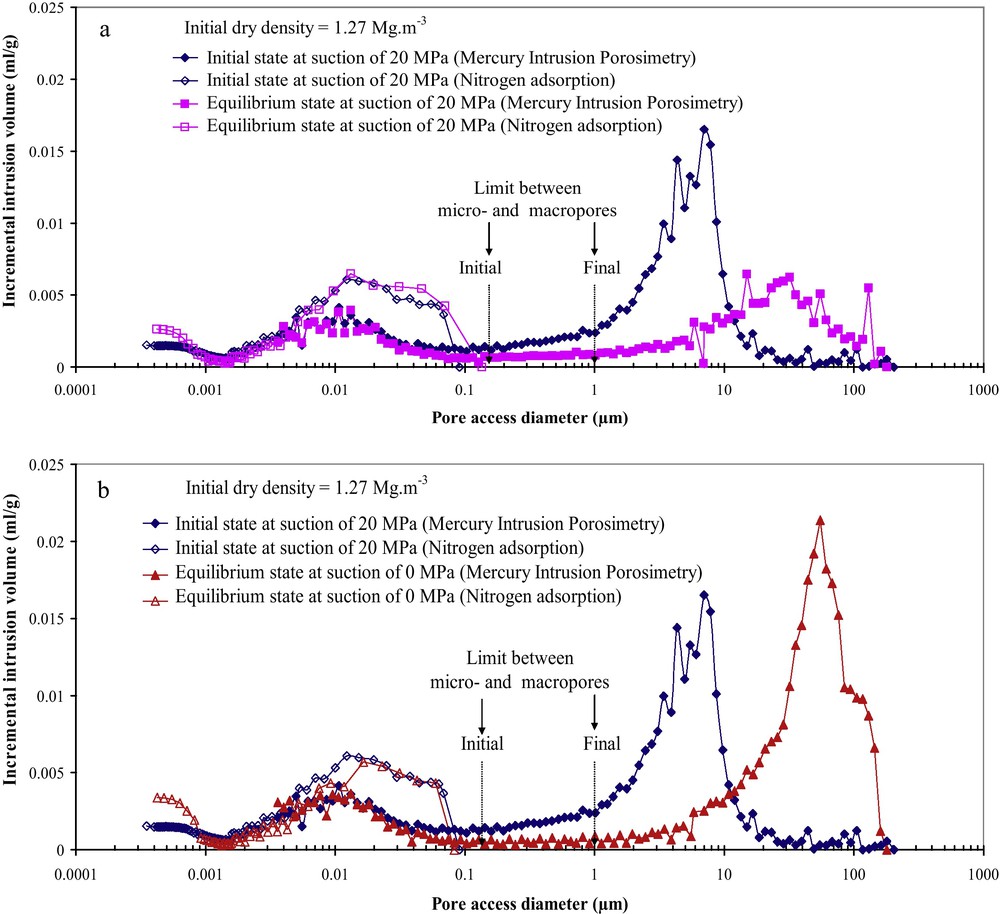
Influence of suction cycles on the soil fabric of a loosely compacted bentonite and silt mixture: a) at the suction of 20 MPa and b) at the saturated state.
Influence de cycles de succion sur la structure interne du mélange de bentonite/limon compacté à l’état lâche : a) à la succion de 20 MPa et b) à l’état saturé.
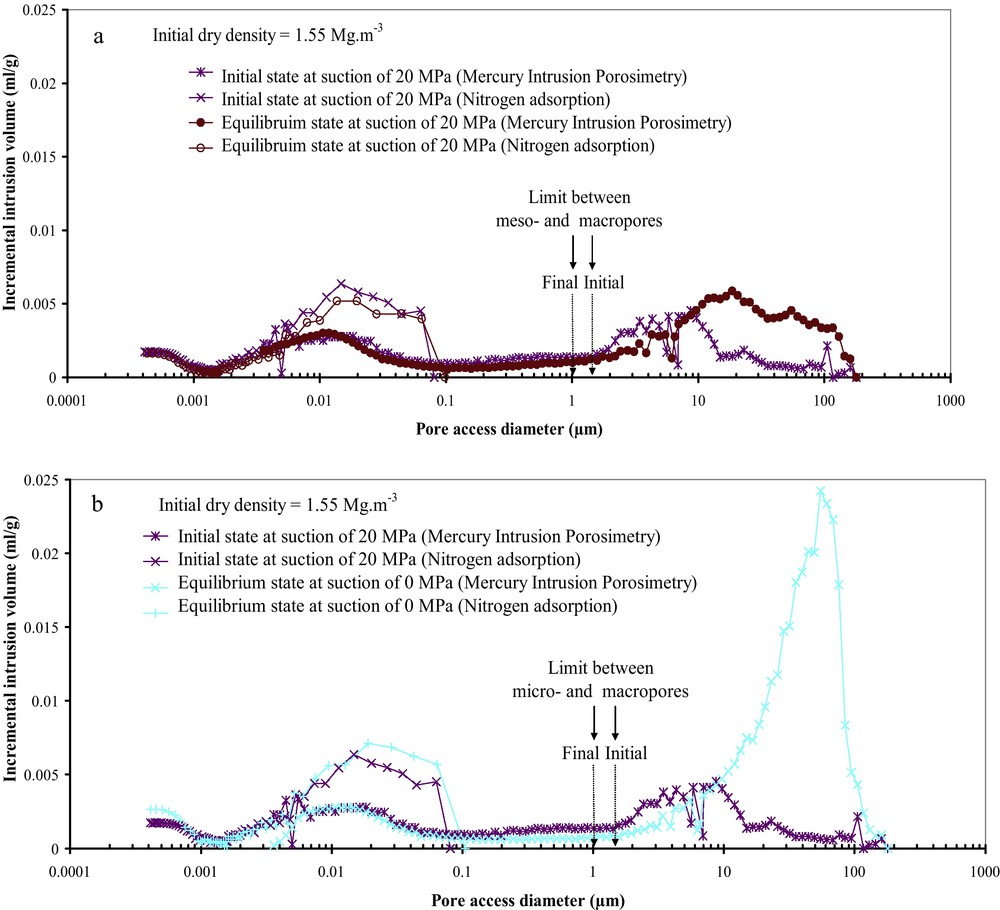
Influence of suction cycles on the soil fabric of a densely compacted bentonite and silt mixture: a) at the suction of 20 MPa and b) at the saturated state.
Influence de cycles de succion sur la structure interne du mélange de bentonite/limon compacté à l’état dense : a) à la succion de 20 MPa et b) à l’état saturé.
Based on the experimental results presented in Fig. 3, since the (sm/M)Sh value was not modified by the drying path for both studied materials, we propose this constant suction value of 0.3 MPa as the final suction limit for the meso- and macropores at the equilibrium state. In this state, a constant diameter limit of 1 μm can be taken between the meso- and macropores for both samples in Figs. 7 and 8.
For the loose soil, a comparison of the initial and final states at the suction of 20 MPa shows that the suction cycles significantly decreased the size of the macropores due to shrinkage accumulation during the suction cycles (Fig. 7a). At the equilibrium state, the wetting and drying cycles respectively decreased and increased the size of the largest macropores (Fig. 7b).
On the other hand, the macropores of the dense sample increased at a suction of 20 MPa (Fig. 8a). The results showed the same pattern for the largest macropores during the last wetting and drying cycles (Fig. 8b).
Based on the results presented in Figs. 5–8, we can state that in general at the equilibrium state after several hydric cycles:
- • the diameter limit between the meso- and macropores decreased from 1.5 to 1 μm for the dense sample, and increased from 0.15 to 1 μm for the loose samples,
- • the defined limit of 0.002 μm for the meso- and micropores is not modified for both of the studied samples, and
- • multi-structural soils reached the elastic void ratio (e0el) showed less active macropores. In this stage, the distance between macro- and mesopore mode reaches its maximum value.
We compared the nitrogen gas adsorption technique with the MIP results (Figs. 5–8) to confirm that the diameter limit between meso- and micropores was not modified by the suction cycles, although the correspondence between these two methods is not completely satisfying. It should be mentioned again that the nitrogen gas desorption technique produces a better agreement with the MIP results for all of the performed tests, but there were not sufficient points for the pores smaller than the diameter limit for the meso- and micropores.
5 Discussion
The successive wetting and drying cycles cause the value of (sm/M)Sw to approach (sm/M)Sh. Since the initial (sm/M)Sw and (sm/M)Sh are closer for the dense samples, we suppose that a small number of wetting and drying cycles are necessary to reach the equilibrium state. At the equilibrium state, the hydric cycles may stabilise the (sm/M) suction limit at a value of 0.3 MPa for both samples. A diameter limit of 1 μm can be related to this suction value according to Jurin-Laplace equation.
The surface limit between micro- and mesopores (sn/m) in this study is not activated during the hydromechanical tests. This value can be estimated as close to 30 MPa, which is the suction of the shrinkage limit.
The state variables employed for the initially developed elastoplastic constitutive models for unsaturated soils include the following: the net stresses (σv or p), the suction (s), and the specific volume (v = 1 + e) (e.g., Alonso et al., 1990, 1999). Several models for unsaturated soils have added a degree of saturation (Sr) to the term for effective stress (σ’v = σv + Sr × s or p′ = p + Sr × s), to explain the complex behaviour of these soils (Gallipoli et al., 2003; Laloui and Nuth, 2005; Wheeler et al., 2003). For swelling unsaturated soils, we suggest that the elastic void ratio (e0el) is another independent parameter. The compacted soils at this state present an elastic hydric behaviour for the different suctions.
6 Conclusion
The experimental results made it possible to define the suction limit between macro- and mesopores (sm/M) and the suction limit between the meso- and micropores (sn/m). The suction limit (sm/M) completely depended on the soil fabric and the diameter separating the macro- and mesopores. The (sn/m) can be taken equal to the “shrinkage limit” suction.
This article also showed the influence of successive wetting and drying cycles on the soil fabrics of loosely and densely compacted bentonite and silt mixtures. In general, we found that the suction cycles stabilised the (sm/M) at an estimated value of 0.3 MPa without modifying the value of (sn/m) estimated close to 30 MPa.
We predict that there is an elastic void ratio (e0el) for which the compacted sample produces no volumetric strain accumulation during the wetting and drying cycles. It could be considered that the equilibrium state is a characteristic of the soil, with loose and dense samples of the same soil presenting the same hydric behaviour.


