Capillary force due to water between two grains of soil
DDiameter of soil's particles
u aPressure in the air phase
s eSuction of air entry
u wPressure in the water phase
σcCapillary stress
A REVCross-sectional area of the REV in the plane normal to the direction observed
γWater-air surface tension
eVoid ratio
RA non-physical parameter to fix yield function
sSuction
pTotal mean stress
p′Effective mean stress
qDeviatoric stress
TTemperature
M(T)Slope of critical state line influenced by temperature
p′c(σc, T)Preconsolidation stress influenced by capillary stress and temperature
a1, a2Parameters defining thermal softening curve
αThermal expansion parameter
λ(σc)Stiffness parameter for changes in effective mean stress for virgin states of the soil influenced by capillary stress
κElastic stiffness parameter for changes in effective mean stress
kParameter controlling the rate of increase of preconsolidation stress with suction
e 0Initial void ratio
GShear modulus
dɛveIncrement of elastic volumetric strain induced by changes in effective mean stress or temperature
dɛvpIncrement of plastic volumetric strain induced by changes in effective mean stress or temperature
dɛseIncrement of elastic deviatoric strain induced by changes in deviatoric stress
dɛspIncrement of plastic deviatoric strain induced by changes in deviatoric stress
1 Introduction
Thermohydromechanical (THM) behaviour of unsaturated soils is a subject of interest for civil engineers, for example, in the use of geothermal energy or for nuclear waste disposal. Over the past three decades, the study of THM behaviour and non-isothermal mass flow in porous media has been a key area of research in environmental geomechanics.
Many studies have been carried out in the last forty years concerning the impact of temperature changes on saturated soil behaviour during isotropic and oedometric loadings. Studies had for object the influence of temperature on preconsolidation stress (Eriksson, 1989; Tidfors and Sàllfors, 1989), on stiffness parameters (cs or κ and cc or λ) (Burghignoli et al., 2000; Campanella and Mitchell, 1968; Cekerevac and Laloui, 2004; Despax, 1976; Eriksson, 1989; Fleureau, 1972; Graham et al., 2001; Tidfors and Sàllfors, 1989) and the evolution of thermal conductivity on a thermo-hydro-mechanical path (Djéran-Maigre, 1993; Djéran-Maigre et al., 1997).
Concerning the failure criterion, defined by the slope M of the critical state line in the (p′, q) stress plane, the experimental results obtained by several researchers show some divergence: Belanteur et al. (1997), Burghignoli et al. (2000), De Bryn (1999), Despax (1976), Hicher (1974), Hueckel and Pellegrini (1989), Hueckel and Baldi (1990) noted a reduction of the slope M with temperature. Other results were obtained by Cekerevac and Laloui (2004), Graham et al. (2001, 2004), Hueckel and Pellegrini (1989) and highlighted the absence of influence of temperature on M. All these results led us to be particularly attentive concerning the kind of material tested, the initial state and the way of preparation of the specimens. Hueckel and Baldi (1990) and Cekerevac and Laloui (2004) showed that the reduction of the strength of soils with temperature is amplified for low values of the OCR.
In the case of unsaturated soils, there are few results in the literature (Recordon, 1993; Saix, 1991; Saix et al., 2000; Romero, 1999; Weibe et al., 1998). On triaxial paths, Romero (1999) on Boom clay and Weibe et al. (1998) on samples of compacted sand-expansive clay mixtures, showed a contraction of the yield surface with temperature at any suction. On the other hand, the works of Jamin et al. (2004) showed a thermo-dilatancy of the yield surface for samples of sand-loam mixture. These observations highlight the major role of the clay fraction of the soil on the yield surface change (El-Youssoufi, 2006).
1.1 Modelling
Two points of view have been proposed in literature to model the THM behaviour of unsaturated soils, one based on independent stress analysis (Alonso et al., 1990; Mathyas and Radhakrishna, 1968), and the other, on the effective stress concept.
In the latter case, it is admitted that, as for saturated soils, the behaviour of unsaturated soils depends only on one parameter, which is the combination of stress and suction. This concept, in association with a hardening model of soil with suction, presents many advantages, in particular because it assures a continuous passage from saturated to unsaturated medium. The validity of the model highly depends on the correct definition of the capillary stress which is the contribution of suction to the effective stress (Aboubekr, 1995; Biarez et al., 1993; Modaressi and Aboubekr, 1994; Loret and Khalili, 2002; Taibi, 1994). Under non-isothermal conditions, the expression of the constitutive laws for unsaturated soils is formulated in the same way as under isothermal conditions. Lewis et al. (1986, 1998) have developed a finite elements model for studying the hydromechanical behaviour and heat transfer in saturated and unsaturated porous media.
Recently, two new models, one based on a generalised effective stress concept (Loret and Khalili, 2002), and the other one based on the independent variable approach (Wenhua et al., 2004), have been developped. In their model, Loret and Khalili (2002) propose a thermohydromechanical model for unsaturated soils, based on the effective stress definition of Bishop, with the χ parameter being a function of suction. On the other hand, for Wenhua et al. (2004), the THM model for unsaturated soils is an extension of the thermomechanical models for saturated soils proposed by Hueckel and Borsetto (1990) and Cui et al. (2000).
2 Thermohydromechanical model for unsaturated soil
2.1 Effective stress in unsaturated soils
A simple way to define effective stresses is to start from the expression of the intergranular forces between two particles in an idealized medium at the microscopic scale (Aboubekr, 1995; Biarez et al., 1993; Taibi, 1994). The method consists in calculating the capillary force Fcap due to water between two grains of soil modelled by rigid spheres with the same diameter D (Fig. 1).
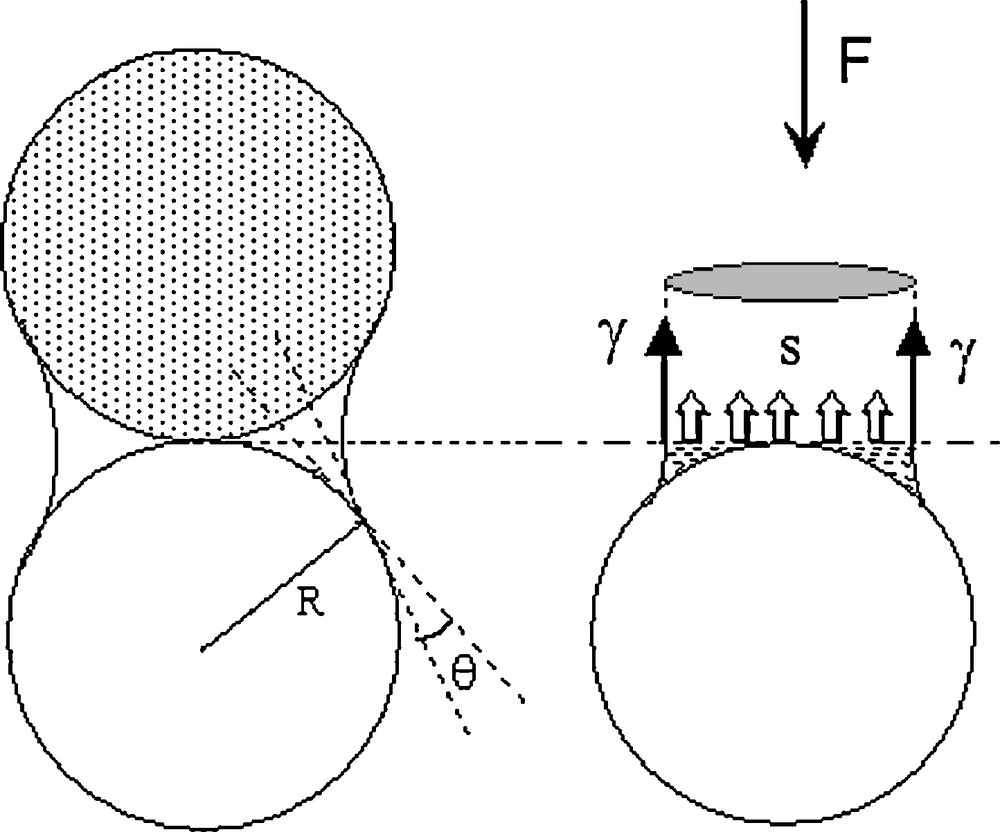
Schematic representation of two particles bonded with meniscus.
Représentation schématique de deux particules liées par un ménisque.
In a representative elementary volume (REV), the capillary stress σc in any direction is defined by:
| (1) |
| (2) |
| (3) |
Fig. 2 illustrates the transient between the two cases in the (s, σc) plane. For the highest suctions, capillary stress reaches a horizontal asymptote, where σc is equal to σcmax defined as:
| (4) |
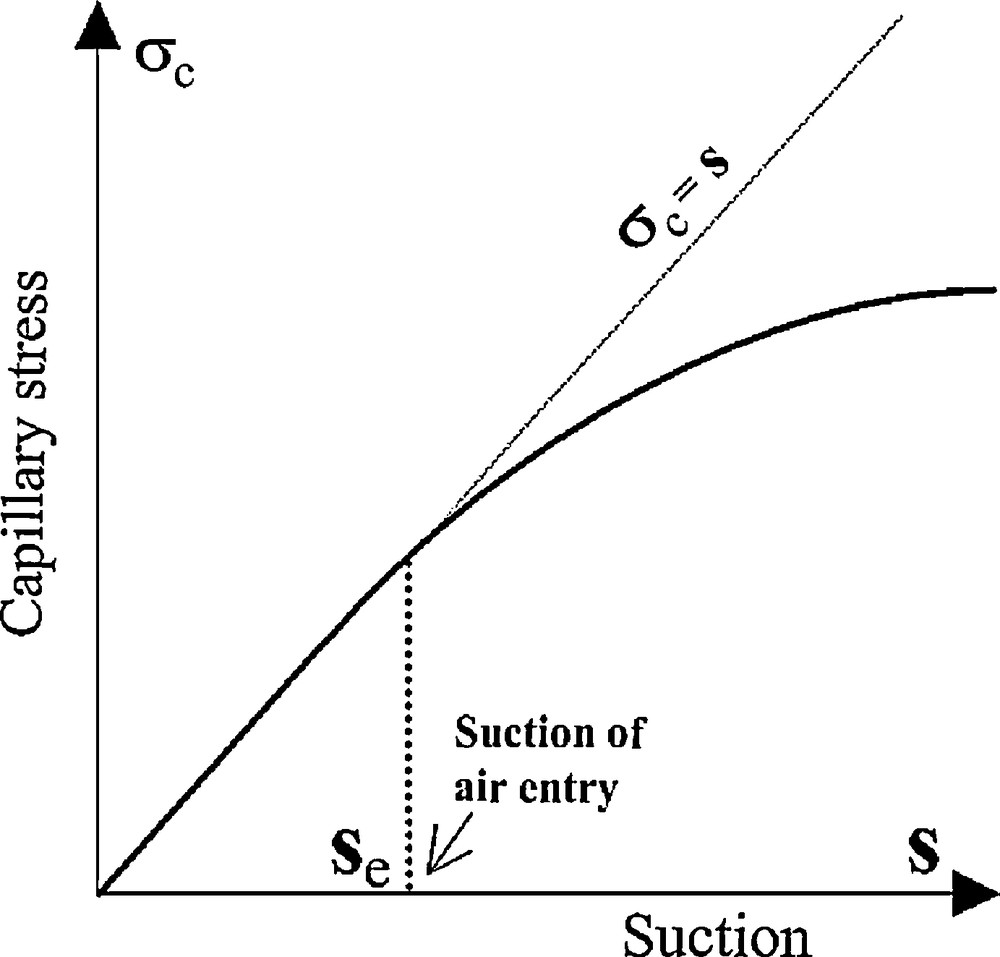
Capillary stress σc as a function of suction s.
Contrainte capillaire σc en fonction de la succion s.
The capillary stress appears as an isotropic pressure, that replaces the matrix suction when the water phase is discontinuous. The expression of the effective stress tensor becomes:
| (5) |
When considering a real soil with different diameters of particles, the determination of the capillary stress is difficult, because of the need to choose a “characteristic diameter” D equivalent to the real grain-size distribution. In practice, this diameter is a parameter of the model and must be derived from experimental data (Biarez et al., 1993, 1994).
2.2 The elastoplastic general framework
The purpose of the model presented in this article is to associate the capillary stress defined for unsaturated soils in the previous part with an elastic-plastic behaviour law like Modified Cam-Clay. The yield function used in this model is based on the Khalili and Loret (2001) yield function in which suction is replaced by the capillary stress σc. Moreover, the increase of preconsolidation stress with suction is proposed and defined as a function p′c(σc) = f((pc0, k, σc) where k is a parameter depending of soils. The thermal effect is coupled in the model with the thermal softening curve as explained by Wenhua et al. (2004).
Concerning the influence of temperature on M, the slope of the critical state line in the plane (p′,q), experimental results (De Bryn, 1999; Despax, 1976) show a decrease of M and qmax with temperature. These results lead us to introduce a function defining the evolution of M with temperature as follows:
| (6) |
The yield function is described by two distinct expressions depending on the
| (7) |
| (8) |
2.3 The thermal and the capillary stress softening curves
Many authors have carried out thermomechanical tests consisting in oedometric and triaxial loadings, under constant temperature, on overconsolidated samples in a saturated state. They have observed a nonlinear decrease in the preconsolidation stress when the temperature increases (Eriksson, 1989; Ghembaza, 2004; Tidfors and Sàllfors, 1989). This form was adopted to define a yield surface in the (p′, T) plane by Hueckel and Borsetto (1990) and also by Wenhua et al. (2004) who used it in their model as thermal softening curve (TS). This expression has the following form:
| (9) |
| (10) |
| (11) |
To couple the effect of temperature with that of suction, the relationship is derived from that of Wenhua et al. (2004) in which suction has been replaced by capillary stress. The relationship between the preconsolidation pressure p′c(σc, T), the capillary stress and temperature T in unsaturated soils becomes:
| (12) |
For this coupling between temperature and capillary stress for unsaturated soils, p′c0(T) must first be calculated from p′c0 using the TS relation then p′c(σc, T).
The response of the volumetric elastic strain to a change in p′ and temperature T becomes:
| (13) |
| (14) |
2.4 Plastic behaviour
The set of constitutive equations for the plastic part consists in the following incremental relations. For an isotropic test in which a soil sample, at a given suction, is submitted to mechanical load increments along the normally consolidated (NC) line, the incremental volumetric plastic strain is given by:
| (15) |
For suction values higher than se, p′c(σc) increases faster than p′ and this leads to hardening of the soil. Consequently, only elastic strains occur.
Concerning NC or slightly overconsolidated (OC) materials at ambient temperature, an increase in temperature induces volumetric plastic strains due to activation of Thermal Softening mechanism (TS). If p′c(σc, T) > p′, the preconsolidation stress p′c(σc, T) decreases when temperature increases and p′c(σc, T) is equal to the effective mean stress p′ in some cases. For these particular cases, the preconsolidation stress decrease is stopped because p′c(σc, T) cannot be lower than p′. Plastic strains appear and are calculated as indicated below:
| (16) |
| (17) |
| (18) |
3 Simulations of typical phenomena of unsaturated soils
Table 1 gathers the parameters used for simulations below.
3.1 Collapse path
In unsaturated soil, wetting under constant net mean stress may result in collapse (volumetric contraction). When an unsaturated soil is loaded then wetted, the preconsolidation stress p′c(σc, T) decreases faster than the effective mean stress p′. As long as p′c(σc, T) is higher than p′, elastic swelling is observed and may be calculated using relation (13). When p′c(σc, T) is equal to p′, the yield surface evolves to produce only irreversible contraction calculated with relation (16).
Fig. 3 illustrates collapse. The corresponding stress path is shown in Fig. 3a. The soil is first dried to a suction of 5 MPa (larger than the air entry suction se = 1 MPa). Afterwards, mechanical loading is applied up to p = 1000 kPa with p′ = p′c(σc), followed by a wetting path (Fig. 3b). During this wetting step, capillary stress decreases like p′c(σc) and irreversible contraction appears (Fig. 3c) highlighting the collapse phenomenon. This phenomenon takes place as long as s > se. When s < se, elastic swelling is observed (Fig. 3c).
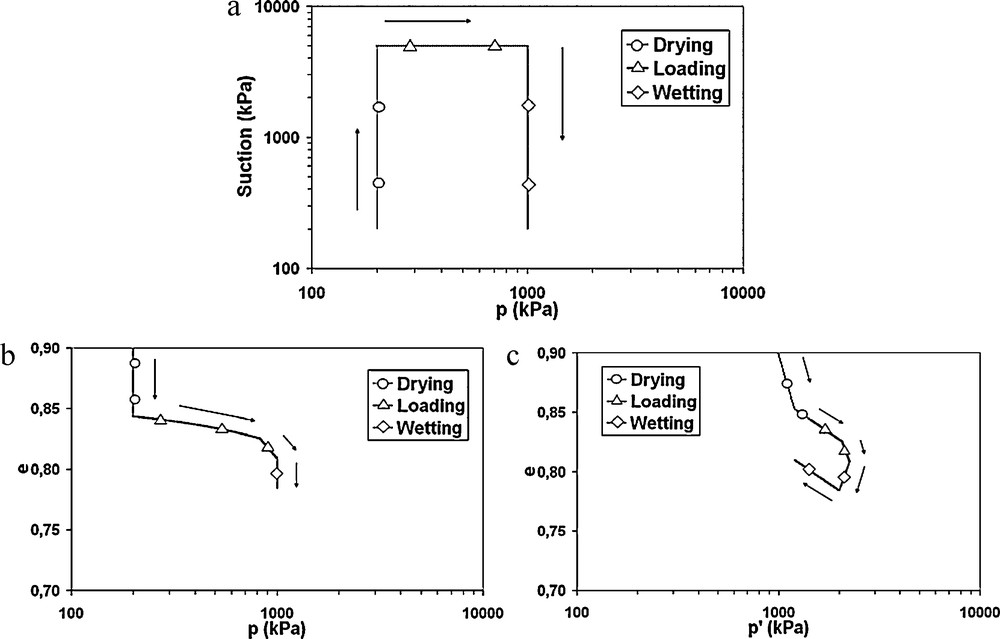
Wetting and drying cycle path in current soil mechanic planes normally consolidated soil.
Cycle de dessiccation-humidification dans les plans usuels pour un sol normalement consolidé.
3.2 Coupled drying-heating loading
Fig. 4 shows a coupled drying-heating path with a constant total stress (p = 200kPa) on normally consolidated samples in the (T, e), (ln s, e), (ln p′, e); (s, p′c) and (T, p′c) planes. During the drying step, the same observations as those described in section 3.1 for the drying path can be done. After the drying step, a heating path is simulated by a temperature increase. At the beginning of the heating, the behaviour is elastic as evidenced by the yield surface position (Fig. 4b), and the preconsolidation stress p′c(σc) which is larger than the effective mean stress p′. The behaviour is first elastic with thermal expansion and the preconsolidation stress decreases according to the relation 20.
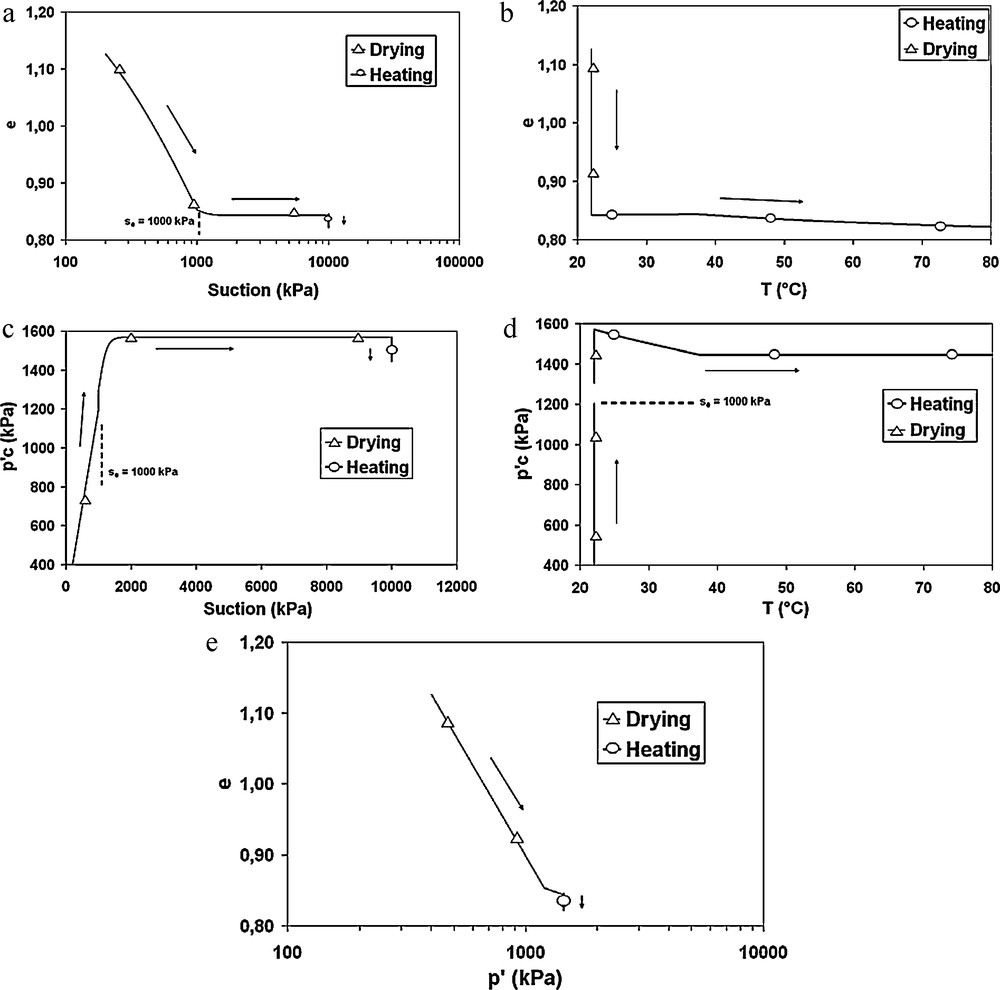
Drying and heating on normally consolidated soil.
Dessiccation et chauffe d’un sol normalement consolidé.
As long as temperature continues to increase, p′c(σc, T) is equal to p′, temperature continues to increase and results in irreversible deformations and irreversible contraction as shown in Fig. 4b. In this case, p′c(σc, T) keeps a constant value, as shown in Fig. 4e.
This simulation on a normally consolidated sample shows the predominant effect of the drying path in the saturated zone, which induces the larger part of total and plastic strains. Concerning reversible strains, the part linked to the drying path in the unsaturated zone is larger than the part linked to heating but stays of the same order of magnitude (Fig. 4a and b).
3.3 Deviatoric path under constant suction and imposed temperature
Fig. 5 shows the effect of temperature on the coefficient M, the slope of the Critical State Line in the (T, M) plane (Despax, 1976). When the sample is heated from 22 °C to 80 °C, M decreases from 0.8 to 0.4.
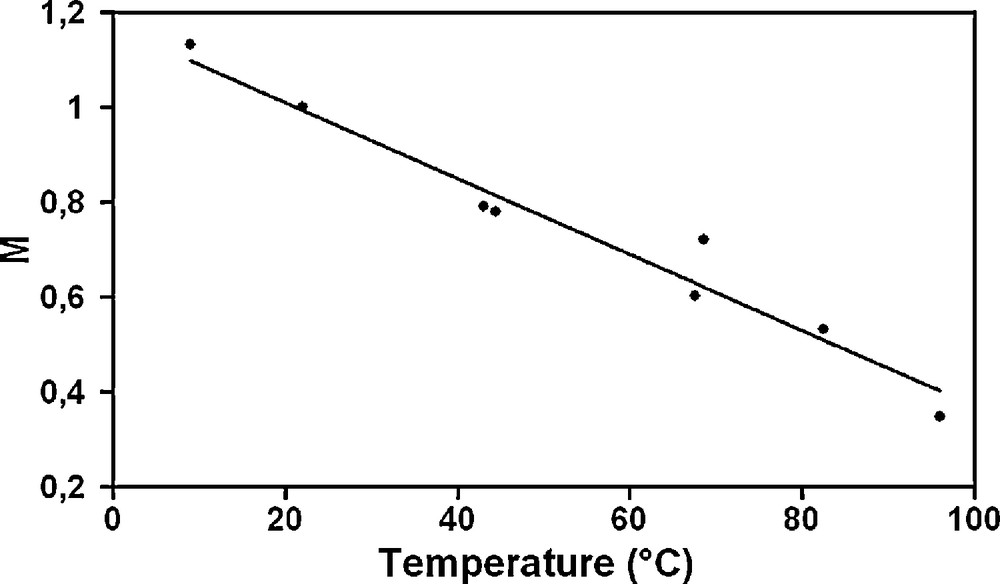
M as a function of temperature T (Despax, 1976).
M en fonction de la température T (Despax, 1976).
Fig. 6 shows the results of two triaxial tests at reference temperature (T = 22 °C) and high temperature (T = 80 °C) under constant net mean stress (p = 800 kPa) and suction (s = 10 MPa), higher than air entry suction value (se = 1000 kPa) in the (ɛ1, q), (p′, q), (ɛ1, e), (ln p′, e) planes. Both samples have been first isotropically consolidated in saturated state at ambient temperature up to p = 800 kPa. Then, suction (s = 10 MPa) has been applied and one of it has been heated to 80 °C before starting triaxial tests.
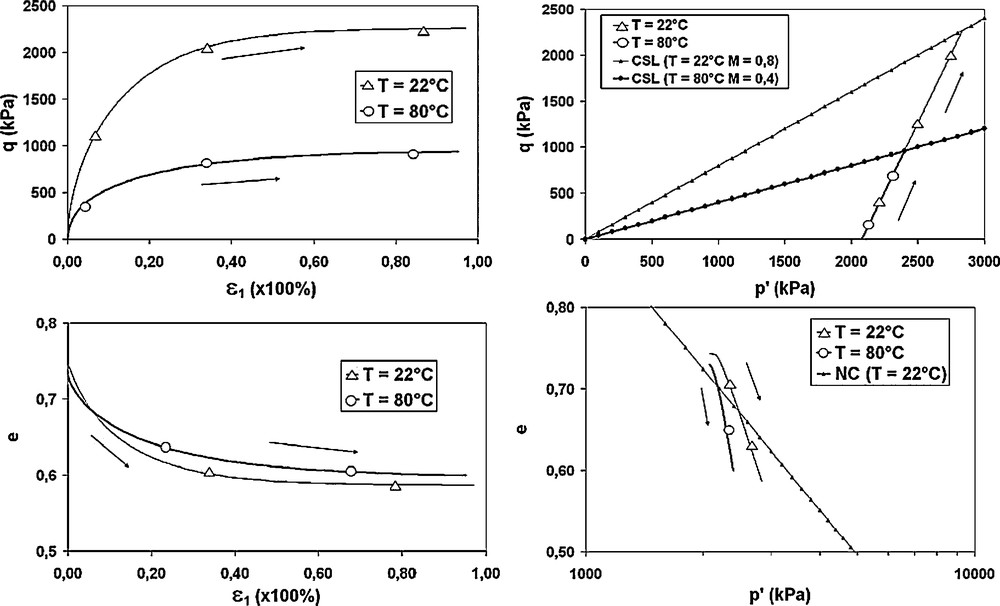
Triaxial tests with constant suction and imposed temperature.
Essais triaxiaux à succion constante et température imposée.
For the sample at ambient temperature, the path is first elastic then elastoplastic. This phenomenon is due to suction and capillary stress that increase the preconsolidation stress p′c(σc) and consequently the yield surface. Elastic strains are calculated by relation (13). When the yield surface is activated, elastic and plastic strains occur that are estimated by the increase in the preconsolidation stress and flow rules described in section 2. In the (q, ɛ1) plane, the elastic part of the strains for the test at 80 °C is smaller than those calculated for the test at reference temperature. For the sample heated before the triaxial test, the preconsolidation stress is reduced with the yield surface contraction. The behaviour is only elastoplastic (Fig. 6a), because with thermal expansion, the preconsolidation stress decreases according to the relation (12) and p′c(σc, T) is equal to p′ when triaxial test begins. Both samples reach a plateau for different values because the slope of the Critical State Line decreases and the failure criterion is reached for a lower effective mean stress p′.
For sample at ambient temperature, the void ratio first follows a straight line (slope κ) when the behaviour is elastic, and it reaches the critical state line when the yield surface is activated and the stresses are close to the failure criterion.
4 Comparison of model predictions with experimental results
4.1 Drying and wetting cycle
Fig. 7 shows a drying-wetting cycle on a mixture of kaolin and sand prepared at a water content of 1.5 wL (where wL is the liquid limit): specimens were first dried up to 10 MPa of suction, then they were wetted (Ghembaza, 2004). The air entry suction se is almost equal to 0.3 MPa. As shown in Fig. 7, the model has the capacity to simulate this kind of path. For s > se, the increase in suction has a limited influence on void ratio and volumetric strain. Moreover, the irreversible strains on the drying and wetting paths are well simulated.
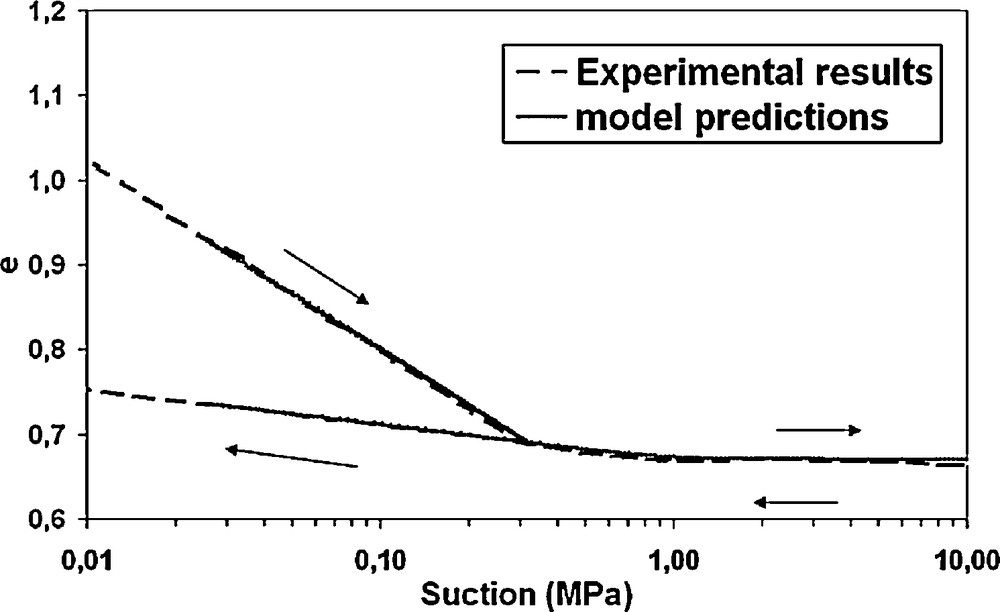
Drying and wetting on normally consolidated mixture of kaolin-sand. Comparison of measured and predicted void ratio – suction relationship.
Dessiccation et humidification d’un mélange sable-kaolinite. Comparaison des résultats expérimentaux et modélisés dans le plan indice des vides – succion.
4.1.1 Deviatoric path under constant suction
Fig. 8 shows the results of triaxial tests on the same kaolin-sand mixture under constant suction (Ghembaza, 2004). The samples are first consolidated to an effective mean stress p′ = 1250 kPa under saturated condition, then suction is applied. After stabilization under the required suctions (3 MPa and 8.5 MPa), deviatoric loading begins.

Shear tests on partially saturated kaolin-sand mixture.
Essai de cisaillement sur un mélange sable-kaolinite non saturé.
5 Concluding remarks
The modified Cam-Clay model has been chosen as a plastic driver to keep the model for unsaturated soils and thermal effects as simple as possible. The replacement of suction by capillary stress in Terzaghi's effective stress definition is used to extend relations defined for saturated soils to unsaturated soils. Moreover, this capillary stress is based on a microstructural model and calculated from attraction forces due to water menisci.
The introduction of the thermal softening curve to describe the thermal effect on soils in the elastoplastic model allows to reproduce some coupled paths like a drying path under mechanical stress with transition between saturated and unsaturated states, a heating path under constant suction or a deviatoric path with imposed suction and temperature.
The typical compression phenomena observed in saturated normally or slightly overconsolidated soils, or the swelling of overconsolidated soils (OCR > R) submitted to coupled thermomechanical loading have been highlighted in this study.
In the (p′, q) plane, the failure criterion is intrinsic and its slope M remains constant for a given saturated or unsaturated soil at ambient temperature. This criterion is affected by temperature, and the introduction of the decreasing function M = f(T) in the model allows to reproduce the decrease in shear strength during a triaxial test at high temperature.


