Plan
Comptes Rendus
no. 1

External geophysics, climate
Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India
[Analyse de tendance et modélisation ARIMA des données de pluviosité de pré-mousson pour l’Ouest de l’Inde]

Présenté par : Michel Petit

Priya Narayanan1 ; Ashoke Basistha2 ; Sumana Sarkar1 ; Sachdeva Kamna1 
1 Department of Natural Resources, TERI University, 10, institutional Area, Vasant Kunj, New Delhi 110070, India
2 DGM (Hydro Civil), Lahmeyer International India Pvt. Ltd, New Delhi, India
Comptes Rendus. Géoscience, Volume 345 (2013) no. 1, pp. 22-27.

Résumés

Spatial and temporal variability of rainfall over different seasons influence physical, social and economic parameters. Pre-monsoon (March, April and May – MAM) rainfall over the country is highly variable. Since heat lows and convective rainfall in MAM have an impact on the intensity of the ensuing monsoons, hence the pre-monsoon period was chosen for the study. The pre-whitened Mann Kendall test was used to explore presence of rainfall trend during MAM. The results indicate presence of significant (at 10% level) increasing trend in two stations (Ajmer, Bikaner). The practical significance of the change in rainfall was also explored as percentage changes over long term mean, using Theil and Sen's median slope estimator. Forecast using univariate ARIMA model for pre-monsoon months indicates that there is a significant rise in the pre-monsoon rainfall over the northwest part of the country.

La variabilité spatiotemporelle de la pluviosité sur différentes saisons influence les paramètres physiques, sociaux et économiques. La pluviosité pré-mousson (mars, avril et mai – MAM) sur la région est extrêmement variable. La période pré-mousson a été choisie pour cette étude, étant donné que l’abaissement de chaleur et la pluviosité convective pour la période MAM ont un impact sur l’intensité des moussons qui suivent. Le test Mann Kendall de pré-blanchiment a été utilisé pour explorer la possibilité d’une évolution de la pluviosité pendant la période MAM. Les résultats indiquent une tendance significative à l’accroissement (à un niveau de 10 %) dans deux stations (Ajmer et Bikaner). La signification pratique du changement dans la pluviosité a aussi été explorée dans le sens de changements sur une moyenne à long terme utilisant l’estimateur de pente moyenne de Theil et Sen. La prévision utilisant le modèle ARIMA à une variable pour les mois de pré-mousson indique une augmentation significative de la pluviosité de pré-mousson dans la partie nord-occidentale de la région.

Métadonnées
Reçu le :
Accepté le :
Publié le :
DOI : 10.1016/j.crte.2012.12.001
Keywords: Pre-monsoon, Rainfall trend, India, Pre-whitened Mann Kendall Test, Theil and Sen's Median Slope, Forecast, Auto Regressive Integrated Moving Average (ARIMA)
Mots-clés : Pré-mousson, Tendance de la pluviosité, Test Mann Kendall de pré-blanchiment, Pente médiane de Theil et Sen, Prévision, Moyenne mobile intégrée régressive automatique (ARIMA)

Priya Narayanan 1 ; Ashoke Basistha 2 ; Sumana Sarkar 1 ; Sachdeva Kamna 1

1 Department of Natural Resources, TERI University, 10, institutional Area, Vasant Kunj, New Delhi 110070, India
2 DGM (Hydro Civil), Lahmeyer International India Pvt. Ltd, New Delhi, India 
@article{CRGEOS_2013__345_1_22_0,
     author = {Priya Narayanan and Ashoke Basistha and Sumana Sarkar and Sachdeva Kamna},
     title = {Trend analysis and {ARIMA} modelling of pre-monsoon rainfall data for western {India}},
     journal = {Comptes Rendus. G\'eoscience},
     pages = {22--27},
     publisher = {Elsevier},
     volume = {345},
     number = {1},
     year = {2013},
     doi = {10.1016/j.crte.2012.12.001},
     language = {en},
}
TY  - JOUR
AU  - Priya Narayanan
AU  - Ashoke Basistha
AU  - Sumana Sarkar
AU  - Sachdeva Kamna
TI  - Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India
JO  - Comptes Rendus. Géoscience
PY  - 2013
SP  - 22
EP  - 27
VL  - 345
IS  - 1
PB  - Elsevier
DO  - 10.1016/j.crte.2012.12.001
LA  - en
ID  - CRGEOS_2013__345_1_22_0
ER  - 
%0 Journal Article
%A Priya Narayanan
%A Ashoke Basistha
%A Sumana Sarkar
%A Sachdeva Kamna
%T Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India
%J Comptes Rendus. Géoscience
%D 2013
%P 22-27
%V 345
%N 1
%I Elsevier
%R 10.1016/j.crte.2012.12.001
%G en
%F CRGEOS_2013__345_1_22_0
Priya Narayanan; Ashoke Basistha; Sumana Sarkar; Sachdeva Kamna. Trend analysis and ARIMA modelling of pre-monsoon rainfall data for western India. Comptes Rendus. Géoscience, Volume 345 (2013) no. 1, pp. 22-27. doi : 10.1016/j.crte.2012.12.001. https://comptes-rendus.academie-sciences.fr/geoscience/articles/10.1016/j.crte.2012.12.001/

Version originale du texte intégral

Le texte intégral ci-dessous peut contenir quelques erreurs de conversion par rapport à la version officielle de l'article publié.

1 Introduction

Climate variability in the dry and arid parts of India poses a great risk to the people and resources of these regions (INCCA, 2010) as the smallest fluctuations of weather parameters like precipitation not only damage the agriculture and economy of the region but disturb the overall water cycle (Krishna Kumar et al., 2004; Zhang et al., 2011). Study of the space-time variability of rainfall assumes great importance for India, as its economy is largely dependent on agriculture (Davey and Peilke, 2005). Undeniable regional and global impacts have been observed due to the slightest variability in the precipitation patterns (Dash et al., 2004; New et al., 2001; Pal and Al-Tabbaa, 2009). Time series analysis is used to understand this random mechanism and to predict future series based on past data.

The study explores the rainfall behavior in the pre-monsoon season over a period 1949–2009 for the western part of India; the importance of this study is that it uses long series station-wise data for western part of India, which is semi-arid and has extremely low pressure conditions and intense dust storms during this season. Differential heating of land and sea is the precursor for monsoons, so understanding the trend of rainfall during these months in the north-western part of India is important to understand the overall pattern of monsoon (Bhutiyani et al., 2009; Chatterjee et al., 2009; Das et al., 2002).

The statistical and practical significance of trend was analyzed using a pre-whitened Mann Kendall test, percentage changes over the long term mean were calculated using Theil Sen's median slope estimator. Forecast was done using ARIMA model for a period 2010 to 2030. We have tried to understand the changes in pre-monsoon rainfall which is distinctly convective in nature and has direct influence on different monsoon branches. Computation of trends during the pre-monsoon season gives a clear indication of performance of subsequent monsoons if correlated with meteorological attributes. The study indirectly focuses on the changes and connection in the western branch (which is special because this region is influenced by dust storms) of the monsoon, and the overall trend of pre-monsoon rainfall in the country.

2 Methodology and data

Data used for this study were obtained from Indian Meterological Department (IMD). Monthly Rainfall data for March, April, May (MAM) for six stations (Abu (Ab), Ahemdabad (Ah), Ajmer (Aj), Amritsar (Am), Bikaner (Bk), Jodhpur (Jd)) for a period of 60 years were analyzed. Consistency checks and data gaps were filled according to standard procedures. Trend analysis was performed on rainfall data using a pre-whitened Mann Kendall Test, autocorrelation removal was done in the required datasets at the chosen level of significance (α = 10%). The magnitude and practical significance of trend has been estimated using the Theil and Sen's median slope estimator, and by assessing the percentage change over the mean for the period concerned (Yue and Hashino, 2003; Yue et al., 2002).

In this study, a rank-based non-parametric Mann Kendall (MK) test is used. The MK test is the most common test used for trend analysis of hydro meteorological data (Yue et al., 2002). The limitation of the MK test is that in the case of positive autocorrelation present in series, it shows a positive trend even when trend is not present (Bayazit and Önöz, 2007). The pre-whitened Mann Kendall (PWMK) test was developed by Von Storch to remove the effect of autocorrelation from the series (Bayazit and Önöz, 2007). The pre-whitened Mann Kendall test removes the autocorrelation at lag 1 assuming an AR (1) model and then applies Mann Kendall test to the independent series (Bayazit and Önöz, 2007; Yue et al., 2002), in case autocorrelation is detected at the same significance level.

2.1 Mann Kendall test

The null hypothesis H0 states that the data series is independent and identically distributed and the alternate hypothesis H1 states existence of a trend.

The general MK test has test statistics S defined as:

S=∑i=1n−1∑j=i+1nxj−xi(1)
where xj is the sequential data series, n is the length of the data set and
Sgny=1   if   y>00   if   y=0−1   if   y<0(2)

Results of Mann Kendall test are supposed to be normally distributed for n ≥ 8 with mean and variance described as:

ES=0(3)
VS=nn−12n+5+∑titi−12ti+518(4)
where ti is the number of ties present with i as extent. The standardized Z statistics is computed by
Z=S−1/VS  S>0 0     S=0S+1VS        S<0(5)

The standard MK statistic Z follows the standard normal distribution with zero mean and unit variance.

2.2 Pre-whitened Mann Kendall test

A modification of the MK test, PWMK test is generally applied in presence of autocorrelation. The removal of autocorrelation is accomplished by:

x′t=xt+1−r1xt(6)
where r1 is the autocorrelation coefficient at lag 1 and is represented as:
r1=∑t=1n−1xt−x¯txt+1−x¯t+1∑t=1n−1xt−x¯t2xt+1−x¯t+1212(7)

Here x¯t and Var (xt) are the sample mean and sample variance of the first (n–1) terms and x¯t+1 and Var (xt+1) is the sample mean and sample variance of the next (n–1) terms. The presence of significant autocorrelation in the series is checked by Student's t test (Cunderlik and Burn, 2004), where the null hypothesis of no autocorrelation is rejected if t≥tα/2

t=r1n−21−r2(8)

The MK test was applied after the removal of the autocorrelation wherever it was present at the chosen level of significance (α = 10%).

2.3 Theil and Sen's median slope estimator

The magnitude of trend has been estimated using the Theil and Sen's median slope estimator. This method gives a robust estimate of trend (Yue et al., 2002) as it is not influenced by outliers. The slope estimates of N pairs of data are first computed by

Qi=xj−xk/j−kfor   i=1,n(9)

Here xj and xk are data values at time j and k, respectively, where (j > k).

The median of the N values of Qi is the Sen's estimator of slope where:

N=nn−1/2(10)

The trends which have statistical significance might not have practical significance and vice versa (Yue and Hashino, 2003), hence the practical significance of trend was assessed by estimating the Theil and Sen's median slope and assessing the percentage change over the mean for the period concerned.

3 Forecasting

Climate modelling using GCMs has been used extensively to predict pattern of climatic variables globally (IPCC, 2007). However, GCM forecasts have certain limitations (Sun et al., 2009; INCCA, 2010). In recent years, time series modelling approach for climatic variables is gaining popularity amongst researchers (Boochabun et al., 2004; Chattopadhyay and Chattopadhyay, 2010), and has been followed here.

3.1 Choice of model and parsimony

In the current study, ARIMA model has been used for forecasting rainfall for the period 2010–2030. ARIMA modeling predicts future values as a product of several past observations and random errors (Yurekli et al., 2007). As a modeling technique, ARIMA has been beneficial for predicting hydro meteorological parameters (Boochabun et al., 2004; Chattopadhyay and Chattopadhyay, 2010; Chattopadhyay et al., 2011; Hipel et al., 1977).

The ARIMA (p, d, q) can be expressed as (Box et al., 2007):

z¯t=ϕ1z¯t−1+ϕ2z¯t−2+⋯+ϕ3z¯t−p+at−θ1z¯t−1−θ2z¯t−2−⋯θ3z¯t−q(11)
where z¯t=zt−μ, and at is the shock. By introducing the Backward shift operator (B), Eq. (11) can be written as:
ϕB1−Bdzt=θBat(12)

The modeling process includes model identification and diagnostic checking. The identification test is done to obtain the value of order of differencing ‘d’ in ARIMA (p, d, q) and also the values of AR and MA operators. The need for differencing to make the series stationary has been thoroughly explained by Dickey and Fuller (1979).

3.2 ADF test for unit roots

Δyt=α0+βt+α1Yt−1+∑i=1pdiΔyt−1+ut(13)
where ΔYt = Yt – Yt−1, with the null hypothesis H0: α1 ≠ 0 versus H1: α1 = 0, tested on the basis of the t-statistic. H0 is rejected if the t-statistic is smaller than the critical value at 10% significance level (–1.62).

Climatic data has no fixed mean, and for ARIMA modeling, stationarity is a prerequisite. So when the observed data exhibits trend and heteroscedasticity, application of differencing, a log or a square root transformation is required to reduce it to a stationary series (Yurekli et al., 2007). Parsimonious model selection was done by using Akaike Information Criterion (AIC), a model with minimum AIC being considered.

The AIC is expressed in the form:

AICp,q=N Inσε2+2p+q(14)
where p and q are the lags of the ARIMA (p, d, q).

After fitting the parsimonious model, the residuals were subjected to a diagnostic test to check the randomness of the residuals. An ARIMA model with random residuals at particular significance level (α = 10%) is considered as the best fit model. The randomness was checked using the Ljung–Box test statistics for checking the presence of autocorrelation in the residual series.

The Rank test was used as another test of randomness. It is particularly suitable for detecting presence of linear trend in the time series. Here P is defined as the number of pairs (i, j) such that yj > yi (Brockwell and Davis, 2009). The assumption of randomness of the series yj is rejected at level α if P−μP/σP>ϕ1−α/2.

The whiteness of the residual was checked by examining the Residual ACFs (RACF) of the models. The RACF can be calculated by Hipel et al. (1977):

rkaˆ=∑t=K+1naˆtaˆt−k/∑t=1naˆt2(2)
where aˆ is the residual series.

The ARIMA model for each station was then used to forecast the rainfall values until 2030.

4 Results and discussions

Sixty years of data have been analysed for six stations on the western side of India. Table 1 represents the location of stations and the mean rainfall. The stations located on the western side of India fall in the semi-arid zone which is characterized by both scant and random convective rainfall. Statistical significance at (α = 10%) level is analysed for all six stations, From Fig. 1 it is evident in terms of Z statistics that an overall positive trend is observed in April, May for almost all the stations and negative trend in March for four stations; however, at the α = 10% level of significance, two stations (Ah), (Ab) do not show any trend in rainfall during MAM. Significant trend in rainfall is observed in (Bk), (Jd) in April and (Bk), (Am) in May. Two stations (Aj), (Bk) show significant trend for the entire pre-monsoon season. Monthly level analysis of the percentage change in rainfall showed an overall rise for two stations Bk, Am during MAM.

Table 1

Stations avec leur localisation géographique et la pluviosité moyenne pré-mousson.

Station Latitude Longitude Altitude
(msl)		 Mean MAM rainfall
(mm)		 Standard deviation
(mm)
Abu (Ab) 24.48 72.78 1722 21.2 43.5
Ahmdabad (Ah) 23.1 72.6 55 10.5 21
Ajmer (Aj) 26.45 74.63 486 21.3 25.9
Amritsar (Am) 31.6 74.9 234 74.3 57.2
Bikaner (Bk) 28 73.3 227 47.1 81.2
Jodhpur (Jd) 26.28 73.03 230 32.9 58.2
Fig. 1

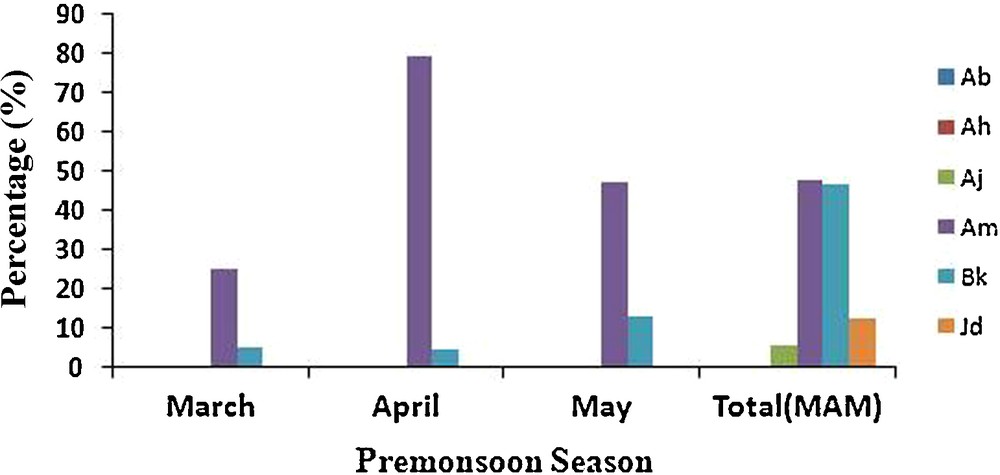
Percentage change (α = 10%) rainfall for different stations during pre-monsoon season.

Pourcentage de changement de pluviosité (α = 10 % pour différentes stations pendant la saison de pré-mousson.

Rainfall in the pre-monsoon period is due to formation of semi permanent heat lows over the northwest parts of India and central parts of Pakistan during the summer months (Chandrashekhar, 2010). The rise in the surface air temperature since 1971 (Krishna Kumar et al., 2004) during the months of March, April and May probably suggests intensification of the convective heating over the region extending from 24°N to 37°N and 68°E to 89°E (Indo Gangetic Plain, Northwest Rajasthan, western India, Indian peninsular region); the trends obtained in the study are consistent with these observations. Similar findings have been reported by Kothawale et al., 2010, indicating the presence of an increasing trend in the number of hot days and hot nights over entire India. The increasing trend in rainfall in the northwest parts of Rajasthan especially in (Bk) and (Aj) might be due to intense heat lows and resultant rainfall. Further, the month of May is characterized by major reversal of surface winds that brings warm, moist and unstable air from Indian Ocean into the Indian Peninsular region under the influence of land sea thermal contrast, which plays a major role in the establishment of planetary scale monsoon circulation over the entire subcontinent for coming months (Chandrashekhar, 2010). Recent studies on the impacts of aerosols on the Indian Summer Monsoon rainfall (Gautam et al., 2009; Lau et al., 2006; Nigam and Bollasina, 2010) have found increasing aerosol loading in the pre-monsoon months (MAM). Lau et al. (2006) reports build up of aerosol loading in the MAM, peaking up in May over the entire North, Northwest India and Indo Gangetic Plains. The source of aerosol in these regions are from the dust transported from deserts of Saudi Arabia, Afghanistan and Pakistan along with black carbon from local emissions (Gautam et al., 2009; Lau et al., 2006). Studies by Beegum et al. (2009), Bollasina and Nigam (2009) and Kumar et al. (2009) have found increased black carbon loading in the recent period. These changes in atmospheric aerosol loading can be correlated with the changes in the rainfall trends.

4.1 ARIMA forecasting

ARIMA modeling was done for forecasting the pre-monsoon rainfall for all the six stations. Root Mean Square Error (RMSE) was computed to check the accuracy of model fitting in Table 2, and Fig. 2 by comparing the forecast results for 2000 to 2009 using input data from 1949 to 1999. The most parsimonious model with minimum AIC, which passed the test of randomness were selected for forecasting rainfall until 2030. The model parameters, along with diagnostic statistics and predicted rainfall as percentage, change over long term mean, see Table 2. From forecast results stations (Ab), (Ah) show negative change in pre-monsoon rainfall: this could be attributed to rapid local change in land use land cover. The stations like Bk show positive change in rainfall; this could be due to the high fine aerosols load in that region (Sarkar et al., 2005).

Table 2

Modèles ARIMA sélectionnés et prévision des données de pluviosité pré-mousson pour toutes les stations.

Station ARIMA Model AIC RMSE Test of Randomness % change for 2030
LBQ/P Rank test Statistics
Ab (2,2,3) 334.26 11.82 0.31 0.39 –0.86
Ah (2,2,1) 303.81 26.58 0.15 0.2 –0.4
Aj (2,2,2) 308.52 24.08 0.61 0.23 20.9
Am (1,0,4) 126.02 33.33 0.12 0.54 13.21
Bk (1,2,1) 358.46 57.83 0.22 0.25 31.13
Jd (2,2,1) 348.93 95.27 0.45 0.68 25.66
Fig. 2

Percentage change of rainfall for observed (1949–2009) and predicted (2010–2030) years for all stations.

Pourcentage de changement de pluviosité pour les années observées (1949–2009) et prévisionnelles (2010–2030) pour toutes les stations.

This part of India has extremely high temperatures, and the further convective nature of rainfall in MAM makes it more sensitive to local land use land cover changes. Hence detecting the long term change in mean values, as done in this study, gives a possible idea of changes in rainfall pattern in the study area.

5 Conclusion

Analysis of long-term time series (1949–2009) for western region stations using the non-parametric pre-whitened Mann Kendall test showed evident changes in rainfall pattern during the pre-monsoon season. Four stations (Amritsar, Bikaner, Jodhpur and New Delhi) in the north-western and western part of the country show increase in pre-monsoon rainfall of 10% or more; while at two stations (Ajmer and Bikaner) it was statistically significant. Analysis at a monthly level shows statistically significant increasing trend in May rainfall at six stations distributed over a wide expanse. Forecast results from ARIMA modelling show that (Ab), (Ah) have negative change due to rapid local change in land use. Further studies are needed to understand factors affecting pre-monsoon rainfall.

Acknowledgements

Authors extend sincere thanks to following people and agencies for the support: IMD, Helmut Lutkepohl and Markus Kratzig (for software JMulTi), Brockwell and Davis (for ITSM 2000 ARIMA model) and University Grants Commission (UGC) for the financial support.

Bibliographie

[Bayazit and Önöz, 2007] M. Bayazit; B. Önöz To prewhiten or not to prewhiten in trend analysis, Hydrol. Sci. J., Volume 52 (2007) no. 4, pp. 611-624

[Beegum et al., 2009] N.S. Beegum; K. Krishna Moorthy; S. Suresh Babu; S.K. Satheesh; V. Vinoj; K.V.S. Badarinath; P.D. Safai; P.V.S. Devara; S. Singh; D.U.C. Vinod; P. Pant Spatial distribution of aerosol black carbon over India during Pre-monsoon Season, Atmos. Environ., Volume 43 (2009), pp. 1071-1078

[Bhutiyani et al., 2009] R.M. Bhutiyani; S.V. Kale; J.N. Pawar Climate change and the precipitation variations in the northwestern Himalaya: 1866–2006, Int. J. Climatol., Volume 30 (2009) no. 4, pp. 535-548

[Bollasina and Nigam, 2009] M. Bollasina; S. Nigam Absorbing aerosols and pre-summer monsoon hydro climate variability over the Indian subcontinent: the challenge in investigating links, Atmos. Environ., Volume 94 (2009), pp. 338-344

[Boochabun et al., 2004] K. Boochabun; W. Tych; N.A. Chappell; P.A. Carling; K. Lorsirirat; S. Pa-Obsaeng Statistical modelling of rainfall and river flow in Thailand, J. Geol. Soc. India, Volume 64 (2004), pp. 503-515

[Box et al., 2007] G.E.P. Box; G.M. Jenkins; G.C. Reinsel Time Series Analysis: forecasting and control, Pearson Education, 2007 (pp. 8–12)

[Brockwell and Davis, 2009] P. Brockwell; R. Davis Time Series: theory and Methods, Springer International Edition, 2009 (pp. 310–313)

[Chandrashekhar, 2010] A. Chandrashekhar Basics of Atmospheric Sciences, PHI Learning Private Limited, 2010 (pp. 280–306)

[Chatterjee et al., 2009] S. Chatterjee; S. Ghosh; K.U. De Reduction of number of parameters and forecasting convective developments at Kolkata (22.53°N, 88.33°E), India during pre-monsoon season: an application of multivariate techniques, Indian J. Radio Space Phys., Volume 38 (2009), pp. 275-282

[Chattopadhyay and Chattopadhyay, 2010] S. Chattopadhyay; G. Chattopadhyay Univariate modelling of summer-monsoon rainfall time series: comparison between ARIMA and ARNN, CR Geoscience, Volume 342 (2010), pp. 100-107

[Chattopadhyay et al., 2011] S. Chattopadhyay; D. Jhajharia; G. Chattopadhyay Univariate modelling of monthly maximum temperature time series over northeast India: neural network versus Yule–Walker equation based approach, Meteorol. Appl., Volume 18 (2011), pp. 70-82

[Cunderlik and Burn, 2004] J.M. Cunderlik; D.H. Burn Linkages between regional trends in monthly maximum flows and selected climatic variables, J. Hydrol. Eng., Volume 9 (2004) no. 4, pp. 247-255

[Das et al., 2002] M.R. Das; K.R. Mukhopadhyay; M.M. Dandekar; R.S. Kshirsagar Pre-monsoon western disturbances in relation to monsoon rainfall, its advancement over NW India and their trends, Curr. Sci., Volume 11 (2002), pp. 1320-1321

[Dash et al., 2004] S.K. Dash; R.J. Kumar; K.M. Shekhar On the decreasing frequency of monsoon depressions over the Indian region, Curr. Sci., Volume 86 (2004) no. 25, pp. 1404-1411

[Davey and Peilke, 2005] C.A. Davey; R.A. Peilke Microclimate exposures of surface based weather stations: implications for the assessment of long-term temperature trends, Bull. Am. Meteorol. Soc., Volume 86 (2005) no. 4, pp. 497-504

[Dickey and Fuller, 1979] D.A. Dickey; W.A. Fuller Estimators for autoregressive time series with a unit root, J. Am. Stat. Assoc., Volume 74 (1979), pp. 427-431

[Gautam et al., 2009] R. Gautam; N.C. Hsu; K.M. Lau; M. Kafatos Enhanced pre-monsoon warming over the Himalayan-Gangetic region from 1979 to 2007, Ann. Geophys., Volume 27 (2009), pp. 3691-3703

[Hipel et al., 1977] K.W. Hipel; A.I. McLoed; W.C. Lennox Advances in Box Jenkins Modeling. 1. Model Construction, Water Resour. Res., Volume 13 (1977) no. 3, pp. 567-575

[INCCA, 2010] INCCA: Indian Network for Climate Change Assessment, 2010. Climate change and India: a 4X4 assessment a sectoral and regional analysis for 2030s. 15, 36–38.

[IPCC, 2007] IPCC The Physical Science Basis. Contribution of working group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, Cambridge University Press, New York, 2007 (pp. 589–663)

[Kothawale et al., 2010] D.R. Kothawale; J.V. Revadekar; K. Rupa Kumar Recent trends in pre-monsoon daily temperature extremes over India, J. Earth Syst. Sci., Volume 119 (2010) no. 1, pp. 51-65

[Krishna Kumar et al., 2004] K. Krishna Kumar; K. Rupa Kumar; G.R. Ashrit; R.N. Deshpande; W.J. Hansen Climate impacts on Indian agriculture, Int. J. Climatol., Volume 24 (2004), pp. 1375-1393

[Kumar et al., 2009] R. Kumar; K. Narasimhulua; R.R. Reddy; K. Rama Gopal; L. Reddy; Siva Sankara; G. Balakrishnaiaha; K. Krishna Moorthy; S. Suresh Babu Temporal and spectral characteristics of aerosol optical depths in a semi-arid region of southern India, Sci. Total Environ., Volume 407 (2009), pp. 2673-2688

[Lau et al., 2006] K.M. Lau; M.K. Kim; K.M. Kim Asian Summer monsoon anomalies induced by aerosol direct forcing; the role of Tibetian Plateau, Climate Dyn., Volume 26 (2006), pp. 864-885

[Nigam and Bollasina, 2010] S. Nigam; M. Bollasina “Elevated heat pump” hypothesis for the aerosol–monsoon hydro climate link: “Grounded” in observations, J. Geophys. Res., Volume 115 (2010), p. D16201

[New et al., 2001] M. New; M. Todd; M. Hulme; P. Jones Precipitation measurement and trend in the twentieth century, Int. J. Climatol., Volume 21 (2001), pp. 1899-1922

[Pal and Al-Tabbaa, 2009] I. Pal; A. Al-Tabbaa Trends in seasonal precipitation extremes – an indicator of “climate change” in Kerala, India, J. Hydrol., Volume 367 (2009), pp. 62-69

[Sarkar et al., 2005] S. Sarkar; R. Chokngamwong; G. Cervone; R.P. Singh; M. Kafatos Variability of aerosol optical depth and aerosol forcing over India, Adv. Space Res. (2005), pp. 1-7

[Sun et al., 2009] D.Z. Sun; Y. Yu; T. Zhang Tropical water vapour and cloud feedbacks in climate models: a further assessment using coupled simulations, J. Climate, Volume 22 (2009) no. 5, pp. 1287-1304

[Yue et al., 2002] S. Yue; P. Pilon; G. Cavadias Power of the Mann Kendall and Spearman's rho test for detecting monotonic trends in hydrological series, J. Hydrol., Volume 259 (2002), pp. 254-271

[Yue and Hashino, 2003] S. Yue; M. Hashino Long term trends of annual and monthly precipitation in Japan, J. Am. Water Resour. Assoc., Volume 39 (2003) no. 3, pp. 587-596

[Yurekli et al., 2007] K. Yurekli; H. Simsek; B. Cemek; S. Karaman Simulating climatic variables by using stochastic approach, Build. Environ., Volume 42 (2007), pp. 3493-3499

[Zhang et al., 2011] Q. Zhang; C. Xu Yu; X. Chen; Z. Zhang Statistical behaviours of precipitation regimes in China and their links with atmospheric circulation 1960–2005, Int. J. Climatol., Volume 31 (2011) no. 11, pp. 1665-1678

Cité par

  • Ramya Hariharan COVID-19: A Boon for Tropical Solar Parks?: A Time Series Based Analysis and Forecasting of Solar Irradiance, Energy Sources, Part A: Recovery, Utilization, and Environmental Effects, Volume 47 (2025) no. 1, p. 2029 | DOI:10.1080/15567036.2020.1839603
  • Lakhan Jain; Bindu Bhatt Modeling and Forecasting Rainfall Patterns of Southwest Monsoons in Kutch District of Gujarat Using Arima, Humanities and Sustainability from Glocal Perspectives Towards Future Earth (2025), p. 331 | DOI:10.1007/978-981-96-0381-7_25
  • Michel Rwema; Mouhamadou Bamba Sylla; Bonfils Safari; Lassi Roininen; Marko Laine Trend analysis and change point detection in precipitation time series over the Eastern Province of Rwanda during 1981–2021, Theoretical and Applied Climatology, Volume 156 (2025) no. 2 | DOI:10.1007/s00704-024-05317-7
  • Swades Pal; Rumki Khatun; Sandipta Debanshi; Rajesh Sarda Measuring the degree of rainfall alteration and eco-deficit/eco-surplus of rainfall using indicators of rainfall alteration approach, Acta Geophysica, Volume 72 (2024) no. 5, p. 3719 | DOI:10.1007/s11600-024-01288-5
  • Ahya Aulia Oktarini; Mariana Marselina; O. Siriratpiriya Discharge Forecasting in Monsoonal Gung Watershed: A Comparative Analysis of F. J. Mock, Markov, and ARIMA Models, E3S Web of Conferences, Volume 557 (2024), p. 02002 | DOI:10.1051/e3sconf/202455702002
  • Benjamin Nnamdi Ekwueme Deep neural network modeling of river discharge in a tropical humid watershed, Earth Science Informatics, Volume 17 (2024) no. 2, p. 1161 | DOI:10.1007/s12145-023-01219-w
  • Md. Abu Saleh; H.M. Rasel; Briti Ray A comprehensive review towards resilient rainfall forecasting models using artificial intelligence techniques, Green Technologies and Sustainability, Volume 2 (2024) no. 3, p. 100104 | DOI:10.1016/j.grets.2024.100104
  • Junaid Qadir; M. Sultan Bhat; Mohammad Suhail Meer Forecasting Pre - post Monsoon Depth to Water Levels using the Autoregressive Integrated Moving Average (ARIMA) Model in Outer Plains of Jammu Himalaya, Journal Of The Geological Society Of India, Volume 100 (2024) no. 11, p. 1557 | DOI:10.17491/jgsi/2024/174015
  • Sharmistha Bhowmik; Bindu Bhatt Drought Monitoring Using MODIS Derived Indices and Google Earth Engine Platform for Vadodara District, Gujarat, Journal of the Indian Society of Remote Sensing, Volume 52 (2024) no. 9, p. 1885 | DOI:10.1007/s12524-024-01922-1
  • Han Wu; Pei Du; Jiani Heng Gated convolution with attention mechanism under variational mode decomposition for daily rainfall forecasting, Measurement, Volume 237 (2024), p. 115222 | DOI:10.1016/j.measurement.2024.115222
  • Md Hibjur Rahaman; Tamal Kanti Saha; Md Masroor; Roshani; Haroon Sajjad Trend analysis and forecasting of meteorological variables in the lower Thoubal river watershed, India using non-parametrical approach and machine learning models, Modeling Earth Systems and Environment, Volume 10 (2024) no. 1, p. 551 | DOI:10.1007/s40808-023-01799-y
  • Rabia Chhachhar; Habibullah Abbasi Hydrological response to land use land cover and climate variability, and simulation of sediment export and water yield in the catchment Kotri Sindh Pakistan using Soil and Water Assessment tool model, Science Progress, Volume 107 (2024) no. 2 | DOI:10.1177/00368504241251655
  • Zhuang Liu; Yibin Cui; Chengcheng Ding; Yonghai Gan; Jun Luo; Xiao Luo; Yongguo Wang The Characteristics of ARMA (ARIMA) Model and Some Key Points to Be Noted in Application: A Case Study of Changtan Reservoir, Zhejiang Province, China, Sustainability, Volume 16 (2024) no. 18, p. 7955 | DOI:10.3390/su16187955
  • Swades Pal; Gargi Ghosh; Rajesh Sarda Introducing an indicator-based novel approach for exploring the degree of rainfall alteration, Theoretical and Applied Climatology, Volume 155 (2024) no. 4, p. 2801 | DOI:10.1007/s00704-023-04777-7
  • Hasan Çağatay Çiftçi; Kutalmış Gümüş; Münevver Gizem Gümüş Analyzing land use and climate change impacts of Suğla water storage in Turkey, Theoretical and Applied Climatology, Volume 155 (2024) no. 7, p. 6797 | DOI:10.1007/s00704-024-05043-0
  • Shahenaz Mulla; Chaitanya B. Pande; Sudhir K. Singh Times Series Forecasting of Monthly Rainfall using Seasonal Auto Regressive Integrated Moving Average with EXogenous Variables (SARIMAX) Model, Water Resources Management, Volume 38 (2024) no. 6, p. 1825 | DOI:10.1007/s11269-024-03756-5
  • Jatinder Kaur; Kulwinder Singh Parmar; Sarbjit Singh Autoregressive models in environmental forecasting time series: a theoretical and application review, Environmental Science and Pollution Research, Volume 30 (2023) no. 8, p. 19617 | DOI:10.1007/s11356-023-25148-9
  • Deyun Wang; Yifei Ren; Yanchen Yang; Haixiang Guo Hybridized gated recurrent unit with variational mode decomposition and an error compensation mechanism for multi-step-ahead monthly rainfall forecasting, Environmental Science and Pollution Research, Volume 31 (2023) no. 1, p. 1177 | DOI:10.1007/s11356-023-31243-8
  • Yanxin Xu; Xuejian Li; Huaqiang Du; Fangjie Mao; Guomo Zhou; Zihao Huang; Di’en Zhu; Qi Chen; Chi Ni; Keruo Guo Spatiotemporal variation in bamboo Solar-induced chlorophyll fluorescence (SIF) in China based on the global Orbiting Carbon Observatory-2 (OCO-2) carbon satellite and study on the response to climate and terrain, GIScience Remote Sensing, Volume 60 (2023) no. 1 | DOI:10.1080/15481603.2023.2253952
  • Sagarika Roy; Ajay Kumar Taloor; Prosun Bhattacharya A geospatial approach for understanding the spatio-temporal variability and projection of future trend in groundwater availability in the Tawi basin, Jammu, India, Groundwater for Sustainable Development, Volume 21 (2023), p. 100912 | DOI:10.1016/j.gsd.2023.100912
  • Mohammad Shad; Y. D. Sharma; Pankaj Narula Forecasting Southwest Indian Monsoon Rainfall Using the Beta Seasonal Autoregressive Moving Average (βSARMA) Model, Pure and Applied Geophysics, Volume 180 (2023) no. 1, p. 405 | DOI:10.1007/s00024-022-03217-3
  • Yanxin Xu; Xuejian Li; Huaqiang Du; Fangjie Mao; Guomo Zhou; Zihao Huang; Weiliang Fan; Qi Chen; Chi Ni; Keruo Guo Improving extraction phenology accuracy using SIF coupled with the vegetation index and mapping the spatiotemporal pattern of bamboo forest phenology, Remote Sensing of Environment, Volume 297 (2023), p. 113785 | DOI:10.1016/j.rse.2023.113785
  • Sayantan Haldar; Moharana Choudhury; Santanu Choudhury; Palas Samanta Trend analysis of long-term meteorological data of a growing metropolitan city in the era of global climate change, Total Environment Research Themes, Volume 7 (2023), p. 100056 | DOI:10.1016/j.totert.2023.100056
  • Jian Chen; Zhikai Guo; Changhui Zhang; Yangyang Tian; Yaowei Li Research on the Application of CEEMD-LSTM-LSSVM Coupled Model in Regional Precipitation Prediction, Water, Volume 15 (2023) no. 8, p. 1465 | DOI:10.3390/w15081465
  • Merri Jayanti; Arwin Sabar; Herto Dwi Ariesyady; Mariana Marselina; Muammar Qadafi A comparison of three water discharge forecasting models for monsoon climate region: A case study in cimanuk-jatigede watershed Indonesia, Water Cycle, Volume 4 (2023), p. 17 | DOI:10.1016/j.watcyc.2023.01.002
  • Sajid Gul; Jingli Ren Application of non-parametric innovative trend analysis of different time scale precipitation during (1951–2016) in Khyber Pakhtunkhwa, Pakistan, Acta Geophysica, Volume 70 (2022) no. 1, p. 485 | DOI:10.1007/s11600-021-00703-5
  • Zeinu Ahmed Rabba; Tomeu Rigo Trend Analysis of Hydrometeorological Data of Gilgel Gibe Catchment, Ethiopia, Advances in Meteorology, Volume 2022 (2022), p. 1 | DOI:10.1155/2022/7485270
  • Deepa Rawat; Pradeep Mishra; Soumik Ray; Himasha Harshani Fernando Warnakulasooriya; Sarswati Prakash Sati; Gaurav Mishra; Hussein Alkattan; Mostafa Abotaleb Modeling of rainfall time series using NAR and ARIMA model over western Himalaya, India, Arabian Journal of Geosciences, Volume 15 (2022) no. 23 | DOI:10.1007/s12517-022-10994-7
  • Yanhui Song; Jiayi Cao An ARIMA-based study of bibliometric index prediction, Aslib Journal of Information Management, Volume 74 (2022) no. 1, p. 94 | DOI:10.1108/ajim-03-2021-0072
  • Vikas Bajpai; Anukriti Bansal; Ramit Agarwal; Shashwat Kumar; Namit Bhandari; Shivam Kejriwal Rainfall Estimation and Prediction Using Artificial Intelligence: a Survey, Congress on Intelligent Systems, Volume 111 (2022), p. 807 | DOI:10.1007/978-981-16-9113-3_59
  • K SatishKumar; E. Venkata Rathnam Comparison of six trend detection methods and forecasting for monthly groundwater levels – a case study, ISH Journal of Hydraulic Engineering, Volume 28 (2022) no. sup1, p. 412 | DOI:10.1080/09715010.2020.1715270
  • Harshada; Satyanarayana; K. S. Jayappa Forecast of Sea Surface Temperature and Chlorophyll-a Using ARIMA, South-Eastern Arabian Sea, Karnataka, India, Innovative Trends in Hydrological and Environmental Systems, Volume 234 (2022), p. 189 | DOI:10.1007/978-981-19-0304-5_15
  • P Kabbilawsh; D Sathish Kumar; N R Chithra Forecasting long-term monthly precipitation using SARIMA models, Journal of Earth System Science, Volume 131 (2022) no. 3 | DOI:10.1007/s12040-022-01927-9
  • P. Kabbilawsh; D. Sathish Kumar; N. R. Chithra Performance evaluation of univariate time-series techniques for forecasting monthly rainfall data, Journal of Water and Climate Change, Volume 13 (2022) no. 12, p. 4151 | DOI:10.2166/wcc.2022.107
  • Majid Javari Rainfall random variability and its effects on flood risk management in Iran, Modeling Earth Systems and Environment, Volume 8 (2022) no. 1, p. 1109 | DOI:10.1007/s40808-021-01130-7
  • Rajni; Sudip Patra, PROCEEDINGS OF THE THIRD INTERNATIONAL CONFERENCE ON FRONTIERS IN INDUSTRIAL AND APPLIED MATHEMATICS 2020: FIAM-2020, Volume 2435 (2022), p. 020051 | DOI:10.1063/5.0083522
  • Asmae El Mezouari; Abdelaziz El Fazziki; Mohammed Sadgal Hadoop–Spark Framework for Machine Learning-Based Smart Irrigation Planning, SN Computer Science, Volume 3 (2022) no. 1 | DOI:10.1007/s42979-021-00856-6
  • Sabyasachi Swain; S. K. Mishra; Ashish Pandey; Deen Dayal A Stochastic Model-Based Monthly Rainfall Prediction Over a Large River Basin, Sustainability of Water Resources, Volume 116 (2022), p. 133 | DOI:10.1007/978-3-031-13467-8_9
  • Tayeb Boulmaiz; Hamouda Boutaghane; Habib Abida; Mohamed Saber; Sameh A. Kantoush; Yves Tramblay Exploring the Spatio-Temporal Variability of Precipitation over the Medjerda Transboundary Basin in North Africa, Water, Volume 14 (2022) no. 3, p. 423 | DOI:10.3390/w14030423
  • R. Sarma; S. K. Singh A Comparative Study of Data-driven Models for Groundwater Level Forecasting, Water Resources Management, Volume 36 (2022) no. 8, p. 2741 | DOI:10.1007/s11269-022-03173-6
  • Can Chen; Qing Lv; Qian Tang Simulating and predicting soil water dynamics using three models for the Taihu Lake region of China, Water Supply, Volume 22 (2022) no. 4, p. 4030 | DOI:10.2166/ws.2022.032
  • Youssef NaitMalek; Mehdi Najib; Mohamed Bakhouya; Mohamed Essaaidi Embedded Real-time Battery State-of-Charge Forecasting in Micro-Grid Systems, Ecological Complexity, Volume 45 (2021), p. 100903 | DOI:10.1016/j.ecocom.2020.100903
  • Shyamal Dutta; Sufia Rehman; Soumen Chatterjee; Haroon Sajjad Analyzing seasonal variation in the vegetation cover using NDVI and rainfall in the dry deciduous forest region of Eastern India, Forest Resources Resilience and Conflicts (2021), p. 33 | DOI:10.1016/b978-0-12-822931-6.00003-4
  • Ning Yu; Timothy Haskins Bagging Machine Learning Algorithms: A Generic Computing Framework Based on Machine-Learning Methods for Regional Rainfall Forecasting in Upstate New York, Informatics, Volume 8 (2021) no. 3, p. 47 | DOI:10.3390/informatics8030047
  • Yongbao Zhang; Jingqi Gao; Xiaowei Luo; Xiang Wu; Haoqi Bao; Xander Wang Dynamic Evolution of Public’s Positive Emotions and Risk Perception for the COVID-19 Pandemic: A Case Study of Hubei Province of China, Mathematical Problems in Engineering, Volume 2021 (2021), p. 1 | DOI:10.1155/2021/6680303
  • P. H. Hrudya; Hamza Varikoden; R. Vishnu Regional variabilities of rainfall and convective parameters during the summer monsoon period: their linkage with El Niño Southern Oscillation, Meteorology and Atmospheric Physics, Volume 133 (2021) no. 4, p. 1223 | DOI:10.1007/s00703-021-00802-4
  • Asmae El Mezouari; Mehdi Najib; Abdelaziz El Fazziki Towards a Smart Irrigation Scheduling System Through Massive Data and Predictive Models, Advanced Intelligent Systems for Sustainable Development (AI2SD’2019), Volume 1103 (2020), p. 375 | DOI:10.1007/978-3-030-36664-3_42
  • Sinan Q. Salih; Ahmad Sharafati; Isa Ebtehaj; Hadi Sanikhani; Ridwan Siddique; Ravinesh C. Deo; Hossein Bonakdari; Shamsuddin Shahid; Zaher Mundher Yaseen Integrative stochastic model standardization with genetic algorithm for rainfall pattern forecasting in tropical and semi-arid environments, Hydrological Sciences Journal, Volume 65 (2020) no. 7, p. 1145 | DOI:10.1080/02626667.2020.1734813
  • Pengcheng Zhang; Yangyang Jia; Jerry Gao; Wei Song; Hareton Leung Short-Term Rainfall Forecasting Using Multi-Layer Perceptron, IEEE Transactions on Big Data, Volume 6 (2020) no. 1, p. 93 | DOI:10.1109/tbdata.2018.2871151
  • Mozafar Ansari; Faridah Othman; El-Shafie Integrating Fuzzy System and Meta-Heuristic Algorithms to Predict Influent Parameters for a Sewage Treatment, IOP Conference Series: Earth and Environmental Science, Volume 498 (2020) no. 1, p. 012076 | DOI:10.1088/1755-1315/498/1/012076
  • Kasturi Singh; Jagabandhu Panda; Sunny Kant A study on variability in rainfall over India contributed by cyclonic disturbances in warming climate scenario, International Journal of Climatology, Volume 40 (2020) no. 6, p. 3208 | DOI:10.1002/joc.6392
  • Ch. Praveenkumar; V. Jothiprakash Spatio-temporal trend and homogeneity analysis of gridded and gauge precipitation in Indravati River basin, India, Journal of Water and Climate Change, Volume 11 (2020) no. 1, p. 178 | DOI:10.2166/wcc.2018.183
  • R. D. Putra; M. P. Suhana; D. Kurniawn; M. Abrar; R. M. Siringoringo; N. W. P. Sari; H. Irawan; E. Prayetno; T. Apriadi; A. Suryanti, Volume 2094 (2019), p. 020024 | DOI:10.1063/1.5097493
  • Asmae EL Mezouari; Mehdi Najib, 2019 15th International Conference on Signal-Image Technology Internet-Based Systems (SITIS) (2019), p. 681 | DOI:10.1109/sitis.2019.00111
  • Y. NaitMalek; M. Najib; M. Bakhouya; M. Essaaidi, 2019 4th World Conference on Complex Systems (WCCS) (2019), p. 1 | DOI:10.1109/icocs.2019.8930731
  • Y. NaitMalek; M. Najib; M. Bakhouya; M. Essaaidi, 2019 IEEE International Smart Cities Conference (ISC2) (2019), p. 408 | DOI:10.1109/isc246665.2019.9071705
  • Sheikh Mohammad Idrees; M. Afshar Alam; Parul Agarwal; Lubna Ansari Effective Predictive Analytics and Modeling Based on Historical Data, Advances in Computing and Data Sciences, Volume 1046 (2019), p. 552 | DOI:10.1007/978-981-13-9942-8_52
  • M. Godsoe; M. Ladd; R. Cox Assessing Canada’s disaster baselines and projections under the Sendai Framework for Disaster Risk Reduction: a modeling tool to track progress, Natural Hazards, Volume 98 (2019) no. 1, p. 293 | DOI:10.1007/s11069-019-03599-z
  • Rakesh Meghwal; Deep Shah; Vimal Mishra On the Changes in Groundwater Storage Variability in Western India Using GRACE and Well Observations, Remote Sensing in Earth Systems Sciences, Volume 2 (2019) no. 4, p. 260 | DOI:10.1007/s41976-019-00026-6
  • Suman Kumar Kundu; Tarun Kumar Mondal Analysis of long-term rainfall trends and change point in West Bengal, India, Theoretical and Applied Climatology, Volume 138 (2019) no. 3-4, p. 1647 | DOI:10.1007/s00704-019-02916-7
  • Deen Dayal; S. Swain; A. K. Gautam; S. S. Palmate; A. Pandey; S. K. Mishra, World Environmental and Water Resources Congress 2019 (2019), p. 264 | DOI:10.1061/9780784482339.027
  • Xiaodong Liu; Jinyu Deng; Jingli Yang; Yue Li, 2018 Eighth International Conference on Instrumentation Measurement, Computer, Communication and Control (IMCCC) (2018), p. 1827 | DOI:10.1109/imccc.2018.00376
  • Lu-Tao Zhao; Yi Wang; Shi-Qiu Guo; Guan-Rong Zeng A novel method based on numerical fitting for oil price trend forecasting, Applied Energy, Volume 220 (2018), p. 154 | DOI:10.1016/j.apenergy.2018.03.060
  • Georgia Papacharalampous; Hristos Tyralis; Demetris Koutsoyiannis One-step ahead forecasting of geophysical processes within a purely statistical framework, Geoscience Letters, Volume 5 (2018) no. 1 | DOI:10.1186/s40562-018-0111-1
  • Abass Gibrilla; Geophrey Anornu; Dickson Adomako Trend analysis and ARIMA modelling of recent groundwater levels in the White Volta River basin of Ghana, Groundwater for Sustainable Development, Volume 6 (2018), p. 150 | DOI:10.1016/j.gsd.2017.12.006
  • Hesham Fouli; Rabie Fouli; Bashar Bashir; Oumar A. Loni Seasonal Forecasting of Rainfall and Runoff Volumes in Riyadh Region, KSA, KSCE Journal of Civil Engineering, Volume 22 (2018) no. 7, p. 2637 | DOI:10.1007/s12205-017-0726-3
  • S. Swain; S. Nandi; P. Patel Development of an ARIMA Model for Monthly Rainfall Forecasting over Khordha District, Odisha, India, Recent Findings in Intelligent Computing Techniques, Volume 708 (2018), p. 325 | DOI:10.1007/978-981-10-8636-6_34
  • Muhammad Farooq Iqbal; H. Athar Variability, trends, and teleconnections of observed precipitation over Pakistan, Theoretical and Applied Climatology, Volume 134 (2018) no. 1-2, p. 613 | DOI:10.1007/s00704-017-2296-1
  • Mohamed Yassine Samiri; Mehdi Najib; Abdelaziz El Fazziki; Jaouad Boukachour Toward a Self-Adaptive Workflow Management System Through Learning and Prediction Models, Arabian Journal for Science and Engineering, Volume 42 (2017) no. 2, p. 897 | DOI:10.1007/s13369-016-2372-3
  • Adil M. Bagirov; Arshad Mahmood; Andrew Barton Prediction of monthly rainfall in Victoria, Australia: Clusterwise linear regression approach, Atmospheric Research, Volume 188 (2017), p. 20 | DOI:10.1016/j.atmosres.2017.01.003
  • Lida Barba; Nibaldo Rodríguez A Novel Multilevel-SVD Method to Improve Multistep Ahead Forecasting in Traffic Accidents Domain, Computational Intelligence and Neuroscience, Volume 2017 (2017), p. 1 | DOI:10.1155/2017/7951395
  • Bahram Choubin; Arash Malekian Combined gamma and M-test-based ANN and ARIMA models for groundwater fluctuation forecasting in semiarid regions, Environmental Earth Sciences, Volume 76 (2017) no. 15 | DOI:10.1007/s12665-017-6870-8
  • Taher Abunama; Faridah Othman Time Series Analysis and Forecasting of Wastewater Inflow into Bandar Tun Razak Sewage Treatment Plant in Selangor, Malaysia, IOP Conference Series: Materials Science and Engineering, Volume 210 (2017), p. 012028 | DOI:10.1088/1757-899x/210/1/012028
  • Subana Shanmuganathan; Ajit Narayanan; Nishantha Priyanka Kumara Medagoda Temporal Data Analysis and Mining Methods for Modelling the Climate Change Effects on Malaysia's Oil Palm Yield at Different Regional Scales, Natural Resources Management (2017), p. 499 | DOI:10.4018/978-1-5225-0803-8.ch024
  • Tahoora Sheikhy Narany; Ahmad Zaharin Aris; Anuar Sefie; Saskia Keesstra Detecting and predicting the impact of land use changes on groundwater quality, a case study in Northern Kelantan, Malaysia, Science of The Total Environment, Volume 599-600 (2017), p. 844 | DOI:10.1016/j.scitotenv.2017.04.171
  • Sanjay Kumar Srivastava; Anu Rani Sharma; Kamna Sachdeva An observation‐based climatology and forecasts of winter fog in Ghaziabad, India, Weather, Volume 72 (2017) no. 1, p. 16 | DOI:10.1002/wea.2743
  • Subana Shanmuganathan; Ajit Narayanan; Nishantha Priyanka Kumara Medagoda Temporal Data Analysis and Mining Methods for Modelling the Climate Change Effects on Malaysia's Oil Palm Yield at Different Regional Scales, Handbook of Research on Climate Change Impact on Health and Environmental Sustainability (2016), p. 482 | DOI:10.4018/978-1-4666-8814-8.ch025
  • T. A. Fathima; V. Jothiprakash Consequences of Continuous Zero Values and Constant Values in Time Series Modeling: Understanding through Chaotic Approach, Journal of Hydrologic Engineering, Volume 21 (2016) no. 7 | DOI:10.1061/(asce)he.1943-5584.0001367
  • Nelio Moura De Figueiredo; Claudio José Cavalcante Blanco Water level forecasting and navigability conditions of the Tapajós River - Amazon - Brazil, La Houille Blanche, Volume 102 (2016) no. 3, p. 53 | DOI:10.1051/lhb/2016031
  • Majid Javari Spatial-temporal Variability of Seasonal Precipitation in Iran, The Open Atmospheric Science Journal, Volume 10 (2016) no. 1, p. 84 | DOI:10.2174/1874282301610010084
  • Priya Narayanan; Sumana Sarkar; Ashoke Basistha; Kamna Sachdeva Trend analysis and forecast of pre-monsoon rainfall over India, Weather, Volume 71 (2016) no. 4, p. 94 | DOI:10.1002/wea.2699
  • Priya Narayanan; Ashoke Basistha; Kamna Sachdeva Understanding trends and shifts in rainfall in parts of northwestern India based on global climatic indices, Weather, Volume 71 (2016) no. 8, p. 198 | DOI:10.1002/wea.2746
  • Mahua Bose; Kalyani Mali Two-Level Multivariate Fuzzy Logic Based Integrated Model for Monsoon Rainfall Prediction, Information Systems Design and Intelligent Applications, Volume 339 (2015), p. 53 | DOI:10.1007/978-81-322-2250-7_6
  • Zhihua Zhang; John C. Moore Autoregressive Moving Average Models, Mathematical and Physical Fundamentals of Climate Change (2015), p. 239 | DOI:10.1016/b978-0-12-800066-3.00008-5
  • Wenpeng Wang; Yuanfang Chen; Stefan Becker; Bo Liu Linear Trend Detection in Serially Dependent Hydrometeorological Data Based on a Variance Correction Spearman Rho Method, Water, Volume 7 (2015) no. 12, p. 7045 | DOI:10.3390/w7126673
  • Arpit Baheti; Durga Toshniwal, 2014 IEEE International Congress on Big Data (2014), p. 430 | DOI:10.1109/bigdata.congress.2014.69
  • Anubha Agrawal; Anu Rani Sharma; Shresth Tayal Assessment of regional climatic changes in the Eastern Himalayan region: a study using multi-satellite remote sensing data sets, Environmental Monitoring and Assessment, Volume 186 (2014) no. 10, p. 6521 | DOI:10.1007/s10661-014-3871-x
  • Yudie Du; Yue Cai; Mingxin Chen; Wei Xu; Hui Yuan; Tao Li A Novel Divide-and-Conquer Model for CPI Prediction Using ARIMA, Gray Model and BPNN, Procedia Computer Science, Volume 31 (2014), p. 842 | DOI:10.1016/j.procs.2014.05.335
  • Lida Barba; Nibaldo Rodríguez; Cecilia Montt Smoothing Strategies Combined with ARIMA and Neural Networks to Improve the Forecasting of Traffic Accidents, The Scientific World Journal, Volume 2014 (2014), p. 1 | DOI:10.1155/2014/152375

Cité par 89 documents. Sources : Crossref

Commentaires - Politique

Ces articles pourraient vous intéresser

Univariate modelling of summer-monsoon rainfall time series: Comparison between ARIMA and ARNN

Surajit Chattopadhyay; Goutami Chattopadhyay

C. R. Géos (2010)

Trend estimation and univariate forecast of the sunspot numbers: Development and comparison of ARMA, ARIMA and Autoregressive Neural Network models

Surajit Chattopadhyay; Deepak Jhajharia; Goutami Chattopadhyay

C. R. Géos (2011)